Загрузить PDF
Загрузить PDF
Вычислить средневзвешенную величину, также известную как среднее взвешенное, не так просто, как найти среднее арифметическое. Среднее взвешенное — это величина, вычисляемая на основе чисел, «ценность» или «вес» которых не равнозначны. Например, если нужно вычислить среднее взвешенное оценки, помните, что оценки за разные задания составляют определенные проценты от финальной оценки. Метод вычисления зависит от того, равна ли сумма всех весов 1 (100 %) или нет.
-
1
Запишите все числа, среднее взвешенное которых нужно вычислить. Например, если нужно найти среднее взвешенное оценок, сначала запишите все оценки.[1]
- Например, вы получили 82 балла за тесты, 90 баллов за экзамен и 76 баллов за курсовую работу.
-
2
Определите вес (или «ценность») каждого числа. Например, оценка за тест составляет 20 % от финальной оценки, оценка за экзамен — 35 %, оценка за курсовую работу — 45 %. В этом случае сумма весов равна 1 (или 100 %).[2]
- Чтобы использовать проценты в вычислениях, необходимо преобразовать их в десятичные дроби. Полученные числа называются «весовыми коэффициентами».
Совет: чтобы преобразовать проценты в десятичную дробь, добавьте десятичную запятую в конец процентов, а затем переместите ее на 2 позиции влево. Например, 75 % = 0,75.
-
3
Умножьте каждое число (х) на соответствующий весовой коэффициент (w). Затем сложите полученные значения, чтобы вычислить среднее взвешенное.[3]
- Например, если за тест вы получили 82 балла, а оценка за тест составляет 20 % от финальной оценки, умножьте 82 x 0,2. В этом случае х = 82 и w = 0,2.
-
4
Сложите полученные значения, чтобы найти среднее взвешенное. Формула для вычисления среднего взвешенного, когда сумма весов равна 1: x1(w1) + x2(w2) + x3(w3) + …, где x1, ч2, … — это числа, w1, w2, … — это соответствующие весовые коэффициенты.[4]
Чтобы найти среднее взвешенное, просто умножьте каждое число на его весовой коэффициент, а затем сложите полученные значения.- В нашем примере: 82(0,2) + 90(0,35) + 76(0,45) = 16,4 + 31,5 + 34,2 = 82,1. Это означает, что за предмет вы получили 82,1%.
Реклама
-
1
Запишите все числа, среднее взвешенное которых нужно вычислить. Помните, что сумма весов не всегда равна 1 (или 100 %), но в любом случае сначала запишите все нужные числа.[5]
- Например, нужно вычислить среднюю продолжительность вашего ежедневного сна в течение 15 недель, причем продолжительность сна менялась — вы спали 5, 8, 4, 7 и так далее часов в сутки.
-
2
Определите вес (или «ценность») каждого числа. Например, допустим, что в течение 15 недель было несколько недель, когда вы спали дольше. Такие недели имеют больший вес (потому что вы спали дольше, чем обычно). В качестве весового коэффициента используйте количество недель, связанное со средней продолжительностью сна. Например:[6]
- 9 недель, в течение которых продолжительность сна в среднем составляла 7 часов в сутки.
- 3 недели, в течение которых продолжительность сна в среднем составляла 5 часов в сутки.
- 2 недели, в течение которых продолжительность сна в среднем составляла 8 часов в сутки.
- 1 неделя, в течение которой продолжительность сна в среднем составляла 4 часа в сутки.
- Количество недель, связанное с количеством часов, является весовым коэффициентом. В нашем примере вы спали 7 часов в сутки в течение большинства недель, а бо́льшая или меньшая продолжительность сна приходится на меньшее число недель.
-
3
Вычислите сумму весов. Для этого просто сложите все веса. В нашем примере сумма весов f = 15, потому что вы исследуете продолжительность сна в течение 15 недель. [7]
- Общее количество недель, которые вы рассматриваете, складывается следующим образом: 3 недели + 2 недели + 1 неделя + 9 недель = 15 недель.
-
4
Умножьте числа на соответствующие веса, а затем сложите результаты. В нашем примере умножьте среднюю продолжительность сна на соответствующее число недель. Вы получите:[8]
- 5(часов в сутки)*3(недели) + 8(часов в сутки)*2(недели) + 4(часа в сутки)*1(неделя) + 7(часов в сутки)*9(недель) = 5(3) + 8(2) + 4( 1) + 7(9) = 15 + 16 + 4 + 63 = 98
-
5
Разделите полученный результат на сумму весов, чтобы найти среднее взвешенное. В нашем примере:[9]
- 98/15 = 6,53. Это означает, что средняя продолжительность вашего ежедневного сна в течение 15 недель составила 6,53 часа.
Реклама
Об этой статье
Эту страницу просматривали 95 286 раз.
Была ли эта статья полезной?
Среднее арифметическое — это статистический показатель, иллюстрирующий среднее значение набора данных, который рассчитывается как сумма всех значений, деленная на их количество. Это важный коэффициент, получивший широкое распространение в прикладных науках.
Что такое среднее арифметическое
Суть данного показателя проще всего продемонстрировать на примере. Торговец продает на рынке яблоки. В понедельник ему удалось продать 54 кг, во вторник — 47 кг, а в среду — 61 кг. Торговец хочет спланировать свои продажи и ему интересно, сколько килограмм фруктов он продает в среднем за день. Вот здесь на сцену и выходит среднее арифметическое. Для его определения необходимо суммировать значения показателей и разделить на их количество.
Среднее = (54 + 47 + 61) / 3 = 54 кг
Торговец выяснил, что в среднем он продает 54 кг яблок в день и может грамотно спрогнозировать свои затраты на покупку товара. Так как килограмм яблок стоит 10 рублей, то в день наш коммерсант зарабатывает в среднем 540 рублей.
Среднее арифметическое широко используется в статистике в случаях, если рассматривается набор однородных данных. В нашем случае это были только яблоки. Однако если торговец расширит свой ассортимент и добавит на прилавки еще и апельсины? Как изменится средняя стоимость одной единицы товара?
Пусть в понедельник торговец реализовал 23 кг апельсинов, во вторник — 28 кг, а в среду — 21 кг. Средний уровень продаж апельсинов составит:
Среднее = (28 + 21 + 23) / 3 = 24 кг.
Так как цена одного килограмма цитрусов составляет 20 рублей, то средний доход от продажи апельсинов составит 480 рублей в день.
Теперь решим простую на первый взгляд задачу. Какова средняя стоимость реализации одного килограмма любого товара? Неискушенный аналитик решит эту задачу как:
Среднее = (20 + 10) / 2 = 15 рублей,
за килограмм апельсинов или яблок. Однако не все так просто. В случае с разнородными данными важно учитывать их вес.
Среднее арифметическое взвешенное
Данный показатель используется при расчете среднего арифметического для разных данных, каждое из которых имеет свой вес. Для определения взвешенного параметра необходимо каждое значение умножить на свой вес, суммировать эти произведения, после чего разделить на сумму весов.
В данном случае у нас есть средний вес каждого вида фруктов и его необходимо учесть для определения средней цены одного килограмма товара. На практике это выглядит так:
Среднее взвешенное = (20 × 24 + 10 × 54) / (24 + 54) = 13,07.
Естественно, 13,07 не сильно отличается от 15, однако чем больше слагаемых и больший разброс весов, тем сильнее отличается среднее взвешенное от простого среднего арифметического. Также очевидно, что если все веса равны единице, то среднее взвешенное становится равным среднему арифметическому.
Что выбрать?
Если требуется найти среднее значение одного элемента из однородного набора, то достаточно отыскать среднее арифметическое. Именно это мы делали при поиске среднего уровня продажи яблок или апельсинов за день. Если требуется найти среднее между разными элементами, принадлежащими к разным группам или отыскать среднее средних, то для расчета используется среднее арифметическое взвешенное.
Наша программа представляет собой калькулятор для расчета среднего арифметического и его взвешенного варианта. В меню калькулятора вы можете выбрать тип искомого параметра. Для расчета среднего арифметического вам понадобится ввести только значения параметров. В случае необходимости вы можете добавить дополнительные ячейки.
Для расчета взвешенного среднего выберите соответствующий пункт в меню калькулятора, укажите значения и их вес. Рассмотрим на примерах, как рассчитывать взвешенное значение.
Примеры из реальной жизни
Подсчет средней зарплаты
Пусть на вашем предприятии числятся сотрудники, каждый из которых получает зарплату в соответчики с должностью. Для рекламного проспекта о поиске персонала вы хотите уточнить, на какую среднюю зарплату может рассчитывать соискатель. Вы знаете, что:
- 10 человек получают зарплату в размере 15 000 рублей;
- 5 сотрудников — 12 000 рублей;
- 12 человек — 19 000 рублей;
- 5 человек — 25 000 рублей;
- 3 сотрудника — 30 000 рублей;
- 2 сотрудника — 35 000 рублей.
Для вычисления средней зарплаты на предприятии вам потребуется ввести в ячейки значений размер зарплаты, а в ячейки весов — количество сотрудников, которые ее получают. Калькулятор мгновенно выдаст вам результат, что средняя зарплата равна 19 540 рублей. Без учета веса значений среднее арифметическое было бы равно 22 666 рублей, что уже значительно отличается от взвешенного значения.
Средняя скорость автомобиля
Допустим, водитель ехал по городскому проспекту со скоростью 60 км/ч в течение одного часа. Затем он выехал на автомагистраль, увеличил скорость до 120 км/ч и ехал так три часа, после чего свернул на проселочную дорогу и со скоростью 40 км/ч ехал еще два часа. С какой средней скоростью ехал водитель? В этой задаче в качестве веса выступает время езды, а значений — скорость. Выглядит это так:
- 60 км/ч — 1 час;
- 120 км/ч — 3 часа;
- 40 км/ч — 2 часа.
Введем эти данные в форму калькулятора и получим ответ: средняя скорость автомобиля составляет 83,3 км/ч. Без учета времени средняя скорость была бы равна 73,3 км/ч, что неверно.
Заключение
Расчет среднего арифметического взвешенного широко используется в прикладных науках. Этот параметр популярен не только в статистике, но и в физике, экономике или финансах. Используйте наши калькуляторы в качестве помощника для решения практических и теоретических задач.
Метод средневзвешенного значения — это инструмент, используемый в учебных аудиториях, статистическом анализе и бухгалтерии, а также в других областях. Взвешенное среднее помогает пользователю получить более точный взгляд на набор данных, чем обычное среднее. Точность чисел, полученных с помощью этого метода, определяется весом, который вы придаете конкретным переменным в наборе данных.
В этой статье мы рассмотрим, как рассчитать средневзвешенное значение двумя методами. Мы предлагаем
Ключевые выводы:
-
Средневзвешенное среднее — это среднее значение набора чисел, каждое из которых имеет различные веса или значения.
-
Чтобы найти средневзвешенное значение, умножьте каждое число на его вес, а затем сложите результаты.
-
Если весовые коэффициенты не равны единице, найдите сумму всех переменных, умноженную на их вес, а затем разделите на сумму весовых коэффициентов.
Что такое средневзвешенное значение?
Средневзвешенное среднее — это среднее значение набора данных, при котором определенные числа считаются более важными, чем другие. Средневзвешенные средние обычно используются в статистическом анализе, портфелях акций и средних оценках учителей. Это важный инструмент для учета колебаний запасов, неравномерных или искаженных данных, а также для обеспечения равенства представленных аналогичных точек данных в пропорции.
Пример средневзвешенного значения
Средневзвешенная стоимость — это один из способов, с помощью которого бухгалтеры рассчитывают стоимость товаров. В некоторых отраслях промышленности, где количество смешанное или слишком большое для подсчета, полезен метод средневзвешенной стоимости. Это число входит в расчет себестоимости проданных товаров. Другие методы калькуляции себестоимости включают метод последний вошел, первый вышел и первый вошел, первый вышел , или LIFO и FIFO соответственно.
Пример:
Производитель закупает 20 000 единиц товара по цене $1 за штуку, 15 000 единиц по цене $1.15 за штуку и 5 000 по 2 доллара за штуку. Используя единицы продукции в качестве веса, а общее количество единиц продукции как сумму всех весов, мы получаем следующий расчет:
$1(20,000) + $1.15 (15,000) + $2 (5,000) (20,000 + 15,000 + 5,000) = ($20,000 + $17,250 + $10,000) ($20,000 + 15,000 + 5,000) = $47,250 40,000 = $1.18
Это равняется средневзвешенной стоимости в $1.18 за единицу.
Как рассчитать средневзвешенное значение
Средневзвешенное среднее отличается от обычного среднего значения набора данных, поскольку общее отражает, что некоторые части данных имеют больший вес , или большую значимость, чем другие, или встречаются чаще. Вы можете рассчитать средневзвешенное значение набора чисел, умножив каждое значение в наборе на его вес, а затем сложив полученные продукты.
Для более подробного объяснения приведенной выше формулы средневзвешенного значения выполните следующие шаги:
1. Определите вес каждой точки данных
Вы определяете вес точек данных, учитывая, какие цифры являются наиболее важными. Например, преподаватели часто оценивают тесты и работы более весомо, чем контрольные работы и домашние задания. В больших статистических наборах данных, таких как поиск данных о потребительском поведении или перепись населения, для определения важности переменной в наборе данных используются рандомизированные деревья данных. Это помогает обеспечить несмещенное распределение важности. Этот процесс обычно выполняется с помощью компьютерной программы. Для бухгалтерских и финансовых целей в качестве весового коэффициента используется количество единиц продукта.
Пример:
-
Вы набрали 76 баллов на тесте, который составляет 20% от вашей итоговой оценки. Процент от вашей оценки — это вес, который она имеет.
-
Инвестор приобретает 50 акций по 100 долларов каждая. В качестве веса выступают купленные акции.
2. Умножьте вес на каждое значение
Как только вы узнаете вес каждого значения, умножьте вес на каждую точку данных.
Пример:
В наборе данных из четырех тестов, где последний тест имеет больший вес, чем остальные:
-
50(.15) = 7.5
-
76(.20) = 15.2
-
80(.20) = 16
-
98(.45) = 44.1
3. Сложите результаты второго шага вместе
Рассчитайте сумму всех взвешенных значений, чтобы получить средневзвешенное значение.
Пример:
7.5 + 15.2 + 16 + 44.1 = 82.8
Средневзвешенное значение равно 82.8%. Используя обычное среднее, когда мы вычисляем сумму и делим ее на количество переменных, средний балл будет равен 76%. Метод средневзвешенного значения подчеркивает важность выпускного экзамена по сравнению с другими.
Расчет средневзвешенного значения
| Результат теста | Присвоенный вес | Тестовый балл Взвешенное значение |
| 50 | .15 | 7.5 |
| 76 | .20 | 15.2 |
| 80 | .20 | 16 |
| 98 | .45 | 44.1 |
| Средневзвешенное значение | 82.8 |
Как рассчитать средневзвешенное значение, если весовые коэффициенты не равны единице
Иногда вам может понадобиться рассчитать среднее значение набора данных, которое не может быть равно 1 или 100%. Это происходит при случайном сборе данных из популяций или случаев в исследовании. Вы можете рассчитать средневзвешенное значение этого набора чисел, умножив каждое значение в наборе на его вес, затем сложив продукты и разделив сумму продуктов на сумму всех весов.
Для более подробного объяснения приведенной выше формулы средневзвешенного, когда веса не складываются в единицу, выполните следующие действия:
1. Определите вес каждого числа
Чтобы определить вес каждого числа, подумайте о его важности для вас или частоте появления. Если вы пытаетесь рассчитать среднее количество деловых предложений, которые вы получаете, вы можете предположить, что предложения, которые превращаются в продажи, будут иметь больший вес, чем холодные звонки. Чтобы найти средневзвешенное значение без дополнительного смещения, рассчитайте частоту встречаемости числа как вес переменной. Это отражает его влияние на весь набор данных.
Пример: Рассчитайте среднее время, которое вы тратите на физические упражнения четыре дня в неделю в течение месяца или четырех недель. Время, которое вы потратили на физические упражнения в любой конкретный день, является набором данных. Количество дней, в течение которых вы занимались спортом в среднем, — это вес, который вы будете использовать.
-
7 дней вы занимались спортом в течение 20 минут
-
3 дня вы занимались спортом в течение 45 минут
-
4 дня вы занимались спортом в течение 15 минут
-
2 дня, когда вы должны были заниматься спортом, но не делали этого
2. Найдите сумму всех весов
Следующим шагом для нахождения средневзвешенного значения набора данных, не равного 1, является сложение суммы общего веса. Из нашего предыдущего примера следует, что в общей сложности вы потратили на физические упражнения 16 дней:
-
7+3+4+2 = 16
3. Рассчитайте сумму каждого числа, умноженную на его вес
Используя числа частот, умножьте каждое из них на время, в течение которого вы занимались спортом. Общий итог дает сумму переменных, умноженную на их соответствующие веса.
Пример:
-
20(7) = 140
-
45(3) = 135
-
15(4) = 60
-
0(2) = 0
-
140 + 135 + 60 + 0 = 335
4. Разделите результаты третьего шага на сумму всех весов
Формула для нахождения средневзвешенного показателя — это сумма всех переменных, умноженная на их вес, затем деленная на сумму весов.
Пример:
Сумма переменных (вес) сумма всех весов = средневзвешенное значение
33516 = 20.9
Средневзвешенное значение времени, которое вы потратили на тренировки в течение месяца, равно 20.9 минут.
Что такое взвешенное среднее?
Уравнение средневзвешенного значения — это статистический метод, который вычисляет среднее значение путем умножения весов на их соответствующее среднее значение и получения его суммы. Это тип среднего значения, в котором весам присваиваются отдельные значения для определения относительной важности каждого наблюдения.
Оглавление
- Что такое взвешенное среднее?
- Формула взвешенного среднего
- Расчет средневзвешенного значения (шаг за шагом)
- Примеры
- Актуальность и использование формулы взвешенного среднего
- Рекомендуемые статьи
Формула взвешенного среднего
Средневзвешенное значение рассчитывается путем умножения веса на количественный результат и сложения всех продуктов. Если все веса равны, то средневзвешенное и среднее арифметическое будут одинаковыми.
Средневзвешенное значение = ∑ni=1 (xi*wi)/∑ni=1wi
Это подразумевает, что Средневзвешенное значение = w1x1+w2x2+…+wnxn/w1+w2+…+wn
Где
- ∑ обозначает сумму
- w — веса и
- х это значение
В случаях, когда сумма весов равна 1,
Средневзвешенное значение = ∑ni (xi* wi)
Расчет средневзвешенного значения (шаг за шагом)
Выполните следующие шаги.
- Запишите числа и веса в табличной форме. Представление в табличной форме не является обязательным, но упрощает расчеты.
- Умножьте каждое число и соответствующий вес, назначенный этому числу (w1 на x1, w2 на x2 и т. д.)..
- Сложите числа, полученные на шаге 2 (∑x1wi).
- Найдите сумму весов (∑wi).
- Разделите сумму значений, полученных на шаге 3, на сумму весов, полученных на шаге 4 (∑x1wi/∑wi).
Примечание: Если сумма весов равна 1, то сумма значений, полученных на шаге 3, будет средневзвешенным.
Примеры
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel для формулы взвешенного среднего здесь — Формула взвешенного среднего Excel Шаблон
Пример №1
Ниже приведены 5 чисел и веса, присвоенные каждому числу. Затем вычислите средневзвешенное значение приведенных выше чисел.
Решение:
ВМ будет –

Генеральный директор компании решил, что он продолжит бизнес только в том случае, если рентабельность капитала превышает + [Cost of Debt * % of Debt * (1-Tax Rate)]” url=” средняя стоимость капитала”взвешенный”. Компания получает доход в размере 14% от своего капитала. Капитал состоит из собственных и заемных средств на 60% и 40% соответственно. Стоимость собственного капитала составляет 15%, а стоимость долгаСтоимость долгаСтоимость долга представляет собой ожидаемую норму прибыли для держателя долга и обычно рассчитывается как эффективная процентная ставка, применимая к обязательствам фирмы. Это неотъемлемая часть анализа дисконтированных оценок, который рассчитывает текущую стоимость фирмы путем дисконтирования будущих денежных потоков по ожидаемой норме прибыли для держателей капитала и долговых обязательств. Читать далее 6%. Посоветуйте генеральному директору, следует ли компании продолжать свою деятельность.
Решение:
Давайте сначала представим данную информацию в табличной форме, чтобы понять сценарий.
Для расчета будем использовать следующие данные.
ВМ = 0,60*0,15 + 0,40*0,06
= 0,090 + 0,024
Поскольку рентабельность капитала в размере 14% больше, чем средневзвешенная стоимость капитала в размере 11,4%, генеральный директор должен продолжать свою деятельность.
Пример №3
Трудно оценить будущий экономический сценарий. Доходность акций может быть затронута. Финансовый консультант разрабатывает различные бизнес-сценарии и ожидаемую доходность акций для каждого сценария. Следовательно, это позволит ему принять лучшее инвестиционное решение. Рассчитайте средневзвешенное значение из приведенных выше данных, чтобы помочь инвестиционному консультанту продемонстрировать ожидаемую доходность акций своим клиентам.
Решение:
Для расчета будем использовать следующие данные.
=0,20*0,25 + 0,30*(-0,10) + 0,50*0,05
= 0,050 – 0,030 + 0,025
ВМ будет –
Ожидаемая доходность акций составляет 4,5%.
Пример №4
Джей — торговец рисом, который продает различные виды риса в Махараштре. Некоторые сорта риса более высокого качества и продаются по более высокой цене. Он хочет, чтобы вы вычислили средневзвешенное значение из следующих данных:
Решение:
Для расчета будем использовать следующие данные.
Шаг 1: В Excel есть встроенная формула для вычисления произведений чисел и их суммы, что является одним из шагов при вычислении средневзвешенного значения. Выберите пустую ячейку и введите эту формулу = СУММПРОИЗВСУММПРОИЗВФункция Excel СУММПРОИЗВ умножает числа двух или более массивов и суммирует полученные продукты. Подробнее (B2: B5, C2: C5), где диапазон B2: B5 представляет веса и диапазон C2: C5 представляет числа.
Шаг 2: Вычислите сумму весов по формуле =СУММ(B2:B5), где диапазон B2:B5 представляет веса.
Шаг 3: Вычислить =C6/B6,
ВМ будет –
Это дает WM как 51,36 рупий.
Актуальность и использование формулы взвешенного среднего
Средневзвешенное значение может помочь человеку в принятии решений, когда некоторые атрибуты имеют большее значение, чем другие. Например, его обычно используют для расчета итоговой оценки за конкретный курс. В курсах комплексный экзамен обычно имеет большее значение для оценки, чем тесты по главам. Таким образом, если кто-то плохо справляется с тестами по главам, но хорошо сдает выпускные экзамены, средневзвешенное значение оценок будет относительно высоким.
Его можно использовать в описательном статистическом анализе, таком как вычисление индексов. Например, индексы фондового рынка, такие как Nifty или BSE Sensex, вычисляются с использованием метода средневзвешенного значения. Его также можно применить в физике для нахождения центра масс и моментов инерции объекта с известным распределением плотности.
Люди в бизнесе часто рассчитывают средневзвешенное значение для оценки средних цен на товары, приобретенные у разных продавцов, где количество считается весом. Это дает бизнесмену лучшее понимание своих расходов.
Можно применить формулу средневзвешенного значения для расчета средней доходности портфеля, состоящего из различных финансовых инструментов. , акции, переводные векселя, форварды, FRA или соглашение о форвардной ставке и т. д. одной организации и в качестве обязательства другой организации и используются исключительно в торговых целях. подробнее. Например, предположим, что собственный капитал состоит из 80% портфеля, а остаток долга — из 20%. Доходность собственного капитала составляет 50%, а заемного капитала – 10%. Простое среднее будет (50%+10%)/2, что составляет 30%.
Это дает неправильное представление о доходах, поскольку капитал составляет большую часть портфеля. Следовательно, мы рассчитываем средневзвешенное значение, которое составляет 42%. Это число в 42% намного ближе к доходности собственного капитала в размере 50%, так как основной капитал составляет большую часть портфеля. Другими словами, доходность зависит от веса собственного капитала, равного 80%.
Рекомендуемые статьи
Эта статья представляет собой руководство по формуле взвешенного среднего. Здесь мы обсуждаем расчет средневзвешенного значения с практическими примерами и загружаемым шаблоном Excel. Вы можете узнать больше о моделировании в Excel из следующих статей:
- Формула среднего арифметическогоАрифметическая формула среднегоАрифметическое среднее обозначает среднее значение всех наблюдений ряда данных. Это совокупность всех значений в наборе данных, деленная на общее количество наблюдений.Подробнее
- Что такое средневзвешенные акции в обращении?
- Среднее против средневзвешенного Среднее против. Средневзвешенное значение В Excel слова среднее значение и средневзвешенное значение различаются. Среднее — это метод вычисления центральной точки заданного набора данных, который выполняется с использованием традиционного метода сложения чисел и деления суммы на количество имеющихся наборов данных. С другой стороны, взвешенное среднее — это среднее значение, рассчитанное таким же образом, но с весом, умноженным на каждый набор данных.Подробнее
- Среднее по сравнению с медианнымСреднее по сравнению с. MedianMean — это среднее значение заданных чисел. Он суммирует числа и делит их на количество чисел, которое дает нам среднее значение. С другой стороны, медиана возвращает среднее число из всего набора данных.Подробнее
Онлайн калькулятор поможет найти среднее арифметическое взвешенное набора чисел. Основные числа и веса могут быть и вещественными, и комплексными. При этом сумма весов не может быть 0, но могут быть некоторые, равные 0. В том случае, если все веса равны между собой, среднее арифметическое взвешенное будет равно среднему арифметическому.
Формула для вычисления средней арифметической взвешенной:
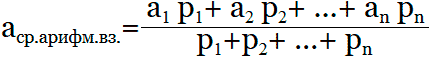
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»
























