Памятка по нахождению неизвестных компонентов действий.
Скачать:
Предварительный просмотр:
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
По теме: методические разработки, презентации и конспекты
- Мне нравится
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
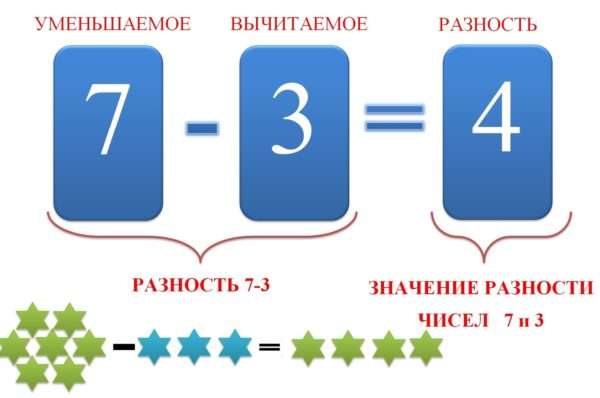
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | 11 | = | 7 | |
| 14 | 5 | = | 9 | |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Поиск вычитаемого, уменьшаемого и разности для первоклассников
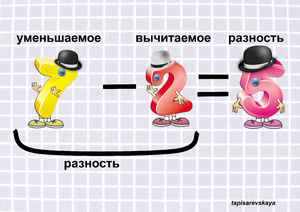
Теперь рассмотрим правила вычисления каждого из этих компонентов на простых примерах.
Чтобы сделать юным математикам понимание азов науки проще и доступнее, представим эти сложные и пугающие термины именами чисел в уравнении. Ведь у каждого человека есть имя, по которому к нему обращаются, чтобы о чем-то спросить, что-то рассказать, обменяться информацией. Учитель в классе, вызывая ученика к доске, смотрит на него и называет по имени. Так и мы, глядя на числа в уравнении, можем очень легко понять, какое число как зовут. А после уже и обратиться к числу, чтобы правильно решить уравнение или даже найти потерявшееся число, об этом чуть позже.
Но, ничего не зная о числах в уравнении, давайте сначала с ними познакомимся. Для этого приведем пример: уравнение 5−3= 2. Первое и самое большое число 5 после того, как мы от него отняли 3, становится меньше, уменьшается. Поэтому в мире математики его так и называют — Уменьшаемое. Второе число 3, которое мы отнимаем от первого, тоже легко узнать и запомнить — оно Вычитаемое. Глядя на третье число 2, мы видим разницу между Уменьшаемым и Вычитаемым — это Разность, то, что мы получили в результате вычитания. Вот так.
Как найти неизвестные

Но бывают случаи, когда какое-то из чисел теряется или просто неизвестно. Что же делать? Все очень просто — для того, чтобы такое число найти, нам нужно знать только два других значения, а также несколько правил математики, и, конечно, уметь ими пользоваться. Начнём с самой лёгкой ситуации, когда нам нужно найти Разность.
Как найти разность
Представим, что мы купили 7 яблок, подарили 3 яблока своей сестре и оставили какое-то количество себе. Уменьшаемое — это наши 7 яблок, число которых уменьшилось. Вычитаемое — это те 3 подаренных нами яблока. Разность — это количество оставшихся яблок. Что сделать, чтобы узнать это количество? Решить уравнение 7−3= 4. Таким образом, хотя мы и подарили 3 яблока сестре, у нас ещё осталось 4.
Правило поиска уменьшаемого
Теперь узнаем, что делать, если потерялось Уменьшаемое.
Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.
- Теперь, чтобы быть уверенными, сделаем небольшую проверку — подставим все на свои места и вычислим разность. Итак, 10 -4= 6. Разность совпадает, а значит мы сделали все верно. У нас было 10 яблок, мы съели 4, осталось 6.
Как найти вычитаемое
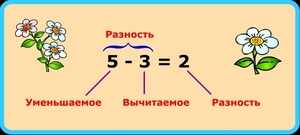
На всякий случай можно проверить наши успехи и подставить отыскавшееся Вычитаемое в исходный пример. 7−3= 4. Разность не изменилась, а значит мы сделали все правильно. Было 7 яблок, съели 3, осталось 4.
Правила очень простые, но, чтобы быть уверенными и ничего не забыть, можно поступить так — самому для себя придумать лёгкий и понятный пример на вычитание и, решая другие примеры, отыскивать неизвестные значения, просто подставляя цифры и легко находить правильный ответ. Например, 5−3= 2. Мы уже знаем, как найти и Уменьшаемое 5, и Вычитаемое 3, поэтому решая более сложное уравнение, скажем, 25-Х= 13, мы можем вспомнить наш простой пример и понять, что, чтобы найти неизвестное Вычитаемое, нужно лишь отнять от 25 число 13, то есть 25 -13= 12.
Ну вот, теперь мы познакомились с вычитанием, его главными участниками.
Мы умеем отличать их друг от друга, находить, если они неизвестны и решать любые уравнения с их участием. Пусть эти знания помогут и пригодятся вам в начале интересного и увлекательного пути в страну Математики. Удачи!
Памятка «Нахождение неизвестных компонентов сложения и вычитания в уравнениях»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
ПРАВИЛА НАХОЖДЕНИЯ НЕИЗВЕСТНЫХ КОМПОНЕНТОВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
Нужно найти неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое
Нужно найти сумму
Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое
Нужно найти уменьшаемое
Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое
Нужно найти вычитаемое
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность
Нужно найти разность
Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого
ПРАВИЛА НАХОЖДЕНИЯ НЕИЗВЕСТНЫХ КОМПОНЕНТОВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
Нужно найти неизвестное слагаемое
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое
Нужно найти сумму
Чтобы найти сумму, нужно к первому слагаемому прибавить второе слагаемое
Нужно найти уменьшаемое
Чтобы найти неизвестное уменьшаемое, нужно к разность прибавить вычитаемое
Нужно найти вычитаемое
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность
Нужно найти разность
Чтобы найти неизвестную разность, нужно из уменьшаемого вычесть вычитаемого
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 939 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 686 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 313 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 590 273 материала в базе
Материал подходит для УМК
«Математика (в 2 частях)», Муравин Г.К., Муравина О.В.
3. Нахождение неизвестных компонентов сложения и вычитания
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 02.05.2020
- 250
- 3
- 02.05.2020
- 210
- 2
- 02.05.2020
- 188
- 1
- 02.05.2020
- 177
- 0
- 01.05.2020
- 423
- 30
- 01.05.2020
- 377
- 5
- 01.05.2020
- 434
- 3
- 01.05.2020
- 198
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 02.05.2020 7510
- DOCX 14.9 кбайт
- 534 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Логинов Вячеслав Дмитриевич. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 4 года и 11 месяцев
- Подписчики: 1
- Всего просмотров: 14421
- Всего материалов: 24
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
Минпросвещения подключит студотряды к обновлению школьной инфраструктуры
Время чтения: 1 минута
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Каждый второй ребенок в школе подвергался психической агрессии
Время чтения: 3 минуты
РДШ организовало сбор гуманитарной помощи для детей из ДНР
Время чтения: 1 минута
Университет им. Герцена и РАО создадут портрет современного школьника
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.

Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
http://infourok.ru/pamyatka-nahozhdenie-neizvestnyh-komponentov-slozheniya-i-vychitaniya-v-uravneniyah-4279339.html
http://tvercult.ru/nauka/chto-takoe-vyichitaemoe-umenshaemoe-i-raznost-pravilo
Содержание материала
- Предварительный просмотр:
- Видео
- Нахождение неизвестного множителя
- Поиск вычитаемого
- Правила нахождения уменьшаемого
- Свойства сложения
- Общие правила
- Другие методы
- Сложение в столбик многозначных чисел
Предварительный просмотр:
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Выучи названия компонентов действий и правила нахождения неизвестных компонентов:
- Сложение: слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Вычитание: уменьшаемое, вычитаемое, разность. Чтобы найти уменьшаемое, нужно к вычитаемому прибавить разность. Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
- Умножение: множитель, множитель, произведение. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
- Деление: делимое, делитель, частное. Чтобы найти делимое, нужно делитель умножить на частное. Чтобы найти делитель, нужно делимое разделить на частное.
Видео
Нахождение неизвестного множителя
Посмотрим на два уравнения: x·2=20 и 3·x=12. В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a·b=c при a и b, не равных , c: a=b, c: b=c и наоборот.
Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2. Проводим деление натуральных чисел и получаем 10. Запишем последовательность равенств:
x·2=20x=20:2x=10.
Подставляем десятку в исходное равенство и получаем, что 2·10=20. Значение неизвестного множителя было выполнено правильно.
Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x·=11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.
Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.
Поиск вычитаемого
Нахождение вычитаемого — это такой же простой процесс, как и поиск уменьшаемого. Уравнение может иметь следующий вид: 7-x=3. Мы имеем разность — результат вычитания, и уменьшаемое число. Формулировка правила: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Так, если мы вычитаем из одного числа неизвестное число и получаем определённый результат (разность), значит, для поиска неизвестного вычитаемого вычтем из известного числа разность. В нашем примере x=7−3, результат равен 4. Для проверки вычтем 4 из 7, и получим 3 — решение верное. Ещё один вариант проверки — сложить 3 и 4. Так как сумма равна 7, решение правильное.
Правила нахождения уменьшаемого

При поиске уменьшаемого уравнение может выглядеть следующим образом: x-2=4. Мы имеем разность — результат вычитания и число, которое вычитаем. Необходимо найти уменьшаемое — самое большое число в примере. Формулировка правила: чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Так, если мы вычитаем из неизвестного числа другое число и получаем результат, известный нам, то для поиска уменьшаемого необходимо сложить разность и вычитаемое. Простейший пример: дома были конфеты. Их количество мы не знаем. После того как Дима съел 2 конфеты, их осталось 4. Вопрос: сколько их всего было изначально? Для того чтобы узнать, прибавим 2 к 4 и получим результат — было 6 конфет. Для проверки вычтем 2 из 6. Получим результат 4 — решение верное.
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Общие правила
Для того чтобы гораздо быстрее решать элементарные уравнения, необходимо знать некоторые правила математики и логики. Здесь даже навыки арифметики не имеют такого решающего значения, как понимание того, что именно необходимо находить.
В случае с неизвестным слагаемым оно находится очень просто. От перестановки слагаемых сумма не меняется. То есть совершенно неважно, какой вид имеет уравнение x+2=6, или 2+x=6. В любом случае компонент x будет равен 4.

Дело в том, что уравнения с одним неизвестным предусмотрены школьной программой третьего класса. А ученики могут путаться и испытывать трудности в их решении, не зная этого правила.
Первое, с чего стоит начинать развитие навыка решения — это многократное повторение. Достаточно решать 5—10 уравнений в день с одним неизвестным компонентом, и уже через несколько дней ученик будет справляться с подобными заданиями гораздо быстрее. И только потом можно переходить к более сложным заданиям.

А также для улучшения понимания необходимо решать обратные уравнения. Что это значит? Вычитание — процесс, обратный сложению. То есть при сложении 3 и 4 сумма равна 7. А при вычитании 4 из 7 разность равна 3. В первом уравнении можно искать неизвестные слагаемые. При этом решать его с теми же числами, но на поиск уменьшаемого или вычитаемого.
Решение подобных уравнений точно не навредит ученику, это лишь ускорит процесс формирования навыка. При проверке и решении обратных уравнений в голове откладывается взаимосвязь между всеми компонентами примеров, а их решение практически доводит до автоматизма. Главное — постоянно тренировать этот навык.
Другие методы
Правило, которое позволяет быстро найти неизвестное слагаемое, довольно простое. Однако для того, чтобы облегчить его понимание, из него можно вывести правила, связанные с вычитанием.
Так, в примерах со сложением мы имеем два слагаемых и сумму: 3+5=8. Здесь 3 и 5 — слагаемые, а 8 — сумма. А в примерах с вычитанием мы имеем:
- Уменьшаемое.
- Вычитаемое.
- Разность.
Например, 7 — 4=3. В этом случае уменьшаемое — 7, вычитаемое — 3, а разность — 4. Уменьшаемое и вычитаемое также могут быть неизвестными. И крайне важно знать, как их вычислять.
Сложение в столбик многозначных чисел
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Итак, допустим, что нам нужно найти сумму : 5728+803
Теги
Содержание
- Вычитание чисел
- Уменьшаемое, вычитаемое и разность
- Проверка вычитания
- Уменьшаемое
- Смотреть что такое «Уменьшаемое» в других словарях:
- Что такое вычитаемое уменьшаемое и разность: правило
- Значение терминов
- Что такое разность чисел в математике
- Что такое уменьшаемое и вычитаемое
- Полезное видео: уменьшаемое, вычитаемое, разность
- Правила нахождения неизвестного элемента
- Как найти уменьшаемое
- Как найти вычитаемое
- Полезное видео: как найти неизвестное уменьшаемое
- Вывод
- Общее представление о вычитании натуральных чисел
- Общий смысл процесса вычитания
- Основные понятия, связанные с вычитанием
- Для решения каких задач нужно знать вычитание
Вычитание чисел
Вычитание чисел — это арифметическое действие, с помощью которого от единиц одного числа отнимают столько единиц, сколько их содержится в другом числе.
Пример. На столе лежало 9 конфет, 5 из них съели. Сколько конфет осталось на столе?
Чтобы ответить на этот вопрос, надо из общего количества конфет вычесть количество конфет, которые были съедены:
Отнимая 5 раз по одной конфете от общего количества конфет, мы получим количество конфет, которые остались лежать на столе, то есть 4.
Вычесть – значит от одного числа отнять столько единиц, сколько их содержится в другом.
Для записи вычитания используется знак — (минус), который ставится между числами. Например:
Эта запись означает, что от 9 надо отнять пять. Справа от записи вычитания ставится знак = (равно), после которого записывается полученный результат:
Уменьшаемое, вычитаемое и разность
Уменьшаемое — это число, из которого вычитают. Вычитаемое — это число, которое вычитают. Например, в записи:
9 — это уменьшаемое, 4 — вычитаемое.
Разность (остаток) — это число, которое получается в результате вычитания. Например, в записи:
5 — это разность. При этом сама запись 9 — 4 тоже называется разностью.
Эту запись можно прочитать так: разность девяти и четырёх равна пяти , девять минус четыре равно пяти или из девяти вычесть четыре, получится пять .
Вычитание – это арифметическое действие обратное сложению, с помощью которого по сумме и одному слагаемому находится другое слагаемое.
Проверка вычитания
где 15 — это уменьшаемое, 7 — это вычитаемое, а 8 — разность. Чтобы узнать правильно ли было выполнено вычитание, можно:
- Вычитаемое сложить с разностью, если получится уменьшаемое, то вычитание было выполнено верно:
От уменьшаемого отнять разность, если получится вычитаемое, то вычитание было выполнено верно:
Источник
Уменьшаемое
Вычита́ние — одно из четырех арифметических действий; операция, обратная сложению. Обозначается знаком минус «−».
В выражении x − y (читается «икс минус игрек») элемент x называется уменьшаемым, элемент y называется вычитаемым, а результат вычитания называется разностью x и y .
В области положительных чисел вычитание не всегда выполнимо (из меньшего числа нельзя вычесть большее). Это обстоятельство является формальным поводом для введения в арифметику нуля и отрицательных чисел; в расширенной таким образом числовой области вычитание всегда однозначно выполнимо.
Вычитание удобно рассматривать (или даже определять) как разновидность сложения — сложение положительного и отрицательного чисел. К примеру, 7 − 3 = 4 можно рассматривать как сложение чисел 7 и − 3 , то есть 7 − 3 тождественно 7 + ( − 3) .
Операция вычитания не является ассоциативной и коммутативной, она антикоммутативна, то есть x − y = − (y − x) .
Wikimedia Foundation . 2010 .
Смотреть что такое «Уменьшаемое» в других словарях:
уменьшаемое — сократимый Словарь русских синонимов. уменьшаемое сущ., кол во синонимов: 1 • сократимый (2) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
УМЕНЬШАЕМОЕ — элемент операции (см.) число, из которого вычитается др. число. Если вычитание записано как с = а b, то а уменьшаемое … Большая политехническая энциклопедия
УМЕНЬШАЕМОЕ — УМЕНЬШАЕМОЕ, ого, ср. Число или выражение, из к рого вычитают другое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
уменьшаемое — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN minuend … Справочник технического переводчика
Уменьшаемое — см. Вычитание … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Уменьшаемое — ср. Название числа, из которого вычитают другое (в математике). Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
уменьшаемое — уменьш аемое, ого … Русский орфографический словарь
уменьшаемое — Р. уменьша/емого … Орфографический словарь русского языка
уменьшаемое — ого; ср. Матем. Число, из которого вычитают другое при действии вычитания. Вычесть из уменьшаемого четыре. От уменьшаемого отнять десять единиц … Энциклопедический словарь
уменьшаемое — ого; ср.; матем. Число, из которого вычитают другое при действии вычитания. Вычесть из уменьшаемого четыре. От уменьшаемого отнять десять единиц … Словарь многих выражений
Источник
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.

Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Источник
Общее представление о вычитании натуральных чисел
В рамках это материала мы разберемся с таким действием, как вычитание. Для начала мы попробуем дать общее представление о нем, пояснить сам смысл процесса вычитания. Потом введем и поясним необходимые обозначения и определения. В финальной части мы укажем, в решении каких задач нам может потребоваться вычитание.
Общий смысл процесса вычитания
Само по себе вычитание связано с разъединением некого множества на отдельные части. В этом смысле оно обратно сложению, которое, напротив, объединяет их (см. материал о сложении натуральных чисел).
Что конкретно это означает на практике?
Допустим, у нас есть некоторое количество шаров в вазе. Заберем из всей кучи один-два и положим в другое место. Тем самым мы совершили процесс вычитания, т.е. отняли от множества несколько предметов. То есть суть процесса вычитания состоит именно в исключении, отделении одних предметов от других.
Вернемся к сложению. Мы складываем одни числа с другими для того, чтобы получить сведения об их общем, суммарном количестве. А для чего мы вычитаем? Есть два подхода к пониманию сути этого процесса. От того, какой мы используем, будет зависеть смысл, придаваемый вычитаемому числу.
Для натуральных чисел результат вычитания говорит нам:
1) о том, сколько предметов останется, если убрать из их множества некое определенное количество;
2) о том, сколько нужно убрать предметов из заданного множества, чтобы получить требуемое количество.
Разберем сначала первый случай.
У нас на столе лежит 6 шаров. С помощью процесса вычитания мы сможем узнать то количество шаров, которое останется у нас после того, как мы уберем куда-нибудь, скажем, 3 шара. Для этого нам нужно вычесть 3 из 6 .
Ответ: 3 .
А во втором случае мы узнаем:
Сколько шаров надо убрать, чтобы у нас в руках их осталось, например, 2 . Для этого нам надо вычислить разность 6 — 2 и получить то число предметов, которое нужно убрать.
Ответ: 4
В этом смысле процесс вычитания натуральных чисел имеет смысл только тогда, когда вычитаемое число меньше, чем уменьшаемое. В самом деле, как можно убрать больше, чем у нас уже есть? В дальнейшем мы останемся в рамках этого ограничения, пока говорим о действиях с натуральными числами.
В результате вычитания у нас, разумеется, может получиться не только другое натуральное число, но и нуль, который говорит о полном отсутствии предметов. Это происходит тогда, когда уменьшаемое и вычитаемое равны. Получается, если мы уберем все предметы, которые у нас есть, то на столе не останется ни одного.
Основные понятия, связанные с вычитанием
Здесь мы укажем общепринятые обозначения и поясним их.
Для того чтобы указать на письме, что речь идет именно о процессе вычитания, традиционно используется знак минуса. Порядок записи примера таков: сначала уменьшаемое (любое натуральное число), потом минус, а затем вычитаемое (любое натуральное число, которое меньше первого). Примерами таких записей могут быть 10 — 4 , 6 — 3 и т.д. Их принято называть числовыми выражениями.
Выше мы уже использовали термины «уменьшаемое» и «вычитаемое». Легко понять, что они означают:
Уменьшаемое – это то, из чего вычитают, вычитаемое – то, которое вычитают.
Полученное в результате вычитания число принято называть разностью. Также разностью можно назвать и само числовое выражение, состоящее из двух натуральных чисел с минусом. Например, для 8 — 5 восьмерка – это уменьшаемое, пять – вычитаемое, а тройка – разность, и само выражение 8 — 5 – это тоже разность.
Когда требуется определить, что получится в результате вычитания одного числа из другого, используются выражения: «вычислить разность», «найти разность», «вычесть одно число из другого», «отнять от одного числа другое».
В целом можно сказать, что все три компонента (уменьшаемое, вычитаемое и разность ) вместе образуют верное равенство. Например, натуральное число 7 есть результат вычитания 11 из 18 . Это можно записать в виде 18 — 11 = 7 (о знаке равенства мы говорили отдельно). Как правильно прочитать эту запись? «От восемнадцати отнять одиннадцать равно семь», «из восемнадцати вычесть одиннадцать равно семь» или «восемнадцать минус одиннадцать равно семь».
Таким образом, весь процесс вычитания мы можем представить так: уменьшаемое минус вычитаемое равно разность.
Для решения каких задач нужно знать вычитание
С помощью вычитания можно решить широкий спектр задач. Перечислим их:
1. Найти количество предметов, которое получится после разбиения всего их множества на два других. Примером такой задачи может стать задача с шарами на столе, которую мы приводили в пункте о смысле процесса вычитания. Задачи с нахождением числа предметов, которое надо убрать из имеющегося множества, так же относятся в этому виду.
2. Решить задачи, в которых изменяются значения длины, объема, массы, времени и других измерений.
У нас есть полотно, общая площадь которого составляет 9 кв.м. От него отрезали кусок в 5 кв.м. Чтобы узнать, сколько осталось, мы просто вычислим разность 9 — 5 .
Ответ: 4 .
Сейчас на улице 12 градусов мороза, а час назад было 5 .
Если мы отнимем 5 от 12 , мы узнаем разницу температур за прошедшее время.
Ответ: 7 .
3. Узнать разницу между количеством предметов, которые входят в два разных множества, или разницу между двумя любыми величинами (скоростями, массами и др.)
Например, одна машина проехала 50 км, а вторая – 40 . Если мы подсчитаем, сколько будет 50 — 40 , мы узнаем разницу проделанного пути.
Ответ: 10.
Возьмем пример с более сложными числами:
На одно поле высадили 160 растений, а на второе 340 . С помощью вычитания мы узнаем, на сколько отличаются количества саженцев.
Источник


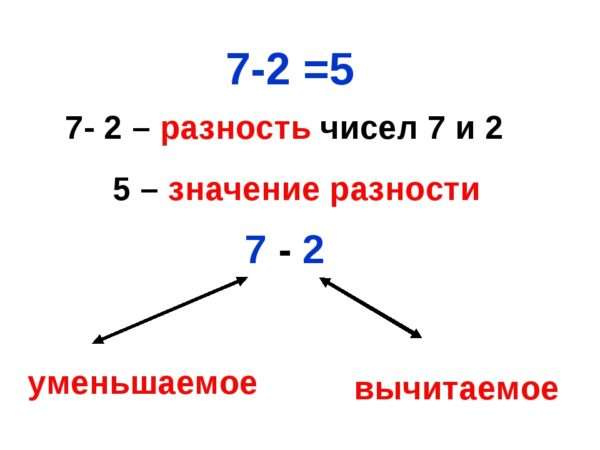

 Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.
Допустим, мы купили один килограмм яблок. Пришли домой, съели 4 яблока, и у нас в корзине осталось 6. Как узнать, сколько яблок у нас было? Ведь мы покупали килограмм, но точное количество не посчитали. В данном случае Уменьшаемое — это как раз и есть первоначальное количество яблок. Вычитаемое — это то число, которое мы съели, а Разность — оставшиеся. Мы не знаем число яблок, которые у нас были, поэтому поставим вместо него букву Х. У нас получается вот такой пример: X-4=6. Чтобы найти неизвестное Уменьшаемое, надо к Вычитаемому прибавить Разность, вот такое простое правило. То есть сложить 3+6=10. И вот оно, наше Уменьшаемое 10.







