Формула томпсона как найти l

Колебательный контур

• Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.

• Свободными называются такие колебания, которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.

При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур.

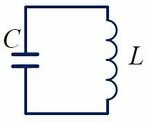
• Идеальный колебательный контур (LC-контур) — электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C.

В отличие от реального колебательного контура, который обладает электрическим сопротивлением R, электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.

На рисунке 1 изображена схема идеального колебательного контура.

Энергии контура

Полная энергия колебательного контура

(W=W_{e} + W_{m}, ; ; ; W_{e} =dfrac{Ccdot u^{2} }{2} = dfrac{q^{2} }{2C}, ; ; ; W_{m} =dfrac{Lcdot i^{2}}{2},)

где W_e — энергия электрического поля колебательного контура в данный момент времени, С — электроемкость конденсатора, u — значение напряжения на конденсаторе в данный момент времени, q — значение заряда конденсатора в данный момент времени, W_m — энергия магнитного поля колебательного контура в данный момент времени, L — индуктивность катушки, i —значение силы тока в катушке в данный момент времени.

Процессы в колебательном контуре

Рассмотрим процессы, которые возникают в колебательном контуре.

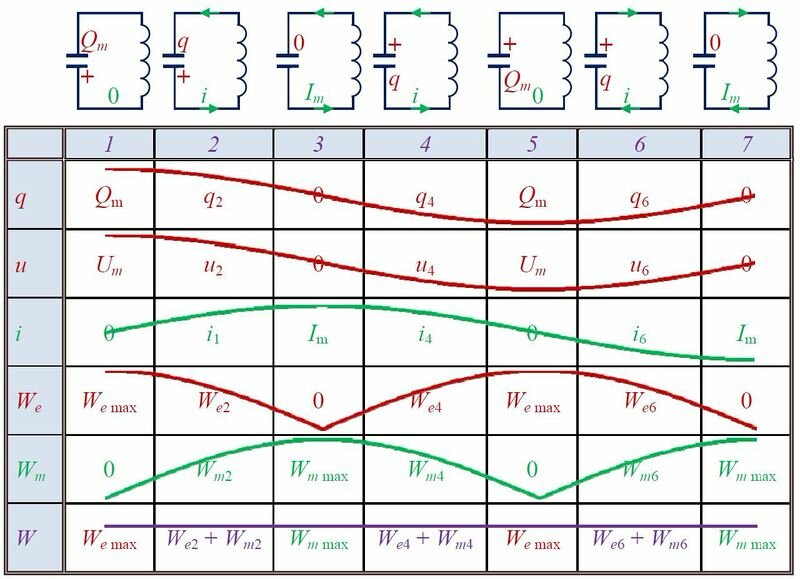
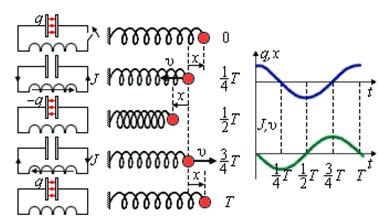
Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q_m (рис. 2, положение 1). С учетом уравнения (U_{m}=dfrac{Q_{m}}{C}) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.

После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2). Вместе с зарядом q будет уменьшаться и напряжение u (left(u = dfrac{q}{C} right).) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.

Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I_m (см. рис. 2, положение 3).

Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I_m (в положении 3) оказывается максимальным значением силы тока в контуре.

Далее сила тока становится равной нулю, а заряд конденсатора достигнет максимального значения Q_m (U_m) (см. рис. 2, положение 5).

И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6)до нуля (см. рис. 2, положение 7). И так далее.

Так как заряд на конденсаторе q (и напряжение u) определяет его энергию электрического поля W_e (left(W_{e}=dfrac{q^{2}}{2C}=dfrac{C cdot u^{2}}{2} right),) а сила тока в катушке i — энергию магнитного поля Wm (left(W_{m}=dfrac{L cdot i^{2}}{2} right),) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Обозначения в таблице:

Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку в нем потерь энергии (нет сопротивления). Тогда

(W=W_{e, max } = W_{m, max } = W_{e2} + W_{m2} = W_{e4} +W_{m4} = …)

Свободные электромагнитные колебания

Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока i, заряда q и напряжения u, причем полная энергия контура при этом будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.

• Свободные электромагнитные колебания в контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.

Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q и сила тока в катушке i достигают своих максимальных значений Q_m и I_m в различные моменты времени.

Свободные электромагнитные колебания в контуре происходят по гармоническому закону:

(q=Q_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; u=U_{m} cdot cos left(omega cdot t+varphi _{1} right), ; ; ; i=I_{m} cdot cos left(omega cdot t+varphi _{2} right).)

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.

Период свободных электромагнитных колебаний в LC-контуре определяется по формуле Томсона:

(T=2pi cdot sqrt{Lcdot C}, ;;; omega =dfrac{1}{sqrt{Lcdot C}}.)

Сточки зрения механической аналогии, идеальному колебательному контурусоответствует пружинный маятник без трения, а реальному — с трением. Вследствиедействия сил трения колебания пружинного маятника затухают с течением времени.

*Вывод формулы Томсона

Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство

(W=dfrac{Q_{m}^{2} }{2C} =dfrac{Lcdot I_{m}^{2} }{2} =dfrac{q^{2} }{2C} +dfrac{Lcdot i^{2} }{2} ={rm const}.)

Получим уравнение колебаний в LC-контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что

(W’=0, ;;; q’=i, ;;; i’=q»,)

получаем уравнение, описывающее свободные колебания в идеальном контуре:

Переписав его в виде:

(q»+omega ^{2} cdot q=0,)

замечаем, что это — уравнение гармонических колебаний с циклической частотой

(omega =dfrac{1}{sqrt{Lcdot C} }.)

Соответственно период рассматриваемых колебаний

(T=dfrac{2pi }{omega } =2pi cdot sqrt{Lcdot C}.)

Литература

1. Жилко, В.В. Физика: учеб. пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, Л.Г. Маркович. — Минск: Нар. Асвета, 2009. — С. 39-43.

Колебательный контур

Формулы

Формула Томпсона

Закон сохранения энергии в колебательном контуре

Видео

Лекции и опыты

Рекомендуем

Последовательный колебательный контур обозначение на схеме

Последовательный колебательный контур — это цепь, состоящая их катушки индуктивности и конденсатора, которые соединяются последовательно.

Идеальный последовательный колебательный контур

 На схемах идеальный последовательный колебательный контур обозначается вот так:

где

L — индуктивность, Гн

С — емкость, Ф

Реальный последовательный колебательный контур

Реальный колебательный контур имеет сопротивление потерь катушки и конденсатора. Это суммарное суммарное сопротивление потерь обозначается буквой R. В результате, реальный последовательный колебательный контур будет иметь такой вид:

R  — это суммарное сопротивление потерь катушки и конденсатора

L — собственно сама индуктивность катушки

С — собственно сама емкость конденсатора

Принцип работы последовательного колебательного контура

Генератор частоты и последовательный колебательный контур

Давайте проведем классический эксперимент, который есть в каждом учебнике по электронике. Для этого соберем вот такую схему:

Генератор (Ген)у нас будет выдавать синус.

Для того, чтобы снять осциллограмму силы тока через последовательный колебательный контур, мы подключим в схему шунтовый резистор с малым сопротивлением в 0,5 Ом и с него уже будем снимать напряжение. То есть в данном случае мы шунт используем для наблюдения силы тока в цепи.

А вот и сама схема в реальности:

Слева-направо: шунтовый резистор, катушка индуктивности и конденсатор. Как вы уже поняли, сопротивление R — это суммарное сопротивление потерь катушки и конденсатора, так как нет идеальных радиоэлементов. Оно «прячется» внутри катушки и конденсатора, поэтому в реальной схеме отдельным радиоэлементом мы его не увидим.

Теперь нам осталось подцепить эту схему к генератору частоты и осциллографу, и прогнать по некоторым частотам, снимая осциллограмму с шунта U_ш , а также снимая осциллограмму с самого генератора U_ГЕН .

С шунта мы будем снимать напряжение, которое у нас отображает поведение силы тока в цепи, а с генератора собственно сам сигнал генератора. Давайте прогоним нашу схемку по некоторым частотам и глянем что есть что.

Влияние частоты генератора на сопротивление колебательного контура

В схеме я взял конденсатор на 1мкФ и катушку индуктивности на 1 мГн. На генераторе настраиваю синус размахом в 4 Вольта. Вспоминаем правило: если в цепи соединение радиоэлементов идет последовательно друг за другом, значит, через них течет одинаковая сила тока.

Красная осциллограмма — это напряжение с генератора частоты, а желтая осциллограмма — отображение силы тока через напряжение на шунтовом резисторе.

Частота 200 Герц с копейками:

Как мы видим, при такой частоте ток в этой цепи есть, но очень слабый

Добавляем частоту. 600  Герц с копейками

Здесь мы уже отчетливо видим, что сила тока возросла, а также видим, что осциллограмма силы тока опережает напряжение. Попахивает реактивным сопротивлением конденсатора.

Добавляем частоту. 2 Килогерца

Сила тока стала еще больше.

3 Килогерца

Сила тока увеличилась. Заметьте также, что сдвиг фаз стал уменьшаться.

4,25 Килогерц

Осциллограммы почти уже сливаются в одну. Сдвиг фаз между напряжением и силой тока становится почти незаметным.

И вот на какой-то частоте у нас сила тока стала максимальной, а сдвиг фаз стал равен нулю. Запомните этот момент. Для нас он будет очень важен.

Ну а давайте далее будем увеличивать частоту. Смотрим, что получается в итоге.

Еще совсем недавно ток опережал напряжение, а сейчас уже стал запаздывать после того, как выровнялся с ним по фазе. Так как ток уже отстает от напряжения, здесь уже попахивает реактивным сопротивлением катушки индуктивности.

Увеличиваем частоту еще больше

Сила тока начинает падать, а сдвиг фаз увеличивается.

22 Килогерца

74 Килогерца

Как вы видите, с увеличением частоты, сдвиг приближается к 90 градусов, а сила тока становится все меньше и меньше.

Резонанс последовательного колебательного контура

Давайте подробнее рассмотрим тот самый момент, когда сдвиг фаз был равен нулю и сила тока, проходящая через последовательный колебательный, контур была максимальна:

Это явление носит название резонанса.

Не будем углубляться  в теорию высшей математики и комплексных чисел. Дело в том, что в этот самый момент реактивное сопротивление катушки и конденсатора становятся равными, но противоположными по знаку. Поэтому, эти реактивные сопротивления как-бы вычитаются друг из друга, что в сумме дает ноль, и в цепи остается только активная составляющая сопротивления, то есть то самое паразитное сопротивление катушки и конденсатора, или иначе, сопротивление потерь R.

Как вы помните, если у нас сопротивление  становится малым, а в данном случае сопротивления потерь катушки и конденсатора очень маленькие, то в цепи начинает течь большая сила тока согласно закону Ома: I=U/R. Если генератор мощный, то напряжение на нем не меняется, а сопротивление становится пренебрежимо малым и вуаля! Ток растет как грибы после дождя, что мы и увидели, посмотрев на желтую осциллограмму при резонансе.

Формула Томсона (резонанса) для последовательного колебательного контура

Если при резонансе у нас реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора X_L=X_C , то можно уравнять их реактивные сопротивления и уже отсюда вычислить частоту, на которой произошел резонанс. Итак, реактивное сопротивление катушки у нас выражается формулой:

Реактивное сопротивление конденсатора вычисляется по формуле:

Приравниваем обе части и вычисляем отсюда F:

В данном случае мы получили формулу резонансной частоты. Это формула по другому называется формулой Томсона, как вы поняли, в честь ученого, который ее вывел.

Давайте по формуле Томсона посчитаем резонансную частоту нашего последовательного колебательного контура. Для этого я буду использовать свой RLC-транзисторметр.

Замеряем индуктивность катушки:

И замеряем нашу емкость:

Высчитываем по формуле нашу резонансную частоту:

У меня получилось 5, 09 Килогерц.

С помощью  регулировки частоты и осциллографа я поймал резонанс на частоте 4,78 Килогерц (написано в нижнем левом углу)

Спишем погрешность в 200 с копейками Герц на погрешность измерений приборов. Как вы видите, формула Томпсона работает.

Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора  падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем  резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты  размах  более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14,  и цепляю поочередно к ним лампочку:

Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L , а на конденсаторе U_C = IX_C . А так как при резонансе у нас X_L = X_C , то получаем что U_L = U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Добротность последовательного колебательного контура

Ну раз уж мы начали задвигать тему колебательных контуров, поэтому мы не можем обойти стороной такой параметр, как добротность колебательного контура. Так как мы уже провели некоторые опыты, то нам будет проще определить добротность, исходя из амплитуды напряжений. Добротность обозначается буквой Q и вычисляется по первой простой формуле:

Давайте посчитаем добротность в нашем случае.

Так как цена деления одного квадратика по вертикали 2 Вольта, следовательно, амплитуда сигнала  генератора частоты 2 Вольта.

А это то, что мы имеем на зажимах конденсатора или катушки. Здесь цена деления одного квадратика по вертикали 5 Вольт. Считаем квадратики и умножаем. 5х4=20 Вольт.

Считаем по формуле добротности:

Q=20/2=10. В принципе немного и не мало. Пойдет. Вот так вот на практике можно найти добротность.

Есть также вторая формула для вычисления добротности.

где

R — сопротивление потерь в контуре, Ом

L — индуктивность, Генри

С — емкость, Фарад

Зная добротность, можно легко найти сопротивление потерь R последовательного колебательного контура.

Также хочу добавить пару слов о добротности. Добротность контура — это качественный показатель колебательного контура. В основном его стараются всегда увеличить различными всевозможными способами. Если взглянуть на формулу выше, то можно понять, для того, чтобы увеличить добротность, нам надо как-то уменьшить сопротивление потерь колебательного контура. Львиная доля потерь относится к катушке индуктивности, так как она уже конструктивно имеет большие потери. Она намотана из провода и в большинстве случаев имеет сердечник. На высоких частотах в проводе начинает проявляться скин-эффект, который еще больше вносит потери в контур.

Видео на тему «Как работает колебательный контур. Резонанс»:

Резюме

Последовательный колебательный контур состоит из катушки индуктивности и конденсатора, соединенных последовательно.

Катушка и конденсатор имеют паразитные омические потери, так как не являются идеальными радиоэлементами. Сумма этих потерь называется сопротивлением потерь R последовательного колебательного контура.

На какой-то частоте реактивное сопротивление катушки становится равным реактивному сопротивлению конденсатора и в цепи последовательного колебательного контура наступает такое явление, как резонанс.

При резонансе реактивные сопротивления катушки и конденсатора хоть и равны по модулю, но противоположны по знаку, поэтому они вычитается и в сумме дают ноль. В цепи остается только активное сопротивление потерь R.

При резонансе сила тока в цепи становится максимальной, так как сопротивление потерь катушки и конденсатора R в сумме дают малое значение.

При резонансе напряжение на катушке равняется напряжению на конденсаторе и превышает напряжение на генераторе.

Коэффициент, показывающий во сколько раз напряжение на катушке либо на конденсаторе превышает напряжение на генераторе, называется добротностью Q последовательного колебательного контура и показывает качественную оценку колебательного контура. В основном стараются сделать Q как можно больше.

На низких частотах колебательный контур имеет емкостную составляющую тока до резонанса, а после резонанса — индуктивную составляющую тока.

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания.

Электромагнитными колебаниями называют периодические взаимосвязанные изменения заряда, силы тока и напряжения.

Свободными колебаниями называют такие, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.

Вынужденными называются колебания в цепи под действием внешней периодической электродвижущей силы

Свободные электромагнитные колебания – это периодически повторяющиеся изменения электромагнитных величин (q – электрический заряд, I – сила тока, U – разность потенциалов), происходящие без потребления энергии от внешних источников. 

Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур или колебательный контур.

Колебательный контур – это система, состоящая из последовательно соединенных конденсатора емкости C, катушки индуктивности L и проводника с сопротивлением R 

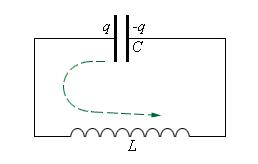
Рассмотрим закрытый колебательный контур, состоящий из индуктивности L и емкости С.

 

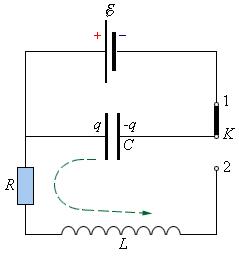
Чтобы возбудить колебания в этом контуре, необходимо сообщить конденсатору некоторый заряд от источника ε. Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер

 

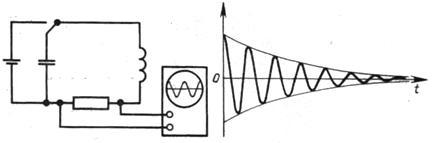
Свободные электромагнитные колебания можно наблюдать на экране осциллографа.

Как видно из графика колебаний, полученного на осцилографе, свободные электромагнитные колебания являются затухающими, т.е.их амплитуда уменьшается с течением времени. Это происходит потому, что часть электрической энергии на активном сопротивлении R превращается во внутреннюю энерги. проводника (проводник нагревается при прохождении по нему электрического тока).

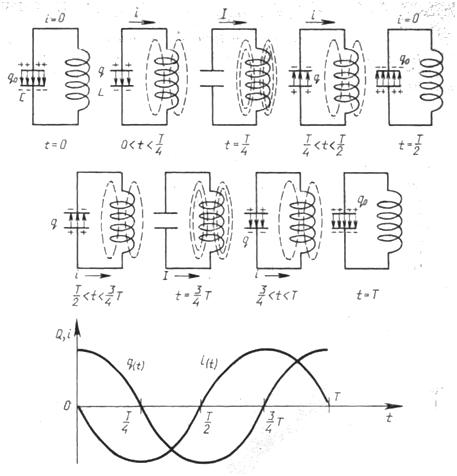
Рассмотрим, как происходят колебания в колебательном контуре и какие изменения энергии при этом происходят. Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0).

Если зарядить конденсатор до напряжения U₀ то в начальный момент времени t₁=0 на обкладках конденсатора установятся амплитудные значения напряжения U₀ и заряда q₀ = CU₀.

Полная энергия W системы равна энергии электрического поля W_эл:

Если цепь замыкают, то начинает течь ток. В контуре возникает э.д.с. самоиндукции

Вследствие самоиндукции в катушке конденсатор разряжается не мгновенно, а постепенно (так как, согламно правилу Ленца, возникающий индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Т.е. магнитное поле индукционного тока не дает мгновенно увеличиться магнитному потоку тока в контуре). При этом ток увеличивается постепенно, достигая своего максимального значения I₀ в момент времени t₂=T/4, а заряд на конденсаторе становится равным нулю.

По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля. Полная энергия контура после разрядки конденсатора равна энергии магнитного поля W_м:

В следующий момент времени ток течет в том же направлении, уменьшаясь до нуля, что вызывает перезарядку конденсатора. Ток не прекращается мгновенно после разрядки конденсатора вследствии самоиндукции (теперь магнитное поле индукционного тока не дает магнитному потоку тока в контуре мгновенно уменьшиться). В момент времени t₃=T/2 заряд конденсатора опять максимален и равен первоначальному заряду q = q₀, напряжение тоже равно первоначальному U = U₀, а ток в контуре равен нулю I = 0.

Затем конденсатор снова разряжается, ток через индуктивность течёт в обратном направлении. Через промежуток времени Т система приходит в исходное состояние. Завершается полное колебание, процесс повторяется.

График изменения заряда и силы тока при свободных электромагнитных колебаниях в контуре показывает, что колебания силы тока отстают от колебаний заряда на π/2.

В любой момент времени полная энергия:

При свободных колебаниях происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается постоянной.

Свободные электрические колебания аналогичны механическим колебаниям. На рисунке приведены графики изменения заряда q(t) конденсатора и смещения x(t) груза от положения равновесия, а также графики тока I(t) и скорости груза υ(t) за один период колебаний.

В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

q(t) = q₀cos(ωt + φ₀)

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний  и период колебаний  — формула Томпсона

Амплитуда q₀ и начальная фаза φ₀ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.

Для колебаний заряда, напряжения и силы тока получаются формулы:

Для конденсатора:

q(t) = q₀cosω₀t

U(t) = U₀cosω₀t

Для катушки индуктивности:

i(t) = I₀cos(ω₀t + π/2)

U(t) = U₀cos(ω₀t + π)

Вспомомним основные характеристики колебательного движения:

q_0, U₀, I₀ — амплитуда – модуль наибольшего значения колеблющейся величины

Т — период – минимальный промежуток времени через который процесс полностью повторяется

ν — Частота – число колебаний в единицу времени

ω — Циклическая частота – число колебаний за 2п секунд

φ — фаза колебаний — величина стоящая под знаком косинуса (синуса) и характеризующая состояние системы в любой момент времени.

Формула Томсона названа в честь английского физика Уильяма Томсона, который вывел её в 1853 году, и связывает период собственных электрических или электромагнитных колебаний в контуре с его ёмкостью и индуктивностью.^[1]

Формула Томсона выглядит следующим образом^[2]:

Она следует из связи периода и циклической частоты колебаний:

См. также

• Колебательный контур
• Уильям Томсон

Примечания

Для улучшения этой статьи по физике желательно: Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).