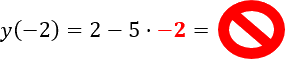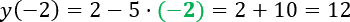Функции как по заданной функции найти остальные - Исправление недочетов и поиск решений вместе с Examum.ru

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».

После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание.
Функция задана формулой «y = 2x − 1»

Вычислить «y» при «x = 15»
Найти значение «x», при котором
значение «y» равно «−19».

Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.

Запись решения выглядит следующим образом.

y(15) = 2 · 15 − 1 = 30 − 1 = 29

Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.

То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .

−19 = 2x − 1

Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.

Запомните!

Не забывайте про правило переноса в уравнениях.

При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.

−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.

−2x = 18 | · (−1)
2x = −18

Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .

2x = −18 | (: 2)
x = −9

Как проверить верно ли равенство для функции

Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».

Верно ли равенство
«f(−2) = −18»?

Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.

Важно!

Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.

Не забывайте использовать
правило знаков.

Неправильно

Правильно

С помощью расчетов мы получили
«f(−2) = 12».

Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию «y = x² −5x + 6»

Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).

Для этой задачи нет необходимости, строить график заданной функции.

Запомните!

Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).

Если получится верное равенство, значит, точка принадлежит функции.

Вернемся к нашему заданию. Подставим в функцию «y = x² − 5x + 6»
координаты точки (1; 2).

Вместо «x» подставим «1».
Вместо «y» подставим «2».

2 = 1² − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)

У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x² − 5x + 6»?

Вместо «x» подставим «0».
Вместо «y» подставим «1».

1 = 0² − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)

В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x² − 5x + 6»

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.

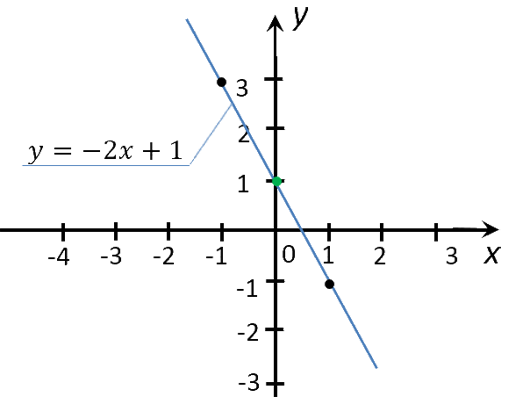
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.

Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.

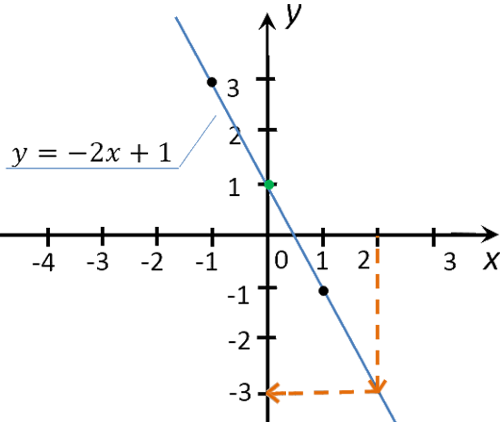
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».

Полученное значение «−3» на оси «Oy» и будет искомым значением «y».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».

Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.

y(2) = −2 · 2 + 1 = −4 + 1 = −3

При расчетах мы также получили y = −3.

Значит, мы правильно получили координаты с графика функции.

Важно!

Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.

При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Только подстановка значений в формулу функции дает точные результаты.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

11 ноября 2018 в 15:46

Веточка Сакуры
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Веточка Сакуры
Профиль
Благодарили: 0

Сообщений: 1

Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= — x² — 8x.Найдите значение фун. в т. минимума (y min).

0
Спасибо thanks
Ответить

12 ноября 2018 в 3:25
Ответ для Веточка Сакуры

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

y_min= y(4) = -16.

0
Спасибо thanks
Ответить

17 сентября 2018 в 13:28

Alesger Mammedov
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Alesger Mammedov
Профиль
Благодарили: 0

Сообщений: 1

Добрый день помогите пожалуйста с задачкой
f(x²-3x)=3x²+5x-4
f(3)=?

0
Спасибо thanks
Ответить

17 сентября 2018 в 23:01
Ответ для Alesger Mammedov

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

f(3) = 26 ± 7√21

0
Спасибо thanks
Ответить

13 ноября 2016 в 6:43

Роман Безбородов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Роман Безбородов
Профиль
Благодарили: 0

Сообщений: 1

определите вид графика

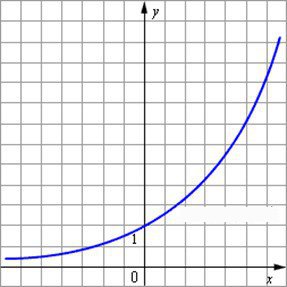
0
Спасибо thanks
Ответить

14 ноября 2016 в 17:30
Ответ для Роман Безбородов

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

y = a^x; a > 1.

0
Спасибо thanks
Ответить

7 сентября 2016 в 22:08

Иван Баранов
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Иван Баранов
Профиль
Благодарили: 0

Сообщений: 3

у=Х²+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10

0
Спасибо thanks
Ответить

8 сентября 2016 в 15:26
Ответ для Иван Баранов

Юлия Анарметова
(^-^)
Профиль
Благодарили: 0

Сообщений: 11

(^-^)
Юлия Анарметова
Профиль
Благодарили: 0

Сообщений: 11

аргумент это х значит у=(-2)²+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5

0
Спасибо thanks
Ответить

Источник

Мы знакомы с примерами функций и способами их задания. Рассмотрим понятия области определения и области значения функции, а также свойства функции.
1. Область определения и область значений функции
Найти область определения функции можно как по формуле, задающей функцию, так и по графику.

Определение:
Область определения функции — это допустимые значения независимой переменной (переменной x). Обозначается область определения функции D(f).

Чтобы лучше понять что такое область определения функции рассмотрим несколько примеров.
Если функция задана аналитически:

Найти область определения функции, если она задана формулой:

1) y=12x+7

2)f(x)=(5x-3)/(8x-16)

Функция задана формулой значит, для того чтобы найти ее область определения, нужно ответить на вопрос: «Какие значения можно подставлять в формулу вместо х?»
1) В формулу функции вместо х можно подставлять

любые

действительные числа. Значит область определения функции — любые действительные числа. Записывают следующим образом:

D(y)=(-ထ; +ထ)

2) Поскольку знаменатель функции не должен равняться нулю:

8x-16≠0

х≠2

Значит, D(y)=(-ထ; 2)U(2; +ထ)

Найти область определения функции если она задана графически еще проще, для этого необходимо обратить внимание на то, какие значения принимает «х» на графике. Попробуйте выполнить задание самостоятельно, а затем сравните с решением.

По графику видно что D(f)=[-7;7]

Далее рассмотрим понятие область значений функции

Определение:
Область значений функции — это множество всех действительных значений y, которые принимает функция. Обозначается область значений функции E(f).

Рассмотрим примеры на нахождение области определения если функция задана аналитически и графически.

Для того чтобы найти область значений функции необходимо ответить на вопрос: » какие значения может принимать у«

1) Если вместо х любое действительное число, то у, в данном случае, также может принимать любые значения, следовательно

E(y)=(-ထ; +ထ)

2) Так как, при подстановке любого действительного числа вместо х, функция (у) из-за модуля будет принимать только неотрицательные значения, то

E(y)=[0; +ထ)

Для нахождения области значений функции, если она задана графически необходимо обратить внимание на то, какие значения принимает «у» на графике. Попробуйте выполнить задание самостоятельно, а затем сравните с решением.

По графику видно что E(f)=[-7;7]

2. Нули функции

Нули функции можно найти как по формуле, задающей функцию, так и по графику.

Определение:
Нули функции– это значение аргумента, при которых функция обращается в ноль.

Если необходимо найти нули функции по графику, то нужно определить точки пересечения графика с осью ОХ:

На данном примере график функции пересекает ось ОХ при х=-4; х=5,5 и х=8. Эти точки пересечения выделены красным цветом.
Обратите внимание!:

Существуют функции, которые не будут иметь точек пересечения с осью ОХ, следовательно нулей у такой функции нет

Для того чтобы найти нули функции заданной аналитически нужно:

Прировнять «у» к нулю
Решить получившееся уравнение

а. y=-11х+22
б. y=(х+76)(х-95)

а. y=-11х+22
1) у=0
т.е:

-11х+22=0

2) Решим получившееся уравнение

-11х+22=0

-11х=-22

х=2

Ответ: 2
б. y=(х+76)(х-95)
1) у=0
получим:

(х+76)(х-95)=0

2) Решим уравнение

(х+76)(х-95)=0

х+76=0 или х-95=0

х=-76 х=95

Ответ: -76; 95

3. Промежутки знакопостоянства

Промежутки знакопостоянства функции также можно определить как по формуле, задающей функцию, так и по графику.

Определение:
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

Если необходимо найти промежутки знакопостоянства у функции заданной графически, то достаточно определить по графику где функция принимает положительные и отрицательные значения. Для примера возьмем график функции для которой мы находили нули функции :

На рисунке синим цветом выделены части графика в промежутках [-8; -4) U (-4; 5,5) U (8;9] , которые расположены выше оси ОХ. Зеленым цветом выделены части графика в промежутке (5,5 ; который расположен выше оси х.
Значит, что в промежутках [-8; -4) U (-4; 5,5) U (8;9] функция принимает положительные значения, а в промежутке (5,5 ; она принимает отрицательные значения. Это и есть промежутки знакопостоянства.

Что делать если функция задана аналитически?
Чтобы определить знаки постоянства достаточно понимать как решаются неравенства и запомнить алгоритм:

Рассматриваем случай когда у>0
Решаем получившееся неравенство, полученный промежуток показывает при каких «х» функция положительна
Аналогично рассматриваем случай у<0
Решаем неравенство, полученный промежуток показывает при каких «х» функция отрицательна

Рассмотрите пример с решением или попробуйте выполнить задание самостоятельно с помощью алгоритма описанного выше:

а. y=-11х+22
1) y>0
Следовательно

-11х+22>0

-11(x+2)>0

x+2<0

x<-2

3) y<0
Следовательно

-11х+22<0

-11(x+2)<0

x+2>0

x>2

Ответ: Функция положительна (у>0) при х∈ (-∞;-2)

Функция отрицательна (у<0) при х∈ (-2;+∞)

б. y=|x+14|
1) y>0
Следовательно

|x+14|>0

2) |x+14|>0

Неравенство верно при любых «х» кроме х=-14

3) y<0
Следовательно

|x+14|<0

4) |x+14|<0

Неравенство неверно при любых «х»

Ответ: Функция положительна (у>0) при х∈ (-∞;-14) U (-14;+∞)

Функция не принимает отрицательных значений

4. Монотонность

В курсе средней школы монотонность функции будем определять исключительно по ее графическому заданию, но в старших классах промежутки возрастания и убывания можно определить и аналитически с помощью производной

Определение:
Функцию у=f(x) называют возрастающей на промежутке, если для любых двух точек x1 и x2 промежутка, таких, что x1 < x2, выполняется неравенство f(x1) < f(x2)

Функцию у=f(x) называют убывающей на промежутке, если для любых двух точек x1 и x2 промежутка, таких, что x1 < x2, выполняется неравенство f(x1) > f(x2)

Иными словами формальное определение можно интерпретировать следующим образом:
Функция называется возрастающей на промежутке если график визуально «идет наверх», аналогично функция называется убывающей если график визуально «идет вниз».
В качестве примера найдем промежутки монотонности графика функции, рассматриваемого выше:

На рисунке голубым цветом выделены части графика в промежутках (-4; 1) U (7;9) на которых график функции возрастает. Розовым цветом выделены части графика в промежутке (-8 ; 4) U (1;7) на которых график функции убывает. Это и есть промежутки монотонности исходной функции.

5. Четность и нечетность

Исследовать функцию на четность и нечетность можно как аналитически так и графически. Рассмотрим определения четной и нечетной функции, а также алгоритмы для ее проверки.

Определение:
Функцию у=f(x) называют четной, если для любого значения «х» выполняется равенство f(-x)=f(x)
Функцию у=f(x) называют нечетной, если для любого значения «х» выполняется равенство f(-x)=-f(x)

Важно!

Существуют четные функции, нечетные функции, а также функции которые не являются ни четными, ни нечетными.

Не существует функций которые одновременно являются четными и нечетными

Если функция y=f(x) задана аналитически, то для ее исследования на четность и нечетность применим следующий алгоритм:

Записать выражение y=f(-x). Для этого необходимо в формуле задания функции заменить «х» на «-х»;
Сопоставить выражения f(-x) и f(x):

Если f(-x) = f(x), то функция является четной;
Если f(-x) = -f(x), то функция является нечетной;
Если ни первое, ни второе условие не выполняется то функция не является ни четной, ни нечетной.

Рассмотрим пример:

а. y=-11х+22

1) f(-x)= -11·(-x)+22=11х+22
2) Сравним f(x) и f(-x)
-11х+22 ≠ 11х+22, то есть f(-x) ≠ f(x)
-11х+22 ≠ -(-11х-22), то есть f(-x) ≠ -f(x)
Значит, функция не является четной и не является нечетной

б. y=|x|

1) f(-x)=|-x|
2) Сравним f(x) и f(-x)
|x|=|-x|, то есть f(-x) = f(x)
Значит функция является четной

Если функция y=f(x) задана графически, то для ее исследования на четность и нечетность будем применять следующие правила:

Четная и нечетная функция y=f(x) имеет симметричную область определения D(f)

Если график функции y=f(x) симметричен относительно оси ординат, то y=f(x) — четная функция
Например:

Если график функции y=f(x) симметричен относительно начала координат, то y=f(x) — четная функция
Например:

На этом рассмотрение свойств функций закончено. Помимо тех свойств, которые разобраны в данном разделе существуют и другие, такие как ограниченность и неограниченность функции, периодичность функции и так далее, которые в курсе алгебры 7-9 класса не рассматриваются.

Источник

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a<0), то ветви параболы направлены вниз.

— Если (a>1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

— Аналогично с (a<-1), только график вытянут вниз.

— Если (a∈(0;1)), то график сжат в (a) раз (по сравнению с «базовым» графиком с (a=1)). Вершина при этом остается на месте.

— Аналогично (a∈(-1;0)), только ветви направлены вниз.
Парабола пересекает ось y в точке (c).
(b) напрямую по графику не видно, но его можно посчитать с помощью (x_в) — абсциссы (икса) вершины параболы:

(x_в=-frac{b}{2a})
(b=-x_вcdot 2a)

Пример (ЕГЭ):

Решение:
Во-первых, надо разобраться, где тут (f(x)), а где (g(x)). По коэффициенту (c) видно, что (f(x)) это функция, которая лежит ниже – именно она пересекает ось игрек в точке (4).

Значит нужно найти коэффициенты у параболы, которая лежит повыше.
Коэффициент (c) у неё равен (1).
Ветви параболы направлены вниз – значит (a<0). При этом форма этой параболы стандартная, базовая, значит (a=-1).

Найдем (b). (x_в=-2), (a=-1).

(x_в=-frac{b}{2a})
(-2=-frac{b}{-2})
(b=-4)

Получается (g(x)=-x^2-4x+1). Теперь найдем в каких точках функции пересекаются:

(-x^2-4x+1=-2x^2-2x+4)
(-x^2-4x+1+2x^2+2x-4=0)
(x^2-2x-3=0)
(D=4+4cdot 3=16=4^2)
(x_1=frac{2-4}{2}=-1); (x_2=frac{2+4}{2}=3).

Ответ: (3).

2 способ – находим формулу по точкам

Это самый надежный способ, потому что его можно применить практически в любой ситуации, но и самый не интересный, потому что думать тут особо не надо, только уметь решать системы линейных уравнений. Алгоритм прост:

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Пример: (A(-4;5)), (B(-5;5)), (C(-6;3)).

(begin{cases}5=a(-4)^2+b(-4)+c\5=a(-5)^2+b(-5)+c\3=a(-6)^2+b(-6)+c end{cases})
Решаем систему.
Пример:

(begin{cases}5=16a-4b+c\5=25a-5b+c\3=36a-6b+c end{cases})

Вычтем из второго уравнения первое:

(0=9a-b)
(b=9a)

Подставим (9a) вместо (b):

(begin{cases}5=16a-36a+c\5=25a-45a+c\3=36a-54a+c end{cases})
(begin{cases}5=-20a+c\5=-20a+c\3=-18a+c end{cases})

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

(2=-2a)
(a=-1)

Найдем (b):

(b=-9)

Подставим в первое уравнение (a):

(5=20+c)
(c=-15).

Получается квадратичная функция: (y=-x^2-9x-15).

Пример (ЕГЭ):

Решение:

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

(begin{cases}8=a(-1)^2+b(-1)+4\2=a+b+4 end{cases})

(begin{cases}8=a-b+4\2=a+b+4 end{cases})

(begin{cases}4=a-b\-2=a+b end{cases})

Сложим 2 уравнения:

(2=2a)
(a=1)

Подставим во второе уравнение:

(-2=1+b)
(b=-3)

Получается:

(g(x)=x^2-3x+4)

Теперь найдем точки пересечения двух функций:

(-3x+13=x^2-3x+4)
(x^2-9=0)
(x=±3)

Теперь можно найти ординату второй точки пересечения:

(f(-3)=-3cdot (-3)+13)
(f(-3)=9+13)
(f(-3)=22)

Ответ: (22).

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

(y=x^2-10x+25-4)
(y=x^2-10x+21)

Готово.

Пример (ЕГЭ):

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
Получается (y=-2(x^2-4x+4)+4=)(-2x^2+8x-8+4=-2x^2+8x-4).
(f(6)=-2cdot 6^2+8cdot 6-4=-72+48-4=-28)

Смотрите также:
Как найти k и b по графику линейной функции?

Источник

Как найти значение функции по значению аргумента

Как найти значение функции по значению аргумента? Это можно сделать с помощью формулы, задающей функцию.

Если функция задана формулой y=f(x), чтобы найти значение функции по данному значению аргумента, надо в формулу функции вместо каждого икса подставить это значение и вычислить значение y.

Пример.

1) Линейная функция задана формулой y=10x-7.

Найти значение функции, соответствующее значению аргумента, равному 3; -2,5; 1,4; 0.

Решение:

При x=3

$[y = 2 cdot {10^3} + 5 cdot {10^2} - 1 = ]$

при x=-2,5

при x=1,4

при x=0

2) Функция задана формулой

$[y = 2{x^3} + 5{x^2} - 1.]$

Найти значение функции при x, равном 10; -2; 1; 0.

Решение:

При x=10

$[y = 2 cdot {10^3} + 5 cdot {10^2} - 1 = ]$

при x=-2

$[y = 2 cdot {( - 2)^3} + 5 cdot {( - 2)^2} - 1 = ]$

при x=1

$[y = 2 cdot {1^3} + 5 cdot {1^2} - 1 = 2 cdot 1 + 5 cdot 1 - 1 = 6;]$

при x=0

$[y = 2 cdot {0^3} + 5 cdot {0^2} - 1 = ]$

Значение функции по данному значению аргумента можно найти также по графику. Как это сделать, мы рассмотрим в следующий раз.

Источник

Как найти функцию по ее графику

Еще в школе мы подробно изучаем функции и строим их графики. Однако читать график функции и находить ее вид по готовому чертежу, нас, к сожалению, практически не учат. На самом деле, это совсем не сложно, если помнить несколько основных видов функций.Задача описания свойств функции по ее графику часто возникает при экспериментальных исследованиях. По графику можно определить промежутки возрастания и убывания функции, разрывы и экстремумы, а также можно видеть асимптоты.

Инструкция

Если графиком является прямая линия, проходящая через начало координат и образующая с осью ОX угол α (угол наклона прямой к положительной полуоси ОХ). Функция, описывающая эту прямую, будет иметь вид y = kx. Коэффициент пропорциональности k равен tg α. Если прямая проходит через 2-ю и 4-ю координатные четверти, то k < 0, и функция является убывающей, если через 1-ю и 3-ю, то k > 0 и функция возрастает.Пусть график представляет собой прямую линию, располагающуюся различным образом относительно осей координат. Это линейная функция, и она имеет вид y = kx + b, где переменные x и y стоят в первой степени, а k и b могут принимать как положительные, так и отрицательные значения или равны нулю. Прямая параллельна прямой y = kx и отсекает на оси ординат |b| единиц. Если прямая параллельна оси абсцисс, то k = 0, если оси ординат, то уравнение имеет вид x = const.

Кривая, состоящая из двух ветвей, располагающихся в разных четвертях и симметричных относительно начала координат, называется гиперболой. Этот график выражает обратную зависимость переменной y от x и описывается уравнением y = k/x. Здесь k ≠ 0 — коэффициент обратной пропорциональности. При этом если k > 0, функция убывает; если же k < 0 — функция возрастает. Таким образом, областью определения функции является вся числовая прямая, кроме x = 0. Ветви гиперболы приближаются к осям координат как к своим асимптотам. С уменьшением |k| ветки гиперболы все больше «вдавливаются» в координатные углы.

Квадратичная функция имеет вид y = ax2 + bx + с, где a, b и c – величины постоянные и a  0. При выполнении условия b = с = 0, уравнение функции выглядит, как y = ax2 (простейший случай квадратичной функции), а ее график является параболой, проходящей через начало координат. График функции y = ax2 + bx + с имеет ту же форму, что и простейший случай функции, однако ее вершина (точка пересечения параболы с осью OY) лежит не в начале координат.

Параболой является также график степенной функции, выраженной уравнением y = xⁿ, если n – любое четное число. Если n — любое нечетное число, график такой степенной функции будет иметь вид кубической параболы.
В случае, если n – любое отрицательное число, уравнение функции приобретает вид. Графиком функции при нечетном n будет гипербола, а при четном n их ветви будут симметричны относительно оси ОУ.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник