Гамма функция как найти - Исправление недочетов и поиск решений вместе с Examum.ru

Гамма-функция и ее свойства

Содержание

Обнаружили ошибку?
Выделите ее мышью
и нажмите

Введение

Гамма функция находит
очень широкое применение в прикладном анализе. С гамма-функцией
связаны функции Бесселя используемые при синтезе фильтров и
спектральном анализе, а также другие специальные функции:
бета-функция, К-функции, G-функции. В
статистике широко используется гамма-распределение, частными случаями
которого являются экспоненциальное распределение и распределение
хи-квадрат. В данной статье введено понятие гамма-функции, приведены
ее основные свойства, а также показан алгоритм ее численного
расчета.

Определение гамма-функции

В математике вводится
понятие факториала для натурального числа:

(1)

При этом можно заметить,
что

(2)

Гамма-функция
,
распространяет понятие факториала на дробные, отрицательные и даже
комплексные значения аргумента
.
Гамма функция не выражается через элементарные функции, но может быть
представлена как интеграл вида:

(3)

Для натуральных значений
аргумента гамма функция совпадает со значением факториала:

(4)

При этом для любых
комплексных значений

справедливо равенство:

(5)

Данное рекуррентное
соотношение является очень важным и используется при расчете
гамма-функции. Приведем также формулу дополнения:

(6)

Можно заметить, что при
отрицательных значениях
,
,
при этом гамма-функция для отрицательного аргумента может быть
вычислена по формуле:

(7)

Необходимо
отметить, что при целых
,

и гамма-функция претерпевает разрыв. График гамма-функции для
вещественного аргумента представлен на рисунке 1.

Рисунок 1: График гамма-функции вещественного аргумента

Некоторые значения гамма-функции

Рассмотрим
некоторые значения гамма-функции. Из выражения (4)
следует, что:

(8)

Рассмотрим
,
для этого воспользуемся выражением (6):

(9)

Рассмотрим

,
для этого воспользуемся выражением (5):

(10)

Рассмотрим

,
для этого воспользуемся выражением (7):

(11)

Расчет гамма-функции

Теперь рассмотрим очень
важный вопрос, касающийся расчета гамма-функции. Для этого
рассмотрим несколько возможных интервалов аргумента
.

Пусть
,
тогда в соответствии с (5) можно вычислить:

(12)

где
,
другими словами значение гамма функции при

может быть вычилено через значения гамма функции при
.

Пусть
,
тогда можно снова воспользоваться выражением (5), которое можно
переписать к виду:

(13)

При этом
,
и если продолжать, то можно свести к вычислению гамма-функции в
интервале
.

Рассмотрим на примере:

(14)

То есть опять свели к
вычислению гамма-функции в интервале
.

Пусть теперь
,
тогда при вычислении по формуле (7)

можно рекуррентно вычислять путем сведения к гамма-функции в
интервале
.

Теперь для вычисления
гамма-функции необходимо получить алгоритм ее расчета при
.
На практике для этого производят аппроксимацию гамма функции на
данном интервале в виде:

(15)

где

и

— полиномы 8 степени:

(16)

Коэффициенты полиномов
аппроксимации подобраны так, чтобы обеспечивать наименьшую ошибку
аппроксимации. Значения коэффициентов полиномов приведены в таблице:

1	2	3	4	5	6	7	8
6.65e+4	-3.61e+4	-3.14e+4	866.97	629.33	-379.8	24.77	-1.716
-1.15e+5	-1.35e+5	4.76e+3	2.25e+4	-3107.8	-1015.2	315.35	-30.84

Таким образом, используя
полиномиальную аппроксимацию и рекуррентные соотношения можно
вычислить значения гамма-функции для любого вещественного аргумента.
Программная реализация функции расчета гамма-функции на C
приведена ниже.

При численном расчете гамма-функции необходимо соблюдать
осторожность, так как скорость роста гамма-функции как у факториала и при 32 битной разрядности
процессора вычислять гамма-функцию без переполнения разрядности можно только для аргумента меньшего 170.
Например, значение гамма-функции для аргумента 50 равно 6e+62.

Выводы

Таким образом в данной статье мы ввели понятие гамма-функции, рассмотрели ее свойства и привели алгоритм численного расчета гамма-функции на основе
полиномиальной аппроксимации. В конце приведен пример программной реализации гамма-функции

Программная реализациия гамма-функции

Следующая программа использует рекуррентные соотношения для расчета гамма-функции.

gamma_ex.c


#include <stdio.h>
#include <stdlib.h>
#define _USE_MATH_DEFINES
#include <math.h>


//***************************************************
// аппроксимация гамма-функции в интервале от 1 до 2
// отношением полиномов 8 степени
double gammaapprox(double x)
{
  double p[]={-1.71618513886549492533811e+0,
               2.47656508055759199108314e+1,
              -3.79804256470945635097577e+2,
               6.29331155312818442661052e+2,
               8.66966202790413211295064e+2,
              -3.14512729688483675254357e+4,
              -3.61444134186911729807069e+4,
               6.64561438202405440627855e+4};

  double q[]={-3.08402300119738975254353e+1,
                3.15350626979604161529144e+2,
               -1.01515636749021914166146e+3,
               -3.10777167157231109440444e+3,
                2.25381184209801510330112e+4,
                4.75584627752788110767815e+3,
               -1.34659959864969306392456e+5,
               -1.15132259675553483497211e+5};
  double z = x - 1.0;
  double a = 0.0;
  double b = 1.0;
  int i;
  for(i = 0; i < 8; i++)
  { 
    a =(a + p[i]) * z;
    b = b * z + q[i];
  }
  return (a / b + 1.0);
}


//***************************************************
// Гамма-функция вещественного агрумента
// возвращает значение гамма-функции аргумента z
double gamma(double z)
{
  
  // рекурентное соотношение для 0
  if((z>0.0)&&(z<1.0))   
    return gamma(z+1.0)/z;   
  
  // рекурентное соотношение для z>2
  if(z>2)
    return (z-1)*gamma(z-1); 

  // рекурентное соотношение для z<=0
  if(z<=0)
    return M_PI/(sin(M_PI*z)*gamma(1-z));

  // 1<=z<=2 использовать аппроксимацию
  return gammaapprox(z); 
}


//***************************************************
// Основная программа для рассчета значения 
// гамма-функции вещественного аргумента
int main(){
  float z = 12.0;
  double g = gamma((double)z);
  printf("gamma(%.2f) = %en", z,g);
  return 0;
}

Последнее изменение страницы: 12.05.2022 (19:43:02)

Страница создана Latex to HTML translator ver. 5.20.11.14

Источник

For the gamma function of ordinals, see Veblen function. For the gamma distribution in statistics, see Gamma distribution. For the function used in video and image color representations, see Gamma correction.

Gamma
The gamma function along part of the real axis
General information
General definition	${displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}e^{-t},dt}$
Fields of application	Calculus, mathematical analysis, statistics, physics

In mathematics, the gamma function (represented by Γ, the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,

Derived by Daniel Bernoulli, for complex numbers with a positive real part, the gamma function is defined via a convergent improper integral:

${displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}e^{-t},dt, qquad Re (z)>0,.}$

The gamma function then is defined as the analytic continuation of this integral function to a meromorphic function that is holomorphic in the whole complex plane except zero and the negative integers, where the function has simple poles.

The gamma function has no zeros, so the reciprocal gamma function 1/Γ(z) is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential function:

${displaystyle Gamma (z)={mathcal {M}}{e^{-x}}(z),.}$

Other extensions of the factorial function do exist, but the gamma function is the most popular and useful. It is a component in various probability-distribution functions, and as such it is applicable in the fields of probability and statistics, as well as combinatorics.

Motivation[edit]

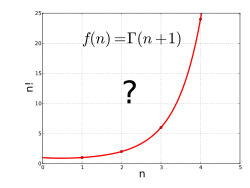
The gamma function interpolates the factorial function to non-integer values.

The gamma function can be seen as a solution to the following interpolation problem:

«Find a smooth curve that connects the points (x, y) given by y = (x − 1)! at the positive integer values for x.»

A plot of the first few factorials suggests that such a curve can be drawn, but it would be preferable to have a formula that precisely describes the curve, in which the number of operations does not depend on the size of x. The simple formula for the factorial, x! = 1 × 2 × ⋯ × x, cannot be used directly for non-integer values of x since it is only valid when x is a natural number (or positive integer). There are, relatively speaking, no such simple solutions for factorials; no finite combination of sums, products, powers, exponential functions, or logarithms will suffice to express x!; but it is possible to find a general formula for factorials using tools such as integrals and limits from calculus. A good solution to this is the gamma function.^[1]

There are infinitely many continuous extensions of the factorial to non-integers: infinitely many curves can be drawn through any set of isolated points. The gamma function is the most useful solution in practice, being analytic (except at the non-positive integers), and it can be defined in several equivalent ways. However, it is not the only analytic function that extends the factorial, as adding to it any analytic function that is zero on the positive integers, such as k sin mπx for an integer m, will give another function with that property.^[1] Such a function is known as a pseudogamma function, the most famous being the Hadamard function.^[2]

The gamma function, Γ(z) in blue, plotted along with Γ(z) + sin(πz) in green. Notice the intersection at positive integers. Both are valid analytic continuations of the factorials to the non-integers.

A more restrictive property than satisfying the above interpolation is to satisfy the recurrence relation defining a translated version of the factorial function,^[3]^[4]

for any positive real number x. But this would allow for multiplication by any function g(x) satisfying both g(x) = g(x+1) for all real numbers x and g(0) = 1, such as the function g(x) = e^{k sin 2mπx}. One of several ways to resolve the ambiguity comes from the Bohr–Mollerup theorem. It states that when the condition that f be logarithmically convex (or «super-convex»,^[5] meaning that is convex) is added, it uniquely determines f for positive, real inputs. From there, the gamma function can be extended to all real and complex values (except the negative integers and zero) by using the unique analytic continuation of f.^[6]

Definition[edit]

Main definition[edit]

The notation is due to Legendre.^[1] If the real part of the complex number z is strictly positive (), then the integral

${displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}e^{-t},dt}$

converges absolutely, and is known as the Euler integral of the second kind. (Euler’s integral of the first kind is the beta function.^[1]) Using integration by parts, one sees that:

Plot of the absolute value of the gamma function in complex plane in 3D with color and legend and 1000 plot points created with Mathematica

${displaystyle {begin{aligned}Gamma (z+1)&=int _{0}^{infty }t^{z}e^{-t},dt\&={Bigl [}-t^{z}e^{-t}{Bigr ]}_{0}^{infty }+int _{0}^{infty }zt^{z-1}e^{-t},dt\&=lim _{tto infty }left(-t^{z}e^{-t}right)-left(-0^{z}e^{-0}right)+zint _{0}^{infty }t^{z-1}e^{-t},dt.end{aligned}}}$

Recognizing that ${displaystyle -t^{z}e^{-t}to 0}$ as

${displaystyle {begin{aligned}Gamma (z+1)&=zint _{0}^{infty }t^{z-1}e^{-t},dt\&=zGamma (z).end{aligned}}}$

We can calculate :

${displaystyle {begin{aligned}Gamma (1)&=int _{0}^{infty }t^{1-1}e^{-t},dt\&=int _{0}^{infty }e^{-t},dt\&=1.end{aligned}}}$

Thus we can show that for any positive integer n by induction. Specifically, the base case is that , and the induction step is that .

The identity ${textstyle Gamma (z)={frac {Gamma (z+1)}{z}}}$ can be used (or, yielding the same result, analytic continuation can be used) to uniquely extend the integral formulation for to a meromorphic function defined for all complex numbers z, except integers less than or equal to zero.^[1] It is this extended version that is commonly referred to as the gamma function.^[1]

Alternative definitions[edit]

There are many equivalent definitions.

Euler’s definition as an infinite product[edit]

For a fixed integer , as the integer increases, we have that ^[7]

${displaystyle lim _{nto infty }{frac {n!,left(n+1right)^{m}}{(n+m)!}}=1,.}$

If is not an integer then it is not possible to say whether this equation is true because we have not yet (in this section) defined the factorial function for non-integers. However, we do get a unique extension of the factorial function to the non-integers by insisting that this equation continue to hold when the arbitrary integer is replaced by an arbitrary complex number ,

${displaystyle lim _{nto infty }{frac {n!,left(n+1right)^{z}}{(n+z)!}}=1,.}$

Multiplying both sides by gives

${displaystyle {begin{aligned}Gamma (z)&=(z-1)!\[8pt]&={frac {1}{z}}lim _{nto infty }n!{frac {z!}{(n+z)!}}(n+1)^{z}\[8pt]&={frac {1}{z}}lim _{nto infty }(1cdots n){frac {1}{(1+z)cdots (n+z)}}left({frac {2}{1}}cdot {frac {3}{2}}cdots {frac {n+1}{n}}right)^{z}\[8pt]&={frac {1}{z}}prod _{n=1}^{infty }left[{frac {1}{1+{frac {z}{n}}}}left(1+{frac {1}{n}}right)^{z}right].end{aligned}}}$

This infinite product, which is due to Euler,^[8] converges for all complex numbers except the non-positive integers, which fail because of a division by zero. Intuitively, this formula indicates that is approximately the result of computing for some large integer , multiplying by ${displaystyle (n+1)^{z}}$ to approximate , and using the relationship backwards n+1 times to get an approximation for ; and furthermore that this approximation becomes exact as increases to infinity.

Weierstrass’s definition[edit]

The definition for the gamma function due to Weierstrass is also valid for all complex numbers z except the non-positive integers:

${displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{n=1}^{infty }left(1+{frac {z}{n}}right)^{-1}e^{z/n},}$

where is the Euler–Mascheroni constant.^[1] This is the Hadamard product of in a rewritten form.

Proof of equivalence of the three definitions
Equivalence of the integral definition and Weierstrass definition By the integral definition, the relation and Hadamard factorization theorem, ${displaystyle {frac {1}{Gamma (z)}}=ze^{c_{1}z+c_{2}}prod _{n=1}^{infty }e^{-{frac {z}{n}}}left(1+{frac {z}{n}}right),quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}}$ for some constants ${displaystyle c_{1},c_{2}}$ since is an entire function of order . Since as , ${displaystyle c_{2}=0}$ (or an integer multiple of ) and since , ${displaystyle {begin{aligned}e^{-c_{1}}&=prod _{n=1}^{infty }e^{-{frac {1}{n}}}left(1+{frac {1}{n}}right)\&=exp left(lim _{Nto infty }sum _{n=1}^{N}left(log left(1+{frac {1}{n}}right)-{frac {1}{n}}right)right)\&=exp left(lim _{Nto infty }left(log(N+1)-sum _{n=1}^{N}{frac {1}{n}}right)right)\&=exp left(lim _{Nto infty }left(log N+log left(1+{frac {1}{N}}right)-sum _{n=1}^{N}{frac {1}{n}}right)right)\&=exp left(lim _{Nto infty }left(log N-sum _{n=1}^{N}{frac {1}{n}}right)right)\&=e^{-gamma }.end{aligned}}}$ Whence ${displaystyle c_{1}=gamma +2pi ik}$ for some integer . Since for ${displaystyle zin mathbb {R} setminus mathbb {Z} _{0}^{-}}$ , we have and ${displaystyle {frac {1}{Gamma (z)}}=ze^{gamma z}prod _{n=1}^{infty }e^{-{frac {z}{n}}}left(1+{frac {z}{n}}right),quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}.}$ Equivalence of the Weierstrass definition and Euler definition ${displaystyle {begin{aligned}Gamma (z)&={frac {e^{-gamma z}}{z}}prod _{n=1}^{infty }left(1+{frac {z}{n}}right)^{-1}e^{z/n}\&={frac {1}{z}}lim _{nto infty }e^{zleft(ln n-1-{frac {1}{2}}-{frac {1}{3}}-cdots -{frac {1}{n}}right)}{frac {e^{zleft(1+{frac {1}{2}}+{frac {1}{3}}+cdots +{frac {1}{n}}right)}}{left(1+zright)left(1+{frac {z}{2}}right)cdots left(1+{frac {z}{n}}right)}}\&={frac {1}{z}}lim _{nto infty }{frac {1}{left(1+zright)left(1+{frac {z}{2}}right)cdots left(1+{frac {z}{n}}right)}}e^{zln left(nright)}\&=lim _{nto infty }{frac {n!n^{z}}{z(z+1)cdots (z+n)}},quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}end{aligned}}}$ Let ${displaystyle Gamma _{n}(z)={frac {n!n^{z}}{z(z+1)cdots (z+n)}}}$ and ${displaystyle G_{n}(z)={frac {(n-1)!n^{z}}{z(z+1)cdots (z+n-1)}}.}$ Then ${displaystyle Gamma _{n}(z)={frac {n}{z+n}}G_{n}(z)}$ and ${displaystyle lim _{nto infty }G_{n+1}(z)=lim _{nto infty }G_{n}(z)=lim _{nto infty }Gamma _{n}(z)=Gamma (z),}$ therefore ${displaystyle Gamma (z)=lim _{nto infty }{frac {n!(n+1)^{z}}{z(z+1)cdots (z+n)}},quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}.}$ Then ${displaystyle {frac {n!(n+1)^{z}}{z(z+1)cdots (z+n)}}={frac {(2/1)^{z}(3/2)^{z}(4/3)^{z}cdots ((n+1)/n)^{z}}{z(1+z)(1+z/2)(1+z/3)cdots (1+z/n)}}={frac {1}{z}}prod _{k=1}^{n}{frac {(1+1/k)^{z}}{1+z/k}},quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}}$ and taking gives the desired result.

Proof of equivalence of the three definitions

Equivalence of the integral definition and Weierstrass definition

By the integral definition, the relation and Hadamard factorization theorem,

${displaystyle {frac {1}{Gamma (z)}}=ze^{c_{1}z+c_{2}}prod _{n=1}^{infty }e^{-{frac {z}{n}}}left(1+{frac {z}{n}}right),quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}}$

for some constants ${displaystyle c_{1},c_{2}}$ since is an entire function of order . Since as , ${displaystyle c_{2}=0}$ (or an integer multiple of 2pi i ) and since ,

${displaystyle {begin{aligned}e^{-c_{1}}&=prod _{n=1}^{infty }e^{-{frac {1}{n}}}left(1+{frac {1}{n}}right)\&=exp left(lim _{Nto infty }sum _{n=1}^{N}left(log left(1+{frac {1}{n}}right)-{frac {1}{n}}right)right)\&=exp left(lim _{Nto infty }left(log(N+1)-sum _{n=1}^{N}{frac {1}{n}}right)right)\&=exp left(lim _{Nto infty }left(log N+log left(1+{frac {1}{N}}right)-sum _{n=1}^{N}{frac {1}{n}}right)right)\&=exp left(lim _{Nto infty }left(log N-sum _{n=1}^{N}{frac {1}{n}}right)right)\&=e^{-gamma }.end{aligned}}}$

Whence ${displaystyle c_{1}=gamma +2pi ik}$ for some integer . Since for ${displaystyle zin mathbb {R} setminus mathbb {Z} _{0}^{-}}$ , we have k=0 and

${displaystyle {frac {1}{Gamma (z)}}=ze^{gamma z}prod _{n=1}^{infty }e^{-{frac {z}{n}}}left(1+{frac {z}{n}}right),quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}.}$

Equivalence of the Weierstrass definition and Euler definition

${displaystyle {begin{aligned}Gamma (z)&={frac {e^{-gamma z}}{z}}prod _{n=1}^{infty }left(1+{frac {z}{n}}right)^{-1}e^{z/n}\&={frac {1}{z}}lim _{nto infty }e^{zleft(ln n-1-{frac {1}{2}}-{frac {1}{3}}-cdots -{frac {1}{n}}right)}{frac {e^{zleft(1+{frac {1}{2}}+{frac {1}{3}}+cdots +{frac {1}{n}}right)}}{left(1+zright)left(1+{frac {z}{2}}right)cdots left(1+{frac {z}{n}}right)}}\&={frac {1}{z}}lim _{nto infty }{frac {1}{left(1+zright)left(1+{frac {z}{2}}right)cdots left(1+{frac {z}{n}}right)}}e^{zln left(nright)}\&=lim _{nto infty }{frac {n!n^{z}}{z(z+1)cdots (z+n)}},quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}end{aligned}}}$

Let

${displaystyle Gamma _{n}(z)={frac {n!n^{z}}{z(z+1)cdots (z+n)}}}$

and

${displaystyle G_{n}(z)={frac {(n-1)!n^{z}}{z(z+1)cdots (z+n-1)}}.}$

Then

${displaystyle Gamma _{n}(z)={frac {n}{z+n}}G_{n}(z)}$

and

${displaystyle lim _{nto infty }G_{n+1}(z)=lim _{nto infty }G_{n}(z)=lim _{nto infty }Gamma _{n}(z)=Gamma (z),}$

therefore

${displaystyle Gamma (z)=lim _{nto infty }{frac {n!(n+1)^{z}}{z(z+1)cdots (z+n)}},quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}.}$

Then

${displaystyle {frac {n!(n+1)^{z}}{z(z+1)cdots (z+n)}}={frac {(2/1)^{z}(3/2)^{z}(4/3)^{z}cdots ((n+1)/n)^{z}}{z(1+z)(1+z/2)(1+z/3)cdots (1+z/n)}}={frac {1}{z}}prod _{k=1}^{n}{frac {(1+1/k)^{z}}{1+z/k}},quad zin mathbb {C} setminus mathbb {Z} _{0}^{-}}$

and taking gives the desired result.

Properties[edit]

General[edit]

Other important functional equations for the gamma function are Euler’s reflection formula

${displaystyle Gamma (1-z)Gamma (z)={frac {pi }{sin pi z}},qquad znot in mathbb {Z} }$

which implies

${displaystyle Gamma (z-n)=(-1)^{n-1};{frac {Gamma (-z)Gamma (1+z)}{Gamma (n+1-z)}},qquad nin mathbb {Z} }$

and the Legendre duplication formula

${displaystyle Gamma (z)Gamma left(z+{tfrac {1}{2}}right)=2^{1-2z};{sqrt {pi }};Gamma (2z).}$

Derivation of Euler’s reflection formula
Proof 1 We can use Euler’s infinite product ${displaystyle Gamma (z)={frac {1}{z}}prod _{n=1}^{infty }{frac {(1+1/n)^{z}}{1+z/n}}}$ to compute ${displaystyle {frac {1}{Gamma (1-z)Gamma (z)}}={frac {1}{(-z)Gamma (-z)Gamma (z)}}=zprod _{n=1}^{infty }{frac {(1-z/n)(1+z/n)}{(1+1/n)^{-z}(1+1/n)^{z}}}=zprod _{n=1}^{infty }left(1-{frac {z^{2}}{n^{2}}}right)={frac {sin pi z}{pi }},,}$ where the last equality is a known result. A similar derivation begins with Weierstrass’s definition. Proof 2 First we prove that ${displaystyle I=int _{-infty }^{infty }{frac {e^{ax}}{1+e^{x}}},dx=int _{0}^{infty }{frac {v^{a-1}}{1+v}},dv={frac {pi }{sin pi a}},quad ain (0,1).}$ Consider the positively oriented rectangular contour $C_{R}$ with vertices at , , and where ${displaystyle Rin mathbb {R} ^{+}}$ . Then by the residue theorem, ${displaystyle int _{C_{R}}{frac {e^{az}}{1+e^{z}}},dz=-2pi ie^{api i}.}$ Let ${displaystyle I_{R}=int _{-R}^{R}{frac {e^{ax}}{1+e^{x}}},dx}$ and let ${displaystyle I_{R}'}$ be the analogous integral over the top side of the rectangle. Then ${displaystyle I_{R}to I}$ as and ${displaystyle I_{R}'=-e^{2pi ia}I_{R}}$ . If denotes the right vertical side of the rectangle, then ${displaystyle left\|int _{A_{R}}{frac {e^{az}}{1+e^{z}}},dzright\|leq int _{0}^{2pi }left\|{frac {e^{a(R+it)}}{1+e^{R+it}}}right\|,dtleq Ce^{(a-1)R}}$ for some constant and since , the integral tends to as . Analogously, the integral over the left vertical side of the rectangle tends to as . Therefore ${displaystyle I-e^{2pi ia}I=-2pi ie^{api i},}$ from which ${displaystyle I={frac {pi }{sin pi a}},quad ain (0,1).}$ Then ${displaystyle Gamma (1-z)=int _{0}^{infty }e^{-u}u^{-z},du=tint _{0}^{infty }e^{-vt}(vt)^{-z},dv,quad t>0}$ and ${displaystyle {begin{aligned}Gamma (z)Gamma (1-z)&=int _{0}^{infty }int _{0}^{infty }e^{-t(1+v)}v^{-z},dv,dt\&=int _{0}^{infty }{frac {v^{-z}}{1+v}},dv\&={frac {pi }{sin pi (1-z)}}\&={frac {pi }{sin pi z}},quad zin (0,1).end{aligned}}}$ Proving the reflection formula for all proves it for all by analytic continuation.

Derivation of Euler’s reflection formula

Proof 1

We can use Euler’s infinite product

${displaystyle Gamma (z)={frac {1}{z}}prod _{n=1}^{infty }{frac {(1+1/n)^{z}}{1+z/n}}}$

to compute

${displaystyle {frac {1}{Gamma (1-z)Gamma (z)}}={frac {1}{(-z)Gamma (-z)Gamma (z)}}=zprod _{n=1}^{infty }{frac {(1-z/n)(1+z/n)}{(1+1/n)^{-z}(1+1/n)^{z}}}=zprod _{n=1}^{infty }left(1-{frac {z^{2}}{n^{2}}}right)={frac {sin pi z}{pi }},,}$

where the last equality is a known result. A similar derivation begins with Weierstrass’s definition.

Proof 2

First we prove that

${displaystyle I=int _{-infty }^{infty }{frac {e^{ax}}{1+e^{x}}},dx=int _{0}^{infty }{frac {v^{a-1}}{1+v}},dv={frac {pi }{sin pi a}},quad ain (0,1).}$

Consider the positively oriented rectangular contour $C_{R}$ with vertices at , , R+2pi i and where ${displaystyle Rin mathbb {R} ^{+}}$ . Then by the residue theorem,

${displaystyle int _{C_{R}}{frac {e^{az}}{1+e^{z}}},dz=-2pi ie^{api i}.}$

Let

${displaystyle I_{R}=int _{-R}^{R}{frac {e^{ax}}{1+e^{x}}},dx}$

and let ${displaystyle I_{R}'}$ be the analogous integral over the top side of the rectangle. Then ${displaystyle I_{R}to I}$ as and ${displaystyle I_{R}'=-e^{2pi ia}I_{R}}$ . If A_R denotes the right vertical side of the rectangle, then

${displaystyle left|int _{A_{R}}{frac {e^{az}}{1+e^{z}}},dzright|leq int _{0}^{2pi }left|{frac {e^{a(R+it)}}{1+e^{R+it}}}right|,dtleq Ce^{(a-1)R}}$

for some constant and since a<1 , the integral tends to as . Analogously, the integral over the left vertical side of the rectangle tends to as . Therefore

${displaystyle I-e^{2pi ia}I=-2pi ie^{api i},}$

from which

${displaystyle I={frac {pi }{sin pi a}},quad ain (0,1).}$

Then

${displaystyle Gamma (1-z)=int _{0}^{infty }e^{-u}u^{-z},du=tint _{0}^{infty }e^{-vt}(vt)^{-z},dv,quad t>0}$

and

${displaystyle {begin{aligned}Gamma (z)Gamma (1-z)&=int _{0}^{infty }int _{0}^{infty }e^{-t(1+v)}v^{-z},dv,dt\&=int _{0}^{infty }{frac {v^{-z}}{1+v}},dv\&={frac {pi }{sin pi (1-z)}}\&={frac {pi }{sin pi z}},quad zin (0,1).end{aligned}}}$

Proving the reflection formula for all proves it for all by analytic continuation.

Derivation of the Legendre duplication formula
The beta function can be represented as ${displaystyle mathrm {B} (z_{1},z_{2})={frac {Gamma (z_{1})Gamma (z_{2})}{Gamma (z_{1}+z_{2})}}=int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1},dt.}$ Setting ${displaystyle z_{1}=z_{2}=z}$ yields ${displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}=int _{0}^{1}t^{z-1}(1-t)^{z-1},dt.}$ After the substitution ${displaystyle t={frac {1+u}{2}}}$ we get ${displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}={frac {1}{2^{2z-1}}}int _{-1}^{1}left(1-u^{2}right)^{z-1},du.}$ The function ${displaystyle (1-u^{2})^{z-1}}$ is even, hence ${displaystyle 2^{2z-1}Gamma ^{2}(z)=2Gamma (2z)int _{0}^{1}(1-u^{2})^{z-1},du.}$ Now assume ${displaystyle mathrm {B} left({frac {1}{2}},zright)=int _{0}^{1}t^{{frac {1}{2}}-1}(1-t)^{z-1},dt,quad t=s^{2}.}$ Then ${displaystyle mathrm {B} left({frac {1}{2}},zright)=2int _{0}^{1}(1-s^{2})^{z-1},ds=2int _{0}^{1}(1-u^{2})^{z-1},du.}$ This implies ${displaystyle 2^{2z-1}Gamma ^{2}(z)=Gamma (2z)mathrm {B} left({frac {1}{2}},zright).}$ Since ${displaystyle mathrm {B} left({frac {1}{2}},zright)={frac {Gamma left({frac {1}{2}}right)Gamma (z)}{Gamma left(z+{frac {1}{2}}right)}},quad Gamma left({frac {1}{2}}right)={sqrt {pi }},}$ the Legendre duplication formula follows: ${displaystyle Gamma (z)Gamma left(z+{frac {1}{2}}right)=2^{1-2z}{sqrt {pi }};Gamma (2z).}$

Derivation of the Legendre duplication formula

The beta function can be represented as

${displaystyle mathrm {B} (z_{1},z_{2})={frac {Gamma (z_{1})Gamma (z_{2})}{Gamma (z_{1}+z_{2})}}=int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1},dt.}$

Setting ${displaystyle z_{1}=z_{2}=z}$ yields

${displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}=int _{0}^{1}t^{z-1}(1-t)^{z-1},dt.}$

After the substitution ${displaystyle t={frac {1+u}{2}}}$ we get

${displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}={frac {1}{2^{2z-1}}}int _{-1}^{1}left(1-u^{2}right)^{z-1},du.}$

The function ${displaystyle (1-u^{2})^{z-1}}$ is even, hence

${displaystyle 2^{2z-1}Gamma ^{2}(z)=2Gamma (2z)int _{0}^{1}(1-u^{2})^{z-1},du.}$

Now assume

${displaystyle mathrm {B} left({frac {1}{2}},zright)=int _{0}^{1}t^{{frac {1}{2}}-1}(1-t)^{z-1},dt,quad t=s^{2}.}$

Then

${displaystyle mathrm {B} left({frac {1}{2}},zright)=2int _{0}^{1}(1-s^{2})^{z-1},ds=2int _{0}^{1}(1-u^{2})^{z-1},du.}$

This implies

${displaystyle 2^{2z-1}Gamma ^{2}(z)=Gamma (2z)mathrm {B} left({frac {1}{2}},zright).}$

Since

${displaystyle mathrm {B} left({frac {1}{2}},zright)={frac {Gamma left({frac {1}{2}}right)Gamma (z)}{Gamma left(z+{frac {1}{2}}right)}},quad Gamma left({frac {1}{2}}right)={sqrt {pi }},}$

the Legendre duplication formula follows:

${displaystyle Gamma (z)Gamma left(z+{frac {1}{2}}right)=2^{1-2z}{sqrt {pi }};Gamma (2z).}$

The duplication formula is a special case of the multiplication theorem (see ^[9] Eq. 5.5.6):

${displaystyle prod _{k=0}^{m-1}Gamma left(z+{frac {k}{m}}right)=(2pi )^{frac {m-1}{2}};m^{{frac {1}{2}}-mz};Gamma (mz).}$

A simple but useful property, which can be seen from the limit definition, is:

In particular, with z = a + bi, this product is

${displaystyle |Gamma (a+bi)|^{2}=|Gamma (a)|^{2}prod _{k=0}^{infty }{frac {1}{1+{frac {b^{2}}{(a+k)^{2}}}}}}$

If the real part is an integer or a half-integer, this can be finitely expressed in closed form:

${displaystyle {begin{aligned}|Gamma (bi)|^{2}&={frac {pi }{bsinh pi b}}\[1ex]left|Gamma left({tfrac {1}{2}}+biright)right|^{2}&={frac {pi }{cosh pi b}}\[1ex]left|Gamma left(1+biright)right|^{2}&={frac {pi b}{sinh pi b}}\[1ex]left|Gamma left(1+n+biright)right|^{2}&={frac {pi b}{sinh pi b}}prod _{k=1}^{n}left(k^{2}+b^{2}right),quad nin mathbb {N} \[1ex]left|Gamma left(-n+biright)right|^{2}&={frac {pi }{bsinh pi b}}prod _{k=1}^{n}left(k^{2}+b^{2}right)^{-1},quad nin mathbb {N} \[1ex]left|Gamma left({tfrac {1}{2}}pm n+biright)right|^{2}&={frac {pi }{cosh pi b}}prod _{k=1}^{n}left(left(k-{tfrac {1}{2}}right)^{2}+b^{2}right)^{pm 1},quad nin mathbb {N} \[-1ex]&end{aligned}}}$

Proof of absolute value formulas for arguments of integer or half-integer real part
First, consider the reflection formula applied to . ${displaystyle Gamma (bi)Gamma (1-bi)={frac {pi }{sin pi bi}}}$ Applying the recurrence relation to the second term, we have ${displaystyle -bicdot Gamma (bi)Gamma (-bi)={frac {pi }{sin pi bi}}}$ which with simple rearrangement gives ${displaystyle Gamma (bi)Gamma (-bi)={frac {pi }{-bisin pi bi}}={frac {pi }{bsinh pi b}}}$ Second, consider the reflection formula applied to ${displaystyle z={tfrac {1}{2}}+bi}$ . ${displaystyle Gamma ({tfrac {1}{2}}+bi)Gamma left(1-({tfrac {1}{2}}+bi)right)=Gamma ({tfrac {1}{2}}+bi)Gamma ({tfrac {1}{2}}-bi)={frac {pi }{sin pi ({tfrac {1}{2}}+bi)}}={frac {pi }{cos pi bi}}={frac {pi }{cosh pi b}}}$ Formulas for other values of for which the real part is integer or half-integer quickly follow by induction using the recurrence relation in the positive and negative directions.

Proof of absolute value formulas for arguments of integer or half-integer real part

First, consider the reflection formula applied to .

${displaystyle Gamma (bi)Gamma (1-bi)={frac {pi }{sin pi bi}}}$

Applying the recurrence relation to the second term, we have

${displaystyle -bicdot Gamma (bi)Gamma (-bi)={frac {pi }{sin pi bi}}}$

which with simple rearrangement gives

${displaystyle Gamma (bi)Gamma (-bi)={frac {pi }{-bisin pi bi}}={frac {pi }{bsinh pi b}}}$

Second, consider the reflection formula applied to ${displaystyle z={tfrac {1}{2}}+bi}$ .

${displaystyle Gamma ({tfrac {1}{2}}+bi)Gamma left(1-({tfrac {1}{2}}+bi)right)=Gamma ({tfrac {1}{2}}+bi)Gamma ({tfrac {1}{2}}-bi)={frac {pi }{sin pi ({tfrac {1}{2}}+bi)}}={frac {pi }{cos pi bi}}={frac {pi }{cosh pi b}}}$

Formulas for other values of for which the real part is integer or half-integer quickly follow by induction using the recurrence relation in the positive and negative directions.

Perhaps the best-known value of the gamma function at a non-integer argument is

${displaystyle Gamma left({tfrac {1}{2}}right)={sqrt {pi }},}$

which can be found by setting ${textstyle z={frac {1}{2}}}$ in the reflection or duplication formulas, by using the relation to the beta function given below with ${textstyle z_{1}=z_{2}={frac {1}{2}}}$ , or simply by making the substitution in the integral definition of the gamma function, resulting in a Gaussian integral. In general, for non-negative integer values of we have:

${displaystyle {begin{aligned}Gamma left({tfrac {1}{2}}+nright)&={(2n)! over 4^{n}n!}{sqrt {pi }}={frac {(2n-1)!!}{2^{n}}}{sqrt {pi }}={binom {n-{frac {1}{2}}}{n}}n!{sqrt {pi }}\[8pt]Gamma left({tfrac {1}{2}}-nright)&={(-4)^{n}n! over (2n)!}{sqrt {pi }}={frac {(-2)^{n}}{(2n-1)!!}}{sqrt {pi }}={frac {sqrt {pi }}{{binom {-1/2}{n}}n!}}end{aligned}}}$

where the double factorial . See Particular values of the gamma function for calculated values.

It might be tempting to generalize the result that ${textstyle Gamma left({frac {1}{2}}right)={sqrt {pi }}}$ by looking for a formula for other individual values where is rational, especially because according to Gauss’s digamma theorem, it is possible to do so for the closely related digamma function at every rational value. However, these numbers are not known to be expressible by themselves in terms of elementary functions. It has been proved that is a transcendental number and algebraically independent of for any integer and each of the fractions ${textstyle r={frac {1}{6}},{frac {1}{4}},{frac {1}{3}},{frac {2}{3}},{frac {3}{4}},{frac {5}{6}}}$ .^[10] In general, when computing values of the gamma function, we must settle for numerical approximations.

The derivatives of the gamma function are described in terms of the polygamma function, ψ⁽⁰⁾(z):

${displaystyle Gamma '(z)=Gamma (z)psi ^{(0)}(z).}$

For a positive integer m the derivative of the gamma function can be calculated as follows:

Plot of gamma function in the complex plane from -2-2i to 6+2i with colors created in Mathematica

${displaystyle Gamma '(m+1)=m!left(-gamma +sum _{k=1}^{m}{frac {1}{k}}right)=m!left(-gamma +H(m)right),,}$

where H(m) is the mth harmonic number and γ is the Euler–Mascheroni constant.

For the th derivative of the gamma function is:

${displaystyle {frac {d^{n}}{dz^{n}}}Gamma (z)=int _{0}^{infty }t^{z-1}e^{-t}(ln t)^{n},dt.}$

(This can be derived by differentiating the integral form of the gamma function with respect to , and using the technique of differentiation under the integral sign.)

Using the identity

${displaystyle Gamma ^{(n)}(1)=(-1)^{n}n!sum limits _{pi ,vdash ,n},prod _{i=1}^{r}{frac {zeta ^{*}(a_{i})}{k_{i}!cdot a_{i}}}qquad zeta ^{*}(x):={begin{cases}zeta (x)&xneq 1\gamma &x=1end{cases}}}$

where is the Riemann zeta function, and is a partition of given by

${displaystyle pi =underbrace {a_{1}+cdots +a_{1}} _{k_{1}{text{ terms}}}+cdots +underbrace {a_{r}+cdots +a_{r}} _{k_{r}{text{ terms}}},}$

we have in particular the Laurent series expansion of the gamma function ^[11]

${displaystyle Gamma (z)={frac {1}{z}}-gamma +{tfrac {1}{2}}left(gamma ^{2}+{frac {pi ^{2}}{6}}right)z-{tfrac {1}{6}}left(gamma ^{3}+{frac {gamma pi ^{2}}{2}}+2zeta (3)right)z^{2}+O(z^{3}).}$

Inequalities[edit]

When restricted to the positive real numbers, the gamma function is a strictly logarithmically convex function. This property may be stated in any of the following three equivalent ways:

The last of these statements is, essentially by definition, the same as the statement that ${displaystyle psi ^{(1)}(x)>0}$ , where ${displaystyle psi ^{(1)}}$ is the polygamma function of order 1. To prove the logarithmic convexity of the gamma function, it therefore suffices to observe that ${displaystyle psi ^{(1)}}$ has a series representation which, for positive real x, consists of only positive terms.

Logarithmic convexity and Jensen’s inequality together imply, for any positive real numbers $x_{1},ldots ,x_{n}$ and ,

${displaystyle Gamma left({frac {a_{1}x_{1}+cdots +a_{n}x_{n}}{a_{1}+cdots +a_{n}}}right)leq {bigl (}Gamma (x_{1})^{a_{1}}cdots Gamma (x_{n})^{a_{n}}{bigr )}^{frac {1}{a_{1}+cdots +a_{n}}}.}$

There are also bounds on ratios of gamma functions. The best-known is Gautschi’s inequality, which says that for any positive real number x and any s ∈ (0, 1),

${displaystyle x^{1-s}<{frac {Gamma (x+1)}{Gamma (x+s)}}<left(x+1right)^{1-s}.}$

Stirling’s formula[edit]

Representation of the gamma function in the complex plane. Each point is colored according to the argument of . The contour plot of the modulus is also displayed.

3-dimensional plot of the absolute value of the complex gamma function

The behavior of for an increasing positive real variable is given by Stirling’s formula

${displaystyle Gamma (x+1)sim {sqrt {2pi x}}left({frac {x}{e}}right)^{x},}$

where the symbol sim means asymptotic convergence; the ratio of the two sides converges to 1 in the limit .^[1] This growth is faster than exponential, , for any fixed value of beta .

Another useful limit for asymptotic approximations for is:

${displaystyle {Gamma (x+alpha )}sim {Gamma (x)x^{alpha }},qquad alpha in mathbb {C} .}$

Residues[edit]

The behavior for non-positive is more intricate. Euler’s integral does not converge for , but the function it defines in the positive complex half-plane has a unique analytic continuation to the negative half-plane. One way to find that analytic continuation is to use Euler’s integral for positive arguments and extend the domain to negative numbers by repeated application of the recurrence formula,^[1]

${displaystyle Gamma (z)={frac {Gamma (z+n+1)}{z(z+1)cdots (z+n)}},}$

choosing such that is positive. The product in the denominator is zero when equals any of the integers . Thus, the gamma function must be undefined at those points to avoid division by zero; it is a meromorphic function with simple poles at the non-positive integers.^[1]

For a function of a complex variable , at a simple pole , the residue of is given by:

${displaystyle operatorname {Res} (f,c)=lim _{zto c}(z-c)f(z).}$

For the simple pole we rewrite recurrence formula as:

${displaystyle (z+n)Gamma (z)={frac {Gamma (z+n+1)}{z(z+1)cdots (z+n-1)}}.}$

The numerator at is

and the denominator

${displaystyle z(z+1)cdots (z+n-1)=-n(1-n)cdots (n-1-n)=(-1)^{n}n!.}$

So the residues of the gamma function at those points are:^[12]

${displaystyle operatorname {Res} (Gamma ,-n)={frac {(-1)^{n}}{n!}}.}$

The gamma function is non-zero everywhere along the real line, although it comes arbitrarily close to zero as z → −∞. There is in fact no complex number for which , and hence the reciprocal gamma function ${textstyle {frac {1}{Gamma (z)}}}$ is an entire function, with zeros at .^[1]

Minima and maxima[edit]

On the real line, the gamma function has a local minimum at z_min ≈ +1.46163214496836234126^[13] where it attains the value Γ(z_min) ≈ +0.88560319441088870027.^[14] The gamma function rises to either side of this minimum. The solution to Γ(z − 0.5) = Γ(z + 0.5) is z = +1.5 and the common value is Γ(1) = Γ(2) = +1. The positive solution to Γ(z − 1) = Γ(z + 1) is z = φ ≈ +1.618, the golden ratio, and the common value is Γ(φ − 1) = Γ(φ + 1) = φ! ≈ +1.44922960226989660037.^[15]

The gamma function must alternate sign between its poles at the non-positive integers because the product in the forward recurrence contains an odd number of negative factors if the number of poles between and is odd, and an even number if the number of poles is even.^[12] The extrema values of the Gamma function between the non-positive integers are Γ(-0.50408300826454938526…^[16]) = -3.54464361115500508912…,
Γ(-1.57349847316239045877…^[17]) = 2.30240725833968013582…, Γ(-2.61072086844414465000…^[18]) = -0.88813635840124192009…,
Γ(-3.63529336643690109783…^[19]) = 0.24512753983436625043…, Γ(-4.65323776174314244171…^[20]) = -0.05277963958731940076…, etc.

Integral representations[edit]

There are many formulas, besides the Euler integral of the second kind, that express the gamma function as an integral. For instance, when the real part of z is positive,^[21]

${displaystyle Gamma (z)=int _{-infty }^{infty }e^{zt-e^{t}},dt}$

and^[22]

${displaystyle Gamma (z)=int _{0}^{1}left(log {frac {1}{t}}right)^{z-1},dt,}$

${displaystyle Gamma (z)=2int _{0}^{infty }t^{2z-1}e^{-t^{2}},dt}$

where the three integrals respectively follow from the substitutions ${displaystyle t=e^{-x}}$ , ^[23] and ${displaystyle t=x^{2}}$ ^[24] in Euler’s second integral. The last integral in particular makes clear the connection between the gamma function at half integer arguments and the Gaussian integral: if we let we get ${textstyle Gamma (1/2)={sqrt {pi }}=2int _{0}^{infty }e^{-t^{2}},dt}$ .

Binet’s first integral formula for the gamma function states that, when the real part of z is positive, then:^[25]

${displaystyle log Gamma (z)=left(z-{frac {1}{2}}right)log z-z+{frac {1}{2}}log(2pi )+int _{0}^{infty }left({frac {1}{2}}-{frac {1}{t}}+{frac {1}{e^{t}-1}}right){frac {e^{-tz}}{t}},dt.}$

The integral on the right-hand side may be interpreted as a Laplace transform. That is,

${displaystyle log left(Gamma (z)left({frac {e}{z}}right)^{z}{sqrt {2pi z}}right)={mathcal {L}}left({frac {1}{2t}}-{frac {1}{t^{2}}}+{frac {1}{t(e^{t}-1)}}right)(z).}$

Binet’s second integral formula states that, again when the real part of z is positive, then:^[26]

${displaystyle log Gamma (z)=left(z-{frac {1}{2}}right)log z-z+{frac {1}{2}}ln(2pi )+2int _{0}^{infty }{frac {arctan(t/z)}{e^{2pi t}-1}},dt.}$

Let C be a Hankel contour, meaning a path that begins and ends at the point ∞ on the Riemann sphere, whose unit tangent vector converges to −1 at the start of the path and to 1 at the end, which has winding number 1 around 0, and which does not cross [0, ∞). Fix a branch of by taking a branch cut along [0, ∞) and by taking to be real when t is on the negative real axis. Assume z is not an integer. Then Hankel’s formula for the gamma function is:^[27]

${displaystyle Gamma (z)=-{frac {1}{2isin pi z}}int _{C}(-t)^{z-1}e^{-t},dt,}$

where ${displaystyle (-t)^{z-1}}$ is interpreted as . The reflection formula leads to the closely related expression

${displaystyle {frac {1}{Gamma (z)}}={frac {i}{2pi }}int _{C}(-t)^{-z}e^{-t},dt,}$

again valid whenever z is not an integer.

Continued fraction representation[edit]

The gamma function can also be represented by a sum of two continued fractions:^[28]^[29]

${displaystyle Gamma (z)={cfrac {e^{-1}}{2+0-z+1{cfrac {z-1}{2+2-z+2{cfrac {z-2}{2+4-z+3{cfrac {z-3}{2+6-z+4{cfrac {z-4}{2+8-z+5{cfrac {z-5}{2+10-z+ddots }}}}}}}}}}}}+{cfrac {e^{-1}}{z+0-{cfrac {z+0}{z+1+{cfrac {1}{z+2-{cfrac {z+1}{z+3+{cfrac {2}{z+4-{cfrac {z+2}{z+5+{cfrac {3}{z+6-ddots }}}}}}}}}}}}}}}$

where .

Fourier series expansion[edit]

The logarithm of the gamma function has the following Fourier series expansion for

${displaystyle ln Gamma (z)=left({frac {1}{2}}-zright)(gamma +ln 2)+(1-z)ln pi -{frac {1}{2}}ln sin(pi z)+{frac {1}{pi }}sum _{n=1}^{infty }{frac {ln n}{n}}sin(2pi nz),}$

which was for a long time attributed to Ernst Kummer, who derived it in 1847.^[30]^[31] However, Iaroslav Blagouchine discovered that Carl Johan Malmsten first derived this series in 1842.^[32]^[33]

Raabe’s formula[edit]

In 1840 Joseph Ludwig Raabe proved that

${displaystyle int _{a}^{a+1}ln Gamma (z),dz={tfrac {1}{2}}ln 2pi +aln a-a,quad a>0.}$

In particular, if a=0 then

${displaystyle int _{0}^{1}ln Gamma (z),dz={tfrac {1}{2}}ln 2pi .}$

The latter can be derived taking the logarithm in the above multiplication formula, which gives an expression for the Riemann sum of the integrand. Taking the limit for gives the formula.

Pi function[edit]

An alternative notation that was originally introduced by Gauss is the -function, which, in terms of the gamma function, is

${displaystyle Pi (z)=Gamma (z+1)=zGamma (z)=int _{0}^{infty }e^{-t}t^{z},dt,}$

so that for every non-negative integer .

Using the pi function the reflection formula takes on the form

${displaystyle Pi (z)Pi (-z)={frac {pi z}{sin(pi z)}}={frac {1}{operatorname {sinc} (z)}}}$

where sinc is the normalized sinc function, while the multiplication theorem takes on the form

${displaystyle Pi left({frac {z}{m}}right),Pi left({frac {z-1}{m}}right)cdots Pi left({frac {z-m+1}{m}}right)=(2pi )^{frac {m-1}{2}}m^{-z-{frac {1}{2}}}Pi (z) .}$

We also sometimes find

${displaystyle pi (z)={frac {1}{Pi (z)}} ,}$

which is an entire function, defined for every complex number, just like the reciprocal gamma function. That pi (z) is entire entails it has no poles, so , like , has no zeros.

The volume of an n-ellipsoid with radii r₁, …, r_n can be expressed as

${displaystyle V_{n}(r_{1},dotsc ,r_{n})={frac {pi ^{frac {n}{2}}}{Pi left({frac {n}{2}}right)}}prod _{k=1}^{n}r_{k}.}$

Relation to other functions[edit]

In the first integral above, which defines the gamma function, the limits of integration are fixed. The upper and lower incomplete gamma functions are the functions obtained by allowing the lower or upper (respectively) limit of integration to vary.
The gamma function is related to the beta function by the formula

${displaystyle mathrm {B} (z_{1},z_{2})=int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1},dt={frac {Gamma (z_{1}),Gamma (z_{2})}{Gamma (z_{1}+z_{2})}}.}$
The logarithmic derivative of the gamma function is called the digamma function; higher derivatives are the polygamma functions.
The analog of the gamma function over a finite field or a finite ring is the Gaussian sums, a type of exponential sum.
The reciprocal gamma function is an entire function and has been studied as a specific topic.
The gamma function also shows up in an important relation with the Riemann zeta function, .

${displaystyle pi ^{-{frac {z}{2}}};Gamma left({frac {z}{2}}right)zeta (z)=pi ^{-{frac {1-z}{2}}};Gamma left({frac {1-z}{2}}right);zeta (1-z).}$

It also appears in the following formula:

${displaystyle zeta (z)Gamma (z)=int _{0}^{infty }{frac {u^{z}}{e^{u}-1}},{frac {du}{u}},}$

which is valid only for . The logarithm of the gamma function satisfies the following formula due to Lerch:

${displaystyle log Gamma (z)=zeta _{H}'(0,z)-zeta '(0),}$

where ${displaystyle zeta _{H}}$ is the Hurwitz zeta function, is the Riemann zeta function and the prime (′) denotes differentiation in the first variable.
The gamma function is related to the stretched exponential function. For instance, the moments of that function are

${displaystyle langle tau ^{n}rangle equiv int _{0}^{infty }dt,t^{n-1},e^{-left({frac {t}{tau }}right)^{beta }}={frac {tau ^{n}}{beta }}Gamma left({n over beta }right).}$

Particular values[edit]

Including up to the first 20 digits after the decimal point, some particular values of the gamma function are:

${displaystyle {begin{array}{rcccl}Gamma left(-{tfrac {3}{2}}right)&=&{tfrac {4{sqrt {pi }}}{3}}&approx &+2.36327,18012,07354,70306\Gamma left(-{tfrac {1}{2}}right)&=&-2{sqrt {pi }}&approx &-3.54490,77018,11032,05459\Gamma left({tfrac {1}{2}}right)&=&{sqrt {pi }}&approx &+1.77245,38509,05516,02729\Gamma (1)&=&0!&=&+1\Gamma left({tfrac {3}{2}}right)&=&{tfrac {sqrt {pi }}{2}}&approx &+0.88622,69254,52758,01364\Gamma (2)&=&1!&=&+1\Gamma left({tfrac {5}{2}}right)&=&{tfrac {3{sqrt {pi }}}{4}}&approx &+1.32934,03881,79137,02047\Gamma (3)&=&2!&=&+2\Gamma left({tfrac {7}{2}}right)&=&{tfrac {15{sqrt {pi }}}{8}}&approx &+3.32335,09704,47842,55118\Gamma (4)&=&3!&=&+6end{array}}}$

(See sequences A245886, A019707, A002161, A019704, A245884, and A245885 in the OEIS.)
The complex-valued gamma function is undefined for non-positive integers, but in these cases the value can be defined in the Riemann sphere as ∞. The reciprocal gamma function is well defined and analytic at these values (and in the entire complex plane):

${displaystyle {frac {1}{Gamma (-3)}}={frac {1}{Gamma (-2)}}={frac {1}{Gamma (-1)}}={frac {1}{Gamma (0)}}=0.}$

The log-gamma function[edit]

The analytic function log Γ(z)

Because the gamma and factorial functions grow so rapidly for moderately large arguments, many computing environments include a function that returns the natural logarithm of the gamma function (often given the name lgamma or lngamma in programming environments or gammaln in spreadsheets); this grows much more slowly, and for combinatorial calculations allows adding and subtracting logs instead of multiplying and dividing very large values. It is often defined as^[34]

${displaystyle ln Gamma (z)=-gamma z-ln z+sum _{k=1}^{infty }left[{frac {z}{k}}-ln left(1+{frac {z}{k}}right)right].}$

The digamma function, which is the derivative of this function, is also commonly seen.
In the context of technical and physical applications, e.g. with wave propagation, the functional equation

Plot of logarithmic gamma function in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D

is often used since it allows one to determine function values in one strip of width 1 in z from the neighbouring strip. In particular, starting with a good approximation for a z with large real part one may go step by step down to the desired z. Following an indication of Carl Friedrich Gauss, Rocktaeschel (1922) proposed for an approximation for large Re(z):

${displaystyle ln Gamma (z)approx (z-{tfrac {1}{2}})ln z-z+{tfrac {1}{2}}ln(2pi ).}$

This can be used to accurately approximate ln(Γ(z)) for z with a smaller Re(z) via (P.E.Böhmer, 1939)

${displaystyle ln Gamma (z-m)=ln Gamma (z)-sum _{k=1}^{m}ln(z-k).}$

A more accurate approximation can be obtained by using more terms from the asymptotic expansions of ln(Γ(z)) and Γ(z), which are based on Stirling’s approximation.

${displaystyle Gamma (z)sim z^{z-{frac {1}{2}}}e^{-z}{sqrt {2pi }}left(1+{frac {1}{12z}}+{frac {1}{288z^{2}}}-{frac {139}{51,840z^{3}}}-{frac {571}{2,488,320z^{4}}}right)}$

as |z| → ∞ at constant |arg(z)| < π. (See sequences A001163 and A001164 in the OEIS.)

In a more «natural» presentation:

${displaystyle ln Gamma (z)=zln z-z-{tfrac {1}{2}}ln z+{tfrac {1}{2}}ln 2pi +{frac {1}{12z}}-{frac {1}{360z^{3}}}+{frac {1}{1260z^{5}}}+oleft({frac {1}{z^{5}}}right)}$

as |z| → ∞ at constant |arg(z)| < π. (See sequences A046968 and A046969 in the OEIS.)

The coefficients of the terms with k > 1 of z^1−k in the last expansion are simply

${displaystyle {frac {B_{k}}{k(k-1)}}}$

where the B_k are the Bernoulli numbers.

The Gamma function also has Stirling Series (derived by Charles Hermite in 1900) equal to^[35]

${displaystyle log Gamma (1+x)={frac {x(x-1)}{2!}}log(2)+{frac {x(x-1)(x-2)}{3!}}(log(3)-2log(2))+cdots ,quad Re (x)>0.}$

Properties[edit]

The Bohr–Mollerup theorem states that among all functions extending the factorial functions to the positive real numbers, only the gamma function is log-convex, that is, its natural logarithm is convex on the positive real axis. Another characterisation is given by the Wielandt theorem.

The gamma function is the unique function that simultaneously satisfies

,
for all complex numbers except the non-positive integers, and,
for integer n, ${textstyle lim _{nto infty }{frac {Gamma (n+z)}{Gamma (n);n^{z}}}=1}$ for all complex numbers .^[1]

In a certain sense, the ln(Γ) function is the more natural form; it makes some intrinsic attributes of the function clearer. A striking example is the Taylor series of ln(Γ) around 1:

${displaystyle ln Gamma (z+1)=-gamma z+sum _{k=2}^{infty }{frac {zeta (k)}{k}},(-z)^{k}qquad forall ;|z|<1}$

with ζ(k) denoting the Riemann zeta function at k.

So, using the following property:

${displaystyle zeta (s)Gamma (s)=int _{0}^{infty }{frac {t^{s}}{e^{t}-1}},{frac {dt}{t}}}$

we can find an integral representation for the ln(Γ) function:

${displaystyle ln Gamma (z+1)=-gamma z+int _{0}^{infty }{frac {e^{-zt}-1+zt}{tleft(e^{t}-1right)}},dt}$

or, setting z = 1 to obtain an integral for γ, we can replace the γ term with its integral and incorporate that into the above formula, to get:

${displaystyle ln Gamma (z+1)=int _{0}^{infty }{frac {e^{-zt}-ze^{-t}-1+z}{tleft(e^{t}-1right)}},dt,.}$

There also exist special formulas for the logarithm of the gamma function for rational z.
For instance, if and are integers with k<n and then

${displaystyle {begin{aligned}ln Gamma left({frac {k}{n}}right)={}&{frac {,(n-2k)ln 2pi ,}{2n}}+{frac {1}{2}}left{,ln pi -ln sin {frac {pi k}{n}},right}+{frac {1}{pi }}!sum _{r=1}^{n-1}{frac {,gamma +ln r,}{r}}cdot sin {frac {,2pi rk,}{n}}\&{}-{frac {1}{2pi }}sin {frac {2pi k}{n}}cdot !int _{0}^{infty }!!{frac {,e^{-nx}!cdot ln x,}{,cosh x-cos(2pi k/n),}},{mathrm {d} }xend{aligned}}}$

see.^[36]
This formula is sometimes used for numerical computation, since the integrand decreases very quickly.

Integration over log-gamma[edit]

The integral

${displaystyle int _{0}^{z}ln Gamma (x),dx}$

can be expressed in terms of the Barnes G-function^[37]^[38] (see Barnes G-function for a proof):

${displaystyle int _{0}^{z}ln Gamma (x),dx={frac {z}{2}}ln(2pi )+{frac {z(1-z)}{2}}+zln Gamma (z)-ln G(z+1)}$

where Re(z) > −1.

It can also be written in terms of the Hurwitz zeta function:^[39]^[40]

${displaystyle int _{0}^{z}ln Gamma (x),dx={frac {z}{2}}ln(2pi )+{frac {z(1-z)}{2}}-zeta '(-1)+zeta '(-1,z).}$

When z=1 it follows that

${displaystyle int _{0}^{1}ln Gamma (x),dx={frac {1}{2}}ln(2pi ),}$

and this is a consequence of Raabe’s formula as well. O. Espinosa and V. Moll derived a similar formula for the integral of the square of :^[41]

${displaystyle int _{0}^{1}ln ^{2}Gamma (x)dx={frac {gamma ^{2}}{12}}+{frac {pi ^{2}}{48}}+{frac {1}{3}}gamma L_{1}+{frac {4}{3}}L_{1}^{2}-left(gamma +2L_{1}right){frac {zeta ^{prime }(2)}{pi ^{2}}}+{frac {zeta ^{prime prime }(2)}{2pi ^{2}}},}$

where $L_{1}$ is ${displaystyle {frac {1}{2}}ln(2pi )}$ .

D. H. Bailey and his co-authors^[42] gave an evaluation for

${displaystyle L_{n}:=int _{0}^{1}ln ^{n}Gamma (x),dx}$

when n=1,2 in terms of the Tornheim–Witten zeta function and its derivatives.

In addition, it is also known that^[43]

${displaystyle lim _{nto infty }{frac {L_{n}}{n!}}=1.}$

Approximations[edit]

Comparison gamma (blue line) with the factorial (blue dots) and Stirling’s approximation (red line)

Complex values of the gamma function can be approximated using Stirling’s approximation or the Lanczos approximation,

${displaystyle Gamma (z)sim {sqrt {2pi }}z^{z-1/2}e^{-z}quad {hbox{as }}zto infty {hbox{ in }}left|arg(z)right|<pi .}$

This is precise in the sense that the ratio of the approximation to the true value approaches 1 in the limit as |z| goes to infinity.

The gamma function can be computed to fixed precision for by applying integration by parts to Euler’s integral. For any positive number x the gamma function can be written

${displaystyle {begin{aligned}Gamma (z)&=int _{0}^{x}e^{-t}t^{z},{frac {dt}{t}}+int _{x}^{infty }e^{-t}t^{z},{frac {dt}{t}}\&=x^{z}e^{-x}sum _{n=0}^{infty }{frac {x^{n}}{z(z+1)cdots (z+n)}}+int _{x}^{infty }e^{-t}t^{z},{frac {dt}{t}}.end{aligned}}}$

When Re(z) ∈ [1,2] and x geq 1 , the absolute value of the last integral is smaller than ${displaystyle (x+1)e^{-x}}$ . By choosing a large enough , this last expression can be made smaller than ${displaystyle 2^{-N}}$ for any desired value . Thus, the gamma function can be evaluated to bits of precision with the above series.

A fast algorithm for calculation of the Euler gamma function for any algebraic argument (including rational) was constructed by E.A. Karatsuba.^[44]^[45]^[46]

For arguments that are integer multiples of 1/24, the gamma function can also be evaluated quickly using arithmetic–geometric mean iterations (see particular values of the gamma function).^[47]

Applications[edit]

One author describes the gamma function as «Arguably, the most common special function, or the least ‘special’ of them. The other transcendental functions […] are called ‘special’ because you could conceivably avoid some of them by staying away from many specialized mathematical topics. On the other hand, the gamma function Γ(z) is most difficult to avoid.»^[48]

Integration problems[edit]

The gamma function finds application in such diverse areas as quantum physics, astrophysics and fluid dynamics.^[49] The gamma distribution, which is formulated in terms of the gamma function, is used in statistics to model a wide range of processes; for example, the time between occurrences of earthquakes.^[50]

The primary reason for the gamma function’s usefulness in such contexts is the prevalence of expressions of the type ${displaystyle f(t)e^{-g(t)}}$ which describe processes that decay exponentially in time or space. Integrals of such expressions can occasionally be solved in terms of the gamma function when no elementary solution exists. For example, if f is a power function and g is a linear function, a simple change of variables gives the evaluation

${displaystyle int _{0}^{infty }t^{b}e^{-at},dt={frac {1}{a^{b}}}int _{0}^{infty }u^{b}e^{-u}dleft({frac {u}{a}}right)={frac {Gamma (b+1)}{a^{b+1}}}.}$

The fact that the integration is performed along the entire positive real line might signify that the gamma function describes the cumulation of a time-dependent process that continues indefinitely, or the value might be the total of a distribution in an infinite space.

It is of course frequently useful to take limits of integration other than 0 and ∞ to describe the cumulation of a finite process, in which case the ordinary gamma function is no longer a solution; the solution is then called an incomplete gamma function. (The ordinary gamma function, obtained by integrating across the entire positive real line, is sometimes called the complete gamma function for contrast.)

An important category of exponentially decaying functions is that of Gaussian functions

${displaystyle ae^{-{frac {(x-b)^{2}}{c^{2}}}}}$

and integrals thereof, such as the error function. There are many interrelations between these functions and the gamma function; notably, the factor obtained by evaluating ${textstyle Gamma left({frac {1}{2}}right)}$ is the «same» as that found in the normalizing factor of the error function and the normal distribution.

The integrals we have discussed so far involve transcendental functions, but the gamma function also arises from integrals of purely algebraic functions. In particular, the arc lengths of ellipses and of the lemniscate, which are curves defined by algebraic equations, are given by elliptic integrals that in special cases can be evaluated in terms of the gamma function. The gamma function can also be used to calculate «volume» and «area» of n-dimensional hyperspheres.

Calculating products[edit]

The gamma function’s ability to generalize factorial products immediately leads to applications in many areas of mathematics; in combinatorics, and by extension in areas such as probability theory and the calculation of power series. Many expressions involving products of successive integers can be written as some combination of factorials, the most important example perhaps being that of the binomial coefficient

${displaystyle {binom {n}{k}}={frac {n!}{k!(n-k)!}}.}$

The example of binomial coefficients motivates why the properties of the gamma function when extended to negative numbers are natural. A binomial coefficient gives the number of ways to choose k elements from a set of n elements; if k > n, there are of course no ways. If k > n, (n − k)! is the factorial of a negative integer and hence infinite if we use the gamma function definition of factorials—dividing by infinity gives the expected value of 0.

We can replace the factorial by a gamma function to extend any such formula to the complex numbers. Generally, this works for any product wherein each factor is a rational function of the index variable, by factoring the rational function into linear expressions. If P and Q are monic polynomials of degree m and n with respective roots p₁, …, p_m and q₁, …, q_n, we have

${displaystyle prod _{i=a}^{b}{frac {P(i)}{Q(i)}}=left(prod _{j=1}^{m}{frac {Gamma (b-p_{j}+1)}{Gamma (a-p_{j})}}right)left(prod _{k=1}^{n}{frac {Gamma (a-q_{k})}{Gamma (b-q_{k}+1)}}right).}$

If we have a way to calculate the gamma function numerically, it is a breeze to calculate numerical values of such products. The number of gamma functions in the right-hand side depends only on the degree of the polynomials, so it does not matter whether b − a equals 5 or 10⁵. By taking the appropriate limits, the equation can also be made to hold even when the left-hand product contains zeros or poles.

By taking limits, certain rational products with infinitely many factors can be evaluated in terms of the gamma function as well. Due to the Weierstrass factorization theorem, analytic functions can be written as infinite products, and these can sometimes be represented as finite products or quotients of the gamma function. We have already seen one striking example: the reflection formula essentially represents the sine function as the product of two gamma functions. Starting from this formula, the exponential function as well as all the trigonometric and hyperbolic functions can be expressed in terms of the gamma function.

More functions yet, including the hypergeometric function and special cases thereof, can be represented by means of complex contour integrals of products and quotients of the gamma function, called Mellin–Barnes integrals.

Analytic number theory[edit]

An application of the gamma function is the study of the Riemann zeta function. A fundamental property of the Riemann zeta function is its functional equation:

${displaystyle Gamma left({frac {s}{2}}right)zeta (s)pi ^{-{frac {s}{2}}}=Gamma left({frac {1-s}{2}}right)zeta (1-s)pi ^{-{frac {1-s}{2}}}.}$

Among other things, this provides an explicit form for the analytic continuation of the zeta function to a meromorphic function in the complex plane and leads to an immediate proof that the zeta function has infinitely many so-called «trivial» zeros on the real line. Borwein et al. call this formula «one of the most beautiful findings in mathematics».^[51] Another contender for that title might be

${displaystyle zeta (s);Gamma (s)=int _{0}^{infty }{frac {t^{s}}{e^{t}-1}},{frac {dt}{t}}.}$

Both formulas were derived by Bernhard Riemann in his seminal 1859 paper «Ueber die Anzahl der Primzahlen unter einer gegebenen Größe» («On the Number of Primes Less Than a Given Magnitude»), one of the milestones in the development of analytic number theory—the branch of mathematics that studies prime numbers using the tools of mathematical analysis. Factorial numbers, considered as discrete objects, are an important concept in classical number theory because they contain many prime factors, but Riemann found a use for their continuous extension that arguably turned out to be even more important.

History[edit]

The gamma function has caught the interest of some of the most prominent mathematicians of all time. Its history, notably documented by Philip J. Davis in an article that won him the 1963 Chauvenet Prize, reflects many of the major developments within mathematics since the 18th century. In the words of Davis, «each generation has found something of interest to say about the gamma function. Perhaps the next generation will also.»^[1]

18th century: Euler and Stirling[edit]

The problem of extending the factorial to non-integer arguments was apparently first considered by Daniel Bernoulli and Christian Goldbach in the 1720s. In particular, in a letter from Bernoulli to Goldbach dated 6 October 1729 Bernoulli introduced the product representation^[52]

${displaystyle x!=lim _{nto infty }left(n+1+{frac {x}{2}}right)^{x-1}prod _{k=1}^{n}{frac {k+1}{k+x}}}$

which is well defined for real values of x other than the negative integers.

Leonard Euler later gave two different definitions: the first was not his integral but an infinite product that is well defined for all complex numbers n other than the negative integers,

${displaystyle n!=prod _{k=1}^{infty }{frac {left(1+{frac {1}{k}}right)^{n}}{1+{frac {n}{k}}}},,}$

of which he informed Goldbach in a letter dated 13 October 1729. He wrote to Goldbach again on 8 January 1730, to announce his discovery of the integral representation

${displaystyle n!=int _{0}^{1}(-ln s)^{n},ds,,}$

which is valid when the real part of the complex number n is strictly greater than −1 (i.e., ). By the change of variables t = −ln s, this becomes the familiar Euler integral. Euler published his results in the paper «De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt» («On transcendental progressions, that is, those whose general terms cannot be given algebraically»), submitted to the St. Petersburg Academy on 28 November 1729.^[53] Euler further discovered some of the gamma function’s important functional properties, including the reflection formula.

James Stirling, a contemporary of Euler, also attempted to find a continuous expression for the factorial and came up with what is now known as Stirling’s formula. Although Stirling’s formula gives a good estimate of n!, also for non-integers, it does not provide the exact value. Extensions of his formula that correct the error were given by Stirling himself and by Jacques Philippe Marie Binet.

19th century: Gauss, Weierstrass and Legendre[edit]

The first page of Euler’s paper

Carl Friedrich Gauss rewrote Euler’s product as

${displaystyle Gamma (z)=lim _{mto infty }{frac {m^{z}m!}{z(z+1)(z+2)cdots (z+m)}}}$

and used this formula to discover new properties of the gamma function. Although Euler was a pioneer in the theory of complex variables, he does not appear to have considered the factorial of a complex number, as instead Gauss first did.^[54] Gauss also proved the multiplication theorem of the gamma function and investigated the connection between the gamma function and elliptic integrals.

Karl Weierstrass further established the role of the gamma function in complex analysis, starting from yet another product representation,

${displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{k=1}^{infty }left(1+{frac {z}{k}}right)^{-1}e^{frac {z}{k}},}$

where γ is the Euler–Mascheroni constant. Weierstrass originally wrote his product as one for 1/Γ, in which case it is taken over the function’s zeros rather than its poles. Inspired by this result, he proved what is known as the Weierstrass factorization theorem—that any entire function can be written as a product over its zeros in the complex plane; a generalization of the fundamental theorem of algebra.

The name gamma function and the symbol Γ were introduced by Adrien-Marie Legendre around 1811; Legendre also rewrote Euler’s integral definition in its modern form. Although the symbol is an upper-case Greek gamma, there is no accepted standard for whether the function name should be written «gamma function» or «Gamma function» (some authors simply write «Γ-function»). The alternative «pi function» notation Π(z) = z! due to Gauss is sometimes encountered in older literature, but Legendre’s notation is dominant in modern works.

It is justified to ask why we distinguish between the «ordinary factorial» and the gamma function by using distinct symbols, and particularly why the gamma function should be normalized to Γ(n + 1) = n! instead of simply using «Γ(n) = n!«. Consider that the notation for exponents, xⁿ, has been generalized from integers to complex numbers x^z without any change. Legendre’s motivation for the normalization does not appear to be known, and has been criticized as cumbersome by some (the 20th-century mathematician Cornelius Lanczos, for example, called it «void of any rationality» and would instead use z!).^[55] Legendre’s normalization does simplify some formulae, but complicates others. From a modern point of view, the Legendre normalization of the Gamma function is the integral of the additive character e^−x against the multiplicative character x^z with respect to the Haar measure ${textstyle {frac {dx}{x}}}$ on the Lie group R⁺. Thus this normalization makes it clearer that the gamma function is a continuous analogue of a Gauss sum.^[56]

19th–20th centuries: characterizing the gamma function[edit]

It is somewhat problematic that a large number of definitions have been given for the gamma function. Although they describe the same function, it is not entirely straightforward to prove the equivalence. Stirling never proved that his extended formula corresponds exactly to Euler’s gamma function; a proof was first given by Charles Hermite in 1900.^[57] Instead of finding a specialized proof for each formula, it would be desirable to have a general method of identifying the gamma function.

One way to prove would be to find a differential equation that characterizes the gamma function. Most special functions in applied mathematics arise as solutions to differential equations, whose solutions are unique. However, the gamma function does not appear to satisfy any simple differential equation. Otto Hölder proved in 1887 that the gamma function at least does not satisfy any algebraic differential equation by showing that a solution to such an equation could not satisfy the gamma function’s recurrence formula, making it a transcendentally transcendental function. This result is known as Hölder’s theorem.

A definite and generally applicable characterization of the gamma function was not given until 1922. Harald Bohr and Johannes Mollerup then proved what is known as the Bohr–Mollerup theorem: that the gamma function is the unique solution to the factorial recurrence relation that is positive and logarithmically convex for positive z and whose value at 1 is 1 (a function is logarithmically convex if its logarithm is convex). Another characterisation is given by the Wielandt theorem.

The Bohr–Mollerup theorem is useful because it is relatively easy to prove logarithmic convexity for any of the different formulas used to define the gamma function. Taking things further, instead of defining the gamma function by any particular formula, we can choose the conditions of the Bohr–Mollerup theorem as the definition, and then pick any formula we like that satisfies the conditions as a starting point for studying the gamma function. This approach was used by the Bourbaki group.

Borwein & Corless^[58] review three centuries of work on the gamma function.

Reference tables and software[edit]

Although the gamma function can be calculated virtually as easily as any mathematically simpler function with a modern computer—even with a programmable pocket calculator—this was of course not always the case. Until the mid-20th century, mathematicians relied on hand-made tables; in the case of the gamma function, notably a table computed by Gauss in 1813 and one computed by Legendre in 1825.^[59]

A hand-drawn graph of the absolute value of the complex gamma function, from Tables of Higher Functions by Jahnke and Emde [de].

Tables of complex values of the gamma function, as well as hand-drawn graphs, were given in Tables of Functions With Formulas and Curves by Jahnke and Emde [de], first published in Germany in 1909. According to Michael Berry, «the publication in J&E of a three-dimensional graph showing the poles of the gamma function in the complex plane acquired an almost iconic status.»^[60]

There was in fact little practical need for anything but real values of the gamma function until the 1930s, when applications for the complex gamma function were discovered in theoretical physics. As electronic computers became available for the production of tables in the 1950s, several extensive tables for the complex gamma function were published to meet the demand, including a table accurate to 12 decimal places from the U.S. National Bureau of Standards.^[1]

reproduction of a famous complex plot by Janhke and Emde (Tables of Functions with Formulas and Curves, 4th ed., Dover, 1945) of the gamma function from -4.5-2.5i to 4.5+2.5i

Double-precision floating-point implementations of the gamma function and its logarithm are now available in most scientific computing software and special functions libraries, for example TK Solver, Matlab, GNU Octave, and the GNU Scientific Library. The gamma function was also added to the C standard library (math.h). Arbitrary-precision implementations are available in most computer algebra systems, such as Mathematica and Maple. PARI/GP, MPFR and MPFUN contain free arbitrary-precision implementations. In some software calculators, e.g. Windows Calculator and GNOME Calculator, the factorial function returns Γ(x+1) when the input x is a non-integer value.^[61]^[62]

Notes[edit]

^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ Davis, P. J. (1959). «Leonhard Euler’s Integral: A Historical Profile of the Gamma Function». American Mathematical Monthly. 66 (10): 849–869. doi:10.2307/2309786. JSTOR 2309786. Retrieved 3 December 2016.
^ «Is the Gamma function misdefined? Or: Hadamard versus Euler — Who found the better Gamma function?».
^ Beals, Richard; Wong, Roderick (2010). Special Functions: A Graduate Text. Cambridge University Press. p. 28. ISBN 978-1-139-49043-6. Extract of page 28
^ Ross, Clay C. (2013). Differential Equations: An Introduction with Mathematica (illustrated ed.). Springer Science & Business Media. p. 293. ISBN 978-1-4757-3949-7. Expression G.2 on page 293
^ Kingman, J. F. C. (1961). «A Convexity Property of Positive Matrices». The Quarterly Journal of Mathematics. 12 (1): 283–284. Bibcode:1961QJMat..12..283K. doi:10.1093/qmath/12.1.283.
^ Weisstein, Eric W. «Bohr–Mollerup Theorem». MathWorld.
^ Davis, Philip. «Leonard Euler’s Integral: A Historical Profile of the Gamma Function» (PDF). maa.org.
^ Bonvini, Marco (9 October 2010). «The Gamma function» (PDF). roma1.infn.it.
^ Askey, R. A.; Roy, R. (2010), «Series Expansions», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
^ Waldschmidt, M. (2006). «Transcendence of Periods: The State of the Art» (PDF). Pure Appl. Math. Quart. 2 (2): 435–463. doi:10.4310/pamq.2006.v2.n2.a3. Archived (PDF) from the original on 6 May 2006.
^ «How to obtain the Laurent expansion of gamma function around $z=0$?». Mathematics Stack Exchange. Retrieved 17 August 2022.
^ ^a ^b Weisstein, Eric W. «Gamma Function». MathWorld.
^ Sloane, N. J. A. (ed.). «Sequence A030169». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Sloane, N. J. A. (ed.). «Sequence A030171». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Sloane, N. J. A. (ed.). «Sequence A178840». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Sloane, N. J. A. (ed.). «Sequence A175472». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Sloane, N. J. A. (ed.). «Sequence A175473». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Sloane, N. J. A. (ed.). «Sequence A175474». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Sloane, N. J. A. (ed.). «Sequence A256681». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Sloane, N. J. A. (ed.). «Sequence A256682». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ Gradshteyn, I. S.; Ryzhik, I. M. (2007). Table of Integrals, Series, and Products (Seventh ed.). Academic Press. p. 893. ISBN 978-0-12-373637-6.
^ Whittaker and Watson, 12.2 example 1.
^ Detlef, Gronau. «Why is the gamma function so as it is?» (PDF). imsc.uni-graz.at.
^ Pascal Sebah, Xavier Gourdon. «Introduction to the Gamma Function» (PDF). Numbers Computation.
^ Whittaker and Watson, 12.31.
^ Whittaker and Watson, 12.32.
^ Whittaker and Watson, 12.22.
^ «Exponential integral E: Continued fraction representations (Formula 06.34.10.0005)».
^ «Exponential integral E: Continued fraction representations (Formula 06.34.10.0003)».
^ Bateman, Harry; Erdélyi, Arthur (1955). Higher Transcendental Functions. McGraw-Hill.
^ Srivastava, H. M.; Choi, J. (2001). Series Associated with the Zeta and Related Functions. The Netherlands: Kluwer Academic.
^ Blagouchine, Iaroslav V. (2014). «Rediscovery of Malmsten’s integrals, their evaluation by contour integration methods and some related results». Ramanujan J. 35 (1): 21–110. doi:10.1007/s11139-013-9528-5. S2CID 120943474.
^ Blagouchine, Iaroslav V. (2016). «Erratum and Addendum to «Rediscovery of Malmsten’s integrals, their evaluation by contour integration methods and some related results»«. Ramanujan J. 42 (3): 777–781. doi:10.1007/s11139-015-9763-z. S2CID 125198685.
^ «Log Gamma Function». Wolfram MathWorld. Retrieved 3 January 2019.
^ «Leonhard Euler’s Integral: An Historical Profile of the Gamma Function» (PDF). Archived (PDF) from the original on 12 September 2014. Retrieved 11 April 2022.
^ Blagouchine, Iaroslav V. (2015). «A theorem for the closed-form evaluation of the first generalized Stieltjes constant at rational arguments and some related summations». Journal of Number Theory. 148: 537–592. arXiv:1401.3724. doi:10.1016/j.jnt.2014.08.009.
^ Alexejewsky, W. P. (1894). «Über eine Classe von Funktionen, die der Gammafunktion analog sind» [On a class of functions analogous to the gamma function]. Leipzig Weidmanncshe Buchhandluns. 46: 268–275.
^ Barnes, E. W. (1899). «The theory of the G-function». Quart. J. Math. 31: 264–314.
^ Adamchik, Victor S. (1998). «Polygamma functions of negative order». J. Comput. Appl. Math. 100 (2): 191–199. doi:10.1016/S0377-0427(98)00192-7.
^ Gosper, R. W. (1997). « ${displaystyle textstyle int _{n/4}^{m/6}log F(z),dz}$ in special functions, q-series and related topics». J. Am. Math. Soc. 14.
^ Espinosa, Olivier; Moll, Victor H. (2002). «On Some Integrals Involving the Hurwitz Zeta Function: Part 1». The Ramanujan Journal. 6 (2): 159–188. doi:10.1023/A:1015706300169. S2CID 128246166.
^ Bailey, David H.; Borwein, David; Borwein, Jonathan M. (2015). «On Eulerian log-gamma integrals and Tornheim-Witten zeta functions». The Ramanujan Journal. 36 (1–2): 43–68. doi:10.1007/s11139-012-9427-1. S2CID 7335291.
^ Amdeberhan, T.; Coffey, Mark W.; Espinosa, Olivier; Koutschan, Christoph; Manna, Dante V.; Moll, Victor H. (2011). «Integrals of powers of loggamma». Proc. Amer. Math. Soc. 139 (2): 535–545. doi:10.1090/S0002-9939-2010-10589-0.
^ E.A. Karatsuba, Fast evaluation of transcendental functions. Probl. Inf. Transm. Vol.27, No.4, pp. 339–360 (1991).
^ E.A. Karatsuba, On a new method for fast evaluation of transcendental functions. Russ. Math. Surv. Vol.46, No.2, pp. 246–247 (1991).
^ E.A. Karatsuba «Fast Algorithms and the FEE Method».
^ Borwein, J. M.; Zucker, I. J. (1992). «Fast evaluation of the gamma function for small rational fractions using complete elliptic integrals of the first kind». IMA Journal of Numerical Analysis. 12 (4): 519–526. doi:10.1093/IMANUM/12.4.519.
^ Michon, G. P. «Trigonometry and Basic Functions Archived 9 January 2010 at the Wayback Machine». Numericana. Retrieved 5 May 2007.
^ Chaudry, M. A. & Zubair, S. M. (2001). On A Class of Incomplete Gamma Functions with Applications. p. 37
^ Rice, J. A. (1995). Mathematical Statistics and Data Analysis (Second Edition). p. 52–53
^ Borwein, J.; Bailey, D. H. & Girgensohn, R. (2003). Experimentation in Mathematics. A. K. Peters. p. 133. ISBN 978-1-56881-136-9.
^ «Interpolating the natural factorial n! or The birth of the real factorial function (1729 — 1826)».
^ Euler’s paper was published in Commentarii academiae scientiarum Petropolitanae 5, 1738, 36–57. See E19 — De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt, from The Euler Archive, which includes a scanned copy of the original article.
^ Remmert, R. (2006). Classical Topics in Complex Function Theory. Translated by Kay, L. D. Springer. ISBN 978-0-387-98221-2.
^ Lanczos, C. (1964). «A precision approximation of the gamma function». J. SIAM Numer. Anal. Ser. B. 1 (1): 86. Bibcode:1964SJNA….1…86L. doi:10.1137/0701008.
^ Ilker Inam; Engin Büyükaşşk (2019). Notes from the International Autumn School on Computational Number Theory. Springer. p. 205. ISBN 978-3-030-12558-5. Extract of page 205
^ Knuth, D. E. (1997). The Art of Computer Programming, Volume 1 (Fundamental Algorithms). Addison-Wesley.
^ Borwein, Jonathan M.; Corless, Robert M. (2017). «Gamma and Factorial in the Monthly». American Mathematical Monthly. Mathematical Association of America. 125 (5): 400–24. arXiv:1703.05349. Bibcode:2017arXiv170305349B. doi:10.1080/00029890.2018.1420983. S2CID 119324101.
^ «What’s the history of Gamma_function?». yearis.com. Retrieved 5 November 2022.
^ Berry, M. (April 2001). «Why are special functions special?». Physics Today.
^ «microsoft/calculator». GitHub. Retrieved 25 December 2020.
^ «gnome-calculator». GNOME.org. Retrieved 3 March 2023.

This article incorporates material from the Citizendium article «Gamma function», which is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License but not under the GFDL.

External links[edit]

NIST Digital Library of Mathematical Functions:Gamma function
Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
C++ reference for std::tgamma
Examples of problems involving the gamma function can be found at Exampleproblems.com.
«Gamma function», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Wolfram gamma function evaluator (arbitrary precision)
«Gamma». Wolfram Functions Site.
Volume of n-Spheres and the Gamma Function at MathPages

Источник

В математике, гамма-функция (представлена Γ, { displaystyle Gamma,}заглавной буквой гамма из греческого алфавита ) является одним из часто используемых расширений факториальной функции до комплексных чисел. Гамма-функция определена для всех комплексных чисел, кроме целых неположительных. Для любого натурального числа n, { displaystyle n,}

Получено по Даниэлю Бернулли, для комплексных чисел с положительной действительной частью гамма-функция определяется с помощью сходящейся несобственный интеграл :

Γ (z) = ∫ 0 ∞ xz — 1 e — xdx, ℜ (z)>0. { displaystyle Gamma (z) = int _ {0} ^ { infty} x ^ {z-1} e ^ {- x} , dx, qquad Re (z)>0 .} ${displaystyle Gamma (z)=int _{0}^{infty }x^{z-1}e^{-x},dx, qquad Re (z)>0 .}$

аналитическое продолжение этой интегральной функции до мероморфной функции, которая голоморфна во всей комплексной плоскости, кроме неположительные целые числа, где функция имеет простые полюсы.

Гамма-функция не имеет нулей, поэтому обратная гамма-функция 1 / Γ { displaystyle 1 / Gamma}— это целая функция. Фактически, гамма-функция соответствует преобразованию Меллина отрицательной экспоненциальной функции :

Γ (z) = { M e — x} (z). { Displaystyle Gamma (z) = {{ mathcal {M}} e ^ {- x} } (z).} ${ displaystyle Gamma (z) = {{ mathcal {M}} e ^ {- x} } (z).}$

Другие расширения факториальной функции делают существуют, но гамма-функция наиболее популярна и полезна. компонент sa в различных функциях распределения вероятностей, и как таковой он применим в полях вероятность и статистика, а также комбинаторика.

Содержание

1 Мотивация
2 Определение
- 2.1 Основное определение
- 2.2 Альтернативные определения
  - 2.2.1 Определение Эйлера как бесконечного произведения
  - 2.2.2 Определение Вейерштрасса
  - 2.2.3 В терминах обобщенных многочленов Лагерра
3 Свойства
- 3.1 Общие сведения
- 3.2 Неравенства
- 3.3 Формула Стирлинга
- 3.4 Остатки
- 3.5 Минимумы
- 3.6 Интегральные представления
- 3.7 Разложение в ряд Фурье
- 3.8 Формула Раабе
- 3.9 Функция Pi
- 3.10 Связь с другими функциями
- 3.11 Частные значения
4 Логарифмическая гамма-функция
- 4.1 Свойства
- 4.2 Интегрирование по логарифмической гамме
5 Приближение
6 Приложения
- 6.1 Проблемы интеграции
- 6.2 Вычисление продуктов
- 6.3 Аналитическая теория чисел
7 История
- 7.1 XVIII век: Эйлер и Св. irling
- 7.2 XIX век: Гаусс, Вейерштрасс и Лежандр
- 7.3 XIX – XX века: характеристика гамма-функции
- 7.4 Справочные таблицы и программное обеспечение
8 См. также
9 Примечания
10 Далее чтение
11 Внешние ссылки

Мотивация

Гамма-функция интерполирует факториальную функцию к нецелым значениям.

Гамма-функцию можно рассматривать как решение следующей проблемы интерполяции :

«Найдите гладкую кривую, которая соединяет точки (x, y) { displaystyle (x, y)} (x, y)

, заданные как y = ( х — 1)! { displaystyle y = (x-1)!}

при положительных целочисленных значениях для x { displaystyle x}

.»

График первых нескольких факториалов показывает, что такая кривая может быть нарисованным, но было бы предпочтительнее иметь формулу, которая точно описывает кривую, в которой количество операций не зависит от размера x { displaystyle x}. Простая формула факториала x! = 1 × 2 × ⋯ × x { displaystyle x! = 1 times 2 times cdots times x}, не может использоваться непосредственно для дробных значений x { displaystyle x}, поскольку он действителен только тогда, когда x является натуральным числом (или положительным целым числом). Условно говоря, таких простых решений для факториалов не существует; никакая конечная комбинация сумм, произведений, степеней, экспоненциальных функций или логарифмов не будет достаточной для выражения x! { displaystyle x!}; но можно найти общую формулу для факториалов, используя такие инструменты, как интегралы и пределы из исчисления. Хорошим решением этой проблемы является гамма-функция.

Существует бесконечно много непрерывных расширений факториала на нецелые числа: через любой набор изолированных точек можно провести бесконечно много кривых. Гамма-функция — это наиболее полезное решение на практике, поскольку она является аналитической (кроме неположительных целых чисел), и ее можно определить несколькими эквивалентными способами. Однако это не единственная аналитическая функция, которая расширяет факториал, так как добавление к нему любой аналитической функции, которая равна нулю для положительных целых чисел, например, k sin mπx, даст другую функцию с этим свойством.

Гамма-функция, Γ (z) синего цвета, построенная вместе с Γ (z) + sin (πz) зеленым цветом. Обратите внимание на пересечение в положительных целых числах, оба являются допустимыми аналитическими продолжениями факториалов до нецелых чисел

Более ограничивающим свойством, чем удовлетворение приведенной выше интерполяции, является удовлетворение рекуррентного отношения, определяющего переведенную версию факториальная функция,

f (1) = 1, { displaystyle f (1) = 1,}

f (x + 1) = xf (x), { displaystyle f (x + 1) = xf (x),}

для любого положительного действительного числа x. Но это позволило бы производить умножение на любую периодическую аналитическую функцию, которая дает значение 1 для положительных целых чисел, таких как e. Один из нескольких способов окончательно разрешить неоднозначность исходит из теоремы Бора – Моллерупа. Он утверждает, что когда добавляется условие, что f будет логарифмически выпуклым (или «супервыпуклым»), оно однозначно определяет f для положительных, реальных входов. Отсюда гамма-функция может быть расширена на все действительные и комплексные значения (кроме отрицательных целых чисел и нуля) с помощью уникального аналитического продолжения f.

Определение

Основное определение

Обозначение Γ (z) { displaystyle Gamma (z)}связано с Legendre. Если действительная часть комплексного числа z положительна (ℜ (z)>0 { displaystyle Re (z)>0}), затем интеграл

Γ (z) = ∫ 0 ∞ xz — 1 e — xdx { displaystyle Gamma (z) = int _ {0} ^ { infty} x ^ {z-1} e ^ {- x} , dx} ${ displaystyle Gamma (z) = int _ {0} ^ { infty} x ^ {z-1} e ^ {- x} , dx}$

сходится абсолютно и известен как интеграл Эйлера второго рода . (Интеграл Эйлера первого рода — это бета-функция.) Используя интегрирование по частям, видно, что:

Γ (z + 1) = ∫ 0 ∞ xze — xdx = [- xze — x] 0 ∞ + ∫ 0 ∞ zxz — 1 e — xdx = lim x → ∞ (- xze — x) — (- 0 ze — 0) + Z ∫ 0 ∞ xz — 1 е — xdx. { Displaystyle { begin {align} Gamma (z + 1) = int _ {0} ^ { infty} x ^ {z} e ^ {- x} , dx \ = { Big [} -x ^ {z} e ^ {- x} { Big]} _ {0} ^ { infty} + int _ {0} ^ { infty} zx ^ {z-1} e ^ {- x} , dx \ = lim _ {x to infty} (- x ^ {z} e ^ { -x}) — (- 0 ^ {z} e ^ {- 0}) + z int _ {0} ^ { inft y} x ^ {z-1} e ^ {- x} , dx. end {align}}} ${ displaystyle { begin {align} Gamma (z + 1) = int _ {0} ^ { infty} x ^ {z} e ^ {-x} , dx \ = { Big [} -x ^ {z} e ^ {- x} { Big]} _ {0} ^ { infty} + int _ {0} ^ { infty} zx ^ {z-1} e ^ {- x} , dx \ = lim _ {x to infty} (- x ^ {z} e ^ {- x}) - ( -0 ^ {z} e ^ {- 0}) + z int _ {0} ^ { infty} x ^ {z-1} e ^ {- x} , dx. End {align}}}$

Признавая, что — xze — x → 0 { displaystyle -x ^ {z} e ^ {- x} к 0} ${ displaystyle -x ^ {z} е ^ {- x} к 0}$ как x → ∞, { displaystyle x to infty,}

Γ (z + 1) = z ∫ 0 ∞ xz — 1 е — xdx = z Γ (z). { Displaystyle { begin {align} Gamma (z + 1) = z int _ {0} ^ { infty} x ^ {z-1} e ^ {- x} , dx \ = z Gamma (z). end {align}}} ${ displaystyle { begin {align} Gamma (z + 1) = z int _ {0} ^ { infty} x ^ {z-1 } e ^ {- x} , dx \ = z Gamma (z). end {align}}}$

Мы можем вычислить Γ (1): { displaystyle Gamma (1) { text {:}}}

Γ (1) = ∫ 0 ∞ x 1 — 1 e — xdx = [- e — x] 0 ∞ = lim x → ∞ (- e — x) — (- e — 0) = 0 — (- 1) = 1. { displaystyle { begin {align} Gamma (1) = int _ {0} ^ { infty} x ^ {1-1} e ^ {- x} , dx \ = { Big [ } -e ^ {- x} { Big]} _ {0} ^ { infty} \ = lim _ {x to infty} (- e ^ {- x}) — (- e ^ {-0}) \ = 0 — (- 1) \ = 1. end {align}}} ${ displaystyle { begin {align} Gamma (1) = int _ {0} ^ { infty} x ^ {1-1} e ^ {- x} , dx \ = { Big [} -e ^ {- x} { Big]} _ {0} ^ { infty} \ = lim _ {x to infty} (- e ^ {- x}) - ( -e ^ {- 0}) \ = 0 - (- 1) \ = 1. end {align}}}$

Учитывая, что Γ (1) = 1 { displaystyle Gamma (1) = 1}и Γ (n + 1) = n Γ (n), { displaystyle Gamma (n + 1) = n Gamma (n),}

Γ ( п) знак равно 1 ⋅ 2 ⋅ 3 ⋯ (п — 1) знак равно (п — 1)! { displaystyle Gamma (n) = 1 cdot 2 cdot 3 cdots (n-1) = (n-1)!}

для всех положительных целых чисел n. Это можно рассматривать как пример доказательства по индукции.

Тождество Γ (z) = Γ (z + 1) z { textstyle Gamma (z) = { frac { Gamma ( z + 1)} {z}}} ${ textstyle Gamma (z) = { frac { Gamma (z + 1)} {z}}}$ (или, с тем же результатом, может использоваться аналитическое продолжение ), чтобы однозначно расширить интегральную формулировку для Γ (z) { displaystyle Gamma (z)}в мероморфную функцию, определенную для всех комплексных чисел z, кроме целых чисел, меньших или равных нулю. Именно эта расширенная версия обычно называется гамма-функцией.

Альтернативные определения

Определение Эйлера как бесконечного произведения

При приближении z! { displaystyle z!}для комплексного числа z { displaystyle z}эффективно сначала вычислить n! { displaystyle n!}для некоторого большого целого числа n { displaystyle n}. Используйте это, чтобы приблизить значение для (n + z)! { displaystyle (n + z)!}, а затем используйте соотношение рекурсии m! = м (м — 1)! { displaystyle m! = m (m-1)!}назад n { displaystyle n}раз, чтобы приблизить его к z! { displaystyle z!}. Кроме того, это приближение является точным в пределе, поскольку n { displaystyle n}стремится к бесконечности.

В частности, для фиксированного целого числа m { displaystyle m}это тот случай, когда

lim n → ∞ n! (П + 1) м (П + м)! = 1. { displaystyle lim _ {n to infty} { frac {n! ; (n + 1) ^ {m}} {(n + m)!}} = 1 ,.} ${ displaystyle lim _ {n to infty} { frac {n! ; (N + 1) ^ {m}} {(n + m)!}} = 1 ,.}$

Если m { displaystyle m}не является целым числом, поэтому невозможно сказать, верно ли это уравнение, потому что мы еще (в этом разделе) не определили факториальную функцию для нецелых чисел. Однако мы действительно получаем уникальное расширение факториальной функции на нецелые числа, настаивая на том, чтобы это уравнение продолжало выполняться, когда произвольное целое число m { displaystyle m}заменяется произвольным комплексным число z { displaystyle z}.

lim n → ∞ n! (N + 1) Z (N + Z)! = 1. { displaystyle lim _ {n to infty} { frac {n! ; (n + 1) ^ {z}} {(n + z)!}} = 1 ,.} ${ displaystyle lim _ {n to infty} { frac {n! ; (n +1) ^ {z}} {(n + z)!}} = 1 ,.}$

Умножение обе стороны на z! { displaystyle z!}дает

z! = lim n → ∞ n! z! (п + з)! (n + 1) z = lim n → ∞ (1 ⋯ n) 1 (1 + z) ⋯ (n + z) ((2 1) (3 2) ⋯ (n + 1 n)) z = ∏ n = 1 ∞ [1 1 + zn (1 + 1 n) z]. { displaystyle { begin {align} z! = lim _ {n to infty} n! { frac {z!} {(n + z)!}} (n + 1) ^ {z} \ [8pt] = lim _ {n to infty} (1 cdots n) { frac {1} {(1 + z) cdots (n + z)}} left ( left ( { frac {2} {1}} right) left ({ frac {3} {2}} right) cdots left ({ frac {n + 1} {n}} right) справа) ^ {z} \ [8pt] = prod _ {n = 1} ^ { infty} left [{ frac {1} {1 + { frac {z} {n}}}} left (1 + { frac {1} {n}} right) ^ {z} right]. end {align}}} ${ displaystyle { begin {align} z! = lim _ {n to infty} n! { frac {z!} {(n + z)!}} (n + 1) ^ {z} \ [8pt ] = lim _ {n to infty} (1 cdots n) { frac {1} {(1 + z) cdots (n + z)}} left ( left ({ frac { 2} {1}} right) lef t ({ frac {3} {2}} right) cdots left ({ frac {n + 1} {n}} right) right) ^ {z} \ [8pt] = prod _ {n = 1} ^ { infty} left [{ frac {1} {1 + { frac {z} {n}}}} left (1 + { frac {1} {n}) } right) ^ {z} right]. end {align}}}$

Это бесконечное произведение сходится для всех комплексных чисел z { displaystyle z}кроме отрицательных целых чисел, которые не выполняются из-за попытки использовать соотношение рекурсии m! = м (м — 1)! { displaystyle m! = m (m-1)!}назад через значение m = 0 { displaystyle m = 0} m=0 включает деление на ноль.

Аналогично для гамма-функции определение как бесконечное произведение из-за Эйлера действительно для всех комплексных чисел z { displaystyle z}кроме целые неположительные числа:

Γ (z) = 1 z ∏ n = 1 ∞ (1 + 1 n) z 1 + zn. { displaystyle Gamma (z) = { frac {1} {z}} prod _ {n = 1} ^ { infty} { frac { left (1 + { frac {1} {n}) } right) ^ {z}} {1 + { frac {z} {n}}}} ,.} ${ displaystyle Gamma (z) = { frac {1} {z}} prod _ {n = 1} ^ { infty } { frac { left (1 + { frac {1} {n}} right) ^ {z}} {1 + { frac {z} {n}}}} ,.}$

По этой конструкции гамма-функция является единственной функцией, которая одновременно удовлетворяет Γ ( 1) знак равно 1 { Displaystyle Gamma (1) = 1}, Γ (z + 1) = z Γ (z) { displaystyle Gamma (z + 1) = z Gamma (z)}для всех комплексных чисел z { displaystyle z}кроме неположительных целых чисел, и lim n → ∞ Γ (n + z) Γ (n) nz = 1 { textstyle lim _ {n to infty} { frac { Gamma (n + z)} { Gamma (n) ; n ^ {z}}} = 1} ${ textstyle lim _ {n to infty} { frac { Gamma (n + z)} { Gamma (n) ; n ^ {z}}} = 1}$ для всех комплексных чисел z { displaystyle z}.

Определение Вейерштрасса

Определение для гамма-функции из-за Вейерштрасса также действительно для всех комплексных чисел z, кроме не -положительные целые числа:

Γ (z) = e — γ zz ∏ n = 1 ∞ (1 + zn) — 1 ez / n, { displaystyle Gamma (z) = { frac {e ^ {- гамма z}} {z}} prod _ {n = 1} ^ { infty} left (1 + { frac {z} {n}} right) ^ {- 1} e ^ {z / n },} ${ displaystyle Gamma (z) = { frac {e ^ {- gamma z}} {z}} prod _ {n = 1 } ^ { infty} left (1 + { frac {z} {n}} right) ^ {- 1} e ^ {z / n},}$

где e γ ≈ 0,577216 { displaystyle gamma приблизительно 0,577216}— константа Эйлера – Маскерони. Это Произведение Адамара из 1 / Γ (z) { displaystyle 1 / Gamma (z)}в переписанном виде. Действительно, поскольку 1 / Γ (z) { displaystyle 1 / Gamma (z)}— это целое рода 1 с простым нулем в z = 0 { displaystyle z = 0} z = 0 , имеем представление продукта

1 Γ (z) = ze A z + B ∏ ρ (1 — z ρ) ez / ρ, { displaystyle { frac {1} { Gamma (z)}} = ze ^ {Az + B} prod _ { rho} left (1 — { frac {z} { rho}} right) e ^ { z / rho},} ${ displaystyle { frac { 1} { Gamma (z)}} = ze ^ {Az + B} prod _ { rho} left (1 - { frac {z} { rho}} right) e ^ {z / rho},}$

где произведение находится над нулями ρ ≠ 0 { displaystyle rho neq 0}of 1 / Γ (z) { displaystyle 1 / Gamma (z)}. Поскольку Γ (z) { displaystyle Gamma (z)}имеет простые полюса при неположительных целых числах, из этого следует, что 1 / Γ (z) { displaystyle 1 / Gamma (z)}имеет простые нули при неположительных целых числах, поэтому приведенное выше уравнение становится формулой Вейерштрасса с — A z — B { displaystyle -Az-B}вместо — γ z { displaystyle — gamma z}. Вывод констант A = γ { displaystyle A = gamma}и B = 0 { displaystyle B = 0} B = 0 носит несколько технический характер, но может быть выполнено с использованием некоторых идентификаторов, включающих дзета-функцию Римана (см., например, этот идентификатор ). См. Также теорему факторизации Вейерштрасса.

В терминах обобщенных полиномов Лагерра

Представление неполной гамма-функции в терминах обобщенных полиномов Лагерра является

Γ (z, x) знак равно xze — x ∑ n знак равно 0 ∞ L n (z) (x) n + 1, { displaystyle Gamma (z, x) = x ^ {z} e ^ {- x} sum _ {n = 0} ^ { infty} { frac {L_ {n} ^ {(z)} (x)} {n + 1}},} ${ displaystyle Gamma (z, x) = x ^ {z} e ^ {- x} sum _ {n = 0} ^ { infty} { frac {L_ {n} ^ { (z)} (x)} {n + 1}},}$

который сходится для ℜ (z)>- 1 { displaystyle Re (z)>- 1}и x>0 { displaystyle x>0} x>0 .

Свойства

Общие

Другими важными функциональными уравнениями для гамма-функции являются формула отражения Эйлера

Γ (1 — z) Γ (z) = π sin ⁡ (π z), z ∉ Z { displaystyle Gamma (1-z) Gamma (z) = { pi over sin ( pi z)}, qquad z not in mathbb {Z}}

, что означает

Γ (ε — N) знак равно (- 1) N — 1 Γ (- ε) Γ (1 + ε) Γ (n + 1 — ε), { Displaystyle Gamma ( varepsilon -n) = (- 1) ^ {n-1} ; { frac { Gamma (- varepsilon) Gamma (1+ varepsilon)} { Gamma (n + 1- varepsilon)}},} $Gamma ( varepsilon -n) = (- 1) ^ {n-1} ; { frac { Gamma (- varepsilon) Gamma (1+ varepsilon) } { Gamma (п + 1- varepsilon)}},$

и Формула дублирования Лежандра

Γ (z) Γ (z + 1 2) = 2 1 — 2 z π Γ (2 z). { displaystyle Gamma (z) Gamma left (z + { tfrac {1} {2}} right) = 2 ^ {1-2z} ; { sqrt { pi}} ; Gamma ( 2z).} ${ displaystyle Gamma (z) Gamma left (z + { tfrac {1} {2}} right) = 2 ^ {1-2z} ; { sqrt { pi}} ; Gamma ( 2z).}$

Вывод формулы Эйлера отражения
Поскольку e — t = lim n → ∞ (1 — tn) n, { displaystyle e ^ {- t} = lim _ {n to infty} left (1 — { frac {t} {n}} right) ^ {n},} ${ displa ystyle e ^ {- t} = lim _ {n to infty} left (1 - { frac {t} {n}} right) ^ {n},}$ гамма-функция может быть представлена как Γ (z) = lim n → ∞ ∫ 0 нтз — 1 (1 — тн) ндт. { displaystyle Gamma (z) = lim _ {n to infty} int _ {0} ^ {n} t ^ {z-1} left (1 — { frac {t} {n}) } right) ^ {n} , dt.} ${ displaystyle Gamma (z) = lim _ {n to infty} int _ {0} ^ {n} t ^ {z-1} left (1 - { frac {t} {n}} right) ^ {n} , dt.}$ Интегрирование по частям n { displaystyle n}раз дает Γ (z) = lim n → ∞ nnz ⋅ N — 1 N (Z + 1) ⋅ N — 2 N (Z + 2) ⋯ 1 N (Z + N — 1) ∫ 0 NTZ + N — 1 dt, { Displaystyle Gamma (z) = lim _ {n to infty} { frac {n} {nz}} cdot { frac {n-1} {n (z + 1)}} cdot { frac {n-2} {n (z +2)}} cdots { frac {1} {n (z + n-1)}} int _ {0} ^ {n} t ^ {z + n-1} , dt,} ${ displayst yle Gamma (z) = lim _ {n to infty} { frac {n} {nz}} cdot { frac {n-1} {n (z + 1)}} cdot { гидроразрыв {n-2} {n (z + 2)}} cdots { frac {1} {n (z + n-1)}} int _ {0} ^ {n} t ^ {z + n -1} , dt,}$ что равно Γ (z) = lim n → ∞ n! N N ∏ К знак равно 0 N (Z + К) — 1 N Z + N. { displaystyle Gamma (z) = lim _ {n to infty} { frac {n!} {n ^ {n}}} prod _ {k = 0} ^ {n} (z + k) ^ {- 1} n ^ {z + n}.} ${ displaystyle Gamma (z) = lim _ {n to infty} { frac {n!} {N ^ {n }}} prod _ {k = 0} ^ {n} (z + k) ^ {- 1} n ^ {z + n}.}$ Это можно переписать как Γ (z) = lim n → ∞ nzz ∏ k = 1 nkz + k = lim n → ∞ nzz ∏ к знак равно 1 n 1 1 + zk. { displaystyle Gamma (z) = lim _ {n to infty} { frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} { frac {k } {z + k}} = lim _ {n to infty} { frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 + { frac {z} {k}}}}.} ${ displaystyle Gamma (z) = lim _ {n to infty} { frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} { frac {k} {z + k}} = lim _ {n to infty} { frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 + { frac {z} {k}}}}.}$ Тогда, используя функциональное уравнение гамма-функции, получаем — z Γ (- z) Γ (z) = Γ ( 1 — z) Γ (z) = lim n → ∞ 1 z ∏ k знак равно 1 n 1 1 — z 2 k 2. { Displaystyle -z Gamma (-z) Gamma (z) = Gamma (1-z) Gamma (z) = lim _ {n to infty} { frac {1} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 — { frac {z ^ {2}} {k ^ {2}}}}}.} ${ displaystyle -z Gamma (-z) Гамма (z) = Gamma (1-z) Gamma (z) = lim _ {n to infty} { frac {1} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 - { frac {z ^ {2}} {k ^ {2}}}}}.}$ Может быть доказал, что sin ⁡ (π z) = π z ∏ k = 1 ∞ (1 — z 2 k 2). { displaystyle sin ( pi z) = pi z prod _ {k = 1} ^ { infty} left (1 — { frac {z ^ {2}} {k ^ {2}}} right).} ${ displaystyle sin ( pi z) = pi z prod _ {k = 1} ^ { infty} left (1 - { frac {z ^ {2}} {k ^ {2 }}} right).}$ Тогда π sin ⁡ (π z) = lim n → ∞ 1 z ∏ k = 1 n 1 1 — z 2 k 2. { Displaystyle { frac { pi} { sin ( pi z)}} = lim _ {n to infty} { frac {1} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 — { frac {z ^ {2}} {k ^ {2}}}}}.} ${ Displaystyle { frac { pi} { sin ( pi z)}} = lim _ {n to infty} { frac {1} {z}} prod _ {k = 1} ^ { n} { frac {1} {1 - { frac {z ^ {2}} {k ^ {2}}}}}.}$ Формула отражения Эйлера следующая: Γ (1 — z) Γ (z) = π sin ⁡ (π z), z ∉ Z. { Displaystyle Gamma (1-z) Gamma (z) = { frac { pi} { sin ( pi z)}}, qquad z not in mathbb {Z}.} ${ displaystyle Gamma (1-z) Gamma (z) = { frac { pi} { sin ( pi z)}}, qquad z not in mathbb {Z}.}$

Вывод формулы Эйлера отражения

Поскольку e — t = lim n → ∞ (1 — tn) n, { displaystyle e ^ {- t} = lim _ {n to infty} left (1 — { frac {t} {n}} right) ^ {n},} ${ displa ystyle e ^ {- t} = lim _ {n to infty} left (1 - { frac {t} {n}} right) ^ {n},}$

гамма-функция может быть представлена как

Γ (z) = lim n → ∞ ∫ 0 нтз — 1 (1 — тн) ндт. { displaystyle Gamma (z) = lim _ {n to infty} int _ {0} ^ {n} t ^ {z-1} left (1 — { frac {t} {n}) } right) ^ {n} , dt.} ${ displaystyle Gamma (z) = lim _ {n to infty} int _ {0} ^ {n} t ^ {z-1} left (1 - { frac {t} {n}} right) ^ {n} , dt.}$

Интегрирование по частям n { displaystyle n}раз дает

Γ (z) = lim n → ∞ nnz ⋅ N — 1 N (Z + 1) ⋅ N — 2 N (Z + 2) ⋯ 1 N (Z + N — 1) ∫ 0 NTZ + N — 1 dt, { Displaystyle Gamma (z) = lim _ {n to infty} { frac {n} {nz}} cdot { frac {n-1} {n (z + 1)}} cdot { frac {n-2} {n (z +2)}} cdots { frac {1} {n (z + n-1)}} int _ {0} ^ {n} t ^ {z + n-1} , dt,} ${ displayst yle Gamma (z) = lim _ {n to infty} { frac {n} {nz}} cdot { frac {n-1} {n (z + 1)}} cdot { гидроразрыв {n-2} {n (z + 2)}} cdots { frac {1} {n (z + n-1)}} int _ {0} ^ {n} t ^ {z + n -1} , dt,}$

что равно

Γ (z) = lim n → ∞ n! N N ∏ К знак равно 0 N (Z + К) — 1 N Z + N. { displaystyle Gamma (z) = lim _ {n to infty} { frac {n!} {n ^ {n}}} prod _ {k = 0} ^ {n} (z + k) ^ {- 1} n ^ {z + n}.} ${ displaystyle Gamma (z) = lim _ {n to infty} { frac {n!} {N ^ {n }}} prod _ {k = 0} ^ {n} (z + k) ^ {- 1} n ^ {z + n}.}$

Это можно переписать как

Γ (z) = lim n → ∞ nzz ∏ k = 1 nkz + k = lim n → ∞ nzz ∏ к знак равно 1 n 1 1 + zk. { displaystyle Gamma (z) = lim _ {n to infty} { frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} { frac {k } {z + k}} = lim _ {n to infty} { frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 + { frac {z} {k}}}}.} ${ displaystyle Gamma (z) = lim _ {n to infty} { frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} { frac {k} {z + k}} = lim _ {n to infty} { frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 + { frac {z} {k}}}}.}$

Тогда, используя функциональное уравнение гамма-функции, получаем

— z Γ (- z) Γ (z) = Γ ( 1 — z) Γ (z) = lim n → ∞ 1 z ∏ k знак равно 1 n 1 1 — z 2 k 2. { Displaystyle -z Gamma (-z) Gamma (z) = Gamma (1-z) Gamma (z) = lim _ {n to infty} { frac {1} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 — { frac {z ^ {2}} {k ^ {2}}}}}.} ${ displaystyle -z Gamma (-z) Гамма (z) = Gamma (1-z) Gamma (z) = lim _ {n to infty} { frac {1} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 - { frac {z ^ {2}} {k ^ {2}}}}}.}$

Может быть доказал, что

sin ⁡ (π z) = π z ∏ k = 1 ∞ (1 — z 2 k 2). { displaystyle sin ( pi z) = pi z prod _ {k = 1} ^ { infty} left (1 — { frac {z ^ {2}} {k ^ {2}}} right).} ${ displaystyle sin ( pi z) = pi z prod _ {k = 1} ^ { infty} left (1 - { frac {z ^ {2}} {k ^ {2 }}} right).}$

Тогда

π sin ⁡ (π z) = lim n → ∞ 1 z ∏ k = 1 n 1 1 — z 2 k 2. { Displaystyle { frac { pi} { sin ( pi z)}} = lim _ {n to infty} { frac {1} {z}} prod _ {k = 1} ^ {n} { frac {1} {1 — { frac {z ^ {2}} {k ^ {2}}}}}.} ${ Displaystyle { frac { pi} { sin ( pi z)}} = lim _ {n to infty} { frac {1} {z}} prod _ {k = 1} ^ { n} { frac {1} {1 - { frac {z ^ {2}} {k ^ {2}}}}}.}$

Формула отражения Эйлера следующая:

Γ (1 — z) Γ (z) = π sin ⁡ (π z), z ∉ Z. { Displaystyle Gamma (1-z) Gamma (z) = { frac { pi} { sin ( pi z)}}, qquad z not in mathbb {Z}.} ${ displaystyle Gamma (1-z) Gamma (z) = { frac { pi} { sin ( pi z)}}, qquad z not in mathbb {Z}.}$

Вывод формулы дублирования Лежандра
бета-функция может быть представлена как B (z 1, z 2) = Γ (z 1) Γ (z 2) Γ (z 1 + z 2) знак равно ∫ 0 1 tz 1 — 1 (1 — t) z 2 — 1 dt. { Displaystyle mathrm {B} (z_ {1}, z_ {2}) = { frac { Gamma (z_ {1}) Gamma (z_ {2})} { Gamma (z_ {1} + z_ {2})}} = int _ {0} ^ {1} t ^ {z_ {1} -1} (1-t) ^ {z_ {2} -1} , dt.} ${ displaystyle mathrm {B} (z_ {1}, z_ {2}) = { frac { Gamma (z_ {1}) Gamma (z_ {2})} { Gamma (z_ {1} + z_ {2})}} = int _ {0} ^ {1} t ^ {z_ {1} -1} (1-t) ^ {z_ {2} -1} , dt.}$ Установка z 1 = z 2 = z { displaystyle z_ {1} = z_ {2} = z} ${ displaystyle z_ {1} = z_ {2} = z}$ дает Γ 2 (z) Γ (2 z) = ∫ 0 1. tz — 1 (1 — t) z — 1 dt. { Displaystyle { frac { Gamma ^ {2} (z)} { Gamma (2z)}} = int _ {0} ^ {1} t ^ {z-1} (1-t) ^ { z-1} , dt.} ${ displaystyle { frac { Gamma ^ {2} (z)} { Gamma (2z)}} = int _ {0 } ^ {1} t ^ {z-1} (1-t) ^ {z-1} , dt.}$ После замены t = 1 + x 2 { displaystyle t = { frac {1 + x} {2}}} ${ displaystyle t = { frac {1 + x } {2}}}$ получаем Γ 2 (z) Γ (2 z) = 1 2 2 z — 1 ∫ — 1 1 (1 — x 2) z — 1 dx. { displaystyle { frac { Gamma ^ {2} (z)} { Gamma (2z)}} = { frac {1} {2 ^ {2z-1}}} int _ {- 1} ^ {1} left (1-x ^ {2} right) ^ {z-1} , dx.} ${ displaystyle { frac { Gamma ^ {2} (z)} { Gamma ( 2z)}} = { frac {1} {2 ^ {2z-1}}} int _ {- 1} ^ {1} left (1-x ^ {2} right) ^ {z-1 } , dx.}$ Функция (1 — x 2) z — 1 { displaystyle (1- x ^ {2}) ^ {z-1}} ${ displaystyle (1-x ^ {2}) ^ {z-1}}$ четно, поэтому 2 2 z — 1 Γ 2 (z) = 2 Γ (2 z) ∫ 0 1 (1 — x 2) z — 1 дх. { Displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = 2 Gamma (2z) int _ {0} ^ {1} (1-x ^ {2}) ^ {z-1 } , dx.} ${ displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = 2 Gamma (2z) int _ {0} ^ {1} (1-x ^ {2}) ^ { z-1} , dx.}$ Теперь предположим, что B (1 2, z) = ∫ 0 1 t 1 2 — 1 (1 — t) z — 1 dt, t = s 2. { displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = int _ {0} ^ {1} t ^ {{ frac {1} {2}} -1} (1-t) ^ {z-1} , dt, quad t = s ^ {2}.} ${ displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = int _ {0} ^ {1} t ^ {{ frac {1} {2}} - 1} (1-t) ^ {z-1} , dt, quad t = s ^ {2}.}$ Тогда B (1 2, z) = 2 ∫ 0 1 (1 — s 2) z — 1 ds = 2 ∫ 0 1 (1 — x 2) z — 1 dx. { displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = 2 int _ {0} ^ {1} (1-s ^ {2}) ^ {z -1} , ds = 2 int _ {0} ^ {1} (1-x ^ {2}) ^ {z-1} , dx.} ${ displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = 2 int _ {0} ^ {1} (1-s ^ {2}) ^ {z -1} , ds = 2 int _ {0} ^ {1} (1-x ^ {2}) ^ {z-1} , dx.}$ Отсюда следует 2 2 z — 1 Γ 2 (z) = Γ (2 z) B (1 2, z). { displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = Gamma (2z) mathrm {B} left ({ frac {1} {2}}, z right).} ${ displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = Gamma (2z) mathrm {B} left ({ frac {1} {2}}, z right).}$ Поскольку B (1 2, z) = Γ (1 2) Γ (z) Γ (z + 1 2), Γ (1 2) = π, { displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = { frac { Gamma left ({ frac {1} {2}} right) Gamma (z)} { Gamma left (z + { frac {1} {2}} right)}}, quad Gamma left ({ frac {1} {2}} right) = { sqrt { pi}},} ${ displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = { frac { Гамма left ({ frac {1} {2}} right) Gamma (z)} { Gamma left (z + { frac {1} {2}} right)}}, quad Gamma left ({ frac {1} {2}} right) = { sqrt { pi}},}$ формула дублирования Лежандра следует: Γ (z) Γ (z + 1 2) = 2 1 — 2 z π Γ (2 z). { Displaystyle Gamma (z) Gamma left (z + { frac {1} {2}} right) = 2 ^ {1-2z} { sqrt { pi}} ; Gamma (2z).} ${ displaystyle Gamma (z) Gamma влево (z + { frac {1} {2}} right) = 2 ^ {1-2z} { sqrt { pi}} ; Gamma (2z).}$

Вывод формулы дублирования Лежандра

бета-функция может быть представлена как

B (z 1, z 2) = Γ (z 1) Γ (z 2) Γ (z 1 + z 2) знак равно ∫ 0 1 tz 1 — 1 (1 — t) z 2 — 1 dt. { Displaystyle mathrm {B} (z_ {1}, z_ {2}) = { frac { Gamma (z_ {1}) Gamma (z_ {2})} { Gamma (z_ {1} + z_ {2})}} = int _ {0} ^ {1} t ^ {z_ {1} -1} (1-t) ^ {z_ {2} -1} , dt.} ${ displaystyle mathrm {B} (z_ {1}, z_ {2}) = { frac { Gamma (z_ {1}) Gamma (z_ {2})} { Gamma (z_ {1} + z_ {2})}} = int _ {0} ^ {1} t ^ {z_ {1} -1} (1-t) ^ {z_ {2} -1} , dt.}$

Установка z 1 = z 2 = z { displaystyle z_ {1} = z_ {2} = z} ${ displaystyle z_ {1} = z_ {2} = z}$ дает

Γ 2 (z) Γ (2 z) = ∫ 0 1. tz — 1 (1 — t) z — 1 dt. { Displaystyle { frac { Gamma ^ {2} (z)} { Gamma (2z)}} = int _ {0} ^ {1} t ^ {z-1} (1-t) ^ { z-1} , dt.} ${ displaystyle { frac { Gamma ^ {2} (z)} { Gamma (2z)}} = int _ {0 } ^ {1} t ^ {z-1} (1-t) ^ {z-1} , dt.}$

После замены t = 1 + x 2 { displaystyle t = { frac {1 + x} {2}}} ${ displaystyle t = { frac {1 + x } {2}}}$ получаем

Γ 2 (z) Γ (2 z) = 1 2 2 z — 1 ∫ — 1 1 (1 — x 2) z — 1 dx. { displaystyle { frac { Gamma ^ {2} (z)} { Gamma (2z)}} = { frac {1} {2 ^ {2z-1}}} int _ {- 1} ^ {1} left (1-x ^ {2} right) ^ {z-1} , dx.} ${ displaystyle { frac { Gamma ^ {2} (z)} { Gamma ( 2z)}} = { frac {1} {2 ^ {2z-1}}} int _ {- 1} ^ {1} left (1-x ^ {2} right) ^ {z-1 } , dx.}$

Функция (1 — x 2) z — 1 { displaystyle (1- x ^ {2}) ^ {z-1}} ${ displaystyle (1-x ^ {2}) ^ {z-1}}$ четно, поэтому

2 2 z — 1 Γ 2 (z) = 2 Γ (2 z) ∫ 0 1 (1 — x 2) z — 1 дх. { Displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = 2 Gamma (2z) int _ {0} ^ {1} (1-x ^ {2}) ^ {z-1 } , dx.} ${ displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = 2 Gamma (2z) int _ {0} ^ {1} (1-x ^ {2}) ^ { z-1} , dx.}$

Теперь предположим, что

B (1 2, z) = ∫ 0 1 t 1 2 — 1 (1 — t) z — 1 dt, t = s 2. { displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = int _ {0} ^ {1} t ^ {{ frac {1} {2}} -1} (1-t) ^ {z-1} , dt, quad t = s ^ {2}.} ${ displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = int _ {0} ^ {1} t ^ {{ frac {1} {2}} - 1} (1-t) ^ {z-1} , dt, quad t = s ^ {2}.}$

Тогда

B (1 2, z) = 2 ∫ 0 1 (1 — s 2) z — 1 ds = 2 ∫ 0 1 (1 — x 2) z — 1 dx. { displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = 2 int _ {0} ^ {1} (1-s ^ {2}) ^ {z -1} , ds = 2 int _ {0} ^ {1} (1-x ^ {2}) ^ {z-1} , dx.} ${ displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = 2 int _ {0} ^ {1} (1-s ^ {2}) ^ {z -1} , ds = 2 int _ {0} ^ {1} (1-x ^ {2}) ^ {z-1} , dx.}$

Отсюда следует

2 2 z — 1 Γ 2 (z) = Γ (2 z) B (1 2, z). { displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = Gamma (2z) mathrm {B} left ({ frac {1} {2}}, z right).} ${ displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = Gamma (2z) mathrm {B} left ({ frac {1} {2}}, z right).}$

Поскольку

B (1 2, z) = Γ (1 2) Γ (z) Γ (z + 1 2), Γ (1 2) = π, { displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = { frac { Gamma left ({ frac {1} {2}} right) Gamma (z)} { Gamma left (z + { frac {1} {2}} right)}}, quad Gamma left ({ frac {1} {2}} right) = { sqrt { pi}},} ${ displaystyle mathrm {B} left ({ frac {1} {2}}, z right) = { frac { Гамма left ({ frac {1} {2}} right) Gamma (z)} { Gamma left (z + { frac {1} {2}} right)}}, quad Gamma left ({ frac {1} {2}} right) = { sqrt { pi}},}$

формула дублирования Лежандра следует:

Γ (z) Γ (z + 1 2) = 2 1 — 2 z π Γ (2 z). { Displaystyle Gamma (z) Gamma left (z + { frac {1} {2}} right) = 2 ^ {1-2z} { sqrt { pi}} ; Gamma (2z).} ${ displaystyle Gamma (z) Gamma влево (z + { frac {1} {2}} right) = 2 ^ {1-2z} { sqrt { pi}} ; Gamma (2z).}$

Формула дублирования является частным случаем теоремы умножения (см. Уравнение 5.5.6)

∏ k = 0 m — 1 Γ (z + km) = (2 π) m — 1 2 m 1 2 — mz Γ (mz). { Displaystyle prod _ {к = 0} ^ {m-1} Gamma left (z + { frac {k} {m}} right) = (2 pi) ^ { frac {m-1 } {2}} ; m ^ {{ frac {1} {2}} — mz} ; Gamma (mz).} ${ displaystyle prod _ {k = 0} ^ {m-1} Gamma left (z + { frac {k} {m}} right) = (2 pi) ^ { frac {m-1} {2}} ; m ^ {{ frac {1} {2}} - mz} ; Gamma (mz).}$

Простое, но полезное свойство, которое видно из определения предела, есть:

Γ (z) ¯ = Γ (z ¯) ⇒ Γ (z) Γ (z ¯) ∈ R. { Displaystyle { overline { Gamma (z)}} = Gamma ({ overline {z}}) ; Rightarrow ; Gamma (z) Gamma ({ overline {z}}) in mathbb {R}.}

{ Displaystyle { overline { Gamma (z)}} = Gamma ({ overline {z}}) ; Rightarrow ; Gamma (z) Gamma ({ overline {z}}) в mathbb {R}.}

В частности, при z = a + bi этот продукт равен

| Γ (a + b i) | 2 = | Γ (a) | 2 ∏ К знак равно 0 ∞ 1 1 + б 2 (а + К) 2 { Displaystyle | Гамма (а + би) | ^ {2} = | Гамма (а) | ^ {2} prod _ {к = 0} ^ { infty} { frac {1} {1 + { frac {b ^ {2}} {(a + k) ^ {2}}}}}} ${ displaystyle | Gamma (a + bi) | ^ {2} = | Gamma (a) | ^ {2} prod _ {k = 0} ^ { infty} { frac {1} {1 + { frac {b ^) {2}} {(a + k) ^ {2}}}}}}$

Если действительная часть целое или полуцелое число, это может быть конечно выражено в закрытой форме :

| Γ (b i) | 2 = π b sh (π b) | Γ (1 2 + b i) | 2 = π ch ⁡ (π b) | Γ (1 + b i) | 2 = π b sh (π b) | Γ (1 + n + b i) | 2 = π b sinh ⁡ (π b) ∏ k = 1 n (k 2 + b 2), n ∈ N | Γ (- n + b i) | 2 = π b sinh ⁡ (π b) ∏ k = 1 n (k 2 + b 2) — 1, n ∈ N | Γ (1 2 ± n + b i) | 2 знак равно π cosh ⁡ (π b) ∏ К знак равно 1 N ((к — 1 2) 2 + b 2) ± 1, n ∈ N { Displaystyle { begin {выровнены} | Gamma (bi) | ^ { 2} = { frac { pi} {b sinh ( pi b)}} \ [6pt] | Gamma left ({ tfrac {1} {2}} + bi right) | ^ {2} = { frac { pi} { ch ( pi b)}} \ | Gamma left (1 + bi right) | ^ {2} = { frac { pi b } { sinh ( pi b)}} \ | Gamma left (1 + n + bi right) | ^ {2} = { frac { pi b} { sinh ( pi b) }} prod _ {k = 1} ^ {n} left (k ^ {2} + b ^ {2} right), quad n in mathbb {N} \ | Gamma left ( -n + bi right) | ^ {2} = { frac { pi} {b sinh ( pi b)}} prod _ {k = 1} ^ {n} left (k ^ { 2} + b ^ {2} right) ^ {- 1}, quad n in mathbb {N} \ | Gamma left ({ tfrac {1} {2}} pm n + bi right) | ^ {2} = { frac { pi} { cosh ( pi b)}} prod _ {k = 1} ^ {n} left ( left (k — { tfrac {1} {2}} right) ^ {2} + b ^ {2} right) ^ { pm 1}, quad n in mathbb {N} end {align}}} ${ displaystyle { begin {align} | Gamma (bi) | ^ {2} = { frac { pi} {b sinh ( pi b)}} \ [6pt] | Gamma left ({ tfrac {1} {2}} + bi right) | ^ {2} = { frac { pi} { cosh ( pi b)}} \ | Gamma left (1 + bi right) | ^ {2} = { frac { pi b} { sinh ( pi b)}} \ | Gamma left (1 + n + bi right) | ^ {2} = { frac { pi b} { sinh ( pi b)}} prod _ {k = 1} ^ {n} left (k ^ {2} + b ^ {2} right), quad n in mathbb {N} \ | Gamma left (-n + bi right) | ^ {2} = { frac { pi} {b sh ( pi b)}} prod _ {k = 1} ^ {n} left (k ^ {2} + b ^ {2} right) ^ {- 1}, quad n in mathbb {N} \ | Gamma left ({ tfrac {1} {2}} pm n + bi right) | ^ {2} = { frac { pi} { cosh ( pi b)}} prod _ {k = 1} ^ {n} left ( left (k - { tfrac {1} {2}} right) ^ {2} + b ^ {2 } right) ^ { pm 1}, quad n in mathbb {N} end {align}}}$

Доказательство формул для целой или полуцелой вещественной части
Сначала рассмотрим формулу отражения, примененную к z = bi { displaystyle z = bi}. Γ (bi) Γ (1 — bi) = π грех ⁡ (π би) { Displaystyle Гамма (би) Гамма (1-би) = { гидроразрыва { пи } { sin ( pi bi)}}} ${ displaystyle Gamma (bi) Gamma (1-bi) = { frac { pi} { sin ( pi bi)}}}$ Применяя рекуррентное соотношение ко второму члену, получаем — bi ⋅ Γ (bi) Γ (- bi) = π sin ⁡ (π bi) { displaystyle -bi cdot Gamma (bi) Gamma (-bi) = { frac { pi} { sin ( pi bi)}}} ${ displaystyle -bi cdot Gamma (bi) Gamma (-bi) = { frac { pi} { sin ( pi bi)}}}$ , что при простой перестановке дает Γ (bi) Γ (- bi) знак равно π — bi sin ⁡ (π bi) = π b sinh ⁡ (π b) { displaystyle Gamma (bi) Gamma (-bi) = { frac { pi} {- bi sin ( pi bi)}} = { frac { pi} {b sinh ( pi b)}}} ${ displaystyle Gamma (bi) Gamma (-bi) = { frac { pi} {- bi sin ( pi bi)}} = { frac { pi} {b sinh ( pi b)} }}$ Во-вторых, рассмотрим формулу отражения, примененную к z = 1 2 + bi { Displaystyle Z = { tfrac {1} {2}} + bi} ${ displaystyle z = { tfrac {1} {2}} + bi}$ . Γ (1 2 + bi) Γ (1 — (1 2 + bi)) = Γ (1 2 + bi) Γ (1 2 — bi) знак равно π грех ⁡ (π (1 2 + bi)) = π соз ⁡ (π bi) = π cosh ⁡ (π b) { displaystyle Gamma ({ tfrac {1} {2}} + bi) Gamma left (1 — ({ tfrac {1} {2}} + bi) right) = Gamma ({ tfrac {1} {2}} + bi) Gamma ({ tfrac {1 } {2}} — bi) = { frac { pi} { sin left ( pi ({ tfrac {1} {2}} + bi) right)}} = { frac { pi } { cos ( pi bi)}} = { frac { pi} { cosh ( pi b)}}} ${ displaystyle Gamma ({ tfrac {1} {2}} + bi) Gamma left (1 - ({ tfrac {1} {2}} + bi) right) = Gamma ({ tfrac {1} {2}} + bi) Gamma ({ tfrac {1} {2}} - bi) = { frac { pi} { sin left ( pi ({ tfrac {1} {2}} + bi) right)}} = { frac { pi} { cos ( pi bi)}} = { frac { pi} { cosh ( pi b)}}}$ Формулы для других значений z { d isplaystyle z}, для которого действительная часть является целым или полуцелым числом, быстро следует индукция с использованием рекуррентного отношения в положительном и отрицательном направлениях.

Доказательство формул для целой или полуцелой вещественной части

Сначала рассмотрим формулу отражения, примененную к z = bi { displaystyle z = bi}.

Γ (bi) Γ (1 — bi) = π грех ⁡ (π би) { Displaystyle Гамма (би) Гамма (1-би) = { гидроразрыва { пи } { sin ( pi bi)}}} ${ displaystyle Gamma (bi) Gamma (1-bi) = { frac { pi} { sin ( pi bi)}}}$

Применяя рекуррентное соотношение ко второму члену, получаем

— bi ⋅ Γ (bi) Γ (- bi) = π sin ⁡ (π bi) { displaystyle -bi cdot Gamma (bi) Gamma (-bi) = { frac { pi} { sin ( pi bi)}}} ${ displaystyle -bi cdot Gamma (bi) Gamma (-bi) = { frac { pi} { sin ( pi bi)}}}$

, что при простой перестановке дает

Γ (bi) Γ (- bi) знак равно π — bi sin ⁡ (π bi) = π b sinh ⁡ (π b) { displaystyle Gamma (bi) Gamma (-bi) = { frac { pi} {- bi sin ( pi bi)}} = { frac { pi} {b sinh ( pi b)}}} ${ displaystyle Gamma (bi) Gamma (-bi) = { frac { pi} {- bi sin ( pi bi)}} = { frac { pi} {b sinh ( pi b)} }}$

Во-вторых, рассмотрим формулу отражения, примененную к z = 1 2 + bi { Displaystyle Z = { tfrac {1} {2}} + bi} ${ displaystyle z = { tfrac {1} {2}} + bi}$ .

Γ (1 2 + bi) Γ (1 — (1 2 + bi)) = Γ (1 2 + bi) Γ (1 2 — bi) знак равно π грех ⁡ (π (1 2 + bi)) = π соз ⁡ (π bi) = π cosh ⁡ (π b) { displaystyle Gamma ({ tfrac {1} {2}} + bi) Gamma left (1 — ({ tfrac {1} {2}} + bi) right) = Gamma ({ tfrac {1} {2}} + bi) Gamma ({ tfrac {1 } {2}} — bi) = { frac { pi} { sin left ( pi ({ tfrac {1} {2}} + bi) right)}} = { frac { pi } { cos ( pi bi)}} = { frac { pi} { cosh ( pi b)}}} ${ displaystyle Gamma ({ tfrac {1} {2}} + bi) Gamma left (1 - ({ tfrac {1} {2}} + bi) right) = Gamma ({ tfrac {1} {2}} + bi) Gamma ({ tfrac {1} {2}} - bi) = { frac { pi} { sin left ( pi ({ tfrac {1} {2}} + bi) right)}} = { frac { pi} { cos ( pi bi)}} = { frac { pi} { cosh ( pi b)}}}$

Формулы для других значений z { d isplaystyle z}, для которого действительная часть является целым или полуцелым числом, быстро следует индукция с использованием рекуррентного отношения в положительном и отрицательном направлениях.

Возможно, наиболее известное значение гамма-функции при нецелочисленном аргументе:

Γ (1 2) = π, { displaystyle Gamma left ({ tfrac {1} {2}} справа) = { sqrt { pi}},} ${ displaystyle Gamma left ({ tfrac {1} {2}} right) = { sqrt { pi}},}$

, который можно найти, задав z = 1 2 { textstyle z = { frac {1} {2}}} ${ textstyle z = { frac {1} {2}}}$ в формулах отражения или дублирования, используя отношение к бета-функции, приведенной ниже, с x = y = 1 2 { textstyle x = y = { frac {1} {2} }} ${ textstyle x = y = { frac {1} {2}}}$ , или просто сделав замену u = x { displaystyle u = { sqrt {x}}}в интегральном определении гамма-функции, в результате в интеграле Гаусса. В общем, для неотрицательных целочисленных значений n { displaystyle n}мы имеем:

Γ (1 2 + n) = (2 n)! 4 н н! π = (2 п — 1)! ! 2 N π знак равно (N — 1 2 N) п! π Γ (1 2 — п) знак равно (- 4) п п! (2 п)! π знак равно (- 2) п (2 п — 1)! ! π знак равно π (- 1/2 п) п! { displaystyle { begin {align} Gamma left ({ tfrac {1} {2}} + n right) = {(2n)! over 4 ^ {n} n!} { sqrt { pi}} = { frac {(2n-1) !!} {2 ^ {n}}} { sqrt { pi}} = { binom {n — { frac {1} {2}}} {n}} n! { sqrt { pi}} \ [8pt] Gamma left ({ tfrac {1} {2}} — п право) = {(- 4) ^ {п} п! over (2n)!} { sqrt { pi}} = { frac {(-2) ^ {n}} {(2n-1) !!}} { sqrt { pi}} = { frac { sqrt { pi}} {{ binom {-1/2} {n}} n!}} end {align}}} ${ displaystyle { begin {align} Гамма left ({ tfrac {1} {2}} + n right) = {(2n)! over 4 ^ {n} n!} { sqrt { pi}} = { frac {(2n-1) !!} {2 ^ {n}}} { sqrt { pi}} = { binom {n - { frac {1} {2}}} {n}} n! { sqrt { pi}} \ [8pt] Gamma left ({ tfrac {1} {2}} - п право) = {(- 4) ^ {п} п! over (2n)!} { sqrt { pi}} = { frac {(-2) ^ {n}} {(2n-1) !!}} { sqrt { pi}} = { frac { sqrt { pi}} {{ binom {-1/2} {n}} n!}} end {align}}}$

где n! ! { displaystyle n !!} n !! обозначает двойной факториал числа n, а при n = 0 { displaystyle n = 0} n = 0 , n! ! = 1 { displaystyle n !! = 1}. См. Частные значения гамма-функции для расчетных значений.

Может возникнуть соблазн обобщить результат, что Γ (1 2) = π { textstyle Gamma left ({ frac {1} {2}} right) = { sqrt { pi}}} ${ textstyle Gamma left ({ frac {1} {2}} right) = { sqrt { pi}}}$ путем поиска формулы для других индивидуальных значений Γ (r) { displaystyle Gamma (r)}где r { displaystyle r}является рациональным, особенно потому, что согласно теореме Гаусса о дигамме, это возможно для тесно связанной функции дигаммы при любом рациональном значении. Однако неизвестно, что эти числа Γ (r) { displaystyle Gamma (r)}сами по себе выражаются в терминах элементарных функций. Доказано, что Γ (n + r) { displaystyle Gamma (n + r)}является трансцендентным числом и алгебраически независимым из π { displaystyle pi}для любого целого числа n { displaystyle n}и каждой дроби r = 1 6, 1 4, 1 3, 2 3, 3 4, 5 6 { textstyle r = { frac {1} {6}}, { frac {1} {4}}, { frac {1} {3}}, { frac {2} {3}}, { frac {3} {4}}, { frac {5} {6}}} ${ textstyle r = { frac {1} {6}}, { frac {1} {4}}, { frac {1} {3}}, { frac {2} {3}}, { frac {3} {4}}, { frac {5} {6 }}}$ . В общем, при вычислении значений гамма-функции мы должны ограничиваться численными приближениями.

Еще один полезный предел для асимптотических приближений:

lim n → ∞ Γ (n + α) Γ (n) n α = 1, α ∈ C. { displaystyle lim _ {n to infty} { frac { Gamma (n + alpha)} { Gamma (n) n ^ { alpha}}} = 1, qquad alpha in mathbb {C}.} ${ displaystyle lim _ {n to infty } { frac { Gamma (n + alpha)} { Gamma (n) n ^ { alpha}}} = 1, qquad alpha in mathbb {C}.}$

Производные гамма-функции описаны с помощью полигамма-функции. Например:

Γ ′ (z) = Γ (z) ψ 0 (z). { displaystyle Gamma ‘(z) = Gamma (z) psi _ {0} (z).} $Gamma '(z)=Gamma (z)psi _{0}(z).$

Для положительного целого числа m производная гамма-функции может быть вычислена следующим образом (здесь γ { displaystyle gamma} gamma — это постоянная Эйлера – Маскерони ):

Γ ′ (m + 1) = m! (- γ + ∑ k = 1 м 1 к). { displaystyle Gamma ‘(m + 1) = m! left (- gamma + sum _ {k = 1} ^ {m} { frac {1} {k}} right) ,.} ${displaystyle Gamma '(m+1)=m!left(-gamma +sum _{k=1}^{m}{frac {1}{k}}right),.}$

Для ℜ (x)>0 { displaystyle Re (x)>0}n { displaystyle n}-я производная гамма-функции:

Производная функции Γ (z)

dndxn Γ (x) = ∫ 0 ∞ tx — 1 e — t (ln ⁡ t) ndt. { displaystyle { frac {d ^ {n}} {dx ^ {n }}} Gamma (x) = int _ {0} ^ { infty} t ^ {x-1} e ^ {- t} ( ln t) ^ {n} , dt.} ${ displaystyle { frac {d ^ {n}} {dx ^ {n}}} Gamma (x) = int _ {0} ^ { infty} t ^ {х-1} е ^ {- t} ( ln t) ^ {n} , dt.}$

(Это может быть получено путем дифференцирования интегральной формы гамма-функции относительно x { displaystyle x}и использования техники дифференцирования под знаком интеграла.)

Используя тождество

Γ (n) (1) = (- 1) nn! ∑ π ⊢ n ∏ i = 1 r ζ ∗ (ai) ki! ⋅ ai ζ ∗ (x) : знак равно {ζ (Икс) Икс ≠ 1 γ Икс знак равно 1 { Displaystyle Gamma ^ {(n)} (1) = (- 1) ^ {n} п! сумма пределы _ { пи , vda sh , n} , prod _ {i = 1} ^ {r} { frac { zeta ^ {*} (a_ {i})} {k_ {i}! cdot a_ {i}}} qquad zeta ^ {*} (x): = { begin {cases} zeta (x) x neq 1 \ gamma x = 1 end {ases}}} ${ displaystyle Gamma ^ {(n)} (1) = (- 1) ^ {n} n! sum limits _ { pi , vdash , n} , prod _ {i = 1 } ^ {r} { frac { zeta ^ {*} (a_ {i})} {k_ {i}! cdot a_ {i}}} qquad zeta ^ {*} (x): = { begin {case} zeta (x) x neq 1 \ gamma x = 1 end {ases}}$

где ζ (z) { displaystyle zeta (z)}— это дзета-функция Римана,, и π { displaystyle pi}— это раздел из n { displaystyle n}, заданный как

π = a 1 + ⋯ + a 1 ⏟ k 1 термины + ⋯ + ar + ⋯ + ar ⏟ kr термины, { displaystyle pi = underbrace {a_ {1} + cdots + a_ {1}} _ {k_ {1} { text {terms}}} + cdots + underbrace {a_ {r} + cdots + a_ {r}} _ {k_ {r} { text {terms}}},} ${ displaystyle pi = underbrace {a_ {1} + cdots + a_ {1}} _ {k_ {1} { text {terms}}} + cdots + underbrace {a_ {r} + cdots + a_ {r}} _ {k_ {r} { text {terms}}},}$

мы имеем, в частности,

Γ (z) = 1 z — γ + 1 2 (γ 2 + π 2 6) z — 1 6 (γ 3 + γ π 2 2 + 2 ζ (3)) z 2 + O (z 3). { Displaystyle Gamma (z) = { frac {1} {z}} — gamma + { tfrac {1} {2}} left ( gamma ^ {2} + { frac { pi ^ {2}} {6}} right) z — { tfrac {1} {6}} left ( gamma ^ {3} + { frac { gamma pi ^ {2}} {2}} +2 zeta (3) right) z ^ {2} + O (z ^ {3}).} ${ displaystyle Gamma (z) = { frac {1} {z}} - gamma + { tfrac {1} {2}} left ( gamma ^ {2} + { frac { pi ^ {2}} {6}} right) z - { tfrac {1} {6}} left ( gamma ^ {3} + { frac { gamma pi ^ {2}} { 2}} + 2 zeta (3) right) z ^ {2} + O (z ^ {3}).}$

Неравенства

При ограничении положительными действительными числами гамма-функция является строго логарифмически выпуклая функция. Это свойство может быть указано любым из следующих трех эквивалентных способов:

Γ (tx 1 + (1 — t) x 2) ≤ Γ (x 1) t Γ (x 2) 1 — t. { Displaystyle Gamma (tx_ {1} + (1-t) x_ {2}) leq Gamma (x_ {1}) ^ {t} Gamma (x_ {2}) ^ {1-t}. } ${ displaystyle Gamma (tx_ {1} + (1-t) x_ {2 }) Leq Gamma (x_ {1}) ^ {t} Gamma (x_ {2}) ^ {1-t}.}$

Для любых двух положительных действительных чисел x и y, y>x,

(Γ (y) Γ (x)) 1 y — x>exp ⁡ (Γ ′ (x) Γ (x)). { displaystyle left ({ frac { Gamma (y)} { Gamma (x)}} right) ^ { frac {1} {yx}}> exp left ({ frac { Gamma ‘(x)} { Gamma (x)}} right).} ${displaystyle left({frac {Gamma (y)}{Gamma (x)}}right)^{frac {1}{y-x}}> exp left ({ frac { Gamma' (x)} { Gamma (x)}} right).}$

Для любого положительного вещественное число x { displaystyle x},

Γ ″ (x) Γ (x)>Γ ′ (x) 2. { displaystyle Gamma » (x) Gamma (x)> Gamma ‘ (x) ^ {2}.} ${displaystyle Gamma ''(x)Gamma (x)> Gamma '(x) ^ {2}.}$

Последний из этих операторов, по сути, по определению совпадает с утверждением, что ψ (1) (x)>0 { displaystyle psi ^ {(1)} (x)>0} ${displaystyle psi ^{(1)}(x)>0}$ , где ψ (1) { disp laystyle psi ^ {(1)}} ${ displaystyle psi ^ {( 1)}}$ — это полигамма-функция порядка 1. Чтобы доказать логарифмическую выпуклость гамма-функции, достаточно заметить, что ψ (1) { displaystyle psi ^ {(1)}} ${ displaystyle psi ^ {( 1)}}$ имеет представление ряда, которое для положительного действительного x состоит только из положительных членов.

Логарифмическая выпуклость и неравенство Дженсена вместе означают, что для любых положительных действительных чисел x 1,…, xn { displaystyle x_ {1}, ldots, x_ {n}} $x_ {1}, ldots, x_ {n}$ и a 1,…, an { displaystyle a_ {1}, ldots, a_ {n}},

Γ (a 1 x 1 + ⋯ + тревога 1 + ⋯ + an) ≤ (Γ (x 1) a 1 ⋯ Γ (xn) an) 1 a 1 + ⋯ + an. { displaystyle Gamma left ({ frac {a_ {1} x_ {1} + cdots + a_ {n} x_ {n}}) {a_ {1} + cdots + a_ {n}}} right) leq { bigl (} Gamma (x_ {1}) ^ {a_ {1}} cdots Gamma (x_ {n}) ^ {a_ {n}} { bigr)} ^ { frac { 1} {a_ {1} + cdots + a_ {n}}}.} ${ displaystyle Gamma left ({ frac {a_ {1} x_ {1} + cdots + a_ {n} x_ {n}} {a_ {1} + cdots + a_ {n}}} right) leq { bigl (} Gamma (x_ {1}) ^ {a_ {1}} cdots Gamma (x_ {n}) ^ {a_ {n}} { bigr)} ^ { frac {1} {a_ {1} + cdots + a_ {n}}}.}$

Также существуют ограничения на отношения гамма-функций. Наиболее известным является неравенство Гаучи, которое гласит, что для любого положительного действительного числа x и любого s ∈ (0, 1)

x 1 — s < Γ ( x + 1) Γ ( x + s) < ( x + 1) 1 − s. {displaystyle x^{1-s}<{frac {Gamma (x+1)}{Gamma (x+s)}}<(x+1)^{1-s}.} ${ displaystyle x ^ {1-s} <{ frac { Gamma (x + 1)} { Gamma (x + s)}} <(x + 1) ^ {1-s}.}$

формула Стирлинга

Представление гамма-функция в комплексной плоскости. Каждая точка z { displaystyle z}окрашена в соответствии с аргументом Γ (z) { displaystyle Gamma (z)}. Контурный график модуля | Γ (z) | { displaystyle | Gamma (z) |}также отображается. 3-мерный график абсолютного значения комплексной гамма-функции

Поведение Γ (z) { displaystyle Gamma (z)}для возрастающей положительной переменной просто. Он растет быстро, быстрее, чем экспоненциальная функция на самом деле. Асимптотически при z → ∞, { textstyle z to infty ,}величина гамма-функции задается формулой Стирлинга

Γ (z + 1) ∼ 2 π z (ze) z, { displaystyle Gamma (z + 1) sim { sqrt {2 pi z}} left ({ frac {z} {e}} right) ^ {z},} ${ displaystyle Gamma (z + 1) sim { sqrt {2 pi z}} left ({ frac {z} {e}} right) ^ {z},}$

где символ ∼ { displaystyle sim} sim подразумевает асимптотическую сходимость. Другими словами, отношение двух сторон сходится к 1 как z → + ∞ { textstyle z to + infty}.

Остатки

Поведение для неположительных z { displaystyle z}более сложный. Интеграл Эйлера не сходится для z ≤ 0 { displaystyle z leq 0}, но функция, которую он определяет в положительной комплексной полуплоскости, имеет уникальное аналитическое продолжение в отрицательную полуплоскость. Один из способов найти это аналитическое продолжение — использовать интеграл Эйлера для положительных аргументов и расширить область до отрицательных чисел путем повторного применения рекуррентной формулы

Γ (z) = Γ (z + n + 1) z (z + 1) ⋯ (Z + N), { Displaystyle Gamma (z) = { frac { Gamma (z + n + 1)} {z (z + 1) cdots (z + n)}},} ${ displaystyle Gamma (z) = { frac { Gamma (z + n + 1)} {z (z + 1) cdots (z + n)}},}$

выбор n { displaystyle n}так, чтобы z + n { displaystyle z + n}было положительным. Произведение в знаменателе равно нулю, если z { displaystyle z}равно любому из целых чисел 0, — 1, — 2, ⋯ { displaystyle 0, -1, -2., cdots}. Таким образом, гамма-функция должна быть неопределенной в этих точках, чтобы избежать деления на ноль ; это мероморфная функция с простыми полюсами в неположительных целых числах.

Для функции f { displaystyle f}сложной переменной z { displaystyle z}, на простом полюсе c { displaystyle c}, остаток из f { displaystyle f}определяется как:

Res ⁡ (f, c) = lim z → c (z — c) f (z). { displaystyle operatorname {Res} (f, c) = lim _ {z to c} (zc) f (z).} $operatorname {Res} (f, c) = lim _ {z to c} (zc) f ( z).$

Для простого полюса z = — n, { displaystyle z = -n,}перепишем рекуррентную формулу как:

(z + n) Γ (z) = Γ (z + n + 1) z (z + 1) ⋯ (z + n — 1). { Displaystyle (z + n) Gamma (z) = { frac { Gamma (z + n + 1)} {z (z + 1) cdots (z + n-1)}}.} ${ displaystyle (z + n) Gamma (z) = { frac { Gamma (z + n + 1)} {z (z + 1) cdots (z + n-1)}}.}$

Числитель в z = — n, { displaystyle z = -n,}равен

Γ (z + n + 1) = Γ (1) = 1 { displaystyle Гамма (z + n + 1) = Gamma (1) = 1}

{ displaystyle Gamma (z + n + 1) = Gamma (1) = 1}

и знаменатель

z (z + 1) ⋯ (z + n — 1) = — n (1 — n) ⋯ ( п — 1 — п) = (- 1) пп!. { displaystyle z (z + 1) cdots (z + n-1) = — n (1-n) cdots (n-1-n) = (- 1) ^ {n} n !.} ${ displaystyle z (z +1) cdots (z + n-1) = - n (1-n) cdots (n-1-n) = (- 1) ^ {n} n !.}$

Таким образом, вычеты гамма-функции в этих точках равны:

Res ⁡ (Γ, — n) = (- 1) nn!. { displaystyle operatorname {Res} ( Gamma, -n) = { frac {(-1) ^ {n}} {n!}}.} $operatorname {Res} ( Gamma, -n) = { frac {(-1) ^ {n}} {n!}}.$

Гамма-функция не равна нулю везде вдоль действительного линия, хотя она сколь угодно близка к нулю при z → −∞. На самом деле комплексного числа z { displaystyle z}для wh не существует ich Γ (z) = 0 { displaystyle Gamma (z) = 0}, и, следовательно, обратная гамма-функция 1 Γ (z) { textstyle { frac {1} { Gamma (z)}}} ${ textstyle { frac {1} { Gamma (z)} }}$ — это целая функция с нулями в z = 0, — 1, — 2, ⋯ { displaystyle z = 0, -1, -2, cdots}.

Minima

Гамма-функция имеет локальный минимум в z min ≈ +1,46163214496836234126 (усеченный), где достигает значения Γ (z min) ≈ +0,88560319441088870027 (усечено). Гамма-функция должна чередовать знак между полюсами, поскольку произведение в прямом повторении содержит нечетное количество отрицательных факторов, если количество полюсов между z { displaystyle z}и z + n { displaystyle z + n}нечетное число и четное число, если число полюсов четное.

Интегральные представления

Есть много формул, помимо Интеграл Эйлера второго рода, выражающий гамма-функцию как интеграл. Например, когда действительная часть z положительна,

Γ (z) = ∫ 0 1 (log ⁡ 1 t) z — 1 d t. { displaystyle Gamma (z) = int _ {0} ^ {1} left ( log { frac {1} {t}} right) ^ {z-1} , dt.} ${ displaystyle Gamma (z) = int _ {0} ^ {1} left ( log { frac {1} {t}} right) ^ {z -1} , dt.}$

Первая интегральная формула Бине для гамма-функции гласит, что, если действительная часть z положительна, то:

log ⁡ Γ (z) = (z — 1 2) log ⁡ z — z + 1 2 log ⁡ ( 2 π) + ∫ 0 ∞ (1 2 — 1 t + 1 et — 1) e — tztdt. { displaystyle log Gamma (z) = left (z — { frac {1} {2}} right) log z-z + { frac {1} {2}} log (2 pi) + int _ {0} ^ { infty} left ({ frac {1} {2}} — { frac {1} {t}} + { frac {1} {e ^ {t} -1}} right) { frac {e ^ {- tz}} {t}} , dt.} ${ displaystyle log Gamma (z) = left (z - { frac {1} {2}} right) log z-z + { frac {1} {2}} log (2 pi) + int _ {0} ^ { infty} left ({ frac {1} {2}} - { frac {1} {t} } + { frac {1} {e ^ {t} -1}} right) { frac {e ^ {- tz}} {t}} , dt.}$

Интеграл в правой части можно интерпретировать как преобразование Лапласа. То есть

log ⁡ (Γ (z) (e z) z 2 π z) = L (1 2 t — 1 t 2 + 1 t (e t — 1)) (z). { Displaystyle log left ( Gamma (z) left ({ frac {e} {z}} right) ^ {z} { sqrt {2 pi z}} right) = { mathcal {L}} left ({ frac {1} {2t}} — { frac {1} {t ^ {2}}} + { frac {1} {t (e ^ {t} -1) }} right) (z).} ${ displaystyle log left ( Gamma (z) left ({ frac {e} {z}} right) ^ {z} { sqrt {2 pi z}} right) = { mathcal {L}} left ({ frac {1} {2t}} - { frac {1} {t ^ {2}}} + { frac {1} {t (e ^ {t}) -1)}} right) (z).}$

Вторая интегральная формула Бине утверждает, что снова, когда действительная часть z положительна, тогда:

log ⁡ Γ (z) = (z — 1 2) log ⁡ z — z + 1 2 журнал ⁡ (2 π) + 2 ∫ 0 ∞ arctan ⁡ (t / z) e 2 π t — 1 dt. { displaystyle log Gamma (z) = left (z — { frac {1} {2}} right) log z-z + { frac {1} {2}} log (2 pi) +2 int _ {0} ^ { infty} { frac { arctan (t / z)} {e ^ {2 pi t} -1}} , dt.} ${ displaystyle log Gamma (z) = left (z - { frac {1} {2}} right) log z-z + { frac {1} { 2}} log (2 pi) +2 int _ {0} ^ { infty} { frac { arctan (t / z)} {e ^ {2 pi t} -1}} , dt.}$

Пусть C будет a контур Ганкеля, означающий путь, который начинается и заканчивается в точке ∞ на сфере Римана, единичный касательный вектор которого сходится к −1 в начале пути и к 1 в конец, имеющий число обмотки 1 вокруг 0 и не пересекающий [0, ∞). Зафиксируем ветвь журнала ⁡ (- t) { displaystyle log (-t)}, взяв отрезок ветви вдоль [0, ∞) и взяв log ⁡ (- t) { displaystyle log (-t)}быть действительным, когда t находится на отрицательной действительной оси. Предположим, что z не является целым числом. Тогда формула Ганкеля для гамма-функции:

Γ (z) = — 1 2 i sin ⁡ π z ∫ C (- t) z — 1 e — tdt, { displaystyle Gamma (z) = — { frac {1} {2i sin pi z}} int _ {C} (- t) ^ {z-1} e ^ {- t} , dt,} ${ displaystyle Gamma (z) = - { frac {1} {2i sin pi z}} int _ {C} (- t) ^ {z-1} e ^ {- t} , dt,}$

где (- t) z — 1 { displaystyle (-t) ^ {z-1}} ${ displaystyle (-t) ^ {z-1}}$ интерпретируется как exp ⁡ ((z — 1) log ⁡ (- t)) { displaystyle exp ((z-1) log (-t))}. Формула отражения приводит к тесно связанному выражению

1 Γ (z) = i 2 π ∫ C (- t) — ze — tdt, { displaystyle { frac {1} { Gamma (z)}} = { frac {i} {2 pi}} int _ {C} (- t) ^ {- z} e ^ {- t} , dt,} ${ displaystyle { frac {1} { Гамма (z)}} = { frac {i} {2 pi}} int _ {C} (- t) ^ {- z} e ^ {- t} , dt,}$

снова допустимо, если z не является целым числом.

Разложение в ряд Фурье

Логарифм гамма-функции имеет следующее разложение в ряд Фурье для 0 < z < 1 : {displaystyle 0

ln ⁡ Γ (z) = (1 2 — z) (γ + ln ⁡ 2) + (1 — z) ln ⁡ π — 1 2 ln ⁡ sin ⁡ (π z) + 1 π ∑ n = 1 ∞ ln ⁡ nn sin ⁡ (2 π nz), { displaystyle ln Gamma (z) = left ({ frac {1} {2}} — z right) ( gamma + ln 2) + (1-z) ln pi — { frac {1} {2}} ln sin ( pi z) + { frac {1} { pi}} sum _ {n = 1} ^ { infty} { frac { ln n} {n}} sin (2 pi nz),} ${ displaystyle ln Gamma (z) = left ({ frac {1} {2}} - z right) ( gamma + ln 2) + (1-z) ln pi - { frac {1} {2}} ln sin ( pi z) + { frac {1} { pi}} sum _ {n = 1 } ^ { infty} { frac { ln n} {n}} sin (2 pi nz),}$

который долгое время приписывался Эрнсту Куммеру, который вывел его в 1847 году. Однако обнаружил, что Карл Йохан Мальмстен впервые вывел этот ряд в 1842 году.

Формула Раабе

В 1840 году Джозеф Людвиг Раабе доказал, что

∫ aa + 1 ln ⁡ Γ ( z) dz = 1 2 ln ⁡ 2 π + a ln ⁡ a — a, a>0. { displaystyle int _ {a} ^ {a + 1} ln Gamma (z) , dz = { tfrac {1} {2}} ln 2 pi + a ln aa, quad a>0.} ${displaystyle int _{a}^{a+1}ln Gamma (z),dz={tfrac {1}{2}}ln 2pi +aln a-a,quad a>0.}$

В частности, если a = 0 { displaystyle a = 0} a = 0 , то

∫ 0 1 ln ⁡ Γ (z) dz = 1 2 ln ⁡ 2 π. { displaystyle int _ {0} ^ {1} ln Gamma (z) , dz = { tfrac {1} {2}} ln 2 pi.} ${ Displaystyle int _ {0} ^ {1} ln Gamma (z) , dz = { tfrac {1} {2}} ln 2 pi.}$

Последнее может быть выводится логарифмом в приведенной выше формуле умножения, которая дает выражение для суммы Римана подынтегрального выражения. Если взять предел для a → ∞ { displaystyle a rightarrow infty}, получаем формулу.

Функция Пи

Альтернативное обозначение, которое изначально было введено Гауссом и которое иногда использовалось, — это Π { displaystyle Pi}-функция, которая в терминах гамма-функции равна

Π (z) = Γ (z + 1) = z Γ (z) = ∫ 0 ∞ e — ttzdt, { displayst yle Pi (z) = Gamma (z + 1) = z Gamma (z) = int _ {0} ^ { infty} e ^ {- t} t ^ {z} , dt,} ${ displaystyle Pi (z) = Gamma (z + 1) = z Gamma (z) = int _ {0} ^ { infty} e ^ {- t } t ^ {z} , dt,}$

, так что Π (n) = n! { displaystyle Pi (n) = n!}для каждого неотрицательного целого числа n { displaystyle n}.

Используя функцию пи, формула отражения принимает форму

Π (z) Π (- z) знак равно π z грех ⁡ (π z) = 1 грех ⁡ (z) { displaystyle Pi (z) Pi (-z) = { frac { pi z} { sin ( pi z)}} = { frac {1} { operatorname {sinc} (z)}}} ${ displaystyle Pi (z) Pi (-z) = { frac { pi z} { sin ( pi z)}} = { frac {1} { operatorname {sinc} (z)}}}$

где sinc — это нормализованная функция sinc, тогда как теорема умножения принимает форма

Π (zm) Π (z — 1 m) ⋯ Π (z — m + 1 m) = (2 π) m — 1 2 m — z — 1 2 Π (z). { displaystyle Pi left ({ frac {z} {m}} right) , Pi left ({ frac {z-1} {m}} right) cdots Pi left ( { frac {z-m + 1} {m}} right) = (2 pi) ^ { frac {m-1} {2}} m ^ {- z — { frac {1} {2 }}} Pi (z) .} ${ displaystyle Pi left ({ frac {z} {m }} right) , Pi left ({ frac {z-1} {m}} right) cdots Pi left ({ frac {z-m + 1} {m}} right) = (2 pi) ^ { frac {m-1} {2}} m ^ {- z - { frac {1} {2}}} Pi (z) .}$

Иногда мы также находим

π (z) = 1 Π (z), { displaystyle pi (z) = { frac {1} { Pi (z)}} ,} ${ displaystyle pi (z) = { frac {1} { Pi (z)}} ,}$

, которая представляет собой целую функцию, определенную для каждого комплексного числа, как и обратная гамма-функция . π (z) { displaystyle pi (z)} pi (z) целиком влечет за собой отсутствие полюсов, поэтому Π (z) { displaystyle Pi left (z right)}, например Γ (z) { displaystyle Gamma left (z right)}, не имеет нулей.

объем n-эллипсоида с радиусами r 1,…, r n можно выразить как

V n (r 1,…, rn) = π N 2 Π (N 2) ∏ k знак равно 1 nrk. { displaystyle V_ {n} (r_ {1}, dotsc, r_ {n}) = { frac { pi ^ { frac {n} {2}}} { Pi left ({ frac { n} {2}} right)}} prod _ {k = 1} ^ {n} r_ {k}.} ${ displaystyle V_ {n} (r_ {1}, dotsc, r_ {n}) = { frac { pi ^ { frac {n} {2}}} { Pi left ({ frac {n} {2}} right)}} prod _ {k = 1} ^ {n} r_ {k}.}$

Связь с другими функциями

В первом интеграле выше, который определяет гамма-функцию, пределы интегрирования фиксированы. Верхняя и нижняя неполные гамма-функции — это функции, полученные путем изменения нижнего или верхнего (соответственно) предела интегрирования.
Гамма-функция связана с бета-функцией по формуле

B (x, y) = ∫ 0 1 tx — 1 (1 — t) y — 1 dt = Γ (x) Γ (y) Γ (x + y). { displaystyle mathrm {B} (x, y) = int _ {0} ^ {1} t ^ {x-1} (1-t) ^ {y-1} , dt = { frac { Gamma (x) , Gamma (y)} { Gamma (x + y)}}.} ${ displaystyle mathrm {B} (x, y) = int _ {0} ^ {1} t ^ {x-1} (1- t) ^ {y-1} , dt = { frac { Gamma (x) , Gamma (y)} { Gamma (x + y)}}.}$

Логарифмическая производная гамма-функции называется дигамма-функцией ; высшие производные — это полигамма-функции.
Аналогом гамма-функции над конечным полем или конечным кольцом являются суммы Гаусса, a тип экспоненциальной суммы.
обратная гамма-функция — это целая функция, которая изучалась как отдельная тема.
Гамма-функция также показывает вверх в важной связи с дзета-функцией Римана, ζ (z) { displaystyle zeta (z)}.

π — z 2 Γ (z 2) ζ (z) = π — 1 — z 2 Γ (1 — z 2) ζ (1 — z). { displaystyle pi ^ {- { frac {z} {2}}} ; Gamma left ({ frac {z} {2}} right) zeta (z) = pi ^ {- { frac {1-z} {2}}} ; Gamma left ({ frac {1-z} {2}} right) ; zeta (1-z).} $pi ^ {- { fra c {z} {2}}} ; Gamma left ({ frac {z} {2}} right) zeta (z) = pi ^ {- { frac {1-z} {2 }}} ; Gamma left ({ frac {1-z} {2}} right) ; zeta (1-z).$

Это также присутствует в следующей формуле:

ζ (z) Γ (z) = ∫ 0 ∞ uzeu — 1 duu, { displaystyle zeta (z) Gamma (z) = int _ {0} ^ { infty} { frac {u ^ {z}} {e ^ {u} -1}} , { frac {du} {u}},} ${ displaystyle zeta (z) Gamma (z) = int _ {0} ^ { infty} { гидроразрыва {u ^ {z}} {e ^ {u} -1}} , { frac {du} {u}},}$

, который действителен только для ℜ (z)>1 { displaystyle Re (z)>1}

Логарифм гамма-функции удовлетворяет следующей формуле Лерха:

log ⁡ Γ (x) = ζ H ′ (0, Икс) — ζ ′ (0), { Displaystyle log Gamma (x) = zeta _ {H} ‘(0, x) — zeta’ (0),} ${displaystyle log Gamma (x)=zeta _{H}'(0,x)-zeta '(0),}$

где ζ H { displaystyle zeta _ {H}} ${ displaystyle Зет a _ {H}}$

— это дзета-функция Гурвица,, ζ { displaystyle zeta} zeta

— дзета-функция Римана и штрих (′) означает дифференцирование по первая переменная.

Гамма-функция связана с растянутой экспоненциальной функцией. Например, моменты этой функции равны

⟨τ n⟩ ≡ ∫ 0 ∞ d t t n — 1 e — (t τ) β = τ n β Γ (n β). { displaystyle langle tau ^ {n} rangle Equiv int _ {0} ^ { infty} dt , t ^ {n-1} , e ^ {- left ({ frac {t } { tau}} right) ^ { beta}} = { frac { tau ^ {n}} { beta}} Gamma left ({n over beta} right).} ${ displaystyle langle tau ^ {n} rangle Equiv int _ {0} ^ { infty} dt , t ^ {n -1} , e ^ {- left ({ frac {t} { tau}} right) ^ { beta}} = { frac { tau ^ {n}} { beta}} Гамма left ({n over beta} right).}$

Конкретные значения

Включая до первых 20 цифр после десятичной точки, некоторые конкретные значения гамма-функции:

Γ (- 3 2) = 4 3 π ≈ + 2.36327 18012 07354 70306 Γ (- 1 2) = — 2 π ≈ — 3,54490 77018 11032 05459 Γ (1 2) = π ≈ + 1,77245 38509 05516 02729 Γ (1) = 0! = + 1 Γ (3 2) = 1 2 π ≈ + 0,88622 69254 52758 01364 Γ (2) = 1! = + 1 Γ (5 2) = 3 4 π ≈ + 1,32934 03881 79137 02047 Γ (3) = 2! = + 2 Γ (7 2) = 15 8 π ≈ + 3.32335 09704 47842 55118 Γ (4) = 3! = + 6 { displaystyle { begin {array} {rcccl} Gamma left (- { tfrac {3} {2}} right) = { tfrac {4} {3}} { sqrt { pi}} приблизительно + 2.36327 , 18012 , 07354 , 70306 \ Гамма left (- { tfrac {1} {2}} right) = — 2 { sqrt { pi}} приблизительно -3.54490 , 77018 , 11032 , 05459 \ Гамма left ({ tfrac {1} {2}} right) = { sqrt { pi}} приблизительно + 1.77245 , 38509 , 05516 , 02729 \ Гамма (1) = 0! = + 1 \ Гамма left ({ tfrac {3} {2}} right) = { tfrac {1} {2}} { sqrt { pi}} приблизительно + 0.88622 , 69254 , 52758 , 01364 \ Гамма (2) = 1! = + 1 \ Gamma left ({ tfrac {5} {2}} right) = { tfrac {3} {4}} { sqrt { pi}} приблизительно + 1.32934 , 03881 , 79137 , 02047 \ Гамма (3) = 2! = + 2 \ Гамма left ({ tfrac {7} {2}} right) = { tfrac {15} {8}} { sqrt { pi}} приблизительно + 3.32335 , 09704 , 47842 , 55118 \ Гамма (4) = 3! = + 6 end { array}}} ${ displaystyle { begin {array} {rcccl} Gamma left (- { tfrac {3} {2}} right) = { tfrac {4} {3}} { sqrt { pi}} app rox + 2.36327 , 18012 , 07354 , 70306 \ Гамма left (- { tfrac {1} {2}} right) = - 2 { sqrt { pi}} приблизительно -3.54490 , 77018 , 11032 , 05459 \ Гамма left ({ tfrac {1} {2}} right) = { sqrt { pi}} приблизительно + 1.77245 , 38509 , 05516 , 02729 \ Gamma (1) = 0! = + 1 \ Gamma left ({ tfrac {3} {2}} right) = { tfrac {1} {2}} { sqrt { pi}} приблизительно + 0.88622 , 69254 , 52758 , 01364 \ Гамма (2) = 1! = + 1 \ Гамма left ({ tfrac {5} {2}} right) = { tfrac {3} {4}} { sqrt { pi}} приблизительно + 1.32934 , 03881 , 79137 , 02047 \ Gamma (3) = 2! = + 2 \ Gamma left ({ tfrac {7} {2}} right) = { tfrac {15} {8} } { sqrt { pi}} приблизительно + 3.32335 , 09704 , 47842 , 55118 \ Гамма (4) = 3! = + 6 end {array}}}$

Комплексная гамма-функция не определена для неположительных целых чисел, но в этих случаях значение может быть определено в сфере Римана как ∞. обратная гамма-функция является хорошо определенной и аналитической при этих значениях (и во всей комплексной плоскости ):

1 Γ (- 3) знак равно 1 Γ (- 2) = 1 Γ (- 1) = 1 Γ (0) = 0. { displaystyle { frac {1} { Gamma (-3)}} = { frac { 1} { Gamma (-2)}} = { frac {1} { Gamma (-1)}} = { frac {1} { Gamma (0)}} = 0.} ${ displaystyle { frac {1} { Gamma (-3)}} = { frac {1} { Gamma (-2)}} = { frac {1} { Gamma (-1) }} = { frac {1} { Gamma (0)}} = 0.}$

log-гамма-функция

Аналитическая функция log Γ (z)

Поскольку гамма- и факториальные функции растут так быстро для умеренно больших аргументов, многие вычислительные среды включают функцию, которая возвращает натуральный логарифм от гамма-функция (часто именуется lgammaили lngammaв средах программирования или gammalnв электронных таблицах); это растет намного медленнее, и для комбинаторных вычислений позволяет складывать и вычитать журналы вместо умножения и деления очень больших значений. Часто его определяют как

ln ⁡ Γ (z) = — γ z — ln ⁡ z + ∑ k = 1 ∞ [z k — ln ⁡ (1 + z k)]. { Displaystyle ln Gamma (z) = — gamma z- ln z + sum _ {k = 1} ^ { infty} left [{ frac {z} {k}} — ln left (1 + { frac {z} {k}} right) right].} ${ displaystyle ln Gamma (z) = - gamma z- ln z + sum _ {k = 1} ^ { infty} left [{ frac {z} {k}} - ln left (1 + { frac {z} {k}} right) right].}$

Также часто встречается дигамма-функция, которая является производной от этой функции. В контексте технических и физических приложений, например с распространением волн функциональное уравнение

ln ⁡ Γ (z) = ln ⁡ Γ (z + 1) — ln ⁡ z { displaystyle ln Gamma (z) = ln Gamma (z + 1) — ln z}

часто используется, поскольку он позволяет определять значения функции в одной полосе шириной 1 по z из соседней полосы. В частности, начиная с хорошего приближения для z с большой действительной частью, можно шаг за шагом перейти к желаемому z. Следуя указанию Карла Фридриха Гаусса, Роктэшель (1922) предложил вместо ln ⁡ (Γ (z)) { displaystyle ln ( Gamma (z))}приближение для больших Re (z):

ln ⁡ Γ (z) ≈ (z — 1 2) ln ⁡ z — z + 1 2 ln ⁡ (2 π). { displaystyle ln Gamma (z) приблизительно (z — { tfrac {1} {2}}) ln z-z + { tfrac {1} {2}} ln (2 pi).} ${ Displaystyle ln Gamma (z) приблизительно (z - { tfrac {1} {2}}) ln z-z + { tfrac {1} {2}} ln (2 pi).}$

Это можно использовать для точного приближения ln (Γ (z)) для z с меньшим Re (z) с помощью (PEBöhmer, 1939)

ln ⁡ Γ (z — m) = ln ⁡ Γ (z) — ∑ k = 1 m ln ⁡ (z — k). { displaystyle ln Gamma (zm) = ln Gamma (z) — sum _ {k = 1} ^ {m} ln (zk).} ${ displaystyle ln Gamma (zm) = ln Gamma (z) - sum _ {k = 1} ^ {m} ln (zk).}$

Более точное приближение можно получить, используя дополнительные члены из асимптотических разложений ln (Γ (z)) и Γ (z), основанных на приближении Стирлинга.

Γ (z) ∼ zz — 1 2 e — z 2 π (1 + 1 12 z + 1 288 z 2 — 139 51 840 z 3 — 571 2 488 320 z 4) { displaystyle Gamma (z) sim z ^ {z — { frac {1} {2}}} e ^ {- z} { sqrt {2 pi}} left (1 + { frac {1} {12z}} + { frac {1} {288z ^ {2}}} — { frac {139} {51 , 840z ^ {3}}} — { frac {571} {2 , 488 , 320z ^ {4} }} right)} ${ displaystyle Gamma (z) sim z ^ {z - { frac {1} {2}}} e ^ {- z} { sqrt {2 pi}} left (1 + { frac {1} {12z}} + { frac {1} {288z ^ {2}}} - { frac {139} {51 , 840z ^ {3}}} - { frac {571} {2 , 488 , 320z ^ {4}}} right)}$

как | z | → ∞ при постоянном | arg (z) | < π.

В более «естественном» изложении:

ln ⁡ Γ (z) ∼ z ln ⁡ (z) — z — 1 2 ln ⁡ (z 2 π) + 1 12 z — 1 360 z 3 + 1 1260 z 5 { displaystyle ln Gamma (z) sim z ln (z) -z — { tfrac {1} {2}} ln left ({ frac {z} {2 pi} } right) + { frac {1} {12z}} — { frac {1} {360z ^ {3}}} + { frac {1} {1260z ^ {5}}}} ${ displaystyle ln Gamma (z) sim z ln (z) -z - { tfrac {1} {2}} ln left ({ frac {z} {2 pi}} right) + { frac {1} {12z}} - { frac {1} {360z ^ {3}}} + { frac {1} {1260z ^ {5}}}}$

как | z | → ∞ при постоянном | arg (z) | < π.

Коэффициенты членов с k>1 числа z в последнем разложении равны просто

B kk (k — 1) { displaystyle { frac {B_ {k}} {k (k-1)} }} ${ frac {B_ {k}} {k (k-1)}}$

где B k — это числа Бернулли.

Свойства

Теорема Бора – Моллерупа утверждает, что среди всех функций, расширяющих факториалами к положительным действительным числам, только гамма-функция является логарифмически-выпуклой, то есть ее натуральный логарифм является выпуклым на положительной действительной оси. Другая характеристика дается теоремой Виландта.

В определенном смысле функция ln (Γ) является более естественной формой; это делает некоторые внутренние атрибуты функции более понятными. Ярким примером является ряд Тейлора для ln (Γ) около 1:

ln ⁡ Γ (z + 1) = — γ z + ∑ k = 2 ∞ ζ (k) k (- z) k ∀ | z | < 1 {displaystyle ln Gamma (z+1)=-gamma z+sum _{k=2}^{infty }{frac {zeta (k)}{k}},(-z)^{k}qquad forall ;|z|<1} ${ displaystyle ln Gamma (z + 1) = - gamma z + sum _ {k = 2} ^ { infty} { frac { zeta (k)} {k}} , (- z) ^ {k} qquad forall ; | z | <1}$

с ζ (k), обозначающим дзета-функцию Римана в точке k.

Итак, используя следующее свойство:

ζ (s) Γ (s) = ∫ 0 ∞ tset — 1 dtt { displaystyle zeta (s) Gamma (s) = int _ { 0} ^ { infty} { frac {t ^ {s}} {e ^ {t} -1}} , { frac {dt} {t}}} ${ displaystyle zeta (s) Gamma (s) = int _ {0} ^ { infty} { frac {t ^ {s}} {e ^ {t} -1}} , { frac {dt} {t}}}$

мы можем найти интегральное представление для функция ln (Γ):

ln ⁡ Γ (z + 1) = — γ z + ∫ 0 ∞ (e — zt — 1 + zt) t (et — 1) dt { displaystyle ln Gamma ( z + 1) = — gamma z + int _ {0} ^ { infty} { frac {, left (e ^ {- zt} -1 + zt right) ,} {t left ( e ^ {t} -1 right)}} , dt} ${ displaystyle ln Gamma (z + 1) = - gamma z + int _ {0} ^ { infty} { frac {, left (e ^ {- zt} -1 + zt right) ,} {t left (e ^ {t} -1 right)}} , dt}$

или, задав z = 1, чтобы получить интеграл для γ, мы можем заменить член γ его интегралом и включить его в формулу выше, чтобы получаем:

ln ⁡ Γ (z + 1) = ∫ 0 ∞ (e — zt — ze — t — 1 + z) t (et — 1) dt. { displaystyle ln Gamma (z + 1) = int _ {0} ^ { infty} { frac {, left (e ^ {- zt} -ze ^ {- t} -1 + z right) ,} {t (e ^ {t} -1)}} , dt ,.} ${ displaystyle ln Gamma (z + 1) = int _ {0} ^ { infty} { frac {, left (e ^ {- zt} -ze ^ {- t} -1 + z right) ,} {t (e ^ {t} -1)}} , dt ,.}$

Также существуют специальные формулы для логарифма гамма-функции для рационального z. Например, если k { displaystyle k}и n { displaystyle n}являются целыми числами с k < n {displaystyle k К <N и k ≠ n / 2, { displaystyle k neq n / 2 ,,}, затем

пер ⁡ Γ (kn) = (n — 2 k) пер 2 π 2 n + 1 2 {пер π — ln ⁡ sin ⁡ π kn} + 1 π ∑ r = 1 n — 1 γ + ln ⁡ rr ⋅ sin ⁡ 2 π rkn — 1 2 π sin ⁡ 2 π kn ⋅ ∫ 0 ∞ e — nx ⋅ ln ⁡ x ch ⁡ Икс — соз ⁡ (2 π К / N) dx { Displaystyle { begin {align} ln Gamma { biggl (} ! { Frac {k} {n}} ! { Biggr)} = {} { frac {, (n-2k) ln 2 pi ,} {2n}} + { frac {1} {2}} left {, ln pi — ln sin { frac { pi k} {n}} , right } + { frac {1} { pi}} ! sum _ {r = 1} ^ {n-1} { frac {, gamma + ln r ,} {r}} cdot sin { frac {, 2 pi rk ,} {n}} \ {} — { frac {1 } {2 pi}} sin { frac {2 pi k} {n}} cdot ! Int _ {0} ^ { infty} ! ! { Frac {, e ^ { -nx} ! cdot ln x ,} {, cosh x- cos (2 pi k / n) ,}} , { mathrm {d}} x end {выровнено}} } ${ displaystyle { begin {align} ln Gamma { biggl (} ! { Frac {k} {n}} ! { biggr)} = {} { frac {, (n-2k) ln 2 pi ,} {2n}} + { frac {1} {2}} left {, ln pi - ln sin { frac { pi k} {n}} , right } + { frac {1} { pi}} ! sum _ { r = 1} ^ {n-1} { frac {, gamma + ln r ,} {r}} cdot sin { frac {, 2 pi rk ,} {n}} \ {} - { frac {1} {2 pi}} sin { frac {2 pi k} {n}} cdot ! int _ {0} ^ { infty} ! ! { frac {, e ^ {- nx} ! cdot ln x ,} {, ch x- cos (2 pi k / n) ,}} , { mathrm {d}} х конец {выровнено}}}$

см. Эта формула иногда используется для численных расчетов, поскольку подынтегральное выражение уменьшается очень быстро.

Интегрирование по логарифмической гамме

Интеграл

∫ 0 z ln ⁡ Γ (x) dx { displaystyle int _ {0} ^ {z} ln Gamma ( x) , dx} ${ displaystyle int _ {0} ^ {z} ln Gamma (x) , dx}$

можно выразить через G-функцию Барнса (см. G-функцию Барнса для доказательства):

∫ 0 z ln ⁡ Γ (Икс) dx знак равно Z 2 пер ⁡ (2 π) + z (1 — z) 2 + z пер ⁡ Γ (z) — пер ⁡ G (z + 1) { Displaystyle int _ {0} ^ {z} ln Gamma (x) , dx = { frac {z} {2}} ln (2 pi) + { frac {z (1-z)} {2}} + z ln Gamma (z) — ln G (z + 1)} ${ displaystyle int _ {0} ^ {z} ln Gamma (x) , dx = { frac {z} {2}} ln (2 pi) + { frac {z (1-z)} {2}} + z ln Gam ма (z) - пер G (z + 1)}$

где Re (z)>−1.

Его также можно записать в терминах дзета-функции Гурвица :

∫ 0 z ln ⁡ Γ (x) dx = z 2 ln ⁡ (2 π) + z (1 — z) 2 — ζ ′ (- 1) + ζ ′ (- 1, z). { Displaystyle int _ {0} ^ {z} ln Gamma (x) , dx = { frac {z} {2}} ln (2 pi) + { frac {z (1- z)} {2}} — zeta ‘(-1) + zeta’ (-1, z).} ${displaystyle int _{0}^{z}ln Gamma (x),dx={frac {z}{2}}ln(2pi)+{frac {z(1-z)}{2}}-zeta '(-1)+zeta '(-1,z).}$

Когда z = 1 { displaystyle z = 1} z=1 следует, что

∫ 0 1 пер ⁡ Γ (x) dx = 1 2 log log (2 π), { displaystyle int _ {0} ^ {1} ln Gamma (x) , dx = { frac {1} {2}} log (2 pi),} ${ displaystyle int _ {0} ^ { 1} ln Gamma (x) , dx = { frac {1} {2}} log (2 pi),}$

, и это также является следствием формулы Раабе. О. Эспиноза и В. Молл вывели аналогичную формулу для интеграла от квадрата log ⁡ Γ { displaystyle log Gamma}:

∫ 0 1 log 2 ⁡ Γ (x) dx = γ 2 12 + π 2 48 + 1 3 γ L 1 + 4 3 L 1 2 — (γ + 2 L 1) ζ ′ (2) π 2 + ζ ′ ′ (2) 2 π 2, { displaystyle int _ {0 } ^ {1} log ^ {2} Gamma (x) dx = { frac { gamma ^ {2}} {12}} + { frac { pi ^ {2}} {48}} + { frac {1} {3}} gamma L_ {1} + { frac {4} {3}} L_ {1} ^ {2} — left ( gamma + 2L_ {1} right) { frac { zeta ^ { prime} (2)} { pi ^ {2}}} + { frac { zeta ^ { prime prime} (2)} {2 pi ^ {2}} },} ${ displaystyle int _ {0} ^ {1} log ^ {2} Gamma (x) dx = { frac { gamma ^ {2}} {12}} + { frac { pi ^ {2}} {48}} + { frac {1} {3}} gamma L_ {1} + { frac {4} {3}} L_ {1} ^ {2} - left ( gamma + 2L_ {1} right) { frac { zeta ^ { prime} (2)} { pi ^ {2}}} + { frac { zeta ^ { prime prime} (2)} {2 pi ^ {2}}},}$

где L 1 { displaystyle L_ {1}} $L_ {1}$ равно 1 2 log ⁡ (2 π) { displaystyle { frac {1} {2} } log (2 pi)} ${ displaystyle { frac {1) } {2}} log (2 pi)}$ .

D. Х. Бейли и его соавторы дали оценку

L n: = ∫ 0 1 log n ⁡ Γ (x) dx { displaystyle L_ {n}: = int _ {0} ^ {1} log ^ {n} Gamma (x) dx} ${ d isplaystyle L_ {n}: = int _ {0} ^ {1} log ^ {n} Gamma (x) dx}$

когда n = 1, 2 { displaystyle n = 1,2} n=1,2 в терминах дзета-функции Торнхейма-Виттена и ее производные.

Кроме того, также известно, что

lim n → ∞ L n n! = 1. { displaystyle lim _ {n to infty} { frac {L_ {n}} {n!}} = 1.} ${ displaystyle lim _ {n to infty} { frac {L_ {n}} {n!}} = 1. }$

Приближение

Гамма сравнения (синяя линия) с факториалом (синие точки) и приближение Стирлинга (красная линия)

Комплексные значения гамма-функции могут быть вычислены численно с произвольной точностью с использованием приближения Стирлинга или приближения Ланцоша.

Гамма-функция может вычисляться с фиксированной точностью для Re ⁡ (z) ∈ [1, 2] { displaystyle operatorname {Re} (z) in [1,2]}путем применения интегрирование по частям до интеграла Эйлера. Для любого положительного числа x гамма-функция может быть записана

Γ (z) = ∫ 0 xe — ttzdtt + ∫ x ∞ e — ttzdtt = xze — x ∑ n = 0 ∞ xnz (z + 1) ⋯ (z + п) + ∫ x ∞ e — ttzdtt. { displaystyle { begin {align} Gamma (z) = int _ {0} ^ {x} e ^ {- t} t ^ {z} , { frac {dt} {t}} + int _ {x} ^ { infty} e ^ {- t} t ^ {z} , { frac {dt} {t}} \ = x ^ {z} e ^ {- x} sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {z (z + 1) cdots (z + n)}} + int _ {x} ^ { infty} e ^ {- t} t ^ {z} , { frac {dt} {t}}. end {align}}} ${ displaystyle { begin {align} Gamma (z) = int _ {0} ^ {x} e ^ {- t} t ^ {z} , { frac {dt} {t}} + int _ {x} ^ { infty} e ^ {- t} t ^ {z} , { frac {dt} {t}} \ = x ^ {z} e ^ {- x} sum _ {n = 0} ^ { infty} { frac {x ^ {n}} {z (z + 1) cdots (z + n)}} + int _ {x} ^ { infty} e ^ {- t} t ^ {z} , { frac {dt} {t}}. End { выровнено}}}$

Когда Re (z) ∈ [1,2] и x ≥ 1 { displaystyle x geq 1} x geq 1 , абсолютное значение последнего интеграла меньше, чем (x + 1) e — x { displaystyle (x + 1) e ^ {- x}} ${ displaystyle (x + 1) e ^ {- x}}$ . Выбрав достаточно большой x { displaystyle x}, это последнее выражение можно сделать меньше, чем 2 — N { displaystyle 2 ^ {- N}} ${ displaystyle 2 ^ {- N}}$ для любого желаемого значения N { displaystyle N}. Таким образом, гамма-функция может быть оценена с точностью N { displaystyle N}битов с помощью вышеуказанного ряда.

Быстрый алгоритм вычисления гамма-функции Эйлера для любого алгебраического аргумента (в том числе рационального) был построен Е.А. Карацуба,

Для аргументов, которые являются целыми числами, кратными 1/24, гамма-функцию также можно быстро вычислить с помощью итераций среднего арифметико-геометрического (см. конкретные значения гамма-функции и Borwein Zucker (1992) ошибка harvtxt: нет цели: CITEREFBorweinZucker1992 (help )).

Приложения

Один автор описывает гамма-функцию как «Возможно, наиболее распространенную специальную функцию или наименее« особенную »из них. Другие трансцендентные функции […] называются« специальными » потому что вы, вероятно, можете избежать некоторых из них, избегая многих специализированных математических тем. С другой стороны, гамма-функцию y = Γ (x) избежать труднее всего ».

Проблемы интеграции

Гамма-функция находит применение в таких различных областях, как квантовая физика, астрофизика и гидродинамика. гамма-распределение, которое сформулировано в терминах гамма-функции, используется в статистике для моделирования широкого диапазона процессов; например, время между возникновением землетрясений.

Основной причиной полезности гамма-функции в таких контекстах является преобладание выражений типа f (t) e — g (t) { displaystyle f (t) e ^ {- g (t)}} ${ Displaystyle е (т) е ^ {- г (т)}}$ , которые описывают процессы, которые экспоненциально затухают во времени или пространстве. Интегралы таких выражений иногда могут быть решены в терминах гамма-функции, когда элементарного решения не существует. Например, если f — степенная функция, а g — линейная функция, простая замена переменных дает оценку

∫ 0 ∞ t b e — a t d t = Γ (b + 1) a b + 1. { displaystyle int _ {0} ^ { infty} t ^ {b} e ^ {- at} , dt = { frac { Gamma (b + 1)} {a ^ {b + 1}} }.} $int _ {0} ^ { infty} t ^ {b} e ^ {- at} , dt = { frac { Gamma (b +1)} {a ^ {b + 1}}}.$

Тот факт, что интегрирование выполняется по всей положительной действительной линии, может означать, что гамма-функция описывает накопление зависящего от времени процесса, который продолжается бесконечно, или значение может быть суммой распределения в бесконечное пространство.

Конечно, часто бывает полезно использовать пределы интегрирования, отличные от 0 и ∞, для описания кумуляции конечного процесса, и в этом случае обычная гамма-функция больше не является решением; тогда решение называется неполной гамма-функцией. (Обычная гамма-функция, полученная путем интегрирования по всей положительной вещественной линии, иногда называется полной гамма-функцией для контраста.)

Важной категорией экспоненциально убывающих функций является гауссовские функции

ae — (x — b) 2 c 2 { displaystyle ae ^ {- { frac {(xb) ^ {2}} {c ^ {2}}}}} $ae ^ {- { frac {(xb) ^ {2}} {c ^ {2}}}}$

и их интегралы, такие как функция ошибок. Между этими функциями и гамма-функцией существует множество взаимосвязей; в частности, коэффициент π { displaystyle { sqrt { pi}}}, полученный путем вычисления Γ (1 2) { textstyle Gamma left ({ frac {1 } {2}} right)} ${ textstyle Gamma left ({ frac {1} {2} } right)}$ «то же самое», что и найденное в нормирующем множителе функции ошибок и нормальном распределении.

Интегралы, которые мы обсуждали до сих пор, включают трансцендентные функций, но гамма-функция также возникает из интегралов чисто алгебраических функций. В частности, длины дуг эллипсов и лемнискаты, которые представляют собой кривые, определяемые алгебраическими уравнениями, задаются эллиптическими интегралами что в особых случаях может быть оценено с помощью гамма-функции. Гамма-функцию также можно использовать для вычисления «объема» и «площади» n-мерных гиперсфер.

Вычисления продуктов

Возможность гамма-функции немедленно обобщать факториальные произведения приводит к приложениям во многих областях математики; в комбинаторике, а также в таких областях, как теория вероятностей и вычисление степенных рядов. Многие выражения, включающие произведения следующих друг за другом целых чисел, могут быть записаны в виде некоторой комбинации факториалов, наиболее важным примером, возможно, является биномиальный коэффициент

(n k) = n! к! (п — к)!. { displaystyle { binom {n} {k}} = { frac {n!} {k! (nk)!}}.} ${ displaystyle { binom {n} {k}} = { frac {n!} {K! (Nk)!} }.}$

Пример биномиальных коэффициентов объясняет, почему свойства гамма-функции при расширении отрицательные числа естественны. Биномиальный коэффициент дает количество способов выбрать k элементов из набора n элементов; если k>n, то способов конечно нет. Если k>n, (n — k)! является факториалом отрицательного целого числа и, следовательно, бесконечным, если мы используем определение факториалов гамма-функцией — деление на бесконечность дает ожидаемое значение 0.

Мы можем заменить факториал на гамма-функцию, чтобы расширить любую такую формулу к комплексным числам. Как правило, это работает для любого продукта, в котором каждый фактор является рациональной функцией индексной переменной, путем факторизации рациональной функции в линейные выражения. Если P и Q являются моническими многочленами степени m и n с соответствующими корнями p 1,…, p m и q 1,…, q n, имеем

∏ i = ab P (i) Q (i) = (∏ j = 1 m Γ (b — pj + 1) Γ (a — pj)) (∏ k = 1 n Γ (a — qk) Γ (b — qk + 1)). { displaystyle prod _ {i = a} ^ {b} { frac {P (i)} {Q (i)}} = left ( prod _ {j = 1} ^ {m} { frac { Gamma (b-p_ {j} +1)} { Gamma (a-p_ {j})}} right) left ( prod _ {k = 1} ^ {n} { frac { Гамма (a-q_ {k})} { Gamma (b-q_ {k} +1)}} right).} $prod _ {i = a} ^ {b} { frac {P (i)} {Q (i)}} = left ( prod _ {j = 1} ^ {m} { frac { Gamma (b-p_ {j} +1)} { Gamma (a-p_ {j})}} вправо) влево ( prod _ {k = 1} ^ {n} { frac { Gamma (a-q_ {k})} { Gamma (b-q_ {k} +1)}} right).$

Если у нас есть способ вычислить гамма-функцию численно, это несложно рассчитать числовые значения таких продуктов. Количество гамма-функций в правой части зависит только от степени полиномов, поэтому не имеет значения, равно ли b — a 5 или 10. Принимая соответствующие ограничения, уравнение также может выполняться, даже если левое произведение содержит нули или полюсы.

Принимая ограничения, некоторые рациональные продукты с бесконечно большим числом факторов могут быть оценены также с точки зрения гамма-функции. Согласно теореме факторизации Вейерштрасса, аналитические функции могут быть записаны как бесконечные произведения, а иногда они могут быть представлены как конечные произведения или частные гамма-функции. Мы уже видели один поразительный пример: формула отражения по сути представляет синусоидальную функцию как произведение двух гамма-функций. Исходя из этой формулы, экспоненциальная функция, а также все тригонометрические и гиперболические функции могут быть выражены через гамма-функцию.

Еще больше функций, включая гипергеометрическую функцию и ее частные случаи, могут быть представлены с помощью комплексных контурных интегралов произведений и частных гамма-функции, называемых Интегралы Меллина – Барнса.

Аналитическая теория чисел

Элегантное и глубокое применение гамма-функции заключается в исследовании дзета-функции Римана. Основное свойство дзета-функции Римана — это ее функциональное уравнение :

Γ (s 2) ζ (s) π — s 2 = Γ (1 — s 2) ζ (1 — s) π — 1 — s 2. { displaystyle Gamma left ({ frac {s} {2}} right) zeta (s) pi ^ {- { frac {s} {2}}} = Gamma left ({ frac {1-s} {2}} right) zeta (1-s) pi ^ {- { frac {1-s} {2}}}.} $Gamma left ({ frac {s} {2}} right) zeta (s) pi ^ {- { frac {s} {2}}} = Гамма left ({ frac {1-s} {2}} right) zeta (1-s) pi ^ {- { frac {1-s} {2}}}.$

Среди прочего, это обеспечивает явный вид аналитического продолжения дзета-функции до мероморфной функции на комплексной плоскости и приводит к немедленному доказательству того, что дзета-функция имеет бесконечно много так называемых «тривиальных» нулей на действительной прямой. Borwein et al. называют эту формулу «одним из самых прекрасных открытий в математике». Другим чемпионом этого титула может быть

ζ (s) Γ (s) = ∫ 0 ∞ t s e t — 1 d t t. { displaystyle zeta (s) ; Gamma (s) = int _ {0} ^ { infty} { frac {t ^ {s}} {e ^ {t} -1}} , { frac {dt} {t}}.} ${ displaystyle zeta (s) ; Gamma (s) = int _ {0} ^ { infty} { frac {t ^ {s}} {e ^ {t} -1}} , { frac {dt} {t}}.}$

Обе формулы были выведены Бернхардом Риманом в его основополагающей статье 1859 года «Über die Anzahl der Primzahlen unter einer gegebenen Größe» («О числе простых чисел Числа меньше заданного количества »), одна из вех в развитии аналитической теории чисел — раздела математики, изучающего простые числа с помощью инструментов математического анализа. Факториальные числа, рассматриваемые как дискретные объекты, являются важным понятием в классической теории чисел, потому что они содержат много простых множителей, но Риман нашел применение их непрерывному расширению, которое, возможно, оказалось даже более важным.

История

Гамма-функция вызвала интерес некоторых из самых выдающихся математиков всех времен. Его история, особенно задокументированная Филипом Дж. Дэвисом в статье, которая принесла ему в 1963 г. премию Шовене, отражает многие из основных достижений математики с 18 века. По словам Дэвиса, «каждое поколение нашло что-то интересное, чтобы сказать о гамма-функции. Возможно, следующее поколение тоже найдет».

18 век: Эйлер и Стирлинг

Даниэль Бернулли » s письмо Кристиану Гольдбаху, 6 октября 1729 г.

Проблема расширения факториала на нецелые аргументы, по-видимому, впервые была рассмотрена Даниэлем Бернулли и Кристианом Гольдбахом в 1720-х годах и была решена в конце того же десятилетия Леонардом Эйлером. Эйлер дал два разных определения: первое — это не его интеграл, а бесконечное произведение,

n! Знак равно ∏ К знак равно 1 ∞ (1 + 1 к) n 1 + nk, { displaystyle n! = Prod _ {k = 1} ^ { infty} { frac { left (1 + { frac {1 } {k}} right) ^ {n}} {1 + { frac {n} {k}}}} ,,} $n! = Prod _ {k = 1} ^ { infty} { frac { left (1 + { frac {1} {k}} right) ^ {n}} {1 + { frac {n} {k}}}} ,,$

о чем он сообщил Гольдбаху в письме от 13 октября 1729 г. Он снова написал Гольдбаху 8 января 1730 г., чтобы объявить об открытии им интегрального представления

n! Знак равно ∫ 0 1 (- пер ⁡ s) nds, { displaystyle n! = Int _ {0} ^ {1} (- ln s) ^ {n} , ds ,,} ${ Displaystyle п! = int _ {0} ^ {1} (- ln s) ^ {n} , ds ,,}$

, что является действительно для n>0. Заменой переменных t = −ln s это становится знакомым интегралом Эйлера. Эйлер опубликовал свои результаты в статье «De progressionibus transcendentibus seu Quarum termini generales algebraice dari nequeunt» («О трансцендентных прогрессиях, то есть тех, чьи общие термины не могут быть даны алгебраически»), представленной в St. Петербургская академия 28 ноября 1729 года. Эйлер далее открыл некоторые важные функциональные свойства гамма-функции, включая формулу отражения.

Джеймс Стирлинг, современник Эйлера, также попытался найти непрерывное выражение для факториала и придумал то, что теперь известно как формула Стирлинга. Хотя формула Стирлинга дает хорошую оценку n !, также для нецелых чисел, она не дает точного значения. Расширения его формулы, исправляющие ошибку, были даны самим Стирлингом и Жаком Филиппом Мари Бине.

XIX век: Гаусс, Вейерштрасс и Лежандр

Первая страница статьи Эйлера

Карл Фридрих Гаусс переписал произведение Эйлера как

Γ (z) = lim m → ∞ mzm! z (z + 1) (z + 2) ⋯ (z + m) { displaystyle Gamma (z) = lim _ {m to infty} { frac {m ^ {z} m!} {z (z + 1) (z + 2) cdots (z + m)}}} ${ displaystyle Gamma (z) = lim _ {m to infty} { frac {m ^ {z} m!} {Z (z + 1) (z + 2) cdots (z + m)}}}$

и использовал эту формулу для открытия новых свойств гамма-функции. Хотя Эйлер был пионером в теории комплексных переменных, он, похоже, не рассматривал факториал комплексного числа, как сначала сделал Гаусс. Гаусс также доказал теорему умножения гамма-функции и исследовал связь между гамма-функцией и эллиптическими интегралами.

Карл Вейерштрасс далее установил роль гамма-функции в комплексный анализ, начиная с еще одного представления продукта,

Γ (z) = e — γ zz ∏ k = 1 ∞ (1 + zk) — 1 ezk, { displaystyle Gamma (z) = { frac {e ^ {- gamma z}} {z}} prod _ {k = 1} ^ { infty} left (1 + { frac {z} {k}} right) ^ {- 1 } e ^ { frac {z} {k}},} ${ displaystyle Gamma (z) = { frac {e ^ {- gamma z}} {z}} prod _ {k = 1} ^ { infty} left (1 + { frac {z} {k}} right) ^ {- 1} e ^ { frac {z} {k}},}$

где γ — постоянная Эйлера – Маскерони. Первоначально Вейерштрасс писал свое произведение как единицу для 1 / Γ, и в этом случае оно берется по нулям функции, а не по ее полюсам. Вдохновленный этим результатом, он доказал так называемую теорему факторизации Вейерштрасса — что любую целую функцию можно записать как произведение над ее нулями на комплексной плоскости; обобщение фундаментальной теоремы алгебры.

Имя гамма-функция и символ Γ были введены Адрианом-Мари Лежандром около 1811 г.; Лежандр также переписал интегральное определение Эйлера в его современной форме. Хотя символ представляет собой греческую гамму в верхнем регистре, не существует общепринятого стандарта, определяющего, следует ли записывать имя функции «гамма-функция» или «гамма-функция» (некоторые авторы просто пишут «Γ-функция»). Альтернативное обозначение «функции пи» Π (z) = z! из-за Гаусса иногда встречается в более ранней литературе, но примечания Лежандра преобладают в современных работах.

Уместно спросить, почему мы различаем «обычный факториал» и гамма-функцию, используя разные символы, и, в частности, почему гамма-функцию следует нормировать на Γ (n + 1) = n! вместо простого использования «Γ (n) = n!». Учтите, что обозначение показателей x было обобщено с целых чисел на комплексные числа x без каких-либо изменений. Мотивация Лежандра к нормализации, по-видимому, не известна, и некоторые критиковали ее как громоздкую (математик 20-го века Корнелиус Ланцош, например, назвал ее «лишенной всякой рациональности» и вместо этого использовал бы z!). Нормализация Лежандра действительно упрощает некоторые формулы, но усложняет большинство других. С современной точки зрения, нормализация Лежандра гамма-функции представляет собой интеграл аддитивного символа e от мультипликативного символа x относительно меры Хаара dxx { displaystyle { tfrac {dx} {x}}} ${ displaystyle { tfrac {dx} {x}}}$ в группе Ли R. Таким образом, эта нормализация проясняет, что гамма-функция является непрерывным аналогом суммы Гаусса.

XIX – XX веков: характеристика гамма-функции

Несколько проблематично то, что большое количество определений дано для гамма-функции. Хотя они описывают одну и ту же функцию, доказать эквивалентность не совсем просто. Стирлинг так и не доказал, что его расширенная формула точно соответствует гамма-функции Эйлера; доказательство было впервые дано Чарльзом Эрмитом в 1900 году. Вместо поиска специального доказательства для каждой формулы было бы желательно иметь общий метод определения гамма-функции.

Один из способов доказать — это найти дифференциальное уравнение, которое характеризует гамма-функцию. Большинство специальных функций в прикладной математике возникают как решения дифференциальных уравнений, решения которых единственны. Однако гамма-функция, похоже, не удовлетворяет никакому простому дифференциальному уравнению. Отто Гёльдер доказал в 1887 году, что гамма-функция по крайней мере не удовлетворяет никакому алгебраическому дифференциальному уравнению, показав, что решение такого уравнения не может удовлетворять рекуррентной формуле гамма-функции, что делает его трансцендентно трансцендентная функция. Этот результат известен как теорема Гёльдера.

Определенная и общеприменимая характеристика гамма-функции не была дана до 1922 года. Харальд Бор и Йоханнес Моллеруп затем доказали, что такое известная как теорема Бора-Моллерупа : гамма-функция является единственным решением факторного рекуррентного отношения, которое является положительным и логарифмически выпуклым для положительного z и значение 1 равно 1 ( функция является логарифмически выпуклой, если ее логарифм выпуклый). Другая характеристика дается теоремой Виландта.

Теорема Бора – Моллерупа полезна, потому что относительно легко доказать логарифмическую выпуклость для любой из различных формул, используемых для определения гамма-функции. Двигаясь дальше, вместо того, чтобы определять гамма-функцию какой-либо конкретной формулой, мы можем выбрать в качестве определения условия теоремы Бора – Моллерупа, а затем выбрать любую понравившуюся формулу, которая удовлетворяет условиям, в качестве отправной точки для изучения гамма-функции.. Этот подход был использован группой Бурбаки.

Борвейн и Корлессом, изучившим три века работы над гамма-функцией.

Справочные таблицы и программное обеспечение

Хотя гамма-функцию можно вычислить практически так же легко, как любую математически более простую функцию с помощью современного компьютера — даже с помощью программируемого карманного калькулятора — это, конечно, не всегда кейс. До середины 20 века математики полагались на таблицы, сделанные вручную; в случае гамма-функции, в частности, таблица, вычисленная Гауссом в 1813 году, и таблица, вычисленная Лежандром в 1825 году.

Рисованный график абсолютного значения комплексной гамма-функции из таблиц высших функций по Янке и [de ].

Таблицы комплексных значений гамма-функции, а также нарисованные от руки графики были даны в Таблицах высших функций Янке и [de ], впервые опубликованный в Германии в 1909 году. Согласно Майклу Берри, «публикация в JE трехмерного графика, показывающего полюса гамма-функции в комплексной плоскости, приобрела почти культовый статус».

Фактически практически не было необходимости в чем-либо, кроме реальных значений гамма-функции, до 1930-х годов, когда приложения для сложной гамма-функции были обнаружены в теоретической физике. Когда в 1950-х годах стали доступны электронные компьютеры для производства таблиц, для удовлетворения спроса было опубликовано несколько обширных таблиц для комплексной гамма-функции, включая таблицу с точностью до 12 десятичных знаков из США Национальное бюро стандартов.

Абрамовиц и Стегун стал стандартным справочником для этой и многих других специальных функций после его публикации в 1964 году.

Реализации гамма-функции и ее логарифма с плавающей запятой двойной точности теперь доступны в большинстве научных вычислений. библиотеки программного обеспечения и специальных функций, например TK Solver, Matlab, GNU Octave и Научная библиотека GNU. Гамма-функция также была добавлена в стандартную библиотеку C (math.h ). Реализации произвольной точности доступны в большинстве систем компьютерной алгебры, таких как Mathematica и Maple. PARI / GP, MPFR и содержат бесплатные реализации произвольной точности. Малоизвестная особенность приложения калькулятора, входящего в состав операционной системы Android, заключается в том, что оно принимает дробные значения в качестве входных данных для функции факториала и возвращает эквивалентное значение гамма-функции. То же самое и для Windows Calculator (в научном режиме).

См. Также

Примечания

Эта статья включает материалы из Citizendium статья «Гамма-функция », которая находится под лицензией Creative Commons Attribution-ShareAlike 3.0 Unported License, но не по GFDL.

Дополнительная литература

Внешние ссылки

Викискладе есть медиафайлы, относящиеся к Гамма и связанные с ней функции.

Источник

§1. ГАММА-ФУНКЦИЯ

Начнем с определения гамма-функции, или эйлерова интеграла второго рода, для действительных положительных значений аргумента. Рассмотрим несобственный интеграл, зависящий от параметра α , с особенностями в точках x = 0 и x = +∞:

+∞∫ xα−1e−xdx, x , α > 0.

Для исследования сходимости представим его в виде суммы двух интегралов:

+∞∫ xα−1e−xdx = ∫1	xα−1e−xdx + +∞∫ xα−1e−xdx .	(1.1)
0	0	1

Первый интеграл в формуле (1.1) существует при α > 0 . Действительно, при

α ≥1 это собственный интеграл,	а при 0 < α <1 имеем		1e xα−1 ≤ xα−1e−x ≤ xα−1 и
1					x	x	x
∫xα−1dx сходится. Во втором интеграле xα−1e−x = xα−1e−		e−		≤ Ce−		, C = const>0
2	2	2
0
	+∞	x
при x >1и α , а	∫e−		dx	сходится. Таким образом,	оба интеграла
2

сходятся по признаку сравнения. Проведенные рассуждения дают основание дать

Определение 1. Гамма-функция, или эйлеров интеграл второго рода,

определяется формулой

def +∞

Γ(α)= ∫ xα−1e−xdx, x , α (0,+∞).

Теорема 1. Функция Γ(0α) непрерывна и имеет производные всех порядков α > 0 .

Доказательство. Зафиксируем α > 0 . Тогда α [α1,α2 ], α1 > 0 ; α1 и α2

будут выбраны далее. Воспользуемся представлением (1.1). Оба интеграла в
(1.1) равномерно сходятся	на	[α1,α2 ]	по признаку Вейерштрасса:
действительно,		xα−1e−x	< xα1−1	при	x (0,1),	xα−1e−x	< xα2 e−x при x (1,+∞) и

интегралы

∫1 xα1−1dx, +∞∫ xα2 −1e−xdx

0 1

сходятся. Следовательно, в пределе имеем непрерывную функцию.

Докажем существование первой производной. После формального дифференцирования под знаком интеграла в формуле (1.1) получим интегралы

∫1

xα-1 ln x e—xdx ,

+∞∫ xα-1 ln x e—xdx .

(1.2)

Если α >1,

то

lim xα−1 ln x = 0

и нет особенности в нуле. Если 0 < α ≤1, то

x→+0

xα−1 ln x e−x

≤ xα1−1 ln x ,

0 < x <1. Обозначим через ε =1−α1 . Выберем ε2

> 0 так,

чтобы

0 <ε +ε2 <1.

Тогда

xα1−1

ln x

= x−ε

ln x

= xε2

ln x

x−(ε+ε2 ).

Поскольку

lim xε2

ln x

= 0 ,

то

xα1−1

ln x

≤ C x−(ε+ε2 ) ,

C = const>0.

Интеграл

1 x−(ε+ε2 )dx

x→+0

∫

сходится, так как 0 <ε +ε2 <1. Следовательно,

первый интеграл в (1.2) сходится

равномерно на [α1,α2 ]

по признаку Вейерштрасса. Во втором интеграле имеем

оценки

xα−1 ln x e−x

≤ xα2 e−xdx = xα2

e−

≤ Ce−

C = const>0,

x >1.

+∞

Поскольку

∫ e—

dx сходится, то второй интеграл также сходится равномерно

на отрезке

1[α1,α2 ]

по

признаку Вейерштрасса. По

правилу

Лейбница

дифференцирования по параметру несобственного интеграла существует производная

′	+∞
(α)= ∫ x	α−1	ln x e	−x	dx .	(1.3)
Γ
	0

Аналогично можно показать, что существуют и являются непрерывными функциями производные высших порядков

Γ′′(α)= +∞∫ xα−1 (ln x)2 e−xdx , …, Γ(n) (α)= +∞∫ xα−1 (ln x)n e−xdx .

		0	0
	Установим некоторые соотношения.
1.	Γ(α +1)= αΓ(α)	(первое функциональное уравнение).	(1.4)
	Действительно, Γ(α +1)= +∞∫ xαe−xdx = −xαe−x		0+∞ + α+∞∫ xα−1e−xdx = αΓ(α).

		0	0
2.	Γ(n +1)= n!.			(1.5)

Действительно, в силу (1.4)

Γ(n +1)= nΓ(n)= nΓ(n +1−1)= n(n −1)Γ(n −1)=… = n!Γ(1),

Γ(1) = +∞∫e−xdx =1,

откуда и вытекает требуемое утверждение.

3.	Γ(α)=	Γ(α + n)
α (α +1) (α + n −1).	(1.6)

Действительно, применяя n раз (1.4), получим

Γ(α + n)= (α + n −1)Γ(α + n −1)=… = (α + n −1)(α + n − 2)…(α +1)α Γ(α).

Осталось выразить Γ(α) через Γ(α + n).

4.		1	(1.7)
= π .
Γ	2

Действительно,

+∞

−x

+∞

∫

−2

−x

dx = ∫

∫e

−x

2 ∫e

−t2

dt = ∫e

−t2

dx = 2

d x =

x = t

dt = π

−∞

(интеграл Эйлера─Пуассона).

(2n −1)!!

(1.8)

π .

Рассмотрим

−1

= Γ n

= Γ n −

n −

= Γ n −

+1 n −

=… =

−

= Γ n −

n −

…Γ

2n −1

2n −3

2n −5

(2n −1)!!

π .

…Γ

Построим график гамма-функции. Легко видеть,

что

Γ(α)> 0 в силу

определения.

Поскольку

Γ′′(α)> 0, то график функции

Γ(α)

является

выпуклым вниз, а ее производная Γ′(α)

возрастает. Поскольку Γ(1)= Γ(2)=1,

то

по

теореме

Ролля

существует

точка

ξ (1,2)

такая,

что

Γ′(ξ)= 0, Γ′(α)< 0, 0 <α <ξ, Γ′(α)> 0, α >ξ .

Кроме

того,

Γ(α)→ +∞

при

α → +∞.

В силу первого функционального уравнения

Γ(α)= Γ(α +1)

α и

верна

эквивалентность

Γ(α) 1 α, α → +0.

Получаем эскиз

графика гамма-

функции (см. рис.1.1).

§ 2. БЕТА-ФУНКЦИЯ ЭЙЛЕРА. СВЯЗЬ МЕЖДУ ГАММА-ФУНКЦИЕЙ И

БЕТА-ФУНКЦИЕЙ. ФОРМУЛА ДОПОЛНЕНИЯ.

Бета-функция, или эйлеров интеграл первого рода, определяется формулой

B( p,q) = ∫1

xp−1 (1− x)q−1 dx ,

(1.9)

где p,q

─

параметры. При

p ≥1,q ≥1

─

это

собственный интеграл, при

остальных

p > 0, q > 0 ─ это несобственный интеграл с особенностями либо в

точке

x = 0, либо

в точке

x =1,

либо в

обеих

точках. Можно

доказать

следующее утверждение.

B( p,q) определена

Теорема 1.

Функция

непрерывна

области

p > 0, q > 0 по совокупности переменных.

Замечание.

Легко проверить (подстановкой x =1−t ), что

B( p,q) = B(q, p) ,

т.е. бета-функция симметрична относительно p и q.

Сделаем

(1.9) подстановку

x =

, t

(0,+∞), тогда

придем к

1+t

представлению

+∞

t p−1dt

Β( p,q) = ∫0

(1.10)

(1+t)p+q

Замечание. Можно устранить отсутствие симметрии в формуле (1.10).

Представим интеграл (1.10) в виде суммы двух интегралов:

+∞

p−1

+∞

p−1

Β( p,q) = ∫0

t dt

=∫0

t dt

∫1

t dt

(1+t)p+q

Во втором интеграле сделаем подстановку t =1 u, u (0,1), тогда

+∞

p−1

q−1

∫1

t dt

= ∫0

du ,

(1+t)p+q

(1+u)p+q

1 t p−1 +tq−1

Β( p,q) = ∫0 (1+t)p+q dt .

Установим соотношение между функциями гамма и бета.

Теорема 2.

Имеет место соотношение

(1+t)α+β

Β(α,β) =	Γ(α)Γ(β )	, α > 0, β > 0 .	(1.11)
Γ(α + β )
Доказательство. В формуле (1.1) сделаем подстановку x =ty, t > 0 . Тогда
Γ(α)= +∞∫tα−1 yα−1e−tytdy = tα +∞∫ yα−1e−tydy ,
		0		0
и получаем полезную формулу
	Γ(α)	= +∞∫ yα−1e−tydy .		(1.12)
	α
	t	0

Заменим здесь α на α + β и t на 1+ t , получим

Γ(α + β ) = +∞∫ yα+b−1e−(t+1)ydy .

Умножим обе части этого равенства на tα−1 и проинтегрируем по t от 0 до ∞:

+∞		tα−1	+∞	+∞	−(t+1)y
Γ(α + β ) ∫			α−1	α+β−1
		dt = ∫t	dt ∫ y	e	dy .
(1	α+β
0	+t)	0	0

Воспользуемся формулой (1.10) в левой части, а в правой части изменим порядок интегрирования и снова применим (1.12) и определение гаммафункции:

+∞

−y Γ(α)

Γ(α + β )Β(α,β) = ∫

α+b−1 −y

dy ∫t

α−1 −ty

dt = ∫ y

α+β−1

dy =

= Γ(α)+∞∫ yβ−1e−ydy = Γ(α) Γ(β ).

Разделив обе части последнего равенства на Γ(α + β ), получим (1.11).

Теорема 3(формула дополнения). Имеет место формула

Γ(p)Γ(1− p)= Β( p,1− p) =

, 0 < p <1.

(1.13)

sinπ p

Доказательство. В формуле (1.10) положим

q =1− p , тогда

+∞

p−1

Β( p,1− p) =

∫

1+ x

Рассмотрим функцию комплексного переменного z

w(z)=

z p−1

, zP−1 = e(p−1)ln z , ln z = ln

+i arg z ,

1+ z

в плоскости , разрезанной по положительной части действительной оси. На

xp−1

верхнем крае разреза положим w(x +i0)= 1+ x . На нижнем крае разреза,

совершив обход в положительном направлении вокруг начала координат, мы получим

		2πi		p−1		p−1 2πi(p−1)	, w(x −i0)=	xp−1	2iπ(p−1)
z = x −i0	= xe		, z		= x	e		e		.
		1+ x
Рассмотрим замкнутый контур	L , состоящий из отрезка	[0, R]на верхнем

краю разреза, окружности CR	с центром в начале координат и радиусом R и
отрезка [R,0]на нижнем краю разреза. Обход контура совершается против
часовой стрелки.	Внутри контура имеется одна особая точка z = −1, которая,
очевидно, является полюсом первого порядка. По теореме Коши о вычетах
	∫	w(z)dz = 2πi res w	(z),−1 =	2πieiπ(p−1) .

	L
С другой стороны, в силу аддитивности интеграла
∫ w(z)dz = ∫R w(x +i0)dx + ∫ w(z)dz + ∫0 w(x −i0)dx .	(1.14)
L		0		CR	R
Оценим интеграл по окружности CR при больших значениях R. Если		z		= R ,

то

R p−1

w(z) ≤ R −1 ≤ C R p−2 , C = const>0 .

Следовательно, при 0 < p <1

∫ w(z)dz ≤ C Rp−2 2πR = 2πcRp−1 → 0 при R → +∞.

Переходя к пределу при R → ∞ в (1.14), находим, что

+∞

2πieiπ(p−1) = ∫0

xp−1

dx(1−e2πi(p−1) ).

1+ x

Следовательно,

+∞

p−1

iπ(p−1)

∫

dx = 2πi

= 2πi

= −

1+ x

1−e

2πi(p

−1)

−iπ(p−1)

−e

iπ

(p−1)

sinπ (p −1)

sinπ p

Следствие. Пусть p

, тогда Γ

=π Γ

= π .

sin

Замечание. Формулу дополнения называют вторым функциональным уравнением для гамма-функции.

Теорема 4 (формула Лежандра, третье функциональное уравнение).

Γ(α )Γ(α + 12 )=

Γ( 2α ).

(1.15)

α−

Доказательство. Воспользуемся формулой (1.9):

α−1

−(

1 − x )

α−1

1 2

1 −(

1 − x )

z−1

Β(α,α )= ∫xα−1

(1− x )

dx = ∫

dx = 2 ∫

в силу симметрии параболы

y = 14 −(12 − x )2

относительно

прямой

x = 12 .

Сделаем подстановку 1 − x = 1

. Тогда получим

Β(12 ,α ).

Β(α,α )

∫t−

(1−t )α−1 dt =

22α−1

Заменим

в обоих случаях бета-функцию

ее выражением через гамма-

функцию:

Γ(α)Γ(α)

1 Γ(1 2)Γ(α)

Γ(2α)

22α−1

Γ(α +1 2)

Сокращая на Γ(α) и подставляя Γ(12)= π , приходим к формуле Лежандра.

Замечание. Мы знаем, что функция Γ(α) непрерывна вместе со своей

производной для положительных значений аргумента. Кроме того, она удовлетворяет трем функциональным уравнениям

Γ(α +1)=α Γ(α),

Γ(α)Γ(1−α)= sinππα , 0 <α <1,

(		)	(		)		1	(	)	(	)
Γ	α		Γ	α		=			Γ 1 2	Γ	α	.
Γ(2α)		22α−1		Γ(α +1 2)

Оказывается, эти свойства однозначно определяют гамма-функцию.

Рассмотрим важный пример применения бета-функции. В формуле (1.9) положим x =sin2 t, t [0,π 2]. Тогда

π2

1− x =1−sin2 t = cos2 t, dx = 2sint cost ,Β(p,q)= 2 ∫ sin2 p−1 t cos2q−1 tdt .

Обозначим 2 p −1 = m, 2q −1 = n . Так как p > 0, q > 0, то m > −1,n > −1. Итак,

Источник

Почему это интересно?

Многие распределения вероятностей определяются с использованием гамма-функции, я перечислю лишь некоторые: гамма-распределение, бета-распределение, распределение Дирихле, распределение хи-квадрат, т-распределение Стьюдента и так далее.

Для специалистов по данным или инженеров и исследователей машинного обучения гамма-функция, вероятно, одна из наиболее широко используемых функций, потому что она участвует во множестве распределений. Эти распределения затем используются для генеративных статистических моделей (например, латентного размещения Дирихле), стохастических процессов (таких как модели очередей), байесовском выводе и вариационном выводе. Если вы уже хорошо понимаете гамма-функцию, вы сможете лучше понять множество приложений, в которых она появляется!

1. Зачем нам нужна гамма-функция?

Потому что мы хотим генерализовать факториал!

Функция факториала определена только для дискретных точек (для положительных целых чисел — черные точки на графике выше), но мы хотим соединить черные точки. Мы хотим распространить функцию факториала на все комплексные числа. Простую формулу факториала, x! = 1 * 2 * … * x, нельзя использовать непосредственно для дробных значений, потому что она верна только для целых чисел.

Тогда математики стали искать…

“Какие функции плавно соединяют эти точки и предоставляют нам факториалы всех действительных чисел?”

Однако они не могли найти “конечные” комбинации сумм, произведений, степеней, экспонент и логарифмов, которые могли бы выразить x! для действительных чисел, пока…

2. Эйлер в XVIII веке нашел гамма-функцию

Формула выше используется для нахождения значения гамма-функции любого действительного значения z.

Мы хотим вычислить Γ(4.8). Как решить интеграл выше?
Сможете вычислить вручную? Может быть, по частям?

Для меня (и многих других) пока не существует простого и быстрого способа вычислить гамма-функцию дробей вручную (Если вам интересно решить вручную, вот хорошая стартовая точка).

Ладно, забудьте о том, чтобы сделать это аналитически. Вы сможете вычислить этот интеграл от 0 до бесконечности программным способом, добавляя член бесконечное число раз?

Есть несколько способов вычисления. Два из наиболее используемых решений — это формула Стирлинга и приближение Ланцоша.

Для фанатов вычислений: код для гамма-функции (в основном приближение Ланцоша) на более чем 60 языках - C, C++, C#, python, java, etc.

Давайте вычислим Γ(4.8), используя готовый калькулятор.

Мы получим 17.837.

17.837 находится между 3!(= Γ(4) = 6) и 4!(= Γ(5) = 24) — как мы и ожидали.

Когда z — натуральное число, Γ(z) =(z-1)! Скоро мы это докажем.

В отличие от факториала, который принимает только положительные целые числа, мы можем подставлять в z любые действительные или комплексные числа, в том числе и отрицательные. Гамма-функция соединяет черные точки и плавно рисует кривую.

Уточнение: мы интегрируем по x (НЕ по z) от 0 до бесконечности. 
 • x - вспомогательная переменная, которую мы интегрируем.
• Мы НЕ подставляем 4.8 в x. Мы подставляем 4.8 в z.

3. Как гамма-функция может интерполировать функцию факториала?

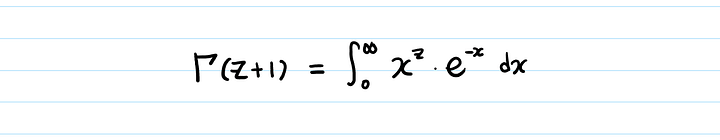
Если вы посмотрите на гамма-функцию, вы заметите две вещи.

Во-первых, это определенно возрастающая функция по отношению к z.

Во-вторых, если z — натуральное число, Γ(z+1) = z!
(Я обещаю, что мы скоро докажем это!)

Значит, можно ожидать, что гамма-функция соединит факториал.

Как гамма-функция получила члены x^z и e^-x?

Я не знаю точно, каким путем шел Эйлер, но именно он открыл натуральное число e, поэтому он, должно быть, много экспериментировал с перемножением e на другие функции, чтобы найти настоящую форму уравнения.

4. Как будет выглядеть график гамма-функции?

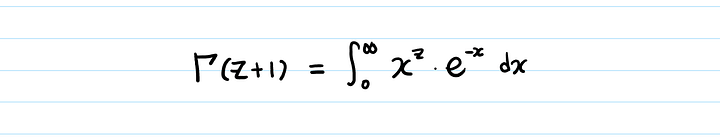
Когда x стремится к бесконечности ∞, первый член (x^z) также стремится к бесконечности ∞, но второй (e^-x) стремится к нулю.

Будет ли гамма-функция сходиться к конечным значениям?

Мы методично покажем, что сходится, используя правило Лопиталя. Но мы также можем увидеть ее сходимость и без особых усилий. Подумаем: мы интегрируем произведение x^z — полиномиальной возрастающей функции — и e^-x —экспоненциально убывающей функции. Так как значение e^-x уменьшается значительно быстрее, чем значение x^z, гамма-функция наверняка сходится и имеет конечные значения.

Давайте построим на каждый график, ведь лучше один раз увидеть, чем сто раз услышать.

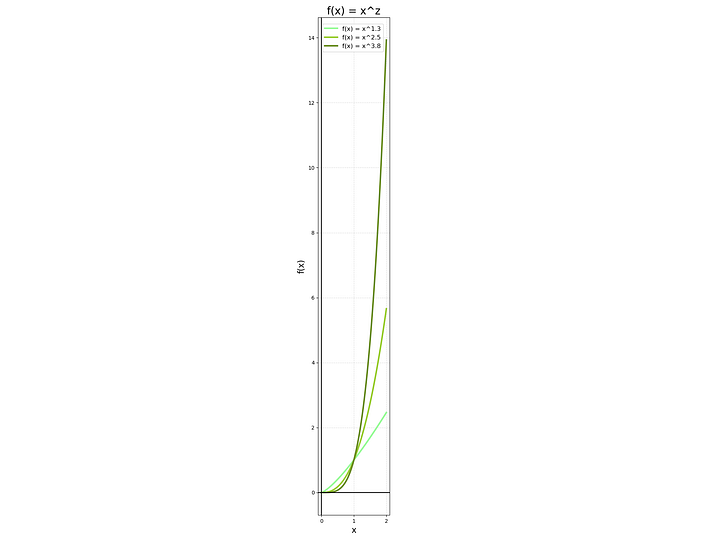
Первый член x^z — полиномиально возрастающая функция.

Второй член e^-x — экспоненциально убывающая функция

График x^z * e^-x

Давайте рассмотрим случай Γ(4.8).

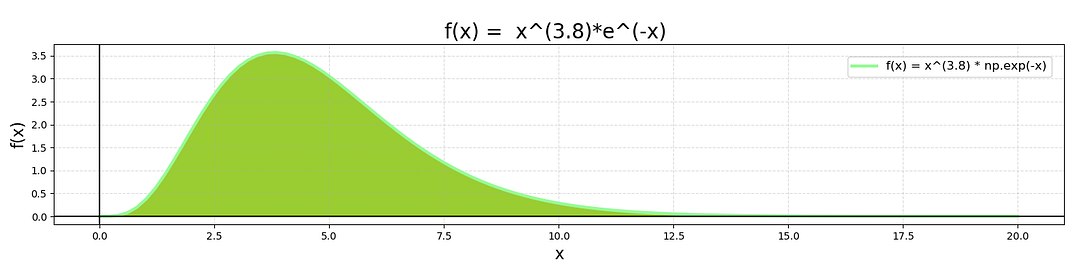
Зеленая область под графиком со значениями от 0 до бесконечности — Γ(4.8) = 3.8!

Для создания красивого графика выше использовался код Python. Постройте такой график сами и увидите, как z меняет форму гамма-функции!

########################
# f(x) = exp(-x) graph #
########################

import matplotlib.pyplot as plt
import numpy as np

# Задаем x и y
x = np.linspace(-2, 20, 100)
y = np.exp(-x)

# Создаем график
fig, ax = plt.subplots()
plt.plot(x, y, label='f(x) = exp(-x)', linewidth=3, color='palegreen')

# Делаем x=0, а y=0 толще
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')

# Добавляем заголовок
plt.title('f(x) = exp(-x)', fontsize=20)

# Добавляем метки X и y
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)', fontsize=16)

# Добавляем шкалу
plt.grid(alpha=.4, linestyle='--')

# Показываем график
plt.show()

####################
# f(x) = x^z graph #
####################

import matplotlib.pyplot as plt
import numpy as np

# Задаем x и y
x = np.linspace(0, 2, 100)
y1 = x**1.3
y2 = x**2.5 
y3 = x**3.8

# Создаем график
fig, ax = plt.subplots()
plt.plot(x, y1, label='f(x) = x^1.3', linewidth=3, color='palegreen')
plt.plot(x, y2, label='f(x) = x^2.5', linewidth=3, color='yellowgreen')
plt.plot(x, y3, label='f(x) = x^3.8', linewidth=3, color='olivedrab')

# Делаем x=0, y=0 толще
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')

# Добавляем заголовок
plt.title('f(x) = x^z', fontsize=20)

# Добавляем метки X и y

plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)', fontsize=16)# Add a grid
plt.grid(alpha=.4, linestyle='--')

# Добавляем легенду
plt.legend(bbox_to_anchor=(1, 1), loc='best', borderaxespad=1, fontsize=12)

# Показываем график
plt.show()

###############################
# f(x) = x^(3.8)*e^(-x) graph #
###############################
import matplotlib.pyplot as plt
import numpy as np

# Задаем x и y
x = np.linspace(0, 20, 100)
y = x**3.8 * np.exp(-x)

# Создаем график
fig, ax = plt.subplots()
plt.plot(x, y, label='f(x) = x^(3.8) * np.exp(-x)', linewidth=3, color='palegreen')
ax.fill_between(x, 0, y, color='yellowgreen')

# Делаем x=0, y=0 толще
ax.set_aspect('equal')
ax.grid(True, which='both')
ax.axhline(y=0, color='k')
ax.axvline(x=0, color='k')

# Добавляем заголовок
plt.title('f(x) =  x^(3.8)*e^(-x) ', fontsize=20)

# Добавляем метки X и y
plt.xlabel('x', fontsize=16)
plt.ylabel('f(x)' ,fontsize=16)

# Добавляем шкалу
plt.grid(alpha=.4, linestyle='--')

# Добавляем легенду
plt.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=1, fontsize=12)

# Показываем график
plt.show()

Код на Github.

5. Свойства гамма-функции

Если усваивать что-то одно из поста, то этот раздел.

Свойство 1.

При z > 1

Γ(z)   = (z-1) * Γ(z-1)
или можно записать так
Γ(z+1) =  z    * Γ(z)

Давайте докажем это, используя интегрирование по частям и определение гамма-функции.

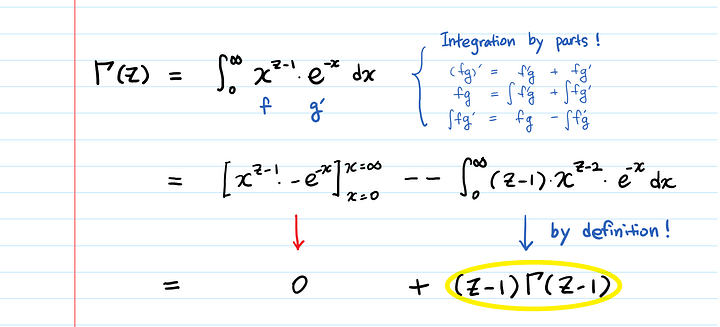
Красная стрелка — значение e^-x уменьшается гораздо быстрее, чем значение x^z

Красивое доказательство!

Свойство 2. 

Если n - положительное целое число 

Γ(n) = (n-1)!

Докажем это, используя свойство 1:

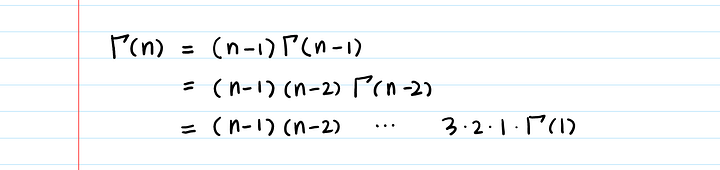
Каково значение Γ(1)?

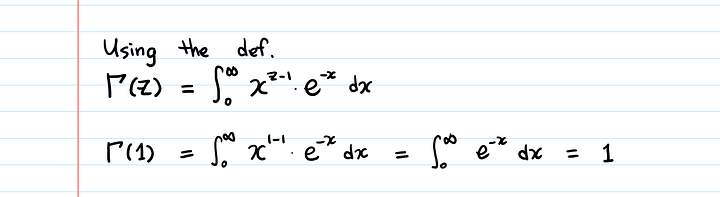
Таким образом, Γ(n) = (n-1)!

Можно также увидеть выражение Γ(n+1) = n! вместо 
Γ(n) = (n-1)!.

Просто чтобы сделать правую часть n! вместо (n-1)! 
Все, что мы сделали, это уменьшили n на 1.

6. Используя свойство гамма-функции, покажем, что плотность вероятности гамма-распределения интегрируется к 1.

Вот доказательство:

Для фанатов доказательств: давайте докажем фрагмент выше, выделенный красным.

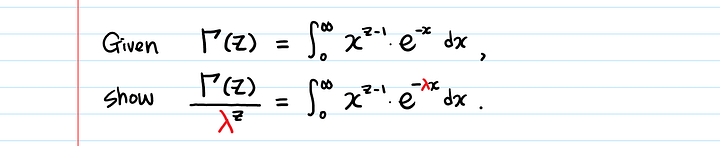
Интегрируем методом подстановки.

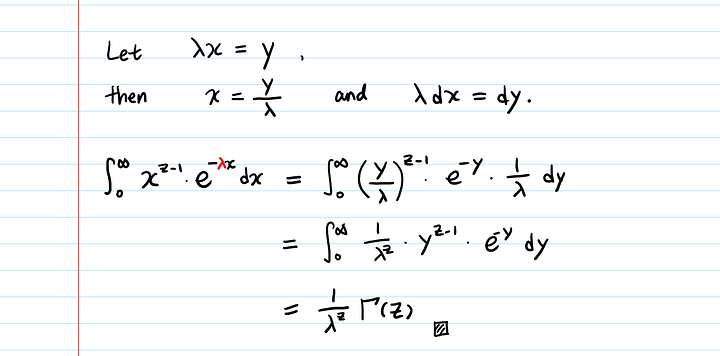
Снова красиво доказано!

Несколько замечаний:

Возраст гамма-функции.

Она весьма стара, ей около 300 лет (работаете ли вы сейчас над чем-то, что будет использоваться 300 лет спустя? 😉

Интересное примечание: Эйлер ослеп в 64 года, однако больше половины своих работ он написал уже после потери зрения.

2. Несколько интересных значений в точках:

Γ(1/2) = sqrt(?)

Множество интересных способов показать это:
https://math.stackexchange.com/questions/215352/why-is-gamma-left-frac12-right-sqrt-pi

Γ(-1/2) = -2 * sqrt(?)

Γ(-1) = Γ(-2) = Γ(-3) = infinity ∞

Сможете доказать?

3. Вот быстрый обзор графиков гамма-функций действительных чисел:

Гамма-функция Γ(z) нарисована синим, Γ(z) + sin(πz) — зеленым. (Заметьте, пересечение в области положительных целых чисел, потому что sin(πz) равен нулю!) Обе являются истинными аналитическими продолжениями факториалов до нецелых чисел.

4. Гамма-функция также появляется в формуле объема n-мерного шара.

Гамма-функция и ее свойства

Motivation[edit]

Definition[edit]

Main definition[edit]

Alternative definitions[edit]

Euler’s definition as an infinite product[edit]

Weierstrass’s definition[edit]

Properties[edit]

General[edit]

Inequalities[edit]

Stirling’s formula[edit]

Residues[edit]

Minima and maxima[edit]

Integral representations[edit]

Continued fraction representation[edit]

Fourier series expansion[edit]

Raabe’s formula[edit]

Pi function[edit]

Relation to other functions[edit]

Particular values[edit]

The log-gamma function[edit]

Properties[edit]

Integration over log-gamma[edit]

Approximations[edit]

Applications[edit]

Integration problems[edit]

Calculating products[edit]

Analytic number theory[edit]

History[edit]

18th century: Euler and Stirling[edit]

19th century: Gauss, Weierstrass and Legendre[edit]

19th–20th centuries: characterizing the gamma function[edit]

Reference tables and software[edit]

See also[edit]

Notes[edit]

Further reading[edit]

External links[edit]

Содержание

Мотивация

Определение

Основное определение

Альтернативные определения

Определение Эйлера как бесконечного произведения

Определение Вейерштрасса

В терминах обобщенных полиномов Лагерра

Свойства

Общие

Неравенства

формула Стирлинга

Остатки

Minima

Интегральные представления

Разложение в ряд Фурье

Формула Раабе

Функция Пи

Связь с другими функциями

Конкретные значения

log-гамма-функция

Свойства

Интегрирование по логарифмической гамме

Приближение

Приложения

Проблемы интеграции

Вычисления продуктов

Аналитическая теория чисел

История

18 век: Эйлер и Стирлинг

XIX век: Гаусс, Вейерштрасс и Лежандр

XIX – XX веков: характеристика гамма-функции

Справочные таблицы и программное обеспечение

См. Также

Примечания

Дополнительная литература

Внешние ссылки

§1. ГАММА-ФУНКЦИЯ

1. Зачем нам нужна гамма-функция?

2. Эйлер в XVIII веке нашел гамма-функцию

3. Как гамма-функция может интерполировать функцию факториала?

4. Как будет выглядеть график гамма-функции?

График x^z * e^-x