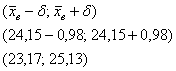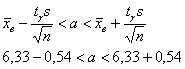Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная дисперсия
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:
С этим понятием также связано понятие генерального среднего квадратического отклонения.
Определение 3
Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_г=sqrt{D_г}]
Выборочная дисперсия
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 4
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 5
Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.
«Дисперсия: генеральная, выборочная, исправленная» 👇
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:
С этим понятием также связано понятие выборочного среднего квадратического отклонения.
Определение 6
Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_в=sqrt{D_в}]
Исправленная дисперсия
Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть
С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Пример задачи на нахождение дисперсии и среднего квадратического отклонения
Пример 1
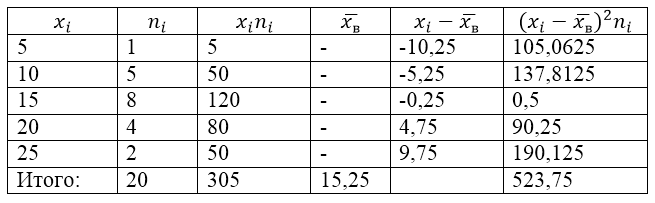
Выборочная совокупность задана следующей таблицей распределения:
Рисунок 1.
Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Решение:
Для решения этой задачи для начала сделаем расчетную таблицу:
Рисунок 2.
Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
То есть
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Найдем выборочную дисперсию по формуле:
[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]
Выборочное среднее квадратическое отклонение:
[{sigma }_в=sqrt{D_в}approx 5,12]
Исправленная дисперсия:
[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]
Исправленное среднее квадратическое отклонение:
[S=sqrt{S^2}approx 5,25]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
-
Числовые характеристики распределений: генеральная средняя и дисперсия; выборочная средняя и дисперсия.
.1.Генеральная
средняя.
Пусть
изучается генеральная совокупность
относительно количественного признака
Х.
Генеральной
средней называют среднее арифметическое
значений признака генеральной
совокупности.
Если
все значения признака различны, то
Если
значения признака имеют частоты N1,
N2,
…, Nk,
где N1
+N2+…+Nk=
N,
то
1.2.Выборочная средняя.
Пусть
для изучения генеральной совокупности
относительно количественного признака
Х извлечена выборка объема
n.
Выборочной
средней называют среднее арифметическое
значение признака выборочной совокупности.
Если
все значения признака выборки различны,
то
если
же все значения имеют частоты n1,
n2,…,nk,
то
Выборочная
средняя является несмещенной и
состоятельной оценкой генеральной
средней.
Замечание:
Если выборка представлена интервальным
вариационным рядом, то за xi
принимают середины частичных интервалов.
1.3. Генеральная дисперсия.
Для
того чтобы охарактеризовать рассеяние
значений количественного признака Х
генеральной совокупности вокруг
своего среднего значения, вводят сводную
характеристику — генеральную дисперсию.
Генеральной
дисперсией Dг
называют
среднее арифметическое квадратов
отклонений значений признака генеральной
совокупности от их среднего значения
.
Если
все значения признака генеральной
совокупности объема N
различны, то
Если
же значения признака имеют соответственно
частоты N1,
N2,
…, Nk,
где N1
+N2+…+Nk=
N,
то
Кроме
дисперсии для характеристики рассеяния
значений признака генеральной
совокупности вокруг своего среднего
значения пользуются сводной характеристикой—
средним квадратическим отклонением.
Генеральным
средним квадратическим отклонением
(стандартом) называют квадратный корень
из генеральной дисперсии:
1.4.Выборочная дисперсия.
Для
того, чтобы наблюдать рассеяние
количественного признака значений
выборки вокруг своего среднего значения
, вводят сводную характеристику-
выборочную дисперсию.
Выборочной
дисперсией называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего значения
.
Если
все значения признака выборки различны,
то
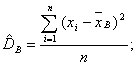
если
же все значения имеют частоты n1,
n2,…,nk,
то
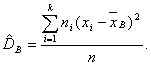
Для
характеристики рассеивания значений
признака выборки вокруг своего среднего
значения пользуются сводной характеристикой
— средним квадратическим отклонением.
Выборочным
средним квадратическим отклоненим
называют квадратный корень из выборочной
дисперсии:
Вычисление
дисперсии- выборочной или генеральной,
можно упростить, используя формулу:
Замечание:
если выборка представлена интервальным
вариационным рядом, то за xi
принимают середины частичных интервалов.
-
Функциональная, статистическая и корреляционная зависимости. Выборочное уравнение регрессии. Отыскание параметров выборочного уравнения прямой линии среднеквадратичной регрессии.
Статистической
называют зависимость, при которой
изменение одной
из величин влечет изменение распреде-
ления другой. В
частности, статистическая зависимость
проявляется в том,
что при изменении одной из величин
изменяется среднее
значение другой; в этом случае ста-
тистическую
зависимость называют корреляционной.
Функциона́льная
зави́симость —
концепция, лежащая в основе многих
вопросов, связанных с реляционными
базами данных,
включая, в частности, их проектирование.
Математически представляет бинарное
отношение
между множествами атрибутов данного
отношения
и является, по сути, связью типа «один
ко многим». Их использование обусловлено
тем, что они позволяют формально и строго
решить многие проблемы.
ВЗЯЛ
ИЗ УЧЕБНИКА В НЕТЕ ЕЩЕ БОЛЬШЕ .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.
Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).
Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”
Что такое дисперсия
Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.
Чтобы найти дисперсию последовательно проведите следующие вычисления:
- Определите среднее (простое среднее арифметическое ряда значений).
- Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
- Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).
Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.
| Порода собаки | Рост в миллиметрах |
| Ротвейлер | 600 |
| Бульдог | 470 |
| Такса | 170 |
| Пудель | 430 |
| Мопс | 300 |
Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.
Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:
Среднее мм.
Итак, среднее (среднеарифметическое) составляет 394 мм.
Теперь нужно определить отклонение роста каждой из собак от среднего:
Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:
Дисперсия мм2.
Таким образом, дисперсия составляет 21704 мм2.
Как найти среднеквадратическое отклонение
Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:
мм (округлено до ближайшего целого значения в мм).
Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).
Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.
То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.
Что такое стандартное отклонение
Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.
Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.
Если есть значений, то:
Все остальные расчеты производятся аналогично, в том числе и определение среднего.
Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:
Дисперсия выборки = мм2.
При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).
Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.
Примечание. Почему именно квадраты разностей?
Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:
.
Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?
.
На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:
.
Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.
А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).
Для первого примера получится:
.
Для второго примера получится:
.
Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.
Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.
И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.
О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич
Выборочная дисперсия, описание
Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.
Определение
Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
Связь выборочной и генеральной дисперсии
Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.
Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.
Как вычислить выборочную дисперсию
Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:
({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)
Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:
({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)
Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:
({widehatsigma}_В=sqrt{{widehat D}_В})
Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:
(D=overline{x^2}-left[overline xright]^2)
Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов.
Пример
Найти выборочную дисперсию выборки со значениями:
- xi: 1, 2, 3, 4;
- ni: 20, 15, 10, 5.
Решение
Для начала необходимо определить выборочную среднюю:
({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)
Затем найдем выборочную дисперсию:
(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)
Исправленная дисперсия
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
(Mleft[D_Bright]=frac{n-1}nD_Г)
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.
Исправить выборочную дисперсию можно путем умножения ее на дробь:
(frac n{n-1})
Получим формулу следующего вида:
(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})
Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2.
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
(S=sqrt{S^2})
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.
Для чего применяют исправленную выборочную дисперсию
Исправленную выборочную используют для точечной оценки генеральной дисперсии.
Пример
Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.
Решение
Сначала вычислим выборочную среднюю:
({overline x}_В=frac{92+94+103+105+106}5=100)
Затем найдем выборочную дисперсию:
(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)
Теперь рассчитаем исправленную дисперсию:
(S^2=frac5{5-1}cdot34=42,5)
4.3. Оценка генеральной средней нормально распределенной совокупности
Если вы не знаете, что такое нормальное
распределение, то это, конечно, большое упущение – обязательно ознакомьтесь с материалом по ссылке. И мы сразу
разберём «заезженную» задачу, которую предлагают даже студентам-гуманитариям:
Пример 19
Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением . Найти доверительный интервал для оценки математического
ожидания с надежностью 0,95, если выборочная
средняя , а объем выборки
.
Прежде всего, обращаю ваше внимание на принципиальный момент: здесь
4.3.1. Известно стандартное отклонение генеральной совокупности
Дело в том, что в похожих задачах оно бывает и не известно, и тогда решение будет отличаться! Этот случай тоже будет. А
сейчас решение таково, разбираемся в ситуации:
– из генеральной совокупности проведена выборка в попугаев и по её результатам найдена выборочная
средняя: (средний рост птицы).
Выборочная средняя – это точечная оценка неизвестной нам генеральной средней . Как отмечалось выше, недостаток точечной оценки
состоит в том, что она может оказаться далёкой от истины. И по условию, требуется найти интервал , который с вероятностью
накроет истинное значение
.
Именно так! Здесь некорректно говорить, что «истинное значение попадёт в этот интервал». Генеральная средняя – это конкретное (пусть
и не известное нам) значение, и оно не может никуда «попасть». В разных выборках мы будем получать разные значения и разные доверительные интервалы, которые могут лишь
накрыть генеральную среднюю. А могут и не накрыть (некоторые из них).
Найдём точность оценки, она рассчитывается по формуле , где
– так
называемый коэффициент доверия. Этот коэффициент отыскивается из соотношения , где
– функция
Лапласа.
По условию, , следовательно:
И по таблице значений функции Лапласа либо пользуясь приложенным к курсу расчётным макетом (пункт 1*), выясняем, что значению соответствует аргумент
.
Таким образом, точность оценки:
и искомый доверительный интервал:
Этот интервал с вероятностью (надёжностью) накрывает истинное генеральное значение
среднего роста попугая. Но всё же остаётся 5%-ная вероятность
того, что генеральная средняя окажется вне найденного интервала.
Ответ: .
И тут возникает светлая мысль уменьшить этот интервал – чтобы получить более точную оценку. Что для этого можно сделать?
Давайте посмотрим на формулу .
Очевидно, что чем меньше стандартное отклонение (мера разброса
значений), тем уже доверительный интервал. Но это в отдельно взятой задаче ни на что не влияет – ведь нам известно
конкретное значение и изменить его невозможно.
Поэтому для уменьшения «дельты» можно уменьшить коэффициент доверия, например, вместо рассмотреть
и тогда
, в
результате чего доверительный интервал –
действительно стал в 2 раза короче. Но засада в том, что упала и доверительная вероятность:
пользуясь таблицей значений функции Лапласа либо расчётным макетом (пункт 1), находим: – то есть о том, что этот более узкий интервал накроет генеральную среднюю, мы
теперь можем утверждать лишь с вероятностью 68,26%. Что, конечно, неудовлетворительно, для серьёзного
статистического исследования.
Поэтому для уменьшения доверительного интервала (при том же значении ) остаётся увеличивать объём выборки
. Что совершенно понятно и без формулы
, ведь чем больше объём выборки, тем точнее она характеризует генеральную совокупность
(при прочих равных условиях). Об объёме выборки мы поговорим позже, ну а пока
творческая задача для самостоятельного решения:
Пример 20
По результатам выборочного исследования объектов найдена выборочная средняя
.
1) С какой вероятностью можно утверждать, что генеральная средняя отличается от найденного значения не более чем на 3,
если известно, что генеральная совокупность распределения нормально с дисперсией 400?
2) Определить доверительный интервал, который с надежностью накроет истинное значение генеральной средней.
Образец в конце книги, таблица либо расчётный
макет (пункты 1 и 1*) в помощь.
И тут, наверное, у вас назрели вопросы – а откуда известно, что генеральная совокупность распределена
нормально, и тем более, откуда известно её стандартное отклонение?
Обычно эта информация известна из предыдущих исследований. Классический пример – измерительный прибор. Очевидно, что его
случайные погрешности удовлетворяют условию теоремы Ляпунова, а значит, распределены
нормально. Кроме того, производитель, как правило, тестирует прибор, и указывает в его паспорте стандартное отклонение случайной погрешности, которое можно принять за
.
Но если установить нормальность распределения достаточно просто (в том числе статистическими методами), то с генеральным
значением всё сложнее – зачастую вычислить его
трудно или невозможно. В такой ситуации остаётся ориентироваться на исправленную
выборочную дисперсию и решение несколько
изменится. Возвращаемся к нашей любимой задаче:
Пример 21
В результате 10 независимых измерений некоторой величины , выполненных с одинаковой точностью, полученные опытные данные, которые представлены в
таблице:
Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение
величины при помощи доверительного интервала,
покрывающего это значение с вероятностью 0,95.
Обратите внимание, что здесь речь идёт уже не о погрешностях прибора, а об измерениях, и помимо технических, велико
влияние других, в частности, человеческого фактора, особенно, если вы используете махрово-аналоговый инструмент – что-нибудь
вроде механического секундомера или линейки.
Решение следует начать с вычисления выборочных характеристик, и задача облегчается тем, что в Примере
13 они уже вычислены: . По условию, требуется оценить
генеральную совокупность (а именно, параметр ),
и поэтому дисперсию нужно обязательно поправить:
– несмещённая оценка неизвестной
генеральной дисперсии . И нас будет интересовать несмещённая оценка генерального стандартного отклонения
:
– исправленное среднее квадратическое
отклонение.
Теперь построим доверительный интервал для оценки истинного (генерального) значения величины
.
4.3.2. Если генеральная дисперсия нормального распределения не известна
то этот интервал строится по похожей формуле:
, с той поправкой, что коэффициент доверия
рассчитывается с помощью распределения Стьюдента. Я
не буду рассказывать об этом распределении и ограничусь технической стороной вопроса.
Значение можно найти с помощью
таблицы значений распределения Стьюдента, в частности популярна таблица, специально
адаптированная для данной задачи*. И, согласно таблице, доверительной вероятности и объёму выборки
соответствует коэффициент доверия:
* в таблице, которую можно встретить чаще, приводятся значения для так
называемого уровня значимости и для количества
степеней свободы .
Другой, более универсальный способ – воспользоваться Экселем, и чтобы далеко не ходить, я добавил этот функционал в расчётный макет: ищем пункт 2б, забиваем значения ,
и получаем «на выходе»
.
Вычислим точность оценки:
Таким образом, искомый доверительный интервал:
– данный интервал с вероятностью
накрывает истинное генеральное значение
измеряемой величины
.
Ответ:
Для самостоятельного решения:
Пример 22
На основании испытаний установлено, что в
среднем для изготовления шавермы полупроводникового диода требуется секунд, а исправленное среднее квадратическое отклонение составляет
секунд. Предположив, что время изготовления диода есть нормальная
случайная величина, определить с надежностью доверительный интервал для оценки среднего времени изготовления диода
Краткое решение в конце книги, таблица или макет (пункт 2б) – в помощь.
Итак, что главное в разобранных задачах? Главное, обратить внимание, генеральное ли нам дано отклонение или исправленное выборочное
. От этого зависит, какую формулу нужно использовать,
эту:
, где
,
или эту:
, где
отыскивается с помощью распределения Стьюдента.
При увеличении объёма выборки , распределение Стьюдента стремится к нормальному распределению, и поэтому уже при
во 2-м случае допускается нахождение
с помощью того же соотношения
. Но я бы не рекомендовал так делать. Потому что если дано
, то предполагается, что решать нужно именно через «Стьюдента», и при
наличии Экселя с этим никаких проблем – можно рассчитать любые значения, которые отсутствуют в таблицах.
Коварные авторы могут предложить «простое» выборочное отклонение , и тогда его следует поправить по формуле:
, которая следует из соотношения дисперсий:
. Иногда бывает предложена и дисперсия (та или
иная). Именно здесь нужно проявлять аккуратность, сами же вычисления достаточно примитивны.


| Оглавление |




![Rendered by QuickLaTeX.com [ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3916a3ccd97d909589dfe1dabb970af0_l3.png)