Геометрия как найти центр фигуры

Как найти центр фигуры

Центр фигуры можно найти несколькими способами, смотря какие данные о ней уже известны. Стоит разобрать нахождение центра окружности, которая является совокупностью точек, располагающихся на равном расстоянии от центра, так как эта фигура — одна из наиболее распространенных.

Вам понадобится

• — угольник;
• — линейка.

Инструкция

Простейший способ найти центр окружности – согнуть листок бумаги, на котором она начерчена, убедившись, глядя на просвет, что она сложилась точно пополам. Затем согните лист перпендикулярно первому сгибу. Так вы получите диаметры, точка пересечения которых и есть центр фигуры.

Конечно, этот способ идеален, только если окружность начерчена на бумаге, достаточно тонкой, чтобы можно было посмотреть на просвет, точно ли сложен лист.

Допустим, рассматриваемую фигуру начертили на твердой, несгибаемой поверхности либо это отдельная деталь, которая также не поддается сгибу. Чтобы найти центр окружности в этом случае, вам нужна линейка.

Диаметр является самым длинным отрезком, соединяющим 2 точки окружности. Как известно, проходит он через центр, поэтому задача нахождения центра окружности сводится к нахождению диаметра и его середины.

Наложите линейку на окружность, после чего зафиксируйте в любой точке фигуры нулевую отметку. Приложите линейку к окружности, получив секущую, а затем двигайте по направлению к центру фигуры. Длина секущей будет возрастать, пока не дойдет до пиковой точки. Вы получите диаметр, а найдя его середину, найдете и центр окружности.

Центр описанной окружности для любого треугольника располагается на пересечении срединных перпендикуляров. В случае, если треугольник прямоугольный, ее центр всегда будет совпадать с серединой гипотенузы. То есть решение кроется в построении внутри окружности прямоугольного треугольника с вершинами, лежащими на окружности.

Трафаретом для прямого угла могут послужить школьный или строительный угольник, линейка или даже лист бумаги/картона. Поместите в любую точку окружности вершину прямого угла, сделайте отметки в тех местах, где стороны угла пересекают границу окружности, соедините их. У вас получился диаметр – гипотенуза.

Таким же способом найдите еще один диаметр, место пересечения двух таких отрезков и будет центром окружности.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure.^{[further explanation needed]} The same definition extends to any object in n-dimensional Euclidean space.^[1]

In geometry, one often assumes uniform mass density, in which case the barycenter or center of mass coincides with the centroid. Informally, it can be understood as the point at which a cutout of the shape (with uniformly distributed mass) could be perfectly balanced on the tip of a pin.^[2]

In physics, if variations in gravity are considered, then a center of gravity can be defined as the weighted mean of all points weighted by their specific weight.

In geography, the centroid of a radial projection of a region of the Earth’s surface to sea level is the region’s geographical center.

History[edit]

The term «centroid» is of recent coinage (1814).^[3] It is used as a substitute for the older terms «center of gravity» and «center of mass» when the purely geometrical aspects of that point are to be emphasized. The term is peculiar to the English language; the French, for instance, use «centre de gravité» on most occasions, and others use terms of similar meaning.

The center of gravity, as the name indicates, is a notion that arose in mechanics, most likely in connection with building activities. It is uncertain when the idea first appeared, as the concept likely occurred to many people individually with minor differences. Nonetheless, the center of gravity of figures was studied extensively in Antiquity; Bossut credits Archimedes (287–212 BCE) with being the first to find the centroid of plane figures, although he never defines it.^[4] A treatment of centroids of solids by Archimedes has been lost.^[5]

It is unlikely that Archimedes learned the theorem that the medians of a triangle meet in a point—the center of gravity of the triangle—directly from Euclid, as this proposition is not in the Elements. The first explicit statement of this proposition is due to Heron of Alexandria (perhaps the first century CE) and occurs in his Mechanics. It may be added, in passing, that the proposition did not become common in the textbooks on plane geometry until the nineteenth century.

Properties[edit]

The geometric centroid of a convex object always lies in the object. A non-convex object might have a centroid that is outside the figure itself. The centroid of a ring or a bowl, for example, lies in the object’s central void.

If the centroid is defined, it is a fixed point of all isometries in its symmetry group. In particular, the geometric centroid of an object lies in the intersection of all its hyperplanes of symmetry. The centroid of many figures (regular polygon, regular polyhedron, cylinder, rectangle, rhombus, circle, sphere, ellipse, ellipsoid, superellipse, superellipsoid, etc.) can be determined by this principle alone.

In particular, the centroid of a parallelogram is the meeting point of its two diagonals. This is not true of other quadrilaterals.

For the same reason, the centroid of an object with translational symmetry is undefined (or lies outside the enclosing space), because a translation has no fixed point.

Examples[edit]

The centroid of a triangle is the intersection of the three medians of the triangle (each median connecting a vertex with the midpoint of the opposite side).^[6]

For other properties of a triangle’s centroid, see below.

Locating[edit]

Plumb line method[edit]

The centroid of a uniformly dense planar lamina, such as in figure (a) below, may be determined experimentally by using a plumbline and a pin to find the collocated center of mass of a thin body of uniform density having the same shape. The body is held by the pin, inserted at a point, off the presumed centroid in such a way that it can freely rotate around the pin; the plumb line is then dropped from the pin (figure b). The position of the plumbline is traced on the surface, and the procedure is repeated with the pin inserted at any different point (or a number of points) off the centroid of the object. The unique intersection point of these lines will be the centroid (figure c). Provided that the body is of uniform density, all lines made this way will include the centroid, and all lines will cross at exactly the same place.

This method can be extended (in theory) to concave shapes where the centroid may lie outside the shape, and virtually to solids (again, of uniform density), where the centroid may lie within the body. The (virtual) positions of the plumb lines need to be recorded by means other than by drawing them along the shape.

Balancing method[edit]

For convex two-dimensional shapes, the centroid can be found by balancing the shape on a smaller shape, such as the top of a narrow cylinder. The centroid occurs somewhere within the range of contact between the two shapes (and exactly at the point where the shape would balance on a pin). In principle, progressively narrower cylinders can be used to find the centroid to arbitrary precision. In practice air currents make this infeasible. However, by marking the overlap range from multiple balances, one can achieve a considerable level of accuracy.

Of a finite set of points[edit]

The centroid of a finite set of points in is^[1]

This point minimizes the sum of squared Euclidean distances between itself and each point in the set.

By geometric decomposition[edit]

The centroid of a plane figure can be computed by dividing it into a finite number of simpler figures , computing the centroid and area of each part, and then computing

Holes in the figure , overlaps between the parts, or parts that extend outside the figure can all be handled using negative areas . Namely, the measures should be taken with positive and negative signs in such a way that the sum of the signs of for all parts that enclose a given point is 1 if belongs to , and 0 otherwise.

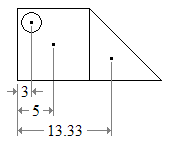
For example, the figure below (a) is easily divided into a square and a triangle, both with positive area; and a circular hole, with negative area (b).

The centroid of each part can be found in any list of centroids of simple shapes (c). Then the centroid of the figure is the weighted average of the three points. The horizontal position of the centroid, from the left edge of the figure is

The vertical position of the centroid is found in the same way.

The same formula holds for any three-dimensional objects, except that each should be the volume of , rather than its area. It also holds for any subset of , for any dimension , with the areas replaced by the -dimensional measures of the parts.

By integral formula[edit]

The centroid of a subset X of can also be computed by the integral

where the integrals are taken over the whole space , and g is the characteristic function of the subset, which is 1 inside X and 0 outside it.^[7] Note that the denominator is simply the measure of the set X. This formula cannot be applied if the set X has zero measure, or if either integral diverges.

Another formula for the centroid is

where C_k is the kth coordinate of C, and S_k(z) is the measure of the intersection of X with the hyperplane defined by the equation x_k = z. Again, the denominator is simply the measure of X.

For a plane figure, in particular, the barycenter coordinates are

where A is the area of the figure X; S_y(x) is the length of the intersection of X with the vertical line at abscissa x; and S_x(y) is the analogous quantity for the swapped axes.

Of a bounded region[edit]

The centroid of a region bounded by the graphs of the continuous functions and such that on the interval , , is given by^[7][8]

where is the area of the region (given by ).^[9][10]

With an integraph[edit]

An integraph (a relative of the planimeter) can be used to find the centroid of an object of irregular shape with smooth (or piecewise smooth) boundary. The mathematical principle involved is a special case of Green’s theorem.^[11]

Of an L-shaped object[edit]

This is a method of determining the centroid of an L-shaped object.

1. Divide the shape into two rectangles, as shown in fig 2. Find the centroids of these two rectangles by drawing the diagonals. Draw a line joining the centroids. The centroid of the shape must lie on this line AB.
2. Divide the shape into two other rectangles, as shown in fig 3. Find the centroids of these two rectangles by drawing the diagonals. Draw a line joining the centroids. The centroid of the L-shape must lie on this line CD.
3. As the centroid of the shape must lie along AB and also along CD, it must be at the intersection of these two lines, at O. The point O might lie inside or outside the L-shaped object.

Of a triangle[edit]

The centroid of a triangle is the point of intersection of its medians (the lines joining each vertex with the midpoint of the opposite side).^[6] The centroid divides each of the medians in the ratio 2:1, which is to say it is located ⅓ of the distance from each side to the opposite vertex (see figures at right).^[12][13] Its Cartesian coordinates are the means of the coordinates of the three vertices. That is, if the three vertices are and then the centroid (denoted C here but most commonly denoted G in triangle geometry) is

The centroid is therefore at in barycentric coordinates.

In trilinear coordinates the centroid can be expressed in any of these equivalent ways in terms of the side lengths a, b, c and vertex angles L, M, N:^[14]

The centroid is also the physical center of mass if the triangle is made from a uniform sheet of material; or if all the mass is concentrated at the three vertices, and evenly divided among them. On the other hand, if the mass is distributed along the triangle’s perimeter, with uniform linear density, then the center of mass lies at the Spieker center (the incenter of the medial triangle), which does not (in general) coincide with the geometric centroid of the full triangle.

The area of the triangle is 1.5 times the length of any side times the perpendicular distance from the side to the centroid.^[15]

A triangle’s centroid lies on its Euler line between its orthocenter H and its circumcenter O, exactly twice as close to the latter as to the former:^[16][17]

In addition, for the incenter I and nine-point center N, we have

If G is the centroid of the triangle ABC, then:

The isogonal conjugate of a triangle’s centroid is its symmedian point.

Any of the three medians through the centroid divides the triangle’s area in half. This is not true for other lines through the centroid; the greatest departure from the equal-area division occurs when a line through the centroid is parallel to a side of the triangle, creating a smaller triangle and a trapezoid; in this case the trapezoid’s area is 5/9 that of the original triangle.^[18]

Let P be any point in the plane of a triangle with vertices A, B, and C and centroid G. Then the sum of the squared distances of P from the three vertices exceeds the sum of the squared distances of the centroid G from the vertices by three times the squared distance between P and G:^[19]

The sum of the squares of the triangle’s sides equals three times the sum of the squared distances of the centroid from the vertices:^[19]

A triangle’s centroid is the point that maximizes the product of the directed distances of a point from the triangle’s sidelines.^[20]

Let ABC be a triangle, let G be its centroid, and let D, E, and F be the midpoints of BC, CA, and AB, respectively. For any point P in the plane of ABC then^[21]

Of a polygon[edit]

The centroid of a non-self-intersecting closed polygon defined by n vertices (x₀,y₀), (x₁,y₁), …, (x_n−1,y_n−1) is the point (C_x, C_y),^[22] where

and

and where A is the polygon’s signed area,^[22] as described by the shoelace formula:

In these formulae, the vertices are assumed to be numbered in order of their occurrence along the polygon’s perimeter; furthermore, the vertex ( x_n, y_n ) is assumed to be the same as (x₀, y₀), meaning on the last case must loop around to . (If the points are numbered in clockwise order, the area A, computed as above, will be negative; however, the centroid coordinates will be correct even in this case.)

Of a cone or pyramid[edit]

The centroid of a cone or pyramid is located on the line segment that connects the apex to the centroid of the base. For a solid cone or pyramid, the centroid is 1/4 the distance from the base to the apex. For a cone or pyramid that is just a shell (hollow) with no base, the centroid is 1/3 the distance from the base plane to the apex.

Of a tetrahedron and n-dimensional simplex[edit]

A tetrahedron is an object in three-dimensional space having four triangles as its faces. A line segment joining a vertex of a tetrahedron with the centroid of the opposite face is called a median, and a line segment joining the midpoints of two opposite edges is called a bimedian. Hence there are four medians and three bimedians. These seven line segments all meet at the centroid of the tetrahedron.^[23] The medians are divided by the centroid in the ratio 3:1. The centroid of a tetrahedron is the midpoint between its Monge point and circumcenter (center of the circumscribed sphere). These three points define the Euler line of the tetrahedron that is analogous to the Euler line of a triangle.

These results generalize to any n-dimensional simplex in the following way. If the set of vertices of a simplex is , then considering the vertices as vectors, the centroid is

The geometric centroid coincides with the center of mass if the mass is uniformly distributed over the whole simplex, or concentrated at the vertices as n+1 equal masses.

Of a hemisphere[edit]

The centroid of a solid hemisphere (i.e. half of a solid ball) divides the line segment connecting the sphere’s center to the hemisphere’s pole in the ratio 3:5 (i.e. it lies 3/8 of the way from the center to the pole).
The centroid of a hollow hemisphere (i.e. half of a hollow sphere) divides the line segment connecting the sphere’s center to the hemisphere’s pole in half.

See also[edit]

• Chebyshev center
• Circular mean
• Fréchet mean
• k-means algorithm
• List of centroids
• Medoid
• Pappus’s centroid theorem
• Spectral centroid
• Triangle center

Notes[edit]

References[edit]

• Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52013504
• Bourke, Paul (July 1997). «Calculating the area and centroid of a polygon».
• Johnson, Roger A. (2007), Advanced Euclidean Geometry, Dover
• Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69012075
• Larson, Roland E.; Hostetler, Robert P.; Edwards, Bruce H. (1998), Calculus of a Single Variable (6th ed.), Houghton Mifflin Company
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
• Sangwin, C.J., Locating the centre of mass by mechanical means (PDF), archived from the original (PDF) on November 13, 2013

External links[edit]

• Weisstein, Eric W. «Geometric Centroid». MathWorld.
• Encyclopedia of Triangle Centers by Clark Kimberling. The centroid is indexed as X(2).
• Characteristic Property of Centroid at cut-the-knot
• Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
• Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.

Среднее («среднее») положение всех точек в форме Центроид треугольника

В математика и физика, центроид или геометрический центр плоской фигуры — это среднее арифметическое положение всех точек на рисунке. Неформально, это точка, в которой вырез формы может быть идеально сбалансирован на кончике булавки.

Определение распространяется на любой объект в n- мерном пространстве : его центроид — это среднее положение всех точек во всех направлениях координат.

В то время как в геометрии слово барицентр является синонимом центроида, в астрофизике и астрономии барицентр — это центр масс двух или более тел, вращающихся по орбите друг с другом. В физике центр масс — это среднее арифметическое всех точек , взвешенных по локальной плотности или удельному весу. Если физический объект имеет однородную плотность, его центр масс совпадает с центроидом его формы.

В geography центроид радиальной проекции области земной поверхности на уровень моря — это географический центр региона.

Содержание

• 1 История
• 2 Свойства
• 3 Примеры
• 4 Расположение
  • 4.1 Метод отвеса
  • 4.2 Метод балансировки
  • 4.3 Из конечного набора точек
  • 4.4 Путем геометрического разложения
  • 4.5 По интегральной формуле
  • 4.6 Ограниченной области
  • 4.7 L-образного объекта
  • 4.8 Треугольника
  • 4.9 Многоугольника
  • 4.10 Конуса или пирамиды
  • 4.11 Тетраэдра и n -мерный симплекс
  • 4.12 Полушария
• 5 См. также
• 6 Примечания
• 7 Ссылки
• 8 Внешние ссылки

История

Термин «центроид» появился недавно чеканка (1814 г.). Он используется в качестве замены старых терминов «центр тяжести » и «центр масс », когда необходимо подчеркнуть чисто геометрические аспекты этой точки. Термин свойственен английскому языку. Французы чаще всего используют «центр притяжения», а другие используют термины схожего значения.

Центр тяжести, как следует из названия, возник в механике, скорее всего, в связи со строительством. Когда, где и кем он был изобретен, неизвестно, так как эта концепция, вероятно, пришла в голову многим людям индивидуально с небольшими различиями.

Хотя возможно Евклид все еще был активен в Александрии в детстве Архимеда (287–212 до н.э.), несомненно, что когда Архимед посетил Александрия, Евклида там больше не было. Таким образом, Архимед не мог усвоить теорему о том, что медианы треугольника пересекаются в точке — центре тяжести треугольника непосредственно от Евклида, поскольку этого утверждения нет в Элементах Евклида. Первое явное утверждение этого предположения принадлежит Герону Александрийскому (возможно, I век н.э.) и встречается в его «Механике». Между прочим, можно добавить, что это положение не входило в учебники по геометрии плоскости до XIX века.

Хотя Архимед прямо не заявляет об этом утверждении, он косвенно ссылается на него, предполагая, что он был с ним знаком. Однако Жан Этьен Монтукла (1725–1799), автор первой истории математики (1758), категорически заявляет (т. I, стр. 463), что центр тяжести твердых тел является предметом Архимеда не трогал.

В 1802 году Шарль Босу (1730–1813) опубликовал двухтомный Essai sur l’histoire générale des mathématiques. Эта книга была высоко оценена современниками, судя по тому, что уже через два года после публикации она была переведена на итальянский (1802–03), английский (1803) и немецкий (1804) языки. Боссут считает, что Архимед обнаружил центроид плоских фигур, но ничего не говорит о твердых телах.

Свойства

Геометрический центроид выпуклого объекта всегда лежит в объект. У невыпуклого объекта центр тяжести может находиться за пределами самой фигуры. Центроид кольца кольца или чаши, например, лежит в центральной пустоте объекта.

Если центроид определен, он является фиксированной точкой всех изометрий в его группе симметрии. В частности, геометрический центр тяжести объекта лежит на пересечении всех его гиперплоскостей симметрии . Центроид многих фигур (правильный многоугольник, правильный многогранник, цилиндр, прямоугольник, ромб, круг, сфера, эллипс, эллипсоид, суперэллипс, суперэллипсоид и т. д.) может определяться только этим принципом.

В частности, центр тяжести параллелограмма является точкой пересечения его двух диагоналей . Это не относится к другим четырехугольникам .

. По той же причине центроид объекта с трансляционной симметрией не определен (или находится за пределами ограничивающего пространства), поскольку сдвиг не имеет фиксированной точки..

Примеры

Центроид треугольника — это пересечение трех медиан треугольника (каждая медиана соединяет вершину с серединой противоположной стороны).

Другие свойства центроида треугольника см. В ниже.

Определение местоположения

Метод отвесной линии

Центроид равномерно плотной плоской пластинки, например, на рисунке (а) ниже, может быть определено экспериментально с использованием отвеса и штифта для нахождения совмещенного центра масс тонкого тела однородной плотности, имеющего такую ​​же форму. Корпус удерживается штифтом, вставленным в точку за пределами предполагаемого центра тяжести, таким образом, что он может свободно вращаться вокруг штифта; затем отвес снимается со штифта (рисунок b). Положение отвеса отслеживается на поверхности, и процедура повторяется со шпилькой, вставленной в любой другой точке (или в нескольких точках) за пределами центроида объекта. Единственной точкой пересечения этих линий будет центроид (рисунок c). При условии, что тело имеет однородную плотность, все линии, построенные таким образом, будут включать центроид, и все линии будут пересекаться в одном и том же месте.

Этот метод может быть расширен (теоретически) на вогнутые формы, где центр тяжести может лежать вне формы, и фактически к твердым телам (опять же с однородной плотностью), где центр тяжести может находиться внутри тела. (Виртуальные) положения отвесов должны быть записаны другими способами, кроме их рисования по форме.

Метод балансировки

Для выпуклых двумерных форм центр тяжести может быть найден путем уравновешивания формы на меньшей форме, такой как вершина узкого цилиндра. Центроид находится где-то в пределах диапазона контакта между двумя формами (и точно в точке, где форма будет балансировать на штифте). В принципе, для определения центра тяжести с произвольной точностью можно использовать все более узкие цилиндры. На практике воздушные потоки делают это невозможным. Однако, отмечая диапазон перекрытия нескольких весов, можно достичь значительного уровня точности.

конечного набора точек

Центроид конечного набора k { displaystyle k}точек x 1, x 2, …, Xk { displaystyle mathbf {x} _ {1}, mathbf {x} _ {2}, ldots, mathbf {x} _ {k}}в R п { displaystyle mathbb {R} ^ {n}}равно

C = x 1 + x 2 + ⋯ + xkk { displaystyle mathbf {C} = { frac { mathbf {x} _ {1} + mathbf {x} _ {2} + cdots + mathbf {x} _ {k}} {k}}}.

Эта точка минимизирует сумму квадратов евклидовых расстояний между собой и каждая точка в наборе.

Путем геометрического разложения

Центроид плоской фигуры X { displaystyle X}можно вычислить, разделив его на конечное число более простых фигур X 1, X 2,…, X n { displaystyle X_ {1}, X_ {2}, dots, X_ {n}}, вычисление центроида C i { displaystyle C_ {i}}и области A i { displaystyle A_ {i}}каждой части, а затем вычисление

C x = ∑ C ix A я ∑ A я, С Y знак равно ∑ С iy A я ∑ A я { displaystyle C_ {x} = { frac { sum C_ {i_ {x}} A_ {i}} { sum A_ {i}} }, C_ {y} = { frac { sum C_ {i_ {y}} A_ {i}} { sum A_ {i}}}}

Отверстия на рисунке X { displaystyle X }, перекрытия между частями или части, выходящие за пределы рисунка, могут быть обработаны с использованием отрицательных областей A i { displaystyle A_ {i}}. А именно, меры A i { displaystyle A_ {i}}следует принимать с положительными и отрицательными знаками таким образом, чтобы сумма знаков A i { displaystyle A_ {i}}для всех частей, которые окружают данную точку p { displaystyle p}равно 1, если p { displaystyle p}принадлежит X { displaystyle X}, иначе 0.

Например, рисунок ниже (а) легко разделить на квадрат и треугольник, оба с положительной площадью; и круглое отверстие с отрицательной площадью (b).

(a) 2D-объект (b) Объект, описанный с использованием более простых элементов (c) Центроиды элементов объекта

Центроид каждой части можно найти в любом списке центроидов простых форм (в). Тогда центроид фигуры — это средневзвешенное значение трех точек. Горизонтальное положение центроида от левого края рисунка

x = 5 × 10 2 + 13,33 × 1 2 10 2 — 3 × π 2,5 2 10 2 + 1 2 10 2 — π 2,5 2 ≈ 8,5 единицы измерения. { displaystyle x = { frac {5 times 10 ^ {2} +13,33 times { frac {1} {2}} 10 ^ {2} -3 times pi 2,5 ^ {2}} {10 ^ {2} + { frac {1} {2}} 10 ^ {2} — pi 2,5 ^ {2}}} приблизительно 8,5 { mbox {units}}.}

Вертикальное положение центроид находится точно так же.

Та же формула верна для любых трехмерных объектов, за исключением того, что каждый A i { displaystyle A_ {i}}должен быть объемом X i { displaystyle X_ {i}}, а не его площадь. Это также справедливо для любого подмножества R d { displaystyle mathbb {R} ^ {d}}, для любого измерения d { displaystyle d}с областями, замененными на d { displaystyle d}-размерные меры частей.

По интегральной формуле

Центроид подмножества X из R n { displaystyle mathbb {R} ^ {n}}также может быть вычислен интегралом

C = ∫ xg (x) dx ∫ g (x) dx { displaystyle C = { frac { int xg (x) ; dx} { int g (x) ; dx}}}

где интегралы берутся по всему пространству R n { displaystyle mathbb {R} ^ {n}}, а g — характеристика функция подмножества, которая равна 1 внутри X и 0 вне его. Обратите внимание, что знаменатель — это просто мера множества X. Эта формула не может быть применена, если у множества X есть нулевая мера или если любой интеграл расходится.

Другая формула для центроида:

C k = ∫ z S k (z) dz ∫ S k (z) dz { displaystyle C_ {k} = { frac { int zS_ {k } (z) ; dz} { int S_ {k} (z) ; dz}}}

где C k — это k-я координата C, а S k (z) — это мера пересечения X с гиперплоскостью, определяемая уравнением x k = z. И снова знаменатель — это просто мера X.

Для плоской фигуры, в частности, координаты центра масс:

C x = ∫ x S y (x) dx A { displaystyle C _ { mathrm {x}} = { frac { int xS _ { mathrm {y}} (x) ; dx} {A}}}

C y = ∫ y S x (y) dy A { displaystyle C _ { mathrm {y}} = { frac { int yS _ { mathrm {x}} (y) ; dy} {A}}}

где A — площадь фигуры X; S y (x) — длина пересечения X с вертикальной линией на абсциссе x; и S x (y) — аналогичная величина для поменяемых местами осей.

ограниченной области

Центроид (x ¯, y ¯) { displaystyle ({ bar {x}}, ; { bar {y}}) }области, ограниченной графиками непрерывных функций f { displaystyle f}и g { displaystyle g}такое, что f (x) ≥ g (x) { displaystyle f (x) geq g (x)}на интервале [a, b] { displaystyle [a, b]}, a ≤ x ≤ b { displaystyle a leq x leq b}, задается как

x ¯ = 1 A ∫ abx [f (х) — g (x)] dx { displaystyle { bar {x}} = { frac {1} {A}} int _ {a} ^ {b} x [f (x) -g ( х)] ; dx}

y ¯ = 1 A ∫ ab [f (x) + g (x) 2] [f (x) — g (x)] dx, { displaystyle { bar {y }} = { frac {1} {A}} int _ {a} ^ {b} left [{ frac {f (x) + g (x)} {2}} right] [f ( x) -g (x)] ; dx,}

где A { displaystyle A}— площадь региона (заданная как ∫ ab [f (x) — g (x)] dx { displaystyle int _ {a} ^ {b} [f (x) -g (x)] ; dx}).

L-образного объекта

Это метод определения ce ntroid L-образного объекта.

1. Разделите фигуру на два прямоугольника, как показано на рис. 2. Найдите центроиды этих двух прямоугольников, нарисовав диагонали. Нарисуйте линию, соединяющую центроиды. Центроид фигуры должен лежать на этой линии AB.
2. Разделите фигуру на два других прямоугольника, как показано на рис. 3. Найдите центроиды этих двух прямоугольников, нарисовав диагонали. Нарисуйте линию, соединяющую центроиды. Центроид L-образной формы должен лежать на этой прямой CD.
3. Поскольку центр тяжести формы должен лежать как вдоль AB, так и вдоль CD, он должен быть на пересечении этих двух линий в точке O. точка O может находиться внутри или снаружи L-образного объекта.

треугольника

Центроид треугольника — это точка пересечения его медиан (линии соединение каждой вершины со средней точкой противоположной стороны). Центроид делит каждую из медиан в соотношении 2: 1, то есть находится на расстояния от каждой стороны до противоположной вершины (см. Рисунки справа). Его декартовы координаты — это означает координат трех вершин. То есть, если три вершины равны L = (x L, y L), { displaystyle L = (x_ {L}, y_ {L}),}M = (x M, y M), { displaystyle M = (x_ {M}, y_ {M}),}и N = (x N, y N), { displaystyle N = (x_ {N}, y_ {N}),}, то центроид (обозначенный здесь C, но чаще всего обозначаемый G в геометрии треугольника ) равен

C = 1 3 (L + M + N) = (1 3 (x L + x M + x N), 1 3 (y L + y M + y N)). { displaystyle C = { frac {1} {3}} (L + M + N) = left ({ frac {1} {3}} (x_ {L} + x_ {M} + x_ {N) }), ; ; { frac {1} {3}} (y_ {L} + y_ {M} + y_ {N}) right).}

Следовательно, центроид находится в 1 3: 1 3: 1 3 { displaystyle { tfrac {1} {3}}: { tfrac {1} {3}}: { tfrac {1} {3}}}дюйм барицентрические координаты.

В трилинейных координатах центроид может быть выражен любым из этих эквивалентных способов с точки зрения длин сторон a, b, c и углов при вершинах L, M, N:

C = 1 a: 1 b: 1 c = bc: ca: ab = csc ⁡ L: csc ⁡ M: csc ⁡ N = cos ⁡ L + cos ⁡ M ⋅ cos ⁡ N: cos ⁡ M + cos ⁡ N ⋅ cos ⁡ L: cos ⁡ N + cos ⁡ L ⋅ cos ⁡ M = sec ⁡ L + sec ⁡ M ⋅ sec ⁡ N: sec ⁡ M + sec ⁡ N ⋅ sec ⁡ L: sec ⁡ N + sec ⁡ L ⋅ sec ⁡ М. { displaystyle { begin {align} C = { frac {1} {a}}: { frac {1} {b}}: { frac {1} {c}} = bc: ca: ab = csc L: csc M: csc N \ [6pt] = cos L + cos M cdot cos N: cos M + cos N cdot cos L: cos N + cos L cdot cos M \ [6pt] = sec L + sec M cdot sec N: sec M + sec N cdot sec L: sec N + sec L cdot sec M. end {выровнено }}}

Центроид также является физическим центром масс, если треугольник сделан из однородного листа материала; или если вся масса сосредоточена в трех вершинах и поровну разделена между ними. С другой стороны, если масса распределена по периметру треугольника с равномерной линейной плотностью, то центр масс находится в центре Шпикера (центр среднего треугольника ), который (в общем случае) не совпадает с геометрическим центром тяжести полного треугольника.

Площадь треугольника в 1,5 раза превышает длину любой стороны, умноженную на перпендикулярное расстояние от стороны до центроида.

Центроид треугольника лежит на его прямой Эйлера между его ортоцентром H и его центром описанной окружности O, ровно в два раза ближе к последнему, чем к первому:

CH ¯ = 2 CO ¯. { displaystyle { overline {CH}} = 2 { overline {CO}}.}

Кроме того, для инцентратора I и центра по девяти точкам N, имеем

CH ¯ = 4 CN ¯ CO ¯ = 2 CN ¯ IC ¯ < H C ¯ I H ¯ < H C ¯ I C ¯ < I O ¯ {displaystyle {begin{aligned}{overline {CH}}=4{overline {CN}}\[5pt]{overline {CO}}=2{overline {CN}}\[5pt]{overline {IC}}<{overline {HC}}\[5pt]{overline {IH}}<{overline {HC}}\[5pt]{overline {IC}}<{overline {IO}}end{aligned}}}

Если G — центр тяжести треугольника ABC, то:

(Площадь △ ABG) = (Площадь △ ACG) = (Площадь △ BCG) = 1 3 (Площадь △ ABC) { displaystyle displaystyle ({ text {Площадь}} треугольник mathrm {ABG}) = ({ text {Площадь}} треугольник mathrm {ACG}) = ({ text {Площадь}} треугольник mathrm {BCG}) = { frac {1} {3}} ({ text {Площадь}} треугольник mathrm {ABC })}

изогонально сопряженным центроиду треугольника является его симедианная точка.

Любая из трех медиан, проходящих через центроид, делит площадь треугольника пополам. Это неверно для других линий, проходящих через центроид; наибольшее отклонение от деления на равные площади происходит, когда линия, проходящая через центр тяжести, параллельна стороне треугольника, образуя меньший треугольник и трапецию ; в этом случае площадь трапеции равна 5/9 площади исходного треугольника.

Пусть P — любая точка на плоскости треугольника с вершинами A, B, C и центроидом G. Тогда сумма Квадрат расстояний P от трех вершин превышает сумму квадратов расстояний от центроида G до вершин в три раза больше квадрата расстояния между P и G:

PA 2 + PB 2 + PC 2 = GA 2 + GB 2 + GC 2 + 3 PG 2. { displaystyle PA ^ {2} + PB ^ {2} + PC ^ {2} = GA ^ {2} + GB ^ {2} + GC ^ {2} + 3PG ^ {2}.}

сумма квадратов сторон треугольника равна троекратной сумме квадратов расстояний от центроида до вершин:

AB 2 + BC 2 + CA 2 = 3 (GA 2 + GB 2 + GC 2). { displaystyle AB ^ {2} + BC ^ {2} + CA ^ {2} = 3 (GA ^ {2} + GB ^ {2} + GC ^ {2}).}

Центроид треугольника равен точка, которая максимизирует произведение ориентированных расстояний от точки до сторон треугольника.

Пусть ABC — треугольник, пусть G — его центр тяжести, а D, E и F — середины BC, CA и AB соответственно. Для любой точки P в плоскости ABC тогда

P A + P B + P C ≤ 2 (P D + P E + P F) + 3 P G. { displaystyle PA + PB + PC leq 2 (PD + PE + PF) + 3PG.}

многоугольника

Центроид несамопересекающегося замкнутого многоугольника, определяемое n вершинами (x 0,y0), (x 1,y1),…, (x n − 1, y n − 1), является точкой ( C x, C y), где

C x = 1 6 A ∑ i = 0 n — 1 (xi + xi + 1) (xiyi + 1 — xi + 1 yi), { displaystyle C _ { mathrm {x}} = { frac {1} {6A}} sum _ {i = 0} ^ {n-1} (x_ {i} + x_ {i + 1}) (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}),}и

C y = 1 6 A ∑ i = 0 п — 1 (yi + yi + 1) (xiyi + 1 — xi + 1 yi), { displaystyle C _ { mathrm {y}} = { frac {1} {6A}} sum _ {i = 0 } ^ {n-1} (y_ {i} + y_ {i + 1}) (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}),}

и где A — подписанная площадь многоугольника, как описано формулой шнурка :

A = 1 2 ∑ i = 0 n — 1 (xiyi + 1 — xi + 1 yi). { displaystyle A = { frac {1} {2}} sum _ {i = 0} ^ {n-1} (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}).}

В этих формулах предполагается, что вершины пронумерованы в порядке их появления по периметру многоугольника; кроме того, вершина (x n, y n) предполагается такой же, как (x 0, y 0), значение i + 1 { displaystyle i + 1}в последнем случае должно выполняться в цикле до i = 0 { displaystyle i = 0}. (Если точки пронумерованы по часовой стрелке, площадь A, вычисленная, как указано выше, будет отрицательной; однако координаты центроида будут правильными даже в этом случае.)

Конуса или пирамиды

Центроид конуса или пирамиды расположен на отрезке линии, который соединяет вершину с центроидом основания. Для твердого конуса или пирамиды центр тяжести составляет 1/4 расстояния от основания до вершины. Для конуса или пирамиды, представляющих собой просто оболочку (полую) без основания, центроид составляет 1/3 расстояния от плоскости основания до вершины.

тетраэдра и n-мерного симплекса

A тетраэдр представляет собой объект в трехмерном пространстве, имеющий четыре треугольника в качестве его граней. Отрезок, соединяющий вершину тетраэдра с центром тяжести противоположной грани, называется срединной, а отрезок, соединяющий середины двух противоположных ребер, называется бимедианой. Следовательно, есть четыре медианы и три бимедианы. Эти семь отрезков пересекаются в центре тетраэдра. Медианы делятся на центроид в соотношении 3: 1. Центроид тетраэдра — это середина между его точкой Монжа и центром описанной области (центром описанной сферы). Эти три точки определяют линию Эйлера тетраэдра, которая аналогична прямой Эйлера треугольника.

Эти результаты обобщаются на любой n-мерный симплекс следующим образом. Если набор вершин симплекса равен v 0,…, vn { displaystyle {v_ {0}, ldots, v_ {n}}}, то рассматриваемые вершины как векторов, центроид равен

C = 1 n + 1 ∑ i = 0 nvi. { displaystyle C = { frac {1} {n + 1}} sum _ {i = 0} ^ {n} v_ {i}.}

Геометрический центроид совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как n + 1 равных масс.

полушария

Центроид твердого полушария (т.е. половина твердого шара) делит отрезок прямой, соединяющий центр шара с полюсом полушария в соотношении 3: 5 (т.е. лежит на 3/8 пути от центра до полюса). Центроид полого полушария (то есть половина полой сферы) делит отрезок прямой, соединяющий центр сферы с полюсом полушария пополам.

См. Также

• Центр Чебышева
• Среднее Фреше
• Алгоритм k-средних
• Список центроидов
• Определение центра масс
• Медоид
• Теорема Паппа о центроидах
• Спектральный центроид
• Центр треугольника

Примечания

Ссылки

• Альтшиллер-Корт, Натан (1925), Геометрия колледжа: Введение в современную геометрию треугольника и круга (2-е изд..), Нью-Йорк: Barnes Noble, LCCN 52013504
• Бурк, Пол (июль 1997 г.). «Расчет площади и центра тяжести многоугольника».
• Джонсон, Роджер А. (2007), Advanced Euclidean Geometry, Dover
• Kay, David C. (1969), College Geometry, Нью-Йорк : Holt, Rinehart and Winston, LCCN 69012075
• Larson, Roland E.; Хостетлер, Роберт П.; Эдвардс, Брюс Х. (1998), Исчисление одной переменной (6-е изд.), Houghton Mifflin Company
• Protter, Murray H.; Морри, младший, Чарльз Б. (1970), College Calculus with Analytic Geometry (2-е изд.), Чтение: Addison-Wesley, LCCN 76087042

External ссылки

• Энциклопедия центров треугольников Кларка Кимберлинга. Центроид индексируется как X (2).
• Характеристическое свойство центроида в точке срезать узел
• Барицентрические координаты в точке разрезать узел
• Интерактивный анимация, показывающая Центроид треугольника и Построение центроида с компасом и линейкой
• Экспериментальное определение медиан и центроида треугольника в Эскизы динамической геометрии, интерактивный эскиз динамической геометрии с использованием симулятора гравитации Золушки.