Фо́кусное
расстоя́ние —
физическая характеристика оптической
системы.
Для центрированной оптической системы,
состоящей из сферических поверхностей,
описывает способность собирать лучи в
одну точку при условии, что эти лучи
идут из бесконечности параллельным
пучком параллельно оптической
оси.
Для
системы линз, как и для простой линзы конечной
толщины, фокусное расстояние зависит
от радиусов кривизны поверхностей,
показателей преломления стёкол и толщин.
Определяется
как расстояние от передней главной
точки до переднего
фокуса (для
переднего фокусного расстояния), и как
расстояние от задней главной точки
дозаднего
фокуса (для заднего
фокусного расстояния).
При этом, под главными точками
подразумеваются точки пересечения
передней (задней) главной
плоскости соптической
осью.
Величина заднего
фокусного расстояния является
основным параметром, которым принято
характеризовать любую оптическую
систему.
Парабола (или параболоид вращения)
фокусирует параллельный пучок лучей в
одну точку
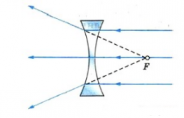
Фо́кус (от лат. focus —
«очаг») оптической (или работающей с
другими видами излучения)
системы — точка, в которой пересекаются
(«фокусируются»)
первоначально параллельные лучи после
прохождения через собирающую систему
(либо где пересекаются их продолжения,
если система рассеивающая). Множество
фокусов системы определяет её фокальную
поверхность. Главный фокус системы
является пересечением её главной оптической
оси и
фокальной поверхности. В настоящее
время[1],
вместо термина главный
фокус (передний
или задний) используются термины задний
фокус и передний
фокус.
Опти́ческая
си́ла —
величина, характеризующая преломляющую
способность осесимметричных линз и
центрированных оптических
систем из
таких линз. Измеряется оптическая сила
в диоптриях (в СИ):
1 дптр=1 м-1.
Обратно
пропорциональна фокусному
расстоянию системы:
где —
фокусное расстояние линзы.
Оптическая
сила положительна у собирающих систем
и отрицательна в случае рассеивающих.
Оптическая
сила системы, состоящей из двух находящихся
в воздухе линз с оптическими силами и
,
определяется формулой[1]:
где —
расстояние между задней главной
плоскостью первой линзы и передней
главной плоскостью второй линзы. В
случае тонких линзсовпадает
с расстоянием между линзами.
Обычно
оптическая сила используется для
характеристики линз, используемых
в офтальмологии,
в обозначениях очков и для упрощённого
геометрического определения траектории
луча.
Для
измерения оптической силы линз используют
диоптриметры[2],
которые позволяют проводить измерения
в том числе астигматических и контактных
линз.
18. Формула сопряжённых фокусных расстояний. Построение изображения линзой.
Сопряжённое
фо́кусное расстоя́ние —
расстояние от задней главной
плоскости объектива до
изображения объекта, когда объект
расположен не в бесконечности, а на
некотором расстоянии от объектива.
Сопряженное фокусное расстояние всегда
большефокусного
расстояния объектива и
тем больше, чем меньше расстояние от
объекта допередней
главной плоскости объектива .
Эта зависимость приведена в таблице, в
которой расстоянияи
выражены
в величинах.
|
Изменение |
|
|
Расстояние |
Расстояние |
|
4f |
1,33f |
|
2f |
2f |
|
1,5f |
3f |
|
1,2f |
6f |
|
1,1f |
11f |
Для линзы эти
расстояния связаны отношением,
непосредственно следующим из формулы
линзы:
или,
если d и R выразить в величинах фокусного
расстояния :
б) Построение
изображения в линзах.
Для
построения хода луча в линзе применяются
те же законы, что и для вогнутого зеркала.
Луч, параллельный
оси,
проходит через фокус и наоборот.
Центральный луч (луч, идущий через
оптический центр линзы) проходит через
линзу без
отклонения;
в толстых
линзах
он немного смещается параллельно самому
себе (как в плоскопараллельной пластинке,
см. рис. 214). Из обратимости хода лучей
следует, что каждая линза имеет два
фокуса, которые находятся на одинаковых
расстояниях от линзы (последнее верно
лишь для тонких линз). Для тонких
собирающих линз и центральных лучей
справедливы следующие законы
построения изображений:
g >2F; изображение
обратное, уменьшенное,
действительное, b >F (рис.221).
g = 2F; изображение
обратное, равное, действительное, b = F.
F <g < 2F;
изображение обратное, увеличенное,
действительное, b > 2F.
g < F; изображение
прямое, увеличенное, мнимое, — b > F.
При g < F лучи
расходятся, на продолжении пересекаются
и дают мнимое
изображение.
Линза действует как увеличительное
стекло (лупа).
Изображения
в рассеивающих линзах всегда мнимые,
прямые и уменьшенные (рис.223).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Построение в линзах
Для введённых нами линз существует два условно разных типа задач:
- задачи на построение в собирающей и рассеивающей линзах
- задачи на формулу для тонкой линзы
Первый тип задач основан на фактическом построении хода лучей от источника и поиска пересечения преломлённых в линзах лучей. Рассмотрим ряд изображений, полученных от точечного источника, который будем помещать на различных расстояниях от линз. Для собирающей и рассеивающей линзу существуют рассмотренные (не нами) траектории распространения луча (рис. 1) от источника .
Рис.1. Собирающая и рассеивающая линзы (ход лучей)
Для собирающей линзы (рис. 1.1) лучи:
- синий. Луч, идущий вдоль главной оптической оси, после преломления проходит через передний фокус.
- зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
- красный. Луч, идущий через передний фокус, после преломления распространяется параллельно главной оптической оси.
Пересечение любых из этих двух лучей (чаще всего выбирают лучи 1 и 2) дают изображение ( ).
Для рассеивающей линзы (рис. 1.2) лучи:
- синий. Луч, идущий параллельно главной оптической оси, преломляется так, что продолжения луча проходит через задний фокус.
- зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
Пересечение продолжений рассмотренных лучей даёт изображение ( ).
Аналогично сферическому зеркалу, получим набор изображений от предмета, расположенного на различных расстояниях от зеркала. Введём те же обозначения: пусть — расстояние от предмета до линзы, — расстояние от изображения до линзы, — фокусное расстояние (расстояние от фокуса до линзы).
Для собирающей линзы:
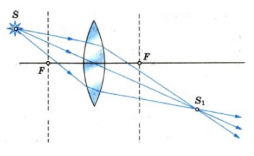
- (источник находится очень далеко от линзы). В этом случае мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 2). Пустим два луча параллельно главной оптической оси линзы.
Рис. 2. Собирающая линза (источник в бесконечности)
Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе проходят через фокус, то точка фокуса и является точкой пересечения преломлённых лучей, тогда она же и есть изображение источника (точечное, действительное).
- 2F’ title=’displaystyle d>2F’/> (источник находится за двойным фокусным расстоянием) (рис. 3).
Рис. 3. Собирающая линза (источник за двойным фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Для визуализации изображения введём описание предмета через стрелку. Точка пересечения преломившихся лучей — изображение (уменьшенное, действительное, перевёрнутое). Положение — между фокусом и двойным фокусом.
- (источник находится ровно в двойном фокусе) (рис. 4).
Рис. 4. Собирающая линза (источник в двойном фокусе)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (того же размера, действительное, перевёрнутое). Положение — ровно в двойном фокусе.
- d>F’ title=’displaystyle 2F>d>F’/> (источник между фокусом и двойным фокусом) (рис. 5)
Рис. 5. Собирающая линза (источник между двойным фокусом и фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (увеличенное, действительное, перевёрнутое). Положение — за двойным фокусом.
- (источник находится ровно в фокусе собирающей линзы) (рис. 6)
Рис. 6. Собирающая линза (источник в фокусе)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). В этом случае, оба преломлённых луча оказались параллельными друг другу, т.е. точка пересечения отражённых лучей отсутствует. Это говорит о том, что изображения нет.
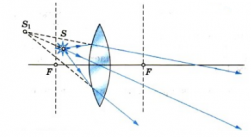
- (источник находится между фокусом и главным оптическим центром) (рис. 7)
Рис. 7. Собирающая линза (источник перед фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Однако преломлённые лучи расходятся, т.е. сами преломлённые лучи не пересекутся, зато могут пересечься продолжения этих лучей. Точка пересечения продолжений преломлённых лучей — изображение (увеличенное, мнимое, прямое). Положение — по ту же сторону, что и предмет.
Для рассеивающей линзы построение изображений предметов практически не зависит от положения предмета, так что ограничимся произвольным положением самого предмета и характеристикой изображения.
- (источник находится очень далеко от линзы). В этом случае, мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 8). Пустим два луча параллельно главной оптической оси линзы.
Рис. 8. Рассеивающая линза (источник в бесконечности)
Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе должны проходить через фокус (свойство фокуса), однако после преломления в рассеивающей линзе лучи должны расходится. Тогда в фокусе сходятся продолжения преломившихся лучей. Тогда точка фокуса и является точкой пересечения продолжений преломлённых лучей, т.е. она же и есть изображение источника (точечное, мнимое).
- любое другое положение источника (рис. 9).
Рис. 9. Рассеивающая линза (произвольное положение источника)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (продолжение отражённого луча проходит через передний фокус) и идущего через главный оптический центр линзы (не преломляется). Тогда изображением будет пересечение продолжений преломлённых лучей.
Второй тип задач связан с формулой тонкой линзы. Такие задачи основываются на числовых данных параметров, характеризующих положение источника, изображения или фокуса линзы. Рассмотрим произвольную систему (рис. 10). Пусть положение источника ( ), изображения ( ) и фокуса системы ( ) задано.
Рис. 10. Формула тонкой линзы
Тогда взаимосвязь между параметрами положения элементов можно описать формулой:
- где
- — фокусное расстояние линзы,
- — расстояние от предмета до линзы,
- — расстояние от изображения до линзы.
Важно: для использования формулы (1) необходимо помнить правило расстановки знаков. Если линза собирающая, то 0′ title=’displaystyle F>0′/>, если рассеивающая, то . В случае действительных предметов и изображений: 0′ title=’displaystyle d>0′/>, 0′ title=’displaystyle f>0′/>, а в случае мнимых предметов и изображений: и .
И последним параметром, характеризующим линзы или систему линз, является оптическая сила линзы ( ). Её нахождение довольно простое:
- где
- — оптическая сила линзы/системы линз,
- — фокус линзы/системы линз.
Размерность оптической силы линзы: м =дптр (диоптрии). Оптическая сила собирающей линзы положительна, рассеивающей — отрицательна.
Вывод: задачи с линзами, в целом, разделены на два класса. Задачи на построение основываются на рисунках 2-9. Достаточно проанализировать ход лучей и найти изображение (рис.1). Численные значения в дано указывают на задачи на формулу тонкой линзы (1).
Источник
Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.
Определение
Линза — прозрачное тело, ограниченное сферическими поверхностями.
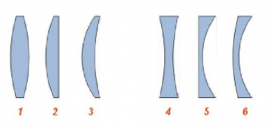
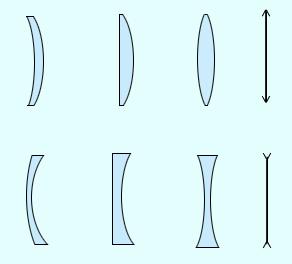
Какими бывают линзы?
По форме различают следующие виды линз:
- Выпуклые — линзы, которые посередине толще, чем у краев.
- Вогнутые — линзы, которые посередине тоньше, чем у краев.
Выпуклые линзы тоже имеют разновидности:
- Двояковыпуклая — линза, ограниченная с обеих сторон выпуклыми сферическими поверхностями (СП). Такая линза изображена ниже на рисунке 1.
- Плосковыпуклая — линза, ограниченная выпуклой СП с одной стороны и плоской поверхностью с другой (рис. 2)
- Вогнуто-выпуклая — линза, ограниченной с одной стороны вогнутой СП, а с другой — выпуклой СП (рис. 3).
Разновидности вогнутых линз:
- Двояковогнутая — линза, ограниченная с обеих сторон вогнутыми СП (рис. 4).
- Плосковогнутая — линза, ограниченная вогнутой СП с одной стороны и плоской поверхностью с другой (рис. 5)
- Выпукло-вогнутая — линза, ограниченной с одной стороны выпуклой СП, а с другой — вогнутой СП (рис. 6).
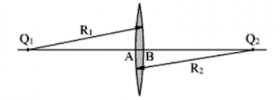
Тонкая линза
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R1 и R2. Такие линзы называют тонкими.
Определение
Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.
Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O1O2).
Оптический центр линзы – точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.
Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.
Изображение в линзе
Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.
Определение
Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.
Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.
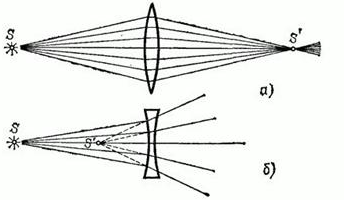
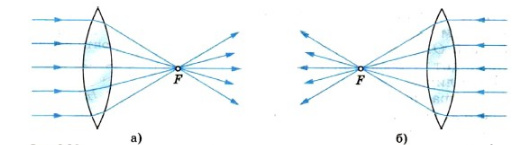
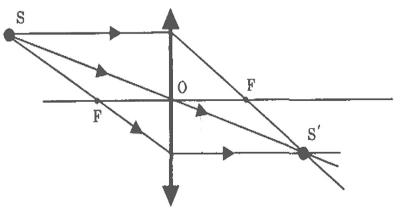
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.
Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.
Собирающая линза
Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.
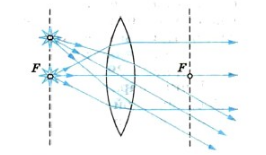
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.
Главный фокус линзы обозначают буквой F.
Определение
Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).
В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.
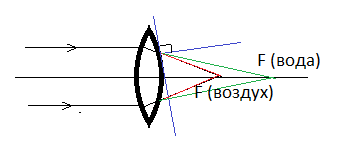
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?
Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.
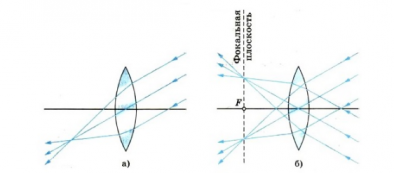
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.
Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.
Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.
Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.
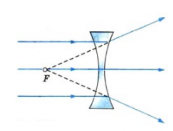
Рассеивающая линза
Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.
Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.
Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.
Оптическая сила линзы
Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.
Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.
Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:
D=±1|F|
D > 0, если линза собирающая, D < 0, если линза рассеивающая. Чем ближе к линзе ее фокусы, тем сильнее линза преломляет лучи, собирая или рассеивая их, и тем больше оптическая сила линзы.
Пример №2. Найти фокусное расстояние линзы, если ее оптическая сила равна –5 дптр.
Так как оптическая силы линзы отрицательная, речь идет о рассеивающей линзе. Следовательно, будем использовать формулу:
D=−1|F|
Отсюда:
|F|=−1D=−1−5=0,2 (м)
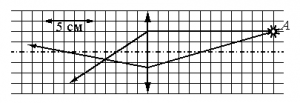
Задание EF18041
Ответ:
а) 14 дптр
б) 20 дптр
в) 17 дптр
г) 33 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы определяется формулой:
D=1F
На рисунке видно, что 5 клеток = 5 см. Следовательно, 1 клетка = 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в главном фокусе, который лежит на этой оси. Значит, фокус находится в точке пересечения этой оси и луча. От него до линзы 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17706
Стеклянную линзу (показатель преломления стекла nстекла = 1,54), показанную на рисунке, перенесли из воздуха (nвоздуха = 1) в воду (nводы = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?
Ответ:
а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.
б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.
в) Фокусное расстояние и оптическая сила увеличились.
г) Фокусное расстояние и оптическая сила уменьшились.
Алгоритм решения
1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.
2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.
Решение
Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:
nвоздух−стекло=nстеклоnвоздух=1,541=1,54
nвода−стекло=nстеклоnвода=1,541,33≈1,16
Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.
Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18076
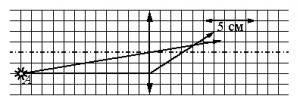
Какова приблизительно оптическая сила этой линзы?
Ответ:
а) –33,3 дптр
б) 7,7 дптр
в) 25,0 дптр
г) 33,3 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
2.Рассчитать длину 1 клетки.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы находится по формуле:
D=1F
На рисунке видно, что 5 соответствуют 5 см. Следовательно, 1 клетка равна 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в фокусе, который лежит на этой оси. Из рисунка видно, фокус находится в точке пересечения этой оси и луча, параллельного ей. Эту точку и линзу разделяют 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33,3 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.9k
Оптические приборы — устройства, в которых излучение какой-либо области спектра (ультрафиолетовой, видимой, инфракрасной) преобразуется (пропускается, отражается, преломляется, поляризуется).
Отдавая дань исторической традиции, оптическими обычно называют приборы, работающие в видимом свете.
При первичной оценке качества прибора рассматриваются лишь основные его характеристики:
- светосила — способность концентрировать излучение;
- разрешающая сила — способность различать соседние детали изображения;
- увеличение — соотношение размеров предмета и его изображения.
- Для многих приборов определяющей характеристикой оказывается поле зрения — угол, под которым из центра прибора видны крайние точки предмета.
Разрешающая сила (способность) — характеризует способность оптических приборов давать раздельные изображения двух близких друг к другу точек объекта.
Наименьшее линейное или угловое расстояние между двумя точками, начиная с которого их изображения сливаются, называется линейным или угловым пределом разрешения.
Способность прибора различать две близкие точки или линии обусловлена волновой природой света. Численное значение разрешающей силы, например, линзовой системы, зависит от умения конструктора справиться с аберрациями линз и тщательно отцентрировать эти линзы на одной оптической оси. Теоретический предел разрешения двух соседних изображаемых точек определяется как равенство расстояния между их центрами радиусу первого темного кольца их дифракционной картины.
Увеличение. Если предмет длиной H перпендикулярен оптической оси системы, а длина его изображения h, то увеличение m определяется по формуле:
m = h/H.
Увеличение зависит от фокусных расстояний и взаимного расположения линз; для выражения этой зависимости существуют соответствующие формулы.
Важной характеристикой приборов для визуального наблюдения является видимое увеличение М. Оно определяется из отношения размеров изображений предмета, которые образуются на сетчатке глаза при непосредственном наблюдении предмета и рассматривании его через прибор. Обычно видимое увеличение М выражают отношением M = tgb /tga, где a — угол, под которым наблюдатель видит предмет невооруженным глазом, а b — угол, под которым глаз наблюдателя видит предмет через прибор.
Основной частью любой оптической системы является линза. Линзы входят в состав практически всех оптических приборов.
Линза – оптически прозрачное тело, ограниченное двумя сферическими поверхностями.
Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой.
Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше.
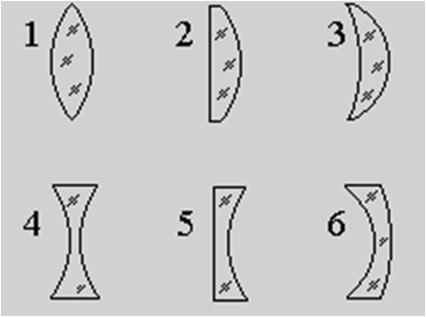
Виды линз:
- выпуклые:
- двояковыпуклые (1)
- плосковыпуклые (2)
- вогнуто-выпуклые (3)
- вогнутые:
- двояковогнутые (4)
- плосковогнутые (5)
- выпукло-вогнутые (6)
Основные обозначения в линзе:
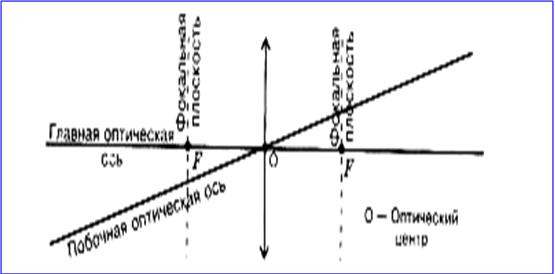
Прямая, проходящая через центры кривизны O1 и O2 сферических поверхностей, называется главной оптической осью линзы.
В случае тонких линз приближенно можно считать, что главная оптическая ось пересекается с линзой в одной точке, которую принято называть оптическим центром линзы O . Луч света проходит через оптический центр линзы, не отклоняясь от первоначального направления.
Оптический центр линзы – точка, сквозь которую световые лучи проходят не преломляясь в линзе.
Главная оптическая ось – прямая, проходящая через оптический центр линзы, перпендикулярно линзе.
Все прямые, проходящие через оптический центр, называются побочными оптическими осями.
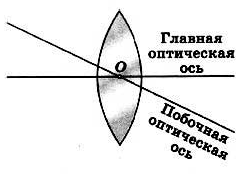
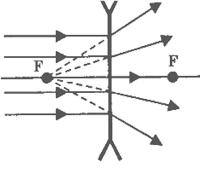
Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. У тонкой линзы имеются два главных фокуса, расположенных симметрично на главной оптической оси относительно линзы. У собирающих линз фокусы действительные, у рассеивающих – мнимые.
Пучки лучей, параллельных одной из побочных оптических осей, после прохождения через линзу также фокусируются в точку F’, которая расположена при пересечении побочной оси с фокальной плоскостью Ф, то есть плоскостью, перпендикулярной главной оптической оси и проходящей через главный фокус.
Фокальная плоскость – прямая, перпендикулярная главной оптической оси линзы и проходящая через фокус линзы.
Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием. Оно обозначаетcя той же буквой F.
Преломление параллельного пучка лучей в собирающей линзе.
Преломление параллельного пучка лучей в рассеивающей линзе.
Точки O1 и O2 – центры сферических поверхностей, O1O2 – главная оптическая ось, O – оптический центр, F – главный фокус, F’ – побочный фокус, OF’ – побочная оптическая ось, Ф – фокальная плоскость.
На чертежах тонкие линзы изображают в виде отрезка со стрелками:
собирающая: 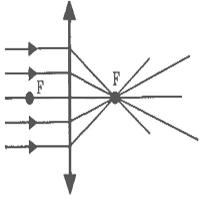
Основное свойство линз – способность давать изображения предметов. Изображения бывают прямыми и перевернутыми, действительными и мнимыми, увеличенными и уменьшенными.
Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей. Для построения изображения в линзе используют любые два из трех лучей:
-
Луч, падающий на линзу параллельно оптической оси, после преломления идет через фокус линзы.
-
Луч, проходящий через оптический центр линзы не преломляется.
-
Луч, проходя через фокус линзы после преломления идет параллельно оптической оси.
Положение изображения и его характер (действительное или мнимое) можно также рассчитать с помощью формулы тонкой линзы. Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:
Величину D, обратную фокусному расстоянию называют оптической силой линзы.
Единицей измерения оптической силы является диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = м–1
Фокусным расстояниям линз принято приписывать определенные знаки: для собирающей линзы F > 0, для рассеивающей F < 0.
Величины d и f также подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов (то есть реальных источников света, а не продолжений лучей, сходящихся за линзой) и изображений;
d < 0 и f < 0 – для мнимых источников и изображений.
Тонкие линзы обладают рядом недостатков, не позволяющих получать высококачественные изображения. Искажения, возникающие при формировании изображения, называются аберрациями. Главные из них – сферическая и хроматическая аберрации.
Сферическая аберрация проявляется в том, что в случае широких световых пучков лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула тонкой линзы справедлива только для лучей, близких к оптической оси. Изображение удаленного точечного источника, создаваемое широким пучком лучей, преломленных линзой, оказывается размытым.
Хроматическая аберрация возникает вследствие того, что показатель преломления материала линзы зависит от длины волны света λ. Это свойство прозрачных сред называется дисперсией. Фокусное расстояние линзы оказывается различным для света с разными длинами волн, что приводит к размытию изображения при использовании немонохроматического света.
В современных оптических приборах применяются не тонкие линзы, а сложные многолинзовые системы, в которых удается приближенно устранить различные аберрации.
Формирование собирающей линзой действительного изображения предмета используется во многих оптических приборах, таких как фотоаппарат, проектор и т. д.
При желании создать качественный оптический прибор следует оптимизировать набор его основных характеристик — светосилы, разрешающей способности и увеличения. Нельзя сделать хороший, например, телескоп, добиваясь лишь большого видимого увеличения и оставляя малой светосилу (апертуру). У него будет плохое разрешение, так как оно прямо зависит от апертуры. Конструкции оптических приборов весьма разнообразны, и их особенности диктуются назначением конкретных устройств. Но при воплощении любой спроектированной оптической системы в готовый оптико-механический прибор необходимо расположить все оптические элементы в строгом соответствии с принятой схемой, надежно закрепить их, обеспечить точную регулировку положения подвижных деталей, разместить диафрагмы для устранения нежелательного фона рассеянного излучения. Нередко требуется выдерживать заданные значения температуры и влажности внутри прибора, сводить к минимуму вибрации, нормировать распределение веса, обеспечить отвод тепла от ламп и другого вспомогательного электрооборудования. Значение придается внешнему виду прибора и удобству обращения с ним.
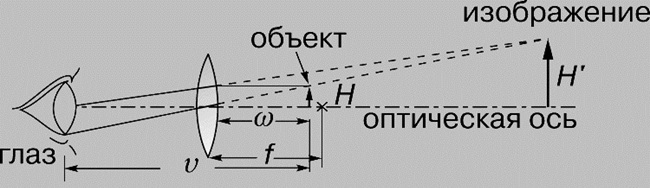
Микроскоп, лупа, увеличительное стекло.
Если рассматривать через положительную (собирающую) линзу предмет, расположенный за линзой не дальше ее фокальной точки, то видно увеличенное мнимое изображение предмета. Такая линза представляет собой простейший микроскоп и называется лупой или увеличительным стеклом.
Из оптической схемы можно определить размер увеличенного изображения.
Когда глаз настроен на параллельный пучок света (изображение предмета находится на неопределенно большом расстоянии, а это означает, что предмет расположен в фокальной плоскости линзы), видимое увеличение M можно определить из соотношения: M = tgb /tga = (H/f)/(H/v) = v/f, где f — фокусное расстояние линзы, v — расстояние наилучшего зрения, т.е. наименьшее расстояние, на котором глаз хорошо видит при нормальной аккомодации. M увеличивается на единицу, когда глаз настраивается так, что мнимое изображение предмета оказывается на расстоянии наилучшего зрения. Способности к аккомодации у всех людей разные, с возрастом они ухудшаются; принято считать 25 см расстоянием наилучшего зрения нормального глаза. В поле зрения одиночной положительной линзы при удалении от ее оси резкость изображения быстро ухудшается из-за поперечных аберраций. Хотя и бывают лупы с увеличением в 20 крат, типичная их кратность от 5 до 10. Увеличение сложного микроскопа, именуемого обычно просто микроскопом, доходит до 2000 крат.
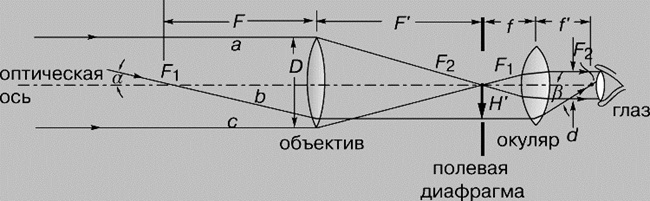
Телескоп.
Телескоп увеличивает видимые размеры удаленных предметов. В схему простейшего телескопа входят две положительные линзы.
Лучи от удаленного предмета, параллельные оси телескопа (лучи a и c на схеме), собираются в заднем фокусе первой линзы (объектива). Вторая линза (окуляр) удалена от фокальной плоскости объектива на свое фокусное расстояние, и лучи a и c выходят из нее вновь параллельно оси системы. Некоторый луч b, исходящий не из тех точек предмета, откуда пришли лучи a и c, падает под углом a к оси телескопа, проходит через передний фокус объектива и после него идет параллельно оси системы. Окуляр направляет его в свой задний фокус под углом b. Поскольку расстояние от переднего фокуса объектива до глаза наблюдателя пренебрежимо мало по сравнению с расстоянием до предмета, то из схемы можно получить выражение для видимого увеличения M телескопа: M = -tgb /tga = -F/f’ (или F/f). Отрицательный знак показывает, что изображение перевернуто. В астрономических телескопах оно таким и остается; в телескопах для наблюдений за наземными объектами применяют оборачивающую систему, чтобы рассматривать нормальные, а не перевернутые изображения. В оборачивающую систему могут входить дополнительные линзы или, как в биноклях, призмы.
Бинокль.
Бинокулярный телескоп, обычно именуемый биноклем, представляет собой компактный прибор для наблюдений обоими глазами одновременно; его увеличение, как правило, от 6 до 10 крат. В биноклях используют пару оборачивающих систем (чаще всего — Порро), в каждую из которых входят две прямоугольные призмы (с основанием под 45°), ориентированные навстречу прямоугольными гранями.
Чтобы получить большое увеличение в широком поле зрения, свободном от аберраций объектива, и, следовательно, значительный угол обзора (6-9°), биноклю необходим очень качественный окуляр, более совершенный, чем телескопу с узким углом зрения. В окуляре бинокля предусмотрена фокусировка изображения, причем с коррекцией зрения, — его шкала размечена в диоптриях. Кроме того, в бинокле положение окуляра подстраивается под расстояние между глазами наблюдателя. Обычно бинокли маркируются в соответствии с их увеличением (в кратах) и диаметром объектива (в миллиметрах), например, 8*40 или 7*50.
Оптический прицел.
В качестве оптического прицела можно применить любой телескоп для наземных наблюдений, если в какой-либо плоскости его пространства изображений нанести четкие метки (сетки, марки), отвечающие заданному назначению. Типичное устройство многих военных оптических установок таково, что объектив телескопа открыто смотрит на цель, а окуляр находится в укрытии. Такая схема требует излома оптической оси прицела и применения призм для ее смещения; эти же призмы преобразуют перевернутое изображение в прямое. Системы со смещением оптической оси называются перископическими. Обычно оптический прицел рассчитывается так, что зрачок его выхода удален от последней поверхности окуляра на достаточное расстояние для предохранения глаза наводчика от ударов о край телескопа при отдаче оружия.
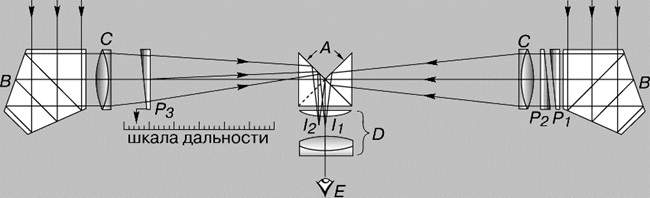
Дальномер.
Оптические дальномеры, с помощью которых измеряют расстояния до объектов, бывают двух типов: монокулярные и стереоскопические. Хотя они различаются конструктивными деталями, основная часть оптической схемы у них одинакова и принцип действия один: по известной стороне (базе) и двум известным углам треугольника определяется неизвестная его сторона. Два параллельно ориентированных телескопа, разнесенных на расстояние b (база), строят изображения одного и того же удаленного объекта так, что он кажется наблюдаемым из них в разных направлениях (базой может служить и размер цели). Если с помощью какого-нибудь приемлемого оптического устройства совместить поля изображений обоих телескопов так, чтобы их можно было рассматривать одновременно, окажется, что соответствующие изображения предмета пространственно разнесены. Существуют дальномеры не только с полным наложением полей, но и с половинным: верхняя половина пространства изображений одного телескопа объединяется с нижней половиной пространства изображений другого. В таких приборах с помощью подходящего оптического элемента проводится совмещение пространственно разнесенных изображений и по относительному сдвигу изображений определяется измеряемая величина. Часто в качестве сдвигающего элемента служит призма или комбинация призм.
МОНОКУЛЯРНЫЙ ДАЛЬНОМЕР. A — прямоугольная призма; B — пентапризмы; C — линзовые объективы; D — окуляр; E — глаз; P1 и P2 -неподвижные призмы; P3 — подвижная призма; I 1 и I 2 — изображения половин поля зрения
В схеме монокулярного дальномера, показанной на рисунке, эту функцию исполняет призма P3; она связана со шкалой, проградуированной в измеряемых расстояниях до объекта. Пентапризмы B используются как отражатели света под прямым углом, поскольку такие призмы всегда отклоняют падающий световой пучок на 90°, независимо от точности их установки в горизонтальной плоскости прибора. Изображения, создаваемые двумя телескопами, в стереоскопическом дальномере наблюдатель видит сразу обоими глазами. База такого дальномера позволяет наблюдателю воспринимать положение объекта объемно, на некоторой глубине в пространстве. В каждом телескопе имеется сетка с марками, соответствующими значениям дальности. Наблюдатель видит шкалу расстояний, уходящую в глубь изображаемого пространства, и по ней определяет удаленность объекта.
Осветительные и проекционные приборы. Прожекторы.
В оптической схеме прожектора источник света, например кратер дугового электрического разряда, находится в фокусе параболического отражателя. Лучи, исходящие из всех точек дуги, отражаются параболическим зеркалом почти параллельно друг другу. Пучок лучей немного расходится потому, что источником служит не светящаяся точка, а объем конечного размера.
Диаскоп.
В оптическую схему этого прибора, предназначенного для просмотра диапозитивов и прозрачных цветных кадров, входят две линзовые системы: конденсор и проекционный объектив. Конденсор равномерно освещает прозрачный оригинал, направляя лучи в проекционный объектив, который строит изображение оригинала на экране. В проекционном объективе предусматриваются фокусировка и замена его линз, что позволяет менять расстояние до экрана и размеры изображения на нем. Оптическая схема кинопроектора такая же.
СХЕМА ДИАСКОПА. A — диапозитив; B — линзовый конденсор; C — линзы проекционного объектива; D — экран; S — источник света
Спектральные приборы.
Основным элементом спектрального прибора может быть дисперсионная призма либо дифракционная решетка. В таком приборе свет сначала коллимируется, т.е. формируется в пучок параллельных лучей, затем разлагается в спектр, и, наконец, изображение входной щели прибора фокусируется на его выходную щель по каждой длине волны спектра.
Спектрометр.
В этом более или менее универсальном лабораторном приборе коллимирующая и фокусирующая системы могут поворачиваться относительно центра столика, на котором расположен элемент, разлагающий свет в спектр. На приборе имеются шкалы для отсчетов углов поворота, например дисперсионной призмы, и углов отклонения после нее разных цветовых составляющих спектра. По результатам таких отсчетов измеряются, например, показатели преломления прозрачных твердых тел.
Спектрограф.
Так называется прибор, в котором полученный спектр или его часть снимается на фотоматериал. Можно получить спектр от призмы из кварца (диапазон 210-800 нм), стекла (360-2500 нм) или каменной соли (2500-16000 нм). В тех диапазонах спектра, где призмы слабо поглощают свет, изображения спектральных линий в спектрографе получаются яркими. В спектрографах с дифракционными решетками последние выполняют две функции: разлагают излучение в спектр и фокусируют цветовые составляющие на фотоматериал; такие приборы применяют и в ультрафиолетовой области.
Фотоаппарат представляет собой замкнутую светонепроницаемую камеру. Изображение фотографируемых предметов создается на фотопленке системой линз, которая называется объективом. Специальный затвор позволяет открывать объектив на время экспозиции.
Особенностью работы фотоаппарата является то, что на плоской фотопленке должны получаться достаточно резкими изображения предметов, находящихся на разных расстояниях.
В плоскости фотопленки получаются резкими только изображения предметов, находящихся на определенном расстоянии. Наведение на резкость достигается перемещением объектива относительно пленки. Изображения точек, не лежащих в плоскости резкого наведения, получаются размытыми в виде кружков рассеяния. Размер d этих кружков может быть уменьшен путем диафрагмирования объектива, т.е. уменьшения относительного отверстия a / F. Это приводит к увеличению глубины резкости.
Объектив современной фотокамеры состоит из нескольких линз, объединенных в оптические системы (например, оптическая схема Тессар). Число линз в объективах самых простых фотокамер — от одной до трех, а в современных дорогих фотоаппаратах их бывает до десяти или даже восемнадцати.
Оптическая схема Тессар
Оптических систем в объективе может быть от двух до пяти. Практически все оптические схемы устроены и работают одинаково – они фокусируют проходящие через линзы лучи света на светочувствительной матрице.
Только от объектива зависит качество изображения на снимке, будет ли фотография резкой, не исказятся ли на снимке формы и линии, хорошо ли она передаст цвета — все это зависит от свойств объектива, поэтому объектив и является одним из самых важных элементов современной фотокамеры.
Линзы объектива делают из специальных сортов оптического стекла или оптической пластмассы. Создание линз одно из самых дорогостоящих операций создания фотокамеры. В сравнении стеклянных и пластмассовых линз стоит отметить, то пластмассовые линзы дешевле и легче. В настоящее время большинство объективов недорогих любительских компактных камер изготавливается из пластмассы. Но, такие объективы подвержены царапинам и не так долговечны, примерно через два-три года они мутнеют, и качество фотографий оставляет желать лучшего. Оптика камер подороже изготавливается из оптического стекла.
В настоящее время большинство объективов компактных фотокамер изготавливается из пластмассы.
Между собой линзы объектива склеивают или соединяют при помощи очень точно рассчитанных металлических оправ. Склейку объективов можно встретить намного чаще, нежели металлические оправы.
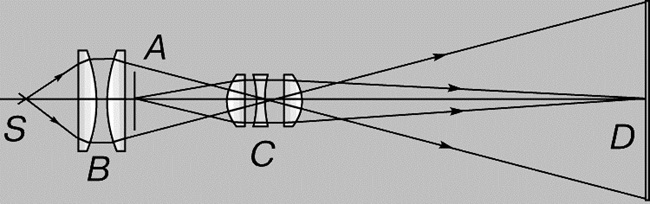
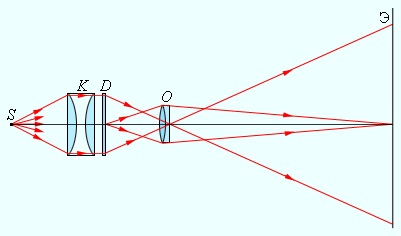
Проекционный аппарат предназначен для получения крупномасштабных изображений. Объектив O проектора фокусирует изображение плоского предмета (диапозитив D) на удаленном экране Э. Система линз K, называемая конденсором, предназначена для того, чтобы сконцентрировать свет источника S на диапозитиве. На экране Э создается действительное увеличенное перевернутое изображение. Увеличение проекционного аппарата можно менять, приближая или удаляя экран Э с одновременным изменением расстояния между диапозитивом D и объективом O.
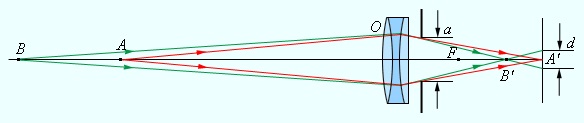
Главные и фокальные точки относятся к кардинальным точкам оптической системы.
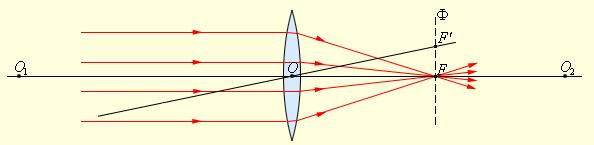
Рассмотрим параксиальную оптическую систему, которая строит изображение предмета (рисунок 1). Роль системы в данном случае исполняет одна линза. Предмет находится на бесконечном расстоянии от нее и центрирован относительно оптической оси системы (пространство предметов на рисунке слева). Так как система параксиальная, она формирует идеальное изображение в точке .
Продлим луч, в пространстве предметов и в пространстве изображений, до пересечения в точке (рисунок 2). Плоскость, которая проходит через эту точку и пересекает оптическую ось под прямым углом, назовем задней главной плоскостью. Точку пересечения этой плоскости с оптической осью
назовем задней главной точкой. Точку изображения предмета
, которая находится на оптической оси, назовем задним главным фокусом.
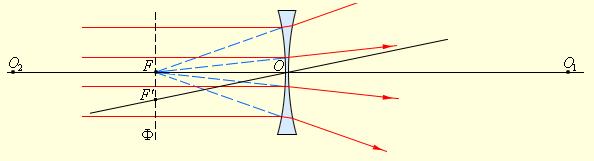
Изменим условия — перенесем предмет вправо на бесконечное расстояние (рисунок 3). Теперь, пространство предметов у нас находится справа, а пространство изображения — слева.
Проведем те же дополнительные построения, которые мы проводили, когда предмет находился слева (рисунок 4). Плоскость, проходящую через точку и пересекающую оптическую ось под прямым углом в точке
, назовем передней главной плоскостью, точку пересечения с осью – передней главной точкой, а точку изображения
– передним главным фокусом.
Заметьте, что в обоих случаях (и когда прдемет был слева, и когда предмет был справа) — лучи проходят через обе точки и , и
(рисунок 5). Дело в том, что точка
является изображением точки
. Другими словами,
и
– сопряженные точки. Очевидно, что коэффициент увеличения для этих точек равен единице, так как они находятся на одинаковом расстоянии от оптической оси.
Передняя и задняя главные плоскости являются сопряженными плоскостями, и коэффициент увеличения для этих плоскостей равен единице. Т.е. для любой точки, принадлежащей передней главной плоскости можно найти сопряженную ей точку в задней главной плоскости и увеличение для этих точек будет равно единице.
Post Views:
1 420