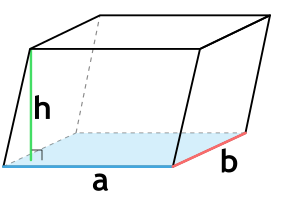
Понятие объема
Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.
Объём — это количественная характеристика пространства, занимаемого телом или веществом.
Другими словами, это то, сколько места занимает предмет.
Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.
За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3).
Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.
Два свойства объёма
- У равных тел равные объёмы. Например, у двух одинаковых пакетов сока равные объемы.
- Если геометрическое тело состоит из нескольких геометрических тел, то его объём равен сумме объёмов этих тел.
Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
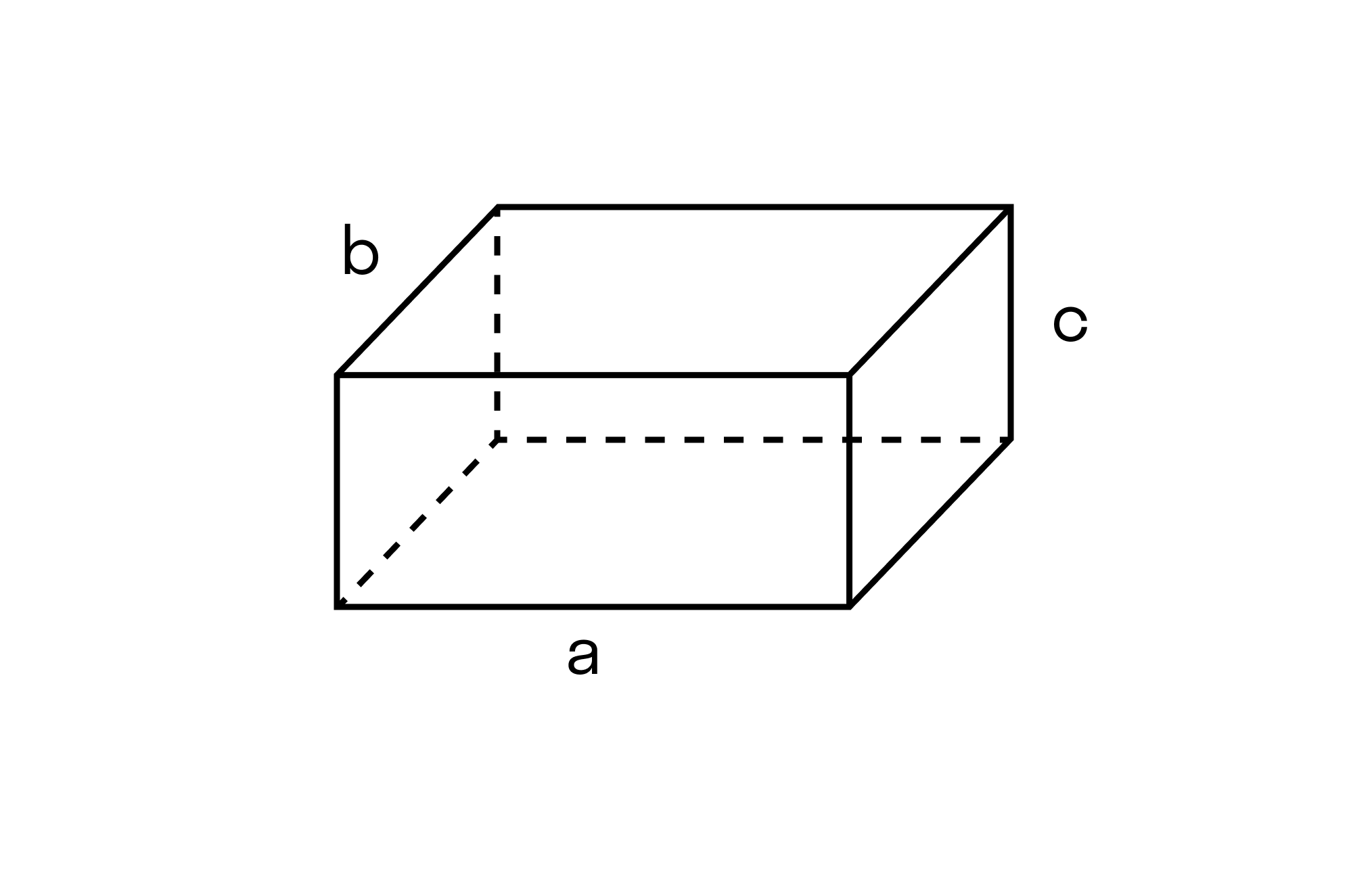
Объем прямоугольного параллелепипеда
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.
Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.
Формула объема прямоугольного параллелепипеда
Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:
V = a × b × h
Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.
|
a |
длина параллелепипеда |
|
b |
ширина параллелепипеда |
|
h |
высота параллелепипеда |
|
P (осн) |
периметр основания |
|
S (осн) |
площадь основания |
|
S (бок) |
площадь боковой поверхности |
|
S (п.п.) |
площадь полной поверхности |
|
V |
объем |
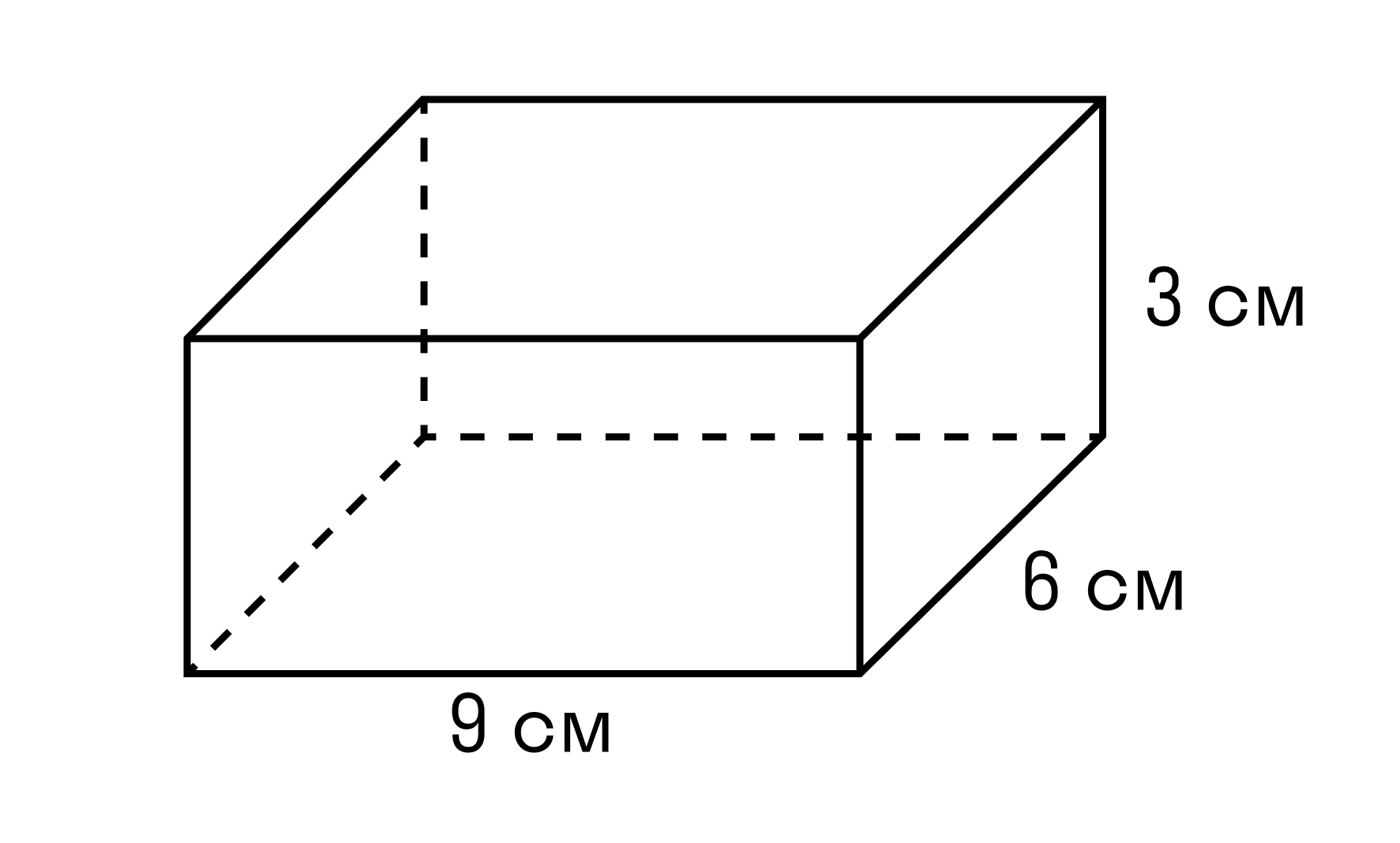
Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.
a = 9 см
b = 6 см
h = 3 см
V = a × b × h
V = 9 × 6 × 3 = 162 см3.
Ответ: объем прямоугольного параллелепипеда равен 162 см3.
Следствие
Объем параллелепипеда равен произведению площади основания на высоту.
V = Sосн × h
Из этого следствия выведем формулу нахождения площади основания параллелепипеда.
Sосн = V : h
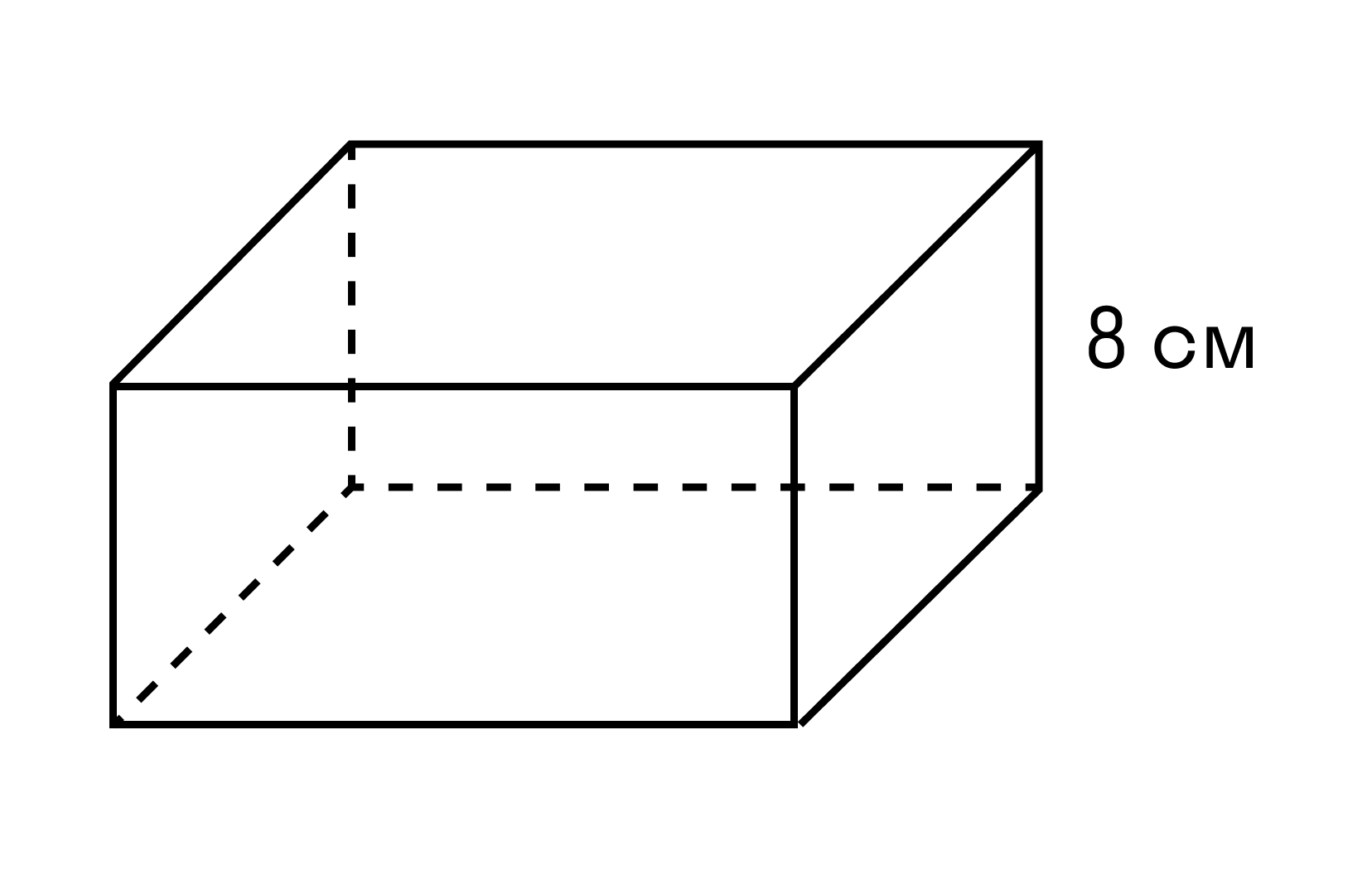
Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см.
V = 96 см3
h = 8 см
V = Sосн × h
Sосн = V : h
Sосн = 82 см3 : 8 см = 12 см2.
Ответ: площадь основания параллелепипеда равна 12 см2.
Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!
Вычисление площади
Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.
Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.
Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sб. п. = 2 (ac + bc)
Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:
- Sп. п. = 2 (ab + ac + bc)
Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2.
Ответ: площадь поверхности параллелепипеда — 108 см2.
Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.
Задачи на самопроверку
Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.
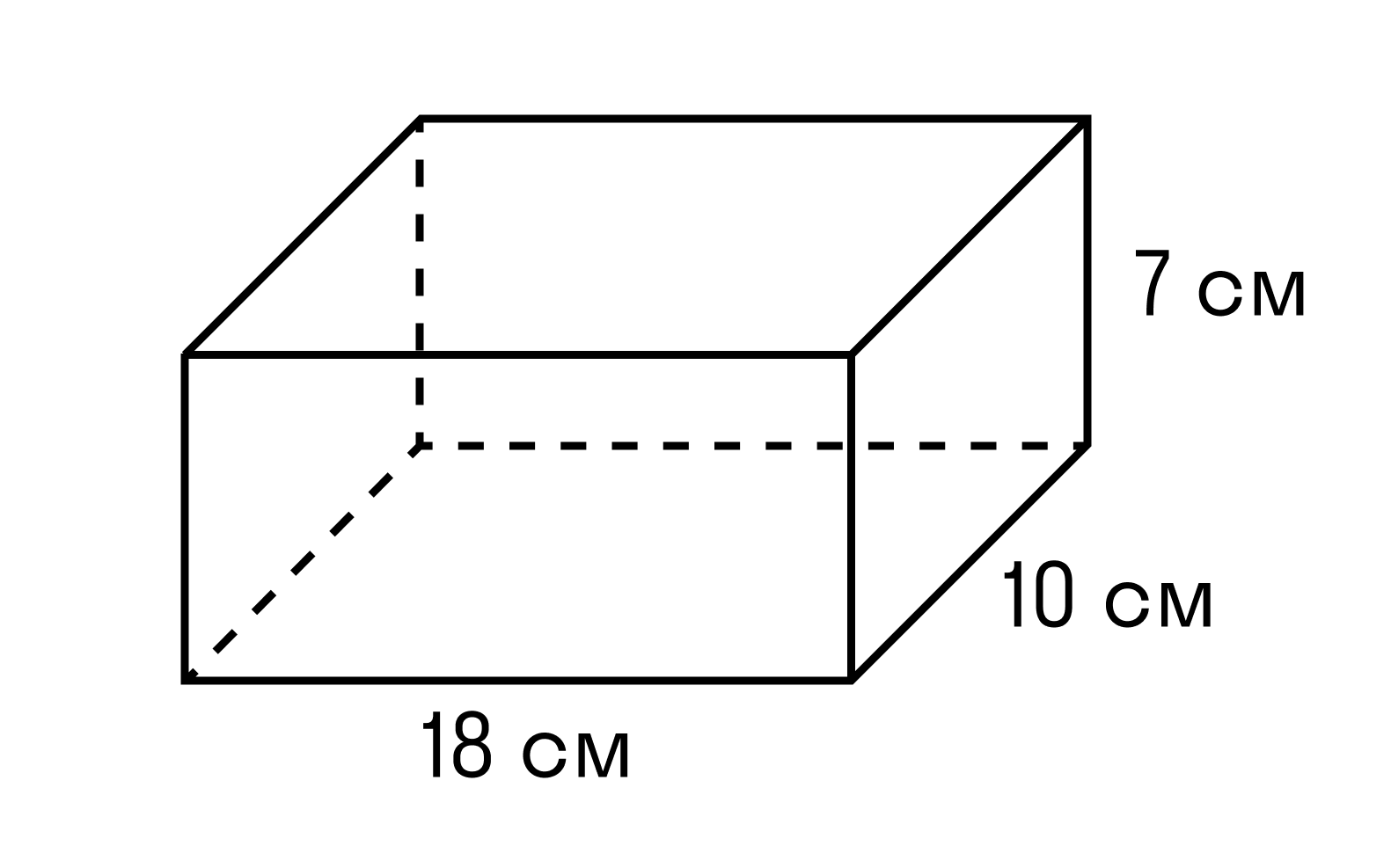
Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.
Как решаем:
a = 18 см
b = 10 см
h = 7 см
Формула нахождения объема параллелепипеда:
V = a × b × h
Подставляем наши числа:
V = 18 × 10 × 7 = 1260 см3.
Ответ: объём параллелепипеда равен 1260 см3.
Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см.
Как решаем:
V = 120 см
h = 15 см
V = Sосн × h
Sосн = V : h
Sосн = 120 см3: 15 см = 8 см2.
Ответ: площадь основания параллелепипеда равна 8 см2.
Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.
Как решаем:
Sп. п. = 2 (ab + ac + bc)
Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2.
Ответ: площадь полной поверхности параллелепипеда равна 1140 см2.
Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.
|
V параллелепипеда |
V = a × b × h |
|
V = Sосн × h |
|
|
S боковой поверхности |
Sб. п. = 2 (ac + bc) |
|
S полной поверхности |
Sп. п. = 2 (ab + ac + bc) |

{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
Формула объема прямоугольного параллелепипеда через три стороны
{V= a cdot b cdot c}
a — длина параллелепипеда
b — ширина параллелепипеда
c — высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab — это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн — площадь основания параллелепипеда
h — высота параллелепипеда
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
{V= a cdot b cdot h}
a — длина основания параллелепипеда
b — ширина основания параллелепипеда
h — высота параллелепипеда
Формула объема наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн — площадь основания параллелепипеда
h — высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
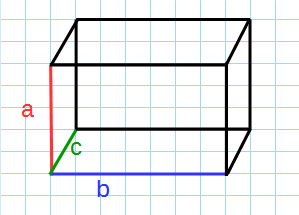
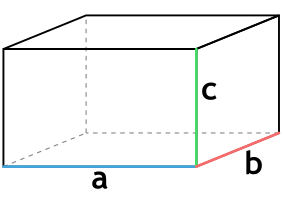
Формула объема параллелепипеда через его ребра:
a,b,c — ребра параллелепипеда.
Через стороны и высоту
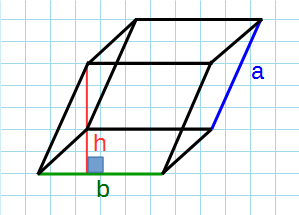
Формула объема параллелепипеда:
a,b — ребра параллелепипеда; h — высота параллелепипеда.
Параллелепипед — это призма, основанием которой является параллелограмм.
Онлайн-калькулятор объема параллелепипеда
Как и у куба, у этого многогранного тела есть двенадцать ребер, шесть граней и восемь вершин. Вид параллелепипеда зависит от геометрической фигуры, лежащей в основании, и от угла, образованного им при пересечении с гранями.
Если его гранями являются прямоугольники, то он называется прямоугольным.
Если такие прямоугольники имеют отношение только к боковым граням, то он называется прямым.
Иногда бывают случаи, когда эти грани образуют не прямой угол с основанием. Тогда в данном случае параллелепипед является наклонным.
Если он состоит исключительно из равных ромбов, то он называется ромбоэдром.
Если все грани параллелепипеда являются одинаковыми квадратами, то получаем куб. Таким образом, куб — это частный случай параллелепипеда.
Формула объема прямоугольного параллелепипеда
Объемом такого параллелепипеда называется произведение всех его трех измерений: длины, ширины, высоты. Вычисляется он так:
V=a⋅b⋅cV=acdot bcdot c
a,b,ca, b, c — длина, ширина и высота прямоугольного параллелепипеда.
Рассмотрим несколько примеров.
Найти объем прямоугольного параллелепипеда, если известны его длина, равная 5 см.5text{ см.}, ширина, имеющая длину 10 см.10text{ см.} и высота длиной в 7 см.7text{ см.}
Решение
a=5a=5
b=10b=10
c=7c=7
Сразу подставляем в формулу численные значения:
V=a⋅b⋅c=5⋅10⋅7=350 см3V=acdot bcdot c=5cdot 10cdot 7=350text{ см}^3
Ответ
350 см3.350text{ см}^3.
Формула объема наклонного параллелепипеда
V=Sосн⋅hV=S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания наклонного параллелепипеда;
hh — его высота.
Вычислить объем наклонного параллелепипеда, если в его основании лежит прямоугольник со сторонами в 4 см.4text{ см.} и 5 см.5text{ см.}, а высота его равна 10 см.10text{ см.}
Решение
a=4a=4
b=5b=5
h=10h=10
Находим площадь основания, то есть площадь прямоугольника:
Sосн=a⋅b=4⋅5=20S_{text{осн}}=acdot b=4cdot 5=20
Сам объем равен:
V=Sосн⋅h=20⋅10=200 см3V=S_{text{осн}}cdot h=20cdot 10=200text{ см}^3
Ответ
200 см3.200text{ см}^3.
Формула объема параллелепипеда через определитель
Альтернативным способом нахождения объема параллелепипеда является вычисление смешанного произведения векторов, на которых построен данный параллелепипед.
Пусть параллелепипед построен на векторах a⃗vec{a}, b⃗vec{b} и c⃗vec{c} с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующего параллелепипеда это определитель, составленный из этих координат:
V=∣axayazbxbybzcxcycz∣V=begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем параллелепипеда через смешанное произведение векторов, координаты которых таковы: a⃗=(2,3,5)vec{a}=(2, 3, 5), b⃗=(1,4,4)vec{b}=(1, 4, 4), c⃗=(3,5,7)vec{c}=(3, 5, 7).
Решение
a⃗=(2,3,5)vec{a}=(2, 3, 5)
b⃗=(1,4,4)vec{b}=(1, 4, 4)
c⃗=(3,5,7)vec{c}=(3, 5, 7)
По формуле:
V=∣235144357∣=2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7=56+36+25−60−40−21=−4V=begin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 — 5cdot4cdot3 — 2cdot4cdot5 — 3cdot1cdot7 = 56 + 36 + 25 — 60 — 40 — 21 = -4
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=4 см3V=4text{ см}^3
Ответ
4 см3.4text{ см}^3.
У вас не получается решить задачу по геометрии? Наши эксперты помогут вам!
Тест по теме «Объем параллелепипеда»
Калькулятор для расчета объема параллелепипеда
C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер «a», «b», «c» и нажмите кнопку «Рассчитать». Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
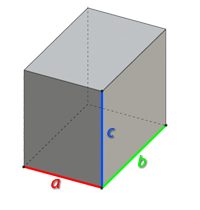
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку «Рассчитать»
Округлить результат до
знаков после запятой
Рассчитать
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.