Гипербола: определение, свойства, построение
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и
есть величина постоянная
, меньшая расстояния
между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Фокальное свойство гиперболы
Точки и
называются фокусами гиперболы, расстояние
между ними — фокусным расстоянием, середина
отрезка
— центром гиперболы, число
— длиной действительной оси гиперболы (соответственно,
— действительной полуосью гиперболы). Отрезки
и
, соединяющие произвольную точку
гиперболы с ее фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение , где
, называется эксцентриситетом гиперболы. Из определения
следует, что
.
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:
(3.50)
Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и
. Для произвольной точки
, принадлежащей гиперболе, имеем:
Записывая это уравнение в координатной форме, получаем:
Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:
где , т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При
, когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство гиперболы). Здесь
и
— один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
В самом деле, например, для фокуса и директрисы
(рис.3.41,а) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса
и директрисы
:
Уравнение гиперболы в полярной системе координат
Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид
, где
— фокальный параметр гиперболы.
В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке
, принадлежащий прямой
, но не содержащий точки
(рис.3.41,б). Тогда для произвольной точки
, принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение гиперболы имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замены
:
что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы,
для эллипса).
Геометрический смысл коэффициентов в уравнении гиперболы
Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения:
. Следовательно, вершины имеют координаты
. Длина отрезка, соединяющего вершины, равна
. Этот отрезок называется действительной осью гиперболы, а число
— действительной полуосью гиперболы. Подставляя
, получаем
. Длина отрезка оси ординат, соединяющего точки
, равна
. Этот отрезок называется мнимой осью гиперболы, а число
— мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.
Замечания 3.10.
1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).
2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).
Для равносторонней гиперболы, описываемой уравнением (т.е. при
), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат
(рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид
(гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).
В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами
Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем
3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.
Действительно, если точка принадлежит гиперболе
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат той же гиперболе.
Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.
4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму гиперболы. Чем больше
, тем шире ветви гиперболы, а чем ближе
к единице, тем ветви гиперболы уже (рис.3.43,а).
Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника:
. Учитывая, что
и
, получаем
Чем больше , тем больше угол
. Для равносторонней гиперболы
имеем
и
. Для
угол
тупой, а для
угол
острый (рис.3.43,а).
6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и
называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы
приводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет гиперболу с центром в точке
, оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение
определяет сопряженную гиперболу с центром в точке
.
Параметрическое уравнение гиперболы
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
где — гиперболический косинус, a
гиперболический синус.
Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .
Пример 3.21. Изобразить гиперболу в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось,
— мнимая полуось гиперболы. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя
в уравнение гиперболы, получаем
Следовательно, точки с координатами и
принадлежат гиперболе. Вычисляем фокусное расстояние
эксцентриситет ; фокальныи параметр
. Составляем уравнения асимптот
, то есть
, и уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Гипербола: определение, свойства, построение
Гиперболой
называется геометрическое место точек
плоскости, модуль разности расстояний
от каждой из которых до двух заданных
точек и
есть
величина постоянная,
меньшая расстояниямежду
этими заданными точками (рис.3.40,а). Это
геометрическое определение
выражаетфокальное
свойство гиперболы.
Фокальное
свойство гиперболы
Точки и
называются
фокусами гиперболы, расстояниемежду
ними — фокусным расстоянием,
серединаотрезка
—
центром гиперболы, число—
длиной действительной оси гиперболы
(соответственно,—
действительной полуосью гиперболы).
Отрезкии
,
соединяющие произвольную точкугиперболы
с ее фокусами, называются фокальными
радиусами точки.
Отрезок, соединяющий две точки гиперболы,
называется хордой гиперболы.
Отношение ,
где,
называетсяэксцентриситетом
гиперболы.
Из определения следует,
что.
Геометрическое
определение гиперболы,
выражающее ее фокальное свойство,
эквивалентно ее аналитическому
определению — линии, задаваемой
каноническим уравнением гиперболы:
|
(3.50) |
Действительно,
введем прямоугольную систему координат
(рис.3.40,б). Центр гиперболы
примем за начало системы координат;
прямую, проходящую через фокусы (фокальную
ось), примем за ось абсцисс (положительное
направление на ней от точкик
точке);
прямую, перпендикулярную оси абсцисс
и проходящую через центр гиперболы,
примем за ось ординат (направление на
оси ординат выбирается так, чтобы
прямоугольная система координатоказалась
правой).
Составим
уравнение гиперболы, используя
геометрическое определение, выражающее
фокальное свойство. В выбранной системе
координат определяем координаты
фокусов и
.
Для произвольной точки,
принадлежащей гиперболе, имеем:
Записывая
это уравнение в координатной форме,
получаем:
Выполняя
преобразования, аналогичные преобразованиям,
используемым при выводе уравнения
эллипса (т.е. избавляясь от иррациональности),
приходим к каноническому уравнению
гиперболы:
где ,
т.е. выбранная система координат является
канонической.
Проводя
рассуждения в обратном порядке, можно
показать, что все точки, координаты
которых удовлетворяют уравнению (3.50),
и только они, принадлежат геометрическому
месту точек, называемому гиперболой.
Таким образом, аналитическое определение
гиперболы эквивалентно его геометрическому
определению.
Директориальное
свойство гиперболы
Директрисами
гиперболы называются две прямые,
проходящие параллельно оси ординат
канонической системы координат на
одинаковом расстоянии от
нее (рис.3.41,а). При,
когда гипербола вырождается в пару
пересекающихся прямых, директрисы
совпадают.
Гиперболу
с эксцентриситетом можно
определить, как геометрическое место
точек плоскости, для каждой из которых
отношение расстояния до заданной
точки(фокуса)
к расстоянию до заданной прямой(директрисы),
не проходящей через заданную точку,
постоянно и равно эксцентриситету(директориальное
свойство гиперболы).
Здесь и
—
один из фокусов гиперболы и одна из ее
директрис, расположенные по одну сторону
от оси ординат канонической системы
координат.
В
самом деле, например, для фокуса и
директрисы(рис.3.41,а)
условиеможно
записать в координатной форме:
Избавляясь
от иррациональности и заменяя ,
приходим к каноническому уравнению
гиперболы (3.50). Аналогичные рассуждения
можно провести для фокусаи
директрисы:
Уравнение
гиперболы в полярной системе координат
Уравнение
правой ветви гиперболы в полярной
системе координат (рис.3.41,б)
имеет вид
,
где —фокальный
параметр гиперболы.
В
самом деле, выберем в качестве полюса
полярной системы координат правый
фокус гиперболы,
а в качестве полярной оси — луч с началом
в точке,
принадлежащий прямой,
но не содержащий точки(рис.3.41,б).
Тогда для произвольной точки,
принадлежащей правой ветви гиперболы,
согласно геометрическому определению
(фокальному свойству) гиперболы, имеем.
Выражаем расстояние между точкамии
(см.
пункт 2 замечаний 2.8):
Следовательно,
в координатной форме уравнение гиперболы
имеет в
Уединяем
радикал, возводим обе части уравнения
в квадрат, делим на 4 и приводим подобные
члены:
Выражаем
полярный радиус и
делаем замены:
что
и требовалось доказать. Заметим, что в
полярных координатах уравнения гиперболы
и эллипса совпадают, но описывают разные
линии, поскольку отличаются эксцентриситетами
(для
гиперболы,для
эллипса).
Геометрический
смысл коэффициентов в уравнении гиперболы
Найдем
точки пересечения гиперболы (рис.3.42,а)
с осью абсцисс (вершины гиперболы).
Подставляя в уравнение ,
находим абсциссы точек пересечения:.
Следовательно, вершины имеют координаты.
Длина отрезка, соединяющего вершины,
равна.
Этот отрезок называется действительной
осью гиперболы, а число—
действительной полуосью гиперболы.
Подставляя,
получаем.
Длина отрезка оси ординат, соединяющего
точки,
равна.
Этот отрезок называется мнимой осью
гиперболы, а число—
мнимой полуосью гиперболы. Гипербола
пересекает прямую, содержащую
действительную ось, и не пересекает
прямую, содержащую мнимую ось.
Замечания
3.10.
1. Прямые ограничивают
на координатной плоскости основной
прямоугольник, вне которого находится
гипербола (рис.3.42,а).
2. Прямые ,
содержащие диагонали основного
прямоугольника, называются асимптотами
гиперболы (рис.3.42,а).
Для равносторонней
гиперболы,
описываемой уравнением (т.е.
при),
основной прямоугольник является
квадратом, диагонали которого
перпендикулярны. Поэтому асимптоты
равносторонней гиперболы также
перпендикулярны, и их можно взять в
качестве координатных осей прямоугольной
системы координат(рис.3.42,б).
В этой системе координат уравнение
гиперболы имеет вид(гипербола
совпадает с графиком элементарной
функции, выражающей обратно-пропорциональную
зависимость).
В
самом деле, повернем каноническую
систему координат на угол (рис.3.42,б).
При этом координаты точки в старой и
новой системах координат связаны
равенствами
Подставляя
эти выражения в уравнение равносторонней
гиперболы и приводя подобные члены,
получаем
3. Координатные
оси (канонической системы координат)
являются осями симметрии гиперболы
(называются главными осями гиперболы),
а ее центр — центром симметрии.
Действительно,
если точка принадлежит
гиперболе.
то и точкии
,
симметричные точкеотносительно
координатных осей, также принадлежат
той же гиперболе.
Ось
симметрии, на которой располагаются
фокусы гиперболы, является фокальной
осью.
4. Из
уравнения гиперболы в полярных
координатах (см.
рис.3.41,б) выясняется геометрический
смысл фокального параметра — это
половина длины хорды гиперболы, проходящей
через ее фокус перпендикулярно фокальной
оси (при
).
5. Эксцентриситет характеризует
форму гиперболы. Чем больше,
тем шире ветви гиперболы, а чем ближек
единице, тем ветви гиперболы уже
(рис.3.43,а).
Действительно,
величина угла
между асимптотами гиперболы, содержащего
ее ветвь, определяется отношением сторон
основного прямоугольника:.
Учитывая,чтои
,
получаем
Чем
больше ,
тем больше угол.
Для равносторонней гиперболыимеем
и
.
Дляугол
тупой,
а дляугол
острый
(рис.3.43,а).
6.
Две гиперболы, определяемые в одной и
той же системе координат
уравнениями и
называютсясопряженными
друг с другом.
Сопряженные гиперболы имеют одни и те
же асимптоты (рис.3.43,б). Уравнение
сопряженной гиперболы приводится
к каноническому при помощи переименования
координатных осей (3.38).7. Уравнение определяет
гиперболу с центром в точке,
оси которой параллельны координатным
осям (рис.3.43,в). Это уравнение сводится
к каноническому при помощи параллельного
переноса (3.36). Уравнениеопределяет
сопряженную гиперболу с центром в
точке.
Параметрическое
уравнение гиперболы
Параметрическое
уравнение гиперболы в канонической
системе координат имеет вид
где —
гиперболический косинус, aгиперболический
синус.
Действительно,
подставляя выражения координат в
уравнение (3.50), приходим к основному
гиперболическому тождеству .
Пример
3.21. Изобразить
гиперболу в
канонической системе координат.
Найти полуоси, фокусное расстояние,
эксцентриситет, фокальный параметр,
уравнения асимптот и директрис.
Решение. Сравнивая
заданное уравнение с каноническим,
определяем полуоси: —
действительная полуось,—
мнимая полуось гиперболы. Строим основной
прямоугольник со сторонамис
центром в начале координат (рис.3.44).
Проводим асимптоты, продлевая диагонали
основного прямоугольника. Строим
гиперболу, учитывая ее симметричность
относительно координатных осей. При
необходимости определяем координаты
некоторых точек гиперболы. Например,
подставляяв
уравнение гиперболы, получаем
Следовательно,
точки с координатами и
принадлежат
гиперболе. Вычисляем фокусное расстояние
эксцентриситет ;
фокальныи параметр.
Составляем уравнения асимптот,
то есть,
и уравнения директрис:.
Парабола
и её каноническое уравнение
Определение. Параболой
называется геометрическое место точек,
для каждой из которых расстояние до
некоторой фиксированной точки плоскости,
называемой фокусом, равно расстоянию
до некоторой фиксированной прямой, не
проходящей через фокус и называемой
директрисой.
Определение. Расстояние
от фокуса параболы до её директрисы
называется параметром параболы.
Эксцентриситет параболы принимается
равным единице.
Опустим
из фокуса перпендикуляр
на директрисуи
точку пересечения этого перпендикуляра
с директрисой параболы обозначим
буквой.
Введём на плоскости ДПСК, поместив
начало координатв
центре отрезка,
принимая за осьпрямую
,
с положительным направлением отк
(См.
рис.176).
Рис.
176
|
|
Расстояние от
фокусадо
директрисыобозначим
буквой(это
параметр параболы). В выбранной системе
координат фокусимеет
координаты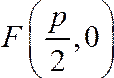
Уравнение директрисы
Пусть —
произвольная точка плоскости. Обозначим
черезрасстояние
от
точкидо
фокусапараболы,
а через—
расстояниеот
точкидо
директрисы этой параболы.
Точка лежит
на данной параболе тогда и
только
тогда, когда .
Так как
а 
то уравнение параболы имеет вид:

Это уравнение эквивалентно следующему
уравнению: 
Или: (1)
Определение. Уравнение
(1) называется каноническим уравнением
параболы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
Equation of chord of hyperbola joining points $(asecphi,btanphi)$ and $(asecphi_1,btanphi_1) $ $$y-btanphi=frac{btanphi-btanphi_1}{asecphi-asec phi_1}(x-asecphi) $$ This reduces to $$frac{y}{b}sinBig(frac{phi+phi_1}{2}Big)-frac{x}{a}cosBig(frac{phi-phi_1}{2}Big)=tanphi sinBig(frac{phi+phi_1}{2}Big)-secphi cosBig(frac{phi-phi_1}{2}Big) $$
Now I want to reduce this in the form$$-frac{y}{b}sinBig(frac{phi+phi_1}{2}Big)+frac{x}{a}cosBig(frac{phi-phi_1}{2}Big)=cosBig(frac{phi+phi_1}{2}Big) $$
How to get this form ? Most of the books use this one but they dont give the proof which I seek.
asked Oct 20, 2015 at 6:47
mathemathermathemather
2,70518 silver badges39 bronze badges
$endgroup$
$begingroup$
If you multiply both sides of $$frac{y}{b}sinBig(frac{phi+phi_1}{2}Big)-frac{x}{a}cosBig(frac{phi-phi_1}{2}Big)=tanphi sinBig(frac{phi+phi_1}{2}Big)-secphi cosBig(frac{phi-phi_1}{2}Big)$$ by $-1$ you get:
$$frac{x}{a}cosBig(frac{phi-phi_1}{2}Big)-frac{y}{b}sinBig(frac{phi+phi_1}{2}Big)=secphi cosBig(frac{phi-phi_1}{2}Big)-tanphi sinBig(frac{phi+phi_1}{2}Big)$$
which means that all we need to show is that:
$$ secphi cosBig(frac{phi-phi_1}{2}Big)-tanphi sinBig(frac{phi+phi_1}{2}Big)=cosleft(frac{phi+phi_1}{2}right) $$
which you can prove by doing the following:$$
sec phileft[ cosBig(frac{phi-phi_1}{2}Big)-sinphi sinBig(frac{phi+phi_1}{2}Big)right]$$
then decompose the cosine and sine using the addition formula:
$$ sec phi left[
cosleft(frac{phi}{2}right)cosleft(frac{phi_1}{2}right)+sinleft(frac{phi}{2}right)sinleft(frac{phi_1}{2}right)
\
-sinphileft( sinleft(frac{phi}{2}right) cosleft(frac{phi_1}{2}right)+cosleft(frac{phi}{2}right)sinleft(frac{phi_2}{2}right)
right)
right] $$
then use the identity $sinphi=2sinleft(frac{phi}{2}right)cosleft(frac{phi}{2}right)$ and collect some like terms together to get:
$$
sec phi left[
cosleft(frac{phi}{2}right)cosleft(frac{phi_1}{2}right)left[ 1-2sin^2left(frac{phi}{2}right)right]+sinleft(frac{phi}{2}right)sinleft(frac{phi_1}{2}right)left[ 1-2cos^2left(frac{phi}{2}right) right]
right]
$$
then you can use the identities
$$cosphi=2cos^2left(frac{phi}{2}right)-1=1-2sin^2left(frac{phi}{2}right)$$
to get:
$$ sec phi left[
cosleft(frac{phi}{2}right)cosleft(frac{phi_1}{2}right)left[cosphiright]+sinleft(frac{phi}{2}right)sinleft(frac{phi_1}{2}right)left[-cosphi right]
right]$$
which gives:
$$
cosleft(frac{phi}{2}right)cosleft(frac{phi_1}{2}right)-sinleft(frac{phi}{2}right)sinleft(frac{phi_1}{2}right)
$$
which, of course is:
$$ cosleft(frac{phi+phi_1}{2}right) $$
which is what we needed to show.
answered Oct 22, 2015 at 14:43
JayJay
1,8451 gold badge14 silver badges21 bronze badges
$endgroup$
$begingroup$
The rhs of your second and third equations should be equal and opposite, as one can verify:
$$
tanphi sin { phi + phi_1 over 2} — sec phi cos {phi — phi_1 over 2} + cos {phi + phi_1 over 2} =
{1 over cos phi} left( sin phi sin {phi+ phi_1 over 2} — cos { phi- phi_1 over 2} + cos phi cos { phi+ phi_1 over 2}
right)=
{1 over cos phi} left( cos { phi — phi_1 over 2} — cos {phi — phi_1 over 2} right) = 0
$$
where in the third line, I used the trig identity
$$
cos (a — b) = cos a cos b + sin a sin b
$$
answered Oct 22, 2015 at 14:42
$endgroup$
$begingroup$
Another method which does not require ingenious use of trigonometric identities goes as follows
Equation of tangent to hyperbola at point $(asec A,btan A)$ is $$frac{x}{a}sec A-frac{y}{b}tan A=1 $$
Equation of tangent to hyperbola at point $(asec B,btan B)$ is $$frac{x}{a}sec B-frac{y}{b}tan B=1 $$
The intersection of these two tangents is the point $$Bigg(afrac{cosfrac{A-B}{2}}{cosfrac{A+B}{2}},bfrac{sinfrac{A+B}{2}}{cosfrac{A+B}{2}}Bigg) $$
The equation of chord of contact from a point on a conic is $T=0$. Hence equation of chord is $$frac{x}{a^2}afrac{cosfrac{A-B}{2}}{cosfrac{A+B}{2}} -frac{y}{b^2}bfrac{sinfrac{A+B}{2}}{cosfrac{A+B}{2}}=1 $$ Which on simplification gives $$frac{x}{a}{cosfrac{A-B}{2}}-frac{y}{b}sinfrac{A+B}{2}=cosfrac{A-B}{2} $$
answered May 13, 2016 at 15:06
mathemathermathemather
2,70518 silver badges39 bronze badges
$endgroup$
0
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
|
0 / 0 / 0 Регистрация: 07.04.2018 Сообщений: 30 |
|
|
1 |
|
Длина хорды гиперболы18.04.2018, 06:11. Показов 2377. Ответов 4
Найти длину хорды гиперболы (x^2/a^2)-(y^2/b^2) проходящей через ее фокусы и перпендикулярной к факельной оси
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
18.04.2018, 06:11 |
|
Ответы с готовыми решениями:
Из точки Р(х,у) проведены касательные к…
нарисовать хорды в долях maxsize — размер всего поля рисования Задача про хорды. 4 |
|
Nacuott |
|
18.04.2018, 07:05
|
|
Не по теме: Denis2299 , вы бы переставили в предпоследнем слове буквы а и е, тогда вам точно помогут.
0 |
|
Любитель математики 1476 / 987 / 282 Регистрация: 27.01.2014 Сообщений: 3,275 |
|
|
18.04.2018, 09:26 |
3 |
|
Denis2299, уравнение гиперболы имеет вид
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,668 Записей в блоге: 4 |
|
|
18.04.2018, 13:05 |
4 |
|
Параметр p это половина хорды. А как известно p=b^2/a, ну или p=a^2/b. Здесь всё зависит от того, как ТС ответит на справедливый вопрос angor6.
0 |
|
0 / 0 / 0 Регистрация: 07.04.2018 Сообщений: 30 |
|
|
20.04.2018, 11:27 [ТС] |
5 |
|
Да всем спасибо. Уже разобрался
0 |
фокусы которой расположены на оси абсцисс
симметрично относительно начала координат, зная,
кроме того, что:
515.1
515.2
фокусами 2c=10 и ось 2b=8;
515.3
фокусами 2c=6 и эксцентриситет e=3/2;
515.4
эксцентриситет e=5/4;
515.5
515.6
директрисами равно 228/13 и расстояние между
фокусами 2c=26;
515.7
директрисами равно 32/5 и ось 2b=6;
515.8
директрисами равно 8/3 и эксцентриситет e=3/2;
515.9
равно 64/5;
уравнение гиперболы, фокусы которого
расположены на оси ординат симметрично
относительно начала координат, зная, кроме того,
что:
(буквой а мы обозначаем полуось гиперболы,
расположенной на оси абсцисс);
фокусами 2с=10 и эксцентриситет e=5/3;
516.3
48;
директрисами равно 50/7 и эксценриситет e=7/5;
равно 32/5.
а и b каждой из следующих гипербол:
эксцентриситет, уравнения асимптот, уравнения
директрис.
эксцентриситет, уравнения асимптот, уравнения
директрис.
треугольника, образованного асимптотами
гиперболы
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
уравнения прямых, на которых лежат фокальные
радиусы точки М1.
точка М1(-5; 9/4) лежит
на гиперболе
М1.
гиперболы e=2, фокальный радиус ее точки М,
проведенный из некоторого фокуса, равен 16.
Вычислить расстояние от точки М до односторонней
с этим фокусом директрисы.
гиперболы e=3, расстояние от точки М гиперболы до
директрисы e=3, расстояние от точки М гиперболы до
директрисы равно 4. Вычислить расстояние от точки
М до фокуса, одностороннего с этой директрисой.
гиперболы e=2, центр ее лежит в начале координат,
один из фокусов F(12; 0). Вычислить расстояние от
точки М1 гиперболы
с абсциссой, равной 13, до директрисы,
соответствующей заданному фокусу.
гиперболы e=3/2, центр ее лежит в начале координат,
одна из директрис дана уравнением x=-8. Вычислить
расстояние от точки М1 гиперболы с абсциссой, равной 10, до
фокуса, соответствующего заданной директрисе.
гиперболы
правого фокуса равно 4,5.
гиперболы
левого фокуса равно 7.
гиперболы
ее оси, содержащей вершины. Определить
расстояние от фокусов до точек пересечения этого
перпендикуляра с гиперболой.
циркулем, построить фокусы гиперболы
что оси координат изображены и масштабная
единица задана).
уравнение гиперболы, фокусы которой лежат на оси
абсцисс симметрично относительно начала
координат, если даны:
-1), M2(-8;
3) гиперболы и эксцентриситет e=
-1) гиперболы с уравнения асимптот
5/2) гиперболы и уравнения
директрис
533
эксцентриситет равносторонней гиперболы.
эксцентриситет гиперболы, если отрезок между ее
вершинами виден из фокусов сопряженной
гиперболы под углом 600.
совпадают с фокусами эллипса
уравнение гиперболы, если ее эксцентриситет e=2.
уравнение гиперболы, фокусы которой лежат в
вершинах эллипса
проходят через фокусы этого эллипса.
расстояние от фокуса гиперболы
асимптоты равно b.
произведение расстояний от любой точки
гиперболы
величина постоянная, равная
площадь параллелограмма, ограниченного
асимптотами гиперболы
прямыми, проведенными через любую ее точку
параллельно асимптотами, есть величина
постоянная, равная ab/2.
уравнение гиперболы, если известны ее полуоси a и
b, центр C(x0; y0) и фокусы расположены на прямой:
каждое из следующих уравнений определяет
гиперболу, и найти координаты ее центра С,
полуоси, эксцентриситет, уравнения асимптот и
уравнения директрис:
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
542.1
542.2
уравнение гиперболы, зная, что:
вершинами равно 24 и фокусы суть F1(-10;
2), F2(16; 2);
расстояние между директрисами равно 3,6;
асимптотами равен 900 и фокусы суть F1(4; -4), F2(-2;
2).
уравнение гиперболы, если известны ее
эксцентриситет e=5/4, фокус F(5; 0) и уравнение
соответствующей директрисы
уравнение гиперболы, если известны ее
эксцентриситет e=13/12, фокус F(0; 13) и уравнение
соответствующей директирсы
на гиперболе, фокус которой F(-2; -3), а
соответствующая директриса дана уравнением
уравнение гиперболы, если известны ее
эксцентриситет e=
уравнение соответствующей директрисы
-2) лежит на гиперболе, фокус
которой F(-2; 2), а соответстующая директриса дана
уравнением
равносторонней гиперболы
ее уравнение в новой системе, приняв за оси
координат ее асимптоты.
каждое из следующих уравнений определяет
гиперболу, найти для каждой из них центр, полуоси,
уравнения асимптот и построить их на чертеже:
пересечения прямой
пересечения прямой
пересечения прямой
определить, как расположена прямая относительно
гиперболы: пересекает ли, касается или проходит
вне ее:
каких значениях m прямая
гиперболу
гиперболы.
при котором прямая
уравнение касательной к гиперболе
точке M1(x1; y1).
касательные к гипербле, проведенные в концах
одного и того же диаметра, параллельны.
уравнения касательных к гиперболе
к прямой
уравнения касательных к гиперболе
прямой
касательные к гиперболе
прямой
вычислить расстояние d от точки М1 до этой прямой.
уравнение касательной к гиперболе
из точки А(-1; -7).
проведены касательные к гиперболе
уравнение хорды, соединяющей точки касания.
проведены касательные к гиперболе
расстояние d от точки Р до хорды гиперболы,
соединяющей точки касания.
через точку А(
уравнение этой гиперболы при условии, что ее оси
совпадают с осями координат.
уравнение гиперболы, касающейся прямых
условии, что ее оси совпадают с осями координат.
точки пересечения эллипса
гиперболы
составить уравнения его сторон.
точка пересечения касательной с осью Ох, Q –
проекция точки касания на ту же ось. Доказать, что
фокусы гиперболы расположены по разные стороны
от любой ее касательной.
произведение расстояний от фокусов до любой
касательной к гиперболе
величина постоянная, равная b2.
гиперболы, фокусы которой находятся в точках F1(-3;
0), F2(3; 0). Составить
уравнение этой гиперболы.
уравнение гиперболы, фокусы которой расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
гиперболе
вершинами 2а=8.
прямая, касающаяся гиперболы в некоторой точке М,
составляет равные углы с фокальными радиусами F1M, F2M и проходит
внутри угла F1MF2.
гиперболы
оси Ох направлен луч света. Известно, что
до гиперболы, луч от нее отразился. Составить
уравнение прямой, на которой лежит отраженный
луч.
эллипс и гипербола, имеющие общие фокусы,
пересекаются под прямым углом.
равномерного сжатия плоскости к оси Ох равен 4/3.
Определить уравнение линии, в котороую при этом
сжатии преобразуется гипербола
равномерного сжатия плоскости к оси Оу равен 4/5.
Определить уравнение линии, в которую при этом
сжатии преобразуется гипербола
линии, в которую преобразуется гипербола
равноменых сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ох и Оу соответствуют 2/3 и 5/3.
коэффициент q равномерного сжатия плоскости к
оси Ох, при котором гипербола
в гиперболу
коэффициент q равномерного сжатия плоскости к
оси Оу, при котором гипербола
в гиперболу
коэффициенты q1, q2 двух последовательных равномерных
сжатий плоскости к осям Ох и Оу, при которых
гипербола

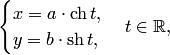
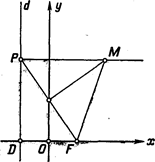

 Вычислить длину хорды
Вычислить длину хорды