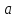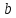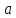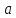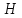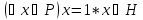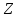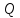Идеал кольца как найти - Исправление недочетов и поиск решений вместе с Examum.ru

What Bill say in the comments is that there is no method to determine all ideals of a ring. Even if you specialize and look just for the maximal ideals in a given ring it might imply hard work!

A great example is to look at $H^infty(mathbb{D})$ which is the collection of all power series $$f(z)=sum_{nge0}a_nz^n$$ such that
$$sup_{|z|<1}|f(z)|<infty.$$
In other words, the space of all bounded analytic functions on the unit disc $mathbb{D}$.
It is fairly easy to see that $R=H^infty(mathbb{D})$ is a ring under point-wise operations.
However, for long it was unknown how the maximal ideals ideals looks like. That problem was solved in 1962 by L. Carleson and is known as the Corona Theorem. I recommend reading this popular text regarding the Corona theorem.

In this day no one knows for sure how the the maximals looks like in $H^infty(mathbb{D}timesmathbb{D})$, that is the space of bounded analytic functions in the bi-disc in $mathbb{C}^2$.

Edit: The old link to the popular presentation of the Corona theorem has changed — using google with the following string

"corona theorem site:http://www.abelprize.no/"

(without quotes) led me to the present link.

Источник

Содержание

Идеал кольца

Левый идеал

Определение 1. Подмножество $rho$ кольца $R$ называется левым идеалом¹⁾, если является подгруппой $(R,+)$ и $rho$ является подмодулем $R$ , рассматриваемого как левый модуль над собой, то есть выполнено условие

для всех $ain R$ и .

Пример 1. Пусть $R$ — кольцо, и $ain R$ . Тогда — левый идеал в $R$ . Такой идеал называется главным левым идеалом²⁾ кольца.

Определение 2. Левый идеал $rho$ кольца $R$ называется собственным³⁾, если .

Определение 3. Левый идеал $rho$ кольца $R$ называется максимальным⁴⁾, если он не совпадает с кольцом и не содержится ни в каком собственном левом идеале $alpha$ , то есть .

Определение 4. Левый идеал $rho$ кольца $R$ называется регулярным⁵⁾, или модулярным⁶⁾, если существует такой элемент $ain R$ , что для всех $xin R$ .

Пример 2. В любом ассоциативном кольце с единицей $R$ каждый его левый идеал $rho$ является регулярным, так как .

Определение 5. Если $rho$ — левый идеал в $R$ , то объект называется частным.

Предложение 1. Если $rho$ — регулярный левый идеал кольца $R$ , то $rho$ можно вложить в максимальный левый идеал, который также регулярен.

Предложение 2. Пусть $rho$ — максимальный левый идеал в $R$ . Предположим, что он регулярен и – соответствующий ему неприводимый левый модуль. Тогда аннулятор $A(M)$ модуля $ M $ совпадает с и является наибольшим двусторонним идеалом $R$ , лежащим в $rho$ .

Правый идеал

Определение 1. Подмножество $rho$ кольца $R$ называется правым идеалом⁷⁾, если является подгруппой $(R,+)$ и $rho$ является подмодулем $R$ , рассматриваемого как правый модуль над собой, то есть выполнено условие

для всех и .

Пример 1. Пусть $R$ — кольцо, и $ain R$ . Тогда — правый идеал в $R$ . Такой идеал называется главным правым идеалом кольца.

Определение 2. Правый идеал $rho$ кольца $R$ называется собственным⁹⁾, если .

Определение 3. Правый идеал $rho$ кольца $R$ называется максимальным¹⁰⁾, если он не совпадает с кольцом и не содержится ни в каком собственном правом идеале $alpha$ , то есть .

Определение 4. Правый идеал $rho$ кольца $R$ называется регулярным¹¹⁾, или модулярным¹²⁾, если существует такой элемент $ain R$ , что для всех $xin R$ .

Пример 2. В любом ассоциативном кольце с единицей $R$ каждый его правый идеал $rho$ является регулярным, так как .

Определение 5. Если $rho$ — правый идеал в $R$ , то положим .

Предложение 1. Если $rho$ — регулярный правый идеал кольца $R$ , то $rho$ можно вложить в максимальный правый идеал, который также регулярен.

Предложение 2. Пусть $rho$ — максимальный правый идеал в $R$ . Предположим, что он регулярен и – соответствующий ему неприводимый правый модуль. Тогда аннулятор $A(M)$ модуля $ M $ совпадает с и является наибольшим двусторонним идеалом $R$ , лежащим в $rho$ .

Двусторонний идеал

См. также

Литература

Наверх

Источник

Левый
идеал — подкольцо

кольца
,
в котором
.

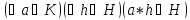
Правый
идеал — подкольцо

кольца
,
в котором
.

Двусторонний
идеал — подкольцо

кольца
,
в котором
,
то есть подкольцо

кольца

замкнуто относительно умножения на
любой элемент кольца.

Когда

— коммутативное кольцо, определения
левого, правого и двустороннего идеалов
совпадают. В таком случае используется
просто слово «идеал».

Далее
будем рассматривать только двусторонние
идеалы и писать просто «идеал».

В
кольце

всегда есть два несобственных идеала
—

(нулевой идеал) и всё кольцо

(пишут «единичный идеал»:
).
То есть
.
Все остальные идеалы — собственные.

Примеры.

Множество чётных чисел

образуют идеал в кольце

всех целых чисел. Действительно,
произведение любого чётного числа и
любого целого числа есть чётное число,
то есть принадлежит этому идеалу.
Множество

— идеал в кольце
.
Множество квадратных матриц порядка

с элементами из некоторого коммутативного
кольца

— некоммутативное по умножению кольцо,
поэтому в нём нужно различать односторонние
и двухсторонние (настоящие) идеалы.

Пусть
дано коммутативное кольцо

и
.
Подмножество

является идеалом в
,
который называется идеалом, порождённым
элементами
,
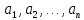
и обозначается
.

Главный
идеал

— идеал кольца
,
состоящий из кратных элемента

(то есть порождается одним элементом
).

Кольцо
главных идеалов — кольцо, в котором
все идеалы главные.

Пример.

— кольцо главных идеалов (все идеалы
имеют вид
,
то есть порождаются одним элементом
).
Доказательство. Пусть

— произвольный идеал в
.
Если
,
то доказывать нечего. Если же в

есть ещё элемент
,
то

содержит и элемент

(исходя из определений кольца и идеала),
а один из этих элементов является
положительным числом. Пусть

— наименьшее положительное число в
идеале
.
Если

— произвольное число в идеале

и

— остаток от деления числа

на число

(понятно, что
),
то
.
Так как

и

принадлежат идеалу
,
то число

тоже принадлежит этому идеалу. Так как
,
то обязательно

(
— наименьшее положительное число в
идеале
).
Следовательно,
,
то есть все числа идеала

являются кратными числа
.
Отсюда следует, что
;
следовательно,

— главный идеал.

Пример.
В кольце

также все идеалы главные, так как вместе
с любыми элементами

идеал всегда содержит их НОД.

Теорема.
Любое поле не содержит идеалов, кроме

и
.

Доказательство.

Так
как в любом кольце всегда есть два
несобственных идеала:

и
,
то любое поле также имеет два несобственных
идеала (любое поле является кольцом) —
это очевидно.

Пусть

— ненулевой идеал в поле
.
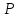
Так как

— ненулевой, то в нём есть элемент
.
В поле всякий ненулевой элемент

обратим:
.
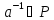
Тогда ввиду замкнутости

относительно умножения на любой элемент
поля

имеем:
.
То есть единица принадлежит идеалу
.
Тогда

(ибо
,
а

— идеал). То есть
,
и тогда, с учётом

(по условию), имеем
.
То есть этот идеал

совпадает со всем полем
.
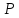
Таким образом, из предположения, что
идеал не является нулевым, мы вывели,
что он совпадает со всем полем. Теорема
доказана.

Замечание.
В любом кольце
,
отличном от поля, любой необратимый
элемент

порождает идеал
,
отличный от

и
.
Например, так как в кольце

нет обратных элементов

(кроме
),
то

— не поле и в нём существуют идеалы:
…

Замечание.
Всякий идеал в кольце является подкольцом.
Обратное неверно. Например, кольцо

целых чисел в поле

рациональных чисел является подкольцом,
но не идеалом.

Источник