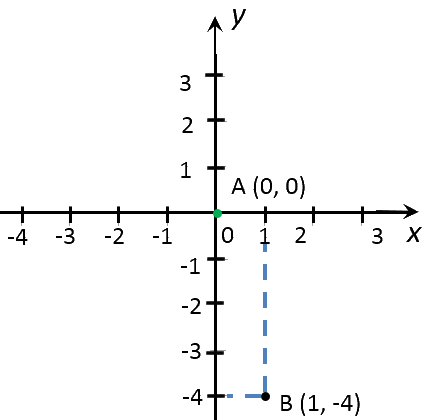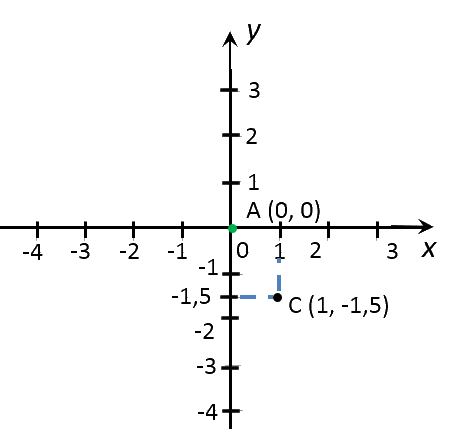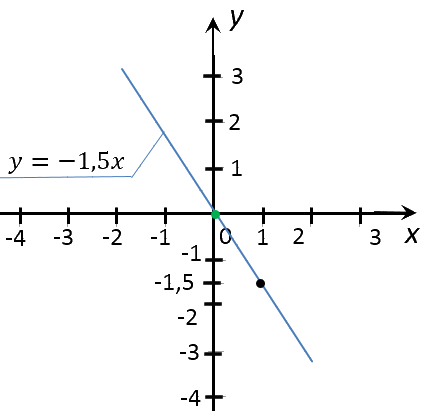Игрек равно ка икс как найти ка

Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Функция «y = kx» — это первый тип функции, который изучается в математике.

Другими словами, можно сказать, что «y = kx» — это семейство всевозможных функций, где вместо
«k» стоит число.

Примеры функций вида «y = kx».

• y = 4x
• y = −1,5x
• y = x

Давайте определим для каждой из функций выше, чему в них равен числовый коэффициент
«k».

Функция	Коэффициент «k»
y = 4x	k = 4
y = −1,5x	k = −1,5
y = 1 2 x	k = 1 2

Как построить график функции «y = kx»

Из геометрии вспомним аксиому (утверждение, которое не требует доказательства),
что через любые две точки можно провести прямую и притом только одну.

Исходя из этой аксиомы, что
чтобы построить график функции вида «у = kx» нам будет достаточно найти всего
две точки.

Для примера построим график функции «y = −4x».

Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».

x	Расчет «y»
0	y(0) = −4 · 0 = 0
1	y(1) = −4 · 1 = −4

Полученные значения «x» и «y» — это координаты точек графика

функции «y = −4x».

Запишем полученные координаты точек «y = −4x» в таблицу.

Точка	Координата по оси «Оx» (абсцисса)	Координата по оси «Оy» (ордината)
(·)A	0	0
(·)B	1	−4

Отметим полученные точки на системе координат.

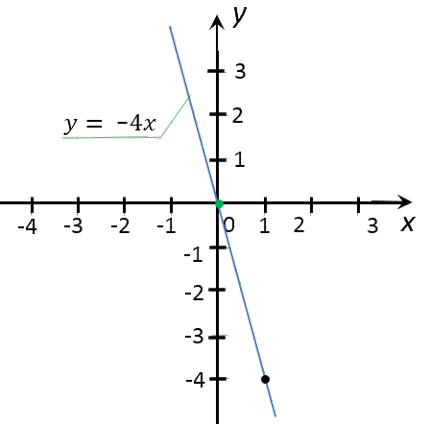
Теперь проведем прямую через отмеченные точки. Эта прямая и будет
являться графиком функции «y = −4x».

После построения не забудьте подписать график функции.

Как решать задачи на функцию «y = kx»

Рассмотрим задачу.

---

Построить график функции «y = −1,5x». Найти по графику:

1. значение «y» соответствующее значению «x» равному 1; 0; 2; 3;
2. значение «x», если значение «y» равно
   −3; 4,5; 6;
3. несколько целых значений «x», при которых значения
   «y» положительны (отрицательны).

---

Вначале построим график функции «y = −1,5x».

Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = −1,5x» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = −1,5 · 0 = 0
(·)B	1	y(1) = −1,5 · 1 = −1,5

Отметим полученные точки на прямоугольной системе координат.

Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = −1,5x».

---

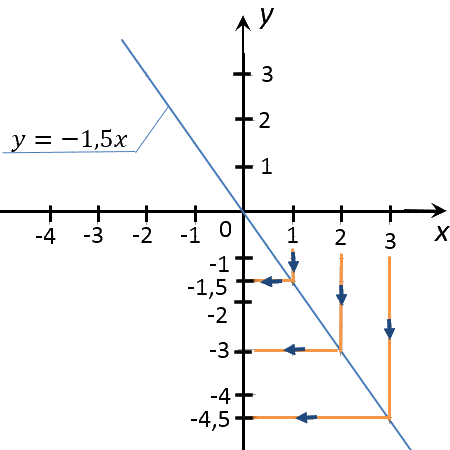
Теперь работаем с построенным графиком функции «y = −1,5x».

Требуется найти значение «y»,
соответствующее значению «x» равному 1; 0; 2; 3.

---

Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

По правилам выше найдем на построенном ранее графике функции «y = −1,5x»
необходимые значения функции «y» для
«x» равным 1; 0; 2; 3.

Запишем полученные результаты в таблицу.

Заданное значение «x»	Полученное с графика значение «y»
0	0
1	−1,5
2	−3
3	−4,5

---

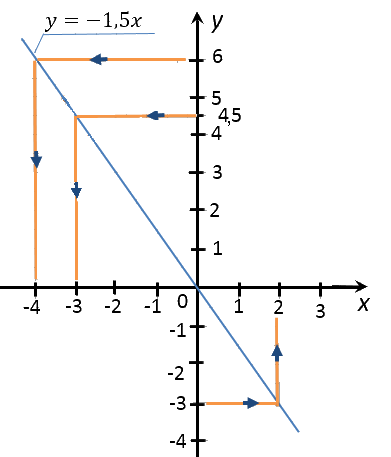
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно −3; 4,5; 6.

---

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры
от оси «Oy».

Запишем полученные результаты в таблицу.

Заданное значение «y»	Полученное с графика значение «x»
−3	2
4,5	−3
6	−4

---

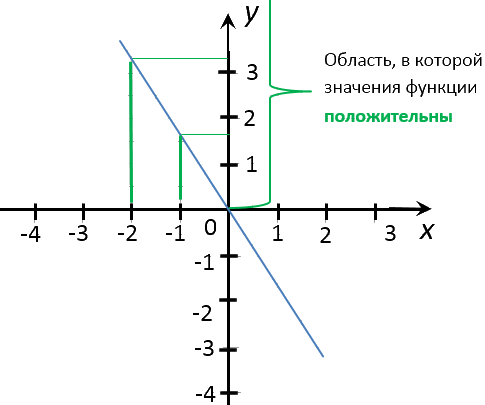
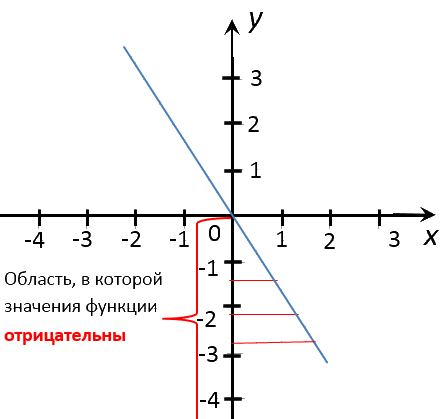
Перейдем к последнему заданию. Нас просят найти несколько целых значений «x»,
при которых значения «y» положительны (отрицательны).

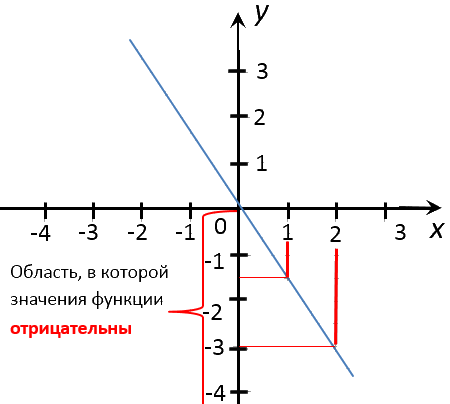
Для решения этой задачи необходимо внимательно изучить
график функции
«y = −1,5x».

Отметим область на оси
«Oy», где значения «y» для графика функции «y = −1,5x»
положительны.

Из этой области проведем от графика функции несколько перпендикуляров
к оси «Ox».

Помните, что по заданию, нас просят найти несколько «целых» значений «x».
Поэтому перпендикуляры мы будем проводить к оси «Ox» в целые числовые значения.

Запишем ответ. При x = −2; x = −1 значения
y > 0.

---

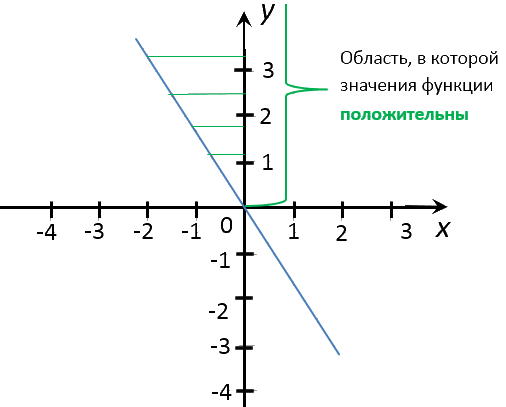
Теперь найдем при каких «x», значения
«y» отрицательны.
Отметим область на оси «Oy», где значения
«y» на графике функции отрицательны.

Проведем перпендикуляры из отмеченной области к оси «Ox» в
целые числовые значения «x».

Запишем ответ. При x = 1; x = 2 значения
y < 0.

---

Рассмотрим другую задачу.

Какие из точек A(5; −3), D(2; 1)
принадлежат графику функции, заданной
формулой
«y = x»?

---

Подробный разбор задачи «Как проверить, что точка принадлежит графику функции» мы приводили в уроке
«Как решать задачи на функцию».

В этом уроке мы вспомним только основные моменты решения подобных задач.

Подставим в функцию
«y = x»
координаты точки (·)A(5; −3).

−3 = · 5

              
−3 = (неверно)

Это означает, что точка (·)А(5; −3)
не принадлежит графику функции «y = x»

Проверим точку (·)D(2; 1).
Также подставим её координаты в функцию «y = x».

1 = ·2

1 =

            
1 = 1(верно)

Это означает, что точка (·)D(2; 1)
принадлежит графику функции «y = x».

---

Ваши комментарии

Оставить комментарий:

---

Общие сведения

Функцией называется некоторая зависимость переменных друг от друга. В некоторых случаях неизвестные величины могут быть выражены системой конкретных значений, интервалами, а также другими функциональными выражениями. Последний класс называется сложным или составным. Различают зависимые и независимые переменные (аргументы). Второй тип может принимать любые значения, кроме тех, которые превращают выражение в неопределенность.

Однако аргументы необходимо также обследовать, поскольку они могут обратить тождество в пустое множество. Одним из таких примеров является функция у = к / х. Ее аргумент x может принимать любые значения, кроме 0. Именно это число превращает уравнение в неопределенность, поскольку в математике существует следующее правило: запрещается делить на 0.

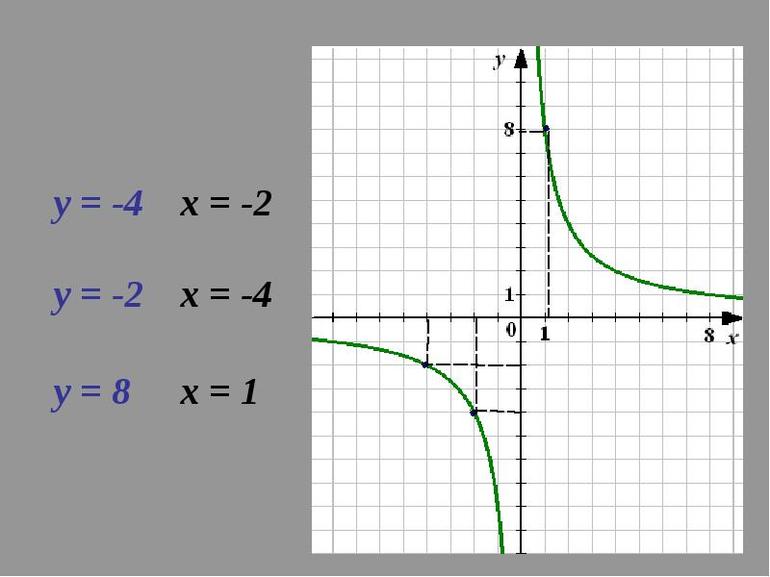
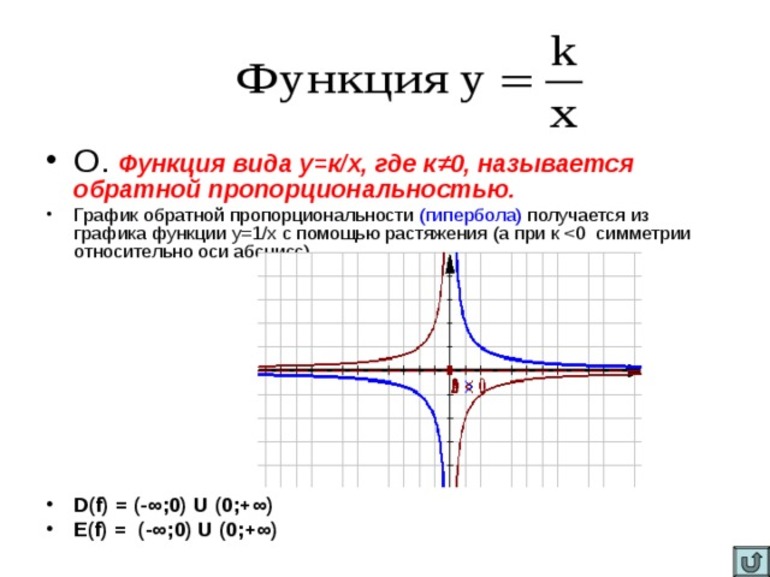
Следует отметить, что существует функция y = k/x и ее график — кривая, имеющая название гипербола. Многие путают его с параболой (в степени 2). Однако она является квадратичной. График строится в системе координат, которая называется декартовой. Кроме того, в математике встречается еще одно уравнение вида y = кх. Ее графиком является прямая.

Прямоугольная система координат

В математике существуют специальные инструменты для построения графиков функций. Одним из них считается распространенная прямоугольная система координат. Она может быть на плоскости и в пространстве. Поскольку y = k/x и y = kx являются элементарными, то для иллюстрации их графиков используется однородная прямоугольная декартовая система координат (рис. 1), элементом которой является точка.

Для декартовой системы на плоскости имеется только две координаты: по взаимно перпендикулярным осям ординат (ОУ) и абсцисс (ОХ). Они пересекаются в некоторой точке О, которая называется началом координат.

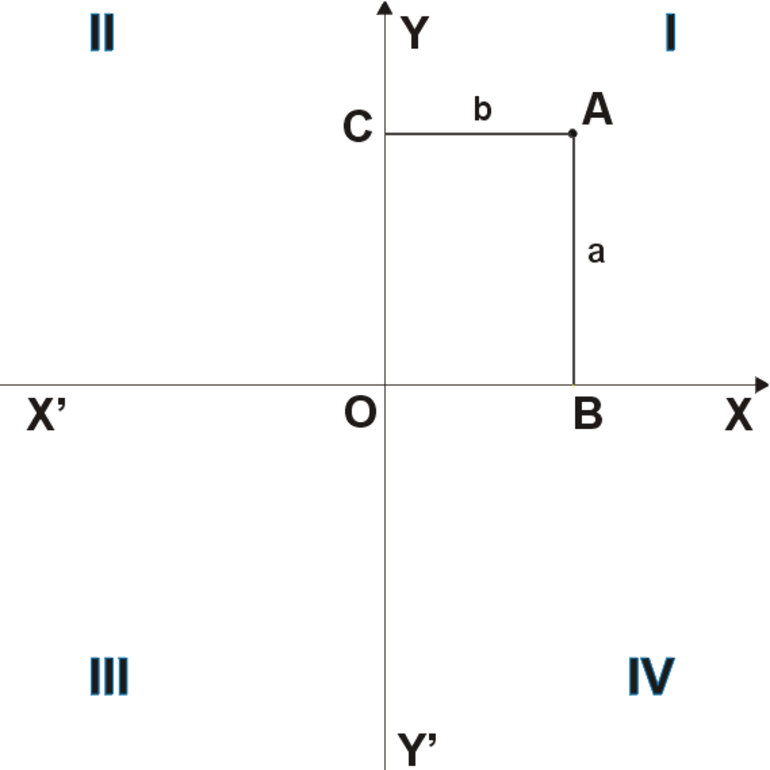
Рисунок 1. Прямоугольная декартова система координат (ДСК).

При указании координат нужно учитывать четверть. От нее зависит знак. Оси ординат (игрек) и абсцисс (икс) делят систему на четыре четверти. Они обозначаются римскими цифрами (рис. 1) и имеют такие свойства:

• Первая — I: координаты x и y являются положительными числами, т. е. x > 0 и y > 0.
• II: x < 0 и y > 0.
• III: x < 0 и y < 0.
• IV: x > 0 и y < 0.

Базовыми знаниями являются правильное нахождение координат произвольной точки и их запись. Например, на рисунке 1 нужно найти координаты С. Их нужно искать по следующему алгоритму:

• Опустить из точки перпендикуляры на ОУ и ОХ: b и a соответственно.
• Найти координаты по х и у (размерность шкалы деления осей нужно задавать при построении ДСК): B и С соответственно.
• Записать значения: C(В;С).

Допускается задавать одну шкалу в одних единицах, а вторую — в других. Например, при построении графика y = 100x можно задавать х в виде единичных значений, а вот уже у будут исчисляться сотнями. Чтобы приступать к дальнейшему изучению материала, математики рекомендуют потренироваться в нахождении координат любых точек.

Коэффициент пропорциональности

В математических дисциплинах бывает два типа пропорциональности — прямая и обратная. Они применяются для описания различных процессов, исследования дифференциальных уравнений, физических величин и законов.

Прямой пропорциональностью называется некоторая линейная функция вида y = kx, в которой аргументом является х, а к — коэффициент прямой пропорциональности. Иными словами, произведение к на аргумент x есть величина, определяющая прямую пропорциональную зависимость одной величины от другой. Обратной пропорциональностью называется некоторая функция вида y = k/x, значение аргумента которой никогда не равно нулю.

Графиком линейной функции вида y = kx является прямая, проходящая через начало координат в точке О(0;0). От к зависит угол наклона прямой. Если к > 0, то он является острым, т. е. его значение меньше 90 градусов. При к < 0 угол наклона больше 90 градусов (тупой).

Для обратной пропорциональности, заданной уравнением у = к / х, значение коэффициента влияет на расположение гиперболы в четвертях ДСК. Если к > 0, то она располагается в I и III. Когда к < 0, тогда ее расположение заключено во II и IV четвертях.

Исследование функции

Для полного анализа поведения функции применяется методика или алгоритм ее исследования. Это нужно прежде всего для подробного графика. Однако перед началом выполнения этой операции следует ознакомиться с основными пунктами полного исследования заданной функции. К ним относятся следующие:

• Область определения — D(f).
• Область допустимых значений — E(f).
• Нули.
• Знаковые промежутки.
• Периодичность.
• Параметры четности.
• Экстремумы (MAX и MIN).
• Монотонность (интервалы).

Однако некоторые пункты можно опускать или менять местами. После этого необходимо строить график, учитывая все необходимые материалы исследования. Следует подробно разобрать каждый пункт, поскольку только верное решение дает возможность построить правильный график. Кроме того, специалисты рекомендуют освоить интервалы и их правильную запись.

Правила записи интервалов

В некоторых пунктах алгоритма исследования функции встречается термин «промежуток» или «интервал». От правильности его задания зависит решение задачи. Во всем мире приняты обозначения, которые помогут сделать запись понятной и грамотной:

• Обозначение жесткой границы (включительно) квадратными скобками [], а значения, не входящего в интервал (не включительно), — круглыми скобками ().
• Тип границ можно комбинировать.
• Для объединения промежутков применяется специальный символ U.
• Бесконечность можно обозначать символом или inf. Например, (-inf;inf).
• Перед и после бесконечности всегда ставится круглая скобка.
• Порядок комбинации промежутков (интервалов или числовых отрезков): последовательно от большего к меньшему. Например, (-inf;-8) U (-4;0] U [5;8] U (10;15).

Обозначение inf используется в некоторых языках программирования или математических пакетах. В дисциплине «Алгебра и начало анализа» интервалы встречаются очень часто, поскольку она основана на исследовании выражений, уравнений, неравенств, функций и т. д. После ознакомления с правилами записи промежутков следует переходить к первому пункту — нахождению D(f).

Область определения и допустимые значения

Все значения аргумента, при которых существует заданная функция вида z = f(y), называется областью ее определения. Обозначается параметр комбинацией букв D(имя функции), т. е. D(z) или D(f(y)). Величина D(z) зависит от типа функции, в том числе от ее сложности. Если она состоит из нескольких простых элементов, то нужно рассматривать D(z) для каждого из них. Параметр всегда записывается в виде промежутка, на котором существует зависимая переменная.

Областью допустимых значений функции z = f(y) являются все значения, при которых она существует. Обозначается величина литерой Е(имя функции). Например, запись для z = f(y) выглядит таким образом: Е(z) или Е(f(y)). Этот параметр тоже зависит от типа выражения, как и D(z). Задается в виде интервала. Для его задания необходимо выяснить, при каких значениях функция не существует. Например, для z = 2 / y. В искомом выражении у не может быть равен 0. Следовательно, у принадлежит следующему интервалу: (-inf;0) U (0;inf). Для z = 3y параметр Е(z) = (-inf;inf), поскольку при любых значениях функция существует.

Нули и знаковые промежутки

Нулями функции называются все значения независимой переменной, при которых ее график пересекается с осями ОУ и ОХ. Для нахождения точки пересечения с ОУ необходимо подставить х = 0 в выражение и выполнить расчеты. Чтобы найти пересечение или пересечения с осью иксов, нужно решить уравнение, приравняв его к 0.

Знаковые промежутки (интервал знакопостоянства) — отрезки, на которых функция меняет знак на противоположный. Если интервал положительный, то короткая запись выглядит таким образом: f(x) > 0 при х, принадлежащим промежутку (2;6) U [8;10]. Аналогично указывается отрезок, на котором заданная функция принимает отрицательные значения (f(x) < 0). Математики рекомендуют воспользоваться методом интервалов. Он представлен таким алгоритмом:

• Найти D(z).
• Определить нули с ОХ.
• Начертить ось ОХ отдельно.
• Отложить на ней точки разрыва, нули функции.
• Определить знаки на интервалах.

Следует отметить, что на числовой прямой обозначаются только те точки, которые входят в ее область определения.

Периодичность и четность

Периодической является функция, повторяющая значения через некоторый период Т (регулярный интервал). Ее значения не меняются при добавлении к аргументу некоторого числа, неравного нулевому значению. Математическая запись для z = f(y) имеет такой вид: z = f(y + T) = f(y — T). Для любой периодической функции справедливо также следующее равенство: z = f(y + nT). Коэффициент n — любое целочисленной значение.

Для выявления признака четности следует воспользоваться очень простым соотношением f(y) = f(-y). Для этого необходимо подставить в выражение положительное, а затем отрицательное значение аргумента. Если в первом и втором случаях равенство будет выполняться, то можно сделать вывод о четности. Когда соотношение не выполняется, тогда исходная функция является нечетной.

Монотонность и экстремумы

Монотонная — функция z = f(x), которая может только возрастать или убывать (понижение) на всей области определения. Для исследования нужно воспользоваться следующим алгоритмом:

• Найти первую производную.
• Определить критические точки, приравняв производную к 0.
• Выяснить знаки производной на промежутках.
• Сделать выводы.

Далее нужно определить экстремумы, т. е. минимальное и максимальное значения функции на всей области ее определения. В этом случае также существуют определенные правила:

• Найти D(z) и сравнить его с отрезком, на котором нужно найти экстремумы (должен принадлежать D(z)).
• Найти производную заданной функции.
• Выполнить поиск стационарных точек (производная приравнивается к 0 и решается уравнение).
• Подставить корни уравнения в исходную функцию.
• Найти минимальное и максимальное значения.

Следует учесть все точки. Однако перед выполнением 4 пункта следует отсеять ложные корни. Для этого следует подставить в уравнение корни. Они должны соответствовать равенству. Если этого не происходит, то корень отсеивается.

Информация о свойствах

В некоторых источниках описываются свойства y = k/x и ее график. Следует отметить, что они получаются при исследовании последней. Существует два состояния. При первом коэффициент пропорциональности больше 0 (k > 0). Следовательно, она обладает такими свойствами:

• График: кривая-гипербола.
• D(y) = (-inf;0) U (0;+inf).
• Если x > 0, то y > 0.
• При отрицательных величинах аргумента функция принимает отрицательные значения.
• Она убывает на интервалах: (-inf;0) и (0;+inf).
• Точек экстремума нет.
• Непрерывна, кроме точки х = 0.
• Непериодическая.
• Нечетная.

Когда к < 0, тогда ее свойства отличаются только в 3 и 4 пунктах: y > 0 при отрицательных значениях аргумента, а y < 0 при x > 0. Функция y = kx обладает такими свойствами (k > 0):

• График: прямая.
• D(y) = (-inf;+inf).
• Если x > 0, то y > 0. Когда x < 0, то y < 0.
• Всегда возрастает по всей D(y).
• Минимумов и максимумов нет.
• Непрерывна.
• Нечетная.
• Непериодическая.

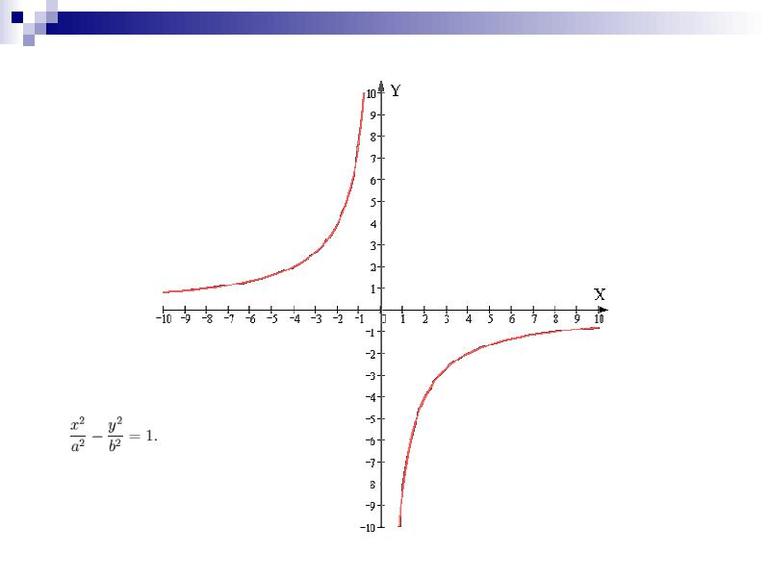
При k < 0 она обладает такими же свойствами, но есть такие отличия в пункте 3: y > 0 при x < 0. Следует отметить, что в высшей математике уравнения гиперболы отличаются. Каноническая форма имеет такой вид: [x^2 / a] — [у^2 / b] = 1 (a и b — некоторые целые числа).

Пример решения

Существует некоторый тип задач, в которых нужно исследовать и построить график функции y = k/x. Разобрать решение можно на примере y = 5 / (x — 3). Следует воспользоваться алгоритмом:

• D(5 / (x — 3)) = (-inf;3) U (3;+inf).
• Нули функции. По ОУ: y = 5 / (0 — 3) = — 5/3. По ОХ: 5 / (x — 3) = 0. Если решить уравнения, то у него нет корней.
• Знаковые промежутки: (-inf;3) и (3;+inf).
• Непериодическая.
• Четность: 5 / (-x — 3) = — 5 / (x + 3). Нечетная: — 5 / (x + 3) не равно 5 / (x — 3).
• Экстремумы: y’ = [5 / (x — 3)] = — 5 / (x — 3)^2 = 0. Уравнение не имеет решений, а это значит, что максимума и минимума нет.
• Не является монотонной.

Чтобы построить график функции y = k / x + 3 (к = 5), нужно составить таблицу для его построения.

х	-4	-3	-2	-1	0	1	2	3	4
у	-5/7	-5/6	-1	-1,2	-5/3	-2,5	-5	нет	5

Таблица 1. Зависимость значения функции от ее аргумента.

После составления таблицы нужно начертить ДСК. На ней следует отмечать точки, а затем их плавно соединить (рис. 2).

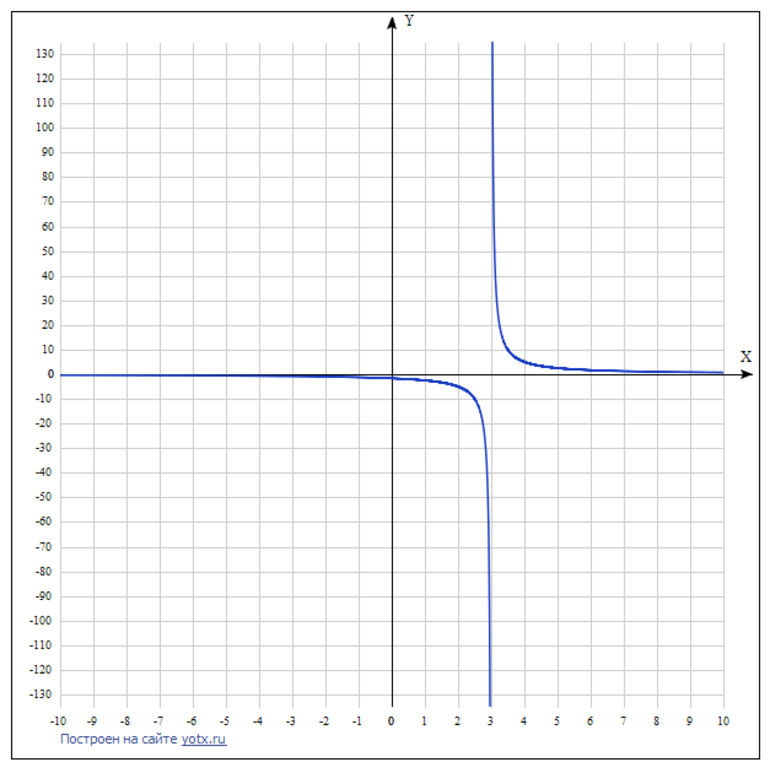
Рисунок 2. График обратной пропорциональности y = k / x — 3 при к = 5.

Математики рекомендуют для проверки применять специализированные веб-приложения. Одним из них является онлайн-сервис, который называется yotx.

Таким образом, графиком обратной пропорциональности является гипербола, а прямой пропорциональности — прямая. Поведение функции исследуется по специальному алгоритму, который позволяет легко построить ее график и выяснить некоторые свойства.

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции, т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

1. Линейная функция пересекает ось (y) в точке (b).
   Примеры:

   

   Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

   Примеры:

   

2. Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

   Примеры:

   

3. Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

   Примеры:

   

Пример (ЕГЭ)

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k<0).

Достроим прямую до прямоугольного треугольника. Вершинами будут жирные точки, которые нам дали в задаче.

(k=-frac{AC}{BC}=-frac{1}{3}). Получается (g(x)=-frac{1}{3}x+3).

Способ 1 быстрее способа 2, но не во всех ситуациях помогает. Поэтому важно владеть и вторым способом тоже.

Способ 2

Вы обращали внимание, что в задачах ЕГЭ на прямых всегда жирно выделяют 2 точки? Так вот, чтобы найти формулу линейной функции, достаточно подставить координаты этих точек в формулу (f(x)=kx+b) и решить получившуюся систему уравнений.

Пример (ЕГЭ)

Обозначим жирные точки какими-нибудь буквами и найдем их координаты.

(A(-2;2)) и (B(2;-5)) подставим эти значения вместо (x) и (f(x)) в формулу (f(x)=kx+b):

Получим:

(begin{cases}2=-2k+b\-5=2k+bend{cases})

Теперь найдем (k) и (b), решив эту систему.

Для этого сложим уравнения друг с другом, чтобы исчезло (k):

(2+(-5)=-2k+b+2k+b)
(-3=2b)
(b=-1,5)

Теперь подставим найденное (b) во второе уравнение системы и найдем (k):

(-5=2k-1,5)
(-5+1,5=2k)
(-3,5=2k)
(k=-1,75)

Получается (f(x)=-1,75x-1,5). Остается последний шаг – вычислим при каком иксе функция, то есть (f(x)), равна (16):

(16=-1,75x-1,5)
(17,5=-1,75x)
(x=-10).

Ответ: (-10).

Пример (ЕГЭ)

Чтоб решить задачу, нам понадобятся формулы каждой из двух функций. Давайте формулу нижней функции найдем с помощью способа 1, а формулу верхней с помощью способа 2. Начнем с нижней функции.

Функция (f(x)) возрастает, значит (k>0). (k=+frac{AC}{BC}=frac{4}{4}=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

(begin{cases}4=-2k+b\1=-4k+bend{cases})

Вычтем второе уравнение из первого, чтоб убрать (b):

(4-1=-2k+b-(-4k+b))
(3=2k)
(k=1,5)

Найдем (b):

(4=-2cdot 1,5+b)
(4=-3+b)
(b=7)

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

(x+1=1,5x+7)
(x-1,5x=7-1)
(-0,5x=6)
(x=6:(-0,5))
(x=-12).

Ответ: (-12).

Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».

Смотрите также:
Как определить a, b и c по графику параболы

Скачать статью