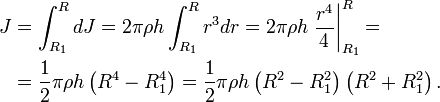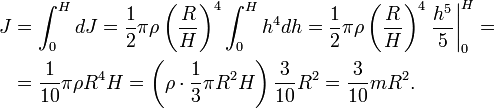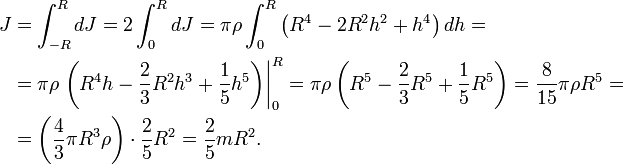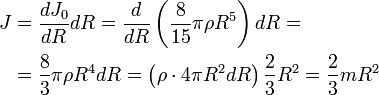Инерция шара как найти радиус - Исправление недочетов и поиск решений вместе с Examum.ru

Радиус инерции

Осевые моменты инерции для твердых тел в некоторых случаях задают при помощи массы и радиуса инерции такого тела. Обычно радиус инерции обозначают буквой , но могут встречаться и другие обозначения. Для того чтобы не путать радиус инерции с плотностью вещества радиус инерции идентифицируют при помощи индекса, например пишут: ${rho }_x$ . Особенно часто радиус инерции применяют для выражения осевых моментов инерции тел, имеющих сложную форму.

Определения радиуса инерции

Выражение (1) означает, что ${rho }_x$ равен расстоянию от оси до места в пространстве, в котором следует сосредоточить всю массу тела для того, чтобы момент инерции данной материальной точки был равен моменту инерции тела по отношению к той же оси.

Так, например, момент инерции однородного шара массы радиуса R относительно оси X, проходящей через его центр, равен:

$[J_x=frac{2}{5}mR^2 qquad (2)]$

Момент инерции материальной точки, имеющей массу , находящейся на расстоянии ${rho }_x$ от этой же оси равен:

$[J_x=m{{rho }_x}^2 qquad (3)]$

Приравнивая правые части выражений (2) и (3), выразим радиус инерции и для шара получим:

$[frac{2}{5}mR^2=m{{rho }_x}^2to {rho }_xapprox 0,632 R]$

Используя радиус инерции, можно используя формулу (1) найти момент инерции тела и наоборот.

Радиусом инерции сечения (плоской фигуры) ( ${{rm i}}_{{rm x}}$ ) относительно оси X, называют величину равную:

$[i_x=sqrt{frac{J_x}{S}} qquad (4)]$

Из выражения, определяющего радиус инерции сечения (4), следует, что он равен расстоянию от оси X до точки, в которой необходимо сосредоточить всю площадь рассматриваемого сечения (S), при этом момент инерции этой точки будет равен моменту инерции всего сечения.

Радиусы инерции, которые соответствуют главным осям, называют главными радиусами инерции. Их определяют при помощи выражений:

$[i_{max}=sqrt{frac{J_{max}}{S}};qquad i_{min}=sqrt{frac{J_{min}}{S}; } qquad (5)]$

Радиусы инерции измеряются в метрах в международной системе единиц (СИ).

Примеры решения задач

Источник

Осевые
моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения
Тело	Описание	Положение оси a	Момент инерции J_a
	Материальная точка массы m	На расстоянии r от точки, неподвижная
	Полый тонкостенный цилиндр или кольцо радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁	Ось цилиндра
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Тонкостенная сфера радиуса r и массы m	Ось проходит через центр сферы
	Шар радиуса r и массы m	Ось проходит через центр шара
	Конус радиуса r и массы m	Ось конуса
	Равнобедренный треугольник с высотой h, основанием a и массой m	Ось перпендикулярна плоскости треугольника и проходит через вершину
	Правильный треугольник со стороной a и массой m	Ось перпендикулярна плоскости треугольника и проходит через центр масс
	Квадрат со стороной a и массой m	Ось перпендикулярна плоскости квадрата и проходит через центр масс

Вывод
формул

Тонкостенный
цилиндр (кольцо, обруч)

Момент
инерции тела равен сумме моментов
инерции составляющих его частей. Разобъём
тонкостенный цилиндр на элементы с
массой dm
и моментами инерции dJ_i.
Тогда

Поскольку
все элементы тонкостенного цилиндра
находятся на одинаковом расстоянии от
оси вращения, формула (1) преобразуется
к виду

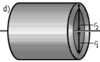
Толстостенный
цилиндр (кольцо, обруч)

Пусть
имеется однородное кольцо с внешним
радиусом R,
внутренним радиусом R₁,
толщиной h
и плотностью ρ. Разобьём его на тонкие
кольца толщиной dr.
Масса и момент инерции тонкого кольца
радиуса r
составит

Момент
инерции толстого кольца найдём как
интеграл

Поскольку
объём и масса кольца равны

получаем
окончательную формулу для момента
инерции кольца

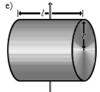
Однородный
диск (сплошной цилиндр)

Рассматривая
цилиндр (диск) как кольцо с нулевым
внутренним радиусом (R₁
= 0), получим формулу для момента инерции
цилиндра (диска):

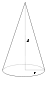
Сплошной
конус

Разобьём
конус на тонкие диски толщиной dh,
перепендикулярные оси конуса. Радиус
такого диска равен

где
R
– радиус основания конуса, H
– высота конуса, h
– расстояние от вершины конуса до диска.
Масса и момент инерции такого диска
составят

Интегрируя,
получим

Сплошной
однородный шар

Разобъём
шар на тонкие диски толщиной dh,
перпендикулярные оси вращения. Радиус
такого диска, расположенного на высоте
h
от центра сферы, найдём по формуле

Масса
и момент инерции такого диска составят

Момент
инерции сферы найдём интегрированием:

Тонкостенная
сфера

Для
вывода воспользуемся формулой момента
инерции однородного шара радиуса R:

Вычислим,
насколько изменится момент инерции
шара, если при неизменной плотности ρ
его радиус увеличится на бесконечно
малую величину dR.

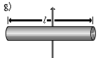
Тонкий
стержень (ось проходит через центр)

Разобъём
стержень на малые фрагменты длиной dr.
Масса и момент инерции такого фрагмента
равна

Интегрируя,
получим

Тонкий
стержень (ось проходит через конец)

При
перемещении оси вращения из середины
стержня на его конец, центр тяжести
стержня перемещается относительно оси
на расстояние l/2.
По теореме Штейнера новый момент инерции
будет равен

Соседние файлы в папке Экзамен 2 поток

Источник

Загрузить PDF

Радиус шара (обозначается как r или R) – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Как и в случае круга, радиус шара является важной величиной, которая необходима для нахождения диаметра шара, длины окружности, площади поверхности и/или объема. Но радиус шара можно найти и по данному значению диаметра, длины окружности и другой величины. Используйте формулу, в которую можно подставить данные значения.

1
Вычислите радиус по диаметру. Радиус равен половине диаметра, поэтому используйте формулу г = D/2. Эта такая же формула, которая используется при вычислении радиуса и диаметра круга.^[1]
- Например, дан шар с диаметром 16 см. Радиус этого шара: r = 16/2 = 8 см. Если диаметр равен 42 см, то радиус равен 21 см (42/2=21).
2
Вычислите радиус по длине окружности. Используйте формулу: r = C/2π. Так как длина окружности C = πD = 2πr, то разделите формулу для вычисления длины окружности на 2π и получите формулу для нахождения радиуса.^[2]
- Например, дан шар с длиной окружности 20 см. Радиус этого шара: r = 20/2π = 3,183 см.
- Такая же формула используется при вычислении радиуса и длины окружности круга.
3
Вычислите радиус по объему шара. Используйте формулу: r = ((V/π)(3/4))^1/3.^[3] Объем шара вычисляется по формуле V = (4/3)πr³. Обособив r на одной стороне уравнения, вы получите формулу ((V/π)(3/4))³ = г, то есть для вычисления радиуса объем шара делим на π, результат умножаем на 3/4, а полученный результат возводим в степень 1/3 (или извлекаем кубический корень).^[4]
- Например, дан шар с объемом 100 см³. Радиус этого шара вычисляется так:
  - ((V/π)(3/4))^1/3 = r
  - ((100/π)(3/4))^1/3 = r
  - ((31,83)(3/4))^1/3 = r
  - (23,87)^1/3 = r
  - 2,88 см = r
4
Вычислите радиус по площади поверхности. Используйте формулу: г = √(A/(4 π)). Площадь поверхности шара вычисляется по формуле А = 4πr². Обособив r на одной стороне уравнения, вы получите формулу √(A/(4π)) = r, то есть, чтобы вычислить радиус, нужно извлечь квадратный корень из площади поверхности, деленной на 4π. Вместо того чтобы извлекать корень, выражение (A/(4π)) можно возвести в степень 1/2.^[5]
- Например, дан шар с площадью поверхности 1200 см³. Радиус этого шара вычисляется так:
  - √(A/(4π)) = r
  - √(1200/(4π)) = r
  - √(300/(π)) = r
  - √(95,49) = r
  - 9,77 см = r
Реклама

1
Запомните основные величины, которые имеют отношение к вычислению радиуса шара. Радиус шара – это отрезок, который соединяет центр шара с любой точкой на его поверхности. Радиус шара можно вычислить по данным значениям диаметра, длины окружности, объема или площади поверхности.
- Диаметр (D) – это отрезок, который соединяет две точки на поверхности шара и проходит через его центр (то есть это наибольшее расстояние между противоположными точками, лежащими на поверхности шара). Диаметр равен удвоенному радиусу.
- Длина окружности (С) представляет собой длину окружности большого круга, то есть круга, который образует секущая плоскость, проходящая через центр шара.
- Объем (V) – это значение трехмерного пространства, занимаемого шаром.^[6]
- Площадь поверхности (А) – это значение двумерного (плоского) пространства, ограниченного поверхностью шара.
- Пи (π) – это постоянная, которая равна отношению длины окружности к ее диаметру. Первыми десятью цифрами этой постоянной являются 3,141592653, но зачастую число Пи округляется до 3,14.
2
Воспользуйтесь значениями данных величин, чтобы найти радиус. Радиус можно вычислить по данным значениям диаметра, длины окружности, объема и площади поверхности. Более того, указанные величины можно найти по данному значению радиуса. Чтобы вычислить радиус, просто преобразуйте формулы для нахождения указанных величин. Ниже приведены формулы (в которых присутствует радиус) для вычисления диаметра, длины окружности, объема и площади поверхности.
- D = 2г. Как и в случае круга, диаметр шара в два раза больше его радиуса.
- C = πD = 2πr. Как и в случае круга, длина окружности шара равна произведению π на диаметр шара. Так как диаметр вдвое больше радиуса, то длина окружности шара равна удвоенному произведению π на радиус шара.
- V = (4/3)πr³. Объем шара равен произведению 4/3 на π и на радиус в кубе.^[7]
- А = 4πr². Площадь поверхности шара равна учетверенному произведению π на радиус в квадрате. Так как площадь круга равна πr², то площадь поверхности шара в четыре раза больше площади круга, который образует секущая плоскость, проходящая через центр шара.
Реклама

1
Найдите координаты (х,у,z) центра шара. Радиус шара равен расстоянию между его центром и любой точкой, лежащей на поверхности шара. Если известны координаты центра шара и любой точки, лежащей на его поверхности, можно найти радиус шара по специальной формуле, вычислив расстояние между двумя точками. Сначала найдите координаты центра шара. Имейте в виду, что так как шар является трехмерной фигурой, то точка будет иметь три координаты (х,у,z), а не две (х,у).
- Рассмотрим пример. Дан шар с центром с координатами (4,-1,12). Воспользуйтесь этими координатами, чтобы найти радиус шара.
2
Найдите координаты точки, лежащей на поверхности шара. Теперь нужно найти координаты (х,у,z) любой точки, лежащей на поверхности шара. Так как все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара, для вычисления радиуса шара можно выбрать любую точку.
- В нашем примере допустим, что некоторая точка, лежащая на поверхности шара, имеет координаты (3,3,0). Вычислив расстояние между этой точкой и центром шара, вы найдете радиус.
3
Вычислите радиус по формуле d = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²). Узнав координаты центра шара и точки, лежащей на его поверхности, вы можете найти расстояние между ними, которое равно радиусу шара. Расстояние между двумя точками вычисляется по формуле d = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²), где d – расстояние между точками, (x₁,y₁,z₁) – координаты центра шара, (x₂,y₂,z₂) – координаты точки, лежащей на поверхности шара.
- В рассматриваемом примере вместо (x₁,y₁,z₁) подставьте (4,-1,12), а вместо (x₂,y₂,z₂) подставьте (3,3,0):
  - d = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²)
  - d = √((3 — 4)² + (3 — -1)² + (0 — 12)²)
  - d = √((-1)² + (4)² + (-12)²)
  - d = √(1 + 16 + 144)
  - d = √(161)
  - d = 12,69. Это искомый радиус шара.
4
Имейте в виду, что в общих случаях r = √((x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)²). Все точки, лежащие на поверхности шара, расположены на одинаковом расстоянии от центра шара. Если в формуле для нахождения расстояния между двумя точками «d» заменить на «r», получится формула для вычисления радиуса шара по известным координатам (x₁,y₁,z₁) центра шара и координатам (x₂,y₂,z₂) любой точки, лежащей на поверхности шара.
- Возведите обе стороны этого уравнения в квадрат, и получите r² = (x₂ — x₁)² + (y₂ — y₁)² + (z₂ — z₁)². Отметьте, что это уравнение соответствует уравнению сферы r² = x² + y² + z² с центром с координатами (0,0,0).
Реклама

Советы

Не забывайте про порядок выполнения математических операций. Если вы не помните этот порядок, а ваш калькулятор умеет работать с круглыми скобками, пользуйтесь ими.
В этой статье рассказывается о вычислении радиуса шара. Но если вы испытываете затруднения с изучением геометрии, лучше начать с вычисления величин, связанных с шаром, через известное значение радиуса.
π (Пи) – это буква греческого алфавита, которая обозначает постоянную, равную отношению диаметра круга к длине его окружности. Число Пи является иррациональным числом, которое не записывается как отношение действительных чисел. Существует множество приближений, например, отношение 333/106 позволит найти число Пи с точностью до четырех цифр после десятичной запятой. Как правило, пользуются приблизительным значением числа Пи, которое равно 3,14.

Об этой статье

Эту страницу просматривали 114 935 раз.

Была ли эта статья полезной?

Источник

Как найти радиус шара

2 методика:Вычисление радиуса по основным величинамВычисление радиуса по центру шара и точке на его поверхности

Радиус шара (r или R) – отрезок, соединяющий центр шара и любую точку на его поверхности. Значение радиуса используется для вычисления диаметра, длины окружности, площади поверхности и объема. Зная перечисленные величины, вы можете найти радиус шара.

Шаги

Метод 1 из 2: Вычисление радиуса по основным величинам

Определение основных величин

1
Радиус можно найти по известным значениям основных величин шара. К таким величинам относятся:
- Диаметр (D) (отрезок, соединяющей две точки на поверхности шара и проходящий через центр шара).
- Длина окружности (C) (длина окружности большого круга – круга, образуемого секущей плоскостью, проходящей через центр шара).
- Объем (V) (значение трехмерного пространства, занимаемого шаром).
- Площадь поверхности (A) (значение двумерного пространства, ограниченного поверхностью шара).
- Число Пи (π) (математическая постоянная, равная отношению длины окружности к ее диаметру; это число применяется при вычислении всех основных величин и обычно округляется до 3,14).
2
Ниже приведены формулы для вычисления основных величин; каждая формула включает радиус. Запомните: обособив радиус на одной стороне формулы, вы сможете найти его по известным значениям основных величин.
- D = 2r. Диаметр вдвое больше радиуса.
- С = πD = 2πr. Длина окружности равна произведению π на ее диаметр. Так как диаметр в два раза больше радиуса, то длина окружности равна произведению π на двойку и на радиус этой окружности.
- V = (4/3) πr3. Объем шара равен произведению 4/3 на радиус в кубе и на π.
- A = 4πr2. Площадь поверхности шара равна произведению квадрата его радиуса на π и на 4.

Вычисление радиуса по формулам

1
Если вам дан диаметр, разделите его пополам (на 2) и получите радиус. Так как D = 2r, то r =D/2.
- Например, если диаметр шара равен 16 см, то радиус шара равен 16/2 = 8 см.
2
Если вам дана длина окружности, разделите ее на 2π и получите радиус. Так как C = 2πr, то r = C/2π.
- Например, если длина окружности шара равна 20 м, то радиус шара: 20/2π = 3,183 м.
3
Если вам дан объем шара, то радиус шара вычисляется по формуле: r = ((V/π)(3/4))1/3. То есть объем делится на π, результат умножается на 3/4 и полученный результат возводится в степень 1/3 (или извлекается кубический корень).
- Например, если объем шара равен 100 см3, то радиус шара вычисляется следующим образом:
  - ((V/π)(3/4))1/3 = r
  - ((100/π)(3/4))1/3 = r
  - ((31,83)(3/4))1/3 = r
  - (23,87)1/3 = r
  - r = 2,88 см
4
Если вам дана площадь поверхности шара, разделите ее на 4π и из полученного значения извлеките квадратный корень, чтобы найти радиус. Так как А = 4πr2, то r = √(A/4π).
- Например, площадь поверхности шара равна 1200 см2. Радиус шара вычисляется следующим образом:
  - √ (A / (4π)) = г
  - √ (1200 / (4π)) = г
  - √ (300 / (π)) = г
  - √ (95,49) = г
  - r = 9,77 см

Метод 2 из 2: Вычисление радиуса по центру шара и точке на его поверхности

1
Найдите координаты (х, у, z) центральной точки шара. Это точка, равноудаленная от любой точки на поверхности шара. Зная координаты центра шара и любой точки на его поверхности вы можете найти расстояние между этими точками, которое и равно радиусу шара. Обратите внимание, что точки шара имеют трехмерные координаты (х, у, z).
- Пример. Дан шар, центр которого имеет координаты (4, -1, 12).
2
Найдите координаты (х, у, z) любой точки на поверхности шара.
- Пример. Точка на поверхности шара имеет координаты (3, 3, 0).
3
Радиус шара вычисляется по формуле d = √((x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2), где d – расстояние между точками, (x1,y1,z1) – координаты центральной точки шара, (x2,y2,z2) – координаты точки на поверхности шара.
- В нашем примере вместо (x1,y1,z1) подставьте (4, -1, 12), а вместо (x2,y2,z2) — (3, 3, 0).
  - d = √((x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2)
  - d = √((3 — 4)2 + (3 — -1)2 + (0 — 12)2)
  - d = √((-1)2 + (4)2 + (-12)2)
  - d = √(1 + 16 + 144)
  - d = √(161)
  - d = 12,69. Это радиус шара.
4
В общих случаях r = √((x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2). Каждая точка, лежащая на поверхности шара, равноудалена от его центра. Если мы возьмем формулу для вычисления расстояния между двумя точками и заменим в ней d на r, то мы получим формулу для вычисления радиуса шара.
- Возведем в квадрат обе части формулы и получим r2 = (x2 — x1)2 + (y2 — y1)2 + (z2 — z1)2. Обратите внимание, что эта формула напоминает уравнение сферы r2 = x2 + y2 + z2 при условии, что центр сферы имеет координаты (0,0,0).

Советы

Соблюдайте определенный порядок выполнения математических операций – начинайте с выражения в скобках, затем возводите в степень/извлекайте корень, затем умножайте/делите, а затем суммируйте/вычитайте.
Если вы сталкиваетесь с объемными фигурами впервые, лучше начать их изучение не с вычисления радиуса, а с нахождения основных величин (см. выше в этой статье).
π – это математическая константа, равная отношение длины окружности к ее диаметру. Это иррациональное число, которое не может быть записано в виде отношения действительных чисел. В большинстве случаев можно использовать приблизительное значение 3,14.

Источник

В данной публикации мы рассмотрим, как можно вычислить радиус шара и разберем примеры решения задач для закрепления материала.