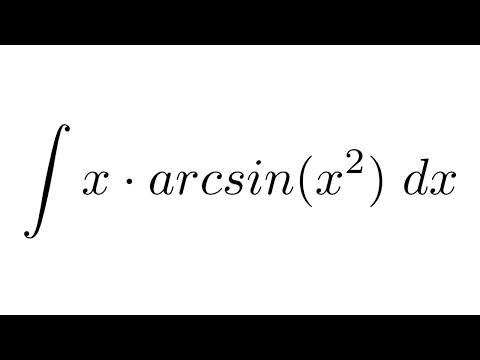Интеграл от арксинуса как найти - Исправление недочетов и поиск решений вместе с Examum.ru

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Интеграл от арксинуса

Интеграл от арксинуса равен сумме произведения переменной интегрирования на этот арксинус и корню квадратному из разности единицы и переменной интегрирования в квадрате плюс константа интегрирования

$[ int{arcsin xdx}=xarcsin x+sqrt{1-{{x}^{2}}}+C ]$

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник

Интеграл от арксинуса

(
int arcsin x d x=x arcsin x+sqrt{1-x^{2}}+C
)

Примеры решения задач

ПРИМЕР 1

Задание

Доказать, что (
int arcsin x d x=x arcsin x+sqrt{1-x^{2}}+C
)

Решение

Для доказательства применим формулу интегрирования по частям:

(
int arcsin x d x|u=underset{d x}{arcsin x}, d v=d x|=x arcsin x-int frac{x d x}{sqrt{1-x^{2}}}left|begin{array}{l}{1-x^{2}=t^{2}} \ {-2 x d x=2 t d t} \ {x d x=-t d t}end{array}right|=
)

(
=x arcsin x-int frac{-t d t}{sqrt{t^{2}}}=x arcsin x+int d t=x arcsin x+t+C=x arcsin x+sqrt{1-x^{2}}+C
)

Что и требовалось доказать.

ПРИМЕР 2

Задание

Найти интеграл (
int arcsin 4 x d x
)

Решение

Сведем данный интеграл к формуле, предварительно сделав в нем замену переменной:

(
int arcsin 4 x d xleft|begin{array}{l}{4 x=t} \ {4 d x=d t} \ {d x=frac{d t}{4}}end{array}right|=int arcsin t cdot frac{d t}{4}=frac{1}{4} int arcsin t d t=
)

(
=frac{1}{4}left(t arcsin t+sqrt{1-t^{2}}right)+C=frac{1}{4}left(4 x arcsin 4 x+sqrt{1-(4 x)^{2}}right)+C=
)

(
=x arcsin 4 x+frac{sqrt{1-16 x^{2}}}{4}+C
)

Ответ

(
int arcsin 4 x d x=x arcsin 4 x+frac{sqrt{1-16 x^{2}}}{4}+C
)

Источник

{2}}}{4}+C
)

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Интеграл степенной функции Интеграл от экспоненты Интеграл от корня Интеграл от дроби

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику
конфиденциальности

Подпишись на рассылку,
чтобы не пропустить информацию об акциях

Интеграл обратного синуса — Примеры, Интеграл арксинуса
- Что такое интеграл обратного от греха?
  - Sin Формула обратного интегрирования
- Интеграл Sin, обратный доказательству с использованием интегрирования по частям
- Доказательство обратного интеграла греха методом подстановки
- Определенный интеграл обратного синуса
- Часто задаваемые вопросы по интегралу обратного синуса
  - Что такое интеграл обратного синуса в исчислении?
  - Как найти обратный интеграл от греха?
  - Что такое интеграл от греха, обратный целому квадрату?
  - Равна ли производная обратного синуса интегралу от арксинуса?
  - Чему равен интеграл от Sin, обратный от 0 до 1?

Интеграл обратного синуса — Примеры, Интеграл арксинуса

Интеграл обратного синуса можно вычислить, используя различные формулы интегрирования. Интеграция есть обратный процесс дифференциации. Интеграл есть не что иное, как антипроизводная. Обратный интеграл sin записывается как ∫sin ^-1 x dx = x sin ^-1 x + √(1 — x ² ) + C, где ∫ — знак интегрирования, dx обозначает, что интегрирование sin обратная по отношению к x, а C — постоянная интегрирования.

Давайте изучим процесс нахождения интеграла от sin, обратного x, используя различные методы, и найдем определенный интеграл от sin, обратный.

1.	Что такое интеграл обратного от греха?
2.	Интеграл Sin, обратный доказательству с использованием интегрирования по частям
3.	Доказательство обратного интеграла греха методом подстановки
4.	Определенный интеграл обратного синуса
5.	Часто задаваемые вопросы по интегралу обратного синуса

Что такое интеграл обратного от греха?

Интеграл, обратный sin, равен x sin ^-1 x + √(1 — x ² ) + C, где C — постоянная интегрирования. Математически обратный интеграл sin записывается как ∫arcsin x dx = ∫sin ^-1 x dx = x sin ^-1 x + √(1 — x ² ) + C. Интеграл от синуса, обратного х, также называют первообразной синуса, обратного х. Интегрирование обратного sin может быть выполнено с использованием различных методов, таких как интегрирование по частям и метод подстановки с последующим интегрированием по частям.

Sin Формула обратного интегрирования

Формула для интеграла от arcsin дается выражением ∫sin ^-1 x dx = x sin ^-1 x + √(1 — x ² ) + C, где C – постоянная интегрирования.

Интеграл Sin, обратный доказательству с использованием интегрирования по частям

Теперь, когда мы знаем, что обратное интегрирование sin равно ∫sin ^-1 x dx = x sin ^-1 x + √(1 — x ² ) + C, мы докажем это, используя интегрирование по формуле части. Мы будем использовать следующие формулы и факты, чтобы доказать обратное интегрирование греха.

Формула интегрирования по частям: ∫f(x)g(x)dx = f(x) ∫g(x)dx — ∫[d(f(x))/dx × ∫g(x) dx ] дх.
Обратите внимание, что sin ^-1 x может быть записано как sin ^-1 x = sin ^-1 x.1.
Имеем f(x) = sin ^-1 x, g(x) = 1
d(sin ^-1 x)/dx = 1/√(1 — x ² )

Используя эти формулы и факты, мы имеем

∫sin ^-1 x dx = ∫sin ^-1 x,1 dx

= sin ^-1 x 05 -1dx — ∫9[dx 1 x)/dx × ∫1 dx] dx

= x sin ^-1 x — ∫[1/√(1 — x ² ) × x] dx

= x sin ^-1 x — ∫x/√(1 — x ² ) dx

= x sin ^-1 x + (1/2) ∫-2x/√(1 — x ² ) dx [Умножение и деление на 2]

= x sin ^-1 x + (1/2) ∫(- 2x)(1 — x ² ) ^-1/2 dx

= x sin ^-1 x + (1/2) [(1 — x ² ) ^{-1/2 + 1} / (-1/2 + 1)] + C {Используя формулу ∫[f(x)] ⁿ f'(x) dx = [f(x)] ^{n + 1} /(n + 1) + С}

= x sin ^-1 x + (1/2) [(1 — x ² ) ^1/2 / (1/2)] + C

= x sin ^-1 x + (1 — x ²

) ^1/2 + C

= x sin ^-1 x + √(1 — x ² ) + C

Доказательство обратного интеграла греха методом подстановки

Мы доказали интеграл от синуса методом интегрирования по частям. Теперь мы докажем обратный интеграл sin методом подстановки интегрирования, а затем методом интегрирования по частям. Чтобы определить интегрирование sin, обратное x, мы заменим x на sin θ. Для определения обратного интеграла от sin будем использовать следующие формулы:

Предположим, что x = sinθ ⇒ sin ^-1 x = sin ^-1 (sinθ) = θ
dx = cosθ dθ
Интегрирование по частям: ∫f(x)g(x)dx = f(x) ∫g(x)dx — ∫[d(f(x))/dx × ∫g(x) dx] dx
sin ² θ + cos ² θ = 1 ⇒ cosθ = √(1 — sin ² θ)

Используя приведенные выше формулы, мы имеем

∫Sin ^-1 x dx = ∫sin ^-1 (sinθ) cosθ dθ

= ∫θ cosθ dθ

= θ ∫cosθ dθ [d (d (d (d (d ( θ)/dθ × ∫cosθ dθ] {Путем замены f(θ) = θ и g(θ) = cosθ в формуле интегрирования по частям}

= θ sinθ — ∫1.sinθ dθ

= θ sinθ — ∫sinθ dθ

= θ sinθ + cosθ + c

= θ sinθ + √ (1 — sin ² θ) + c

= x sin ^-1 x + √(1 — x ² ) + C

Следовательно, мы доказали, что интеграл от arcsin равен x sin ^-1 x + √(1 — x ² ) + C с использованием метода подстановки с последующим интегрированием по частям.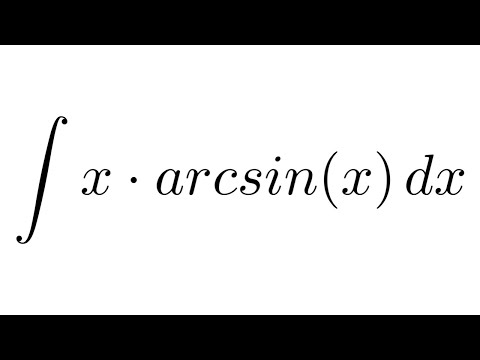

Определенный интеграл обратного синуса

Мы знаем, что интеграл, обратный греху, равен ∫sin 92}+C)\&=dfrac{pi}{2}+0+C-0-1-C\&=dfrac{pi}{2}-1 end{align})

Следовательно, определенный интеграл от sin, обратный x, с пределами от 0 до 1 определяется как π/2 — 1.

Важные замечания об интеграле от sin, обратному угловой синус.

Интеграл, обратный sin, равен x sin ^-1 x + √(1 — x ² ) + C

Производная от sin, обратная 1/√(1 — x ² ), -1 < х < 1

Связанные темы по интегралу обратного синуса

Производное обратного синуса

Интеграл греха x

Интеграция

Часто задаваемые вопросы по интегралу обратного синуса

Что такое интеграл обратного синуса в исчислении?

Интеграл от sin, обратный , равен ∫sin ^-1 x dx = x sin ^-1 x + √(1 — x ² ) + C, где C — постоянная интегрирования.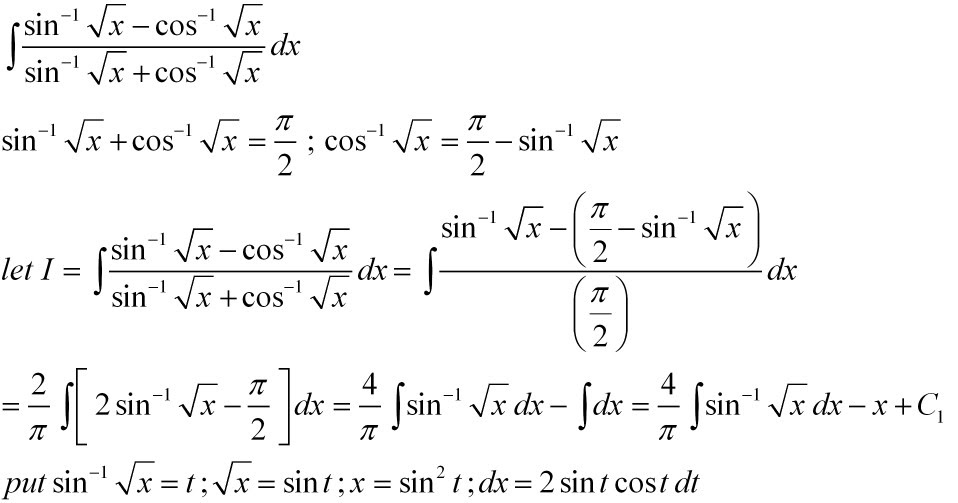

Как найти обратный интеграл от греха?

Интегрирование обратного sin может быть выполнено с использованием различных методов, таких как интегрирование по частям и метод подстановки с последующим интегрированием по частям.

Что такое интеграл от греха, обратный целому квадрату?

Интеграл Sin, обратный целому квадрату, определяется выражением ∫(sin ^-1 x) ² dx = (sin ^-1 x) ² + 2(sin ^-1 x)√(1 — x ² ) — 2x + C, где C — постоянная интегрирования.

Равна ли производная обратного синуса интегралу от арксинуса?

Нет, производная обратного синуса не равна интегралу арксинуса. Производная обратного sin дается выражением d(sin ^-1 x)/dx = 1/√(1 — x ² ), тогда как интеграл обратного sin равен ∫sin ^-1 x dx = x sin ^-1 x + √(1 — x ² ) + C

Чему равен интеграл от Sin, обратный от 0 до 1?

Определенный интеграл от sin, обратный x, в пределах от 0 до 1 равен π/2 — 1.

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

x^{2}-x-6=0
-x+3gt 2x+1
линия:(1,:2),:(3,:1)
f(x)=x^3
доказывать:tan^2(x)-sin^2(x)=tan^2(x)sin^2(x)
frac{d}{dx}(frac{3x+9}{2-x})
(sin^2(theta))’
sin(120)
lim _{xto 0}(xln (x))
int e^xcos (x)dx
int_{0}^{pi}sin(x)dx
sum_{n=0}^{infty}frac{3}{2^n}
Показать больше

Описание

Поэтапное решение задач по алгебре, тригонометрии и исчислению

step-by-step

int arcsinleft(xright)dx

Блог-сообщения, имеющие отношение к Symbolab

Practice, practice, practice

Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing…

Введите Задачу

Сохранить в блокнот!

Войти

Источник