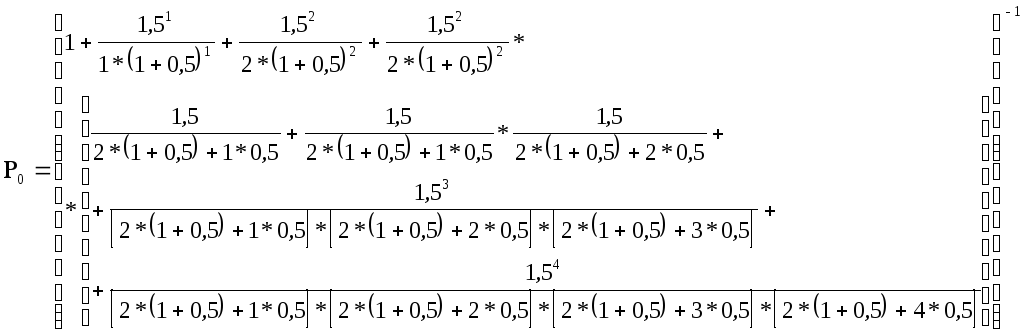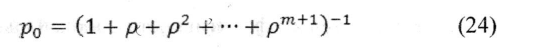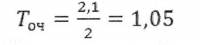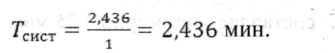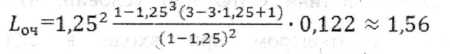Интенсивность потока заявок как найти - Исправление недочетов и поиск решений вместе с Examum.ru

1.1.
Параметры
входящего потока заявок.

1.2.
Параметры структуры СМО:

число каналов
обслуживания — m;
число мест в
очереди — n;
средняя длительность
обслуживания заявки в канале —
;
интенсивность
потока обслуживания
.

2. Характеристики
СМО:

2.1.
Интенсивность выходного потока заявок
.

,
где

— интенсивность
потока обслуженных заявок;

— интенсивность
потока потерянных заявок;

(потери происходят
из-за ухода из СМО «нетерпеливых» заявок
и из-за отказов системы принять заявку
при заполненной очереди).

2.2.
Вероятность обслуживания.

,
где
— интенсивность входящего потока заявок.

2.3.
Вероятность потери заявок.

2.4.
Среднее время ожидания заявок в очереди
.

2.5.
Среднее время пребывания заявки в
системе (время реакции системы)
.

,
где
— среднее время обслуживания.

2.6.
Средняя длина очереди
.

2.7.
Среднее число занятых каналов обслуживания
.

2.8.
Среднее число заявок в системе.

Для СМО без
«выталкивания» заявок и ухода
«нетерпеливых» заявок справедливо
.
Критерий
эффективности СМО (Е) — некоторая функция
-показатель эффективности системы.

В общем виде
,
где— штраф за отказ системы принятьi-ю
заявку;

—
штраф за «выталкивание» i
— ой заявки;

— штраф за уход из
системы i
— ой заявки при превышении

допустимого
времени нахождения заявки в СМО;

M
— количество типов заявок.

Таким образом
критерий эффективности отражает потери
в СМО, вызванные отказами системы принять
заявку, уходом «нетерпеливых» заявок
и «выталкиванием» заявок, имеющих более
низкий приоритет, когда приходит заявка
с высшим приоритетом.

Пусть задано :

k
= 3;
= 6;= 15;= 9;= 0;

B
= 0,5; n
= 4; m
= 2;
= 0,1;= 25;

= 3;
= 2;= 10,

то есть имеется
двухпроцессорная система; число мест
в очереди — 4.

I Формулируем задачу в терминах смо:

Так как рассматриваемая
СМО — бесприоритетная, будем рассматривать
суммарный поток заявок с интенсивностью
с^-1.
Поток обслуживания
для одного канала имеет интенсивность
с^-1.
Находим приведенную
эффективность входного потока для
одного канала :
.
Находим интенсивность
потока уходов :
с^-1.
Находим приведенные
интенсивности потоков уходящих заявок
:

— уход из очереди;

— из каналов
обслуживания;

Рассматриваем возможные состояния системы :

z₀
— в системе нет заявок;
z₁
— в системе одна заявка, очередь
отсутствует;
z₂
— в системе 2 заявки, очередь отсутствует;
z₃
— 3 заявки : 2 заявки на обслуживании, 1 в
очереди;
z₄
— 4 заявки : 2 заявки на обслуживании, 2 в
очереди;
z₅
— 5 заявок : 3 заявки в очереди;
z₆
— 6 заявок : в очереди 4 заявки. Очередь
заполнена.

Вероятность
нахождения системы в i
— ом состоянии находим по формуле [2] :
;

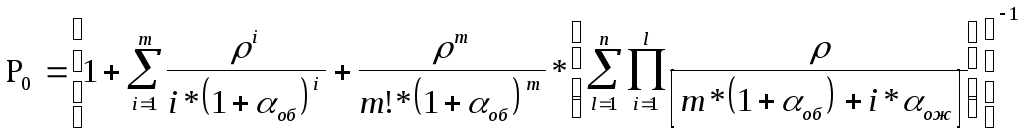
i=1,2,…,m;

l=1,2,…,n,
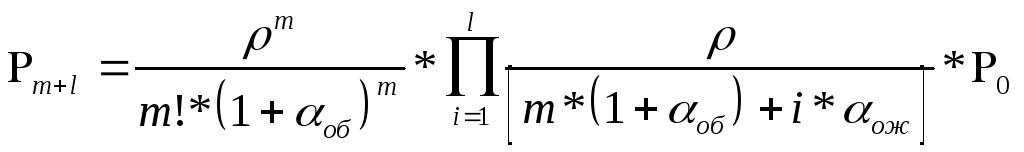
где l
— длина очереди.

Вероятность
состояния z₀
равна

Далее находим

P₀
= 0,3534 P₃
= 0,0757

P₁
= 0,3534 P₄
= 0,0284

P₂
= 0,1767 P₅
= 0,0095

P₆
= 0,0029.

(Для состояний z₀
— z₂
очередь отсутствует.)

Вычисляем характеристики смо :

Среднее число
занятых каналов

(в состоянии P₀
не занят ни один канал;

в состоянии P₁
занят 1 канал;

в состояниях P₂
— P₆
заняты 2 канала).

Средняя длина
очереди
.
Вероятность
отказов
.
Вероятность ухода
заявок из очереди
.
Вероятность ухода
заявки из системы во время обслуживания
.
Суммарная
вероятность ухода «нетерпеливых»
заявок
.
Вероятность потерь
заявок
.
Вероятность
обслуживания заявки
.

Соседние файлы в папке Обработка данных

Источник

Теория массового обслуживания (СМО)

Теория массового обслуживания исследует на основе теорий вероятностей математические методы количественной оценки процессов массового обслуживания. Общей особенностью всех задач, связанных с массовым обслуживанием, является случайный характер исследуемых явлений.

Сервис представлен тремя онлайн-калькуляторами:

Одноканальные СМО.
Многоканальные СМО.
Замкнутые системы массового обслуживания СМО.

Для решения задач на тему Теория массового обслуживания необходимо определиться с типом модели СМО: одноканальные (см. примеры задач для одноканальных СМО) или многоканальные (см. примеры задач для многоканальных СМО). В многоканальных СМО количество устройств обслуживания n (количество рабочих, кассиров, бригад, моек и т.п.) больше одного. Обычно интенсивность потока заявок λ задана явно. Интенсивность потока обслуживания μ может задаваться в виде времени обслуживания t_обс.
В сервисе необходимо ввести либо параметр μ, либо t_обс (только одно из двух).

Выбор СМО зависит как от числа каналов n, так и от допустимой длины очереди m. По указанным признакам различается ряд типов СО, перечисленных в таблице.

№ п/п	Параметры СО	Тип СО
n	m
1	1	0	Одноканальная, без очереди
2	n > 1	0	Многоканальная, без очереди
3	1	1 < m <∞	Одноканальная, с ограниченной очередью
4	n > 1	1 < m<∞	Многоканальная, с ограниченной очередью
5	1	m = ∞	Одноканальная, с неограниченной очередью
6	n > 1	m = ∞	Многоканальная, с неограниченной очередью

По числу обслуживающих каналов различают одноканальные и многоканальные СО.

В зависимости от целочисленного значения m используются следующие названия в классификации типов СО:

m = 0 – без очереди;
m > 0 – с очередью.

Если число мест в очереди m является конечным, то в СО могут происходить отказы в предоставлении обслуживания некоторым заявкам. В связи с этим СО указанного типа называются системами с отказами. Отклоняются от обслуживания те заявки, в момент прихода которых все места в очереди случайно оказались занятыми, или, если m =0, все каналы оказались занятыми. Считается, что заявка, получившая отказ в обслуживании, навсегда теряется для СО. Таким образом, пропускная способность СО этого типа всегда меньше 100%.

Если m не ограничено, что иногда условно записывают как m = ∞ , то соответствующая СО называется системой с ожиданием. В СО данного типа пришедшая заявка при отсутствии возможности немедленного обслуживания ожидает обслуживания, какой бы длинной ни были очередь и продолжительность времени ожидания.

Все СМО делятся на СМО с отказами (параметр m не используется), СМО с ограниченной длиной очереди и СМО с неограниченной очередью. Параметр m (длина очереди) используется для последних двух СМО. При этом в СМО с неограниченной очередью можно указывать любое значение m. Например, m = 3. Тогда будут рассчитаны вероятности нахождения в очереди 1,2,3 заявки.

Временные параметры рассчитываются в часах или в минутах, в зависимости от заданного параметра λ.

Полученное решение сохраняется в файле Word. Для редактирования формул можно использовать редактор формул Microsoft Equation.

Перейти к онлайн решению своей задачи

Решение
Видео решение

Интернет-провайдер в небольшом городе имеет 5 выделенных каналов обслуживания. В среднем на обслуживание одного клиента уходит 25 минут. В систему в среднем поступает 6 заказов в час. Если свободных каналов нет, следует отказ. Определить характеристики обслуживания: вероятность отказа, среднее число занятых обслуживанием линий связи, абсолютную и относительную пропускные способности, вероятность обслуживания. Найти число выделенных каналов, при котором относительная пропускная способность системы будет не менее 0,95. Считать, что потоки заявок и обслуживаний простейшие.

Формулы для расчета параметров простейших СМО

, , , a = , b = , γ =

Показатели эффективности системы	Чистая СМО с отказами (n, a)	СМО с ограничением на время пребывания в очереди (n, a,b)	СМО с ограничением на длину очереди (n, a,m)	Чистая СМО с ожиданием (n, a), γ < 1
1	2	3	4	5
Вероятность того, что все каналы свободны	р₀ =	р₀=	p₀=	р₀ =
Вероятность того, что занято k каналов 0 ≤ k≤ n	Р_k = р₀	Р_k= р₀	р_k= р₀	Р_k = р₀
Вероятность того, что заняты все `n` каналов, `s` заявок в очереди	—	р_n+s = р_n,	р_n_+s= γ^s× р_n; 1 ≤ s ≤ `m`.	р_n+_s=γ^s× р_n
Вероятность отказа	р_отк = р_n	р_отк =	р_отк = р_n+m	р_отк = 0
Вероятность полной загрузки системы	р_n.з = р_n	р_n.з =	р_n.з = р_n	р_n_.з =
Вероятность обслуживания, относительная пропускная способность системы	р_обс = = 1- р_n=	р_обс = = 1 — р_отк =	р_обс = = = 1 — р_n+m =	р_обс = = 1
Абсолютная пропускная способность системы	`l_b = l·р_обс`	`l_b = l·р_обс = l — n·r`	l_b = lр_обс = m × n₃	l_b = l
Вероятность занятости канала	р_зк = k_з =	р_зк = k_з =	р_зк = k_з =	р_зк = k_з =
Среднее число свободных каналов	n₀ =	n₀ =	n₀ =	n₀ =
Вероятность простоя канала p_п.к, коэффициент простоя оборудования к_n	р_n.к = k_n =	р_n.к = k_n =	р_n.к = k_n =	р_n.к = k_n =
1	2	3	4	5
Среднее число заявок в очереди	—	r =	r =	r = р_n
Вероятность наличия очереди	—	р_н.о =	р_н.о = р_n	р_н_.о =p_n
Среднее время наличия очереди	—	—	=	=
Среднее время пребывания заявки в очереди	—	=	=	=
Среднее время пребывания заявки в системе	=	= , `l = n₃ + r`	= , `l = n₃ + r`	= , `l = n₃ + r`
Среднее время занятости канала (любого)	=		= +	=
Среднее время простоя канала
Среднее время полной загрузки системы		—
Среднее время неполной загрузки системы		–

Источник

СМО с ожиданием (очередью): определение и формулы

В качестве показателей эффективности СМО с ожиданием, кроме уже известных показателей — абсолютной и относительной пропускной способности, вероятности отказа $P_{text{otk}}$ , среднего числа занятых каналов к (для многоканальной системы) будем рассматривать также следующие:

1) $L_{text{sist.}}$ — среднее число заявок в системе;

2) $T_{text{sist.}}$ — среднее время пребывания заявки в системе;

3) $L_{text{och.}}$ — среднее число заявок в очереди (длина очереди);

4) $T_{text{och.}}$ — среднее время пребывания заявки в очереди;

5) $P_{text{zan.}}$ — вероятность того, что канал занят (степень загрузки канала).

Одноканальная система с неограниченной очередью

На практике часто встречаются одноканальные СМО с неограниченной очередью (например, телефон-автомат с одной будкой). Рассмотрим задачу.

Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность lambda , а поток обслуживании — интенсивность . Необходимо найти предельные вероятности состояний и показатели эффективности СМО.

Система может находиться в одном из состояний S_0,S_1,S_2,ldots,S_k , по числу заявок, находящихся в СМО: S_0 — канал свободен; S_1 — канал занят (обслуживает заявку), очереди нет; S_2 — канал занят, одна заявка стоит в очереди; — канал занят, (k-1) заявок стоят в очереди и т.д.

Граф состояний СМО представлен на рис. 8.

Граф состояний одноканальной СМО с неограниченной очередью

Это процесс гибели и размножения, но с бесконечным числом состояний, в котором интенсивность потока заявок равна lambda , а интенсивность потока обслуживании .

Прежде чем записать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время ttoinfty , очередь может неограниченно возрастать. Доказано, что если rho<1 , т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если rhogeqslant1 , очередь растет до бесконечности.

Для определения предельных вероятностей состояний воспользуемся формулами (16), (17) для процесса гибели и размножения (здесь мы допускаем известную нестрогость, так как ранее эти формулы были получены для случая конечного числа состояний системы). Получим:

$p_0=left[1+ frac{lambda}{mu}+ left(frac{lambda}{mu}right)^{2}+ldots+ left(frac{lambda}{mu}right)^{k}+ldotsright]^{-1}= left(1+rho+rho^2+ldots+rho^k+ldotsright)^{-1}.$

(32)

Так как предельные вероятности существуют лишь при rho<1 , то геометрический ряд со знаменателем rho<1 , записанный в скобках в формуле (32), сходится к сумме, равной $frac{1}{1-rho}$ . Поэтому

p_0=1-rho,

(33}

и с учетом соотношений (17)

p_1=rhocdot p_0,quad p_2=rho^2cdot p_0,quadldots,quad p_k=rho^kcdot p_0,quadldots

найдем предельные вероятности других состояний

p_1=rho(1-rho),quad p_2=rho^2(1-rho),quadldots,quad p_k=rho^k(1-rho),quad ldots

(34)

Предельные вероятности p_0,p_1,p_2,ldots,p_k,ldots образуют убывающую геометрическую профессию со знаменателем rho<1 , следовательно, вероятность p_0 — наибольшая. Это означает, что если СМО справляется с потоком заявок (при rho<1 ), то наиболее вероятным будет отсутствие заявок в системе.

Среднее число заявок в системе $L_{text{sist.}}$ определим по формуле математического ожидания, которая с учетом (34) примет вид

$L_{text{sist.}}= sum_{k=1}^{infty}kp_k=(1-rho)sum_{k=1}^{infty}krho^k$

(35)

(суммирование от 1 до infty , так как нулевой член 0cdot p_0=0 ).

Можно показать, что формула (35) преобразуется (при rho<1 ) к виду

$L_{text{sist.}}=frac{rho}{1-rho},.$

(36)

Найдем среднее число заявок в очереди $L_{text{och.}}$ . Очевидно, что

$L_{text{och.}}= L_{text{sist.}}- L_{text{ob.}},$

(37)

где $L_{text{ob.}}$ — среднее число заявок, находящихся под обслуживанием.

Среднее число заявок под обслуживанием определим по формуле математического ожидания числа заявок под обслуживанием, принимающего значения 0 (если канал свободен) либо 1 (если канал занят):

$L_{text{ob.}}=0cdot p_0+1cdot (1-p_0),$

т.е. среднее число заявок под обслуживанием равно вероятности того, что канал занят:

$L_{text{ob.}}=P_{text{zan.}}=1-p_0.$

(38)

В силу (33)

$L_{text{ob.}}=P_{text{zan.}}=rho.$

(39)

Теперь по формуле (37) с учетом (36) и (39)

$L_{text{och.}}=frac{rho^2}{1-rho},.$

(40)

Доказано, что при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равна среднему числу заявок в системе (в очереди), деленному на интенсивность потока заявок, т.е.

$T_{text{sist.}}=frac{1}{lambda}cdot L_{text{sist.}} ,$

(41)

$T_{text{och.}}=frac{1}{lambda}cdot L_{text{och.}}.$

(42)

формулы (41) и (42) называются формулами Литтла. Они вытекают из того, что в предельном, стационарном режиме среднее число заявок, прибывающих в систему, равно среднему числу заявок, покидающих ее: оба потока заявок имеют одну и ту же интенсивность lambda .

На основании формул (41) и (42) с учетом (36) и (40) среднее время пребывания заявки в системе определится по формуле:

$T_{text{sist.}}=frac{rho}{lambda(1-rho)},,$

(43)

а среднее время пребывания заявки в очереди —

$T_{text{och.}}=frac{rho^2}{lambda(1-rho)},.$

(44)

Пример 8. В порту имеется один причал для разгрузки судов. Интенсивность потока судов равна 0,4 (судов в сутки). Среднее время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.

Решение. Имеем $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}=0,!4cdot2=0,!8$ . Так как rho=0,!8<1 , то очередь на разгрузку не может бесконечно возрастать и предельные вероятности существуют. Найдем их.

Вероятность того, что причал свободен, по (33) p_0=1-0,!8=0,!2 , а вероятность того, что он занят, $P_{text{zan.}}=1-0,!2=0,!8$ . По формуле (34) вероятности того, что у причала находятся 1, 2, 3 судна (т.е. ожидают разгрузки 0, 1, 2 судна), равны

p_1=0,!8(1-0,!8)=0,!16;quad p_2=0,!8^2(1-0,!8)=0,!128;quad p_3=0,!8^3(1-0,!8)=0,!1024.

Вероятность того, что ожидают разгрузку не более чем 2 судна, равна

P=p_1+p_2+p_3=0,!16+0,!128+0,!1024=0,!3904.

По формуле (40) среднее число судов, ожидающих разгрузки, $L_{text{och.}}=frac{0,!8^2}{1-0,!8}=3,!2$ среднее время ожидания разгрузки по формуле (42) $T_{text{och.}}=frac{3,!2}{0,!8}=4$ (сутки).

По формуле (36) среднее число судов, находящихся у причала, $L_{text{sist.}}=frac{0,!8}{1-0,!8}=4$ (сутки) (или проще по (37) $L_{text{sist.}}=3,!2+0,!8=4$ (сутки), а среднее время пребывания судна у причала по формуле (41) $T_{text{sist.}}=frac{4}{0,!8}=5$ (сутки).

Очевидно, что эффективность разгрузки судов невысокая. Для ее повышения необходимо уменьшение среднего времени разгрузки судна $overline{t}_{text{ob.}}$ либо увеличение числа причалов.

Многоканальная СМО с неограниченной очередью

Рассмотрим задачу. Имеется n-канальная СМО с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность lambda , а поток обслуживании — интенсивность . Необходимо найти предельные вероятности состояний СМО и показатели ее эффективности.

Система может находиться в одном из состояний S_0,S_1,S_2,ldots,S_k,ldots,S_n,ldots нумеруемых по числу заявок, находящихся в СМО: S_0 — в системе нет заявок (все каналы свободны); S_1 — занят один канал, остальные свободны; S_2 — заняты два канала, остальные свободны; ldots,S_k — занято каналов, остальные свободны; ldots,S_n — заняты все каналов (очереди нет); $S_{n+1}$ — заняты все каналов, в очереди одна заявка; $ldots,S_{n+r}$ — заняты все каналов, заявок стоит в очереди, и т.д.

Граф состояний системы показан на рис. 9. Обратим внимание на то, что в отличие от предыдущей СМО, интенсивность потока обслуживании (переводящего систему из одного состояния в другое справа налево) не остается постоянной, а по мере увеличения числа заявок в СМО от 0 до увеличивается от величины до nmu , так как соответственно увеличивается число каналов обслуживания. При числе заявок в СМО большем, чем , интенсивность потока обслуживании сохраняется равной nmu .

Граф состояний многоканальной СМО с неограниченной очередью

Можно показать, что при $frac{rho}{n}<1$ предельные вероятности существуют. Если $frac{rho}{n}geqslant1$ , очередь растет до бесконечности. Используя формулы (16) и (17) для процесса гибели и размножения, можно получить следующие формулы для предельных вероятностей состояний n-канальной СМО с неограниченной очередью

$p_0={left(1+ frac{rho^1}{1!}+ frac{rho^2}{2!}+ldots+frac{rho^n}{n!}+ frac{rho^{n+1}}{n!(n-rho)}right)!}^{-1},$

(45)

$p_1=frac{rho^1}{1!}cdot p_0,~ldots,~ p_k=frac{rho^k}{k!}cdot p_0,~ldots,~ p_n=frac{rho^n}{n!}cdot p_0,$

(46)

$p_{n+1}=frac{rho^{n+1}}{ncdot n!}cdot p_0,~ldots,~p_{n+r}=frac{rho^{n+r}}{n^rcdot n!}cdot p_0,~ldots$

(47)

Вероятность того, что заявка окажется в очереди,

$P_{text{och.}}=frac{rho^{n+1}}{n!(n-rho)}cdot p_0.$

(48)

Для n-канальной СМО с неограниченной очередью, используя прежние приемы, можно найти:

среднее число занятых каналов

$overline{k}=frac{lambda}{mu}=rho,$

(49)

среднее число заявок в очереди

$L_{text{och.}}=frac{rho^{n+1}cdot p_0}{ncdot n!}cdotleft(1-frac{rho}{n}right)^{-2},,$

(50)

среднее число заявок в системе

$L_{text{sist}}=L_{text{och.}}+rho.$

Среднее время пребывания заявки в очереди и среднее время пребывания заявки в системе, как и ранее, находятся по формулам Литтла (42) и (41).

Замечание. Для СМО с неограниченной очередью при rho<1 любая заявка, пришедшая в систему, будет обслужена, т.е. вероятность отказа $P_{text{otk.}}=0$ , относительная пропускная способность Q=1 , а абсолютная пропускная способность равна интенсивности входящего потока заявок, т.е. A=lambda .

Пример 9. В универсаме к узлу расчета поступает поток покупателей с интенсивностью lambda=81 чел. в час. Средняя продолжительность обслуживания контролером-кассиром одного покупателя $overline{t}_{text{ob.}}=2$ мин. Определить:

а. Минимальное количество контролеров-кассиров $n_{min}$ , при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при $n=n_{min}$ .

б. Оптимальное количество $n_{text{opt.}}$ контролеров-кассиров, при котором относительная величина затрат $C_{text{otn.}}$ , связанная с издержками на содержание каналов обслуживания и с пребыванием в очереди покупателей, задаваемая, например, как $C_{text{otn.}}=frac{n}{lambda}+3T_{text{och.}}$ , будет минимальна, и сравнить характеристики обслуживания при $n=n_{min}$ и $n=n_{text{opt.}}$ .

в. Вероятность того, что в очереди будет не более трех покупателей.

Решение. а. По условию lambda=81 (1/ч) $=frac{81}{60}=1,!35$ (1/мин.). По формуле (24) $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}=1,!35cdot2=2,!7$ . Очередь не будет возрастать до бесконечности при условии $frac{rho}{n}<1$ , т.е. при n>rho=2,!7 . Таким образом, минимальное количество контролеров-кассиров $n_{min}=3$ .

Найдем характеристики обслуживания СМО при n=3 .

Вероятность того, что в узле расчета отсутствуют покупатели, по формуле (45)

$p_0={left(1+2,!7+ frac{2,!7^2}{2!}+ frac{2,!7^3}{3!}+ frac{2,!7^4}{3!(3-2,!7)}right)!}^{-1}=0,!025$

т.е. в среднем 2,5% времени контролеры-кассиры будут простаивать.

Вероятность того, что в узле расчета будет очередь, по (48)

$P_{text{och.}}=frac{2,!7^4}{3!cdot(3-2,!7)}cdot0,!025=0,!735.$

Среднее число покупателей, находящихся в очереди, по (50)

$L_{text{och.}}=frac{2,!7^4}{3cdot3!cdot(1-2,!7/3)^2}cdot0,!025=7,!35.$

Среднее время ожидания в очереди по (42)

$T_{text{och.}}=frac{7,!35}{1,!35}=5,!44$ (мин).

Среднее число покупателей в узле расчета по (51)

$L_{text{sist.}}= 7,!35+2,!7=10,!05.$

Среднее время нахождения покупателей в узле расчета по (41)

$T_{text{sist.}}=frac{10,!05}{1,!35}approx7,!44$ (мин).

Среднее число контролеров-кассиров, занятых обслуживанием покупателей, по (49) overline{k}=2,!7 .

Коэффициент (доля) занятых обслуживанием контролеров-кассиров $overline{k}_{text{otn.}}=frac{rho}{n}=frac{2,!7}{3}=0,!9$ .

Абсолютная пропускная способность узла расчета A=1,!35 (1/мин), или 81 (1/ч), т.е. 81 покупатель в час.

Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии трех контролеров-кассиров.

б. Относительная величина затрат при n=3

$C_{text{otn.}}=frac{n}{lambda}+3T_{text{och.}}=frac{3}{1,!35}+3cdot5,!44=5,!44.$

Рассчитаем относительную величину затрат при других значениях (табл. 2).

Расчёт относительных величин затрат

Как видно из табл. 2, минимальные затраты получены при $n=n_{text{opt.}}=5$ контролерах-кассирах.

Определим характеристики обслуживания узла расчета при $n=n_{text{opt.}}=5$ . Получим

$P_{text{och.}}=0,!091;~ L_{text{och.}}= 0,!198;~ T_{text{och.}}=0,!146;~ L_{text{sist.}}=2,!9;~ T_{text{sist.}}=2,!15;~ overline{k}=2,!7;~k_3=0,!54.$

Как видим, при n=5 по сравнению с n=3 существенно уменьшились вероятность возникновения очереди $P_{text{och.}}$ , длина очереди $L_{text{och.}}$ и среднее время пребывания в очереди $T_{text{och.}}$ , и соответственно среднее число покупателей $L_{text{sist.}}$ и среднее время нахождения в узле расчета $T_{text{sist.}}$ , а также доля занятых обслуживанием контролеров k_3 . Но среднее число занятых обслуживанием контролеров-кассиров overline{k} и абсолютная пропускная способность узла расчета естественно не изменились.

в. Вероятность того, что в очереди будет не более 3 покупателей, определится как

$P{rleqslant3}=p_1+p_2+p_3+p_4+p_5+p_{5+1}+p_{5+2}+p_{5+3}=1-P_{text{och.}}+p_{5+1}+p_{5+2}+p_{5+3},$

где каждое слагаемое найдем по формулам (45)–(48). Получим при n=5:

$P{rleqslant3}=1-frac{2,!7^6}{5!(5-2,!3)}cdot 0,!065+frac{2,!7^6}{5cdot5!}cdot0,!065 +frac{2,!7^7}{5^2cdot5!}cdot0,!065 +frac{2,!7^8}{5^3cdot5!}cdot0,!065=0,!986.$

(Заметим, что в случае n=3 контролеров-кассиров та же вероятность существенно меньше: P{rleqslant3}=0,!464 ).

Пример 10. Железнодорожная касса с двумя окошками продает билеты в два пункта и . Интенсивность потока пассажиров, желающих купить билеты, для обоих пунктов одинакова: $lambda_{A}=lambda_{B}=0,!45$ (пассажиров в минуту). На обслуживание пассажиров кассир тратит в среднем 2 мин. Рассматриваются два варианта продажи билетов: первый — билеты продаются в одной кассе с двумя окошками одновременно в оба пункта и , второй — билеты продаются в двух специализированных кассах (по одному окошку в каждой), одна только в пункт , другая — только в пункт . Необходимо:

а. Сравнить два варианта продажи билетов по основным характеристикам обслуживания.

б. Определить, как надо изменить среднее время обслуживания одного пассажира, чтобы по второму варианту продажи пассажиры затрачивали на приобретение билетов в среднем меньше времени, чем по первому варианту.

Решение.
а. По первому варианту имеем двухканальную СМО, на которую поступает поток заявок интенсивностью lambda=0,!45+0,!45=0,!9 ; интенсивность потока обслуживании $mu=frac{1}{2}=0,!5;$ $rho=frac{lambda}{mu}=1,!8$ . Так как $frac{rho}{n}=frac{1,!8}{2}=0,!9<1$ , то предельные вероятности существуют.

Вероятность простоя двух кассиров по (45)

$p_0={left(1+ frac{1,!8}{1!}+ frac{1,!8^2}{2!}+ frac{1,!8^3}{2!cdot(2-1,!8)}right)!}^{-1}approx0,!0526.$

Среднее число пассажиров в очереди по (50)

$L_{text{och.}}=frac{1,!8^3}{2cdot2!cdot(1-1,!8/2)^2}cdot0,!0526=7,!67.$

Среднее число пассажиров у кассы по (51)

$L_{text{sist.}}= 7,!67+1,!8=9,!47.$

Среднее время на ожидание в очереди и покупку билетов равно соответственно (по формулам (42) и (41)):

$T_{text{och.}}=frac{7,!67}{0,!9}=8,!52$ (мин) и $T_{text{sist.}}=frac{9,!47}{0,!9}=10,!5$ (мин).

По второму варианту имеем две одноканальные СМО (два специализированных окошка); на каждую поступает поток заявок с интенсивностью lambda=0,!45 . По-прежнему mu=0,!5; $rho=frac{lambda}{mu}=0,!9<1$ , предельные вероятности существуют. По формулам (40), (36), (42), (41)

$L_{text{och.}}=frac{0,!9^2}{1-0,!9}=8,!1;~ L_{text{sist.}}=frac{0,!9}{1-0,!9}=9;~ T_{text{och.}}=frac{8,!1}{0,!45}=18;~ T_{text{sist.}}=frac{9}{0,!45}=20.$

Итак, по второму варианту увеличились и длина очереди, и среднее время ожидания в ней и в целом на покупку билетов. Такое различие объясняется тем, что в первом варианте (двухканальная СМО) меньше средняя доля времени, которую простаивает каждый из двух кассиров: если он не занят обслуживанием пассажира, покупающего билет в пункт , он может заняться обслуживанием пассажира, покупающего билет в пункт , и наоборот. Во втором варианте такой взаимозаменяемости нет.

Можно заметить, что среднее время на покупку билетов по второму варианту увеличилось более чем в 2 раза. Такое значительное увеличение связано с тем, что СМО работает на пределе своих возможностей (rho=0,!9) : достаточно незначительно увеличить среднее время обслуживания $overline{t}_{text{ob.}}$ , т.е. уменьшить , и rho превзойдет 1, т.е. очередь начнет неограниченно возрастать.

б. Выше было получено, что по первому варианту продажи билетов при среднем времени обслуживания одного пассажира $overline{t}_{text{ob.}}=2$ (мин) среднее время на покупку билетов составит $T_{text{sist.1}}=10,!5$ (мин). По условию для второго варианта продажи $T_{text{sist.2}}<T_{text{sist.1}}$ , или с учетом (36) и (41): $frac{1}{lambda}frac{rho}{1-rho}< T_{text{sist.1}}$ .

Полагая $rho=frac{lambda}{mu}=lambdaoverline{t}_{text{ob.}}$ , получим $-frac{overline{t}_{text{ob.}}}{1-lambdaoverline{t}_{text{ob.}}}<T_{text{sist.1}}$ , откуда найдем $overline{t}_{text{ob.}}<frac{T_{text{sist.1}}}{1+lambda T_{text{sist.1}}}$ или $overline{t}_{text{ob.}}<frac{10,!5}{1+0,!45cdot10,!5}=1,!83$ (мин).

Итак, средние затраты времени на покупку билетов по второму варианту продажи уменьшатся, если среднее время обслуживания одного пассажира уменьшится более чем на 0,17 мин, или более чем на 8,5%.

СМО с ограниченной очередью

СМО с ограниченной очередью отличаются от рассмотренных выше задач лишь тем, что число заявок в очереди ограничено (не может превосходить некоторого заданного ). Если новая заявка поступает в момент, когда все места в очереди заняты, она покидает СМО необслуженной, т.е. получает отказ.

Очевидно: для вычисления предельных вероятностей состояний и показателей эффективности таких СМО может быть использован тот же подход, что и выше, с той разницей, что суммировать надо не бесконечную прогрессию (как, например, мы делали при выводе формулы (33)), а конечную. Соответствующие формулы сведем в табл. 3.

Среднее время пребывания заявки в очереди и в системе, как и ранее, определяем по формулам Литтла (44) и (43).

Таблица 3. Показатели одно- и многоканальной СМО с ограниченной очередью

Показатели одно- и многоканальной СМО с ограниченной очередью

Пример 11. По условию примера 8 найти показатели эффективности работы причала. Известно, что приходящее судно покидает причал (без разгрузки), если в очереди на разгрузку стоит более 3 судов.

Решение. По условию m=3 . Используем формулы, приведенные во второй графе табл. 3.

Вероятность того, что причал свободен:

$p_0=frac{1-0,!6}{1-0,!8^{3+2}}=0,!297.$

Вероятность того, что приходящее судно покинет причал без разгрузки:

$P_{text{otk.}}=0,!8^{3+1}cdot 0,!122.$

Относительная пропускная способность причала:

Q=1-0,!122=0,!878.

Абсолютная пропускная способность причала A=0,!4cdot0,!878=0,!351 , т.е. в среднем в сутки разгружается 0,35 судна.

Среднее число судов, ожидающих разгрузку

$L_{text{och.}}=frac{0,!8^2cdot[1-0,!8^3cdot(3+1-3cdot0,!8)]}{(1-0,!8^{3+2})(1-0,!8)}=0,!861,$

а среднее время ожидания разгрузки по (42)

$T_{text{och.}}=frac{0,!861}{0,!8}=1,!076$ (сутки).

Среднее число судов, находящихся у причала $L_{text{sist.}}=0,!861+(1-0,!297)=1,!564$ , а среднее время пребывания судна у причала по (41):

$T_{text{sist.}}=frac{1,!564}{0,!8}=1,!955$ (сутки).

СМО с ограниченным временем ожидания

На практике часто встречаются СМО с так называемыми «нетерпеливыми» заявками. Такие заявки могут уйти из очереди, если время ожидания превышает некоторую величину. В частности, такого рода заявки возникают в различных технологических системах, в которых задержка с началом обслуживания может привести к потере качества продукции, в системах оперативного управления, когда срочные сообщения теряют ценность (или даже смысл), если они не поступают на обслуживание в течение определенного времени.

В простейших математических моделях таких систем предполагается, что заявка может находиться в очереди случайное время, распределенное по показательному закону с некоторым параметром , т.е. можно условно считать, что каждая заявка, стоящая в очереди на обслуживание, может покинуть систему с интенсивностью .

Соответствующие показатели эффективности СМО с ограниченным временем получаются на базе результатов, полученных для процесса гибели и размножения.

В заключение отметим, что на практике часто встречаются замкнутые системы обслуживания, у которых входящий поток заявок существенным образом зависит от состояния самой СМО. В качестве примера можно привести ситуацию, когда на ремонтную базу поступают с мест эксплуатации некоторые машины: понятно, что чем больше машин находится в состоянии ремонта, тем меньше их продолжает эксплуатироваться и тем меньше интенсивность потока вновь поступающих на ремонт машин. Для замкнутых СМО характерным является ограниченное число источников заявок, причем каждый источник «блокируется» на время обслуживания его заявки (т.е. он не выдает новых заявок). В подобных системах при конечном числе состояний СМО предельные вероятности будут существовать при любых значениях интенсивностей потоков заявок и обслуживании. Они могут быть вычислены, если вновь обратиться к процессу гибели и размножения.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Привет, мой друг, тебе интересно узнать все про расчет показателей эффективности одноканальной смо с ограниченной очередью, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
расчет показателей эффективности одноканальной смо с ограниченной очередью, одноканальная смо с ограниченной очередью , настоятельно рекомендую прочитать все из категории Теория массового обслуживания.

Рассмотрим одноканальную систему массового обслуживания с ожиданием, в которую поступает
простейший поток заявок с интенсивностью X; интенсивность обслуживания и, (т.е. в среднем непрерывно
занятый канал будет выдавать 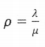обслуженных заявок в единицу (времени).
Длительность обслуживания — случайная величина, подчиненная показательному закону распределения.
Поток обслуживания является простейшим пуассоновским потоком событий.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Предположим, что количество мест в очереди ограничено числом m, т.е. если заявка пришла в момент, когда в очереди
уже стоят m-заявок, она покидает систему не обслуженной.

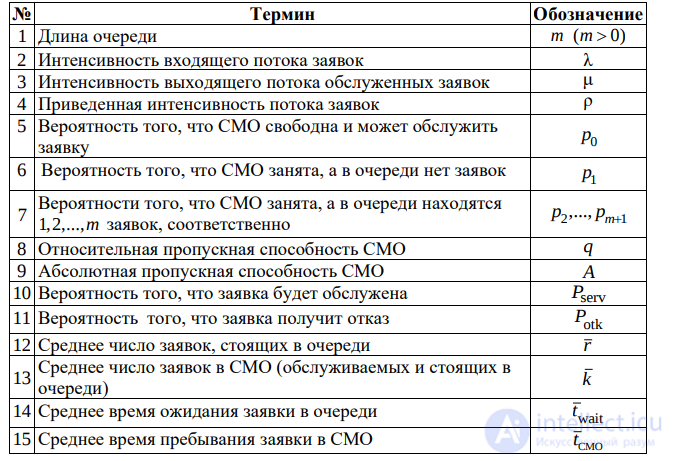
Список используемых терминов и обозначений

Поток обслуживания является простейшим пуассоновским потоком событий.
Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.
Предположим, что количество мест в очереди ограничено числом m, т.е. если заявка пришла в момент, когда в очереди уже стоят m-заявок, она покидает систему не обслуженной.
В качестве показателей эффективности одноканальной
СМО с ограниченной длиной очереди будем рассматривать:
А — абсолютную пропускную способность СМО;
Q — относительную пропускную способность;
Ротк — вероятность отказа;
Lсист — среднее число находящихся в системе заявок;
Теист_ среднее время пребывания заявки в системе;
Lоч — средняя длина очереди;
Точ — среднее время ожидания в очереди.

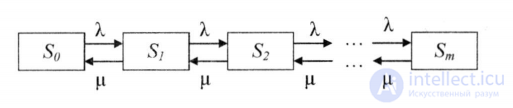
Размеченный граф состояний представлен на рисунке 9.

Рис. 9. Одноканальная СМ О с ограниченной длинной очереди

So — канал обслуживания свободен;
S1 — канал обслуживания занят, но очереди нет;
S2 — канал обслуживания занят, в очереди стоит 1 заявка;

***
Sm — канал обслуживания занят, в очереди все m заявок, любая следующая заявка получает отказ.
Вероятности состояний определяются уравнениями:

Отсюда получаем, что если р 1, то

Тогда остальные предельные вероятности находятся по формулам:

Постановка задачи
Параметры m , λ и μ известны.
Требуется найти

Формулы для расчетов
Приведенная интенсивность потока заявок вычисляется, как и в предыдущих параграфах, по формуле

Вероятности вычисляются по следующим формулам:

Поскольку заявка получает отказ, если СМО занята, а в очереди находятся m заявок, то

Далее получаем

Кроме того, справедливы формулы

Пример 10.
Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой).
Площадка при станции допускает пребывание в очереди на заправку не более пяти машин одновременно (m = 5) . Об этом говорит сайт https://intellect.icu . Если
в очереди уже находятся пять машины, очередная машина, прибывшая к станции, в очередь не становится. Поток
машин, прибывающих для заправки, имеет интенсивность λ = 2 (машина в минуту). Интенсивность потока
обслуживания составляет μ = 2.

Определите характеристики СМО и сделайте вывод об эффективности ее работы.

Решение.

Среднее число находящихся в системе заявок:

Среднее время пребывания машины в системе:

Средняя длина очереди:
Среднее время ожидания в очереди:

Каждому седьмому клиенту отказывают в обслуживании => эффективность СМО низкая.

Пример 11.
В небольшом магазине самообслуживания установлено, что поток покупателей является простейшим с интенсивностью λ = 1 покупатель в минуту. В этом магазине установлен один кассовый аппарат, позволяющий добиться такой производительности труда, при которой среднее время обслуживания одного клиента составляет примерно 1,25 мин. покупателя в минуту.

Определите характеристики СМО при условии, что очередь ограничена контролером при входе в зал самообслуживания: m = 3 покупателей.

Решение: Найдем интенсивность потока обслуживания:

Найдем приведенную интенсивность потока заявок:

Найдем предельные вероятности:

Вероятность отказа:

Относительная пропускная способность СМО:

Абсолютная пропускная способность СМО:

покупателей в мин.
Среднее число покупателей у кассы:

Среднее время пребывания покупателя у кассы:

Среднее число покупателей в очереди:

т.е. среднее число покупателей, ожидающих в очереди у кассы, равно 1,56.
Среднее время ожидания покупателя в очереди:

Вероятность простоя кассира мала, среднее время оживания покупателя не большое, вероятность отказа примерно 0,297. Таким образом, можно сказать, что система работает эффективно.

Задачи для самоконтроля

1. На автомойке один блок для обслуживания и есть место для очереди. Автомобили прибывают по пуассоновскому распределению с интенсивностью 5 авто/час. Среднее время обслуживания одной машины — 10 минут. Найдите все средние характеристики СМО.

Ответ

2. Автосервис (пост диагностики) представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих обслуживания ограничено и равно 3. Если все стоянки заняты, то есть в очереди уже находятся три автомобиля, то очередной автомобиль, прибывший в автосервис на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по показательному закону Пуассона и имеет интенсивность 0,85 (автомобиля в час). Время диагностики распределено по показательному закону и в среднем равно 1,05 час. Определите вероятностные характеристики работы СМО и сделайте вывод об эффективности ее работы.

Ответ:

Как ты считаеешь, будет ли теория про расчет показателей эффективности одноканальной смо с ограниченной очередью улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое расчет показателей эффективности одноканальной смо с ограниченной очередью, одноканальная смо с ограниченной очередью
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Теория массового обслуживания

Источник