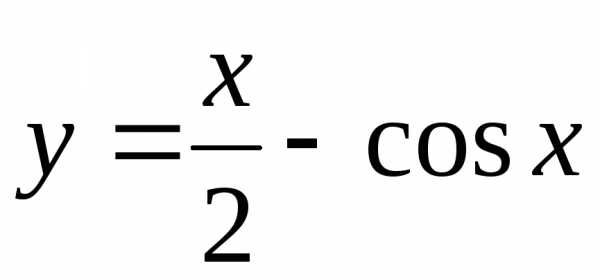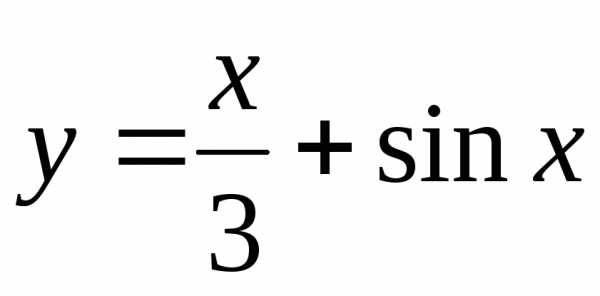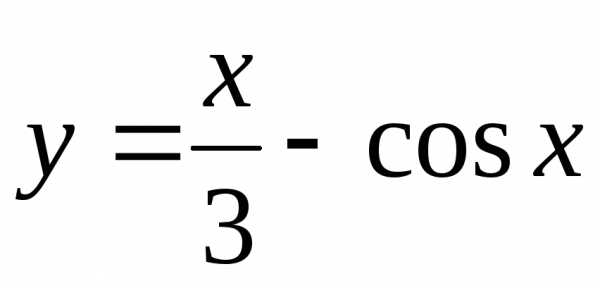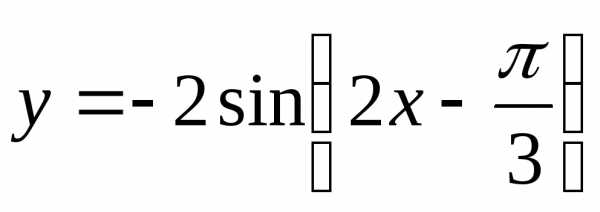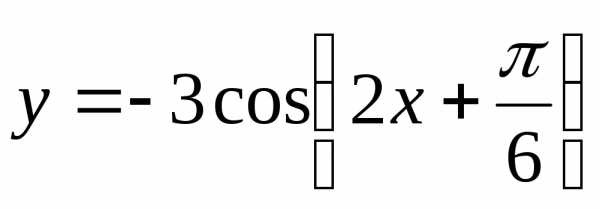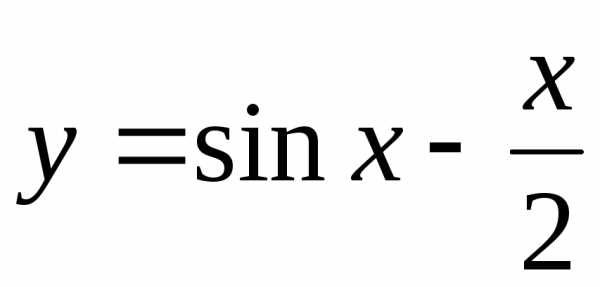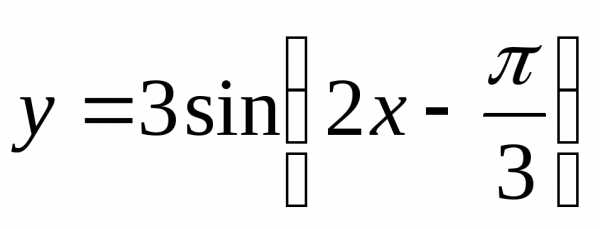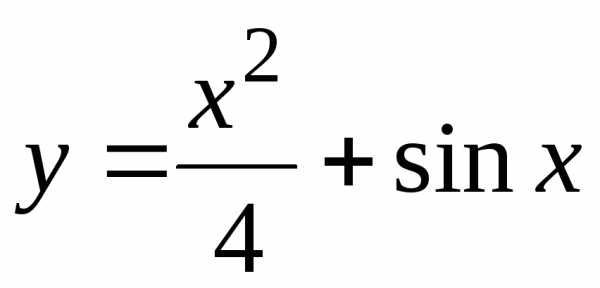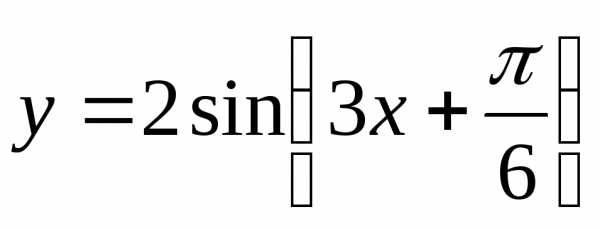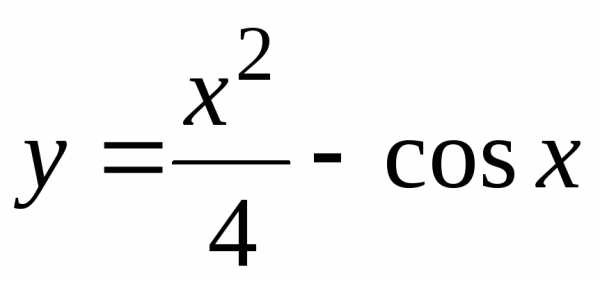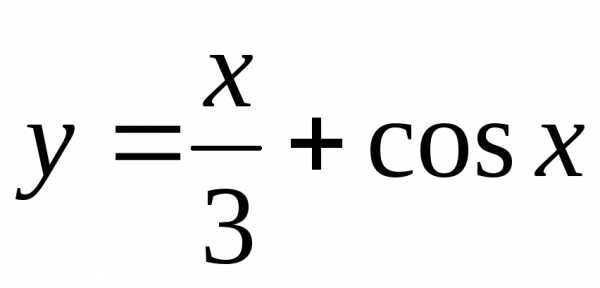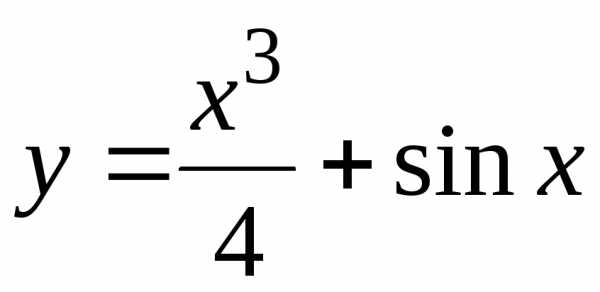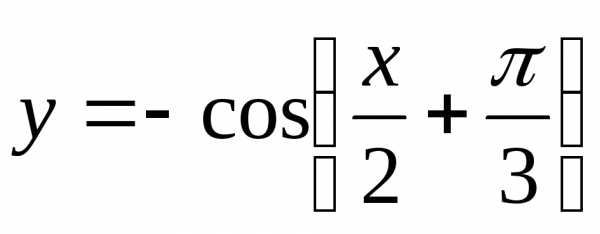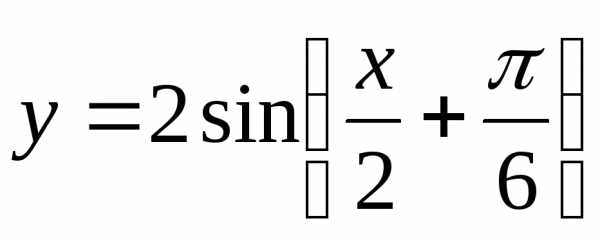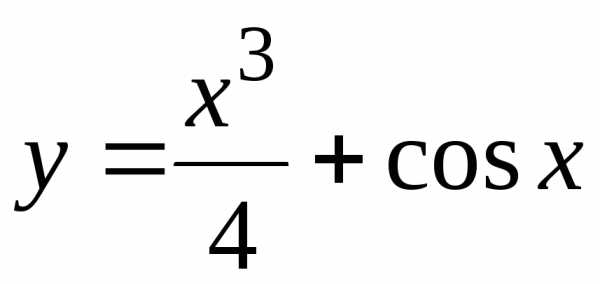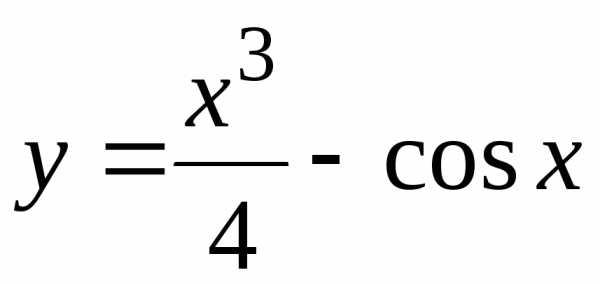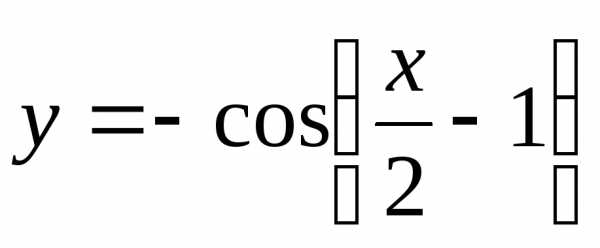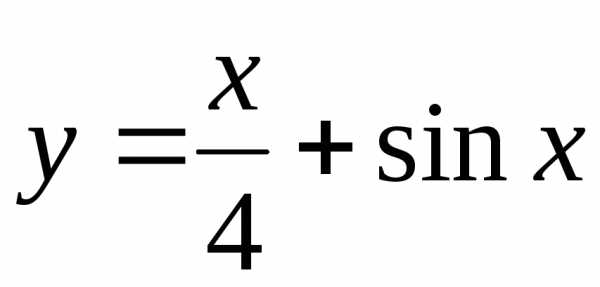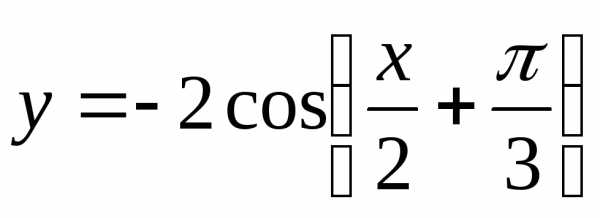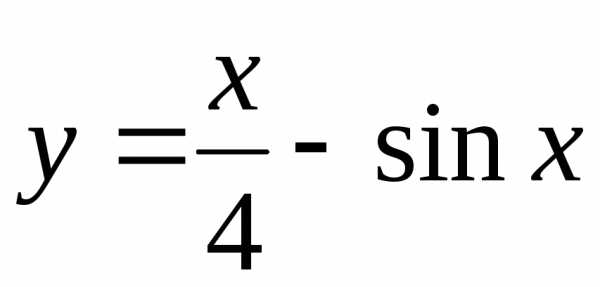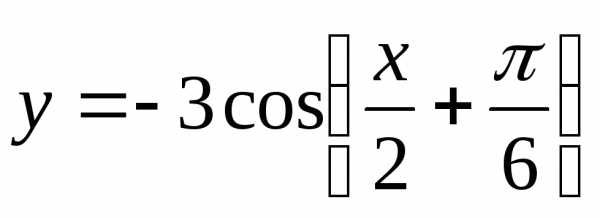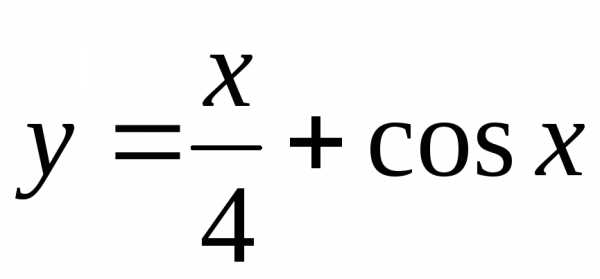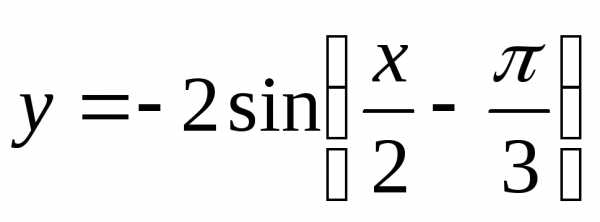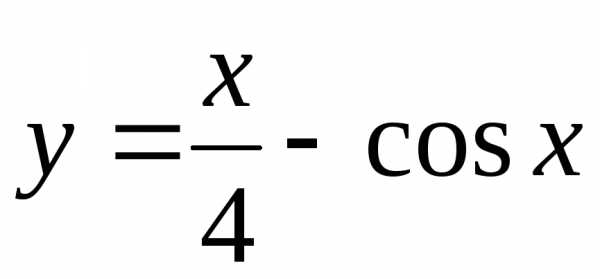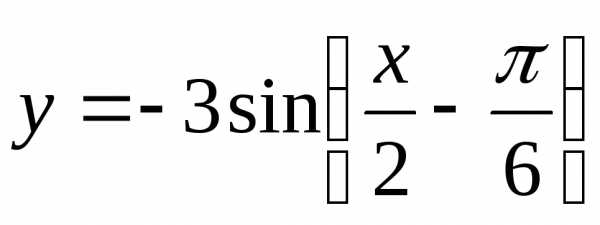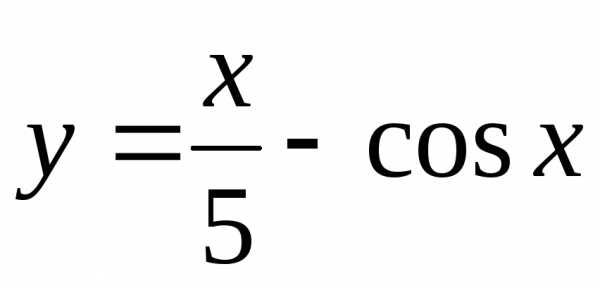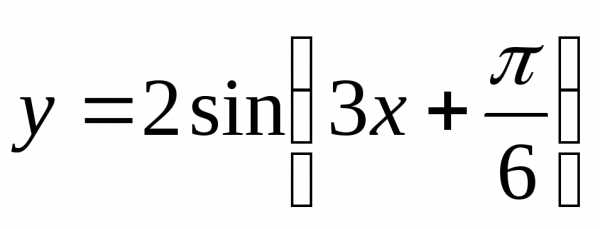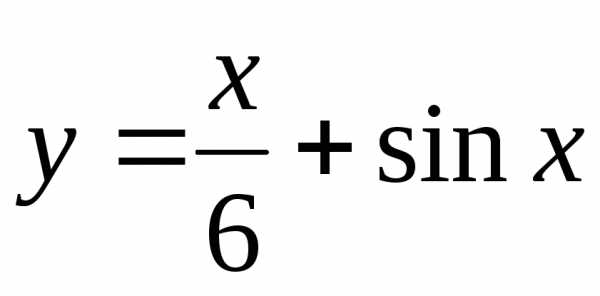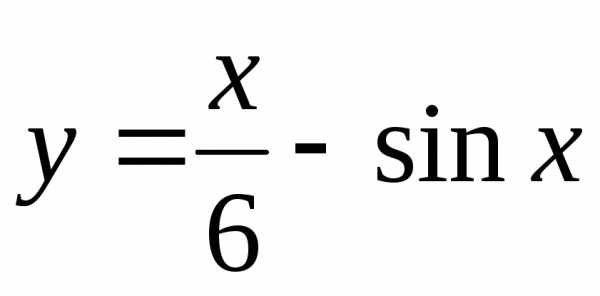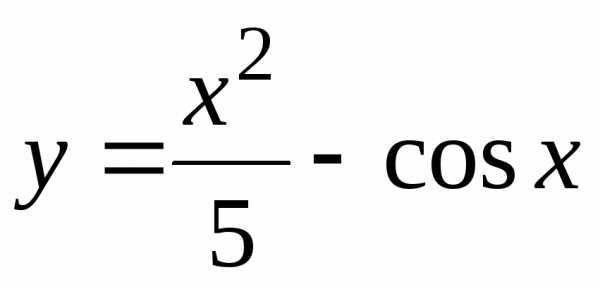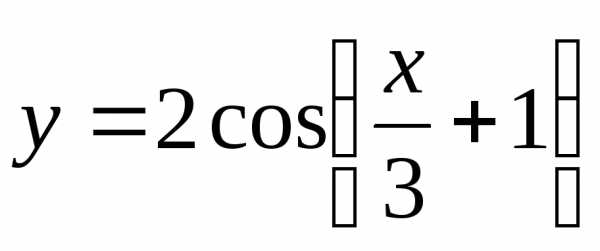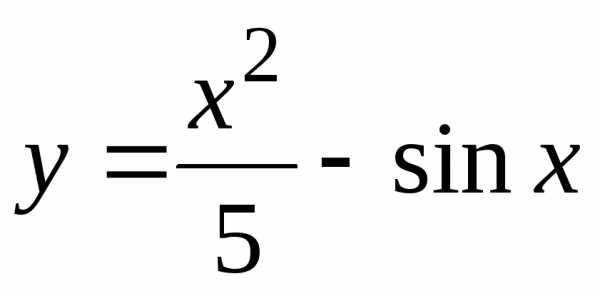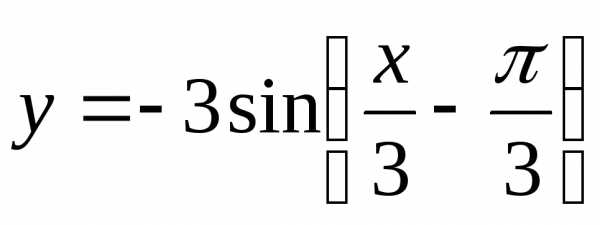Цель: обобщить и систематизировать знания учащихся по теме “Периодичность
функций”; формировать навыки применения свойств периодической функции,
нахождения наименьшего положительного периода функции, построения графиков
периодических функций; содействовать повышению интереса к изучению математики;
воспитывать наблюдательность, аккуратность.
Оборудование: компьютер, мультимедийный проектор, карточки с заданиями,
слайды, часы, таблицы орнаментов, элементы народного промысла
Эпиграф:
“Математика – это то, посредством чего люди управляют природой и собой”
А.Н. Колмогоров
Ход урока
I. Организационный этап.
Проверка готовности учащихся к уроку. Сообщение темы и задач урока.
II. Проверка домашнего задания.
Домашнее задание проверяем по образцам, наиболее сложные моменты обсуждаем.
III. Обобщение и систематизация знаний.
1. Устная фронтальная работа.
Вопросы теории.
1) Сформируйте определение периода функции
2) Назовите наименьший положительный период функций y=sin(x), y=cos(x)
3). Назовите наименьший положительный период функций y=tg(x), y=ctg(x)
4) Докажите с помощью круга верность соотношений:
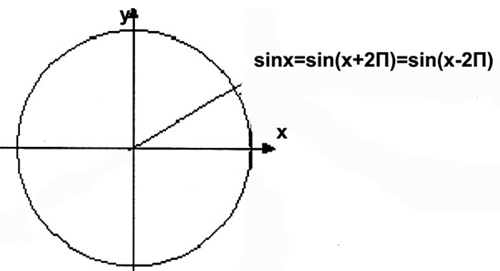
y=sin(x) = sin(x+360º)
y=cos(x) = cos(x+360º)
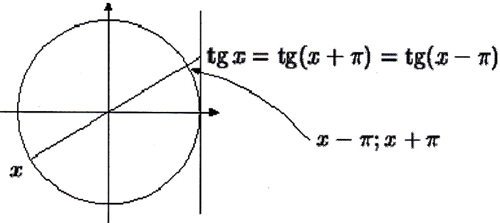
y=tg(x) = tg(x+180º)
y=ctg(x) = ctg(x+180º)
tg(x+πn)=tgx, n € Z
ctg(x+πn)=ctgx, n € Z
sin(x+2πn)=sinx, n € Z
cos(x+2πn)=cosx, n € Z
5) Как построить график периодической функции?
Устные упражнения.
1) Доказать следующие соотношения
a) sin(740º) = sin(20º)
b) cos(54º)
= cos(-1026º)
c) sin(-1000º) = sin(80º)
2. Доказать, что угол в 540º является одним из периодов функции y= cos(2x)
3. Доказать, что угол в 360º является одним из периодов функции y=tg(x)
4. Данные выражения преобразовать так, чтобы входящие в них углы по
абсолютной величине не превышали 90º .
a) tg375º
b) ctg530º
c) sin1268º
d) cos(-7363º)
5. Где вы встречались со словами ПЕРИОД, ПЕРИОДИЧНОСТЬ?
Ответы учащихся: Период в музыке – построение, в котором изложено более или
менее завершенная музыкальная мысль. Геологический период – часть эры и
разделяется на эпохи с периодом от 35 до 90 млн. лет.
Период полураспада радиоактивного вещества. Периодическая дробь.
Периодическая печать – печатные издания, появляющиеся в строго определенные
сроки. Периодическая система Менделеева.
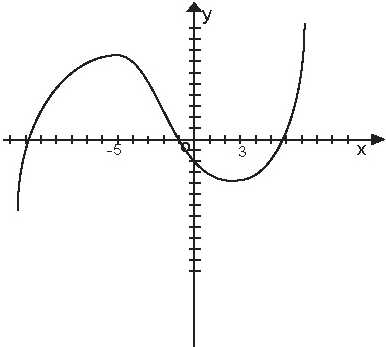
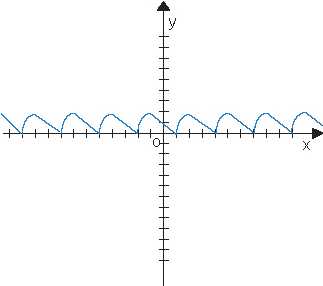
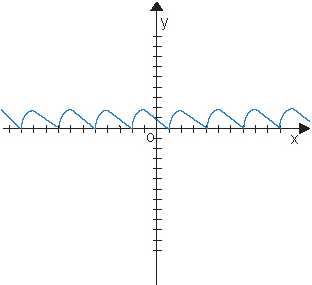
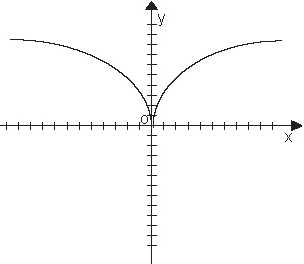
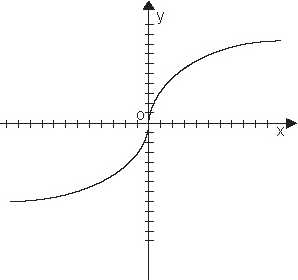
6. На рисунках изображены части графиков периодических функций. Определите
период функции. Определить период функции.
Ответ: Т=2; Т=2; Т=4; Т=8.
7. Где в жизни вы встречались с построением повторяющихся элементов?
Ответ учащихся: Элементы орнаментов, народное творчество.
IV. Коллективное решение
задач.
(Решение задач на слайдах.)
Рассмотрим один из способов исследования функции на периодичность.
При этом способе обходятся трудности, связанные с доказательством того, что
тот или иной период является наименьшим , а также отпадает необходимость
касаться вопросов об арифметических действиях над периодическими функциями и о
периодичности сложной функции. Рассуждение опирается лишь на определение
периодической функции и на такой факт: если Т – период функции, то и nT(n?0) – ее
период.
Задача 1. Найдите наименьший положительный период функции f(x)=1+3{x+q>5}
D(f)=R
Решение: Предположим, что Т-период данной функции. Тогда f(x+T)=f(x) для
всех x € D(f), т.е.
1+3{x+T+0,25}=1+3{x+0,25}
{x+T+0,25}={x+0.25}
Положим x=-0,25 получим
{T}={0}
{T}=0 <=> T=n, n € Z
Мы получили, что все периоды рассматриваемой функции (если они существуют)
находятся среди целых чисел. Выберем среди этих чисел наименьшее положительное
число. Это 1. Проверим, не будет ли оно и на самом деле периодом 1.
f(x+1) =3{x+1+0,25}+1
Так как {T+1}={T} при любом Т, то f(x+1)=3{(x+0.25)+1}+1=3{x+0,25}+1=f(x),
т.е. 1 – период f. Так как 1 – наименьшее из всех целых положительных чисел, то T=1.
Задача 2. Показать, что функция f(x)=cos2(x) периодическая и найти
её основной период.
Решение:
Задача 3. Найдите основной период функции
f(x)=sin(1,5x)+5cos(0,75x)
Решение:
1. D(f)=R
Допустим Т-период функции, тогда для любого х справедливо соотношение
sin1,5(x+T)+5cos0,75(x+T)=sin(1,5x)+5cos(0,75x)
Если х=0, то
sin(1,5T)+5cos(0,75T)=sin0+5cos0
sin(1,5T)+5cos(0,75T)=5
Если х=-Т, то
sin0+5cos0=sin(-1,5Т)+5cos0,75(-Т)
5= – sin(1,5Т)+5cos(0,75Т)
|
|
sin(1,5Т)+5cos(0,75Т)=5
– sin(1,5Т)+5cos(0,75Т)=5 |
Сложив, получим:
10cos(0,75Т)=10
cos=1
=2πn,
n € Z
T=,
n € Z
Выберем из всех “подозрительных” на период чисел
наименьшее положительное и проверим, является ли оно периодом для f. Это число
Имеем:
f(x+)=sin(1,5x+4π)+5cos(0,75x+2π)=
sin(1,5x)+5cos(0,75x)=f(x)
Значит
–
основной период функции f.
Задача 4. Проверим является ли периодической функция f(x)=sin(x)
Решение:
Пусть Т – период функции f. Тогда для любого х
sin|x+Т|=sin|x|
Если х=0, то sin|Т|=sin0, sin|Т|=0 Т=πn,
n € Z.
Предположим. Что при некотором n число
πn является периодом
рассматриваемой функции πn>0.
Тогда sin|πn+x|=sin|x|
Отсюда вытекает, что n должно быть одновременно и четным и нечетным числом, а
это невозможно. Поэтому данная функция не является периодической.
Задача 5. Проверить, является ли периодической функция
f(x)=
Решение:
D(f)=R
Пусть Т – период f, тогда
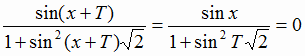
отсюда sinT=0, Т=πn,
n € Z. Допустим, что при некотором n число
πn действительно является периодом
данной функции. Тогда и число 2πn
будет периодом
Так как числители равны, то равны и их знаменатели, поэтому
Значит, функция f не периодическая.
Работа в группах.
Задания для группы 1.
Проверьте является ли функция f периодической и найдите ее основной период
(если существует).
f(x)=|cosx|
Задания для группы 2.
Проверьте является ли функция f периодической и найдите ее основной период
(если существует).
f(x)=cos(2x)+2sin(2x)
Задания для группы 3.
f(x)=|sin|x||
По окончании работы группы презентуют свои решения.
VI. Подведение итогов урока.
Рефлексия.
Учитель выдаёт учащимся карточки с рисунками и предлагает закрасить часть
первого рисунка в соответствии с тем, в каком объёме, как им кажется, они
овладели способами исследования функции на периодичность, а в части второго
рисунка – в соответствии со своим вкладом в работу на уроке.
| Мои умения исследовать функции на периодичность |
Мой вклад в работу на уроке |
|
|
|
VII. Домашнее задание
1). Проверьте, является ли функция f периодической и найдите её основной
период (если он существует)
a). f(x)=√x
b). f(x)=x2-2x+4
c). f(x)=2tg(3x+5)
2). Функция y=f(x) имеет период Т=2 и f(x)=x2+2x при х € [-2; 0].
Найдите значение выражения -2f(-3)-4f(3,5)
Литература/
- Мордкович А.Г. Алгебра и начала анализа с углубленным изучением.
- Математика. Подготовка к ЕГЭ. Под ред. Лысенко Ф.Ф., Кулабухова С.Ю.
- Шереметьева Т.Г. , Тарасова Е.А. Алгебра и начала анализа для
10-11 классов.
Исследование функции и построение графика
На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.
Что будет дальше?
Исследование функции и построение графика
Общая схема исследования
Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.
А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).
Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.
Алгоритм
- Найти область определения. Выделить особые точки (точки разрыва).
- Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
- Найти точки пересечения с осями координат.
- Установить, является ли функция чётной или нечётной.
- Определить, является ли функция периодической или нет (только для тригонометрических функций).
- Найти точки экстремума и интервалы монотонности.
- Найти точки перегиба и интервалы выпуклости-вогнутости.
- Найти наклонные асимптоты. Исследовать поведение на бесконечности.
- Выбрать дополнительные точки и вычислить их координаты.
- Построить график и асимптоты.
В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.
Схема исследования в формате pdf: скачать.
Полный пример решения онлайн
Полезная страница? Сохрани или расскажи друзьям
Провести полное исследование и построить график функции
$$
y(x)=frac{x^2+8}{1-x}.
$$
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, quad Rightarrow quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-infty; 1) cup (1;+infty).
$$
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:
Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.
Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:
Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.
Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).
4) Функция не является ни четной, ни нечетной, так как:
5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.
6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:
Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):
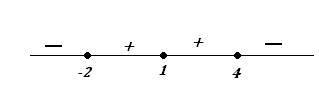
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:
При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.
При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.
При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).
Найдем значения функции в этих точках:
Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.
7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:
Приравняем вторую производную к нулю:
Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y» gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y» lt 0$, то есть функция выпуклая.

.
Так как пределы бесконечны, горизонтальных асимптот нет.
Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:
Получили, у что функции есть одна наклонная асимптота $y=-x-1$.
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
$$
y(-5)=5.5; quad y(2)=-12; quad y(7)=-9.5.
$$
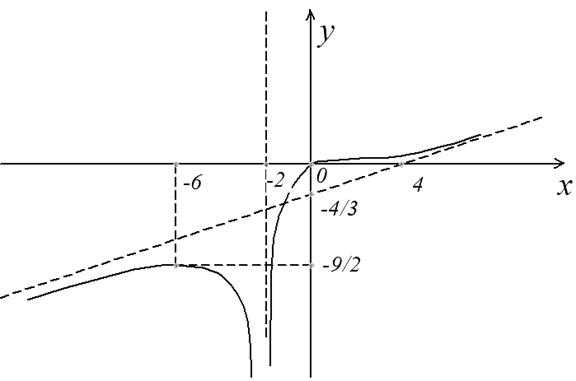
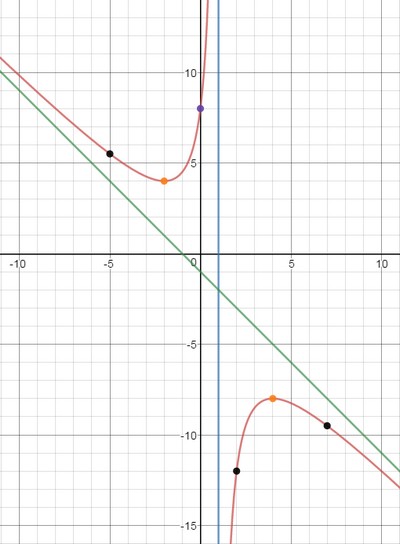
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):
Примеры решений по исследованию функции
Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!
Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.
$$y=frac{e^x}{x}.$$
Задача 2. Исследовать функцию и построить ее график.
$$y=-frac{1}{4}(x^3-3x^2+4).$$
Задача 3. Исследовать функцию с помощью производной и построить график.
$$y=ln frac{x+1}{x+2}.$$
Задача 4. Провести полное исследование функции и построить график.
$$y=frac{x}{sqrt{x^2+x}}.$$
Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.
$$y=frac{x^3-1}{4x^2}.$$
Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.
$$y=frac{x^3}{x^2-1}.$$
Поможем с исследованием функции: быстро, подробно
Задача 7. Проведите исследование функции с построением графика.
$$y=frac{x^3}{2(x+5)^2}.$$
Задача 8. Построить график функции $y=y(x)$, заданной параметрически
$$x=frac{t^2}{t+1}, y=frac{1}{t}-frac{t^3}{3}.$$
Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.
Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.
Задача 11. Провести полное исследование периодической функции
$y = cos 3x – 2 sin 6x$ и построить её график.
Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.
$$y=frac{4-x^3}{x^2}.$$
Задача 13. Провести полное исследование и построить график функции.
$$f(x)=frac{x}{2}-arccosfrac{2x}{1+x^2}.$$
Еще примеры исследования функции (контрольные работы)
Как построить график онлайн?
Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).
Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?
Графический калькулятор Desmos
Desmos.com
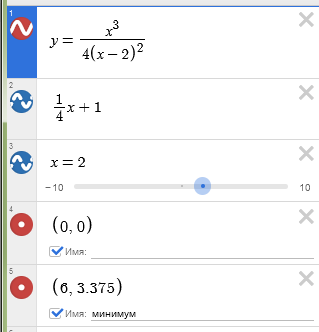
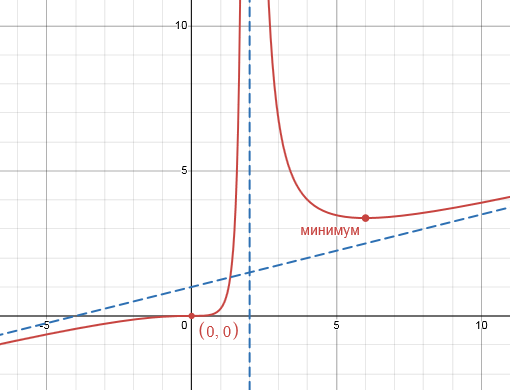
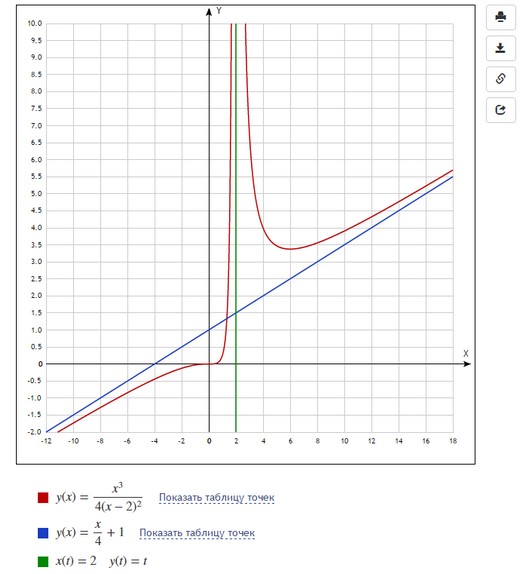
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:
При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.
Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!
Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):
Сайт для построения графиков y(x).ru
y(x).ru
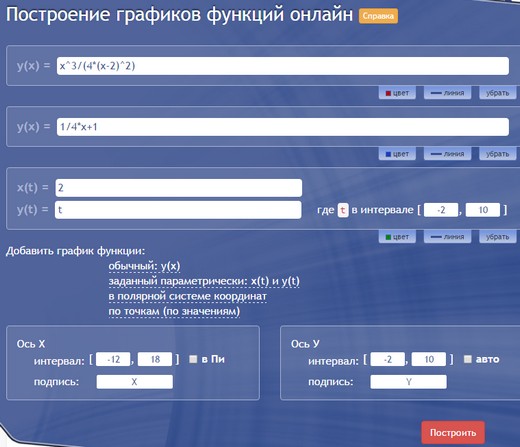
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:
И такой график получается в итоге:
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).
Другие сайты
Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:
- ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
- mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
- easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
- grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет
Больше знаний: теория и практика
Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень «съедобно» даже для полного чайника в математике: Исследование функций от Александра Емелина.
Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.
Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.
Решебник
Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена — около 50 рублей. Может, и ваша задача уже готова? Проверьте!
Полезные видео-ролики
Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.
Классный старый научно-популярный фильм «Математика. Функции и графики». Объяснения на пальцах в прямом смысле слова самых основ.
Закажите полное исследование функции в МатБюро
Лучшее спасибо — порекомендовать эту страницу
В этой статье обсуждаем периодичность функций: как определить, периодична ли функция, и каков ее период.
Функция периодична, если некоторый набор ее значений повторяется раз за разом, и точки с одинаковыми значениями функции расположены на числовой оси с равными промежутками. Это расстояние и будем называть периодом. Периодичная функция может иметь и несколько периодов, самый маленький положительный из них будем называть основным.
Тогда, если мы знаем период, мы можем, зная все значения функции на протяжении данного периода, достроить функцию, либо узнать ее значения в любой точке числовой оси – то есть при любом аргументе.
Периодичная функция
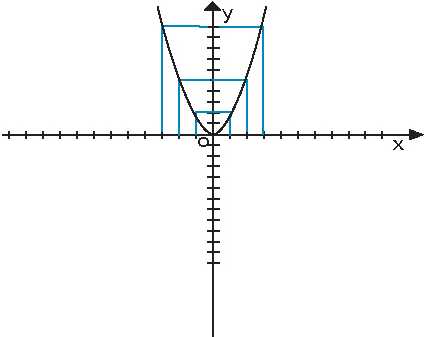
Пример 1: функция 


![x in[-2; 0] x in[-2; 0]](https://easy-physic.ru/img_formuls/math_985.5_76563737120aaab9a7fd96ee3cb53fce.png)

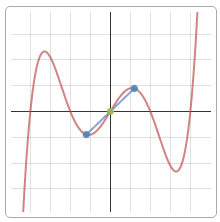
Раз наша функция принимает форму части параболы на отрезке [-2; 0] при периоде, равном 2, значит, такую же форму она будет иметь и на следующем отрезке – [0;2], и на отрезке [2;4]. Изобразим ее:
Определение значения периодичной функции
Видно, что функция принимает одинаковые значения в точках, отстоящих друг от друга на 2, 4, 6 единиц и т.д., тогда 


Теперь найдем значение искомого выражения: 
Строго говоря, функция периодична, если есть такое число Т, что 
Попробуем научиться определять, периодична ли функция или нет. Для этого рассмотрим несколько примеров.
Пример 2. Проверим, периодична ли функция 
Установим, выполняется ли условие: 

Пример 3. Проверим, периодична ли функция 
Функцию для удобства представим в виде: 
Установим, выполняется ли условие: 


Пример 4. Проверим, периодична ли функция 










Определение периода функции
В данном примере делать проверку необязательно, но проверка бывает очень полезна в более сложных задачах, поэтому сделаем ее здесь для тренировки: 
Пример 5. Определить периодичность функции 
Если Т – период, то 
В это равенство подставим какие-нибудь «удобные» точки, например, 
Далее есть два пути отыскания периода, первый – решение этого уравнения, второй – составление еще одного уравнения такого же вида. Если функция имеет период Т, то верно и следующее: 

Пользуясь четностью косинуса и нечетностью синуса можем записать:
Имеем систему:
Уравнения сложим, и получим




Теперь испробуем второй путь, решим это уравнение: 
Оставим в левой части только корень:
Возведем в квадрат:
Тогда либо 


Это уравнение имеет два решения, одно из которых (второе) – посторонний корень, появившийся при возведении в квадрат. Проверка подстановкой его в исходное уравнение позволит нам выявить его и отбросить. Таким образом, получаем:



Здесь также необходимо сделать проверку. Подставим полученный период в условие 

период данной функции — 
Определение периода функции
Пример 6. Определить периодичность функции 
Если Т – период, то
Подставим 

Или 



Проверим:
Определение периода функции
Пример 7. Определим период функции 
Запишем условие периодичности:











Определение периода функции
Пример 8. Доказать, что периодом функции 

Тогда:
Пример 9. Доказать, что периодом функции 

Тогда:
Если 



Удачи вам в учебе и надеюсь, эта статья вам помогла.
Периодичность функций
Функция
называетсяпериодической,
если существует такое число
,
что для любого значениях
из области определения выполняется
равенство
,
число
Т
называется периодом
функции.
Примеры
периодических функций:
,
,
,
.
Заметим,
что периодическую функцию достаточно
исследовать в пределах одного периода,
т.е. при
.
Простейшие преобразования графиков
Пусть
в данной системе координат вычерчен
график некоторой функции
Из
этого графика с помощью специальных
приемов легко получить график сходных
функций; таких как
,
а
также более общего вида
,
где
— некоторые константы.
-
График
функции
получается растяжением
или сжатием
вm
раз исходного графика вдоль оси Оy.
Если
же
,
то, построив сначала график функции,
затем строим симметричный с ним
относительно осиОх
искомый график функции
.
-
График
функции
получается с помощью параллельного
переноса (сдвига) графикавдоль осиОy
вверх
или вниз
наn
единиц.
-
График
функции
получается из графика
сжатием
или растяжением
его ва
раз вдоль оси Ох.
(т.е. к оси Оy).
-
График
функции y=f(x+b)
получается из графика y=f(x)
с помощью параллельного переноса
(сдвига) его вдоль оси Ох
влево (b>0)
или вправо (b<0)
на b
единиц.
Построение
графиков подобного рода в общем случае
сводится
к проведению в соответствующем порядке
операций 1-4.
АЗ-1
1.
.
Вычислить:,
,
,
2.
.
Вычислить:,
,
,
3.
Найти область определения функций:
|
а) |
б) |
в) |
г) |
|
д) |
е) |
ж) |
з) |
|
и) |
к) |
4.
Исследовать функции на четность или
нечетность
|
а) |
б) |
в) |
|
г) |
д) |
е) |
5.
Найти наименьший период функций:
а)
;
б)
6.
Построить графики функций:
|
а) |
б) |
в) |
|
г) |
д) |
е) |
|
ж) |
з) |
и) |
ИДЗ-1
Задание
1. Найти
области определения и значения функций
|
1) |
11) |
21) |
|
2) |
12) |
22) |
|
3) |
13) |
23) |
|
4) |
14) |
24) |
|
5) |
15) |
25) |
|
6) |
16) |
26) |
|
7) |
17) |
27) |
|
|
18) |
28) |
|
9) |
19) |
29) |
|
10) |
20) |
30) |
Задание
2. Исследовать
функцию на четность или нечетность
-
№ зад.
№ вар.
1
2
3
Задание
3. Найти
наименьший период функции
-
1)
16)
2)
17)
3)
18)
4)
19)
5)
20)
6)
21)
7)
22)
23)
9)
24)
10)
25)
11)
26)
12)
27)
13)
28)
14)
29)
15)
30)
Задание
4. Методом
деформации и сдвигов построить график
функции
|
№ зад № вар |
1 |
2 |
3 |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
|
27 |
|
|
|
|
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Исследование функции на четность и на периодичность — Мегаобучалка
Правило Лопиталя. исследование Функции.
Правило Лопиталя расскрытия неопределенностей.
Теорема (правило Лопиталя).
Если или (то есть, если предел отношения в точке приводит к неопределенности вида или ) и предел существует, то
.
Пример 1:
Пример 2:
Пример 3:
Замечание:
1) Неопределенности вида или можно раскрыть по правилу Лопиталя, предворительно преобразовав их к виду или .
Пример 4:
Пример 5:
Пример 6: Таким образом, .
Полное исследование функции
Полное исследование функции проводится по следующей схеме:
1. Нахождение области определения функции;
2. Нахождение точек разрыва, вертикальных и горизонтальных асимптот графика функции;
3. Нахождение (по возможности) точек пересечения графика функции с осями координат;
4. Исследование функции на четность и на периодичность;
5. Нахождение интервалов монотонности и экстремумов функции;
6. Нахождение интервалов выпуклости, вогнутости и точек перегиба графика функции;
7. Нахождение наклонной асимптоты графика функции;
8. Построение графика функции.
Пример 7:Исследовать функцию и построить ее график.
Нахождение области определения функции
Если функция задана только законом соответствия
(то есть область определения не указана), то за область определения функции берется множество { имеет смысл}. — область изменения (множество значений) функции.
1. Область определения функции: { имеет смысл
} .
Нахождение точек разрыва, вертикальных и горизонтальных асимптот графика функции.
По определению непрерывности функции в точке, функция будет непрерывной в точке , если .
Если в точке функция не определена или не является непрерывной ( то есть не выполняется равенство ),
то точка называется точкой разрыва.
Так как функция является элементарной, то она непрерывна в своей области определения, то есть в интервалах
и . — точка разрыва.
Находим пределы функции на концах интервалов и :
Точка — точка разрыва II рода и прямая является вертикальной асимптотой графика функции при и ;
функция не имеет горизонтальную асимптоту.
3. Нахождение (по возможности) точек пересечения графика функции с осями координат
Для нахождения точки пересечения графика функции с осью Ох пологаем , а для нахождения точки пересечения с осью
Оу полагаем х=0:
,следовательно — точка пересечения графика с осью Ох;
, следовательно — точка пересечения графика с осью Оу.
Исследование функции на четность и на периодичность
Функция называется четной (нечетной), если имеет место равенство ( ).
Область определения четной или нечетной функции- симметрична относительно начала координат.
График четной функции симметричен относительно оси Оу, а нечетной функции симметрична относительно начала координат
Функция не обладает четностью (не является ни четной и ни нечетной), так как ее область определения -не симметрична относительно начала координат ( но ).
График функции не является симметричным относительно оси и относительно начала координат О(0;0).
Функция называется периодической, если для некоторого числа имеет место равенство .
=>
функция непериодична.
megaobuchalka.ru
Периодичность функций
Функция
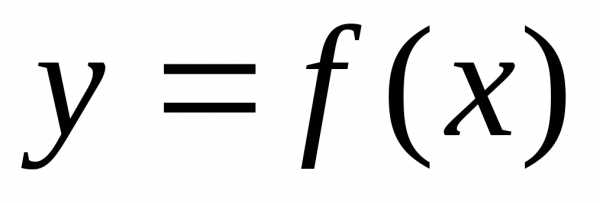
если существует такое число
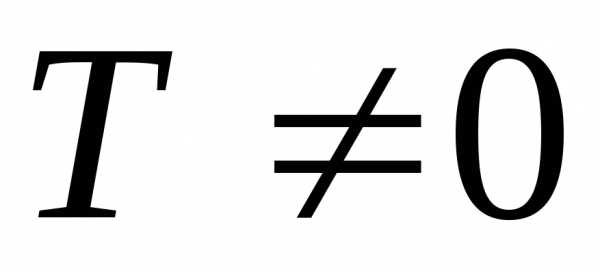
что для любого значениях
из области определения выполняется
равенство
,
число
Т
называется периодом
функции.
Примеры
периодических функций:

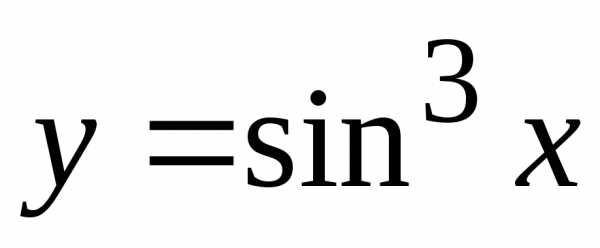
Заметим,
что периодическую функцию достаточно
исследовать в пределах одного периода,
т.е. при
.
Пример.
Найти наименьший период функции
.
Решение.
Период для функций
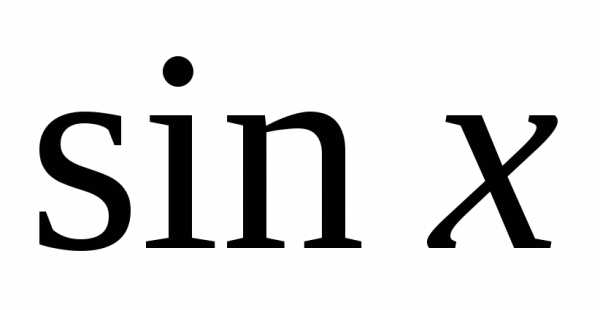


Функцияимеет период в 3 раза меньше, т.е.
Наименьший период суммыдолжен быть таким, чтобы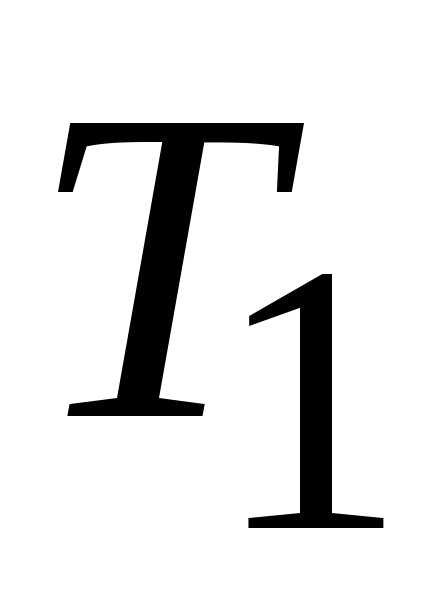

данном случае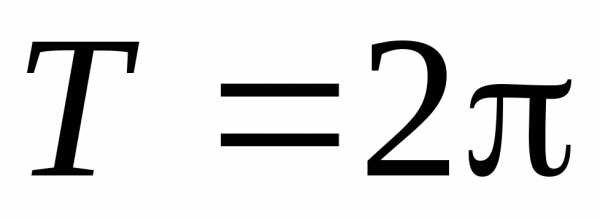
Задание 3. Найти наименьший период функции
-
1)
16)
2)
17)
3)
18)
4)
19)
5)
20)
6)
21)
7)
22)
23)
9)
24)
10)
25)
11)
26)
12)
27)
13)
28)
14)
29)
15)
30)
Простейшие преобразования графиков
Пусть
в данной системе координат вычерчен
график некоторой функции
Из
этого графика с помощью специальных
приемов легко получить график сходных
функций; таких как
,
а
также более общего вида
,
где
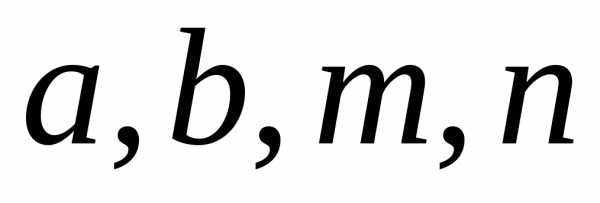
-
График
функции
получается растяжением
или сжатием
вm
раз исходного графика вдоль оси Оy.
Если
же
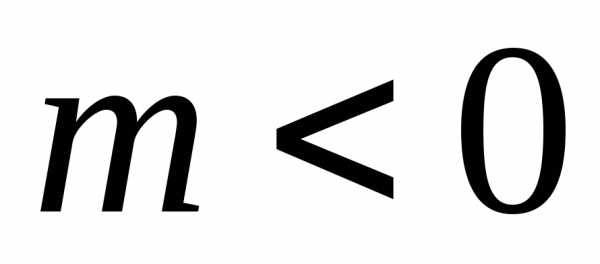
то, построив сначала график функции,
затем строим симметричный с ним
относительно осиОх
искомый график функции
.
-
График
функции
получается с помощью параллельного
переноса (сдвига) графика
вдоль осиОy
вверх
или вниз
наn
единиц.
-
График
функции
получается из графика
сжатием
или растяжением
его ва
раз вдоль оси Ох.
(т.е. к оси Оy).
-
График
функции y=f(x+b)
получается из графика y=f(x)
с помощью параллельного переноса
(сдвига) его вдоль оси Ох
влево (b>0)
или вправо (
b<0)
на b
единиц.
Построение
графиков подобного рода в общем случае
сводится
к проведению в соответствующем порядке
операций 1-4.
Пример.
Построить график функции
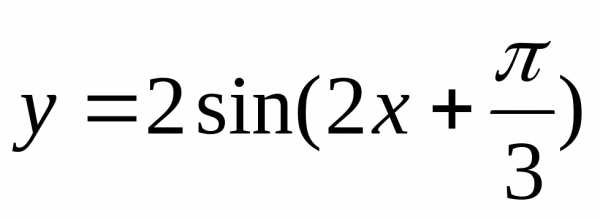
Решение.
-
Строим
график
;
-
сжимаем
его вдоль осив
2 раза, получаем график; -
сдвигаем
график
влево наи получаем график
;
-
растягиваем
график
вдоль оси
в 2 раза и получаем требуемый график.
Пример.
Построить график функции
.
Решение.
1)
строим график
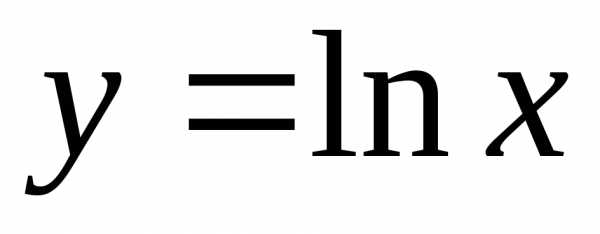
2)
сдвигаем его влево по оси
3)
сжимаем график
вдоль оси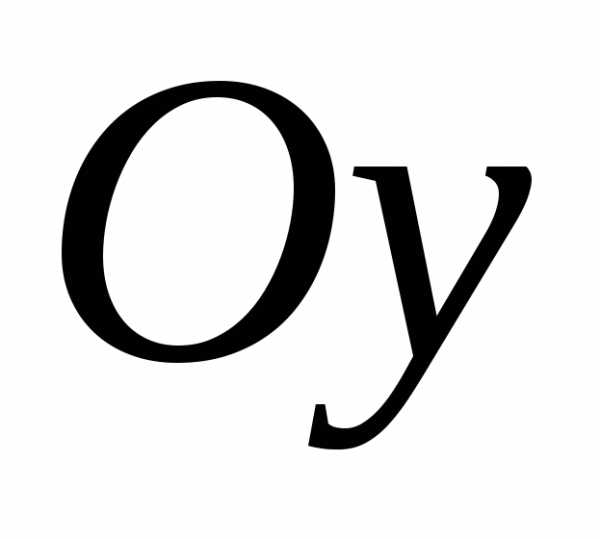
2 раза и строим симметричный ему
относительно оси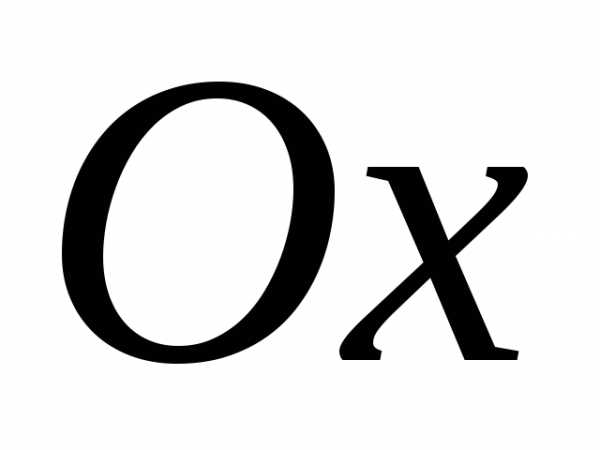
получаем график;
4)
поднимаем график функции
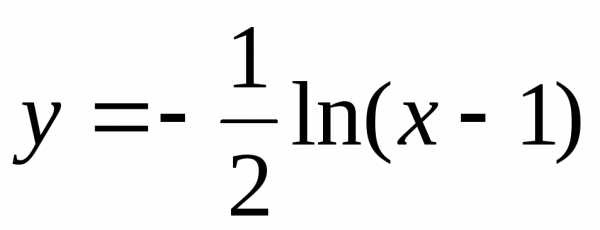
вверх на две единицы, получаем искомый
график.
Задание
4.
Методом
деформации и сдвигов построить график
функции
|
№ зад № вар |
1 |
2 |
3 |
|
1 |
|||
|
2 |
|
||
|
3 |
|
||
|
4 |
|
||
|
5 |
|
||
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
||
|
22 |
|
||
|
23 |
|
|
|
|
24 |
|
||
|
25 |
|
|
|
|
26 |
|
||
|
27 |
|
||
|
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
studfiles.net
Исследование функции
Исследование
функции.
1) D(y)
– Область опрделения: множество всех
тех значений переменной х. при которых
алгебраические выражения f(x)
и g(x)
имеют смысл.
Если функция задана формулой,
то область определения состоит из всех
значений независимой переменной, при
которых формула имеет смысл.
2) Свойства функции:
четность/нечетность, периодичность:
Нечётными
и
чётными
называются
функции,
графики которых обладают
симметрией
относительно
изменения знака аргумента.
-
Нечётная
функция —
функция, меняющая значение на
противоположное при изменении знака
независимой переменной
(симметричная относительно
центра координат). -
Чётная
функция —
функция, не изменяющая своего значения
при изменении знака независимой
переменной (симметричная относительно
оси ординат). -
Ни
чётная ни нечётная функция (функция
общего вида) —
функция, не обладающая симметрией. В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
-
Функции,
не принадлежащие ни одной из категорий
выше, называются ни
чётными ни нечётными (или
функциями общего вида).
Нечётные
функции
Нечётная степень где —
произвольное целое
число.
-
Синус .
-
Тангенс .
Чётные
функции
Чётная
степень где —
произвольное целое
число.
Периоди́ческая
фу́нкция ― функция,
повторяющая свои значения через некоторый
регулярный интервал аргумента, то есть
не меняющая своего значения при добавлении
к аргументу некоторого фиксированного
ненулевого числа (пери́ода функции)
на всей области определения.
-
Говоря
более формально, функция называется
периодической, если существует такое
число T≠0 (период), что на всей области
определения функции выполняется
равенство . -
Исходя
из определения, для периодической
функции справедливо также равенство ,
где —
любое целое число. -
Все тригонометрические
функции являются
периодическими.
3)
Нули
(корни) функции — точки, где она
обращается в ноль.
Нахождение
точки пересечения графика с осью Oy. Для
этого нужно вычислить значение f(0).
Найти также точки пересечения графика
с осью Ox,
для чего найти корни уравнения f(x)
= 0 (или
убедиться в отсутствии корней).
Точки, в
которых график пересекает
ось ,
называют нулями
функции.
Чтобы найти нули функции нужно решить
уравнение ,
то есть найти те
значения «икс»,
при которых функция обращается в ноль.
4)
Промежутки
постоянства знаков, знаки в них.
Промежутки,
где функция f(x) сохраняет знак.
Интервал
знакопостоянства – это интервал, в
каждой точке которого функция
положительна либо отрицательна.
ВЫШЕ
оси абсцисс.
НИЖЕ
оси .
5)
Непрерывность (точки разрыва, характер
разрыва, ассимптоты).
Непрерывная
функция —
функция без «скачков», то есть такая, у
которой малые изменения аргумента приводят
к малым изменениям значения функции.
Устранимые
точки разрыва
Если
предел функции существует,
но функция не определена в этой точке,
либо предел не совпадает со значением
функции в данной точке:
,
то
точка называется точкой
устранимого разрыва функции (в комплексном
анализе —устранимая
особая точка).
Если
«поправить» функцию в
точке устранимого разрыва и положить ,
то получится функция, непрерывная в
данной точке. Такая операция над функцией
называется доопределением
функции до непрерывной или доопределением
функции по непрерывности,
что и обосновывает название точки, как
точки устранимого разрыва.
Точки
разрыва первого и второго рода
Если
функция имеет разрыв в данной точке (то
есть предел функции в данной точке
отсутствует или не совпадает со значением
функции в данной точке), то для числовых
функций возникает два возможных варианта,
связанных с существованием у числовых
функций односторонних
пределов:
-
если
оба односторонних предела существуют
и конечны, то такую точку называют точкой
разрыва первого рода.
Точки устранимого разрыва являются
точками разрыва первого рода; -
если
хотя бы один из односторонних пределов
не существует или не является конечной
величиной, то такую точку называют точкой
разрыва второго рода.
Аси́мпто́та
— прямая,
обладающая тем свойством, что расстояние
от точки кривой до этой прямой стремится
к нулю при удалении точки вдоль ветви
вбесконечность.
Вертикальная
Вертикальная
асимптота — прямая вида при
условии существования предела .
Как
правило, при определении вертикальной
асимптоты ищут не один предел, а два
односторонних (левый и правый). Это
делается с целью определить, как функция
ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон.
Например:
Горизонтальная
Горизонтальная
асимптота — прямая вида при
условии существования предела
.
Наклонная
Наклонная
асимптота — прямая вида при
условии существования пределов
Замечание:
функция может иметь не более двух
наклонных (горизонтальных) асимптот.
Замечание:
если хотя бы один из двух упомянутых
выше пределов не существует (или равен ),
то наклонной асимптоты при (или )
не существует.
если в
п. 2.), то ,
и предел находится
по формуле горизонтальной асимптоты, .
6)
Нахождение
промежутков монотонности. Найти
интервалы монотонности функции f(x)(то
есть интервалы возрастания и убывания).
Это делается с помощью исследования
знака производной f(x).
Для этого находят производную f(x) и
решают неравенство f(x)0.
На промежутках, где это неравенство
выполнено, функция f(x)возрастает.
Там, где выполнено обратное неравенство
f(x)0,
функция f(x)убывает.
Нахождение
локального экстремума. Найдя
интервалы монотонности, мы можем сразу
определить точки локального экстремума
там, где возрастание сменяется убыванием,
располагаются локальные максимумы, а
там, где убывание сменяется возрастанием
— локальные минимумы. Вычислить значение
функции в этих точках. Если функция
имеет критические точки, не являющиеся
точками локального экстремума, то
полезно вычислить значение функции и
в этих точках.
Нахождение
наибольшего и наименьшего значений
функции y = f(x) на отрезке [a; b](продолжение)
|
1. Найти
2. Найти
3. Определить
4. Найти
5. Выбор Замечание. Если |
7)
Нахождение
интервалов выпуклости и вогнутости.
Это делается с помощью исследования
знака второй производной f(x).
Найти точки перегиба на стыках интервалов
выпуклости и вогнутости. Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции. Найдя f(x) ,
мы решаем неравенство f(x)0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f(x)0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
Точка
перегиба функции —
это точка, в которой функция непрерывна
и при переходе через которую функция
меняет направление выпуклости.
Условия
существования
Необходимое
условие существования точки перегиба: если
функция дважды
дифференцируемая в некоторой выколотой
окрестности точки ,
то или .
studfiles.net
Полное исследование функции — шаг за шагом
В статье перечислены основные пункты, по которым принято делать исследование функции. Стать носит теоретический характер, подробно объясняется на «пальцах» что и как нужно исследовать. Поэтому если вас интересуют практические примеры, то смело можно пропускать прочтение данного текста и переходить к примерам, ссылка в конце статьи.
Полное исследование функции включает в себя следующие пункты:
1. Область определения функции D(y).
Область определения D(y) — это множество всех значений аргумента x, на котором задана функция. Другими словами — это промежуток по оси икс, в пределах которого функция f(x) непрерывна и определена.
К примеру, если функция непрерывна, то ответ таков: D(y) = R, где R — это множество всех значений икс, от минус бесконечности до плюс бесконечности. В ином случае, точка разрыва включается в ответ. Пусть функция неопределена в точке х = 1, тогда область определения исключает данную точку: D(y) = (-00; 1),(1;+00). (-00 и +00 это знак бесконечности).
2. Четность, нечетность, периодичность функции.
Четность или нечетность показывает существует ли симметричность функции относительно начала координат или оси ординат. Чтобы определить четность/нечетность, берем икс со знаком минус, подставляем его в исследуемую функцию f(x) на место обычных иксов и считаем. В случае, если на выходе имеем точно такую же функцию, как исходная, с такими же знаками всех коэффициентов, то говорят, что данная функция четная: Записывается так: y(-x) = y(x). График четной функции симметричен относительно центра координат.
В случае, если на выходе получается исходная функция, но со знаком минус за скобками, то говорят что функция нечетная и записывается это так: y(-x) = -y(x). График нечетной функции, симметричен относительно оси ординат. Существует и третий случай, когда на выходе получается «разношерстная» функция, в которой все знаки перемешались и не помогают никакие манипуляции, чтобы функция стала похожей на исходную или исходную со знаком минус. Тогда говорят, что данная функция ни четная, ни нечетная и она не обладает никакой симметрией.
Свойство периодичности присуще тригонометрическим функциям, оно показывает существует ли период или другими словами некоторый повторяющийся регулярный интервал аргумента, при котором функция сохраняет свои значения при добавлении к аргументу этого периода на всей области определения.
3. Точки пересечения с осями координат ОХ и ОУ.
При пересечении графика функции f(x) с осью икс (ОХ), координата у = 0. Найденные точка(и) будет иметь координаты М1(х;0). При пересечении графика функции f(x) оси игрек (ОУ), координата х = 0, соответственно точка(и) пересечения будет иметь координаты М2(0;y).
4. Поиск вертикальных, наклонных или горизонтальных асимптот.
Традиционно исследование начинается с поиска вертикальных асимптот. В случае, если функция f(x) терпит бесконечный разрыв в какой-либо точке х, то прямая, проведенная через эту точку параллельно оси игрек, будет являться вертикальной асимптотой. Чтобы доказать это, необходимо вычислить пределы от исходной функции f(x) при икс стремящемся к минус и плюс бесконечности (если это возможно) или один из этих пределов. В случае, если хоть в одном из них получится ответ бесконечность, это и будет являться доказательством.
Далее идет поиск наклонных или горизонтальных асимптот. Многие иногда путаются в этих понятиях, считая их независимыми, не связанными друг с другом, что конечно же неверно. Наклонная асимптота имеет уравнение y = kx + b, а горизонтальная — это частный случай наклонной, в котором коэффициент при икс равен нулю (k = 0), ее уравнение y = b. Чтобы найти наклонную асимптоту функции необходимо вычислить два предела:
Если коэффициент k = 0, то при поиске коэффициента b будет рассчитываться предел от функции f(x) и при подстановке в формулу y = kx + b мы получим уравнение горизонтальной асимптоты y = b, т.е. прямую, параллельную оси икс. Если коэффициент k будет равен бесконечности, неважно плюс или минус, в таком случае дальнейшие вычисления не осуществляются, а в ответе записываем, что наклонные асимптоты отсутствуют.
5. Промежутки возрастания и убывания (промежутки монотонности), экстремумы функции.
Промежутки монотонности функции f(x) находятся при помощи первой производной. Алгоритм таков: берем первую производную от f(x), приравниваем результат производной к нулю f ‘(x) = 0, находим корень(корни) данного уравнения x1, x2 и т. д. Таким образом мы получаем экстремумы функции. Далее чертим ось икс и отмечаем на ней закрашенными кружочками найденные корни x1, x2…
Нужно помнить, что если функция имеет точки разрыва в области определения, их также необходимо отметить на числовой оси, отмечая пустыми кружочками.
Получаем несколько промежутков, границами которых вперемешку являются точки из корней и точек разрыва, это не страшно, просто нужно будет это учитывать в дальнейшем при оформлении ответа. Далее начинаем исследовать знаки производной на каждом из полученных промежутков. Берем по одному числу из каждого промежутка, подставляем в производную f ‘(x) и отмечаем знаки (плюс или минус), рисуя их прямо над осью в исследуемом промежутке.
Остается самое интересное! Анализируем результаты, изучая каждую точку :
— закрашенная точка, в которой идет смена знаков с плюса на минус ( смотрим слева и справа от точки )- это точка максимума. Под осью икс рисуем стрелочку вверх, там где плюс и стрелочку вниз, там где минус.
— закрашенная точка, в которой идет смена знаков с минуса на плюс — это точка минимума. Также помечаем стрелочками направления вниз и вверх.
— пустая точка (пустой кружок) — это точка разрыва и ее мы не имеем права записать в минимумы или максимумы, в этой точке функция не определена, не существует.
Итак, с экстремумами «рассчитались» и нам остается найти промежутки возрастания и убывания функции, или другими словами — промежутки монотонности. Собственно, здесь все предельно просто: промежутки, в которых стрелочка смотрит вверх это промежутки возрастания функции, где стрелочка вниз — промежутки убывания. Важный момент — учитываем точки разрыва ( незакрашенные точки ), когда записываем ответ.
Если в промежутке (a;b) имеется точка разрыва c (точка с пустым кружочком), то ответ записывается с учетом этой точки: (a;c),(c;b).
6. Промежутки выпуклости и вогнутости, точки перегиба функции.
Чтобы найти промежутки, в которых функция выпукла и вогнута, а также точки перегиба, необходимо найти вторую производную. Вторая производная берется от первой: ( f ‘(x) )’ = f ‘ ‘(x). Далее, как и в предыдущем пункте, приравниваем вторую производную к нулю, находим корни уравнения. Рисуем ось икс, отмечаем найденные корни закрашенными точками, точки разрыва отмечаем пустыми кружочками.
Исследуем знаки второй производной на каждом из промежутков. Там где вторая производная положительна рисуем скобку в виде улыбки, здесь функция вогнута. В ином случае, рисуем унылую скобку, здесь функция выпукла. Соответственно, при записи промежутков вогнутости и выпуклости функции не забываем учитывать точки разрыва. Точки перегиба находим там, где вторая производная меняет свой знак с + на — и наоборот, и точка закрашенная.
7. Построение графика.
Учитывая все предыдущие расчеты и найденные величины — точки разрыва, точки пересечения с осями координат, асимптоты, точки экстремумы, точки перегиба, строим график исследуемой функции. Желательно делать все это на листке в клетку, с масштабом побольше, чтобы как можно точнее получился график функции.
Конечно, сухая теория без практики это не дело, а потому предлагаю перейти к примерам исследования функции с помощью производной.
matematyka.ru
График функции. Возрастание и убывание функции; периодичность, четность, нечетность
Пусть на некоторой плоскости задана прямоугольная система координат. Графиком некоторой функции , (X- область определения) называется множество точек этой плоскости с координатами , где .
Для построения графика нужно изобразить на плоскости множество точек, координаты которых (x;y) связаны соотношением .
Чаще всего графиком функции является некоторая кривая.
Самый простой способ построения графика — построение по точкам.
Составляется таблица, в которой в одной ячейке стоит значение аргумента, а в противоположной ей значение функции от этого аргумента. Затем полученные точки отмечаются на плоскости, и через них проводится кривая.
Пример построения по точкам графика функции :
Построим таблицу.
Теперь строим график.
Но таким способом не всегда возможно построить достаточно точный график — для точности нужно брать очень много точек. Поэтому используют различные методы исследования функции.
С полной схемой исследования функции знакомятся в высших учебных заведениях. Одним из пунктов исследования функции является нахождение промежутков возрастания (убывания) функции.
Функция называется возрастающей (убывающей) на некотором промежутке, если , для любых x2 и x1 из этого промежутка, таких, что x2>x1.
Например, функция, график которой изображен на следующем рисунке, на промежутках возрастает, а на промежутке (-5;3) убывает. То есть, на промежутках график идет «в гору». А на промежутке (-5;3) «под гору».
Еще одним из пунктов исследования функции является исследование функции на периодичность.
Функция называется периодичной, если существует такое число T, что .
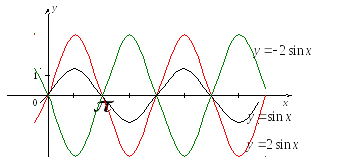
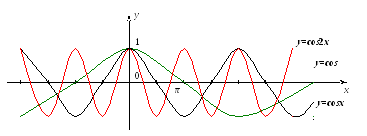
Число T называют периодом функции. Например, функция периодична, здесь период равен 2П, так
Примеры графиков периодичных функций:
Период первой функции равен 3, а второй – 4.
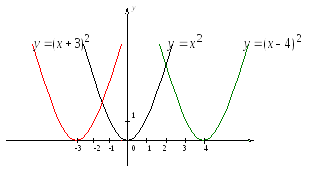
Функция называется четной, если Пример четной функции y=x2.
Функция называется нечетной, если Пример нечетной функции y=x3.
График четной функции симметричен относительно оси ОУ (осевая симметрия).
График нечетной функции симметричен относительно начала координат (центральная симметрия).
Примеры графиков четной (слева) и нечетной (справа) функции:
studyport.ru
П.3. Исследование функций и построение графиков
Полное исследование функции для построения ее графика включает следующие пункты (не обязательно именно в данном порядке).
1) Область определения функции (ООФ) и область ее значений (ОЗФ).
В случае если область определения функции не задана специально, то считают, что она совпадает с областью допустимых значений ее аргумента͵ ᴛ.ᴇ. с множеством всех точек х, для которых выполнима операция f. При нахождении ООФ используют ООФ элементарных функций , , , и др.
Область значений функции находят только в случаях, когда ее можно сразу указать, опираясь на свойства элементарных функций, к примеру, для функции , очевидно, .
2) Четность функции, ее периодичность.
Для установления четности (нечетности) функции , имеющей симметричную область определения, проверяют справедливость равенств ( ) для всех ООФ.
В случае четности или нечетности функции исследование ее поведения и построение графика можно проводить только для , а затем достроить график, используя симметрию: для четной функции график симметричен относительно оси OY, а для нечетной – относительно начала координат.
Для установления периодичности функции проверяют справедливость равенства для ООФ, где Т определяется видом функции. В случае периодической функции исследование проводят для одного промежутка периодичности.
3) Непрерывность функции, точки разрыва, вертикальные асимптоты.
Для определения промежутков непрерывности функции используют непрерывность базовых элементарных функций. В точках, ʼʼподозрительныхʼʼ на разрыв (отдельных точек, не входящих в ООФ), проверяют выполнение условий непрерывности. В случае если функция терпит разрыв в точке х0, то определют тип разрыва.
В случае если функция имеет бесконечный разрыв в некоторой точке х0, то прямая х = х0 является вертикальной асимптотой графика функции. В случае если только один из односторонних пределов при х0– 0 или х0+ 0 является бесконечным, то асимптота принято называть односторонней.
В случае если функция определена не на всей числовой оси, то крайне важно вычислить односторонние пределы функции в точках, ограничивающих промежутки ООФ. В случае если односторонний предел функции в точке а, ограничивающей промежуток ООФ, бесконечен, то х = а является односторонней вертикальной асимптотой графика функции. К примеру, в случае если ООФ: , то нужно найти ; если данный предел окажется бесконечным, то х = а является односторонней вертикальной асимптотой графика функции.
4) Промежутки монотонности и экстремумы.
Для определения промежутков монотонности функции используют достаточный признак монотонности.
Достаточный признак монотонности дифференцируемой функции:
если на интервале хÎ(а, b) производная сохраняет знак, то функция сохраняет монотонность на этом интервале, а именно: если , то f(x) возрастает, в случае если , то f(x) убывает.
Для установления точек экстремумов функции используют необходимый и достаточные признаки существования экстремума.
Необходимое условие существования экстремума функции: если непрерывная функция имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует.
Точки, принадлежащие ООФ, в которых производная равна нулю или не существует, называют критическими точками функции по ее первой производной (точками, ʼʼподозрительными на экстремумʼʼ).
Первый достаточный признак существования экстремума: если при переходе через критическую точку х0 (слева направо) производная изменяет свой знак, то в точке х0 есть экстремум причем это максимум, в случае если знак меняется с плюса на минус, и это минимум, в случае если знак меняется с минуса на плюс. В случае если при переходе через критическую точку х0 производная не изменяет свой знак, то в точке х0 нет экстремума функции .
Второй достаточный признак существования экстремума: если – дважды дифференцируемая функция в точке х0 и , тогда: если , то х0 – точка минимума функции, а если , то х0 – точка максимума.
Стоит сказать, что для нахождения точек экстремумов функции сначала находят критические точки по первой производной. После этого проверяют выполнение в них достаточных условий существования экстремума функции.
5) Промежутки выпуклости, вогнутости графика и точки перегиба.
Дуга кривой L принято называть выпуклой, в случае если все ее точки расположены не выше касательной, проведенной в любой точке этой дуги (рис. 27), и принято называть вогнутой, в случае если все ее точки расположены не ниже касательной, проведенной в любой точке дуги кривой.
Точки, принадлежащие кривой, и отделяющие участки выпуклости от участков вогнутости, называются точками перегиба кривой (рис. 27).
Достаточное условие выпуклости, вогнутости графика функции:если функция является дважды дифференцируемой и ее вторая производная сохраняет знак при всех xÎ(a;b), то график функции имеет постоянное направление выпуклости на этом интервале: при <0 – выпуклость вверх, при >0 – вогнутость (выпуклость вниз).
Необходимое условие для точки перегиба: если х0 – абсцисса точки перегиба графика функции , то ее вторая производная в этой точке равна нулю или не существует.
Точки, принадлежащие графику функции , в которых или не существует, называются критическими точками функции по ее второй производной (точками, ʼʼподозрительными на перегибʼʼ).
Достаточное условие для точек перегиба: если вторая производная при переходе через точку х0, подозрительную на перегиб, изменяет знак, то точка графика с абсциссой х0 является точкой перегиба. В случае если не изменяет знак при переходе через точку х0, то перегиба нет.
При нахождении промежутков выпуклости, вогнутости графика функции сначала находят критические точки по второй производной, после этого выделяют промежутки знакопостоянства второй производной на ООФ: если , то кривая вогнутая, а если , то кривая выпуклая. Точки перегиба определяют, используя достаточные условия перегиба.
6) Наклонные и горизонтальные асимптоты.
Асимптотой кривой, имеющей бесконечную ветвь, принято называть прямая, расстояние до которой от текущей точки М кривой стремится к нулю при удалении точки М от начала координат (рис. 28).
В случае если график функции имеет наклонную асимптоту с уравнением , то параметры k и b в уравнении асимптоты можно найти по формулам:
, (26)
. (27)
В случае если хотя бы один из этих пределов является бесконечным или не существует, то наклонных асимптот нет. В случае, когда k = 0, график имеет горизонтальную асимптоту с уравнением y = b.
В некоторых случаях (как правило, в случае если f(x) выражена через показательную или логарифмическую функцию), график может иметь асимптоты только при или только при .
Иногда ветви графика при и при имеют разные асимптоты.
7) Точки пересечения графика с осями координат или другие дополнительные точки графика.
Дополнительные точки графика находят в случаях, когда недостаточно информации для выбора масштаба по осям координат, ᴛ.ᴇ. когда на некотором промежутке ООФ нет ни точек экстремумов, ни точек перегибов, ни точек пересечения графика с осями координат.
referatwork.ru
Исследование функции и построение её графика
Если требуется построить график функции , то необходимо предварительно провести исследование её свойств. Это можно сделать по следующему плану:
1. Область определения функции .
2. Точки разрыва, поведение функции в окрестности точек разрыва.
3. Вертикальные асимптоты.
4. Точки пересечения графика функции с координатными осями.
5. Интервалы знакопостоянства функции.
6. Чётность, нечётность функции.
7. Периодичность функции.
8. Наклонные асимптоты графика функции.
9. Интервалы монотонности.
10. Экстремумы.
11. Интервалы выпуклости, вогнутости, точки перегиба.
12. Для более точного построения графика, можно найти значения функции в дополнительных точках.
Заметим, что приведённая схема исследования функций не является обязательной, этот порядок исследования может быть изменён в каждом конкретном случае.
Пример.Исследовать функцию и построить её график.
Решение.
1. Область определения функции .
2. – точка разрыва
3. Прямая является вертикальной асимптотой графика функции.
4. Точки пересечения графика функции с координатными осями:
Отсюда видно, что график рассматриваемой функции пересекает обе координатные оси в начале координат, т.е. в точке .
5. Интервалы знакопостоянства функции:
а)
б)
6. Чётность, нечётность функции: рассматриваемая функция не является ни чётной, ни нечётной, поскольку её область определения не симметричная относительно нуля. К этому же выводу можно прийти, рассмотрев
7. Рассматриваемая функция не является периодической.
8. Наклонная асимптота графика имеет уравнение
где
Следовательно, – наклонная асимптота при и при .
9. Интервалы монотонности найдём, исследуя производную функции:
Критические точки:
а) не существует при
б) при
Отсюда видно, что функция возрастает при и при , убывает при .
10. Экстремумы:
Из п. 9 видим, что точкой максимума является вычислим
.
11. Интервалы выпуклости, вогнутости и точки перегиба найдём, исследуя производную второго порядка:
Критические точки II рода:
а) не существует при
б) при
Отсюда видно, что функция имеет выпуклый график на интервале и и вогнутый на интервале .
Кроме того, график имеет точку перегиба, ее вторая координата , таким образом – точка перегиба.
Результаты проведенных исследований можно свести в таблицу:
Похожие статьи:
poznayka.org

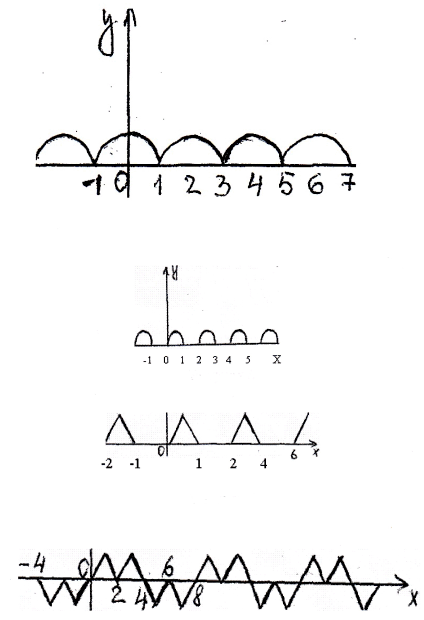

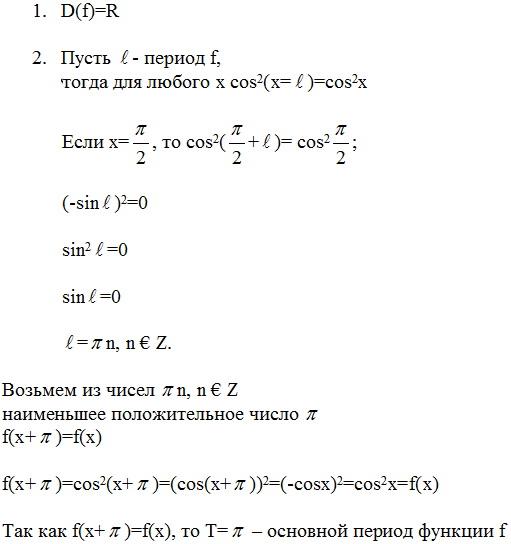
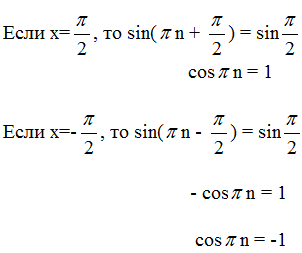
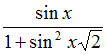
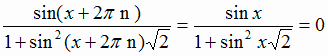
























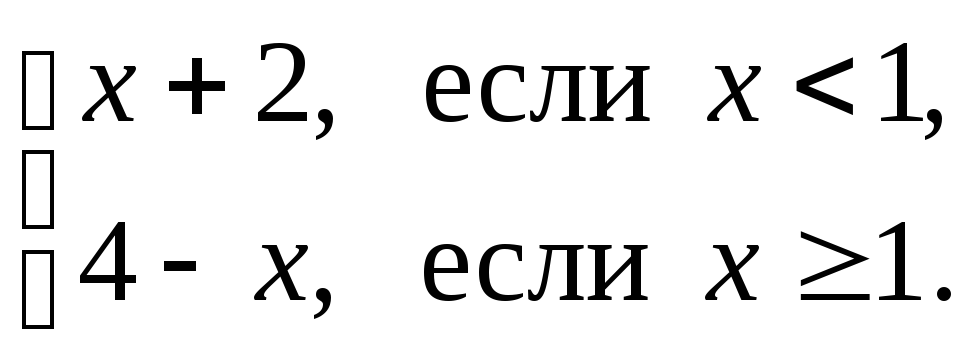
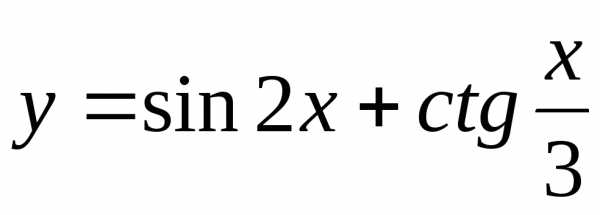
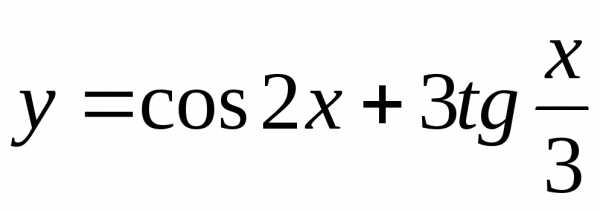
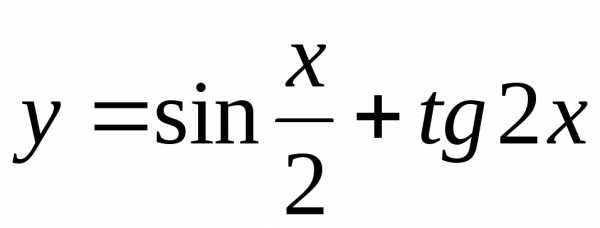

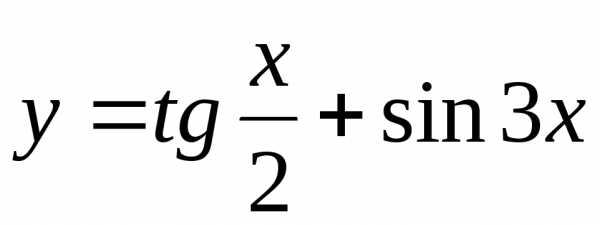
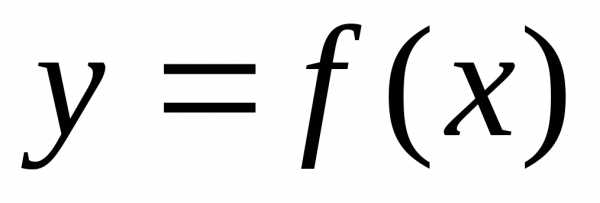
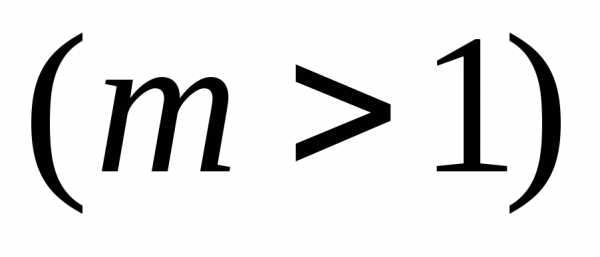 или сжатием
или сжатием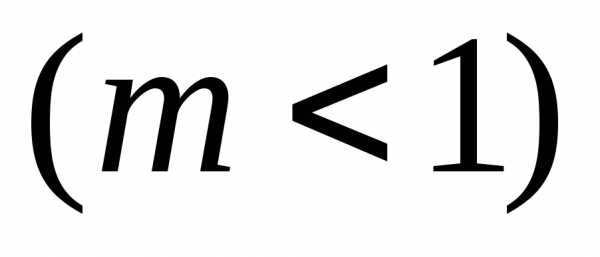 вm
вm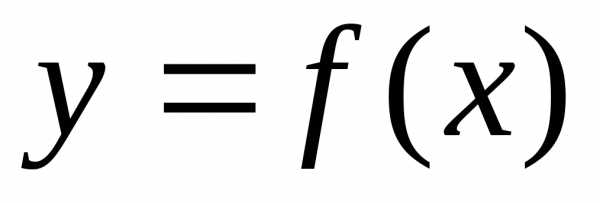 вдоль осиОy
вдоль осиОy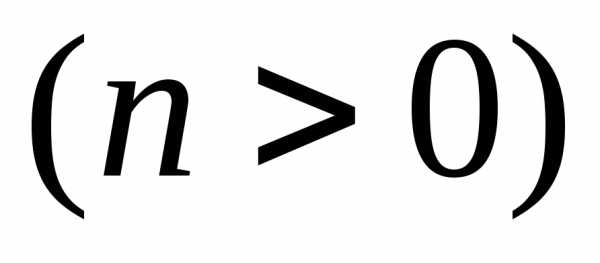
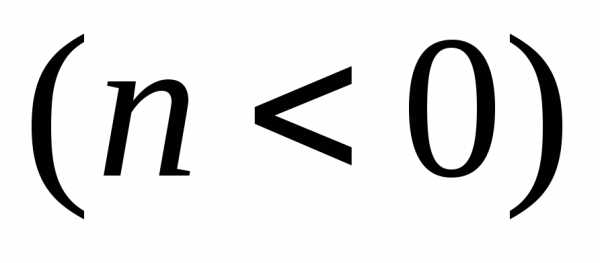 наn
наn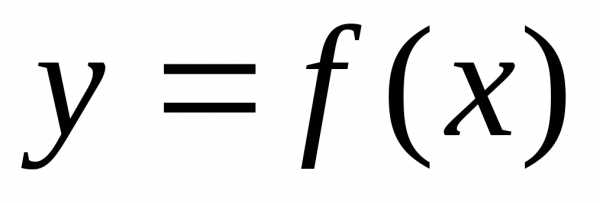 сжатием
сжатием или растяжением
или растяжением его ва
его ва ;
; в
в и получаем график
и получаем график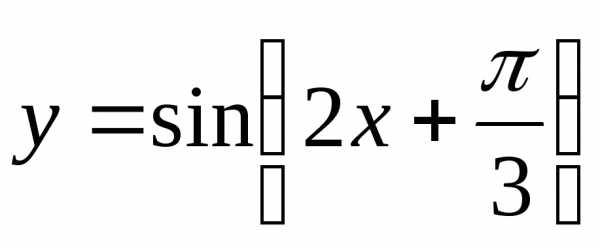 ;
; вдоль оси
вдоль оси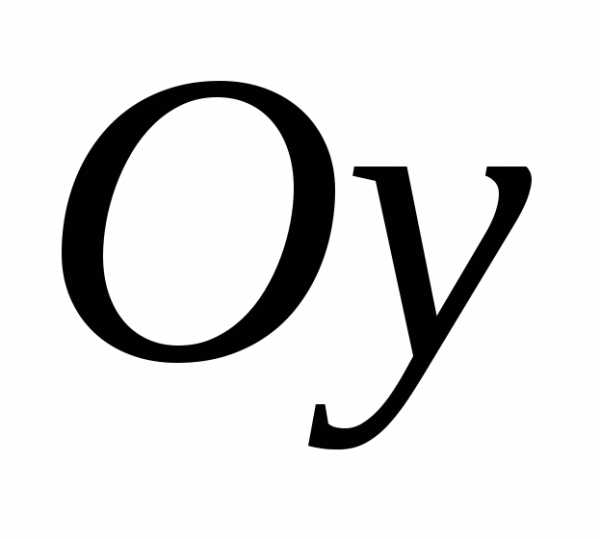 в 2 раза и получаем требуемый график.
в 2 раза и получаем требуемый график.