Известен угол как найти угол между медианами

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Треугольники общего вида

Треугольники общего вида.

Основные свойства треугольников:

1. Сумма всех углов в треугольнике равна $180°$.
2. В равнобедренном треугольнике углы при основании равны.
3. В равнобедренном треугольнике высота, проведенная к основанию, одновременно является медианой и биссектрисой.
4. В равностороннем треугольнике все углы по $60°$.
5. Внешний угол треугольника равен сумме двух углов, не смежных с ним.
6. Средняя линия треугольника параллельна основанию и равна его половине.

$MN$ — средняя линия, так как соединяет середины соседних сторон.

Биссектриса — это линия, которая делит угол пополам.

1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
3. Биссектрисы смежных углов перпендикулярны.
4. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.

Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.

Свойства медиан:

1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.

2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.

3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.

Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.

Свойства высот:

1. Три высоты (или их продолжения) пересекаются в одной точке.

2. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.

3. Высоты треугольника обратно пропорциональны его сторонам:

Прямоугольный треугольник и его свойства:

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна 90 градусов.

2. Катет прямоугольного треугольника, лежащий напротив угла в 30 градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

3. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности (R)

4. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.

5. В прямоугольном треугольнике радиус вписанной окружности равен: $r=/<2>$ , где $а$ и $b$ – это катеты, $с$ – гипотенуза.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$<1>/<2>$	$<√2>/<2>$	$<√3>/<2>$
$cosα$	$<√3>/<2>$	$<√2>/<2>$	$<1>/<2>$
$tgα$	$<√3>/<3>$	$1$	$√3$
$ctgα$	$√3$	$1$	$<√3>/<3>$

Тригонометрические тождества:

1. Основное тригонометрическое тождество:

2. Связь между тангенсом и косинусом одного и того же угла:

3. Связь между котангенсом и синусом одного и того же угла:

Подобие треугольников

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.

Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)

1. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
2. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Признаки подобия треугольников:

1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Теорема синусов

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

В треугольнике $АВС ВС=16, sin∠A=<4>/<5>$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.

Воспользуемся теоремой синусов:

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности

Далее подставим числовые данные и найдем $R$

Теорема косинусов

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Как найти угол между медианой и высотой в прямоугольном треугольнике, если известны его острые углы?

Острые углы прямоугольного треугольника равны α и β (β>α). Найти угол между медианой и высотой, проведенными из вершины прямого угла.

Дано: ∆ ABC, ∠C=90º,

CK — медиана,

CF- высота,

∠A=α, ∠B=β, β>α.

Найти: ∠FCK.

Решение:

Так как сумма острых углов прямоугольного треугольника равна 90º, в треугольнике ABC ∠A+∠B=90º, то есть α+β=90º. Значит, β=90º-α.

По свойству прямоугольного треугольника,

   

Следовательно, треугольник ACK- равнобедренный с основанием AC. Отсюда, ∠ACK=∠A=α (как углы при основании равнобедренного треугольника).

Рассмотрим треугольник ACF — прямоугольный (∠CFA=90º, так как CF — высота).

∠A+∠ACF=90º, откуда ∠ACF=90º-∠A=90º-α=β.

∠FCK=∠ACF-∠ACK=β-α.

Вывод: угол между медианой и высотой, проведёнными к гипотенузе, равен разности острых углов прямоугольного треугольника.

Поскольку две другие высоты прямоугольного треугольника совпадают с его катетами, то угол между медианой и высотой, проведённой к катету, есть угол между медианой и другим катетом. Для нахождения этих углов требуются дополнительные данные.

∠CBP — угол между медианой BP и высотой BC

(высота BC является также катетом).

∠CAE — угол между медианой AE и высотой AC

(высота AC является катетом).

Как найти угол между медианой и стороной

Задача по нахождению угла многоугольника при известных нескольких его параметров достаточно проста. В случае определения угла между медианой треугольника и одной из сторон удобно использовать векторный способ. Для того чтобы задать треугольник, достаточно двух векторов его сторон.

Инструкция

На рис. 1 треугольник достроен до соответствующего ему параллелограмма. При этом известно, что в точке пересечения диагоналей параллелограмма они делятся пополам. Поэтому АО является медианой треугольника АВС, опущенная из А на сторону ВС.
Из этого можно заключить, что необходимо найти угол φ между стороной АС треугольника и медианой АО. Такой же угол, в соответствии с рис. 1, имеется между вектором а и вектором d, соответствующим диагонали параллелограмма AD. По правилу параллелограмма вектор d равен геометрической сумме векторов a и b, d = a + b.

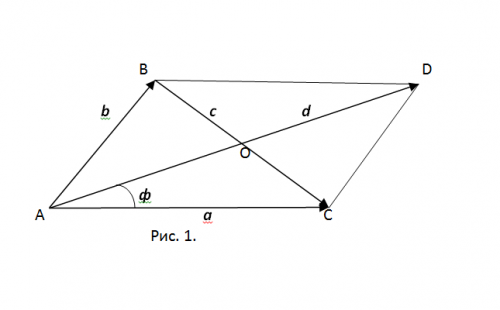
Остается найти способ определения угла φ. Для этого следует использовать скалярное произведение векторов. Скалярное произведение удобнее всего определить на основе тех же векторов a и d, которое определяется по формуле (a, d)= |a||d|cosφ. Здесь φ – угол между векторами a и d. Поскольку скалярное произведение векторов, заданных координатами, определяется выражением:
(a(ax, ay), d(dx, dy))=axdx+aydy, |a|^2= ax^2+ ay^2, |d|^2= dx^2+ dy^2, то
cosφ=(axdx+aydy)/(sqrt(ax^2+ ay^2)sqrt(dx^2+ dy^2)). Кроме того, сумма векторов в координатной форме определяется выражением: d(dx, dy) = a(ax, ay) + b(bx, by)= {ax+bx, ay+by}, то есть dx= ax+bx, dy=ay+by.

Пример. Треугольник АВС задан векторами a(1,1) и b(2, 5) в соответствии с рис.1. Найти угол φ между его медианой АО и стороной треугольника АС.
Решение. Как уже было показано выше, для этого достаточно найти угол между векторами а и d.
Этот угол задается его косинусом и вычисляется в соответствии со следующим тождеством
cosφ=(axdx+aydy)/(sqrt(ax^2+ ay^2)sqrt(dx^2+ dy^2)).
1. d(dx, dy) = {1+2, 1+5} = d(3, 6).
2. cosφ=(3+6)/(sqrt(1+1)sqrt(9+36))=9/(3sqrt(10))=3/sqrt(10).
φ=arcos(3/sqrt(10)).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Итак, что нам известно? Треугольник АВС, ВМ — медиана треугольника, ВМ = АМ = СМ. По сути, это — два равнобедренных треугольника с одной общей стороной, ВМ.

Опускаем из М две медианы: на АВ — медиану МК и на ВС — медиану МН. У нас получается четырёхугольник МКВН.

Поскольку в равнобедренных треугольниках медиана является также и высотой, можно сделать вывод, что углы МКВ и МНВ — прямые, их размер составляет 90*. Треугольник АКМ равен треугольнику КМВ, а треугольник МНВ — треугольнику МНС, по двум сторонам и углу между ними: КМ — общая, АК = ВК по условию (не забудем, что МК — медиана!) и углы между ними равны 90* (она же ещё и высота!). То же самое можно сказать и о треугольниках МНВ и МНС -они равны. Значит, равны и углы КАМ и КВМ, с одной стороны, и НВМ и МСН — с другой. Значит, сумма углов КМВ и ВМН равна сумме углов МВК и МВН. А если у четырёхугольника два противоположных угла прямые и ещё два противоположных угла равны, значит, перед нами — прямоугольник, то есть все углы у него — прямые. И угол АВС составляет 90*.

Для вас несколько заданий — в условии дан прямоугольный треугольник. В условии говорится о вычислении углов между высотой и биссектрисой, медианой и биссектрисой, высотой и медианой проведёнными из прямого угла.

Это группа заданий входит в состав ЕГЭ по математике. Задачи несложные, требуется знание теоремы о сумме углов треугольника, свойств равнобедренного треугольника и немного логики. Да! Есть один нюанс — задачи, в  которых говорится о медиане проведённой к гипотенузе необходимо знать одно свойство, теорию можно посмотреть здесь. Приступим!

Один острый угол прямоугольного треугольника в 4 раза больше другого.  Найдите больший острый угол. Ответ дайте в градусах.

Обозначим меньший острый угол прямоугольного треугольника через x. Тогда больший острый угол данного  треугольника будет равен 4х.

По свойству прямоугольного треугольника сумма его острых углов равна 90^о. Отсюда получаем уравнение  х + 4х = 90^о.

Вычисляем, получим 5х = 90^о,  х = 18^о.

Следовательно больший угол будет равен 18^о ∙ 4 = 72^о

Ответ: 72

Острый угол прямоугольного треугольника равен 32^о. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Нам необходимо найти угол COD. По условию известно, что CE и AD  — это  биссектрисы (делят углы пополам). Это означает, что угол CAD равен 32^о, а угол ACO равен 45^о. По теореме о сумме углов треугольника мы можем найти угол AOC, и далее угол COD. Итак, известно, что сумма углов треугольника равна 180^о, следовательно

Углы AOC и COD  смежные, то есть их сумма равна 180^о. Таким образом, искомый угол (острый угол между данными биссектрисами) равен 61 градусу.

Ответ: 61

*Если в подобных задачах вы сразу не видите ход решения, то ищите те элементы, которые можно найти исходя из условия в первую очередь. А далее уже используйте найденные значения.

Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

В условии нам не даны ни какие величины, кроме того, что угол С прямой. Это говорит  о том, что их необходимо ввести, то есть в данном случае мы можем обозначить угол через переменную,  а далее использовать свойства прямоугольного треугольника и теорему о сумме углов.

Обозначим угол CAD как х. Тогда угол CBA будет равен 90^о – х.

Рассмотрим треугольник AOB:

Можем найти угол AOB:

Значит острый угол между биссектрисами будет равен 45^о, так является смежным углу 135^о.

Как видите, не всегда нужны численные величины в условии. Достаточно знать свойства, включить логику и задача будет решена.

Ответ: 45

В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21^о. Найдите меньший угол данного треугольника. Ответ дайте в градусах. 

Сразу отметим, что в треугольнике CDH нам известны два угла. Используя теорему о сумме углов треугольника мы можем найти угол CDH. То есть:

Теперь мы можем найти угол В в треугольнике CDВ. Так как CD биссектриса, то угол BCD равен 45^о, угол CDB мы нашли.

Значит угол В равен 180^о–45^о–69^о=66^о. По свойству прямоугольного треугольника: сумма острых углов в нём равна 90 градусов.

Следовательно  другой острый угол будет равен 24^о.

Ответ: 24

Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14^о. Найдите меньший угол этого треугольника. Ответ дайте в градусах. 

Нам дан угол MCD равный 14^о. Так же нам известен угол DCB, он равен 45^о, так как CD биссектриса. Можем найти угол MCB: 14^о + 45^о = 59^о.

Как уже сказано, медиана в прямоугольном треугольнике проведённая из прямого угла к гипотенузе равна её половине. То есть, она разбивает прямоугольный треугольник на два равнобедренных треугольника, в данном случае AMC и BMC. Известно, что в равнобедренном треугольнике углы при основании равны, то есть угол MBC равен углу BCM. Таким образом,

То есть, меньший угол равен 31^о.

Ответ: 31

Один острый угол прямоугольного треугольника на 32^о  больше другого. Найдите больший острый угол. Ответ дайте в градусах.

Посмотреть решение

В треугольнике АВС угол С равен 90^о, СН  — высота, угол А равен 34^о. Найдите угол ВСН. Ответ дайте в градусах.

Посмотреть решение

В треугольнике ABC CD  — медиана, угол ACB равен 90^о, угол В равен 58^о. Найдите угол ACD. Ответ дайте в градусах.

Посмотреть решение

Острые углы прямоугольного треугольника равны 29^о  и 61^о. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Посмотреть решение

Острые углы прямоугольного треугольника равны 24^о и 66^о. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Посмотреть решение

В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40^о. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Посмотреть решение

Острые углы прямоугольного треугольника равны 24^о и 66^о. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Посмотреть решение

Какие общие рекомендации можно дать?

1. Используйте теорему о сумме углов треугольника. Это одна из основных теорем, связанных с треугольниками, её нужно всегда помнить.

2. Нужно чётко помнить, что такое медиана, биссектриса, высота (не перепутать).

3. Запомните свойство медианы  в прямоугольном треугольнике.

4. В задачах, где в условии не даны численные величины углов, обозначайте их переменной(ыми) и далее используйте известные вам свойства.

5. Если не видите каким путём строить решение, и сразу не можете увидеть логическую цепочку рассуждений, то исходя из данных в условии ищите то, что возможно найти. Получив новые величины, также смотрите, что вы можете найти при их использовании.

На этом всё. Успеха Вам!

С уважением, Александр

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.