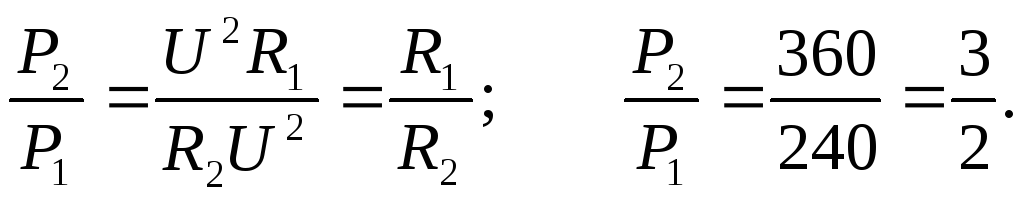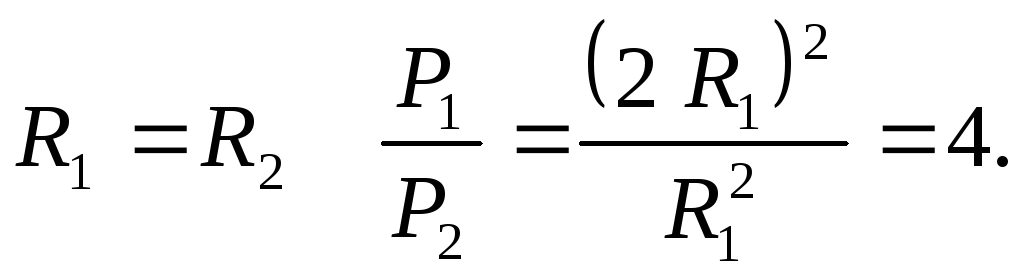Известна мощность как найти внутреннее сопротивление - Исправление недочетов и поиск решений вместе с Examum.ru

Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!

Идеальный источник ЭДС

Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Внутреннее сопротивление источника ЭДС

Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.

Выглядит все это в аккумуляторе примерно вот так:

Цепляем лампочку

Итак, что у нас получается в чистом виде?

Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

На резисторе R падает напряжение U_R , а на внутреннем резисторе r падает напряжение U_r .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Закон Ома для полной цепи

Итак, последнее выражение носит название «закон Ома для полной цепи»

где

Е — ЭДС источника питания, В

R — сопротивление всех внешних элементов в цепи, Ом

I — сила ток в цепи, А

r — внутреннее сопротивление источника питания, Ом

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

[quads id=1]

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

Вывод

Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.

Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.

Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.

Источник

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд q = It . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0) , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина R + r неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0) .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор R + r ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд q = It , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на R + r :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда Кл.

Ответ: 1500.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Полная мощность

(12.10)

Полезная мощность максимальна

(12.11)

Коротким
замыканием называется режим работы
цепи, при котором внешнее сопротивление
R
= 0. При этом

(12.12)

Полезная
мощность Р_а=
0.

Полная мощность

(12.13)

График
зависимости Р_а(I)
– парабола, ветви которой направлены
вниз (рис12.1). На этом же рисунке показаны
зависимость КПД 
от силы тока.

Примеры решения задач

Задача
1. Батарея
состоит из n
= 5 последовательно соединённых элементов
с Е
= 1,4 В и внутренним сопротивлением r
= 0,3 Ом каждый. При каком токе полезная
мощность батареи равна 8 Вт? Какова
наибольшая полезная мощность батареи?

Дано: Решение

n
= 5
При последовательном соединении
элементов ток в цепи

Е
= 1,4 В

(1)

Р_а
= 8 Вт Из формулы полезной
мощности

выразим

внешнее
сопротивление
R
и подставим в формулу (1)

I
— ?
-?

после
преобразований получим квадратное
уравнение, решая которое, найдём значение
токов:

А;
I₂
=
A.

Итак,
при токах I₁
и I₂
полезная мощность одинакова. При анализе
графика зависимости полезной мощности
от тока видно, что при I₁
потери мощности меньше и КПД выше.

Полезная
мощность максимальна при R
= n
r;
R
= 0,3
Ом.

Ответ:
I₁
= 2 A; I₂
=
A;P_amax
=Вт.

Задача
2. Полезная
мощность, выделяемая во внешней части
цепи, достигает наибольшего значения
5 Вт при силе тока 5 А. Найти внутреннее
сопротивление и ЭДС источника тока.

Дано: Решение

P_amax
= 5 Вт Полезная мощность
(1)

I
= 5 A
по закону Ома
(2)

.полезная
мощность максимальна при R
= r,
то из

r
— ? Е
— ? формулы (1)
0,2
Ом.

Из
формулы (2)

В.

Ответ:
r
= 0,2 Ом; Е
= 2 В.

Задача
3. От генератора,
ЭДС которого равна 110В, требуется передать
энергию на расстояние 2,5 км по двухпроводной
линии. Потребляемая мощность равна 10
кВт. Найти минимальное сечение медных
подводящих проводов, если потери мощности
в сети не должны превышать 1 %.

Дано:

Решение

Е
= 110 В
Сопротивление проводов

l
= 510³
м где 
— удельное сопротивление меди; l
– длина проводов;

Р_а
= 10⁴
Вт S
– сечение.

 =
1,710^-8
Ом^.м
Потребляемая мощность P_a
= I
E,
мощность, теряемая

Р_пр
= 100 Вт в
сети P_пр
= I
²
R_пр,
а так как в пороводах и потребителе

S
— ?
ток
одинаковый,
то

откуда

Подставив числовые значения, получим

м².

Ответ:
S
= 710^-3
м².

Задача
4. Найти
внутреннее сопротивление генератора,
если известно, что мощность, выделяемая
во внешней цепи, одинакова при двух
значениях внешнего сопротивления R₁
= 5 Ом и R₂
= 0,2 Ом. Найти КПД генератора в каждом из
этих случаев.

Дано:
Решение

Р₁
= Р₂
Мощность, выделяемая во внешней цепи,
P_a
= I
²
R.
По закону Ома

R₁
= 5 Ом для замкнутой цепи
тогда.

R₂
= 0,2 Ом Используя условие задачи Р₁
= Р₂,
получим

r
-?

Преобразуя
полученное равенство, находим внутреннее
сопротивление источника r:

Ом.

Коэффициентом
полезного действия называется величина

где
Р_а
– мощность, выделяемая во внешней цепи;
Р
– полная мощность.

Ответ:
r
= 1 Ом;
=
83 %;=
17 %.

Задача
5. ЭДС батареи
Е
= 16 В, внутреннее сопротивление r
= 3 Ом. Найти сопротивление внешней цепи,
если известно, что в ней выделяется
мощность Р_а
= 16 Вт. Определить КПД батареи.

Дано:

Решение

Е
= 16 В Мощность, выделяемая во
внешней части цепи Р_а
= I
²
R.

r
= 3 Ом
Силу тока найдём по закону Ома для
замкнутой цепи:

Р_а
= 16 Вт тогда
или

—
? R
— ? Подставляем числовые значения
заданных величин в это квадратное
уравнение и решаем его относительно R:

Ом;
R₂
= 9 Ом.

Ответ:
R₁
= 1 Ом; R₂
= 9 Ом;

Задача
6. Две
электрические лампочки включены в сеть
параллельно. Сопротивление первой
лампочки 360 Ом, сопротивление второй
240 Ом. Какая из лампочек поглощает большую
мощность? Во сколько раз?

Дано:

Решение

R₁
= 360 Ом Мощность, выделяемая в
лампочке,

R₂
= 240 Ом
P
= I ²
R
(1)

—
?
При параллельном соединении на лампочках
будет одинаковое напряжение, поэтому
сравнивать мощности лучше, преобразовав
формулу (1) используя закон Ома

тогда

При параллельном
соединении лампочек большая мощность
выделяется в лампочке с меньшим
сопротивлением.

Ответ:

Задача
7. Два
потребителя сопротивлениями R₁
= 2 Ом и R₂
= 4 Ом подключаются к сети постоянного
тока первый раз параллельно, а второй
– последовательно. В каком случае
потребляется большая мощность от сети?
Рассмотреть случай, когда R₁
= R₂.

Дано:

Решение

R₁
= 2 Ом Потребляемая от сети мощность

R₂
= 4 Ом
(1)

—
? где
R
– общее сопротивление потребителей;
U
– напряжение в сети. При параллельном
соединении потребителей их общее
сопротивление
а при последовательномR
= R₁
+ R₂.

В
первом случае, согласно формуле (1),
потребляемая мощность
а во второмоткуда

Таким образом, при
параллельном подключении нагрузок
потребляется большая мощность от сети,
чем при последовательном.

При

Ответ:

Задача
8.. Нагреватель
кипятильника состоит из четырёх секций,
сопротивление каждой секции R
= 1 Ом. Нагреватель питается от аккумуляторной
батареи с Е
= 8
В и внутренним
сопротивлением r
= 1 Ом. Как следует подключить элементы
нагревателя, чтобы вода в кипятильнике
нагрелась в максимально короткий срок?
Каковы при этом полная мощность,
расходуемая аккумулятором, и его КПД?

Дано:

R₁
= 1 Ом

n
= 4

Е
= 8 В

r
= 1 Ом

Решение

Мак
симальную
полезную мощность источник даёт в
случае, если внешнее сопротивление R
равно внутреннему r.

Следовательно,
чтобы воданагрелась
в максимально короткий срок, нужно
секции включить так,

чтобы
R
= r.
Это условие выполняется при смешанном
соединении секций (рис.12.2.а,б).

Мощность,
которую расходует аккумулятор, равна
Р
= I
E.
По закону Ома для замкнутой цепи
тогда

Вычислим
32
Вт;

Ответ:
Р
= 32 Вт; 
= 50 %.

Задача
9*. Ток в
проводнике сопротивлением R
= 12 Ом равномерно убывает от I₀
= 5 А до нуля в течение времени 
= 10 с. Какое количество теплоты выделяется
в проводнике за это время?

Дано:

R
= 12 Ом

I₀
= 5 А

I
= 0

 =
10 с

Q
— ?

Решение

Так
как сила тока в проводнике изменяется,
то для подсчёта количества теплоты
формулой Q
= I
²R
t
воспользоваться нельзя.

Возьмём
дифференциал dQ
= I
²R
dt,
тогда
В силу равномерности изменения тока
можно записатьI
= k
t,
где k
– коэффициент пропорциональности.

Значение
коэффициента пропорциональности k
найдём из условия, что при 
= 10 с ток I₀
= 5 А, I₀
= k,
отсюда

Подставим
числовые значения:

Дж.

Ответ:
Q
= 1000 Дж.

Соседние файлы в папке Часть 2

Источник

Содержание

1 Как рассчитать сопротивление зная мощность и напряжение?
2 Как узнать амперы зная мощность?
3 Как сопротивление зависит от мощности?
4 Как найти сопротивление Ом?
5 Как рассчитать ток по мощности?
6 Как найти сопротивление из формулы мощности?
7 Сколько идет ампер на 1 квт?
8 Сколько ватт в 1 ампере 12 вольт?
9 Чему равен 1 ампер?
10 Как сила тока зависит от мощности?
11 Как рассчитать мощность?
12 Какая буква обозначает мощность?
13 Как найти сопротивление при параллельном соединении?
14 Как найти общее сопротивление в электрической цепи?

Как рассчитать сопротивление зная мощность и напряжение?

Узнать мощность, если известны напряжение и сопротивление. W = 220 в * 220 в / 500 ом = 96.8 вт.

Как узнать амперы зная мощность?

Таким образом, чтобы получить амперы, нужно ватты разделить на вольты питания — мощность разделить на напряжение I = P/U (вольт в бытовой сети 220-230). Бывает часто, что на сетевом электроприборе мощность указана в киловаттах (кВт), тогда может потребоваться перевести киловатты в амперы.

Как сопротивление зависит от мощности?

Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление. … В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.

Как найти сопротивление Ом?

Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I. Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.

Как рассчитать ток по мощности?

Формула расчета мощности электрического тока

Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.

Как найти сопротивление из формулы мощности?

U = (P*R)
…
Электрическое сопротивление:

R = U / I.
R = U 2/ P.
R = P / I.

Сколько идет ампер на 1 квт?

Сколько ампер в киловатте и сколько киловатт в ампере

Поскольку в одном киловатте 1000 ватт, то для сетевого напряжения в 220 вольт можно принять, что в одном киловатте 4,54 ампера, потому что I = P/U = 1000/220 = 4,54 ампер.

Сколько ватт в 1 ампере 12 вольт?

А значит, если имеем дело с автомобильной сетью на 12 вольт, то 1 ампер — это 12 Ватт, а в бытовой электросети 220 V такая сила тока будет в электроприборе мощностью 220 Вт (0,22 кВт). В промышленном оборудовании, питающемся от 380 Вольт, целых 657 Ватт.

Чему равен 1 ампер?

Ампе́р (обозначение: А) — единица измерения силы электрического тока в системе СИ, а также единица магнитодвижущей силы и разности магнитных потенциалов (устаревшее наименование — ампер-виток). 1 Ампер это сила тока, при которой через проводник проходит заряд 1 Кл за 1 сек.

Как сила тока зависит от мощности?

Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (напряжению) и силе тока в цепи.

Как рассчитать мощность?

Определите мощность источника питания.

Напряжение – это величина, характеризующая электрическое поле, создаваемое током. Мощность равна произведению силы тока на напряжение, то есть 1 Вт = 1 А х 1 В. Формула: Р = I х V. Например, если сила тока равна 3 А, а напряжение равно 110 В, то мощность равна: 3 х 110 = 330 Вт.

Какая буква обозначает мощность?

Обычно в формулах механики обозначается символом N. В электротехнике обычно обозначается символом P — от лат. potestas (сила, мощь, действенность); Иногда используется символ W (от англ.

Как найти сопротивление при параллельном соединении?

Общее сопротивление цепи при параллельном соединении проводников определяется по формуле: 1 R = 1 R 1 + 1 R 2 . Обратное значение общего сопротивления равно сумме обратных значений сопротивлений отдельных проводников. Для проверки формулы можно использовать омметр.

Как найти общее сопротивление в электрической цепи?

Формула для вычисления общего сопротивления последовательной цепи: Req = R1 + R2 + …. Rn где n — общее количество резисторов в цепи, соединенных последовательно. Таким образом, сопротивления всех резисторов просто суммируются. Например, найдем сопротивление цепи, показанной на рисунке.

Источник

Содержание

1 Рассчитать мощность по сопротивлению и напряжению. Расчет мощности по току и напряжению
- 1.1 Негативное воздействие реактивной нагрузки
- 1.2 Расчет потребляемой мощности
- 1.3 Калькулятор мощности онлайн
- 1.4 Способы расчета сопротивления по математическим формулам
2 Закона Ома и применение его на практике
- 2.1 Формула Закона Ома
- 2.2 Формула Закона Джоуля-Ленца
- 2.3 Преобразованные формулы Закона Ома и Джоуля-Ленца
3 Как найти силу тока в цепи
- 3.1 Если известна мощность и напряжение
- 3.2 Если известно напряжение или мощность и сопротивление
- 3.3 Если известно ЭДС, внутреннее сопротивление и нагрузка
- 3.4 Закон Джоуля-Ленца
- 3.5 Несколько примеров
4 Как рассчитать мощность, силу тока и напряжение: разбираемся во взаимосвязях этих величин
- 4.1 Основные понятия величин
- 4.2 Сила электрического тока
- 4.3 Напряжение в бытовых сетях
- 4.4 Нюансы в понятии мощности электроприборов
- 4.5 Линейные и фазные соотношения
- 4.6 Взаимосвязь основных величин
- 4.7 Выводы и полезное видео по теме
5 Закон Ома для участка цепи. Определение, формула расчета, калькулятор
- 5.1 Закон Ома и резистор
- 5.2 Закон Ома — формула
- 5.3 Закон Ома — мощность
- 5.4 Закон Ома — калькулятор

Рассчитать мощность по сопротивлению и напряжению. Расчет мощности по току и напряжению

Расчет электрической мощности

В прошлой статье мы с вами вывели формулу для определения мощности в электрической цепи: умножая напряжение в «вольтах» на силу тока в «амперах», мы получаем мощность в «ваттах». Давайте применим ее к следующей схеме:

В этой схеме есть две известные нам величины: напряжение батареи составляет 18 вольт, а сопротивление лампы — 3 ома. Используя Закон Ома мы определим третью величину — силу тока:

Теперь, зная силу тока, мы можем умножить ее значение на напряжение и получить мощность:

Это означает что лампа рассеивает 108 ватт энергии в форме сета и тепла.

Давайте в этой же схеме увеличим напряжение батареи и посмотрим что произойдет. Интуиция подсказывает нам, что при увеличении напряжения и неизменном сопротивлении, сила тока в цепи также увеличится. А это значит, что увеличится и мощность:

В этой схеме напряжение батареи изменено и составляет 36 вольт вместо прежних 18. Сопротивление лампы не изменилось, и равно 3 омам. Сила тока теперь будет равна:

Давайте обсудим полученное значение. Если I=U/R, и мы удваиваем значение напряжения (U), оставляя неизменным сопротивление, то по логике вещей сила тока у нас тоже должна удвоиться. Действительно, сила тока в данной схеме имеет значение 12 ампер вместо прежних 6. А сейчас давайте вычислим мощность:

Обратите внимание, что мощность у нас также увеличилась по сравнению с предыдущим примером, и увеличилась она значительнее, чем увеличилась сила тока. Почему так получилось? Ответ на этот вопрос прост. Мощность является функцией напряжения умноженного на силу тока, а так как обе эти величины удвоились по сравнению с предыдущими значениями, то мощность увеличилась в 2х2 или в 4 раза. Вы можете проверить эту цифру разделив 432 ватта на 108 ватт и увидев, что соотношение между ними равно 4.

При проектировании любых электрических цепей выполняется расчет мощности. На его основе производится выбор основных элементов и вычисляется допустимая нагрузка. Если расчет для цепи постоянного тока не представляет сложности (в соответствии с законом Ома, необходимо умножить силу тока на напряжение — Р=U*I), то с вычислением мощности переменного тока — не все так просто. Для объяснения потребуется обратиться к основам электротехники, не вдаваясь в подробности, приведем краткое изложение основных тезисов.

В цепях переменного тока расчет мощности ведется с учетом законов синусоидальных изменений напряжения и тока. В связи с этим введено понятие полной мощности (S), которая включает в себя две составляющие: реактивную (Q) и активную (P). Графическое описание этих величин можно сделать через треугольник мощностей (см. рис.1).

Под активной составляющей (Р) подразумевается мощность полезной нагрузки (безвозвратное преобразование электроэнергии в тепло, свет и т.д.). Измеряется данная величина в ваттах (Вт), на бытовом уровне принято вести расчет в киловаттах (кВт), в производственной сфере – мегаваттах (мВт).

Реактивная составляющая (Q) описывает емкостную и индуктивную электронагрузку в цепи переменного тока, единица измерения этой величины Вар.

Рис. 1. Треугольник мощностей (А) и напряжений (В)

В соответствии с графическим представлением, соотношения в треугольнике мощностей можно описать с применением элементарных тригонометрических тождеств, что дает возможность использовать следующие формулы:

S = √P 2 +Q 2, — для полной мощности;
и Q = U*I*cos⁡ φ , и P = U*I*sin φ — для реактивной и активной составляющих.

Эти расчеты применимы для однофазной сети (например, бытовой 220 В), для вычисления мощности трехфазной сети (380 В) в формулы необходимо добавить множитель – √3 (при симметричной нагрузке) или суммировать мощности всех фаз (если нагрузка несимметрична).

Для лучшего понимания процесса воздействия составляющих полной мощности давайте рассмотрим «чистое» проявление нагрузки в активном, индуктивном и емкостном виде.

Возьмем гипотетическую схему, в которой используется «чистое» активное сопротивление и соответствующий источник переменного напряжения. Графическое описание работы такой цепи продемонстрировано на рисунке 2, где отображаются основные параметры для определенного временного диапазона (t).

Рисунок 2. Мощность идеальной активной нагрузки

Мы можем увидеть, что напряжение и ток синхронизированы как по фазе, так и частоте, мощность же имеет удвоенную частоту. Обратите внимание, что направление этой величины положительное, и она постоянно возрастает.

Как видно на рисунке 3, график характеристик емкостной нагрузки несколько отличается от активной.

Рисунок 3. График идеальной емкостной нагрузки

Частота колебаний емкостной мощности вдвое превосходит частоту синусоиды изменения напряжения. Что касается суммарного значения этого параметра, в течение одного периода гармоники оно равно нулю. При этом увеличения энергии (∆W) также не наблюдается. Такой результат указывает, что ее перемещение происходит в обоих направлениях цепи. То есть, когда увеличивается напряжение, происходит накопление заряда в емкости. При наступлении отрицательного полупериода накопленный заряд разряжается в контур цепи.

В процессе накопления энергии в емкости нагрузки и последующего разряда не производится полезной работы.

Представленный ниже график демонстрирует характер «чистой» индуктивной нагрузки. Как видим, изменилось только направление мощности, что касается наращения, оно равно нулю.

Негативное воздействие реактивной нагрузки

В приведенных выше примерах рассматривались варианты, где присутствует «чистая» реактивная нагрузка. Фактор воздействия активного сопротивления в расчет не принимался. В таких условиях реактивное воздействие равно нулю, а значит, можно не принимать его во внимание. Как вы понимаете, в реальных условиях такое невозможно. Даже, если гипотетически такая нагрузка бы существовала, нельзя исключать сопротивление медных или алюминиевых жил кабеля, необходимого для ее подключения к источнику питания.

Реактивная составляющая может проявляться в виде нагрева активных компонентов цепи, например, двигателя, трансформатора, соединительных проводов, питающего кабеля и т.д. На это тратится определенное количество энергии, что приводит к снижению основных характеристик.

Реактивная мощность воздействует на цепь следующим образом:

не производит ни какой полезной работы;
вызывает серьезные потери и нештатные нагрузки на электроприборы;
может спровоцировать возникновение серьезной аварии.

Именно по этому, производя соответствующие вычисления для электроцепи, нельзя исключать фактор влияния индуктивной и емкостной нагрузки и, если необходимо, предусматривать использование технических систем для ее компенсации.

Расчет потребляемой мощности

В быту часто приходится сталкиваться с вычислением потребляемой мощности, например, для проверки допустимой нагрузки на проводку перед подключением ресурсоемкого электропотребителя (кондиционера, бойлера, электрической плиты и т.д.). Также в таком расчете есть необходимость при выборе защитных автоматов для распределительного щита, через который выполняется подключение квартиры к электроснабжению.

В таких случаях расчет мощности по току и напряжению делать не обязательно, достаточно просуммировать потребляемую энергию всех приборов, которые могут быть включены одновременно. Не связываясь с расчетами, узнать эту величину для каждого устройства можно тремя способами:

При расчетах следует учитывать, что пусковая мощность некоторых электроприборов может существенно отличаться от номинальной. Для бытовых устройств этот параметр практически никогда не указывается в технической документации, поэтому необходимо обратиться к соответствующей таблице, где содержатся средние значения параметров стартовой мощности для различных приборов (желательно выбирать максимальную величину).

Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами.

Отцом же науки об электричестве считается французский ученый Кулон — именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор.

Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно — расстоянию между ними, возведенному в квадрат.

Выясним, что же представляет собой понятие электричество? Если коротко, то это — направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз

И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные — притягиваются.

А теперь, перейдем к главному.

Основа-основ науки об электричестве — закон Ома .

Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению:

сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R

Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах.

Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах.

Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах.

Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом .

Вся остальная электротехника «пляшет» от этого.

А теперь — о мощности электрического тока

В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.

Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.

Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:

P = U*I.

Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление .

Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.

Вот так — ничего сложного!

Каждый человек ежедневно пользуется бытовыми приборами, которые имеют электрическую цепь. Онлайн расчет нагрузки в Амперах и Ватах. Это определенная «дорога» для электрического тока, вырабатываемая энергия передается агрегату и запускает его действие.

Все устройства условно разделяются на три группы как источники электроэнергии (первичные и вторичные), преобразующие агрегаты (осветительные и тепловые приборы), а также элементы вспомогательного назначения – коммутаторы, провода, измерительное оборудование, обеспечивающие работу цепи в реальных условиях.

Все эти приборы входят в общий электромагнитный процесс и имеют свой класс электрической цепи, которая создается для обеспечения эффективной функциональности устройства, требуемого режима работы. Быстро узнать сколько Ват в Ампере поможет сервис расчета мощности.

Калькулятор мощности онлайн

Это надежный помощник в работе при расчете мощности электрической цепи, позволяющий за несколько секунд получить готовый 99,9% результат. Пользователь может за считанные минуты продумать массу вариантов и выбрать наиболее оптимальный. Вероятность ошибки сводится к минимуму.J = U/R; U = R×J; R = U/J; P=U²/R

Чтобы осуществить расчет электрических цепей онлайн необходимо вести в готовую таблицу два значения, напряжение (В) и ток (А). А после нажать на кнопку «Вычислить» и получить сиюминутный результат данных сопротивления (Ом) и мощности (Вт) при заданных пользователем параметрах.

Данный онлайн калькулятор мощности для расчета электрических цепей является автоматической, нужно быть внимательными при введении всех показателей. Если число состоит из целой и дробной части, то разделять их нужно точкой, а не запятой.

Способы расчета сопротивления по математическим формулам

Чтобы сделать расчет сопротивления электрических цепей можно применить всем известную формулу Закона Ома

Источник: https://enbima.ru/calculate-the-power-by-resistance-and-voltage-calculation-of-current-and-voltage.html

Закона Ома и применение его на практике

В природе существует два основных вида материалов, проводящие ток и не проводящие (диэлектрики). Отличаются эти материалы наличием условий для перемещения в них электрического тока (электронов).

Из токопроводящих материалов (медь, алюминий, графит, и многие другие), делают электрические проводники, в них электроны не связаны и могут свободно перемещаться.

В диэлектриках электроны привязаны к атомам намертво, поэтому ток в них течь не может. Из них делают изоляцию для проводов, детали электроприборов.

Для того чтобы электроны начали перемещаться в проводнике (по участку цепи пошел ток), им нужно создать условия. Для этого в начале участка цепи должен быть избыток электронов, а в конце – недостаток. Для создания таких условий используют источники напряжения – аккумуляторы, батарейки, электростанции.

Формула Закона Ома

В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.

Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.

Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.

где I – сила тока, измеряется в амперах и обозначается буквой А; U – напряжение, измеряется в вольтах и обозначается буквой В; R – сопротивление, измеряется в омах и обозначается Oм.

Если известны напряжение питания U и сопротивление электроприбора R, то с помощью выше приведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I.

С помощью закона Ома рассчитываются электрические параметры электропроводки, нагревательных элементов, всех радиоэлементов современной электронной аппаратуры, будь то компьютер, телевизор или сотовый телефон.

На практике часто приходится определять не силу тока I, а величину сопротивления R. Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления R, зная протекающий ток I и величину напряжения U.

Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению.

Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения.

Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.

Формула Закона Джоуля-Ленца

Величину резистора для изготовления блока нагрузки для блока питания компьютера мы рассчитали, но нужно еще определить какой резистор должен быть мощности? Тут поможет другой закон физики, который, независимо друг от друга открыли одновременно два ученых физика. В 1841 году Джеймс Джоуль, а в 1842 году Эмиль Ленц. Этот закон и назвали в их честь – Закон Джоуля-Ленца.

Потребляемая нагрузкой мощность прямо пропорциональна приложенной величине напряжения и протекающей силе тока. Другими словами, при изменении величины напряжения и тока будет пропорционально будет изменяться и потребляемая мощность.

где P – мощность, измеряется в ваттах и обозначается Вт; U – напряжение, измеряется в вольтах и обозначается буквой В; I – сила ток, измеряется в амперах и обозначается буквой А.

Зная напряжения питания и силу тока, потребляемую электроприбором, можно по формуле определить, какую он потребляет мощность. Достаточно ввести данные в окошки ниже приведенного онлайн калькулятора.

Закон Джоуля-Ленца позволяет также узнать силу тока, потребляемую электроприбором зная его мощность и напряжение питания. Величина потребляемого тока необходима, например, для выбора сечения провода при прокладке электропроводки или для расчета номинала.

Например, рассчитаем потребляемый ток стиральной машины. По паспорту потребляемая мощность составляет 2200 Вт, напряжение в бытовой электросети составляет 220 В. Подставляем данные в окошки калькулятора, получаем, что стиральная машина потребляет ток величиной 10 А.

Еще один пример, Вы решили в автомобиле установить дополнительную фару или усилитель звука. Зная потребляемую мощность устанавливаемого электроприбора легко рассчитать потребляемый ток и правильно подобрать сечение провода для подключения к электропроводке автомобиля.

Допустим, дополнительная фара потребляет мощность 100 Вт (мощность установленной в фару лампочки), бортовое напряжение сети автомобиля 12 В. Подставляем значения мощности и напряжения в окошки калькулятора, получаем, что величина потребляемого тока составит 8,33 А.

Разобравшись всего в двух простейших формулах, Вы легко сможете рассчитать текущие по проводам токи, потребляемую мощность любых электроприборов – практически начнете разбираться в основах электротехники.

Преобразованные формулы Закона Ома и Джоуля-Ленца

Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой несвязанные между собой четыре сектора и очень удобна для практического применения

По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.

А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.

Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.

Источник: https://YDoma.info/ehlektrotekhnika/electricity-zakon-oma.html

Как найти силу тока в цепи

Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени.

Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций.

В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.

Если известна мощность и напряжение

Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:

P=UI

После несложных мы получаем формулу для вычислений

I=P/U

Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:

Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:

Р1 = Р2/η

Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):

S = P1/cosφ

Определяем потребляемый ток по формуле:

Iном = S/(1,73·U)

Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.

Если известно напряжение или мощность и сопротивление

Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь законом Ома, с его помощью проводим расчёт силы тока через сопротивление и напряжение.

I=U/R

Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:

P=UI

При этом согласно тому же закону Ома:

U=IR

То:

P=I2*R

Значит расчёт проводим по формуле:

I2=P/R

Или возьмем выражение в правой части выражения под корень:

I=(P/R)1/2

Если известно ЭДС, внутреннее сопротивление и нагрузка

Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:

I=E/(R+r)

Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.

Закон Джоуля-Ленца

Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним закон Джоуля-Ленца.

Его формула выглядит так:

Q=I2Rt

Тогда расчет проводите так:

I2=QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt)1/2

Несколько примеров

В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.

1 задача: Рассчитать I в цепи из двух резисторов при последовательном соединении и при параллельном соединении. R резисторов 1 и 2 Ома, источник питания на 12 Вольт.

Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.

R1+R2=1+2=3 Ома

Тогда рассчитать силу тока можно по закону Ома:

I=U/R=12/3=4 Ампера

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67

Тогда дальнейшие вычисления можно проводить так:

I=12*0,67=18А

2 задача: рассчитать ток при смешанном соединении элементов. На выходе источника питания 24В, а резисторы на: R1=1 Ом, R2=3 Ома, R3=3 Ома.

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.

Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома

Теперь схема примет вид:

Далее находим ток по тому же закону Ома:

I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер

Теперь вы знаете, как найти силу тока, зная мощность, сопротивление и напряжение. Надеемся, предоставленные формулы и примеры расчетов помогли вам усвоить материал!

Наверняка вы не знаете:

Источник: https://samelectrik.ru/kak-najti-silu-toka.html

Как рассчитать мощность, силу тока и напряжение: разбираемся во взаимосвязях этих величин

Владельцы квартир, частных домов и других электрифицированных объектов часто сталкиваются с вопросом определения значений основных электрических величин, так как рассчитать мощность по допустимой силе тока и известному напряжению или решить обратную задачу не очень просто.

Прямое применение известного закона Ома без учета особенностей бытовых сетей и приборов может привести к неверному результату.

В этом материале мы разберемся, что такое мощность и расскажем о том, как вычислить этот показатель.

Основные понятия величин

Для электрического тока существует известные зависимости между основными величинами, такими как сила (I, ампер), напряжение (U, вольт), мощность (P, ватт) и сопротивление цепи (R, ом). Обычно, для решения реальных задач, используют первые три параметра, каждый из которых на практике имеет свои нюансы.

Сила электрического тока

Расчет достаточного сечения жил и номинала автоматического выключателя для конкретной ветки электросети проводят согласно значению максимально возможной для этого участка силы тока. Это необходимо для предотвращения ситуации возгорания проводки, что часто приводит к возникновению пожара.

Рабочие параметры автоматов и УЗО выбирают согласно нормативным требованиям. Для определения допустимого сечения жил в зависимости от максимально возможной силы тока необходимо использовать таблицу, предоставленную производителем продукции, потому что кабеля чаще всего произведены по ТУ, а не по ГОСТ.

Имея одинаковую маркировку, кабеля, произведенные по ГОСТу (слева) и по ТУ (справа) отличаются как визуально, так и по основным характеристикам

Так как рассчитать силу электрического тока можно по потребляемой приборами мощности и напряжению сети, то необходимо правильно определить значения этих двух показателей.

Напряжение в бытовых сетях

Многие владельцы квартир считают, что стандартное напряжение в фазе для бытовых нужд приблизительно равно 220 В. В большинство случаев это действительно так. Хотя по ГОСТ 29322-2014 с 01.10.2015 в пределах Российской Федерации должен был произойти переход на совместимую со странами ЕЭС систему 230 В.

Отклонение в 5% от эталона является допустимым на любой срок, а 10% – на период, не превышающий 1 час. Таким образом по старым правилам значение напряжения может колебаться в диапазоне от 198 до 242 В, а по действующему ГОСТу – от 207 до 253 В.

Также есть случаи, когда напряжение в сети длительное время значительно ниже нормативного. Такая ситуация возникает тогда, когда суммарная мощность подключенных к ветке электроприборов гораздо выше запланированной и при включении большинства из них происходит “просадка сети”.

Эта проблема возникает в зоне ответственности организаций, отвечающих за поставку электроэнергии, и связана она с перегрузкой распределительных трансформаторов, изношенностью подстанций или с недостаточным сечением проводов.

Пониженное входное напряжение приводит не только к изменению параметра силы тока и возможному срабатыванию защиты, но и к быстрой поломке электроприборов, содержащих асинхронные электродвигатели или сложную электронику

Для выяснения значения реального напряжения нужно периодически проводить замеры с использованием вольтметра. Если показатели сильно “гуляют”, то необходимо применение стабилизатора или более дорогого преобразователя с функцией накопителя электроэнергии.

Нюансы в понятии мощности электроприборов

Все потребляющие электричество устройства имеют такой параметр как мощность. Чем больше этот показатель, тем больше энергии забирает прибор из цепи.

Всего существует три вида мощности:

Активная (P). Характеризует скорость перевода электрической энергии в иной вид, например электромагнитный или тепловой. Ее нужно учитывать при расчете необратимых затрат электроэнергии, а значит, и стоимости работы прибора. Единица измерения – Вт.
Реактивная (Q). Характеризует энергию, которая приходит от источника (трансформатора) к реактивным элементам потребителя (конденсаторы, обмотки двигателя), но потом практически мгновенно возвращается к источнику. Единица измерения – Вт или вар (расшифровка – вольт-ампер реактивный).
Полная (S). Характеризует нагрузку, которую потребитель налагает на элементы цепи. Ее используют при вычислении площади сечения кабеля и выборе номинала автоматов, то есть расчет силы тока производят по полной мощности всех подключенных в цепь электроприборов. Единица измерения – Вт или V*A (В*А – вольт амперы).

Все эти параметры можно пересчитать через угол сдвига фаз, который возникает между вектором напряжения и током (f):

P = S * cos(f);

Q = S * sin(f);

S2 = P2 + Q2.

К бытовым устройствам, у которых полная мощность может существенно превышать активную, относят холодильники, стиральные машины, люминесцентные и некоторые энергосберегающие лампы, а также блоки силовой электроники.

На двигателях обычно указывают активную мощность и коэффициент. В этом случае полная мощность вычисляется так: S = P / cos(f) = 750 / 0.78 = 962 Вт

Также есть такое понятие как пиковая или стартовая мощность. Дело в том, что для разгона двигателей требуется гораздо больше усилий, чем для поддержания их вращения. Поэтому при включении таких приборов как холодильник или стиральная машина происходит кратковременный всплеск нагрузки на участке цепи.

Стартовые токи могут быть выше рабочих в несколько раз. При расчете необходимого сечения кабелей и подборе номинала автомата следует это учитывать.

Для этого нужно определить прибор с наибольшей разницей стартовой и рабочей мощности и добавить ее к общему значению. Стартовые токи остальных устройств можно не учитывать, так как вероятность одновременного срабатывания на включение двигателей у разных потребителей практически равна нулю.

Линейные и фазные соотношения

Сейчас получила распространение практика подключения бытовых объектов к трехфазным электросетям.

Это обосновано по следующим причинам:

Значительное потребление электроэнергии. В этом случае подведение однофазной сети большой мощности будет очень нерационально по причине большого сечения кабеля и высокой материалоемкости трансформатора.
Наличие приборов, работающих от трех фаз. Реализация схемы подключения такого устройства к однофазной цепи не очень проста и чревата помехами, которые возникают, например, при старте асинхронного двигателя.

Существует два способа подключения трехфазных приборов – “звезда” и “треугольник”.

Принципиальные схемы передачи электроэнергии по трем фазам. Название “звезда” и “треугольник” они получили благодаря геометрической схожести с этими объектами

В цепях типа “звезда” линейные и фазные токи идентичны, а линейное напряжение больше фазного в 1,73 раза:

Iл = Iф;

Uл = 1.73 * Uф.

Эта формула объясняет известное соотношения напряжений для бытовых и низковольтных промышленных сетей частоты 50 Гц: 220 / 380 В (по новому ГОСТу: 230 / 400 В).

При соединении типа треугольник, наоборот, напряжение совпадает, а линейные токи больше фазных:

Iл = 1.73 * Iф;

Эти формулы можно применять только при симметричной нагрузке фаз. Если потребление тока по кабелям отличается (несимметричный приемник), то расчеты проводят с использованием правил векторной алгебры, а возникающий выравнивающий ток компенсируют за счет нейтрального провода. Однако для сетей с подключенными бытовыми приборами такие случаи редки.

Взаимосвязь основных величин

Самая распространенная задача, с которой сталкиваются рядовые потребители, заключаются в расчетах реально действующей силы тока. Так как же правильно рассчитать ампераж по известным значениям напряжения и мощности? Решить ее необходимо при обосновании значений сечения жил и номинала автомата, имея техническую информацию об устройствах, которые будут в эту цепь запитаны.

После вычисления силы тока часто выбирают кабеля с наименьшим допустимым сечением. Однако это не всегда правильно, так как такое решение приводит к существенным ограничениям при необходимости добавления новых электроприборов в сеть.

Иногда необходимо провести обратные вычисления и определить какой суммарной мощности можно подключить приборы при известном напряжении и максимально допустимой силе тока, которая ограничена уже существующей проводкой.

Решить эти две задачи для однофазной цепи можно с помощью простой формулы:

I = S / U;

S = U * I,

где S – суммарная полная мощность всех электропотребителей.

Круговая диаграмма, отражающая закон Ома и выражающая зависимость мощности, силы тока, напряжения и сопротивления подходит для вычисления параметров однофазной цепи

Для решения задачи расчета силы тока по известным или вычисленным значениям мощности и напряжения в трехфазной цепи надо знать суммарную нагрузку, налагаемую на каждую фазу.

И необходимое сечение жил кабеля, и минимально допустимый номинал автомата подбирают по самой загруженной линии, считая что:

S = 3 * max{S1, S2, S3}.

I = S / (U * 1.73).

Допустимую мощность для каждой из фаз можно вычислить по следующей формуле:

S1,2,3 < S / 3 = I * U / 1.73,

где I – максимально допустимая сила тока для существующей проводки.

Выводы и полезное видео по теме

Вычисление силы тока по мощности для подбора сечения кабеля:

Определение потребляемой мощности групп электроприборов на примере частного дома:

Вычисление силы тока для определения параметров проводки или определение допустимой мощности в уже существующей цепи можно сделать самостоятельно. Для правильного решения поставленной задачи необходимо учесть нюансы, возникающие на практике, а не только использовать известные формулы, которые работают при “идеальных” условиях.

Если появились вопросы по теме статьи или вы можете дополнить этот материал интересной информацией, пожалуйста, оставляйте свои комментарии в расположенном ниже блоке.

Источник: https://sovet-ingenera.com/elektrika/docs-elektrika/kak-rasschitat-moshhnost.html

Закон Ома для участка цепи. Определение, формула расчета, калькулятор

В 1827 году Георг Ом опубликовал свои исследования, которые составляют основу формулы, используемую и по сей день. Ом выполнил большую серию экспериментов, которые показали связь между приложенным напряжением и током, протекающим через проводник.

Этот закон является эмпирическим, то есть основанный на опыте. Обозначение «Ом» принято в качестве официальной единицы СИ для электрического сопротивления.

Закон Ома для участка цепи гласит, что электрический ток в проводнике прямо пропорционален разности потенциалов в нем и обратно пропорционален его сопротивлению. Принимая во внимание, что сопротивление проводника (не путать с удельным сопротивлением) величина постоянная, можно оформить это следующей формулой:

где

I — тока в амперах (А)
V — напряжение в вольтах (В)
R — сопротивления в омах (Ом)

Для наглядности: резистор имеющий сопротивление 1 Ом, через который протекает ток силой в 1 А на своих выводах имеет разность потенциалов (напряжение) в 1 В.

Немецкий физик Кирхгоф (известен своими правилами Кирхгофа) сделал обобщение, которое больше используется в физике:

где

σ – проводимость материала
J — плотность тока
Е — электрическое поле.

Закон Ома и резистор

Резисторы являются пассивными элементами, которые оказывают сопротивление потоку электрического тока в цепи. Резистор, который функционирует в соответствии с законом Ома, называется омическим сопротивлением. Когда ток проходит через такой резистор, то падение напряжения на его выводах пропорционально величине сопротивления.

Формула Ома остается справедливой и для цепей с переменным напряжением и током. Для конденсаторов и катушек индуктивности закон Ома не подходит, так как их ВАХ (вольт-амперная характеристика) по сути, не является линейной.

Формула Ома действует так же для схем с несколькими резисторами, которые могут быть соединены последовательно, параллельно или иметь смешанное соединение. Группы резисторов, соединенные последовательно или параллельно могут быть упрощены в виде эквивалентного сопротивления.

В статьях о параллельном и последовательно соединении более подробно описано как это сделать.

Немецкий физик Георг Симон Ом опубликовал в 1827 свою полную теорию электричества под названием «теория гальванической цепи». Он нашел, что падение напряжения на участке цепи является результатом работы тока, протекающего через сопротивление этого участка цепи. Это легло в основу закона, который мы используем сегодня. Закон является одним из основных уравнений для резисторов.

Закон Ома — формула

Формула закона Ома может быть использована, когда известно две из трех переменных. Соотношение между сопротивлением, током и напряжением может быть записано по-разному. Для усвоения и запоминания может быть полезен «треугольник Ома».

или

Ниже приведены два примера использования такого треугольного калькулятора.

Имеем резистор сопротивлением в 1 Ом в цепи с падением напряжения от 100В до 10В на своих выводах.Какой ток протекает через этот резистор?Треугольник напоминает нам, что:

Имеем резистор сопротивлением в 10 Ом через который протекает ток в 2 Ампера при напряжении 120В.Какое будет падение напряжения на этом резисторе?Использование треугольника показывает нам, что:Таким образом, напряжение на выводе будет 120-20 = 100 В.

Закон Ома — мощность

Когда через резистор протекает электрический ток, он рассеивает определенную часть мощности в виде тепла.

Мощность является функцией протекающего тока I (А) и приложенного напряжения V (В):

где

Р — мощность в ваттах (В)

В сочетании с законом Ома для участка цепи, формулу можно преобразовать в следующий вид:

или

Идеальный резистор рассеивает всю энергию и не сохраняет электрическую или магнитную энергию. Каждый резистор имеет предел мощности, которая может быть рассеяна, не оказывая повреждение резистору. Это мощность называется номинальной.

Окружающие условия могут снизить или повысить это значение. Например, если окружающий воздух горячий, то способность рассеять излишнее тепло у резистора снижается, и на оборот, при низкой температуре окружающего воздух рассеиваемая способность резистора возрастает.

На практике, резисторы редко имеют обозначение номинальной мощности. Тем не менее, большинство из резисторов рассчитаны на 1/4 или 1/8 Вт.

Ниже приведена круговая диаграмма, которая поможет вам быстро определить связь между мощностью, силой тока, напряжением и сопротивлением. Для каждого из четырех параметров показано, как вычислить свое значение.

Закон Ома — калькулятор

Данный онлайн калькулятор закона Ома позволяет определить взаимосвязь между силой тока, электрическим напряжением, сопротивлением проводника и мощностью. Для расчета введите любые два параметра и нажмите кнопку расчет:

Для закрепления понимания работы закона Ома, приведем несколько задач для самостоятельного решения.

Какая должна быть минимальным мощность этого резистора? Ответ:
В соответствии с круговой диаграммой Р = I2*R = 0,12*50 = 0,5 Вт. Таким образом, минимальная мощность должна быть не менее 0,5 Вт, но рекомендуется взять более мощный для дополнительной надежности и долговечности.

Какой будет ток в цепи? Ответ:
Это простой пример закона Ома. Напряжение и сопротивление известны, так что мы можем вычислить ток по формуле:I = V / R = 6 / 1,2 = 5 А.

Электронагреватель (резистор) мощностью 1 кВт подключен в цепь с током 10A. Какое будет падение напряжения на нагревателе? Ответ:
Напряжение может быть выражено через ток и мощность по формуле:
V = P / I = 1000/10 = 100 В

Источник: http://www.joyta.ru/8001-zakon-oma-dlya-uchastka-cepi-opredelenie-formula-rascheta/

Источник