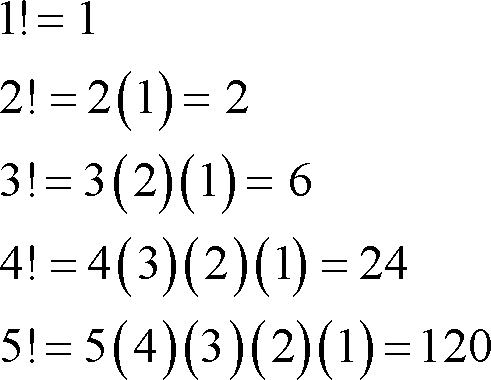Java как найти факториал числа

I found an amazing trick to find factorials in just half the actual multiplications.

Please be patient as this is a little bit of a long post.

For Even Numbers:
To halve the multiplication with even numbers, you will end up with n/2 factors. The first factor will be the number you are taking the factorial of, then the next will be that number plus that number minus two. The next number will be the previous number plus the lasted added number minus two. You are done when the last number you added was two (i.e. 2). That probably didn’t make much sense, so let me give you an example.

8! = 8 * (8 + 6 = 14) * (14 + 4 = 18) * (18 + 2 = 20)

8! = 8 * 14 * 18 * 20 which is **40320** 

Note that I started with 8, then the first number I added was 6, then 4, then 2, each number added being two less then the number added before it. This method is equivalent to multiplying the least numbers with the greatest numbers, just with less multiplication, like so:

8! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 
8! = (1 * 8) * (2 * 7) * (3 * 6) * (4 * 5)
8! = 8 * 14 * 18 * 20

Simple isn’t it

Now For Odd Numbers: If the number is odd, the adding is the same, as in you subtract two each time, but you stop at three. The number of factors however changes. If you divide the number by two, you will end up with some number ending in .5. The reason is that if we multiply the ends together, that we are left with the middle number. Basically, this can all be solved by solving for a number of factors equal to the number divided by two, rounded up. This probably didn’t make much sense either to minds without a mathematical background, so let me do an example:

9! = 9 * (9 + 7 = 16) * (16 + 5 = 21) * (21 + 3 = 24) * (roundUp(9/2) = 5)

9! = 9 * 16 * 21 * 24 * 5 = **362880**

Note: If you don’t like this method, you could also just take the factorial of the even number before the odd (eight in this case) and multiply it by the odd number (i.e. 9! = 8! * 9).

Now let’s implement it in Java:

public static int getFactorial(int num)
{
    int factorial=1;
    int diffrennceFromActualNum=0;
    int previousSum=num;

    if(num==0) //Returning  1 as factorial if number is 0 
        return 1;
    if(num%2==0)//  Checking if Number is odd or even
    { 
        while(num-diffrennceFromActualNum>=2)
        {
            if(!isFirst)
            {
                previousSum=previousSum+(num-diffrennceFromActualNum);  
            }
            isFirst=false;
            factorial*=previousSum;
            diffrennceFromActualNum+=2;
        }
    }
    else // In Odd Case (Number * getFactorial(Number-1))
    {
        factorial=num*getFactorial(num-1);
    }
    return factorial;
}

isFirst is a boolean variable declared as static; it is used for the 1st case where we do not want to change the previous sum.

Try with even as well as for odd numbers.

Factorial program in java. Here is the list of different types of factorial java code along with sample outputs. If you have no idea on how to solve the Factorial in math, do check out our tutorial below so that you will get an idea. The Factorial program in Java, we have written the following program in five different ways, using standard values, using while loop, using for loop, using do while loop, using method or function, using recursion.

If you have any doubts related to the code that we shared below do leave a comment here at the end of the post our team will help you out related to ant query.

Table Of Contents:

Q > So, basically what is factorial?

Def: A factorial is a function that multiplies number by every number. For example 4!= 4*3*2*1=24. The function is used, among other things, to find the number of ways “n” objects can be arranged.

In mathematics, there are n! ( Factorial ways to arrange N Objects ) in sequence.

Q > How to calculate?

For example :

Consider :

• 2! = 2 x 1 = 2

The possibility of 2! is two ways like {2,1}, { 1,2 }.

Same as like :

4! = 4 x 3 x 2 x 1 = 24.

• 24 = the arrangement of 4! is {1,2,3,4}, {2,1,3,4}, {2,3,1,4}, {2,3,4,1}, {1,3,2,4}, etc.

Same as like 5! , 10! , N!.

The following program has been written in 5 different ways, using while loop, for loop, do while loop, using method.

Now, let’s get into the programming part.

Java Program To Calculate Factorial in 5 Different Ways

1. Java Program To Calculate Factorial using standard values with outputs

Standard values – consider the following code is universally applicable- with sample outputs.

output:

2. Java Program Using For Loop

• Using for loop: Here is the program using for loop with sample outputs #example.

Among all three loops, for loop is probably the most used loop. For loop are two types mainly:

1. for each style of for loop
2. normal for loop

output:

3. Using Command Line Arguments

Using command line arguments: Here is the complete guide about command line arguments in Java with examples.

output:

4. Using Function

Java code for calculating Factorial using a user-defined method(using function).

output:

5. Using Recursion 

Recursion: A Recursion is a function call itself – you can check out more information about what is recursion in java here?

output:

        6.Using while loop

Here is the code using the while loop: The definition of while loop is to execute the set of statements as long as the condition is true. Here we share the complete guide on what is while loop in java with sample examples and syntax – do check it out. If you have any doubts related to the following program using while loop, do let us know here.

output:

7.Using Do While Loop

The difference between while loop and do while loop is, wherein do while the condition is checked in each iteration, whereas in while loop the condition is checked at the beginning of each iteration. Here is the complete guide on Java do while with examples and syntax.

output:

That’s it.

Also, check :

• The volume of cylinder Java Program
• The volume of sphere Java Program
• Area of rectangle Java Program

Introduction

Calculating a factorial of a number is a straightforward task. A factorial of a number is the product of that number (positive integer) and all positive integers less than that number. In other words — multiplying a number by all of the whole numbers from that number to 1.

0! equals 1 as well, since you can’t exactly go down from 0 to 1.

It’s simply an agreement that 0! is equal to 1, and a common explanation of this (sadly unattributable to a single person) is: ‘Because there is exactly one way to do nothing.’

A factorial is denoted by the integer and followed by an exclamation mark.

5! denotes a factorial of five. Alternatively, you can simply say five factorial.

And to calculate that factorial, we multiply the number with every positive whole number smaller than it:

$$
5! = 5 * 4 * 3 * 2 * 1
5! = 120
$$

In this tutorial, we’ll learn how to calculate a factorial of an integer in Java. This can be done using loops or recursion — though recursion is arguably a more natural approach. Of course, you should implement the one you’re more comfortable with.

Calculating Factorial Using Loops

Let’s start out calculating factorials using loops — while and for. We can also use do-while loops, but the initial do block doesn’t do much for us here and would introduce a potential erroneous edge-case, so we’ll skip it.

The general process is pretty similar for both loop types — all we need is a parameter as input and a counter to iterate over the numbers.

Let’s start with the for loop:

public static int getFactorialForLoop(int n) {
    int result = 1;
    if (n > 1) {
        for (int i = 1; i <= n; i++) {
            result = result * i;
        }
        return result;
    }
    else {
        System.out.println("n has to be positive");
        return result;
    }
}

We’ve actually strayed a bit away from the original definition here — we’re counting from 1 to n, while the definition of factorial was from the given number down to 1.

When you put it down on paper, though, mathematically:

$$
1 * 2 * 3 * 4 … * n = n * (n-1) * (n-2) * (n-3) * (n-4) … * (n — (n-1))
$$

These are equal statements, and you can really either go from 1 to n, or the other way around.

To simplify, (n - (n-1)) will always be equal to 1.

That means that it doesn’t matter in which direction we’re iterating. It can start from 1 and increase towards the n, or it can start from n and decrease towards 1.

Why?

Well, if you turn the loop the other way around, the method doesn’t get much more complicated, but it’s just a little bit less clean:

public static int getFactorialForLoop(int n) {
    int result = n;
    if (n >= 1) {
        for (int i = n-1; i >= 1; i--) {
            result = result * i;
        }
        return result;
    }
    else {
        System.out.println("n has to be positive");
        return 1;
    }
}

Now that that’s clarified, let’s start breaking the method down.

It takes in a parameter, n, which denotes the number we’re calculating a factorial for. First, we define a variable named result and assign 1 as a value to it.

Why assign 1 and not 0?

If we were to assign 0 to it then all the following multiplications would contain that 0. Naturally, it would collapse the entire operation to a huge 0.

Then we start our for loop with defining i as the counter that starts from 1. Notice that the condition statement is i <= n; in order to include the n itself as well.

Inside the for loop, we multiply the current value of result with the current value of our index i.

Finally, we return the final value of the result. In order to get input from the user, remember to import the java.util.Scanner.

If you’d like to read more about getting user input in Java — read our Guide to the Scanner class.

Let’s test our method and print the results:

Scanner scanner = new Scanner(System.in);
int inp;
	    
System.out.println("Enter a number: "); 
inp = Integer.parseInt(scanner.nextLine());   
	       
System.out.println("The result is: " + getFactorialForLoop(inp));        

	
public static int getFactorialForLoop(int n) {
    int result = 1;
	if (n >= 1) {
	    for (int i = 1; i <= n; i++) {
	        result = result * i;
	    }
	    return result;
	}
	else {
	  System.out.println("n has to be positive");
	  return result;
	}

It will prompt the user to give input. We’ll try it with 4:

Enter a number: 4
The result is: 24

You can use a calculator to verify the result:

4! is 4 * 3 * 2 * 1, which results 24.

Now let’s see how we can calculate factorial using the while loop. Here’s our modified method:

public static int getFactorialWhileLoop(int n){
    int result = 1;
    while (n > 1) {
        result = result * n;
        n -= 1;
    }
    return result;
}

This is pretty similar to the for loop. Except that, this time we’re moving from n towards the 1, closer to the mathematical definition. Let’s test our method:

System.out.println("Enter a number: "); 
inp = Integer.parseInt(scanner.nextLine());   
    
System.out.println("The result is: " + getFactorialWhileLoop(inp));   

We’ll enter 4 as an input once more:

Enter a number: 4
The result is: 24

Although the calculation was 4*3*2*1 the final result is the same as before.

Now let’s take a look at how to calculate the factorial using a recursive method.

Calculating Factorial Using Recursion

A recursive method is a method that calls itself and terminates the call given some condition.

In general, every recursive method has two main components: a base case and a recursive step.

Base cases are the smallest instances of the problem. Also, they must have a break, a case that will return a value and will break out of the recursion. In terms of factorial methods, the base case is when we return the final element of the factorial, which is 1.

Without a base case or with an incorrect base case, your recursive method can run infinitely, causing an overflow.

Recursive steps — as the name implies, are the recursive part of the method, where the whole problem is transformed into something smaller. If the recursive step fails to shrink the problem, then again recursion can run infinitely.

Consider the recurring part of the factorials:

• 5! is 5 * 4 * 3 * 2 * 1.

But we also know that:

• 4! is 4 * 3 * 2 * 1.

In other words 5! is 5 * 4!, and 4! is 4 * 3! and so on.

So we can say that n! = n * (n-1)!. This will be the recursive step of our factorial!

A factorial recursion ends when it hits 1. This will be our base case. We will return 1 if n is 1 or less, covering the zero input.

Let’s take a look at our recursive factorial method:

public static int getFactorialRecursively(int n){
    if (n <= 1){
        return 1;
    }
    else {
        return n * getFactorialRecursively(n-1);
    }
}

As you see the if block embodies our base case, while the else block covers the recursive step.

Let’s test our method:

System.out.println("Enter a number: "); 
inp = Integer.parseInt(scanner.nextLine());   
    
System.out.println("The result is: " + getFactorialRecursively(inp)); 

We will enter 3 as input this time:

Enter a number:3
The result is: 6

We get the same result. But this time, what goes under the hood is rather interesting:

You see, when we enter the input, the method will check with the if block, and since 3 is greater than 1, it will skip to the else block. In this block, we see the line return n * getFactorialRecursively(n-1);.

We know the current value of n for the moment, it’s 3, but getFactorialRecursively(n-1) is still to be calculated.

Then the program calls the same method once more, but this time our method takes 2 as the parameter. It checks the if block and skips to the else block and again encounters the last line. Now, the current value of the n is 2 but the program still must calculate the getFactorialRecursively(n-1).

So it calls the method once again, but this time the if block, or rather, the base class succeeds to return 1 and breaks out from the recursion.

Following the same pattern upwards, it returns each method result, multiplying the current result with the previous n and returning it for the previous method call. In other words, our program first gets to the bottom of the factorial (which is 1), then builds its way up, while multiplying on each step.

Also removing the method from the call stack one by one, up until the final result of the n * (n-1) is returned.

This is generally how recursive methods work. Some more complicated problems may require deeper recursions with more than one base case or more than one recursive step. But for now, this simple recursion is good enough to solve our factorial problem!

Calculating Factorial for Large Numbers

Factorials get large pretty quickly. Everyone knows how exponentials tend to get huge given a small number of steps:

$$
2^6 = 64
$$

$$
6! = 720
$$

As a matter of fact, a factorial of just 20 is equal to:

$$
20! = 2,432,902,008,176,640,000
$$

That’s 2.4 quintillion. The next factorial is 51 quintillion, which is out of range even for longs in Java, which stands at ~9 quintillion. Integers run out at a mere 2.4 billion, so they’re out of the question pretty quickly.

This is where a BigInteger comes into play — the JVM doesn’t pre-allocate known space for the number and dynamically updates its size. You can fill the entire RAM with digits for a BigInteger and only then would you run into the limit:

public static BigInteger getFactorialRecursively(int n) {
    BigInteger value = BigInteger.valueOf(n);
    if (value == BigInteger.ZERO) {
        return BigInteger.ONE;
    } else {
        return value.multiply(getFactorialRecursively(n - 1));
    }
}

Chucking in 21 into this method would result in:

51090942171709440000

Conclusion

In this article, we covered how to calculate factorials using for and while loops. We also learned what recursion is, and how to calculate factorial using recursion.

1. Get Factorial Using the Iterative Method in Java
2. Find Factorial Using the Recursive Method in Java
3. Find Factorial Using the Dynamic Approach in Java
4. Find Factorial Using Apache Commons in Java
5. Find Factorial Using Java 8 Streams
6. Find Factorial Using BigInteger in Java
7. Find Factorial Using BigIntegerMath Library

This tutorial introduces the methods and code examples to calculate factorial in Java.

The factorial of a number n is the multiplication of all the natural numbers between 1 and n. In this tutorial, we will see different ways of calculating the factorial of a number.

We will first look at how the factorial of numbers below and equal to 20 can be calculated. This segregation is because of Java’s limited range of long data types.

The factorials of numbers above 20 are too big to fit in the longs’ range.

Get Factorial Using the Iterative Method in Java

In this example, we created a variable, store_fact, of a long type and initialized it with 1.

We then loop through all the integers from 1 to the number whose factorial is calculated and multiply the loop variable value with the store_fact value. We stored the calculated value into the store_fact variable and updated the loop variable.

To make the above algorithm more clear, we can write it like this:

• initialize n
• initialize store_fact = 1
• do for i = 1 to n
• store_fact = store_fact*n
• increment i
• return store_fact

In the algorithm above, the store_fact variable stores the factorial of the n as follows:

• After the first iteration: store_value = 1 = 1!
• After the second iteration: store_value = 1 X 2 = 2!
• After the third iteration: store_value = 1 X 2 X 3 = 3!
• After the nth iteration: store_value = 1 X 2 X 3 X 4 ........ Xn = n!

Let us now look at the code example for the above algorithm.

import java.util.Scanner;
public class SimpleTesting {
    static long factCalculator(int n){
        long store_fact = 1;
        int i =1;
        while(i <= n){
            store_fact = store_fact*i;
            i++;
        }
        return store_fact;
    }
    public static void main(String args[]) {
      int number;
      Scanner scan = new Scanner(System.in);
      System.out.println("Enter a number: ");
      number = scan.nextInt();
      System.out.println(factCalculator(number));
    }
}

Output:

Find Factorial Using the Recursive Method in Java

The above iterative method can be transformed into a recursive method to find factorial of any number. In this method, we take the base case as:

if( n == 0 || n ==1){
            return 1;
        }

If the base condition is not fulfilled, it returns:

Let’s see the code example below. We used a recursive method, factCalculator(), to find factorial.

import java.util.*;
public class SimpleTesting {
    static long factCalculator(int n){
        if( n == 0 || n ==1){
            return 1;
        }
        else{
            return n * factCalculator(n-1); 
        }
    }
    public static void main(String args[]) {
      int number;
      Scanner scan = new Scanner(System.in);
      System.out.println("Enter a number: ");
      number = scan.nextInt();
      System.out.println(factCalculator(number));
    }
}

Output:

Find Factorial Using the Dynamic Approach in Java

We can also calculate the factorial of a number by using the dynamic programming approach. This method is faster than other methods as it stores the factorial of smaller numbers and calculates the factorials of larger numbers using those factorials.

For example:

• 5! = 5 X 4!
• 4! = 4 X 3!
• 3! = 3 X 2!
• 2! = 2 X 1!
• 1! = 1 X 0!
• 0! = 1

In this method, we create a lookup table. This table stores the factorials of numbers from 0 to 20.

We created the lookup table till 20 only because it is the largest number whose factorial long can store. We initialized 0! as 1.

We then used the value 0! to calculate 1!, the value of 1! to calculate 2! and so on. Look at the code below:

import java.util.*;
public class SimpleTesting {
    static long[] factCalculator(){
        long[] fact_table = new long[21];
        fact_table[0] = 1;
        for(int i=1; i<fact_table.length; i++){
            fact_table[i] = fact_table[i-1] * i;
        }
        return fact_table;
    }
    public static void main(String args[]) {
      long[] table = factCalculator();
      int number;
      Scanner scan = new Scanner(System.in);
      System.out.println("Enter a number: ");
      number = scan.nextInt();
      System.out.println(table[number]);
    }
}

Output:

Find Factorial Using Apache Commons in Java

If you work with the Apache Commons Math library, use the CombinatoricsUtils class with a factorial() method. It is a built-in method to calculate the factorial of any number.

The value returned by this method is of long type; hence, we cannot calculate factorial of numbers greater than 20. See the example below.

import java.util.Scanner;
import org.apache.commons.math3.util.CombinatoricsUtils;
public class SimpleTesting {
    static long factCalculator(int n){
        return CombinatoricsUtils.factorial(n);
    }
    public static void main(String args[]) {
      int number;
      Scanner scan = new Scanner(System.in);
      System.out.println("Enter a number: ");
      number = scan.nextInt();
      System.out.println(factCalculator(number));
    }
}

Output:

Find Factorial Using Java 8 Streams

We can also use Java 8 stream API to calculate the factorial of a number. We will first create a stream of numbers from 1 to n, where n is the number whose factorial is calculated.

We then use the reduce method to perform the reduction operation on the elements. We passed 1 as the identity element and multiplication as the associative accumulation function.

Look at the code below:

import java.util.*;
import java.util.stream.LongStream;
public class SimpleTesting {
    static long factCalculator(int n){
        return LongStream.rangeClosed(1,n).reduce(1, (long num1, long num2) -> num1*num2);
    }
    public static void main(String args[]) {
      int number;
      Scanner scan = new Scanner(System.in);
      System.out.println("Enter a number: ");
      number = scan.nextInt();
      System.out.println(factCalculator(number));
    }
}

Output:

There is a great advantage of using the reduce() function over the iterative or recursive method. The reduce() operation is parallelizable if the function used to process the elements is associative.

Now, we will calculate the factorial of numbers above 20.

Find Factorial Using BigInteger in Java

The BigInteger class is used to handle very large numbers beyond the range of primitive data types. We can use BigInteger to store the value of factorials of numbers above 20.

See the example below.

import java.math.BigInteger;
import java.util.Scanner;

public class SimpleTesting {
    static BigInteger factCalculator(int n){
        BigInteger store_fact = BigInteger.ONE;
    for (int i1 = 2; i1 <= n; i1++){
        store_fact = store_fact.multiply(BigInteger.valueOf(i1));
    }
    return store_fact;
    }
    public static void main(String args[]) {
      int number;
      Scanner scan = new Scanner(System.in);
      System.out.println("Enter a number: ");
      number = scan.nextInt();
      System.out.println(factCalculator(number));
      scan.close();
    }
}

Output:

Enter a number:
50
30414093201713378043612608166064768844377641568960512000000000000

Since we cannot multiply BigInteger using the * operator, we use the multiply() function. This method is just like the iterative method, except that we use BigInteger instead of long.

Find Factorial Using BigIntegerMath Library

The BigIntegerMath library has a built-in factorial() method, which can be used to calculate the factorial of a number. It is a static method and returns a long-type value.

See the example below.

import java.util.*;
import com.google.common.math.BigIntegerMath;
public class SimpleTesting {
    static long factCalculator(int n){
        return BigIntegerMath.factorial(n);
    }
    public static void main(String args[]) {
      int number;
      Scanner scan = new Scanner(System.in);
      System.out.println("Enter a number: ");
      number = scan.nextInt();
      System.out.println(factCalculator(number));
    }
}

Output:

Enter a number:
50
30414093201713378043612608166064768844377641568960512000000000000