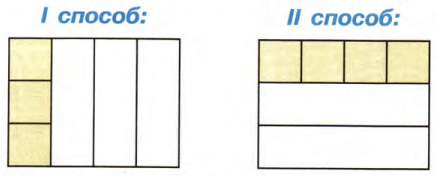
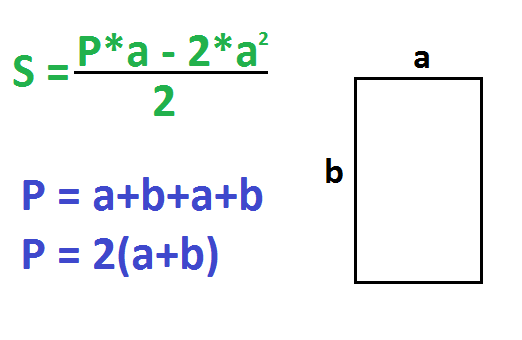Как 2мя способами найти площадь прямоугольника

Длины сторон прямоугольника 3 см и 4 см. Найди его площадь с помощью действия умножения двумя способами.
Задание рисунок 1
а) Как найти площадь прямоугольника? Сделай вывод.
б) Изменится ли результат при изменении порядка множителей? Почему? Сделай вывод.

reshalka.com

ГДЗ учебник по математике 2 класс Петерсон. Урок 23. Площадь прямоугольника. Номер №1

Решение

Способ I:
3 * 4 = 12

− площадь прямоугольника.
Способ II:
4 * 3 = 12

− площадь прямоугольника.
а) Чтобы найти площадь прямоугольника нужно умножить его длину на его ширину, либо ширину на длину.
б) Результат не изменится при изменения порядка множителей, так площадь прямоугольника величина постоянная.

Источник

Выбирайте формулу, ориентируясь на известные величины.

1. Если известны две соседние стороны

Просто перемножьте две стороны прямоугольника.

  • S — искомая площадь прямоугольника;
  • a и b — соседние стороны.

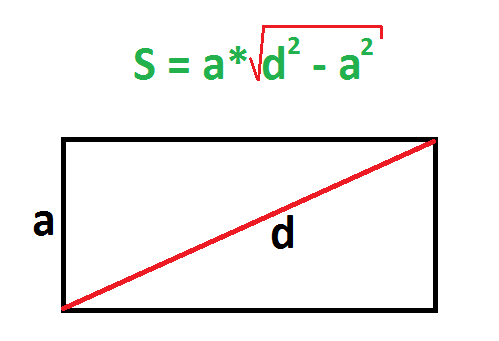
2. Если известны любая сторона и диагональ

Найдите квадраты диагонали и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте длину известной стороны на полученное число.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).

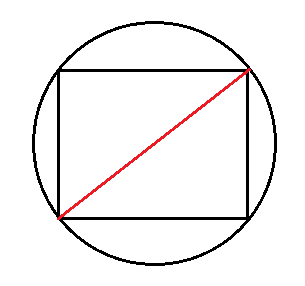
3. Если известны любая сторона и диаметр описанной окружности

Найдите квадраты диаметра и любой стороны прямоугольника.

От первого числа отнимите второе и найдите корень из результата.

Умножьте известную сторону на полученное число.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • D — диаметр описанной окружности.

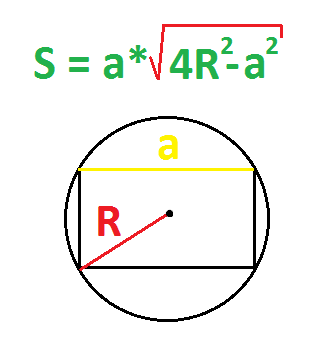
4. Если известны любая сторона и радиус описанной окружности

Найдите квадрат радиуса и умножьте результат на 4.

Отнимите от полученного числа квадрат известной стороны.

Найдите корень из результата и умножьте на него длину известной стороны.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • R — радиус описанной окружности.

5. Если известны любая сторона и периметр

Умножьте периметр на длину известной стороны.

Найдите квадрат известной стороны и умножьте полученное число на 2.

От первого произведения отнимите второе и разделите результат на 2.

  • S — искомая площадь прямоугольника;
  • a — известная сторона;
  • P — периметр прямоугольника (равен сумме всех сторон).

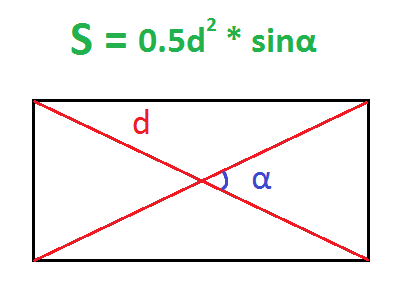
6. Если известны диагональ и угол между диагоналями

Найдите квадрат диагонали.

Разделите полученное число на 2.

Умножьте результат на синус угла между диагоналями.

  • S — искомая площадь прямоугольника;
  • d — любая диагональ прямоугольника;
  • α — любой угол между диагоналями прямоугольника.

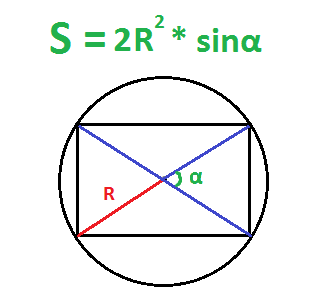
7. Если известны радиус описанной окружности и угол между диагоналями

Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.

Умножьте полученное число на 2, а потом на синус угла между диагоналями.

  • S — искомая площадь прямоугольника;
  • R — радиус описанной окружности;
  • α — любой угол между диагоналями прямоугольника.

Читайте также 🎓❓📐

  • ТЕСТ:​ ​​Умеете ли вы считать в уме?
  • Как легко и быстро считать проценты в уме
  • Как найти площадь любого треугольника
  • ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
  • Как освоить устный счёт школьникам и взрослым
Источник

1. Длины сторон прямоугольника 3 см и 4 см. Найди его площадь с помощью действия умножения двумя способами.

а) Как найти площадь прямоугольника? Сделай вывод.
б) Изменится ли результат при изменении порядка множителей? Почему? Сделай вывод.

Решение

Способ I:
3 * 4 = 12 (см2)
Способ II:
4 * 3 = 12 (см2)
а) Чтобы найти площадь прямоугольника нужно умножить его длину на его ширину, либо ширину на длину.
б) Результат не изменится при изменении порядка множителей, так площадь прямоугольника величина постоянная. Множители можно менять местами (при перемене мест множителей результат не меняется).

2. Измерь стороны прямоугольников и найди их площади:

Решение

А)

a = 4 см;
b = 2 см.
S = a * b = 4 * 2 = 8 (см2) −
площадь прямоугольника.
Ответ: 8 см2

Б)

a = 2 см;
b = 2 см.
S = a * b = 2 * 2 = 4 (см2)  − площадь прямоугольника.
Ответ: 4 см2

3. а) Длина прямоугольного листа бумаги 8 дм, а ширина − 4 дм. Чему равна его площадь?
б) Для игры в классики Таня начертила на асфальте прямоугольник со сторонами 2 м и 3 м. Чему равна его площадь?

Решение

А) S = 8 * 4 = 32 (дм2)− площадь прямоугольника.

Б) S = 2 * 3 = 6 (м2) − площадь прямоугольника

4. Сравни и сделай записи в тетради:

Решение

8 * 5 = 5 * 8

9 * 4 > 4 * 7

6 + 6 + 6 = 3 * 6

31 * 16 = 16 * 31

10 * 17 > 15 * 9

3 + 3 + 3 + 3 = 4 + 4 + 4, так как 3 * 4 = 4 * 3

5. а) Мама заготовила на зиму 25 трехлитровых банок компота. Сколько литров компота заготовила мама?
б) Один карандаш стоит 5 руб. Сколько надо заплатить за 40 таких карандашей?
в) Масса одного пакета с крупой 4 кг. Чему равна масса 72 пакетов?
г) Улитка за одну минуту проползла 3 см. Какое расстояние проползет она за час (60 минут)?

Решение

25 * 3 = 75 (л) − компота
заготовила мама.

5 * 40 = 200 (руб.) − надо заплатить за 40 карандашей.

72 * 4 = 288 (кг) − масса 72 пакетов с крупой.

3 * 60 = 180 (см) − проползет улитка за час.

6. Длина забора вокруг участка треугольной формы равна 275 м. Одна его сторона равна 86 м, а другая − на 5 м больше первой. Найди длину его третьей стороны.

Решение

1) 86 + 5 = 91 (м) − длина второй стороны;
2) 275 − (86 + 91) = 275 − 177 = 98 (м) − длина третьей стороны.
Ответ: 98 метров.

7. Расшифруй слово, расположив ответы в порядке убывания и сопоставив им соответствующие буквы. Кто это? Что ты о нем знаешь?

Решение

17 − 9 = 8
8 + 4 = 12
12 − 6 = 6 = У

27 + 3 = 30
30 − 5 = 25
25 + 8 = 33 = Р

60 − 24 = 36
36 + 40 = 76
76 − 56 = 20 = А

53 + 25 = 78
78 − 15 = 63
63 − 63 = 0 = С

92 + 0 = 92
92 − 12 = 80
80 + 19 = 99 = С

75 − 39 = 36
36 + 18 = 54
54 − 0 = 54 = Т

99(С) > 54(Т) > 33(Р) > 20(А) > 6(У) > 0(С)
Ответ: СТРАУС

8. Найди значения выражений:

Решение

802 − 519 − 81 = 802 − (519 + 81) = 802 − 600 = 202

(398 + 76) + 147 + (124 + 2) + 53 = (398 + 2) + (76 + 124) + (147 + 53) = 400 + 200 + 200 = 800

9. Реши уравнения и сделай проверку:

Решение

x − 214 = 500
x = 500 + 214
x = 714
Проверка:
714 − 214 = 500
500 = 500

x + 679 = 836
x = 836 − 679
x = 157
Проверка:
157 + 679 = 836
836 = 836

407 − x = 348
x = 407 − 348
x = 59
Проверка:
407 − 59 = 348
348 = 348

10. Составь все трехзначные числа, записанные с помощью цифр 4, 5, 0, если известно, что цифры в записи числа:
а) не повторяются;
б) могут повторяться

Решение

А) 450, 540, 405, 504.

Б) 450, 455, 540, 544,
     405, 504, 445, 554,
     444, 555, 400, 500,
     440, 550, 404, 505.

Назад к содержанию

Источник

  • Ответы к учебнику Моро 4 класс 1 часть (2015 г)
  • Ответы к учебнику Моро 4 класс 2 часть (2015 г)
  • Главная страница

7. Реши уравнения.

7

8. 1) Найди площадь прямоугольника ВСКЕ и площадь прямоугольника АЕКD.

2

Измерим линейкой стороны фигур.

ВС=КЕ = 2 см, СК = ВЕ = 2 см. Значит площадь ВСКЕ = 2 • 2 = 4 см².

КD = АЕ = 3 см, ЕК = АD = 2 см. Значит площадь АЕКD = 3 • 2 = 6 см².

2) Найди двумя способами площадь прямоугольника АВСD.

1-й способ:

Площадь прямоугольника АВСD можно найти сложив площади ВСКЕ и АЕКD.

4 + 6 = 6 см².

2-й способ:

Площадь прямоугольника АВСD можно найти перемножив его длину и ширину.

АВ = СD = ВЕ + АЕ = 2 + 3 = 5 см, ВС = АD = 2 см.

5 • 2 = 10 см².

9. 1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной ОК (рис. 1); с общей стороной NP (рис. 2).3

Общая сторона OK есть у трёх фигур: треугольника OKD, четырехугольника OKEA и пятиугольника OKCBF.

Площадь треугольника OKD = (OD • KD) : 2 = (2 см • 3 см) : 2 = 6 см² : 2 = 3 см²

Площадь четырехугольника OKEA = EKDA — OKD = 4 см • 3 см — 3 см² = 12 см² — 3 см² = 9 см²

Площадь пятиугольника OKCBF = ABCD —  OKD= 4 см • 4 см — 3 см²  = 16 см² — 3 см² = 13 см²

Общая сторона NP есть у четырёх фигур: треугольника NPS, квадрата NPLS, треугольника NPT и прямоугольника NPTM.

Площадь квадрата NPLS = NP • LS = 3 см • 3 см = 9 см²

Площадь треугольника NPS = NPLS : 2 = 9 см² : 2 = 4,5 см² (или можно выразить в миллиметрах — 9 см² = 900 мм², площадь треугольника NPS = 900 мм² : 2 = 450 мм²)

Площадь прямоугольника NPTM = NP • NM = 3 см • 2 см = 6 см²

Площадь треугольника NPT = NPTM : 2 = 6 см² : 2 = 3 см²

2) Узнай, площадь какой фигуры меньше: прямоугольника ВСКЕ или треугольника ОKD — и на сколько квадратных сантиметров.

Площадь прямоугольника BCKE = BC  • CK = 4 см • 1 см = 4 см²

Площадь треугольника OKD = (OD • KD) : 2 = (2 см • 3 см) : 2 = 6 см² : 2 = 3 см²

4 см² > 3 см², значит площадь прямоугольника BCKE больше площади треугольника OKD.

4 см² — 3 см² = 1 см². Площадь прямоугольника BCKE больше площади треугольника OKD на 1 см².

На сколько 9 меньше, чем 72?

72 — 9 = 63, значит 9 меньше, чем 72 на 63.

Во сколько раз 6 меньше, чем 54?

54 : 6 = 9, значит 6 меньше, чем 54 в 9 раз.

Задание на полях

54 —> 6 —> 42 —> 100 —>25

  • Ответы к учебнику Моро 4 класс 1 часть (2015 г)
  • Ответы к учебнику Моро 4 класс 2 часть (2015 г)
  • Главная страница

Источник

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

11 474

Как найти площадь прямоугольника – 9 формул с примерами

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

  1. Найти квадрат диагонали, то есть умножить ее на саму себя.
  2. Найти квадрат известной стороны.
  3. Из квадрата диагонали вычесть квадрат стороны.
  4. Найти квадратный корень получившейся разности.
  5. Умножить его на известную сторону.

Ищем площадь по диагонали и стороне

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

  1. Квадрат стороны = 3*3 = 9 см.
  2. Квадрат диагонали = 5*5 = 25 см.
  3. Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
  4. Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
  5. Умножаю корень разности на известную сторону: 16*9 = 144 см.

Ответ: 144 см.

Обратите внимание

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Действия:

  1. Найдите квадрат диаметра – умножьте диаметр на диаметр.
  2. Найдите квадрат известной стороны.
  3. Отнимите от квадрата диаметра квадрат стороны.
  4. Найдите квадратный корень разности.
  5. Умножьте квадратный корень на известную сторону.

По одной стороне и диаметру окружности

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

  1. Квадрат диаметра: 10*10 = 100 см.
  2. Квадрат стороны: 8*8 = 64 см.
  3. Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
  4. Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
  5. Умножаю сторону на корень из разности: 8*6 = 48 см.

Ответ: 48 см.

Лайфхак

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

Диагональ равна диаметру

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

Как найти площадь треугольника – все способы

Как найти площадь треугольника – все способы от самых простых до самых сложных

Зависит от того, какой треугольник.

По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Другой способ:

  1. Найти квадрат радиуса (умножьте радиус на радиус).
  2. Умножить квадрат радиуса на 4.
  3. Найти квадрат известной стороны.
  4. Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
  5. Найти квадратный корень разности.
  6. Умножить корень на известную сторону.

Площадь по стороне и радиусу

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

  1. Квадрат радиуса: 5*5=25 см.
  2. Четыре квадрата радиуса: 4*25 = 100 см.
  3. Квадрат стороны: 6*6 = 36 см.
  4. Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
  5. Нахожу квадратный корень разности. Корень из 64 равен 8 см.
  6. Умножаю корень на сторону: 8*6 = 48 см.

Ответ: 48 см.

Помните

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из  сторон равна 3 см. Найдите площадь.

  1. Нахожу вторую сторону прямоугольника:
    1. P=2(a+b).
    2. P=2a+2b.
    3. 14= 2*3+2b.
    4. 14 = 6+2b.
    5. 2b = 14-6 = 8.
    6. b = 8/2.
    7. b = 4.
  2. Нахожу площадь по основной формуле. S = 3*4 = 12 см.

Ответ: 12 см.

По стороне и периметру – 2 способ

Действия такие:

  1. Умножьте периметр на сторону.
  2. Найдите квадрат стороны.
  3. Умножьте квадрат стороны на 2.
  4. Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
  5. Поделите на 2.

Как найти площадь, если известны периметр и сторона

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

  1. Умножаю периметр на сторону: 8*28 = 224 см.
  2. Нахожу квадрат стороны: 8*8 = 64 см.
  3. Умножаю квадрат стороны на два: 64*2 = 84 см.
  4. Отнимаю из первого третье: 224-84 = 140 см.
  5. Делю разность на два: 140/2 = 70 см.

Ответ: 70 см.

По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Действия:

  1. Найти квадрат диагонали (умножить диагональ на саму себя).
  2. Найти половину этого квадрата – умножить его на 0,5.
  3. Найти синус угла между диагоналями.
  4. Умножить половину квадрата диагонали на синус угла между диагоналями.

Ищем площадь по диагонали и углу

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

  1. Квадрат диагонали: 10*10 = 100 см.
  2. Половина этого квадрата: 0,5*100 = 50 см.
  3. Синус угла между диагоналями: sin 30 градусов = 0,5.
  4. Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.

Ответ: 25 см.

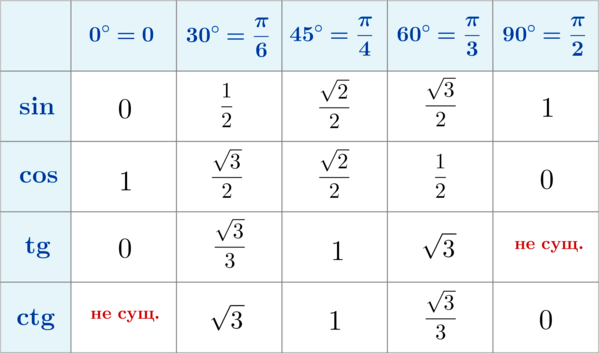
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

Основные значения из тригонометрии

По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

  1. Находим длину диагонали: 6*2 =12 см.
  2. Квадрат диагонали равен 144 см.
  3. Половина квадрата: 72 см.
  4. Синус 30 градусов равен 0,5.
  5. Умножаем половину квадрата на синус: 72*0,5 = 36 см.

Ответ: 36 см.

По радиусу описанной окружности и углу между диагоналями – второй способ

Действия:

  1. Найти квадрат радиуса (умножить радиус на радиус).
  2. Умножить квадрат радиуса на два.
  3. Найти синус угла между диагоналями.
  4. Умножить синус угла на два радиуса в квадрате.

Ищем площадь по радиусу и углу между диагоналями

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

  1. Квадрат радиуса: 6*6 = 36.
  2. Два радиуса в квадрате: 36*2 = 72.
  3. Синус 30 градусов равен 0,5.
  4. Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.

Ответ: 36 см.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

( 1 оценка, среднее 5 из 5 )

Оцените статью

ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА

Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети

ПОДПИСАТЬСЯ

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти программу плагин
  • Как найти координаты центра окружности по формуле
  • Как найти массу газа в кубе
  • Что такое ребус как правильно его составить
  • Как найти плюс в проводке автомобиля мультиметром