Как через диагональ найти сторону куба если

Диагональ стороны куба является диагональю квадрата, который представляет собой грань куба. Исходя из этого, ребро куба может быть вычислено по формуле отношения диагонали стороны куба к корню из двух.
a=d/√2

Тогда площадь стороны куба, равная квадрату его ребра, будет рассчитываться как квадрат диагонали, деленный на два. Чтобы вычислить площадь боковой и полной поверхности куба, необходимо умножить полученное выражение на 4 или 6 соответственно.
S=a^2=d^2/2
S_(б.п.)=4a^2=(4d^2)/2=2d^2
S_(п.п.)=6a^2=(6d^2)/2=3d^2

Чтобы вычислить объем куба, нужно возвести его ребро в третью – кубическую – степень, для этого все выражение, полученное для ребра куба через диагональ его стороны, возводится в степень.
V=a^3=(d/√2)^3=d^3/(2√2)

Периметр куба равен ребру куба, умноженному на двенадцать. Подставив вместо ребра куба выражение через диагональ и сократив коэффициенты, получим следующую формулу для периметра:
P=12a=12d/√2=6√2 d

Диагональ куба через диагональ его стороны можно найти, используя теорему Пифагора, согласно которой квадрат диагонали куба равен сумме квадратов диагонали стороны и бокового ребра, соединенных в прямоугольный треугольник. (рис.2.1.)
a^2+d^2=D^2
D^2=d^2/2+d^2
D^2=(3d^2)/2
D=√(3/2) d

Чтобы вычислить радиус сферы, вписанной в куб, необходимо разделить на два ребро куба, то есть разделить на два корня из двух диагональ его стороны. Радиус сферы, описанной вокруг куба, в свою очередь равен половине диагонали куба, вместо которой также можно использовать полученное через диагональ стороны выражение. (рис.2.2.,2.3)
r=a/2=d/(2√2)
R=D/2=(√(3/2) d)/2

Длина ребра куба

Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Длина ребра куба через объём

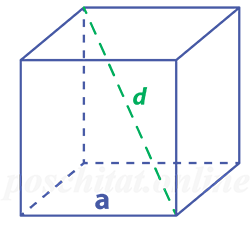
Длина ребра куба через диагональ

Длина ребра куба через площадь поверхности куба

Теория

Как найти ребро куба зная его объём

Как найти ребро куба зная его диагональ

Как найти ребро куба через площадь поверхности

См. также

Пусть нам дан куб ABCDA₁B₁C₁D_1. Обозначим его сторону через a. По условию задачи, диагональ куба ABCDA₁B₁C₁D₁ равна 3 ед.

Требуется вычислить длину а стороны куба.

Диагональ куба

У куба все ребра равны, нижним основанием ABCD и верхним основанием A₁B₁C₁D₁ являются квадраты со стороной а, и боковые ребра AA₁; BB₁; CC₁; DD₁ также равны а.

Диагональю куба называют отрезок, связывающий вершину нижнего основания с противолежащей вершиной верхнего основания, не принадлежащие одной грани. Иначе говоря, это должны быть такие вершины, чтобы отрезок полностью находился внутри куба.

Соответственно, у куба четыре диагонали:

AC₁; BD₁; CA₁; DB₁;

Возьмем любой из прямоугольных треугольников, гипотенузой которого является диагональ куба, а катетами – боковое ребро и диагональ основания, например, треугольник AСC_1. В этом треугольнике диагональ куба AC₁ является гипотенузой, боковое ребро СC₁ и диагональ основания АС – катетами. Все такие треугольники равны друг другу по двум катетам и прямому углу между ними.

Для решения задачи необходимо:

• вычислить диагональ основания АС;
• выразить диагонали куб AC₁ через сторону куба;
• приравнять известной по условию задачи величине и найти сторону куба.

Вычисление стороны куба

Из треугольника АВС:

|АС|^2 = |АВ|^2 + |ВС|^2 = а^2 + а^2 = 2 * а^2;

Из треугольника AСC₁:

|АС₁|^2 = |АС|^2 + |СС₁|^2 = 2 * а^2 + а^2 = 3 * а^2;

Далее:

а^2 = |АС₁|^2 / 3;

а = |АС1| / √3;

Подставляя исходное значение, получаем:

а = 3 / √3 = √3 (ед);

Ответ: сторона куба равна √3 ед.