Как через косинус найти угол в градусах - Исправление недочетов и поиск решений вместе с Examum.ru

Найти угол, зная косинус угла: примеры решения

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.

Существует специальная тригонометрическая функция, которой можно воспользоваться для этого и называется она арккосинусом (записывается как $arccos$).

Замечание 1

Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.

Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:

Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ

Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.

В Windows 10 она обозначается стрелкой как показано на рисунке. При её нажатии кнопка $sin$ поменяется на $sin^{-1}$, а $cos$ на $cos^{-1}$. Теперь для того чтобы узнать значение угла по косинусу — просто набираете значение функции и жмёте кнопку $cos^{-1}$. Не забудьте выбрать нужную единицу измерения — градусы или радианы.

Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ

Пример 1

Найдите, чему равен $arccos 0,456$.

Решение:

Воспользуемся калькулятором в Научном режиме, на рисунке представлен калькулятор Mac OC, кнопка переключения между $sin$ и $sin^{-1}$ обведена красным:

Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ

После нажатия кнопки мы получили значение $α = 27,129°$.

Пример 2

Определите, чему равен угол, если известен его косинус, и он равен $0,95$.

Решение:

Воспользуемся вновь калькулятором и получим, что $α = 18,19°$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 07.05.2023

Источник

Таблица косинусов, найти значения угла косинусов

Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.

Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.

Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.

Таблица косинусов от 0° — 360°

Cos(1°)	0.9998
Cos(2°)	0.9994
Cos(3°)	0.9986
Cos(4°)	0.9976
Cos(5°)	0.9962
Cos(6°)	0.9945
Cos(7°)	0.9925
Cos(8°)	0.9903
Cos(9°)	0.9877
Cos(10°)	0.9848
Cos(11°)	0.9816
Cos(12°)	0.9781
Cos(13°)	0.9744
Cos(14°)	0.9703
Cos(15°)	0.9659
Cos(16°)	0.9613
Cos(17°)	0.9563
Cos(18°)	0.9511
Cos(19°)	0.9455
Cos(20°)	0.9397
Cos(21°)	0.9336
Cos(22°)	0.9272
Cos(23°)	0.9205
Cos(24°)	0.9135
Cos(25°)	0.9063
Cos(26°)	0.8988
Cos(27°)	0.891
Cos(28°)	0.8829
Cos(29°)	0.8746
Cos(30°)	0.866
Cos(31°)	0.8572
Cos(32°)	0.848
Cos(33°)	0.8387
Cos(34°)	0.829
Cos(35°)	0.8192
Cos(36°)	0.809

Cos(37°)	0.7986
Cos(38°)	0.788
Cos(39°)	0.7771
Cos(40°)	0.766
Cos(41°)	0.7547
Cos(42°)	0.7431
Cos(43°)	0.7314
Cos(44°)	0.7193
Cos(45°)	0.7071
Cos(46°)	0.6947
Cos(47°)	0.682
Cos(48°)	0.6691
Cos(49°)	0.6561
Cos(50°)	0.6428
Cos(51°)	0.6293
Cos(52°)	0.6157
Cos(53°)	0.6018
Cos(54°)	0.5878
Cos(55°)	0.5736
Cos(56°)	0.5592
Cos(57°)	0.5446
Cos(58°)	0.5299
Cos(59°)	0.515
Cos(60°)	0.5
Cos(61°)	0.4848
Cos(62°)	0.4695
Cos(63°)	0.454
Cos(64°)	0.4384
Cos(65°)	0.4226
Cos(66°)	0.4067
Cos(67°)	0.3907
Cos(68°)	0.3746
Cos(69°)	0.3584
Cos(70°)	0.342
Cos(71°)	0.3256
Cos(72°)	0.309

Cos(73°)	0.2924
Cos(74°)	0.2756
Cos(75°)	0.2588
Cos(76°)	0.2419
Cos(77°)	0.225
Cos(78°)	0.2079
Cos(79°)	0.1908
Cos(80°)	0.1736
Cos(81°)	0.1564
Cos(82°)	0.1392
Cos(83°)	0.1219
Cos(84°)	0.1045
Cos(85°)	0.0872
Cos(86°)	0.0698
Cos(87°)	0.0523
Cos(88°)	0.0349
Cos(89°)	0.0175
Cos(90°)	0
Cos(91°)	-0.0175
Cos(92°)	-0.0349
Cos(93°)	-0.0523
Cos(94°)	-0.0698
Cos(95°)	-0.0872
Cos(96°)	-0.1045
Cos(97°)	-0.1219
Cos(98°)	-0.1392
Cos(99°)	-0.1564
Cos(100°)	-0.1736
Cos(101°)	-0.1908
Cos(102°)	-0.2079
Cos(103°)	-0.225
Cos(104°)	-0.2419
Cos(105°)	-0.2588
Cos(106°)	-0.2756
Cos(107°)	-0.2924
Cos(108°)	-0.309

Cos(109°)	-0.3256
Cos(110°)	-0.342
Cos(111°)	-0.3584
Cos(112°)	-0.3746
Cos(113°)	-0.3907
Cos(114°)	-0.4067
Cos(115°)	-0.4226
Cos(116°)	-0.4384
Cos(117°)	-0.454
Cos(118°)	-0.4695
Cos(119°)	-0.4848
Cos(120°)	-0.5
Cos(121°)	-0.515
Cos(122°)	-0.5299
Cos(123°)	-0.5446
Cos(124°)	-0.5592
Cos(125°)	-0.5736
Cos(126°)	-0.5878
Cos(127°)	-0.6018
Cos(128°)	-0.6157
Cos(129°)	-0.6293
Cos(130°)	-0.6428
Cos(131°)	-0.6561
Cos(132°)	-0.6691
Cos(133°)	-0.682
Cos(134°)	-0.6947
Cos(135°)	-0.7071
Cos(136°)	-0.7193
Cos(137°)	-0.7314
Cos(138°)	-0.7431
Cos(139°)	-0.7547
Cos(140°)	-0.766
Cos(141°)	-0.7771
Cos(142°)	-0.788
Cos(143°)	-0.7986
Cos(144°)	-0.809

Cos(145°)	-0.8192
Cos(146°)	-0.829
Cos(147°)	-0.8387
Cos(148°)	-0.848
Cos(149°)	-0.8572
Cos(150°)	-0.866
Cos(151°)	-0.8746
Cos(152°)	-0.8829
Cos(153°)	-0.891
Cos(154°)	-0.8988
Cos(155°)	-0.9063
Cos(156°)	-0.9135
Cos(157°)	-0.9205
Cos(158°)	-0.9272
Cos(159°)	-0.9336
Cos(160°)	-0.9397
Cos(161°)	-0.9455
Cos(162°)	-0.9511
Cos(163°)	-0.9563
Cos(164°)	-0.9613
Cos(165°)	-0.9659
Cos(166°)	-0.9703
Cos(167°)	-0.9744
Cos(168°)	-0.9781
Cos(169°)	-0.9816
Cos(170°)	-0.9848
Cos(171°)	-0.9877
Cos(172°)	-0.9903
Cos(173°)	-0.9925
Cos(174°)	-0.9945
Cos(175°)	-0.9962
Cos(176°)	-0.9976
Cos(177°)	-0.9986
Cos(178°)	-0.9994
Cos(179°)	-0.9998
Cos(180°)	-1

Cos(181°)	-0.9998
Cos(182°)	-0.9994
Cos(183°)	-0.9986
Cos(184°)	-0.9976
Cos(185°)	-0.9962
Cos(186°)	-0.9945
Cos(187°)	-0.9925
Cos(188°)	-0.9903
Cos(189°)	-0.9877
Cos(190°)	-0.9848
Cos(191°)	-0.9816
Cos(192°)	-0.9781
Cos(193°)	-0.9744
Cos(194°)	-0.9703
Cos(195°)	-0.9659
Cos(196°)	-0.9613
Cos(197°)	-0.9563
Cos(198°)	-0.9511
Cos(199°)	-0.9455
Cos(200°)	-0.9397
Cos(201°)	-0.9336
Cos(202°)	-0.9272
Cos(203°)	-0.9205
Cos(204°)	-0.9135
Cos(205°)	-0.9063
Cos(206°)	-0.8988
Cos(207°)	-0.891
Cos(208°)	-0.8829
Cos(209°)	-0.8746
Cos(210°)	-0.866
Cos(211°)	-0.8572
Cos(212°)	-0.848
Cos(213°)	-0.8387
Cos(214°)	-0.829
Cos(215°)	-0.8192
Cos(216°)	-0.809

Cos(217°)	-0.7986
Cos(218°)	-0.788
Cos(219°)	-0.7771
Cos(220°)	-0.766
Cos(221°)	-0.7547
Cos(222°)	-0.7431
Cos(223°)	-0.7314
Cos(224°)	-0.7193
Cos(225°)	-0.7071
Cos(226°)	-0.6947
Cos(227°)	-0.682
Cos(228°)	-0.6691
Cos(229°)	-0.6561
Cos(230°)	-0.6428
Cos(231°)	-0.6293
Cos(232°)	-0.6157
Cos(233°)	-0.6018
Cos(234°)	-0.5878
Cos(235°)	-0.5736
Cos(236°)	-0.5592
Cos(237°)	-0.5446
Cos(238°)	-0.5299
Cos(239°)	-0.515
Cos(240°)	-0.5
Cos(241°)	-0.4848
Cos(242°)	-0.4695
Cos(243°)	-0.454
Cos(244°)	-0.4384
Cos(245°)	-0.4226
Cos(246°)	-0.4067
Cos(247°)	-0.3907
Cos(248°)	-0.3746
Cos(249°)	-0.3584
Cos(250°)	-0.342
Cos(251°)	-0.3256
Cos(252°)	-0.309

Cos(253°)	-0.2924
Cos(254°)	-0.2756
Cos(255°)	-0.2588
Cos(256°)	-0.2419
Cos(257°)	-0.225
Cos(258°)	-0.2079
Cos(259°)	-0.1908
Cos(260°)	-0.1736
Cos(261°)	-0.1564
Cos(262°)	-0.1392
Cos(263°)	-0.1219
Cos(264°)	-0.1045
Cos(265°)	-0.0872
Cos(266°)	-0.0698
Cos(267°)	-0.0523
Cos(268°)	-0.0349
Cos(269°)	-0.0175
Cos(270°)	-0
Cos(271°)	0.0175
Cos(272°)	0.0349
Cos(273°)	0.0523
Cos(274°)	0.0698
Cos(275°)	0.0872
Cos(276°)	0.1045
Cos(277°)	0.1219
Cos(278°)	0.1392
Cos(279°)	0.1564
Cos(280°)	0.1736
Cos(281°)	0.1908
Cos(282°)	0.2079
Cos(283°)	0.225
Cos(284°)	0.2419
Cos(285°)	0.2588
Cos(286°)	0.2756
Cos(287°)	0.2924
Cos(288°)	0.309

Cos(289°)	0.3256
Cos(290°)	0.342
Cos(291°)	0.3584
Cos(292°)	0.3746
Cos(293°)	0.3907
Cos(294°)	0.4067
Cos(295°)	0.4226
Cos(296°)	0.4384
Cos(297°)	0.454
Cos(298°)	0.4695
Cos(299°)	0.4848
Cos(300°)	0.5
Cos(301°)	0.515
Cos(302°)	0.5299
Cos(303°)	0.5446
Cos(304°)	0.5592
Cos(305°)	0.5736
Cos(306°)	0.5878
Cos(307°)	0.6018
Cos(308°)	0.6157
Cos(309°)	0.6293
Cos(310°)	0.6428
Cos(311°)	0.6561
Cos(312°)	0.6691
Cos(313°)	0.682
Cos(314°)	0.6947
Cos(315°)	0.7071
Cos(316°)	0.7193
Cos(317°)	0.7314
Cos(318°)	0.7431
Cos(319°)	0.7547
Cos(320°)	0.766
Cos(321°)	0.7771
Cos(322°)	0.788
Cos(323°)	0.7986
Cos(324°)	0.809

Cos(325°)	0.8192
Cos(326°)	0.829
Cos(327°)	0.8387
Cos(328°)	0.848
Cos(329°)	0.8572
Cos(330°)	0.866
Cos(331°)	0.8746
Cos(332°)	0.8829
Cos(333°)	0.891
Cos(334°)	0.8988
Cos(335°)	0.9063
Cos(336°)	0.9135
Cos(337°)	0.9205
Cos(338°)	0.9272
Cos(339°)	0.9336
Cos(340°)	0.9397
Cos(341°)	0.9455
Cos(342°)	0.9511
Cos(343°)	0.9563
Cos(344°)	0.9613
Cos(345°)	0.9659
Cos(346°)	0.9703
Cos(347°)	0.9744
Cos(348°)	0.9781
Cos(349°)	0.9816
Cos(350°)	0.9848
Cos(351°)	0.9877
Cos(352°)	0.9903
Cos(353°)	0.9925
Cos(354°)	0.9945
Cos(355°)	0.9962
Cos(356°)	0.9976
Cos(357°)	0.9986
Cos(358°)	0.9994
Cos(359°)	0.9998
Cos(360°)	1

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Источник

Косинус угла. Таблица косинусов.

Косинус угла через градусы, минуты и секунды

Косинус угла через десятичную запись угла

Как найти угол зная косинус этого угла

У косинуса есть обратная тригонометрическая функция — arccos(y)=x

cos(arccos(y))=y

Пример cos(60°) = 1/2; arccos(1/2) = 60°

Рассчитать арккосинус

Определение косинуса

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

cos(α) = AC/AB

cos(-α) = cos(α)

cos(α ± 2π) = cos(α)

Таблица косинусов в радианах

cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263

Таблица Брадиса косинусы

cos(0) = 1	cos(120) = -0.5	cos(240) = -0.5
cos(1) = 0.9998476952	cos(121) = -0.5150380749	cos(241) = -0.4848096202
cos(2) = 0.999390827	cos(122) = -0.5299192642	cos(242) = -0.4694715628
cos(3) = 0.9986295348	cos(123) = -0.544639035	cos(243) = -0.4539904997
cos(4) = 0.9975640503	cos(124) = -0.5591929035	cos(244) = -0.4383711468
cos(5) = 0.9961946981	cos(125) = -0.5735764364	cos(245) = -0.4226182617
cos(6) = 0.9945218954	cos(126) = -0.5877852523	cos(246) = -0.4067366431
cos(7) = 0.9925461516	cos(127) = -0.6018150232	cos(247) = -0.3907311285
cos(8) = 0.9902680687	cos(128) = -0.6156614753	cos(248) = -0.3746065934
cos(9) = 0.9876883406	cos(129) = -0.629320391	cos(249) = -0.3583679495
cos(10) = 0.984807753	cos(130) = -0.6427876097	cos(250) = -0.3420201433
cos(11) = 0.9816271834	cos(131) = -0.656059029	cos(251) = -0.3255681545
cos(12) = 0.9781476007	cos(132) = -0.6691306064	cos(252) = -0.3090169944
cos(13) = 0.9743700648	cos(133) = -0.6819983601	cos(253) = -0.2923717047
cos(14) = 0.9702957263	cos(134) = -0.6946583705	cos(254) = -0.2756373558
cos(15) = 0.9659258263	cos(135) = -0.7071067812	cos(255) = -0.2588190451
cos(16) = 0.9612616959	cos(136) = -0.7193398003	cos(256) = -0.2419218956
cos(17) = 0.956304756	cos(137) = -0.7313537016	cos(257) = -0.2249510543
cos(18) = 0.9510565163	cos(138) = -0.7431448255	cos(258) = -0.2079116908
cos(19) = 0.9455185756	cos(139) = -0.7547095802	cos(259) = -0.1908089954
cos(20) = 0.9396926208	cos(140) = -0.7660444431	cos(260) = -0.1736481777
cos(21) = 0.9335804265	cos(141) = -0.7771459615	cos(261) = -0.156434465
cos(22) = 0.9271838546	cos(142) = -0.7880107536	cos(262) = -0.139173101
cos(23) = 0.9205048535	cos(143) = -0.79863551	cos(263) = -0.1218693434
cos(24) = 0.9135454576	cos(144) = -0.8090169944	cos(264) = -0.1045284633
cos(25) = 0.906307787	cos(145) = -0.8191520443	cos(265) = -0.08715574275
cos(26) = 0.8987940463	cos(146) = -0.8290375726	cos(266) = -0.06975647374
cos(27) = 0.8910065242	cos(147) = -0.8386705679	cos(267) = -0.05233595624
cos(28) = 0.8829475929	cos(148) = -0.8480480962	cos(268) = -0.0348994967
cos(29) = 0.8746197071	cos(149) = -0.8571673007	cos(269) = -0.01745240644
cos(30) = 0.8660254038	cos(150) = -0.8660254038	cos(270) = 0
cos(31) = 0.8571673007	cos(151) = -0.8746197071	cos(271) = 0.01745240644
cos(32) = 0.8480480962	cos(152) = -0.8829475929	cos(272) = 0.0348994967
cos(33) = 0.8386705679	cos(153) = -0.8910065242	cos(273) = 0.05233595624
cos(34) = 0.8290375726	cos(154) = -0.8987940463	cos(274) = 0.06975647374
cos(35) = 0.8191520443	cos(155) = -0.906307787	cos(275) = 0.08715574275
cos(36) = 0.8090169944	cos(156) = -0.9135454576	cos(276) = 0.1045284633
cos(37) = 0.79863551	cos(157) = -0.9205048535	cos(277) = 0.1218693434
cos(38) = 0.7880107536	cos(158) = -0.9271838546	cos(278) = 0.139173101
cos(39) = 0.7771459615	cos(159) = -0.9335804265	cos(279) = 0.156434465
cos(40) = 0.7660444431	cos(160) = -0.9396926208	cos(280) = 0.1736481777
cos(41) = 0.7547095802	cos(161) = -0.9455185756	cos(281) = 0.1908089954
cos(42) = 0.7431448255	cos(162) = -0.9510565163	cos(282) = 0.2079116908
cos(43) = 0.7313537016	cos(163) = -0.956304756	cos(283) = 0.2249510543
cos(44) = 0.7193398003	cos(164) = -0.9612616959	cos(284) = 0.2419218956
cos(45) = 0.7071067812	cos(165) = -0.9659258263	cos(285) = 0.2588190451
cos(46) = 0.6946583705	cos(166) = -0.9702957263	cos(286) = 0.2756373558
cos(47) = 0.6819983601	cos(167) = -0.9743700648	cos(287) = 0.2923717047
cos(48) = 0.6691306064	cos(168) = -0.9781476007	cos(288) = 0.3090169944
cos(49) = 0.656059029	cos(169) = -0.9816271834	cos(289) = 0.3255681545
cos(50) = 0.6427876097	cos(170) = -0.984807753	cos(290) = 0.3420201433
cos(51) = 0.629320391	cos(171) = -0.9876883406	cos(291) = 0.3583679495
cos(52) = 0.6156614753	cos(172) = -0.9902680687	cos(292) = 0.3746065934
cos(53) = 0.6018150232	cos(173) = -0.9925461516	cos(293) = 0.3907311285
cos(54) = 0.5877852523	cos(174) = -0.9945218954	cos(294) = 0.4067366431
cos(55) = 0.5735764364	cos(175) = -0.9961946981	cos(295) = 0.4226182617
cos(56) = 0.5591929035	cos(176) = -0.9975640503	cos(296) = 0.4383711468
cos(57) = 0.544639035	cos(177) = -0.9986295348	cos(297) = 0.4539904997
cos(58) = 0.5299192642	cos(178) = -0.999390827	cos(298) = 0.4694715628
cos(59) = 0.5150380749	cos(179) = -0.9998476952	cos(299) = 0.4848096202
cos(60) = 0.5	cos(180) = -1	cos(300) = 0.5
cos(61) = 0.4848096202	cos(181) = -0.9998476952	cos(301) = 0.5150380749
cos(62) = 0.4694715628	cos(182) = -0.999390827	cos(302) = 0.5299192642
cos(63) = 0.4539904997	cos(183) = -0.9986295348	cos(303) = 0.544639035
cos(64) = 0.4383711468	cos(184) = -0.9975640503	cos(304) = 0.5591929035
cos(65) = 0.4226182617	cos(185) = -0.9961946981	cos(305) = 0.5735764364
cos(66) = 0.4067366431	cos(186) = -0.9945218954	cos(306) = 0.5877852523
cos(67) = 0.3907311285	cos(187) = -0.9925461516	cos(307) = 0.6018150232
cos(68) = 0.3746065934	cos(188) = -0.9902680687	cos(308) = 0.6156614753
cos(69) = 0.3583679495	cos(189) = -0.9876883406	cos(309) = 0.629320391
cos(70) = 0.3420201433	cos(190) = -0.984807753	cos(310) = 0.6427876097
cos(71) = 0.3255681545	cos(191) = -0.9816271834	cos(311) = 0.656059029
cos(72) = 0.3090169944	cos(192) = -0.9781476007	cos(312) = 0.6691306064
cos(73) = 0.2923717047	cos(193) = -0.9743700648	cos(313) = 0.6819983601
cos(74) = 0.2756373558	cos(194) = -0.9702957263	cos(314) = 0.6946583705
cos(75) = 0.2588190451	cos(195) = -0.9659258263	cos(315) = 0.7071067812
cos(76) = 0.2419218956	cos(196) = -0.9612616959	cos(316) = 0.7193398003
cos(77) = 0.2249510543	cos(197) = -0.956304756	cos(317) = 0.7313537016
cos(78) = 0.2079116908	cos(198) = -0.9510565163	cos(318) = 0.7431448255
cos(79) = 0.1908089954	cos(199) = -0.9455185756	cos(319) = 0.7547095802
cos(80) = 0.1736481777	cos(200) = -0.9396926208	cos(320) = 0.7660444431
cos(81) = 0.156434465	cos(201) = -0.9335804265	cos(321) = 0.7771459615
cos(82) = 0.139173101	cos(202) = -0.9271838546	cos(322) = 0.7880107536
cos(83) = 0.1218693434	cos(203) = -0.9205048535	cos(323) = 0.79863551
cos(84) = 0.1045284633	cos(204) = -0.9135454576	cos(324) = 0.8090169944
cos(85) = 0.08715574275	cos(205) = -0.906307787	cos(325) = 0.8191520443
cos(86) = 0.06975647374	cos(206) = -0.8987940463	cos(326) = 0.8290375726
cos(87) = 0.05233595624	cos(207) = -0.8910065242	cos(327) = 0.8386705679
cos(88) = 0.0348994967	cos(208) = -0.8829475929	cos(328) = 0.8480480962
cos(89) = 0.01745240644	cos(209) = -0.8746197071	cos(329) = 0.8571673007
cos(90) = 0	cos(210) = -0.8660254038	cos(330) = 0.8660254038
cos(91) = -0.01745240644	cos(211) = -0.8571673007	cos(331) = 0.8746197071
cos(92) = -0.0348994967	cos(212) = -0.8480480962	cos(332) = 0.8829475929
cos(93) = -0.05233595624	cos(213) = -0.8386705679	cos(333) = 0.8910065242
cos(94) = -0.06975647374	cos(214) = -0.8290375726	cos(334) = 0.8987940463
cos(95) = -0.08715574275	cos(215) = -0.8191520443	cos(335) = 0.906307787
cos(96) = -0.1045284633	cos(216) = -0.8090169944	cos(336) = 0.9135454576
cos(97) = -0.1218693434	cos(217) = -0.79863551	cos(337) = 0.9205048535
cos(98) = -0.139173101	cos(218) = -0.7880107536	cos(338) = 0.9271838546
cos(99) = -0.156434465	cos(219) = -0.7771459615	cos(339) = 0.9335804265
cos(100) = -0.1736481777	cos(220) = -0.7660444431	cos(340) = 0.9396926208
cos(101) = -0.1908089954	cos(221) = -0.7547095802	cos(341) = 0.9455185756
cos(102) = -0.2079116908	cos(222) = -0.7431448255	cos(342) = 0.9510565163
cos(103) = -0.2249510543	cos(223) = -0.7313537016	cos(343) = 0.956304756
cos(104) = -0.2419218956	cos(224) = -0.7193398003	cos(344) = 0.9612616959
cos(105) = -0.2588190451	cos(225) = -0.7071067812	cos(345) = 0.9659258263
cos(106) = -0.2756373558	cos(226) = -0.6946583705	cos(346) = 0.9702957263
cos(107) = -0.2923717047	cos(227) = -0.6819983601	cos(347) = 0.9743700648
cos(108) = -0.3090169944	cos(228) = -0.6691306064	cos(348) = 0.9781476007
cos(109) = -0.3255681545	cos(229) = -0.656059029	cos(349) = 0.9816271834
cos(110) = -0.3420201433	cos(230) = -0.6427876097	cos(350) = 0.984807753
cos(111) = -0.3583679495	cos(231) = -0.629320391	cos(351) = 0.9876883406
cos(112) = -0.3746065934	cos(232) = -0.6156614753	cos(352) = 0.9902680687
cos(113) = -0.3907311285	cos(233) = -0.6018150232	cos(353) = 0.9925461516
cos(114) = -0.4067366431	cos(234) = -0.5877852523	cos(354) = 0.9945218954
cos(115) = -0.4226182617	cos(235) = -0.5735764364	cos(355) = 0.9961946981
cos(116) = -0.4383711468	cos(236) = -0.5591929035	cos(356) = 0.9975640503
cos(117) = -0.4539904997	cos(237) = -0.544639035	cos(357) = 0.9986295348
cos(118) = -0.4694715628	cos(238) = -0.5299192642	cos(358) = 0.999390827
cos(119) = -0.4848096202	cos(239) = -0.5150380749	cos(359) = 0.9998476952

Похожие калькуляторы

Источник

Как найти угол зная косинус

Кроме прямых тригонометрических функций синус и косинус, существуют и обратные им арксинус и арккосинус. С их помощью можно вычислять величины углов по известным значениям прямых функций. Есть несколько вариантов практической реализации таких расчетов.

Инструкция

Используйте функцию, обратную косинусу (арккосинус) для нахождения угла по известному значению косинуса. Нужное значение арктангенса, а по нему и величину угла, можно найти, например, в «таблицах Брадиса». Бумажные экземпляры этого справочника есть в библиотеках и книжных магазинах, а электронные можно найти в интернете.

Найдите в сети он-лайн калькуляторы для вычисления обратных тригонометрических функций и определите с их помощью нужное значение. Пользоваться такими сервисами намного удобнее, чем искать значения в таблицах. К тому же они могут упростить расчеты, так как многие такие калькуляторы позволяют вычислять не только отдельные значения, но и получать результаты на основе введенных формул, составленных из нескольких операций с тригонометрическими функциями.

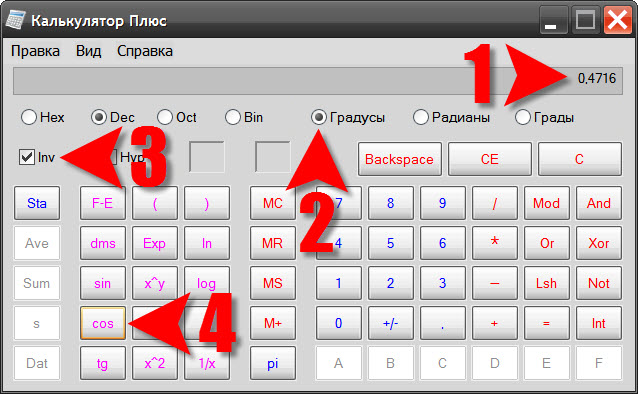
Воспользуйтесь стандартным калькулятором ОС Windows, если хотите обойтись без выхода в интернет. Команда запуска калькулятора помещена в главное меню на кнопке «Пуск». Открыв его, перейдите в раздел «Все программы», затем в подраздел «Стандартные» и щелкните пункт «Калькулятор». По умолчанию он запустится с простейшим интерфейсом, не имеющим инструментов для тригонометрических вычислений. Раскройте в его меню раздел «Вид» и выберите пункт с надписью «Инженерный».

Введите значение косинуса с клавиатуры, или щелкая соответствующие кнопки интерфейса калькулятора. Можно использовать для ввода операции копирования (CTRL + C) и вставки (CTRL + V). Затем выберите единицы измерения, в которых должен быть представлен результат (градусы, радианы или грады) — соответствующий селектор находится строчкой ниже поля ввода числа. После этого надо выставить отметку инвертирования функций в чекбоксе Inv. Этим все приготовления заканчиваются, щелкните кнопку cos и калькулятор рассчитает значение обратной косинусу функции (арккосинус) заданного значения и представит вам результат в выбранных единицах.

Источники:

как найти значение косинуса если есть угол

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Загрузить PDF

Теорема косинусов широко применяется в тригонометрии. Ее используют при работе с неправильными треугольниками, чтобы находить неизвестные величины, например стороны и углы. Теорема схожа с теорема Пифагора, и ее довольно легко запомнить. Теорема косинусов гласит, что в любом треугольнике $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ .

1
Запишите известные величины. Чтобы найти неизвестную сторону треугольника, нужно знать две другие стороны и угол между ними.^[1]
- Например, дан треугольник XYZ. Сторона YX равна 5 см, сторона YZ равна 9 см, а угол Y равен 89°. Чему равна сторона XZ?
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — неизвестная сторона, — косинус угла, противоположного неизвестной стороне, и — две известные стороны.^[2]
3
4
Найдите косинус известного угла. Сделайте это с помощью калькулятора. Введите значение угла, а затем нажмите кнопку . Если у вас нет научного калькулятора, найдите онлайн-таблицу значений косинусов, например, здесь.^[4] Также в Яндексе можно ввести «косинус Х градусов» (вместо X подставьте значение угла), и поисковая система отобразит косинус угла.
- Например, косинус 89° ≈ 0,01745. Итак: $c^{{2}}=5^{{2}}+9^{{2}}-2(5)(9)(0,01745)$ .
5

Перемножьте числа. Умножьте на косинус известного угла.
6

Сложите квадраты известных сторон. Помните, чтобы возвести число в квадрат, его нужно умножить на само себя. Сначала возведите в квадрат соответствующие числа, а затем сложите полученные значения.
7

Вычтите два числа. Вы найдете $c^{{2}}$ .
8

Извлеките квадратный корень из полученного значения. Для этого воспользуйтесь калькулятором. Так вы найдете неизвестную сторону.^[5]

Реклама

1
Запишите известные величины. Чтобы найти неизвестный угол треугольника, нужно знать все три стороны треугольника.^[6]
- Например, дан треугольник RST. Сторона СР = 8 см, ST = 10 см, РТ = 12 см. Найдите значение угла S.
2

Запишите формулу теоремы косинусов. Формула: $c^{{2}}=a^{{2}}+b^{{2}}-2abcos {C}$ , где — косинус неизвестного угла, — известная сторона, противолежащая неизвестному углу, и — две другие известные стороны. ^[7]
3
4
Перемножьте числа. Умножьте на косинус неизвестного угла.
- Например, $12^{{2}}=8^{{2}}+10^{{2}}-160cos {C}$ .
5
Возведите в квадрат. То есть умножьте число само себя.
- Например, $144=8^{{2}}+10^{{2}}-160cos {C}$
6

Сложите квадраты и . Но сначала возведите соответствующие числа в квадрат.
7

Изолируйте косинус неизвестного угла. Для этого вычтите сумму $a^{{2}}$ и $b^{{2}}$ из обеих частей уравнения. Затем разделите каждую часть уравнения на коэффициент (множитель) при косинусе неизвестного угла.
8
Вычислите арккосинус. Так вы найдете значение неизвестного угла.^[9] На калькуляторе функция арккосинуса обозначается $COS^{{-1}}$ .
- Например, арккосинус 0,0125 равен 82,8192. Итак, угол S равен 82,8192°.
Реклама

1

Найдите неизвестную сторону треугольника. Известные стороны равны 20 см и 17 см, а угол между ними равен 68°.
2

Найдите угол H в треугольнике GHI. Две стороны, прилегающие к углу Н, равны 22 и 16 см. Сторона, противоположная углу H, равна 13 см.
3

Найдите длину тропы. Речная, Холмистая и Болотная тропы образуют треугольник. Длина Речной тропы — 3 км, длина Холмистой тропы — 5 км; эти тропы пересекаются друг с другом под углом 135°. Болотная тропа соединяет два конца других троп. Найдите длину Болотной тропы.

Реклама

Советы

Проще пользоваться теоремой синусов. Поэтому сначала выясните, можно ли применить ее к данной задаче.

Об этой статье

Эту страницу просматривали 5444 раза.

Была ли эта статья полезной?

Источник