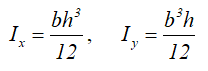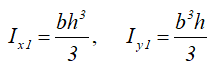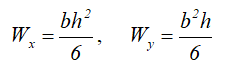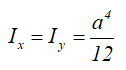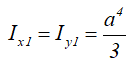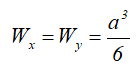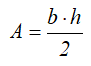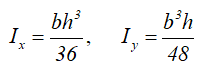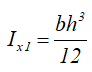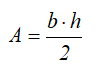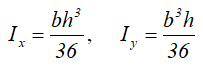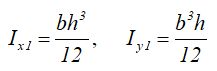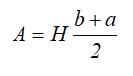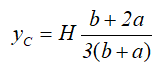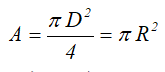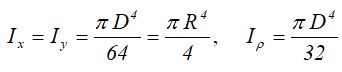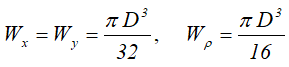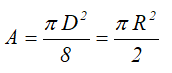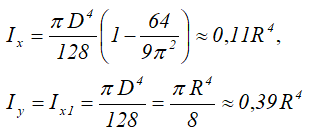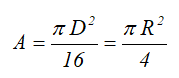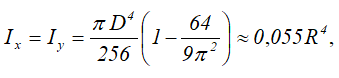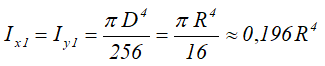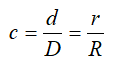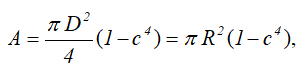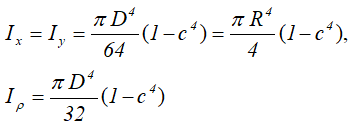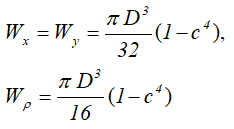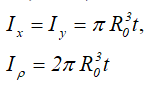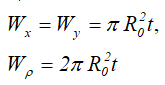Как через площадь найти центр фигуры

На этой странице представлена справочная информация с формулами для вычисления площадей простых фигур (сечений) с указанием положения их центров тяжестей.

Эта страничка будет полезна при расчёте более сложных фигур (составных поперечных сечений): определении положения центра тяжести, а также общей площади.

Центры тяжести

Для всех фигур, положение центра тяжести в статье обозначается буквой – C, это наиболее используемый вариант. Также иногда центр тяжести обозначают буквой – O.

Формулы для расчёта площадей

В сопромате площадь поперечного сечения обозначается буквой – A, однако, в некоторой литературе ты можешь встретить обозначения с буквой – F.

Другую справочную информацию, размещённую на сайте – ssopromat.ru, можешь найти, перейдя по указанной ссылке.

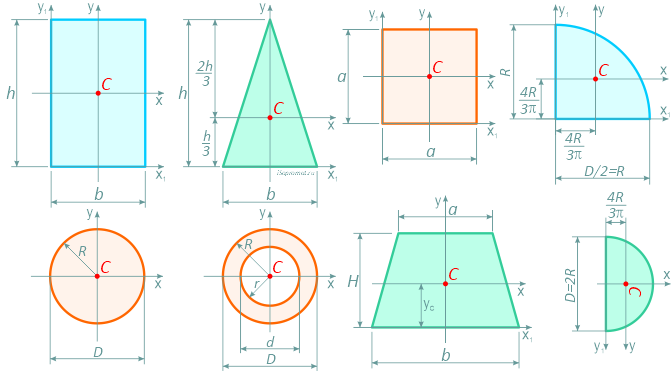
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.

Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
I_x , I_y — осевые моменты инерции сечения относительно главных осей;
I_x1 , I_y1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
I_ρ — полярный момент инерции сечения;
W_x , W_y — осевые моменты сопротивления;
W_ρ — полярный момент сопротивления

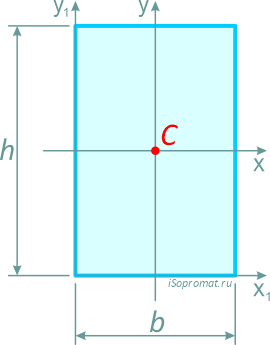
Прямоугольник

Прямоугольник высотой h и шириной b.

Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.

Площадь

Центральные осевые моменты инерции прямоугольника

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевые моменты сопротивления прямоугольного сечения

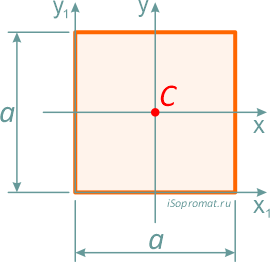
Квадрат

Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.

Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.

Площадь

Центральные осевые моменты инерции квадрата

Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку

Осевой момент сопротивления квадратного сечения

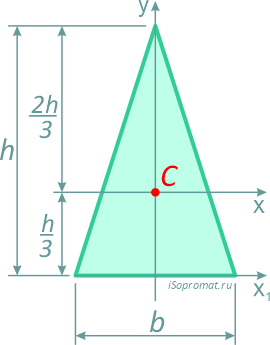
Треугольник равнобедренный

Равнобедренный треугольник высотой h и шириной основания b.

Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.

Площадь

Центральные осевые моменты инерции треугольника

Момент инерции относительно смещенной оси x₁, проходящей через его основание

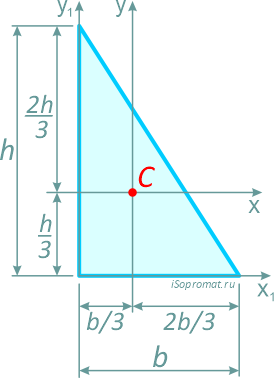
Прямоугольный треугольник

Прямоугольный треугольник высотой h и шириной основания b.

Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.

Площадь

Центральные осевые моменты инерции прямоугольного треугольника

Моменты инерции относительно смещенных осей x₁ и y₁, проходящих через точку, соединяющую его катеты

Трапеция

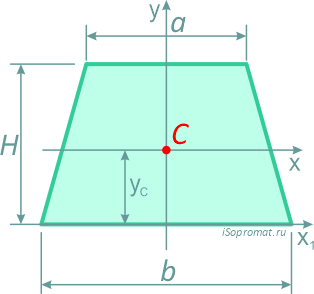
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.

Площадь трапеции

Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:

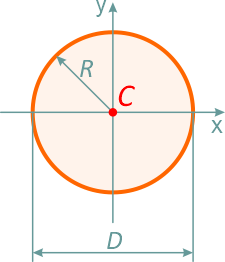
Круг

Круг диаметром D (d) или радиусом R (r)

Площадь круга через его диаметр и радиус

Центральные осевые и полярный моменты инерции круга

Осевые и полярный моменты сопротивления

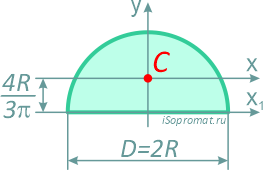
Полукруг

Половина круга диаметром D (d) или радиусом R (r)

Площадь

Осевые моменты инерции полукруга

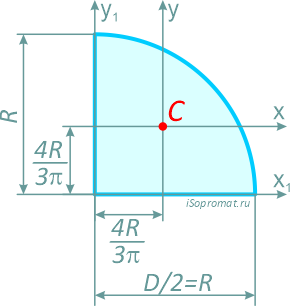
Четверть круга

Четверть круга диаметром D (d) или радиусом R (r)

Площадь

Центральные осевые моменты инерции четверти круга

Моменты инерции относительно смещенных осей x₁ и y₁

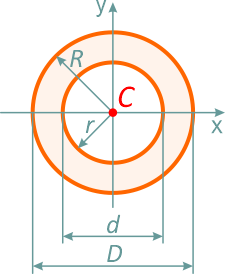
Кольцо

Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)

Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.

Площадь

Центральные осевые и полярный моменты инерции кольца

Осевые и полярный моменты сопротивления

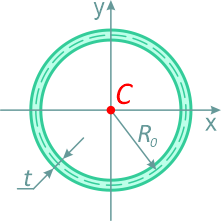
Тонкостенное сечение (труба)

Тонкостенный профиль (сечение трубы) средним радиусом R₀ и толщиной стенки трубы t при R₀>>t

Площадь

Центральные осевые и полярный моменты инерции трубного сечения

Осевые и полярный моменты сопротивления

Пример определения координат центра тяжести сложной фигуры:

Другие видео

Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Содержание:

1. Центр масс
2. Центр параллельных сил
3. Центр тяжести
4. Центры тяжести некоторых плоских однородных фигур
5. Центр тяжести дуги окружности
6. Центр тяжести кругового сектора
7. Центр тяжести кругового сегмента
8. Центр тяжести треугольника
9. Центр тяжести трапеции
10. Примеры решения задач на тему: Центр масс
11. Способы определения координат центра тяжести тела
12. Метод симметрии
13. Метод разбиения
14. Метод дополнения
15. Экспериментальные способы
16. Центры тяжести некоторых однородных тел
17. Центр тяжести дуги окружности
18. Центр тяжести треугольника
19. Центр тяжести сектора

Центр масс — это геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Центр масс

Центр масс — это некоторое положение, определяемое относительно объекта или системы объектов и это среднее положение всех частей системы, взвешенное в соответствии с их массами.

Центр параллельных сил

Если на тело действует система параллельных сил , ,…, , то точка , через которую проходит равнодействующая этой системы сил, называется центром параллельных сил (рис.9.1).

Координаты центра параллельных сил определяются по зависимостям:

где  — координаты точек приложения сил .

Центр параллельных сил имеет ту особенность, что через него обязательно будет проходить линия действия равнодействующей при вращении линий действия всех сил системы вокруг точек их приложения на один и тот же угол в одну и ту же сторону. Модули сил при вращении не должны меняться.

Центр тяжести

Если твердое тело находится возле поверхности Земли, то на каждую материальную часть этого тела действует сила тяжести­ , которая направлена к центру Земли. Поскольку размеры тела небольшие по сравнению с размерами Земли, то образованную систему сил можно рассматривать как параллельную. Равнодействующая этой параллельной системе сил , которая равна их сумме, называется тяжестью тела, а центр этой системы — точка называется центром тяжести тела (рис.9.2).

Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил:

где  — сила тяжести элементарной частицы тела;

 — тяжесть тела;

 — координаты центра тяжести;

 — координаты элементарной частицы тела.

Если тело однородное, то есть удельный вес не меняется по объему , то:

где  — объем тела;

 — объем элементарной частицы.

Тогда формулы для определения координат центра тяжести твердого тела приобретут вид:

Положение центра тяжести однородного тела зависит только от формы объема, что занимает тело, и называется центром тяжести этого объема.

Если однородное тело имеет форму тонкой пластины, то его можно рассматривать как материальную плоскую фигуру. В этом случае положение центра тяжести плоской фигуры определяется двумя координатами  и и зависит от формы площади фигуры:

где  — площадь элементарной части плоской фигуры;

 — площадь плоской фигуры.

Центр тяжести однородной пластины называется центром тяжести плоской фигуры.

Если выбранный элементарный объем  (площадь элементарной площадки в плоском случае) направить к нулю, то формулы для вычисления координат центра тяжести приобретут интегральный вид:

а) для однородного твердого тела:

где  — объем тела, интегрирование выполняется по всему объему тела;

б) для однородной поверхности:

где  — площадь поверхности, интегрирование выполняется по всей поверхности тела;

в) для однородной плоской фигуры, лежащей в плоскости xy:

г) для однородной линии:

где  — длина линии, интегрирование выполняется по всей длине линии.

Центры тяжести некоторых плоских однородных фигур

Для упрощения определения центра тяжести используются следующие вспомогательные правилами:

1. Если тело имеет плоскость симметрии, то центр тяжести лежит на этой плоскости.
2. Если тело симметрично относительно оси, то центр тяжести лежит на этой оси.
3. Если тело симметрично относительно точки, то центр тяжести лежит в центре симметрии.
4. Если тело состоит из нескольких частей, центры тяжести которых можно определить, то центр тяжести такого тела находят как центр тяжести нескольких материальных точек, а именно тех, в которых расположены весы каждой отдельной части тела.

Центр тяжести дуги окружности

Центр тяжести дуги окружности  (рис.9.3) лежит на ее оси симметрии и на расстоянии от центра окружности:

где  — радиус окружности;

 — половина центрального угла, опирающегося на дугу .

Центр тяжести кругового сектора

Центр тяжести кругового сектора лежит на оси симметрии и имеет координаты:

где  — радиус окружности;

 — половина центрального угла сектора.

Центр тяжести кругового сегмента

Центр тяжести кругового сегмента лежит на оси симметрии сегмента и имеет координаты:

где  — радиус окружности;

 — половина центрального угла сегмента.

Центр тяжести треугольника

Центр тяжести треугольника (рис. 9.6) лежит в точке пересечения его медиан — на расстоянии 1/3 каждой медианы от соответствующего основания треугольника.

Центр тяжести трапеции

Центр тяжести трапеции (рис.9.7) с основаниями  и  и высотой лежит на прямой , которая соединяет середины основ.

Расстояния  и центра тяжести площади трапеции от ее основ определяются по формулам:

Наиболее распространенный способ определения положения центра тяжести однородного тела сложной формы заключается в том, что его разбивают на такие части, положение центров тяжести которых известно, или может быть легко определено.

Например, однородную плоскую фигуру (рис.9.8) разбивают на три части 1,2 и 3, положения центров тяжести которых, можно определить.

Координаты центра тяжести фигуры определяются по формулам:

где  — координаты центра тяжести первой части плоской фигуры;

 — площадь первой части и т.п.

Этим способом удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.9.9).

В этом случае площадь плоской фигуры можно записать в виде разницы площадей сплошной фигуры 1 (площадь положительная) и вырезанной части 2 (площадь отрицательная), то есть .

Координаты центра тяжести фигуры равны:

где  — координаты центра тяжести сплошной фигуры 1, площадь которой равна ;

 — координаты центра тяжести вырезанной части 2, площадь которой равна — .

Первый из этих методов имеет название «метод разбиения», второй — «метод дополнения», или «метод отрицательных масс». В общем случае формулы для определения центра тяжести плоской фигуры имеют вид:

где  — площадь всей фигуры.

Примеры решения задач на тему: Центр масс

Задача № 1

Найти центр тяжести двутаврового профиля, размеры которого в сантиметрах указаны на рис.9.10.

Решение. Поскольку форма сечения имеет ось симметрии, ось направим вдоль оси симметрии, а ось перпендикулярно ей.

В силу симметричности профиля относительно оси центр тяжести будет лежать на этой оси, то есть

Линиями и поделим профиль на три прямоугольника 1, 2 и 3.

Запишем уравнение для определения абсциссы центра тяжести площади:

где  — абсциссы центров тяжести прямоугольников 1, 2, 3;

 — площади этих прямоугольников.

Поскольку центры тяжести прямоугольников и лежат на пересечении их диагоналей, то (рис.9.10):

Площади этих прямоугольников соответственно равны:

Тогда: 

Таким образом, центр тяжести фигуры лежит в точке с координатами: 

Ответ: 

Задача № 2

Найти координаты центра тяжести поперечного пересечения разностороннего угольника (рис.9.11), полки которого имеют ширину  и толщину

Решение. Разделим пересечение линией на два прямоугольника и , центры тяжести которых лежат на пересечении соответствующих диагоналей.

Запишем формулы для координат  и  центра тяжести пересечения:

где  и  — координаты центров тяжести прямоугольников 1 и 2;

,  — площади прямоугольников 1 и 2.

С рис.9.11 видим, что

Тогда: 

Ответ: 

Задача № 3

Определить положение центра тяжести плоской фигуры (рис.9.12), ограниченной полуокружностью  радиуса и двумя прямыми равной длины и , причем

Решение. Данная площадь имеет ось симметрии, вдоль которой направим ось . Поскольку центр тяжести площади лежит на оси симметрии, то

Разделим площадь линией на две части: полуокружность и равнобедренный треугольник .

Абсцисса центра тяжести площади будет равняться:

где  — координата центра тяжести половины круга ;

 — координата центра тяжести треугольника ;

,  — площади половины круга и треугольника.

Для определения воспользуемся приведенными в разделе 9.3.2 координатами центра тяжести кругового сектора

В случае половины круга 

Площадь половины круга равна:

Центр тяжести треугольника лежит на пересечении его медиан (раздел 9.3.4). Поскольку треугольник равнобедрен, то линия  будет его медианой и расстояние будет равняться третьей части от :

Площадь треугольника равна:

Подставив найденные значения , ,  и  в уравнение для , получим:

Ответ: 

Задача № 4

Найти координаты центра тяжести квадратной пластины с вырезом в виде сегмента радиуса (рис.9.13), если

Решение. Осью симметрии рассматриваемой фигуры будет диагональ прямоугольника

Поэтому направим ось вдоль этой линии, а ось — перпендикулярно (рис.9.13).

Центр тяжести пластины будет лежать на оси , то есть

Площадь фигуры можно представить как разницу площадей квадрата (положительная площадь) и сектора (отрицательная площадь).

Абсцисса центра тяжести фигуры будет равняться:

где  — абсцисса центра тяжести квадрата ;

 — абсцисса центра тяжести сектора ;

 и  — площади квадрата и сектора.

Для квадрата получим:

Как следует из рис. 9.13, равняется

где  — расстояние от точки к центру тяжести кругового сектора .

Для кругового сектора (раздел 9.3.2) получим:

Поскольку  и , то 

Таким образом, абсцисса равняется:

Площадь кругового сектора :

Подставив значение , ,  и  в формулу для , получим:

Ответ:  

Задача № 5

Найти координаты центра тяжести площади, ограниченной (рис.9.14) правой веткой параболы , осью  и прямой

Решение. На расстоянии  от оси выделяем элементарную площадку шириной (заштрихованная область).

Площадь выделенной элементарной площадки будет равняться:

Площадь фигуры, что ограничена заданными линиями:

Поскольку точка представляет собой пересечение параболы и прямой , то 

Отсюда: 

Тогда:

Абсцисса центра тяжести

Для определения координаты выделим элементарную площадку шириной на расстоянии  от оси .

Площадь выделенной площадки:

Ордината центра тяжести:

Тогда: 

Ответ: 

Способы определения координат центра тяжести тела

Существует несколько способов определения координат центра тяжести тел. среди них различают: метод симметрии, метод разбиения и дополнения, экспериментальные способы.

Рассмотрим последовательно эти способы.

Метод симметрии

Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, или на оси симметрии, или в центре симметрии.

Таким образом, центр тяжести однородных симметричных тел, таких как кольца,
прямоугольные пластины, прямоугольные параллелепипеды, шары и другие тела, которые
имеют центр симметрии, расположенный в геометрических центрах (центры симметрии) этих тел.

Метод разбиения

Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести нетрудно определяется, то координаты центра тяжести всего тела можно определить непосредственно по формулам выше. Причем количество слагаемых в числителе каждого из указанных выражений будет равно количеству частей, на которое разбивается тело.

Приведем пример определения центра тяжести тела методом разбиения его на отдельные тела, центры тяжести которых известны.

Пример:

Определить координаты центра тяжести однородной пластины. Размеры в
мм заданные на рис. 1.64

Решение.

Выберем оси координат x и y. Разбиваем пластину на отдельные прямоугольные части. Для каждого прямоугольника проводим диагонали, точки пересечения которых c₁, c₂ и c₃ соответствуют центрам веса каждого прямоугольника. В принятой системе координат нетрудно получить значение координат этих точек. А именно: c₁ (–1,1), c₂ (1,5), c₃ (5,9). Площади каждого тела соответственно равны: I — s₁ = 4 см²; II — s₂ = 20 см²; III — s₃ = 12 см². Площадь всей пластины равна: S = s₁ + s₂ + s₃ = 36 см².

Для определения координат центра тяжести заданной пластины используем выражение выше. Подставив значения всех известных величин в уравнения, получим

По вычисленным значениям координат центра тяжести пластины можно обозначить точку C на рисунке. Как видим, центр тяжести (геометрическая точка) пластины расположен за ее пределами.

Метод дополнения

Способ, о котором говорится далее, является некоторым случаем способа разбиения. Он может применяться к телам, которые имеют вырезы, полости, причем без учета выреза, или вырезанной части тела положение центра тяжести тела известно. Рассмотрим пример применения такого метода.

Пример. Определить положение центра тяжести круглой пластины радиусом R, имеет круговое отверстие радиуса r (рис. 1.65). Расстояние C₁C₂ = a.

Решение.

Как видно из рисунка, центр тяжести пластины находится на оси симметрии пластины x, то есть на прямой, проходящей через точки C₁ и C₂. Таким образом, для определения положения центра тяжести этой пластины необходимо вычислить только одну координату x_C, поскольку вторая координата y_C равна нулю. Покажем оси координат x, y. Примем, что пластина состоит из двух тел — с полного круга (без учета выреза) и тела,
образовано вырезом. В принятой системе координаты x для указанных тел будут равны: x₁ = 0; x₂ = C₁C₂ = a. Площади тел равны: Общая площадь всего тела будет равна физической разницы между площадями первого и второго тел, а именно
Для определения неизвестной координаты центра тяжести
заданной пластины используем первое уравнение выражения.

Подставив значения всех известных величин в это уравнение, получим

Таким образом, значение координаты x_C отрицательное, а потому, поскольку вторая координата 0 y_C = 0, то центр тяжести пластины C размещен на оси x слева от точки C₁.

Экспериментальные способы

Эти способы нашли широкое применение при отыскании положения центра тяжести тел сложных форм и конфигураций, для которых другие способы почти непригодны вследствие громоздкости и сложности. К таким телам, в первую очередь, следует отнести комбайны, тракторы, сложные сельскохозяйственные машины и орудия. При применении экспериментальных способов отыскания положения
центра тяжести наиболее широко используют метод подвешивания и метод взвешивания тел.

При применении метода подвешивания тело на тросе подвешивают за различные его точки. Направление троса, будет давать каждый раз направление силы веса тела. Тогда точка пересечения этих направлений и дает положение центра тяжести тела.

Использование второго метода — взвешивание требует измерения веса всего тела, а также отдельных его частей. Рассмотрим пример применения этого метода.

Пример.

Определим продольную координату центра тяжести трактора, у которого продольная база составляет l (рис. 1.66).

Решение.

Сначала поставим на платформу весов задние колеса трактора, как это показано на рисунке. Итак, определяем силу давления задних колес на платформу, или реакцию . Аналогично определяем вес переднего моста, или реакцию . Вполне понятно, что сумма этих реакций равна общему весу трактора, а именно:

Q = R_A + R_B.

Теперь составим алгебраическую сумму моментов всех сил относительно точки A. Она равна

Откуда определяем продольную координату центра тяжести:

x_C = .

Для определения поперечной координаты центра тяжести трактора необходимо знать реакции левых колес (переднего и заднего) и правых, а также поперечную базу трактора. Дальше аналогичным выражением определяется эти координаты центра тяжести.

Центры тяжести некоторых однородных тел

Определим далее координаты центров тяжести некоторых простых однородных тел.

Центр тяжести дуги окружности

Рассмотрим дугу AB окружности радиусом R, в которой центральный угол OAB равен 2α (радиан) (рис. 1.67). Покажем оси координат x, y начало которых разместим в точке O. Вследствие того, что дуга имеет ось симметрии Ox, то центр ее тяжести будет расположен именно на этой оси (y_C = 0). Остается только вычислить координату x_C.

Используем для вычисления этой координаты первое уравнение выражения, а именно

Определим составляющие, которые необходимо подставить в это уравнение. Для этого выделим на дуге AB элемент M M₁ длиной dl, равной:

dl = R · dφ.

Если φ — угол, определяющий положение элемента M M₁ на дуге AB, то координата x элемента M M₁ будет равна:

x = Rcosφ.

Общая длина дуги AB равна:

L = 2α · R.

Подставим эти значения в первое уравнение выражения. При этом считается, что интеграл в числителе данного выражения должен быть определенным по всей длине дуги. Будем иметь:

Таким образом, координата x_C будет равняться

x_C = .

Центр тяжести треугольника

Есть произвольный треугольник, вершины которого в принятой системе координат Oxy соответствуют точкам с координатами A₁ (x₁, y₁), A₂ (x₂, y₂), A₃ (x₃, y₃) (рис. 1.68). Если провести прямые, которые будут параллельны основе A₁A₃ и провести их достаточное количество, то вся площадь треугольника будет состоять из полос бесконечно малой ширины, центры тяжести которых будут размещены посередине каждой полосы, а потому и центр тяжести треугольника будет расположенный на его медиане. А если провести линии, параллельные другой стороне треугольника, то и в этом случае центр тяжести будет размещен на соответствующей медиане. Таким образом, совершенно очевидно, что центр тяжести треугольника C будет расположен в точке пересечения его медиан.

Определим координаты этой точки. По курсу аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями

где x₁, x₂, …, y₃  — координаты вершин треугольника.

Полезно также знать, что

Центр тяжести сектора

Рассмотрим круговой сектор OAB радиуса R, центральный угол которого равен 2α (радиан) (рис. 1.69). Центр тяжести сектора, вполне очевидно, лежит на оси его симметрии, то есть на биссектрисе угла AOB. Эту биссектрису примем за ось x и найдем на этой оси положение центра C. Разобьем площадь сектора на бесконечно большое число элементарных секторов с центральными углами ∆φ.

Будем рассматривать каждый сектор как треугольник с основанием R · ∆φ и высотой R. Центр тяжести каждого треугольника расположен на расстоянии  от центра сектора. Таким образом, центры тяжести всех треугольников расположены на дуге A´B´. Итак, если 0 ∆φ → 0, то центры тяжести образуют дугу AB, тогда необходимо найти центр тяжести дуги A´B´. Используем формулу, по которой определяется центр тяжести дуги окружности радиусом r:

Тогда учитывая, что

Будем иметь

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика материальной точки
24. Динамика механической системы
25. Динамика плоского движения твердого тела
26. Динамика относительного движения материальной точки
27. Динамика твердого тела
28. Кинематика простейших движений твердого тела
29. Общее уравнение динамики
30. Работа и мощность силы
31. Обратная задача динамики
32. Поступательное и вращательное движение твердого тела
33. Плоскопараллельное (плоское) движение твёрдого тела
34. Сферическое движение твёрдого тела
35. Движение свободного твердого тела
36. Сложное движение твердого тела
37. Сложное движение точки
38. Плоское движение тела
39. Статика твердого тела
40. Равновесие составной конструкции
41. Равновесие с учетом сил трения
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

Как найти центр фигуры

Центр фигуры можно найти несколькими способами, смотря какие данные о ней уже известны. Стоит разобрать нахождение центра окружности, которая является совокупностью точек, располагающихся на равном расстоянии от центра, так как эта фигура — одна из наиболее распространенных.

Вам понадобится

• — угольник;
• — линейка.

Инструкция

Простейший способ найти центр окружности – согнуть листок бумаги, на котором она начерчена, убедившись, глядя на просвет, что она сложилась точно пополам. Затем согните лист перпендикулярно первому сгибу. Так вы получите диаметры, точка пересечения которых и есть центр фигуры.

Конечно, этот способ идеален, только если окружность начерчена на бумаге, достаточно тонкой, чтобы можно было посмотреть на просвет, точно ли сложен лист.

Допустим, рассматриваемую фигуру начертили на твердой, несгибаемой поверхности либо это отдельная деталь, которая также не поддается сгибу. Чтобы найти центр окружности в этом случае, вам нужна линейка.

Диаметр является самым длинным отрезком, соединяющим 2 точки окружности. Как известно, проходит он через центр, поэтому задача нахождения центра окружности сводится к нахождению диаметра и его середины.

Наложите линейку на окружность, после чего зафиксируйте в любой точке фигуры нулевую отметку. Приложите линейку к окружности, получив секущую, а затем двигайте по направлению к центру фигуры. Длина секущей будет возрастать, пока не дойдет до пиковой точки. Вы получите диаметр, а найдя его середину, найдете и центр окружности.

Центр описанной окружности для любого треугольника располагается на пересечении срединных перпендикуляров. В случае, если треугольник прямоугольный, ее центр всегда будет совпадать с серединой гипотенузы. То есть решение кроется в построении внутри окружности прямоугольного треугольника с вершинами, лежащими на окружности.

Трафаретом для прямого угла могут послужить школьный или строительный угольник, линейка или даже лист бумаги/картона. Поместите в любую точку окружности вершину прямого угла, сделайте отметки в тех местах, где стороны угла пересекают границу окружности, соедините их. У вас получился диаметр – гипотенуза.

Таким же способом найдите еще один диаметр, место пересечения двух таких отрезков и будет центром окружности.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?