|
1. Описано многократно, вот например https://5terka.com/node/532 |
Ток
контура,
создаваемый напряжением генератора,
проходя через конденсатор, поочередно
заряжает и разряжает его. При этомна конденсаторе получается
переменная разность потенциалов ес,
называемая электродвижущей
силой (э. д. с.)
конденсатора3.
В
начале первой четверти периода разность
потенциалов (э. д. с.) между обкладками
конденсатора увеличивается быстро, а
к концу – медленнее.
Это означает, что зарядный ток в начале
четверти периода велик, а к концу
уменьшается. В течение первой четверти
периода конденсатор заряжается, и
энергия поступает из генератора в
конденсатор. Э. д. с. емкости в этом случае
действует навстречу току (см. рис.3).
Рис.3.
Векторная и временная диаграммы токов
и напряжений на конденсаторе
В
течение второй четверти периода
мгновенное значение напряжения генератора
уменьшается, конденсатор разряжается
и отдает энергию генератору. В этом
случае напряжение генератора действует
навстречу току. О количестве электричества,
которое отдает конденсатор, можно судить
по изменению разности потенциалов между
его пластинами: в начале второй четверти
периода она изменяется медленно, а в
конце – быстро. Э. д. с.
емкости препятствует прохождению
переменного тока по цепи и обусловливает
емкостное сопротивление
конденсатора.
Амплитудное значение этой э. д. с. равно
амплитудному значению приложенного
напряжения. Количество электричества,
требующегося для заряда конденсатора
доопределенной разности
потенциалов, зависит от его емкости.
Чем больше емкость конденсатора, тем
большее количество электричества
необходимо для создания между его
пластинами определенной разности
потенциалов. Этим объясняется зависимость
емкостного сопротивления от емкости
конденсатора.
Электродвижущая
сила емкости опережает по фазе на
четверть периода (90°) ток, проходящий в
цепи и равна напряжению, которое требуется
для преодоления емкостного сопротивления:
.
Знак минус говорит
о противофазности э. д. с. и напряжения.
Падение напряжения
на конденсаторе
.
1.3.2. Электродвижущая сила катушки индуктивности
Переменный
синусоидальный ток, проходя через
катушку, возбуждает в ней электродвижущую
силу индукции. В течение первой четверти
периода (рис.4), когда
мгновенное значение тока возрастает,
в катушке согласно правилу Ленца
возникает э. д. с. индукции, препятствующая
увеличению тока.
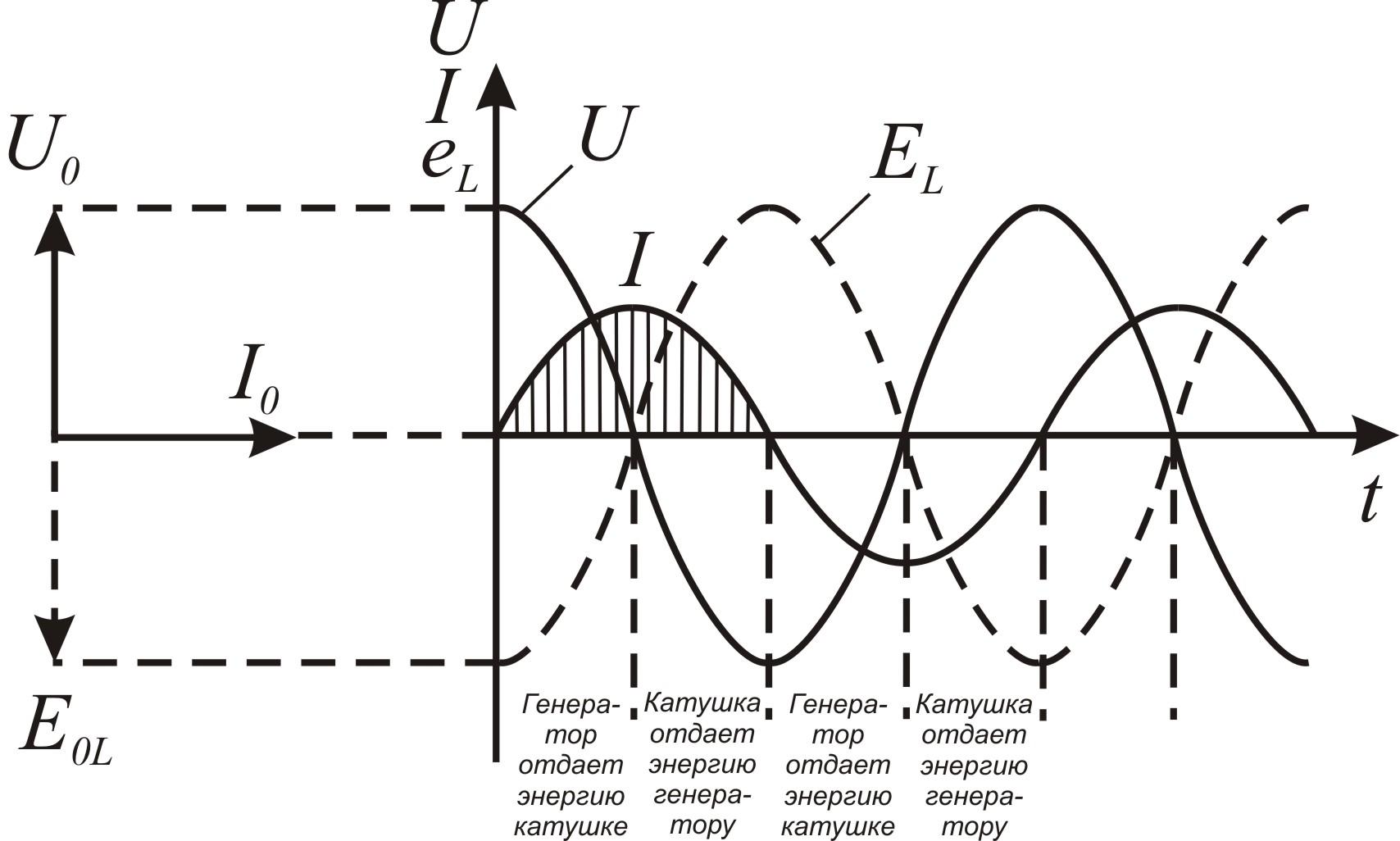
Рис.4.
Векторная и временная диаграммы токов
и напряжений на катушке индуктивности
В
течение второй четверти периода, когда
мгновенное значение тока уменьшается,
в катушке возникает э. д. с. индукции,
которая препятствует уменьшению тока.
Можно считать, что в течение второй
четверти периода источником энергии
является катушка, а нагрузкой –
генератор.
Величина
э. д. с. индукции определяется скоростью
изменения тока. Э. д. с. индукции в любой
момент уравновешивает напряжение
генератора. В цепи, содержащей
индуктивность, ток отстает по фазе на
четверть периода (90°) от напряжения
генератора и опережает на четверть
периода э. д. с. индукции. Э. д. с. индукции
отстает по фазе от тока, ее создавшего,
на четверть периода. Э. д. с. индукции
препятствует изменению тока через
катушку и обусловливает индуктивное
сопротивление катушки
переменному току.
Напряжение,
требующееся для преодоления индуктивного
сопротивления катушки, равно
.
Э. д. с. индукции и
падение напряжения на индуктивном
сопротивлении равны и уравновешивают
друг друга:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
31. Электродинамика (расчетная задача)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Электростатика. Конденсаторы
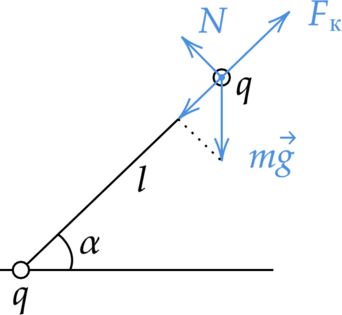
На столе закреплен непроводящий наклонный стержень. На него нанизана бусина с зарядом (q) и массой (m), которая может двигаться без трения. Ниже на стержне закреплена бусина такого же по величине заряда (q), но с нулевой массой. Расстояние между бусинами (l), угол (alpha=30^circ). На рисунке показать все силы, действующие на верхнюю бусину. Найти заряд (q), ответ в общем виде.
“Основная волна 2020 Вариант 4”
Запишем второй закон Ньютона на ось, сопадающую с направлением стержня [mg sin alpha = kdfrac{q^2}{l^2} Rightarrow q=lsqrt{dfrac{mgsin alpha}{k}}]
Ответ: $q=lsqrt{dfrac{mgsin alpha}{k}}$
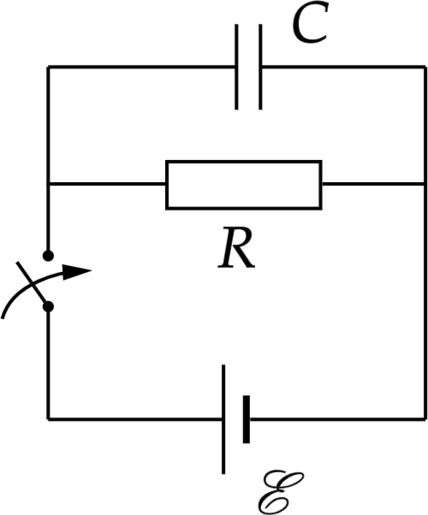
Электрическая цепь, схема которой изображена на рисунке, состоит из конденсатора, резистора, источника тока и ключа. Первоначально ключ был разомкнут. Найти ЭДС источника, если известно, что сила тока через источник сразу после замыкания ключа в (n = 2) раза больше установившейся силы тока в цепи, а установившееся напряжение на конденсаторе (U = 1,75) В. Ответ дайте в В.
Сразу после замыкания ключа ток через резистор не течет, поэтому ток через источник paset [I_{1}=frac{xi}{r}] После того, как ток установится, сила тока будет равна [I_{2}=frac{xi}{R+r}]
так как по условию ток первоначально в ( n ) раз больше, то
[frac{frac{xi}{r}}{frac{xi}{R+r}}=n Rightarrow frac{R+r}{r}=n Rightarrow frac{R}{r}=n-1] Taк как конденсатор и резистор подключены параллельно, то напряжение на резисторе равно установившемуся напряжению на конденсаторе и равно [U=I_{2} R=frac{xi R}{R+r}=frac{xi(n-1)}{n}] Откуда ЭДС источника равно [xi=frac{U n}{n-1}=2 U=3,5 text{ В}]
Ответ: 3,5
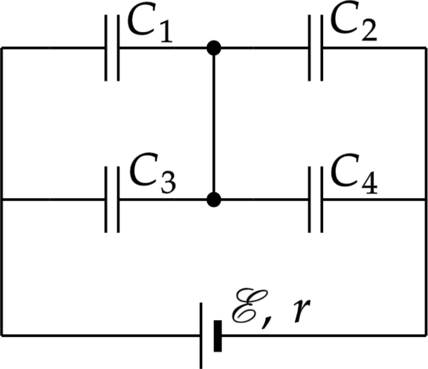
Четыре конденсатора подключены к источнику тока, как показано на рисунке. ЭДС источника равно (xi=10) В его внутреннее сопротивление (r), ёмкости конденсаторов (C_1=3C), (C_2=2C), (C_3=4C), (C_4=C=100) мкФ. Определите энергию на конденсаторе (C_2). Ответ дайте в мДж.
Пусть потенциал между блоком из конденсаторов 1–3 и блоком конденсаторов 2–4 равен (phi), тогда напряжение на блоке 1–3 равно (U_{13}=xi-phi), а напряжение на блоке 2–4 равно(U_{24}=phi-0=phi). Найдем емкости блоков конденсаторов [C_{13}=3C+4C=7C hspace{10 mm} C_{24}=2C+C=3C] Так как блок 1–3 и блок 2–4 подключены последовательно, то на них одинаковый заряд [q_{13}=q_{24} Rightarrow 7C(xi-phi)=3C phi Rightarrow phi=dfrac{7xi}{10}] Так как конденсаторы 2 и 4 подключены параллельно, то напряжение на втором конденсаторе равно напряжению 2–4, а значит энергия второго конденсатора равна [Q_2=dfrac{C 49xi^2}{100cdot 2}=dfrac{49Cxi^2}{200}=dfrac{49 cdot 200cdot 10^{-6}text{ Ф}cdot 100text{ В$^2$}}{200}=4,9text{ мФ}]
Ответ: 4,9
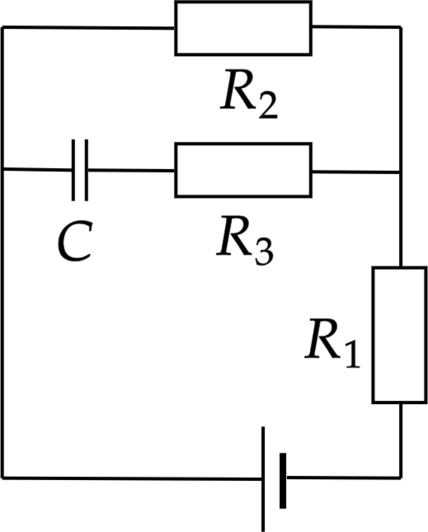
Конденсатор емкостью 2 мкФ присоединен к источнику постоянного тока с ЭДС 3,6 В и внутренним сопротивлением 1 Ом. Сопротивления резисторов (R_1 =) 4 Ом, (R_2) = 7 Ом, (R_3) = 3 Ом. Каков заряд на левой обкладке конденсатора? Ответ дайте в мкКл.
При установившемся токе в цепи ток через конденсатор не будет идти, а значит резистор (R_3) не будет включен в цепь.
По закону Ома для полной цепи, ток в цепи равен [I=frac{xi}{r+R_{1}+R_{2}}] Так как резистор (R_{2} ) и конденсатор подключены параллельно, то напряжение на конденсаторе напряжению на резисторе [U_{C}=U_{R_{2}}=I R_{2}=frac{xi R_{2}}{r+R_{1}+R_{2}}] Заряд на конденсаторе и напряжение связаны фopмулой: [q=C U_{C}] Найдем заряд на левой обкладке, ом будет равен заряду конденсатора, при этом он будет положительным. [q=2 cdot 10^{-6} Phi frac{3,6 text{ В} cdot 7 text{ Ом}}{1 text{ Ом}+4 text{ Ом}+7 text{ Ом}}=4,2 text{ мкКл}]
Ответ: 4,2
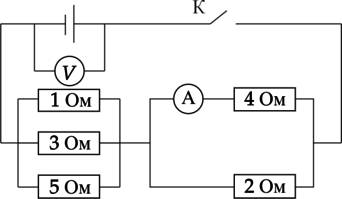
В электрической схеме до замыкания ключа К показание идеального вольтметра 9 В. После замыкания ключа показание идеального амперметра 1 А. Найдите внутреннее сопротивление батарейки.
“Досрочная волна 2019 вариант 2”
1) Поскольку вначале ключ разомкнут, то вольтметр показывает ЭДС источника тока (xi=9) В.
2) Найдём ток в цепи. Поскольку сопротивления 4 и 2 включены между собой параллельно, то напряжения на них равны друг другу. По закону Ома для участка цепи мы можем расписать каждое из напряжений и можем найти токи через резистор 2. При [U_2=U_4 Leftrightarrow I_2R_2=I_4R_4 Leftrightarrow1text{ А}cdot 4text{ Ом}=I_2cdot 2text{ Ом}Leftrightarrow I_2=2text{ А}] 3) Общий ток в цепи — это сумма токов на резисторах 4 и 2: [I=I_4+I_2=2text{ А}+1text{ А}=3text{ А}] 4) Найдём общее сопротивление цепи. Оно будет равно сумме сопротивлений на участках 1–3–5 и 2–4. А на каждом из этих участков мы найдём сопротивления по закону параллельного сопротивления проводников. [dfrac{1}{R_{1-3-5}}=dfrac{1}{R_1}+dfrac{1}{R_3}+dfrac{1}{R_5}=dfrac{1}{1}+dfrac{1}{3}+dfrac{1}{5}=dfrac{23}{15}Leftrightarrow R_{1-3-5}=dfrac{15}{23}text{ Ом}] Найдем общее сопротивление: [R_0=R_{1-3-5}+R_{2-4}=dfrac{15}{23}text{ Ом}+dfrac{4}{3}text{ Ом}=dfrac{137}{69}text{ Ом}] 5) Внутреннее сопротивление можно найти через закон Ома для полной цепи: [I=dfrac{xi}{R+r} Rightarrow r =dfrac{xi}{I}-R=dfrac{9text{ В}}{3text{ А}}-dfrac{137}{69}text{ Ом}approx 1,01 text{ Ом}]
Ответ: 1,01
Конденсатор подключен к источнику с постоянным напряжением (U=10) В, (С=10) мкФ. Как изменится энергия конденсатора, если расстояние между обкладками заполнить диэлектриком с диэлектрической проницаемостью (varepsilon=2)
“Основная волна 2020 Вариант 5”
Ёмкость конденсатора: [C=dfrac{varepsilonvarepsilon_0S}{d},] где (S) — -площадь пластин, (d) – расстояние между пластинами
Площадь пластин и расстояние между ними не изменяют, а диэлектрическая проницаемость воздуха 1, следовательно, ёмкость конденсатора увеличится в 2 раза при внесениии диэлектрика и станет равной (C=20) мкФ.
Конденсатор не отключают от напряжения, следовательно, изменение энергии конденсатора будет равно [Delta W =W_2-W_1=dfrac{2CU^2}{2}-dfrac{CU^2}{2}=dfrac{CU^2}{2}=dfrac{10text{ мкФ}cdot 100text{ В}}{2}=500text{ мкДж}]
Ответ: 37
Конденсатор ёмкостью 100 мкФ заряжен до напряжения 300 В, к нему подключают параллельно второй незаряженный конденсатор ёмкостью 200 мкФ. Найдите чему будет равно количество теплоты, которое выделится при этом. Ответ дайте в Дж.
Заряд на конденсаторе находится по формуле: [q=CU,] где (C) – ёмкость конденсатора, (U) – напряжение на конденсаторе.
Запишем закон сохранения заряда для цепи [C_1U=(C_1+C_2)U_1, quad (1)] где (C_1) и (C_2) – ёмкость первого и второго конденсаторов, (U) – напряжение на конденсаторе до подключения второго конденсатора, (U_1) – напряжение на конденсаторах после подключения второго конденсатора.
Закон сохранения в этом случае выглядит следующим образом [W_1=Q+W_2, quad (2)] где (W_2) и (W_1) – конечная и начальная энергия в цепи.
Энергия на конденсаторе же равна [W=dfrac{CU^2}{2} quad (3)] Объединим (1), (2) и (3) [Q=dfrac{C_1U^2}{2}-dfrac{(C_1+C_2)U_1^2}{2}=U^2left(dfrac{(C_1+C_2)C_1}{2(C_1+C_2)}-dfrac{C_1^2}{2(C_1+C_2)}right)=U^2left(dfrac{C_1C_2}{2(C_1+C_2)}right)] Подставим числа из условия [Q=9cdot 10^4text{ В$^2$} left(dfrac{100text{ мкФ}cdot 200text{ мкФ}}{2(100text{ мкФ}+200text{ мкФ})}right)=3text{ Дж}]
Ответ: 3

УСТАЛ? Просто отдохни
Разряд конденсатора с выделением тепла
Переходные процессы — сложная тема, сложная даже для студентов, тем более — для школьников. Помните: постоянный ток не протекает через конденсатор. Напряжение на конденсаторе определяется его подключением: если параллельно резистору — то напряжение такое же, как на резисторе, если последовательно с источником — то конденсатор зарядится до ЭДС источника, после чего ток исчезнет. Если дать конденсатору возможность разрядиться — то энергия, запасенная в нем, превратится в тепло на резисторе.
Задача 1.
Источник постоянного тока с ЭДС В и внутренним сопротивлением
Ом подсоединен к параллельно соединенным резисторам
Ом,
Ом и конденсатору. Определите емкость конденсатора С, если энергия электрического поля конденсатора равна
мкДж.
К задаче 1
Определить емкость легко из энергии конденсатора, только надо знать напряжение:
Объединим резисторы в один:
Ток в неразветвленной части цепи равен
Напряжение на внутреннем сопротивлении тогда равно
Тогда на резисторах и конденсаторе напряжение
Емкость равна
Ответ: мкФ.
Задача 2.
Источник постоянного напряжения с ЭДС 100 В подключен через резистор к конденсатору переменной емкости, расстояние между пластинами которого можно изменять (см. рис.). Пластины медленно раздвинули. Какая работа была совершена против сил притяжения пластин, если за время движения пластин на резисторе выделилось количество теплоты 10 мкДж и заряд конденсатора изменился на 1 мкКл?
К задаче 2
У конденсатора была энергия до того, как пластины раздвинули – пусть . И после тоже была – пусть
. В процессе раздвижения пластин совершили работу (которую надо найти), и, так как заряд уменьшился (а он именно уменьшился, так как напряжение осталось тем же), то источник тоже совершил работу. Поэтому закон сохранения энергии запишется так:
Заряд на конденсаторе сначала: , потом —
. Тогда изменение заряда равно
Работа источника
Тогда наш закон сохранения можно переписать:
Ответ: 60 мкДж
Задача 3.
Заряженный конденсатор мкФ включен в последовательную цепь из резистора
Ом, незаряженного конденсатора
мкФ и разомкнутого ключа К (см. рис.). После замыкания ключа в цепи выделяется количество теплоты
мДж. Чему равно первоначальное напряжение на конденсаторе
?
К задаче 3
Первоначально на конденсаторе есть заряд:
После замыкания ключа заряд разделится:
Но напряжение на конденсаторах одно и то же:
Тогда
Откуда:
Энергия до замыкания, запасенная в конденсаторе , сохраняется:
Ответ:
Задача 4.
В электрической схеме, показанной на рисунке, ключ К замкнут. ЭДС батарейки В, сопротивление резистора
Ом, заряд конденсатора 2 мкКл. После размыкания ключа К в результате разряда конденсатора на резисторе выделяется количество теплоты 20 мкДж. Найдите внутреннее сопротивление батарейки
.
К задаче 4
Сначала на конденсаторе напряжение такое же, как на резисторе (потому что они включены параллельно):
Определим ток. Он замыкается в контуре , потому что постоянный ток не течет через конденсатор:
Тогда напряжение на резисторе и конденсаторе:
С другой стороны, когда ключ разомкнется, вся энергия, запасенная в конденсаторе, рассеется в виде тепла через резистор:
То есть
Приравняем:
А внутреннее сопротивление равно
Ответ: