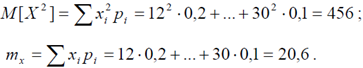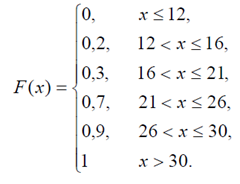Как графически найти среднее квадратическое отклонение - Исправление недочетов и поиск решений вместе с Examum.ru

Дисперсией
называется средний квадрат отклонений
индивидуальных значений признака от
их средней величины. Дисперсия
обозначается греческой буквой
(сигама) в квадрате и равна:

Пир
равенстве весов или когда они равны 1

Дисперсия
имеет большое значение в статистическом
анализе. Однако ее применение как меры
вариации в ряде случаев бывает не совсем
удобным, потому что размерность дисперсии
равна квадрату размерности изучаемого
признака. В таких случаях для измерения
вариации признака вычисляют среднее
квадратическое отклонение.

Среднее
квадратическое отклонение равно корню
квадратному из суммы квадратов отклонений
индивидуальных значений признака от
их средней, т.е. из дисперсии

А
при равенстве весов или когда они равны
1

Исчисление
дисперсии и среднего квадратического
отклонения позволяет устранить недостаток
среднего линейного отклонения. Ведь
любое число, положительное или
отрицательное, возведенное в квадрат,
будет числом положительным.

5. Коэффициент вариации

Дисперсия
и среднее квадратическое отклонение
недостаточно полно характеризуют
колеблемость признака, так как показывают
абсолютный размер отклонений, что
затрудняет сравнение изменчивости
различных признаков.

Для
характеристики колеблемости явления
среднее квадратическое отклонение
сопоставляют с его средней величиной
и выражают в процентах. Такой показатель
называется коэффициентом вариации,
обозначается буквой V
и рассчитывается по формуле

Коэффициент
вариации представляет собой отношение
среднего квадратического отклонения
к средней арифметической. Выражая его
в процентах, различные абсолютные
среднеквадратические отклонения
приводят к одному основанию и дают
возможность сравнивать, оценивать
колеблемость величин различных признаков
при помощи коэффициента вариации
возможно, например, сравнение размера
колеблемости производительности труда
групп рабочих, занятых производством
различных видов продукции, размера
колеблемости урожая различных
сельскохозяйственных культур и т.д.
Чем меньше коэффициент вариации, тем
меньше колеблемость признака, и
наоборот.

Если
взять отношение среднего линейного
отклонения к средней арифметической в
процентах, то получим линейный
коэффициент вариации

Отношение
размаха вариации к средней арифметической
в процентах называется коэффициентом
осцилляции

Самым
распространенным относительным
показателем колеблемости является
коэффициент вариации. Он более точно,
чем абсолютный, характеризует различие
колеблемости признаков.

По
величине коэффициента вариации можно
судить о степени вариации признаков
совокупности. Чем больше его величина,
тем больше разброс значений вокруг
средней, тем менее однородна совокупность
по своему составу и представительна
средняя.

Коэффициент
вариации важен и в тех случаях, когда
нужно сравнить средние квадратические
отклонения, выраженные в разных
единицах измерения.

6. Графическое изображение вариационного ряда

Графическое
изображение вариационных рядов облегчает
их анализ и позволяет судить о форме
распоряжения. Для графического
изображения вариационного ряда в
статистике строят гистограмму, полигон
и кумуляту распределения.

Гистограмма
— столбиковая диаграмма, для построения
которой на оси абсцисс откладывают
отрезки, равные величине интервалов
вариационного ряда. На отрезках строят
прямоугольники, высотка которых в
принятом масштабе по оси ординат
соответствует частотам (частностям).

Для
построения гистограммы по оси абсцисс
указывают значения границ интервалов
и на их основании строят прямоугольники,
высота которых пропорциональна частотам
(или частостям).

На рис. 1
изображена гистограмма распределения
населения России в 1997 г. по возрастным
группам.

Все население	В том числе в возрасте
	до 10	10-20	20-30	30-40	40-50	50-60	60-70	70 и старше	Всего
Численность населения	12,1	15,7	13,6	16,1	15,3	10,1	9,8	7,3	100,0

Рис. 2.
Распределение населения России по
возрастным группам

Условие:
Приводится распределение 30 работников
фирмы по размеру месячной заработной
платы

Размер заработной платы руб. в месяц	Численность работников чел.
до 5000	4
5000 — 7000	12
7000 — 10000	8
10000 — 15000	6
Итого:	30

Задача:
Изобразить интервальный вариационный
ряд графически в виде гистограммы

и
кумуляты

Решение:

Неизвестная граница
открытого (первого) интервала определяется
по величине второго интервала: 7000 —
5000 = 2000 руб. С той же величиной находим
нижнюю границу первого интервала: 5000
— 2000 = 3000 руб.
Для построения
гистограммы в прямоугольной системе
координат по оси абсцисс откладываем
отрезки, величины которых соответствуют
интервалам варицонного ряда.

Эти
отрезки служат нижним основанием, а
соответствующая частота (частость) —
высотой образуемых прямоугольников.
Построим гистограмму:

Для построения кумуляты
необходимо рассчитать накопленные
частоты (частости). Они определяются
путем последовательного суммирования
частот (частостей) предшествующих
интервалов и обозначаются S. Накопленные
частоты показывают, сколько единиц
совокупности имеют значение признака
не больше, чем рассматриваемое.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

Определите среднее (простое среднее арифметическое ряда значений).
Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее $=frac{600+470+170+430+300}{5} = 394$ мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

$[ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]$

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия $= frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{5} = 21704$ мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки = $frac{108520}{4}=27130$ мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

$frac{4+4-4-4}{4}=0$ .

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

$frac{4+4+|-4|+|-4|}{4} = frac{4+4+4+4}{4}=4$ .

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

$frac{7+1+|-6|+|-2|}{4} = frac{7+1+6+2}{4}=4$ .

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

$sqrt{frac{4^2+4^2+(-4)^2+(-4)^2}{4}}=4$ .

Для второго примера получится:

$sqrt{frac{7^2+1^2+(-6)^2+(-2)^2}{4}}=4.74$ .

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Источник

Создание вариационного
ряда, вариационной кривой, определение среднего значения и среднеквадратичного
отклонения.

Для селекционера,
например, важно знать, сколько зерен содержит колос выведенного (выводимого) им
нового сорта пшеницы. В этой ситуации совершенно ясно, что подсчетом количества
зерен только в одном колосе не обойтись. Для определения числа зерен надо
воспользоваться достаточно большим количеством колосьев, скажем не менее сотни.
Приведем пример математической обработки результатов селекции.

Все поле
пшеницы, которое вырастил селекционер можно на математическом языке назвать
генеральной совокупностью. Подсчитать количество зерен в колосьях всей
генеральной совокупности, очевидно, не представляется возможным, но из всей
генеральной совокупности можно выбрать, скажем, сто колосьев и подсчитать
количество зерен в них. Эти сто колосьев будут называться выборкой из генеральной
совокупности, и они с определенной точностью будут отражать число зерен во всем
поле (генеральной совокупности). Чтобы по данным выборки иметь возможность
судить обо всей генеральной совокупности, она должна быть отобрана случайно.
Так в нашем случае селекционер ни в коем случае не должен отдавать предпочтение
тем или иным колосьям (по размерам, внешнему виду, месту произрастания на поле
и т.п.) в процессе их выборки. Наиболее целесообразно в данной ситуации
совершать выбор колосьев из непрозрачного мешка наугад. У всех выбранных
колосьев производится подсчет числа зерен, и результаты фиксируются в виде ряда
чисел, с которыми в дальнейшем и предстоит совершать математические действия. В
данном примере можно предложить следующую их последовательность.

2.1 Создание вариационного ряда.

Вариационным
рядом называется ранжированный в порядке возрастания или убывания ряд вариантов
с соответствующими им весами (частотами или частностями). Вариационный ряд
будет дискретным, если любые его варианты отличаются на постоянную величину, и
непрерывным, если варианты могут отличатся один от другого на сколь угодно
малую величину.

Иными словами в вариационном ряду
полученные значения располагаются в порядке их увеличения и, если значение
повторяется, то рядом записывается число его повторений. Т.е. в данном примере
по числу зерен в колосьях ряд может выглядеть так (таб. 2):

Таблица 2

Число зерен в колосе	17	18	19	20	21	22	23	24	25
Число колосьев	1	2	2	4	6	8	8	9	10
Число зерен в колосе	26	27	28	29	30	31	32	33	34
Число колосьев	9	9	9	8	6	4	3	1	1

Полученный вариационный ряд
позволяет выявить закономерности распределения колосьев по числу зерен в них.

2.2 Создание вариационной
кривой.

Закономерности распределения
можно представить более наглядно, создав вариационную кривую, называемую
полигоном (рис 3), или представить в виде столбчатой диаграммы, которая здесь
будет называться гистограммой (рис 4).

2ю1

2ю2

Из полученных схем уже можно наглядно судить о закономерностях
распределения.

Диаграммы
строятся при помощи «Excel»
так:

Ø Ввести в окно программы данные вариационного
ряда.

Ø Запустить «Мастер диаграмм», нажатием
кнопки .

Ø В графе «тип» выбирать или «гистограмма», или
«график».

Ø Нажать кнопку «Далее».

Ø В «шаге 2 из 4» найти строку с названием
«Диапазон» и щелкнуть по кнопке, расположенной справа от надписи и пустого
поля, при этом «Мастер диаграмм» несколько свернется.

Ø Выделить данные в окне программы (в примере это
значения в ячейках В1 – В18).

Ø Снова щелкнуть по кнопке в «Мастере диаграмм».
«Мастер» развернется. В окне «Мастера» появится эскиз гистограммы или полигона.

Ø В этом же шаге (2 из 4) щелкнуть по закладке с
надписью «Ряд».

Ø В открывшейся страничке найти строчку с надписью
«Подписи оси Х».

Ø Щелкнуть по кнопке справа от надписи и пустого
поля.

Ø Выделить значения в окне программы, которые
будут на диаграмме представляться в качестве данных оси Х. (в примере значения
в ячейках А1 – А18).

Ø Щелкнуть по кнопке в свернутом «Мастере».

Ø Щелкнуть по кнопке «Далее» (шаг 3 из 4).

Ø При необходимости, в графе «Заголовки» выполнить
подписи осей Х и Y, а
так же дать диаграмме название.

Ø Щелкнуть по кнопке далее, затем готово и в
результате получится готовая гистограмма или полигон (рис 3).

2.3 Определение среднего значения признака.

Среднее
значение ряда данных находится обычным образом. Суммируются все значения
признака и делятся на количество этих значений. Т.е. здесь общее число зерен в
100 колосках равно 2551, то среднее значение будет равно 2551/100 = 25.51.

Для определения
среднего значения признака с использованием «Excel» надо выполнить следующие шаги:

Ø Ввести в столбец А окна программы все значения
признака, в том числе и повторяющиеся. Т.е. здесь все 100 значений зерен в
колосках. Ввод можно осуществлять в любой последовательности – по возрастанию,
по убыванию или в разнобой. Введенный массив чисел лучше сохранить, так как он
пригодится для расчета отклонения.

Ø Щелкнуть в окне программы по любой пустой
ячейке. По окончании расчетов в ней появится соответствующее среднее значение.

Ø В меню «Вставка» выбрать «Функция».

Ø В появившемся списке функций выбрать функцию
«СРЗНАЧ».

Ø Щелкнуть по кнопке «ОК». Появится окно
«Аргументы функции».

Ø Щелкнуть по кнопке правее надписи «Число 1» и
поля (окно свернется).

Ø Выделить в окне программы весь числовой массив,
среднее значение которого необходимо определить.

Ø Щелчком по кнопке справа от поля с надписями
развернуть окно «Аргументы функции».

Ø Щелкнуть по кнопке «ОК». В выбранной
предварительно ячейке появится среднее значение массива чисел.

2.4 Определение среднего квадратического
отклонения.

Вариационная кривая имеет
определенную ширину. Нетрудно догадаться, что чем больше ширина вариационной
кривой, тем сильнее разброс значений относительно средней величины.

2ю3

2ю4

Как показано на рисунках 5 и 6 при
одном и том же среднем значении, равном 25.51, полигон первого рисунка шире
полигона второго.

Оценить
степень разброса данных относительно среднего значения можно рассчитав значение
дисперсии S²,
или среднее квадратическое отклонение S, равное корню квадратному из дисперсии. Дисперсией вариационного ряда называется
средняя арифметическая квадратов отклонений вариантов от их средней
арифметической. Значением среднего квадратического отклонения пользоваться
удобнее, так как оно выражается в тех же единицах, что и значение признака. Так
среднее квадратическое отклонение данных, представленных графически на первом
полигоне равно 3.70, а на втором полигоне 2.65. Видим, что отклонение первое
больше второго и это как раз и отражается на ширине полигона.

Алгоритм
расчета среднего квадратического отклонения
и дисперсии такой же, как и для расчета среднего арифметического
значения, только в списке функций надо выбрать «СТАНДОТКЛОН» для вычисления отклонения, или «ДИСП» для расчета дисперсии.

Источник

Главная
Полезные советы
Найти среднее квадратическое отклонение, привести аналитическое и графическое изображение функции распределения F(x).

По заданному закону распределения дискретной случайной величины X, найти ее среднее квадратическое отклонение, привести аналитическое и графическое изображение функции распределения F(x), построить многоугольник распределения вероятностей.

Решение:

Среднее квадратическое отклонение дискретной случайной величины X равно

где

Отсюда

Функция распределения F(x) имеет вид

Если испытываете трудности в написании контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена — от 99 рублей.

Источник

Загрузить PDF

Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.^[1] Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.^[2] Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.

1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.^[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
2
Для вычисления среднего значения понадобятся все числа данного набора данных.^[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
3
Сложите все числа вашего набора данных.^[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.^[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама

1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.^[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.^[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.^[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 2², 0², 2², 0², 0², и (-4)² = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
4
Сложите квадраты значений, то есть найдите сумму квадратов.^[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.^[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама

1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.^[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.^[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.^[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама

Об этой статье

Эту страницу просматривали 64 925 раз.

Была ли эта статья полезной?

Источник