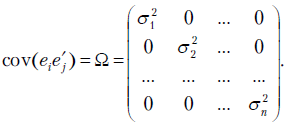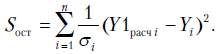Понимание гетероскедастичности в регрессионном анализе
17 авг. 2022 г.
читать 3 мин
В регрессионном анализе гетероскедастичность (иногда пишется как гетероскедастичность) относится к неравномерному разбросу остатков или ошибок. В частности, это относится к случаю, когда имеет место систематическое изменение разброса невязок по диапазону измеренных значений.
Гетероскедастичность является проблемой, потому что обычная регрессия методом наименьших квадратов (OLS) предполагает, что остатки поступают из совокупности с гомоскедастичностью , что означает постоянную дисперсию.
Когда в регрессионном анализе присутствует гетероскедастичность, его результатам становится трудно доверять. В частности, гетероскедастичность увеличивает дисперсию оценок коэффициента регрессии, но регрессионная модель этого не учитывает.
Это повышает вероятность того, что регрессионная модель объявит термин в модели статистически значимым, хотя на самом деле это не так.
В этом руководстве объясняется, как обнаружить гетероскедастичность, причины гетероскедастичности и потенциальные способы решения проблемы гетероскедастичности.
Как обнаружить гетероскедастичность
Самый простой способ обнаружить гетероскедастичность — использовать график сопоставления значения и остатка .
После того, как вы подгоните линию регрессии к набору данных, вы можете создать диаграмму рассеяния, которая показывает подобранные значения модели в сравнении с остатками этих подобранных значений.
На приведенной ниже диаграмме рассеяния показано типичное подобранное значение по сравнению с остаточным графиком , на котором присутствует гетероскедастичность.
Обратите внимание, как остатки становятся намного более разбросанными по мере того, как подобранные значения становятся больше. Эта форма «конуса» является явным признаком гетероскедастичности.
Что вызывает гетероскедастичность?
Гетероскедастичность возникает естественным образом в наборах данных с большим диапазоном наблюдаемых значений данных. Например:
- Рассмотрим набор данных, который включает годовой доход и расходы 100 000 человек в Соединенных Штатах. Для лиц с более низкими доходами изменчивость соответствующих расходов будет ниже, поскольку у этих людей, вероятно, достаточно денег только для оплаты самого необходимого. Для людей с более высокими доходами будет более высокая изменчивость соответствующих расходов, поскольку у этих людей есть больше денег, которые они могут потратить, если захотят. Некоторые люди с более высоким доходом предпочтут тратить большую часть своего дохода, в то время как некоторые могут предпочесть быть бережливыми и тратить только часть своего дохода, поэтому изменчивость расходов среди этих людей с более высоким доходом по своей сути будет выше.
- Рассмотрим набор данных, включающий население и количество цветочных магазинов в 1000 различных городах США. Для городов с небольшим населением может быть обычным наличие только одного или двух цветочных магазинов. Но в городах с большим населением будет гораздо большая вариабельность количества цветочных магазинов. В этих городах может быть от 10 до 100 магазинов. Это означает, что когда мы создаем регрессионный анализ и используем население для прогнозирования количества цветочных магазинов, по своей сути будет большая изменчивость остатков для городов с более высоким населением.
Некоторые наборы данных просто более склонны к гетероскедастичности, чем другие.
Как исправить гетероскедастичность
Существует три распространенных способа исправить гетероскедастичность:
1. Преобразуйте зависимую переменную
Один из способов исправить гетероскедастичность — каким-то образом преобразовать зависимую переменную. Одним из распространенных преобразований является просто получение журнала зависимой переменной.
Например, если мы используем численность населения (независимая переменная) для прогнозирования количества цветочных магазинов в городе (зависимая переменная), вместо этого мы можем попытаться использовать численность населения для прогнозирования логарифма количества цветочных магазинов в городе.
Использование журнала зависимой переменной, а не исходной зависимой переменной, часто приводит к исчезновению гетероскедастичности.
2. Переопределите зависимую переменную
Другой способ исправить гетероскедастичность — переопределить зависимую переменную. Один из распространенных способов сделать это — использовать скорость для зависимой переменной, а не необработанное значение.
Например, вместо использования численности населения для прогнозирования количества цветочных магазинов в городе мы можем вместо этого использовать численность населения для прогнозирования количества цветочных магазинов на душу населения.
В большинстве случаев это снижает изменчивость, которая естественным образом возникает среди больших групп населения, поскольку мы измеряем количество цветочных магазинов на человека, а не простое количество цветочных магазинов.
3. Используйте взвешенную регрессию
Другой способ исправить гетероскедастичность — использовать взвешенную регрессию. Этот тип регрессии присваивает вес каждой точке данных на основе дисперсии ее подобранного значения.
По сути, это дает небольшие веса точкам данных с более высокой дисперсией, что уменьшает их квадраты невязок. Когда используются правильные веса, это может устранить проблему гетероскедастичности.
Вывод
Гетероскедастичность — довольно распространенная проблема, когда дело доходит до регрессионного анализа, потому что многие наборы данных по своей природе склонны к непостоянной дисперсии.
Однако, используя график сравнения подобранного значения с остатком , можно довольно легко обнаружить гетероскедастичность.
А путем преобразования зависимой переменной, переопределения зависимой переменной или использования взвешенной регрессии проблему гетероскедастичности часто можно устранить.
Существует
множество методов устранения
гетероскедастичности остатков модели
регрессии. Рассмотрим некоторые из них.
Наиболее
простым методом устранения
гетероскедастичности остатков модели
регрессии является взвешивание параметров
модели регрессии. В этом случае отдельным
наблюдениям независимой переменой,
характеризующимся максимальным
среднеквадратическим отклонением
случайной ошибки, придаётся больший
вес, а остальным наблюдениям с минимальным
среднеквадратическим отклонением
случайной ошибки придаётся меньший
вес. После данной процедуры свойство
эффективности оценок неизвестных
коэффициентов модели регрессии
сохраняется.
Если
для устранения гетероскедастичности
был использован метод взвешивания, то
в результате мы получим взвешенную
модель регрессии с весами
Предположим,
что на основе имеющихся данных была
построена линейная модель парной
регрессии, в которой было доказано
наличие гетероскедастичности остатков
Рассмотрим
подробнее процесс взвешивания для
данной модели регрессии.
Разделим
каждый член модели регрессии на
среднеквадратическое отклонение
случайной ошибки G(
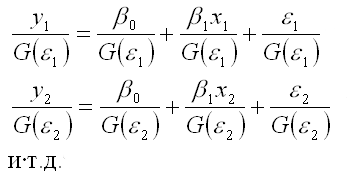
В
общем виде процесс взвешивания для
линейной модели парной регрессии
выглядит следующим образом:
Для
более наглядного представления полученной
модели регрессии воспользуемся методом
замен:
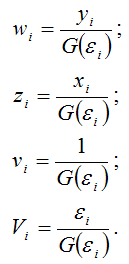
В
результате получим преобразованный
вид взвешенной модели регрессии:
Преобразованная
взвешенная модель регрессии является
двухфакторной моделью регрессии.
Дисперсию
случайной ошибки взвешенной модели
регрессии можно рассчитать по формуле:
Полученный
результат доказывает постоянство
дисперсий случайных ошибок преобразованной
модели регрессии, т. е. о выполнении
условия гомоскедастичности.
Главный
недостаток метода взвешивания заключается
в необходимости априорного знания
среднеквадратических отклонений
случайных ошибок модели регрессии. По
той причине, что в большинстве случаев
данная величина является неизвестной,
приходится использовать другие методы,
в частности методы коррекции
гетероскедастичности.
Определение.
Суть методов коррекции гетероскедастичности
состоит в определении оценки ковариационной
матрицы случайных ошибок модели
регрессии:
Для
определения оценок
используется
метод Бреуше-Пайана, который реализуется
в несколько этапов:
1)
после получения оценок неизвестных
коэффициентов модели регрессии
рассчитывают остатки ei и
показатель суммы квадратов остатков
2)
рассчитывают оценку дисперсии остатков
модели регрессии по формуле:
3)
строят взвешенную модель регрессия,
где весами являются оценка дисперсии
остатков модели регрессии
4)
если при проверке гипотез взвешенная
модель регрессии является незначимой,
то можно сделать вывод, что оценки
матрицы ковариаций являются неточными.
Если
вычислены оценки дисперсий остатков
модели регрессии, то в этом случае можно
использовать доступный обобщённый или
взвешенный методы наименьших квадратов
для вычисления оценок коэффициентов
модели регрессии, которые отличаются
только оценкой
Если
гетероскедастичность остатков не
поддаётся корректировке, то можно
рассчитать оценки неизвестных
коэффициентов модели регрессии с помощью
классического метода наименьших
квадратов, но затем подвергнуть
корректировке ковариационную матрицу
оценок коэффициентов
т.
к. условие гетероскедастичности приводит
к увеличению данной матрицы.
Ковариационная
матрица оценок коэффициентов
может
быть скорректирована методом Уайта:
где N –
количество наблюдений;
X –
матрица независимых переменных;
– квадрат
остатков модели регрессии;
– транспонированная
i-тая строка матрицы данных Х.
Корректировка
ковариационной матрицы оценок
коэффициентов
методом
Уайта приводит к изменению t-статистики
и доверительных интервалов для
коэффициентов регрессии.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Важное предположение о линейной регрессии заключается в том, что остатки не имеют гетероскедастичности. Проще говоря, дисперсия остатка не будет увеличиваться с установленным значением переменной отклика. В этой статье я объясню, почему важно обнаруживать гетероскедастичность? Как определить гетероскедастичность модели? Если существует, как исправить эту проблему с помощью кода R. Этот процесс иногда называютОстаточный анализ。
Почему важно определять гетероскедастичность?
Как только выПостроение модели линейной регрессииОбычно гетероскедастичность остатков должна быть обнаружена. Причина в том, что мы хотим проверить, может ли установленная модель объяснить некоторые шаблоны переменной отклика Y, и в конечном итоге она отображается в остатке. Если есть гетероскедастичность, полученная регрессионная модель неэффективна и нестабильна, и мы можем получить странные результаты предсказания позже.
Как определить гетероскедастичность?
Следующее строится через RcarsМодель регрессии, полученная из набора данных, используется для иллюстрации. Первый проходlm()Функция для построения модели:
lmMod <- lm(dist ~ speed, data=cars) # initial modelТеперь модель готова. Есть два способа определения гетероскедастичности:
-
Графический метод
-
Статистический тест
Графический метод
par(mfrow=c(2,2)) # init 4 charts in 1 panel
plot(lmMod)График выглядит следующим образом:
Нас интересуют две картинки в верхнем левом и нижнем левом углах. Верхний левый угол представляет собой график зависимости остатков от подгоночных значений. Нижний левый угол — это нормализованные остатки, нанесенные на график относительно установленных значений. Если гетероскедастичности нет вообще, вы должны увидеть совершенно случайную точку, точка равномерно распределена по всему диапазону оси X, и вы получите плоскую красную линию.
Однако в этом случае красная линия слегка изогнута от верхнего левого графика, и остаточная ошибка, по-видимому, увеличивается с увеличением значения подгонки. Поэтому предполагается, что гетероскедастичность существует.
Статистический тест
Иногда вам может понадобиться алгоритм для определения гетероскедастичности. Для того, чтобы автоматически оценить его существование и внести изменения. Существует два метода тестирования, чтобы определить, существует ли гетероскедастичность — тест Брейша-Пэгана и тест NCV.
Бреуш языческий тест
lmtest::bptest(lmMod) # Breusch-Pagan test
studentized Breusch-Pagan test
data: lmMod
BP = 3.2149, df = 1, p-value = 0.07297Инспекция NCV
car::ncvTest(lmMod) # Breusch-Pagan test
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 4.650233 Df = 1 p = 0.03104933 Учитывая уровень значимости 0,05, значения P для обоих тестов малы. Следовательно, мы можем отвергнуть нулевую гипотезу о том, что дисперсия остатка постоянна, и сделать вывод, что гетероскедастичность существует, подтверждая тем самым приведенный выше графический вывод.
Как исправить гетероскедастичность?
Перестройте модель прогнозирования
Переменное преобразование, такое как преобразование Бокса-Кокса
Преобразование Бокса-Кокса
Преобразование Бокса-КоксаЭто математическое преобразование, которое превращает переменные в приблизительно нормальное распределение. Обычно преобразование Бокса-Кокса для переменной Y может решить эту проблему, и это именно то, что я хочу сделать.
library(caret)
distBCMod <- caret::BoxCoxTrans(cars$dist)
print(distBCMod)
Box-Cox Transformation
50 data points used to estimate Lambda
Input data summary:
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.00 26.00 36.00 42.98 56.00 120.00
Largest/Smallest: 60
Sample Skewness: 0.759
Estimated Lambda: 0.5 Модельный объект, полученный преобразованием Бокса-Кокса, уже существует, теперь примените его кcar$distЗагрузите и добавьте новый фрейм данных.
cars <- cbind(cars, dist_new=predict(distBCMod, cars$dist)) # append the transformed variable to cars
head(cars) # view the top 6 rows
speed dist dist_new
1 4 2 0.8284271
2 4 10 4.3245553
3 7 4 2.0000000
4 7 22 7.3808315
5 8 16 6.0000000
6 9 10 4.3245553Для новой регрессионной модели преобразованные данные уже доступны. Теперь начните создавать модель и проверьте гетероскедастичность.
lmMod_bc <- lm(dist_new ~ speed, data=cars)
bptest(lmMod_bc)
studentized Breusch-Pagan test
data: lmMod_bc
BP = 0.011192, df = 1, p-value = 0.9157При значении P 0,91 мы не можем отклонить нулевую гипотезу (дисперсия остатка постоянна). Следовательно, дисперсия предполагаемых остатков одинакова. Точно так же используйте график, чтобы проверить гетероскедастичность.
plot(lmMod_bc)График выглядит следующим образом:
Линия вверху слева более плоская, а остатки распределены равномерно. Таким образом, проблема гетероскедастичности была решена.
Эта статья переведена и организована Xueqing Data Network, пожалуйста, обратитесь к оригинальному текстуHow to detect heteroscedasticity and rectify it?Автор Сельва Прабхакаран. Перепечатка, пожалуйста, укажите оригинальную ссылкуhttp://www.xueqing.cc/cms/article/113
Перепечатано по адресу: https://my.oschina.net/u/2605101/blog/603214.
4.3. Последствия гетероскедастичности
При использовании метода наименьших квадратов параметры модели находят по формуле (3.8)
Ранее было доказано, что оценка (3.8) несмещенная. Этот факт основывался на равенстве нулю 

4.4. Подходы к решению проблемы гетероскедастичности
Существует два подхода к решению проблемы гетероскедастичности:
- преобразование данных;
- применение взвешенного и обобщенного метода наименьших квадратов (ОМНК).
Первый подход предполагает такое преобразование исходных данных, чтобы для них модель уже обладала свойством гомоскедастичности. Чаще всего для этого используют два вида преобразований: логарифмирование данных и переход к безразмерным величинам путем деления на некоторые известные величины той же размерности, что и исходные данные. Возможна также стандартизация исходных данных.
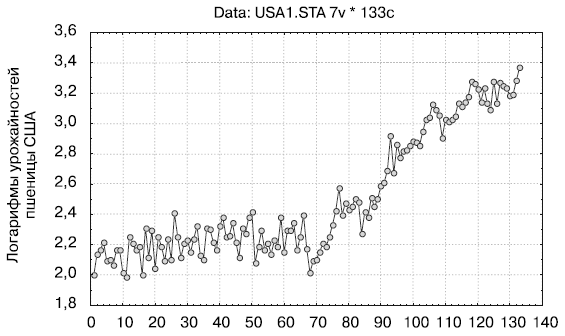
Для примера прологарифмируем ряд данных об урожайности пшеницы в США (рис. 4.2).
Рис.
4.2.
Как видно, преобразованный ряд (см. рис. 4.2) не имеет растущих отклонений от линейного тренда (тенденции роста) и ошибки модели, вероятно, будут гомоскедастическими. Проверим этот факт с помощью критерия Спирмена (табл. 4.2).
Таблица 4.2
Незначимость коэффициента корреляции Спирмена в данном случае очевидна. Факт гомоскедастичности остатков модели вида 
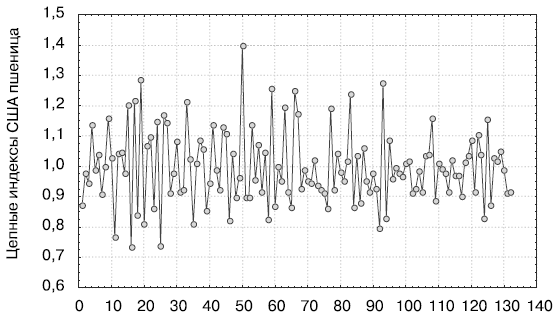
Теперь используем прием уменьшения колеблемости ряда за счет перехода к безразмерным переменным. Перейдем от данных урожайности пшеницы в США за 1866-1998 гг. к цепным индексам (рис. 4.3) по формуле 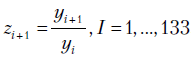
Рис.
4.3.
Цепные индексы США пшеница
Как видно из рис. 4.3, преобразованный ряд уже не показывает экспоненциальную тенденцию технического прогресса и его отклонения от среднего значения, вероятно, будут гомоскедастическими. Проверим этот факт с помощью критерия Спирмена (табл. 4.3).
Таблица 4.3
Коэффициент ранговой корреляции Спирмена оказался незначимым с высокой надежностью.
Второй метод устранения гетероскедастичности состоит, как было сказано, в построении моделей, учитывающих гетероскедастичность ошибок наблюдений. Перейдем к его изучению.
Обобщенная линейная модель множественной регрессии, теорема Айткена и обобщенный метод наименьших квадратов. В теореме Гаусса — Маркова предполагалось, что случайные возмущения имеют постоянную дисперсию и не коррелированы друг с другом. Это означает, что ковариационная матрица имеет вид 


Обобщенная линейная модель множественной регрессии предполагает следующую систему соотношений и условий:
Ранг неслучайной (детерминированной) матрицы 
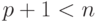



2) 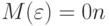
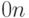

3) 



Итак, в обобщенной линейной регрессионной модели дисперсии и ковариации ошибок наблюдений могут быть произвольными.
Доказано, что при применении обычного МНК для построения оценок коэффициентов в условиях обобщенной модели получается смещенная оценка ковариационной матрицы 
Теорема Айткена. В классе линейных несмещенных оценок вектора коэффициентов модели 
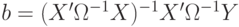 |
(4.1) |
является эффективной (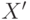

Доказательство состоит в сведении условий теоремы Айткена к условиям теоремы Гаусса — Маркова путем соответствующих преобразований и введения вспомогательных переменных-векторов. Представим (4.1) в виде
Из (4.2) и условия 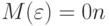






Умножим обе части обобщенной регрессионной модели 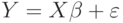

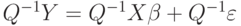
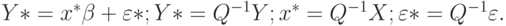 |
(4.3) |
Проверим, что уравнение (4.3) удовлетворяет условиям Гаусса — Маркова и, следовательно, МНК-оценки для коэффициентов уравнения (4.3) эффективные. Легко проверить, что МНК-оценки для коэффициентов уравнения (4.3) являются оценками (4.1) обобщенного МНК для уравнения 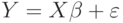
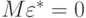

Теперь проверим, что МНК-оценка 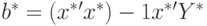
т.е. оценку (4.1). Доказательство теоремы завершено.
Поскольку оценка (4.1) согласно МНК минимизирует остаточную сумму квадратов
оценка ОМНК является точкой минимума обобщенного критерия (4.5).
Устранение гетероскедастичности путем применения обобщенного метода наименьших квадратов (ОМНК) требует знания матрицы ковариаций ошибок наблюдений, что бывает на практике в исключительных случаях. Если же считать все элементы матрицы 
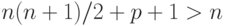

|
|
(4.6) |
Если дисперсии 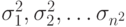


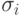
|
|
(4.7) |
В реальных экономических задачах значения 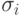
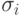
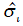
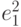
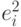
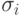
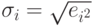
Контрольные вопросы
- Дайте определение гетероскедастичности наблюдений.
- Расскажите о тестировании гетероскедастичности на основе теста Голдфелда — Кванта.
- Опишите, как применяется для обнаружения гетероскедастичности тест ранговой корреляции Спирмена.
- Каковы последствия гетероскедастичности в случае использования МНК для построения модели?
- Опишите подходы к устранению гетероскедастичности, основанные на преобразовании исходных данных.
- Сформулируйте теорему Айткена о коэффициентах обобщенного МНК.
- Опишите алгоритм обобщенного метода наименьших квадратов (ОМНК) для построения уравнения регрессии в случае гетероскедастических наблюдений.




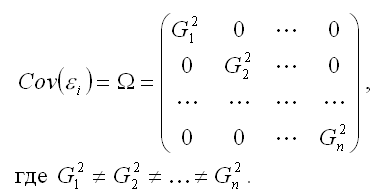


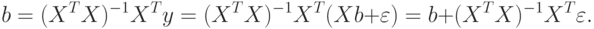



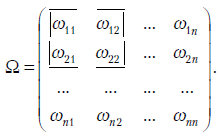
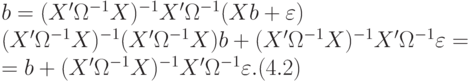
![cov(varepsilon ^*,varepsilon ^*') = M[(Q^{-1}varepsilon )(Q^{-1}varepsilon ')] = M[(Q^{-1}varepsilon varepsilon ' (Q^{-1}) '] =\
= Q^{-1}M(varepsilon varepsilon ')(Q^{-1}) ' = Q^{-1}Omega (Q^{-1})' =\
= Q^{-1}QQ' (Q^{-1}) ' = In. (4.4)](https://new2.intuit.ru/sites/default/files/tex_cache/e81c3cdae08dfae8ff0e29ae1434f908.png)
![b* = (x^*'x^*)-1x^*'Y* = [(Q^{-1}X)' (Q^{-1}X)]-1X' (Q^{-1})'Q^{-1}Y =\
= (X'Omega ^{-1}X)-1X'Omega ^{-1}Y,](https://new2.intuit.ru/sites/default/files/tex_cache/9192e40233abd70fbf1176d16763f7f0.png)