Как исправить рекурсию

Вот несколько самых простых способов на Python (скорее всего, легко портируются и для других языков).

Все их реально применил при решении мной вчера задачи на Stepik (там более сложные примеры, конечно, были, тут упростил для понимания читающих), да и в других случаях применял:

1) При проблеме с допустимой глубиной рекурсии, если не избавляться от самой рекурсии:*

надо добавить в код строку sys.setrecursionlimit (50000) — параметр в скобках с таким большим значением во всех моих случаях решал вопрос (по умолчанию этот параметр равен 1000 или чуть менее, в первом примере ниже ошибка появится при a = 998).
Требуется ещё import sys,конечно.

Повторю, что было написано в начальном вопросе: «В реальной работе это будет означать медленную работу программы либо неэффективное использование ресурсов компьютера». Лучше это не применять без большой необходимости.

*встречавшиеся мне ошибки при превышении глубины рекурсии:

RecursionError: maximum recursion depth exceeded in comparison и

RecursionError: maximum recursion depth exceeded while calling a Python object

2) При рекурсивном вызове в конце функции:

def test (a):
    a -= 1
    if a > 0:
        print (a)
    else:
        return
    test(a)


if __name__ == '__main__':
    a = 997
    test (a)

переделать функцию можем просто с помощью while True, уйдя от рекурсии:

def test (a):
    while True:
        a -= 1
        if a > 0:
            print (a)
        else:
            return

3) При варианте чуть сложнее с рекурсивными вызовами в середине функции:

def test(a, b):
    print ('test start, a, b', a, b)
    if a > 5:
        print('condition a')
        return test(a-1, b)
    if b < 5:
        print('condition b')
        return test(a, b+1)
    print ('test finish, a, b', a, b)


if __name__ == '__main__':
   a = 7
   b = 3

надо еще добавить continue и break, чтобы уйти от рекурсии, помимо while True:

def test(a, b):
    while True:
        print ('test start, a, b', a, b)
        if a > 5:
            print('condition a')
            a -= 1 
            continue
        if b < 5:
            print('condition b')
            b += 1
            continue
        print('test finish, a, b', a, b)
        break

Время на прочтение
4 мин

Количество просмотров 19K

Привет, Хабр! Представляю вашему вниманию перевод статьи «Removing a recursion in Python, part 1» автора Эрика Липперта (Eric Lippert).

На протяжении последних 20 лет я восхищался простоте и возможностям Python, хотя на самом деле никогда не работал с ним и не изучал подробно.

В последнее время я присмотрелся к нему поближе — и он оказался действительно приятным языком.

Недавний вопрос на StackOverflow заставил меня задуматься, как преобразовать рекурсивный алгоритм в итеративный, и оказалось, что Python довольно подходящий язык для этого.
Проблема с которой столкнулся автор вопроса заключалась в следующем:

• Игрок находится в произвольной клетке на пронумерованном поле;
• Цель вернуться в клетку №1;
• Если игрок находится на чётной клетке, он платит одну монету и проходит половину пути к клетке №1;
• Если игрок находится на нечётной клетке, он может заплатить 5 монет и сразу перейти на первую клетку или заплатить одну монету и сделать один шаг к клетке №1 — на чётную клетку.

Вопрос заключается в следующем: какое наименьшее количество монет необходимо заплатить, чтобы вернуться из текущей клетки в первую.

Задача имеет очевидное рекурсивное решение:

def cost(s):
  if s <= 1:
    return 0
  if s % 2 == 0:
    return 1 + cost(s // 2) 
  return min(1 + cost(s - 1), 5)

Однако эта программа падала, достигая максимальной глубины рекурсии, вероятнее всего из-за того, что автор вопроса экспериментировал с очень большими числами.
Следовательно возникает вопрос: как превратить рекурсивный алгоритм в итерационный на Python?

Перед тем как мы начнем, хочу отметить, что конечно существуют более быстрые решения этой конкретной задачи, сама по себе она не очень интересна.

Скорее эта задача послужила лишь отправной точкой в вопросе, как в общем случае избавиться от единственного рекурсивного вызова в программе на Python.

Смысл в том, что можно преобразовать любой простой рекурсивный метод и избавиться от рекурсии, а это всего лишь пример, который оказался под рукой.

Техника, которую я собираюсь показать, конечно не совсем соответствует тому, как принято писать на Python, вероятно решение в Python-стиле использовало бы генераторы или другие возможности языка.

Что я хочу показать здесь, так это как избавиться от рекурсии, используя последовательность маленьких и безопасных преобразований, приводящих функцию к такой форме, в которой легко произвести замену рекурсии на итерацию.

Для начала давайте посмотрим как привести программу к такой форме.

На первом шаге нашего преобразования я хочу чтобы вычисления производимые до рекурсивного вызова сводились к вычислению аргумента, а вычисления, после рекурсивного вызова, производились в отдельном методе, который принимает результат рекурсивного вызова.

def add_one(n):
  return n + 1

def get_min(n):
  return min(n + 1, 5)

def cost(s):
  if s <= 1:
    return 0

  if s % 2 == 0:
    argument = s // 2
    result = cost(argument)
    return add_one(result)

  argument = s - 1
  result = cost(argument)
  return get_min(result)

Вторым шагом я хочу вынести вычисление аргумента в отдельную функцию:

# ...
def get_argument(s):
  if s % 2 == 0:
    return s // 2
  return s - 1

def cost(s):
  if s <= 1:
    return 0

  argument = get_argument(s)
  result = cost(argument)

  if s % 2 == 0:
    return add_one(result) 
  return get_min(result)

На третьем шаге, я хочу добавить вспомогательную функцию, которая будет выбирать функцию-продолжение, вызываемую после возврата из рекурсии.

Обратите внимание, что вспомогательная функция возвращает функцию.

#...
def get_after(s):
  if s % 2 == 0:
    return add_one
  return get_min

def cost(s):
  if s <= 1:
    return 0

  argument = get_argument(s)
  after = get_after(s) # after это функция!
  result = cost(argument)
  return after(result) 

Теперь запишем это в более общей и краткой форме:

#...
def is_base_case(s):
  return s <= 1

def base_case_value(s):
  return 0

def cost(s):
  if is_base_case(s):
    return base_case_value(s)

  argument = get_argument(s)
  after = get_after(s)
  return after(cost(argument)) 

Видно, что каждое проделанное изменение сохраняло смысл программы.

Сейчас проверка на чётность числа выполняется дважды, хотя до изменений проверка была одна.

Если мы захотим, то можем решить эту проблему объединив две вспомогательные функции в одну, возвращающую кортеж.

Но давайте не будем беспокоиться об этом в рамках решения этой задачи.

Мы свели наш рекурсивный метод до максимально общей формы.

• В базовом случае:
  • вычисляем значение, которое нужно вернуть;
  • возвращаем его.
• В не базовом случае:
  • вычисляем аргумент рекурсии;
  • производим рекурсивный вызов;
  • вычисляем возвращаемое значение;
  • возвращаем его.

Кое-что важное на что необходимо обратить внимание на этом шаге — это то, что after не должен сам содержать вызовов cost.

Способ, который я показываю здесь, удаляет единственный рекурсивный вызов.

Если у вас 2 и более рекурсии, то нам понадобится другое решение.

Как только мы привели наш рекурсивный алгоритм к такой форме, преобразовать его в итеративный уже просто.

Хитрость в том, чтобы представить, что происходит в рекурсивной программе.

Как мы делаем рекурсивный спуск: мы вызываем get_argument перед рекурсивным вызовом и вызываем функцию after после возврата из рекурсии.

То есть, все вызовы get_argument происходят перед всеми вызовами after.
Поэтому мы можем преобразовать это в 2 цикла: первый вызывает get_argument и формирует список функций after, а второй вызывает все функции after:

#...
def cost(s):
  # Создаём стек из функций "after". Все эти функции
  # принимают результат рекурсивного вызова и возвращают
  # значение, которое вычисляет рекурсивный метод.
  afters = [ ]
  while not is_base_case(s):
    argument = get_argument(s)
    after = get_after(s)
    afters.append(after)
    s = argument
  # Теперь у нас есть стек функций "after" :
  result = base_case_value(s)
  while len(afters) != 0:
    after = afters.pop()
    result = after(result)
  return result

Больше никакой рекурсии!

Выглядит как магия, но все что мы здесь делаем — то же самое, что делала рекурсивная версия программы и в том же порядке.

Этот пример отражает мысль, которую я часто повторяю о стеке вызовов: его цель сообщить то, что произойдёт дальше, а не то, что уже произошло!

Единственная полезная информация в стеке вызовов в рекурсивной версии программы — это какое значение имеет after, поскольку эта функция вызывается следующей, а все остальное на стеке не важно.

Вместо использования стека вызовов, как неэффективного и громоздкого способа хранения стека after, мы можем просто хранить стек функций after.

В следующий раз мы рассмотрим более сложный способ удаления рекурсии на Python.

import java.util.*;

class NonTerminal{

    private String name;

    private ArrayList<String> rules;

    public NonTerminal(String name) {

        this.name = name;

        rules = new ArrayList<>();

    }

    public void addRule(String rule) {

        rules.add(rule);

    }

    public void setRules(ArrayList<String> rules) {

        this.rules = rules;

    }

    public String getName() {

        return name;

    }

    public ArrayList<String> getRules() {

        return rules;

    }

    public void printRule() {

        System.out.print(name + " -> ");

        for (int i = 0; i < rules.size(); i++){

            System.out.print(rules.get(i));

            if (i != rules.size() - 1)

                System.out.print(" | ");

        }

        System.out.println();

    }

}

class Grammar{

    private ArrayList<NonTerminal> nonTerminals;

    public Grammar() {

        nonTerminals = new ArrayList<>();

    }

    public void addRule(String rule) {

        boolean nt = false;

        String parse = "";

        for (int i = 0; i < rule.length(); i++){

            char c = rule.charAt(i);

            if (c == ' ') {

                if (!nt) {

                    NonTerminal newNonTerminal = new NonTerminal(parse);

                    nonTerminals.add(newNonTerminal);

                    nt = true;

                    parse = "";

                } else if (parse.length() != 0){

                    nonTerminals.get(nonTerminals.size() - 1).addRule(parse);

                    parse = "";

                }

            }else if (c != '|' && c != '-' && c != '>'){

                parse += c;

            }

        }

        if (parse.length() != 0){

            nonTerminals.get(nonTerminals.size() - 1).addRule(parse);

        }

    }

    public void inputData() {

        addRule("S -> Sa | Sb | c | d");

    }

    public void solveNonImmediateLR(NonTerminal A, NonTerminal B) {

        String nameA = A.getName();

        String nameB = B.getName();

        ArrayList<String> rulesA = new ArrayList<>();

        ArrayList<String> rulesB = new ArrayList<>();

        ArrayList<String> newRulesA = new ArrayList<>();

        rulesA = A.getRules();

        rulesB = B.getRules();

        for (String rule : rulesA) {

            if (rule.substring(0, nameB.length()).equals(nameB)) {

                for (String rule1 : rulesB){

                    newRulesA.add(rule1 + rule.substring(nameB.length()));

                }

            }

            else{

                newRulesA.add(rule);

            }

        }

        A.setRules(newRulesA);

    }

    public void solveImmediateLR(NonTerminal A) {

        String name = A.getName();

        String newName = name + "'";

        ArrayList<String> alphas= new ArrayList<>();

        ArrayList<String> betas = new ArrayList<>();

        ArrayList<String> rules = A.getRules();

        ArrayList<String> newRulesA = new ArrayList<>();

        ArrayList<String> newRulesA1 = new ArrayList<>();

        rules = A.getRules();

        for (String rule : rules) {

            if (rule.substring(0, name.length()).equals(name)){

                alphas.add(rule.substring(name.length()));

            }

            else{

                betas.add(rule);

            }

        }

        if (alphas.size() == 0)

            return;

        if (betas.size() == 0)

            newRulesA.add(newName);

        for (String beta : betas)

            newRulesA.add(beta + newName);

        for (String alpha : alphas)

            newRulesA1.add(alpha + newName);

        A.setRules(newRulesA);

        newRulesA1.add("u03B5");

        NonTerminal newNonTerminal = new NonTerminal(newName);

        newNonTerminal.setRules(newRulesA1);

        nonTerminals.add(newNonTerminal);

    }

    public void applyAlgorithm() {

        int size = nonTerminals.size();

        for (int i = 0; i < size; i++){

            for (int j = 0; j < i; j++){

                solveNonImmediateLR(nonTerminals.get(i), nonTerminals.get(j));

            }

            solveImmediateLR(nonTerminals.get(i));

        }

    }

    void printRules() {

        for (NonTerminal nonTerminal : nonTerminals){

            nonTerminal.printRule();

        }

    }

}

class Main{

    public static void main(String[] args) {

        Grammar grammar = new Grammar();

        grammar.inputData();

        grammar.applyAlgorithm();

        grammar.printRules();

    }

}

1. Устранение рекурсии в общем случае

Функции
факториала, наибольшего общего делителя,
и BigAddможно упростить устранением хвостовой
рекурсии. Функцию, вычисляющую числа
Фибоначчи, можно упростить, используя
таблицу значений или переформулировав
задачу с использованием подхода снизу
вверх.

Некоторые
рекурсивные алгоритмы настолько сложны,
то применение этих методов затруднено
или невозможно.

Основной
подход при этом заключается в том, чтобы
рассмотреть порядок выполнения рекурсии
на компьютере и затем попытаться
сымитировать шаги, выполняемые
компьютером. Затем новый алгоритм будет
сам осуществлять «рекурсию» вместо
того, чтобы всю работу выполнял компьютер.

Поскольку
новый алгоритм выполняет практически
те же шаги, что и компьютер, можно
поинтересоваться, возрастет ли скорость
вычислений. В VisualBasicэто обычно не выполняется. Компьютер
может выполнять задачи, которые требуются
при рекурсии, быстрее, чем вы можете их
имитировать. Тем не менее, оперирование
этими деталями самостоятельно обеспечивает
лучший контроль над выделением памяти
под локальные переменные, и позволяет
избежать глубокого уровня вложенности
рекурсии.

Обычно,
при вызове подпрограммы, система
выполняет три вещи. Во‑первых,
сохраняет данные, которые нужны ей для
продолжения выполнения после завершения
подпрограммы. Во‑вторых, она проводит
подготовку к вызову подпрограммы и
передает ей управление. В‑третьих,
когда вызываемая процедура завершается,
система восстанавливает данные,
сохраненные на первом шаге, и передает
управление назад в соответствующую
точку программы. Если вы преобразуете
рекурсивную процедуру в нерекурсивную,
вам приходится выполнять эти три шага
самостоятельно.

Рассмотрим
следующую обобщенную рекурсивную
процедуру:

Sub
Subr(num)

<1
блок кода>

Subr(<параметры>)

<2
блок кода>

End
Sub

Поскольку
после рекурсивного шага есть еще
операторы, вы не можете использовать
устранение хвостовой рекурсии для этого
алгоритма.

Вначале
пометим первые строки в 1 и 2 блоках кода.
Затем эти метки будут использоваться
для определения места, с которого
требуется продолжить выполнение при
возврате из «рекурсии». Эти метки
используются только для того, чтобы
помочь вам понять, что делает алгоритм —
они не являются частью кода VisualBasic. В этом примере метки
будут выглядеть так:

Sub
Subr(num)

1 <1
блок кода>

Subr(<параметры>)

2 <2
блок кода>

End
Sub

Используем
специальную метку «0» для обозначения
конца «рекурсии». Теперь можно переписать
процедуру без использования рекурсии,
например, так:

Sub
Subr(num)

Dim
pc As Integer ‘
Определяет, где нужно продолжить
рекурсию.

pc
= 1 ‘ Начать сначала.

Do

Select
Case pc

Case
1

<1
блок кода>

If
(достигнуто условие остановки) Then

‘
Пропустить рекурсию и перейти к блоку
2.

pc
= 2

Else

‘
Сохранить переменные, нужные после
рекурсии.

‘
Сохранить pc = 2. Точка, с
которой продолжится

‘
выполнение после возврата из «рекурсии».

‘
Установить переменные, нужные для
рекурсии.

‘
Например, num = num
— 1.

:

‘
Перейти к блоку 1 для начала рекурсии.

pc
= 1

End
If

Case
2 ‘ Выполнить 2 блок кода

<2
блок кода>

pc
= 0

Case
0

If
(это последняя рекурсия) Then Exit Do

‘
Иначе восстановить pc и
другие переменные,

‘
сохраненные перед рекурсией.

End
Select

Loop

End
Sub

Переменная
pc,
которая соответствует счетчику программы,
сообщает процедуре, какой шаг она должна
выполнить следующим. Например, приpc = 1,
процедура должна выполнить 1 блок кода.

Когда
процедура достигает условия остановки,
она не выполняет рекурсию. Вместо этого,
она присваивает pcзначение 2, и продолжает выполнение 2
блока кода.

Если
процедура не достигла условия остановки,
она выполняет «рекурсию». Для этого она
сохраняет значения всех локальных
переменных, которые ей понадобятся
позже после завершения «рекурсии». Она
также сохраняет значение pcдля участка кода, который она будет
выполнять после завершения «рекурсии».
В этом примере следующим выполняется
2 блок кода, поэтому она сохраняет 2 в
качестве следующего значенияpc.
Самый простой способ сохранения значений
локальных переменных иpcсостоит в использовании стеков, подобных
тем, которые описывались в 3 главе.

Реальный
пример поможет вам понять эту схему.
Рассмотрим слегка измененную версию
функции факториала. В нем переписана
только подпрограмма, которая возвращает
свое значение при помощи переменной, а
не функции, для упрощения работы.

Private
Sub Factorial(num As Integer, value As
Integer)

Dim
partial As Integer

1 If
num <= 1 Then

value
= 1

Else

Factorial(num
— 1, partial)

2 value
= num * partial

End
If

End
Sub

После
возврата процедуры из рекурсии, требуется
узнать исходное значение переменной
num,
чтобы выполнить операцию умноженияvalue = num
* partial.
Поскольку процедуре требуется доступ
к значениюnumпосле возврата из рекурсии, она должна
сохранять значение переменныхpcиnumдо начала рекурсии.

Следующая
процедура сохраняет эти значения в двух
стеках на основе массивов. При подготовке
к рекурсии, она проталкивает значения
переменных numиpcв стеки. После завершения рекурсии, она
выталкивает добавленные последними
значения из стеков. Следующий код
демонстрирует нерекурсивную версию
подпрограммы вычисления факториала.

Private
Sub Factorial(num
As Integer, value
As Integer)

ReDim
num_stack(1 to 200) As Integer

ReDim
pc_stack(1 to 200) As Integer

Dim
stack_top As Integer ‘ Вершина стека.

Dim
pc As Integer

pc
= 1

Do

Select
Case pc

Case
1

If
num <= 1 Then ‘
Это условие остановки. value
= 1

pc
= 0 ‘ Конец рекурсии.

Else ‘
Рекурсия.

‘ Сохранить num и следующее
значение pc.

stack_top
= stack_top + 1

num_stack(stack_top)
= num

pc_stack(stack_top)
= 2 ‘ Возобновить с 2.

‘ Начать рекурсию.

num
= num — 1

‘ Перенести блок управления в начало.

pc
= 1

End
If

Case
2

‘
value содержит результат
последней

‘
рекурсии. Умножить его на num.

value
= value * num

‘
«Возврат» из «рекурсии».

pc
= 0

Case
0

‘
Конец «рекурсии».

‘
Если стеки пусты, исходный вызов

‘
подпрограммы завершен.

If
stack_top <= 0 Then Exit Do

‘
Иначе восстановить локальные переменные
и pc.

num
= num_stack(stack_top)

pc
= pc_stack(stack_top)

stack_top
= stacK_top — 1

End
Select

Loop

End
Sub

Так
же, как и устранение хвостовой рекурсии,
этот метод имитирует поведение
рекурсивного алгоритма. Процедура
заменяет каждый рекурсивный вызов
итерацией цикла While.
Поскольку число шагов остается тем же
самым, полное время выполнения алгоритма
не изменяется.

Так
же, как и в случае с устранением хвостовой
рекурсии, этот метод устраняет глубокую
рекурсию, которая может переполнить
стек.

1. Резюме

При применении рекурсивных алгоритмов
следует избегать трех основных опасностей:

• Бесконечной рекурсии. Убедитесь,
  что условия остановки вашего алгоритма
  прекращают все рекурсивные пути.

• Глубокой рекурсии. Если алгоритм
  достигает слишком большой глубины
  рекурсии, он может привести к переполнению
  стека. Минимизируйте использование
  стека за счет уменьшения числа
  определяемых в процедуре переменных,
  использования глобальных переменных,
  или определения переменных как
  статических. Если процедура все равно
  приводит к переполнению стека, перепишите
  алгоритм в нерекурсивном виде, используя
  устранение хвостовой рекурсии.

• Ненужной рекурсии. Обычно это
  происходит, если алгоритм типа
  рекурсивного вычисления чисел Фибоначчи,
  многократно вычисляет одни и те же
  промежуточные значения. Если вы
  столкнетесь с этой проблемой в своей
  программе, попробуйте переписать
  алгоритм, используя подход снизу вверх.
  Если алгоритм не позволяет прибегнуть
  к подходу снизу вверх, создайте таблицу
  промежуточных значений.

Применение
рекурсии не всегда неправильно. Многие
задачи являются рекурсивными по своей
природе. В этих случаях рекурсивный
алгоритм будет проще понять, отлаживать
и поддерживать, чем его нерекурсивную
версию.

Если
у вас есть алгоритм, который рекурсивен
по своей природе, но вы не уверены, будет
ли рекурсивная версия лишена проблем,
запишите алгоритм в рекурсивном виде
и выясните это. Может быть, проблемы не
возникнут. Если же они возникнут, то,
возможно, окажется проще преобразовать
эту рекурсивную версию в нерекурсивную,
чем написать нерекурсивную версию с
нуля.

Задача
о Ханойских башнях. Имеются три стержня
с номерами 1, 2, 3. На стержень 1 надетоNдисков различного диаметра так, что они
образуют пирамиду. Написать программу
для печати последовательности перемещений
дисков со стержня на стержень, необходимых
для переноса пирамиды со стержня 1 на
стержень 3 при использовании стержня 2
в качестве вспомогательного. При этом
за одно перемещение должен переноситься
только один диск, и диск большего диаметра
не должен помещаться на диск меньшего
диаметра. Доказано, что дляNдисков
минимальное число необходимых перемещений
равно.

Для
решения простейшего случая задачи,
когда пирамида состоит только из одного
диска, необходимо выполнить одно действие
– перенести диск со стержня Iна стерженьJ, что очевидно
(обозначим такой переносIJ).
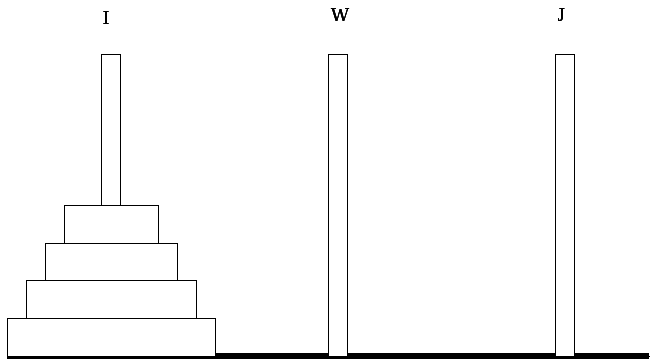
Общий случай задачи изображен на рис
2., когда требуется перенестиNдисков со стержняIна
стерженьJ, считая стерженьWвспомогательным. Сначала
следует перенестиN-1 диск
со стержняIна стерженьWпри вспомогательном
стержнеJ, затем перенести
один диск со стержняIна
стерженьJ, и, наконец,
перенестиN-1 диск изWна стерженьJ, используя
вспомогательный стерженьI.
Итак, задача о переносеNдисков сводится к двум задачам о переносеN-1 диска и одной простейшей
задаче. Схематически это можно записать
так:T(N,I,J,W)≈T(N-1,I,W,J),T(1,I,J,W),T(N-1,W,J,I).

Рекурсивный
вариант процедуры приведен ниже.

Sub Hanoy()

Dim m As Integer

m=InputBox(«Введите количество
дисков», 5)

disk_exch m, 1, 3, 2

End Sub

Sub disk_exch(n As
Integer, i As Integer, j As Integer, w As Integer)

If n > 1 Then

disk_exch n — 1,
i, w, j

disk_exch 1, i,
j, w

disk_exch n — 1,
w, j, i

Else

Debug.Print i &
«—>» & j

End If

End Sub

Протокол
работы для 3-х дисков:

1—>3

1—>2

3—>2

1—>3

2—>1

2—>3

1—>3

Задание:
переписать процедуру без рекурсии.

13

Соседние файлы в папке Самостоятельная работа

• #
• #
• #
• #
• #
• #

Определение:

Говорят, что КС-грамматика содержит левую рекурсию (англ. left recursion), если в ней существует вывод вида .

Методы нисходящего разбора не в состоянии работать с леворекурсивными грамматиками. Проблема в том, что продукция вида может применяться бесконечно долго, так и не выработав некий терминальный символ, который можно было бы сравнить со строкой. Поэтому требуется преобразование грамматики, которое бы устранило левую рекурсию.

Устранение непосредственной левой рекурсии

Опишем процедуру, устраняющую все правила вида , для фиксированного нетерминала .

1. Запишем все правила вывода из в виде:
   , где
   • — непустая последовательность терминалов и нетерминалов ();
   • — непустая последовательность терминалов и нетерминалов, не начинающаяся с .
2. Заменим правила вывода из на .
3. Создадим новый нетерминал .

Изначально нетерминал порождает строки вида . В новой грамматике нетерминал порождает , а порождает строки вида . Из этого очевидно, что изначальная грамматика эквивалентна новой.

Пример

Есть непосредственная левая рекурсия . Добавим нетерминал и добавим правила , .

Новая грамматика:

В новой грамматике нет непосредственной левой рекурсии, но нетерминал леворекурсивен, так как есть

Алгоритм устранения произвольной левой рекурсии

Воспользуемся алгоритмом удаления -правил. Получим грамматику без -правил для языка .

Упорядочим нетерминалы, например по возрастанию индексов, и будем добиваться того, чтобы не было правил вида , где .
Если данное условие выполняется для всех , то в грамматике нет , а значит не будет левой рекурсии.

Пусть — упорядоченное множество всех нетерминалов.

 for 
   for 
     for 
       удалить продукцию  
       for 
         добавить правило 
   устранить непосредственную левую рекурсию для 

Если присутствовал в языке исходной грамматики, добавим новый начальный символ и правила .

После итерации внешнего цикла в любой продукции внешнего цикла в любой продукции вида , должно быть . В результате при следующей итерации внутреннего цикла растет нижний предел всех продукций вида до тех пор, пока не будет достигнуто .

После итерации внешнего цикла в грамматике будут только правила вида , где .
Можно заметить, что неравенство становится строгим только после применения алгоритма устранения непосредственной левой рекурсии. При этом добавляются новые нетерминалы. Пусть новый нетерминал. Можно заметить, что нет правила вида , где самый левый нетерминал, а значит новые нетерминалы можно не рассматривать во внешнем цикле. Для строгого поддержания инвариантов цикла можно считать, что созданный на итерации в процессе устранения непосредственной левой рекурсии нетерминал имеет номер (т.е. имеет номер, меньший всех имеющихся на данный момент нетерминалов).

На итерации внешнего цикла все правила вида где заменяются на где . Очевидно, что одна итерация алгоритма не меняет язык, а значит язык получившийся в итоге грамматики совпадает с исходным.

Оценка времени работы

Пусть количество правил для нетерминала .
Тогда итерация внешнего цикла будет выполняться за , что меньше чем , значит асимптотика алгоритма .

Худший случай

Проблема этого алгоритма в том, что в зависимости от порядка нетерминалов в множестве размер грамматки может получиться экспоненциальным.

Пример грамматики для которой имеет значение порядок нетерминалов

для

Упорядочим множество нетерминалов по возрастанию индексов. Легко заметить, что правила для будут представлять из себя все двоичные вектора длины , а значит размер грамматики будет экспоненциальным.

Порядок выбора нетерминалов

Определение:

Говорят, что нетерминал — прямой левый вывод (англ. direct left corner) из , если существует правило вида .

Определение:

Левый вывод (англ. left corner) — транзитивное, рефлексивное замыкание отношения «быть прямым левым выводом».

Во внутреннем цикле алгоритма для всех нетерминалов и , таких что и — прямой левый вывод из заменяем все прямые левые выводы из на все выводы из .

Это действие удаляет левую рекурсию только если — леворекурсивный нетерминал и содержится в выводе (то есть — левый вывод из ,в то время как — левый вывод из ).

Перестанем добавлять бесполезные выводы, которые не участвуют в удалении левой рекурсии, упорядочив нетерминалы так: если и — прямой левый вывод из , то — левый вывод из .
Упорядочим их по уменьшению количества различных прямых левых выводов из них.

Так как отношение «быть левым выводом» транзитивно,то если — прямой левый вывод из , то каждый левый вывод из С также будет левым выводом из . А так как отношение «быть левым выводом» рефлексивно, явлеяется своим левым выводом, а значит если — прямой левый вывод из — он должен следовать за в упорядоченном множестве, если только не является левым выводом из .

Пример

Дана грамматика:

Среди правил непосредственной рекурсии нет, поэтому во время первой итерации внешнего цикла ничего не происходит.
Во время второй итерации внешнего цикла правило переходит в .

Грамматика имеет вид

Устраняем левую рекурсию для

См. также

• Контекстно-свободные грамматики
• Нормальная форма Хомского
• Удаления -правил из грамматики

Источники информации

• Хопкрофт Д., Мотвани Р., Ульман Д. — Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — Москва, Издательский дом «Вильямс», 2002. — 528 с. : ISBN 5-8459-0261-4 (рус.)
• Robert C. Moore — Removing Left Recursion from Context-Free Grammars