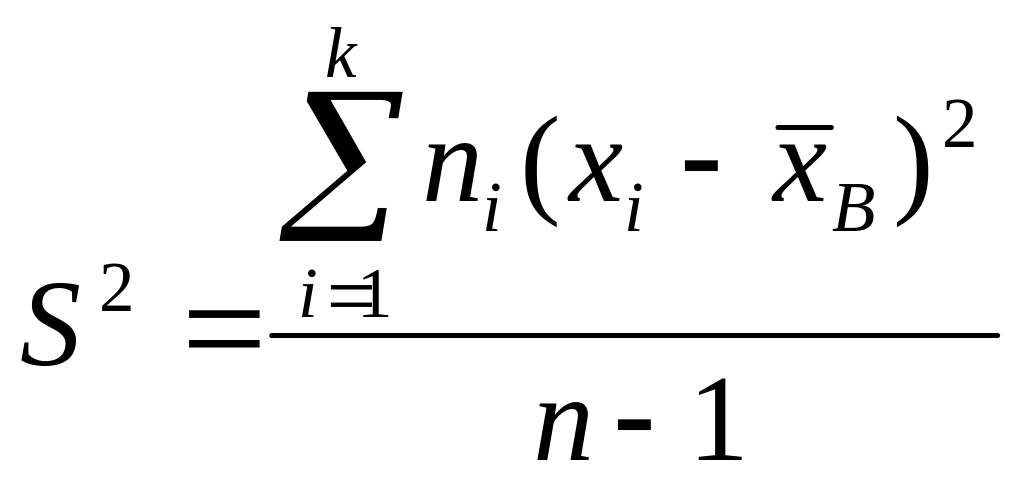Выборочная дисперсия, описание
Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.
Определение
Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
Связь выборочной и генеральной дисперсии
Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.
Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.
Как вычислить выборочную дисперсию
Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:
({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)
Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:
({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)
Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:
({widehatsigma}_В=sqrt{{widehat D}_В})
Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:
(D=overline{x^2}-left[overline xright]^2)
Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов.
Пример
Найти выборочную дисперсию выборки со значениями:
- xi: 1, 2, 3, 4;
- ni: 20, 15, 10, 5.
Решение
Для начала необходимо определить выборочную среднюю:
({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)
Затем найдем выборочную дисперсию:
(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)
Исправленная дисперсия
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
(Mleft[D_Bright]=frac{n-1}nD_Г)
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.
Исправить выборочную дисперсию можно путем умножения ее на дробь:
(frac n{n-1})
Получим формулу следующего вида:
(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})
Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2.
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
(S=sqrt{S^2})
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.
Для чего применяют исправленную выборочную дисперсию
Исправленную выборочную используют для точечной оценки генеральной дисперсии.
Пример
Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.
Решение
Сначала вычислим выборочную среднюю:
({overline x}_В=frac{92+94+103+105+106}5=100)
Затем найдем выборочную дисперсию:
(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)
Теперь рассчитаем исправленную дисперсию:
(S^2=frac5{5-1}cdot34=42,5)
5 способов достичь правильного баланса смещения и дисперсии в модели машинного обучения
Модель машинного обучения хороша ровно настолько, насколько хороши данные, которые в нее поступают.
Универсальная истина в области машинного обучения заключается в том, что производительность модели во многом зависит от данных, которые ей передаются. Однако бывают ситуации, когда производительность модели снижается даже после предоставления данных хорошего качества. Одна из таких распространенных проблем — проблема с высоким смещением и высокой дисперсией (недостаточная подгонка против переоборудования).
Когда мы подбираем коэффициенты (также известные как параметры, веса и т. Д.) Модели машинного обучения, обычно первая цель — минимизировать ошибку обучения. Однако только низкая ошибка обучения не удовлетворяет критериям хорошей модели. То, что алгоритм обучения хорошо подходит для обучающей выборки, не означает, что это хорошая гипотеза. Он может переборщить, и в результате ваши прогнозы по валидации и набору тестов будут плохими. На самом деле, наличие обобщенной модели, которая способна обеспечить низкую ошибку при обучении, а также на невидимых данных, является реальной желаемой моделью.
Как правило, с каждой моделью бывает, что с первого раза вы не можете найти обобщенную модель. На модель может влиять проклятие Высокого смещения или Высокого отклонения, то есть недостаточного или чрезмерного подбора.
Что такое чрезмерная или недостаточная посадка?
Недостаточная и чрезмерная подгонка — распространенные проблемы, которые возникают в процессе построения модели для контролируемых алгоритмов, нейронных сетей и т. Д.
Недостаточная подгонка возникает, когда модели не удается узнать основной шаблон на основе данных обучения. Эти модели обычно имеют высокую систематическую ошибку и низкую дисперсию. Некоторые из возможных причин — ограниченная доступность данных для построения точной модели или когда мы пытаемся построить линейную модель с нелинейными данными. Эта ситуация также возникает, когда модель низкой сложности подгоняется к набору нелинейных данных. например если необходимо использовать полиномиальное уравнение высокой степени, такое как W0 + W1X1 + W2X1² + W3X1³, и мы используем уравнение прямой линии (Y = W0 + W1X1) для моделирования этого.
Чрезмерная подгонка происходит, когда наша модель изучает даже шум вместе с базовым шаблоном в данных. Модель пытается запомнить каждую точку данных из обучающего набора и не может предсказать невидимые данные. Это происходит, когда мы много тренируем нашу модель на зашумленном наборе данных. Эти модели имеют низкую систематическую ошибку и высокую дисперсию.
На приведенных ниже примерах графиков показаны графики для меньшего набора данных с 1 входной функцией и целевой переменной (y).
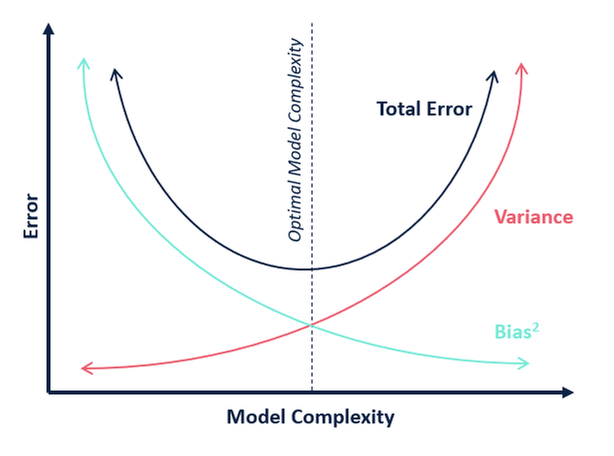
Влияние на производительность модели из-за предвзятости и отклонения
Если на модель машинного обучения влияет систематическая ошибка или дисперсия, она будет иметь тенденцию демонстрировать следующее поведение в отношении ошибок обучения и проверки. Ошибка обучения будет иметь тенденцию уменьшаться по мере увеличения степени сложности полинома или модели. В то же время ошибка проверки будет иметь тенденцию уменьшаться по мере увеличения сложности до определенной точки, а затем она будет увеличиваться, образуя выпуклую кривую, как показано ниже.
- Высокая систематическая погрешность (недостаточная подгонка) — ошибки обучения и проверки будут высокими.
- Высокая дисперсия (чрезмерная подгонка): ошибка обучения будет низкой, а ошибка проверки будет высокой.
Определение наличия у модели сильного смещения или высокого отклонения
Кривые обучения — это один из полезных графиков для проверки правильности работы алгоритма или необходимости повышения его производительности. Вы должны построить график функции затрат на обучающем наборе и наборе проверки по количеству примеров обучения или проверки. Вы найдете проницательные наблюдения на этих графиках, например, ниже:
- Высокое смещение: низкий размер обучающей выборки приводит к тому, что ошибка обучения становится низкой, а ошибка проверки — высокой. При обучении алгоритма на очень небольшом количестве точек данных всегда будет найдена квадратичная кривая, которая касается именно этого количества точек. По мере того, как обучающий набор становится больше, ошибка обучающего набора увеличивается, и после определенного размера обучающего набора он выйдет на плато.
2. Высокая дисперсия: низкий размер обучающего набора приводит к тому, что ошибка обучения становится низкой, а ошибка проверки — высокой. При большом размере обучающего набора ошибка обучения увеличивается, а ошибка проверки продолжает уменьшаться без выравнивания.
Что делать со смещением и дисперсией?
После первоначального запуска модели вы заметите, что модель не справляется с набором валидации, как вы надеялись. Поскольку модель подвержена влиянию из-за высокой систематической ошибки или большой дисперсии. Другими словами, проблема либо в недостаточной, либо в чрезмерной настройке. В идеале нам нужно найти золотую середину между этими двумя, как показано ниже на примере графика. Идея состоит в том, чтобы уменьшить ошибку обучения, а также ошибку проверки и тестирования до точки, при которой модель сможет хорошо обобщать невидимые данные.
Методы достижения оптимального соотношения смещения и дисперсии
- Разделите данные на 3 набора — Обучение, Проверка и Тест с типичной комбинацией 70%, 20% и 10% (это может быть [80%, 10%, 10%] или [60%, 20%, 20%] ). Хорошей практикой является случайное перемешивание данных перед выполнением разделения, чтобы модель не становилась предвзятой из-за какой-либо сортировки или исторической закономерности в данных.
- Начните с простого алгоритма, не тратя слишком много времени на реализацию, и протестируйте его на ранних этапах проверки данных. Часто считается очень хорошей практикой начинать, не создавая очень сложную систему с множеством сложных функций, вместо этого начав с построения очень простого алгоритма.
- Изучите коэффициенты из обучающего набора (70% данных) и сделайте прогноз на основе данных проверки. Постройте кривые обучения, чтобы выяснить, страдает ли модель большой систематической ошибкой или большой дисперсией. Это станет вашей отправной точкой для диагностики и использования метода проб и ошибок, выбрав один из следующих вариантов, чтобы исправить проблему или перейти к следующему решению. Важно отметить, что во всех приведенных ниже методах их необязательно выполнять в указанном порядке. Выбор одного или нескольких из этих методов зависит от ваших конкретных требований, чтобы получить правильный баланс смещения и дисперсии.
- Дополнительные обучающие примеры помогают исправить высокую дисперсию. Если возможно, попробуйте получить больше данных. В качестве альтернативы вам нужно будет использовать некоторые методы увеличения данных, чтобы изменить, модифицировать, обрезать существующие данные.
- Выбирайте меньшие наборы функций, которые устраняют большую дисперсию. Это сложная ситуация, когда вы можете подумать, что все функции важны, но это может быть не так. Вам нужно будет применить различные методы анализа данных, чтобы выяснить корреляцию, взаимосвязь между входными и целевыми переменными. Кроме того, если вы обнаружите, что входные функции имеют одинаковую важность, тогда лучше привлечь бизнес-группы или экспертов в предметной области, чтобы решить, какие функции более важны, чтобы сохранить или удалить.
- Добавление дополнительных функций может помочь исправить высокую систематическую ошибку. Разработка функций — это широкая категория, которая представляет собой итеративный подход к получению новых функций или изменению существующих в зависимости от требований. Например, если набор данных содержит вес и рост как функции, вы можете создать BMI как новую функцию. В другом случае задаются длина и ширина участка, и вы можете создать новый размер участка.
- Добавление полиномиальных функций позволяет соответствовать уравнениям более высокого порядка и устраняет сильное смещение. Полиномы более низкого порядка (низкая сложность модели) имеют высокое смещение и низкую дисперсию. В этом случае модель подходит плохо стабильно. В то время как полиномы более высокого порядка (высокая сложность модели) очень хорошо подходят для обучающих данных, а тестовые — крайне плохо. У них низкая погрешность в данных обучения, но очень высокая дисперсия.
На самом деле, мы хотели бы выбрать модель где-то посередине, которая может хорошо обобщать, но также достаточно хорошо соответствует данным. Чтобы найти правильное полиномиальное уравнение и соответствующую степень полиномиальных функций, выполните следующие действия:
- Составьте список возможных полиномиальных уравнений от низкой до высокой степени.
- Изучите коэффициенты из обучающего набора (70% данных) для каждой степени полинома и найдите ошибку обучения.
- Найдите степень полинома с наименьшей ошибкой, используя набор проверки.
5. Уменьшение λ: устраняет сильное смещение; Увеличение λ: исправляет высокую дисперсию.
По мере увеличения параметра регуляризации лямбда (λ) соответствие модели становится более жесткой. С другой стороны, когда лямбда (λ) приближается к нулю, модель имеет тенденцию чрезмерно соответствовать данным. Теперь вопрос в том, как определить подходящее значение лямбда (λ).
- Создайте список лямбда-значений (т.е. λ ∈ {0,0.01,0.03,0.05,0.07,0.15,0.30}).
- Создайте набор моделей разной степени.
- Переберите лямбду (λ) и для каждой лямбды (λ) пройдитесь по всем моделям, чтобы узнать некоторый коэффициент.
- Вычислите ошибку проверки, используя изученные коэффициенты, вычисленные с λ) и без регуляризации или λ = 0. Выберите лучшую комбинацию, которая дает наименьшую ошибку в наборе проверки.
Наконец, когда вы достигли правильного баланса и нашли обобщенную модель для набора данных проверки, примените модель прогнозирования к невидимому набору тестовых данных.
Резюме
Как объяснялось выше, на каждую модель машинного обучения влияет либо высокая систематическая ошибка, либо дисперсия. Он проходит этот путь применения одного или нескольких решений, чтобы найти правильный баланс смещения и отклонения, и достигает обобщения.
Определение.
Генеральной дисперсией
DГ
называют среднее арифметическое
квадратов отклонения значений признака
Х
генеральной совокупности от его среднего
значения
.
Если
различны, то
,
где N
– объём выборки.
Если
имеют частоты , то
.
Определение.
Генеральным средним квадратическим
отклонением
называют
.
Определение.
Выборочной дисперсией
называют среднее арифметическое
квадратов отклонения наблюдаемых
значений признака от их среднего значения
.
Если
различны, то
.
Если
имеют частоты , то
.
Замечание.
При
решении
практических
задач выборочную дисперсию удобнее
находить по следующей формуле:
(3)
Определение.
Выборочным средним квадратичным
отклонением
называют
.
Задача.
По данным выборки найти оценку
для неизвестной
DГ.
Если
в качестве оценки для DГ
взять DВ,
то эта оценка является смещённой, а
именно
(без доказательства).
(4)
Значит,
эта оценка будет приводить к систематическим
ошибкам (давая заниженное значение
генеральной дисперсии).
Для
получения несмещенной оценки исправим
выборочную дисперсию, умножив её на
.
Определение.
Исправленной (эмпирической) дисперсией
называется
.
(5)
Значит,
,
или
,
где
– несмещённая оценка генеральной
дисперсии DГ.
Действительно,
Можно
доказать, что
– состоятельная оценка DГ,
а значит также состоятельная
оценка
DГ
(т.к. множитель
при
).
Замечание.
При больших значениях n
обе оценки и различаются мало и введение
поправочного коэффициента теряет смысл.
Для
оценки среднего квадратического
отклонения генеральной совокупности
используют исправленное среднее
квадратическое отклонение
.
не
является несмещённой
оценкой Г.
Определение.
Точечной называют
оценку, которая определяется одним
числом.
Рассмотренные оценки являются точечными.
Пример 9.
Выборка задана следующим ДCР.
Найти смещённую и исправленную
оценку для дисперсии.
|
xi |
-2 |
-1 |
0 |
1 |
2 |
|
ni |
10 |
20 |
40 |
20 |
10 |
Решение.
Предварительно найдем для каждой
варианты соответствующую относительную
частоту и результаты внесем в таблицу.
Объём выборки n
= 100.
|
xi |
-2 |
-1 |
0 |
1 |
2 |
|
ni |
10 |
20 |
40 |
20 |
10 |
|
wi |
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
Найдем смещённую
оценку генеральной дисперсии –
воспользуемся формулой (3):
.
Выборочную среднюю
найдем по формуле (2):
.
Отсюда,
.
Несмещённую оценку
генеральной дисперсии найдем по формуле
(5):
.
Задачи
_______________________________________________________
-
Из генеральной
совокупности извлечена выборка. Найти
несмещённую оценку генеральной
средней.xi
2
5
7
10
ni
16
12
8
14
-
Из генеральной
совокупности извлечена выборка. Найти
несмещенную оценку генеральной
средней.xi
1
3
6
26
ni
8
40
10
2
-
Найти выборочную среднюю по данному
распределению выборки:xi
2560
2600
2620
2650
2700
ni
2
3
10
4
1
-
Найти выборочную дисперсию по данному
распределению выборки:xi
340
360
375
380
ni
20
50
18
12
-
Найти выборочную дисперсию по данному
распределению выборки:xi
0,01
0,04
0,08
ni
5
3
2
-
Найти выборочную дисперсию по данному
распределению выборки:xi
0,1
0,5
0,6
0,8
ni
5
15
20
10
-
Найти выборочную дисперсию по данному
распределению выборки:xi
18,4
18,9
19,3
19,6
ni
5
10
20
5
-
Найти исправленную
выборочную дисперсию по данному
распределению выборки:xi
102
104
108
ni
2
3
5
-
Найти исправленную
выборочную дисперсию по данному
распределению выборки:xi
0,1
0,5
0,7
0,9
ni
6
12
1
1
-
Найти исправленную
выборочную дисперсию по данному
распределению выборки:
|
xi |
23,5 |
26,1 |
28,2 |
30,4 |
|
ni |
2 |
3 |
4 |
1 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Приветствую посетителей блога statanaliz.info. В данной статье рассмотрим, что такое «выборочная несмещенная дисперсия».
Тема не нова, так как с таким показателями как размах значений, среднее линейное отклонение, дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации мы уже знакомы.
Понятие о сплошном и выборочном наблюдении
С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.
Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.
Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.
В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.
Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение будет другим. К примеру, провели опрос общественного мнения. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.
У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.
Выборочная несмещенная дисперсия
И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь, тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?
Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.
Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.
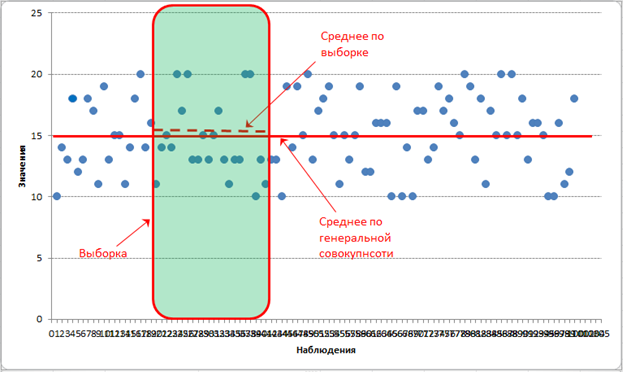
Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.
Отклонение выборочной средней от генеральной показано на рисунке.
Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.
Выборочная смещенная дисперсия:
Выборочная несмещенная дисперсия:
Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.
Теперь посмотрим на практическую сторону отличия смещенной и несмещенной дисперсии. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.
Так, в выборке из 11 наблюдений относительная разница составляет 11/10 = 10%. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.
При переходе к среднеквадратичном отклонению по выборке (корень из выборочной дисперсии) разница становится еще меньше.
Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.
Из данной статьи неплохо бы усвоить следующее.
1. Формула генеральной дисперсии в выборке дает смещенную оценку.
2. В знаменателе несмещенной оценки n-1 вместо n.
3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.
4. Стандартное отклонение по выборке – это корень из выборочной дисперсии.
До новых встреч на блоге statanaliz.info.
Поделиться в социальных сетях:
Несмещенная оценка выборочной дисперсии
Краткая теория
Пусть из генеральной совокупности в результате
независимых наблюдений над количественным
признаком
извлечена повторная выборка объема
:
При этом
Требуется по данным выборки оценить (приближенно найти) неизвестную
генеральную дисперсию
.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то
эта оценка будет приводить в систематическим ошибкам, давая заниженное значение
генеральной дисперсии. Объясняется это тем, что, как можно доказать, выборочная
дисперсия является смещенной оценкой
,
другими словами, математическое ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно:
Легко «исправить» выборочную дисперсию так, чтобы ее математическое
ожидание было равно генеральной дисперсии. Достаточно для этого умножить
на дробь
.
Сделав это, получим исправленную дисперсию, которую обычно обозначают через
:
Исправленная дисперсия является, конечно, несмещенной оценкой
генеральной дисперсии. Действительно:
Итак, в качестве оценки генеральной дисперсии принимают
исправленную дисперсию:
Для оценки среднего квадратического
отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню
из исправленной дисперсии:
При достаточно больших значениях
объема выборки выборочная и исправленная
дисперсия отличаются мало. На практике используются исправленной дисперсией,
если примерно
.
Пример решения задачи
Задача
Найти
несмещенную выборочную дисперсию на основании данного распределения выборки.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, поэтому в статистике применяют также исправленную выборочную дисперсию, которая является несмещенной оценкой генеральной дисперсии.
Сумма
частот:
Вычислим
среднюю:
Средняя квадратов:
Несмещенная
выборочная дисперсия:
Ответ:
Кроме этой задачи на другой странице сайта есть
пример расчета исправленной выборочной дисперсии и среднего квадратического отклонения для интервального вариационного ряда