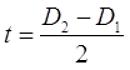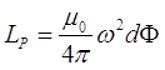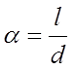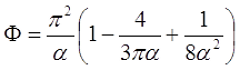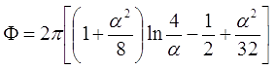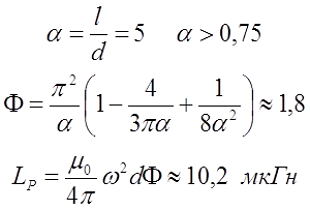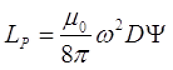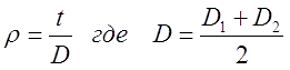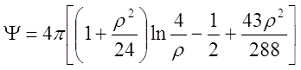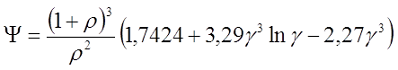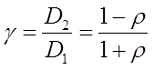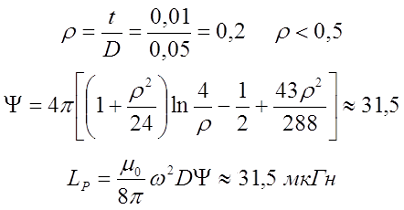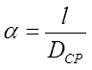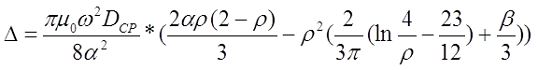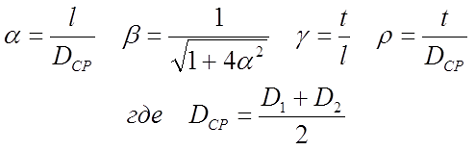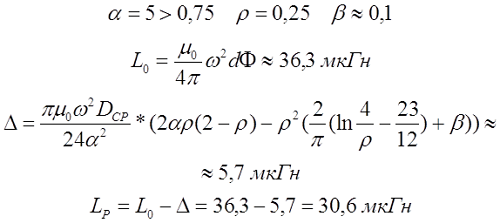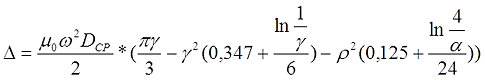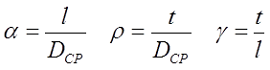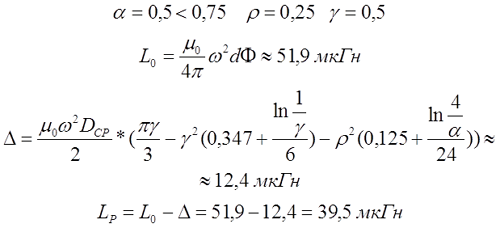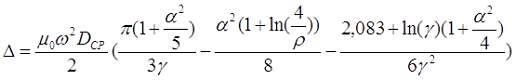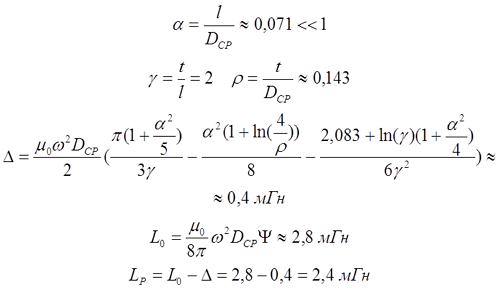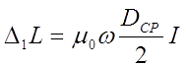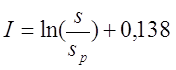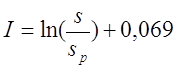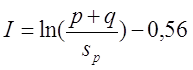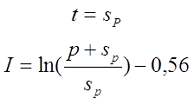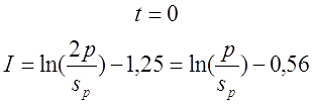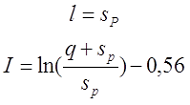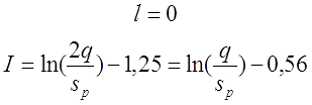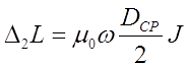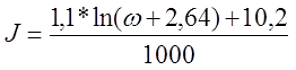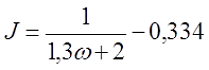Тема: Определить число витков соленоида (Прочитано 23567 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Галина Валерьевна
Здравствуйте срочно нужна помощь в решении. Заранее огромное спасибо
Индуктивность L соленоида, намотанного в один слой на каркас с магнитной проницаемостью µ= 250, равна 0,5 мГн. Длина соленоида l = 0,4 м, диаметр D = 1,5 см. Определить число витков соленоида.
Записан
Kivir
Решение: индуктивность соленоида (катушки, намотанной в один слой), можно определить по формуле:
[ L=mu cdot mu _{0} cdot frac{N^{2} cdot S}{l}, ]
здесь: N — число витков, S — площадь сечения, l — длина катушки, μ – относительная магнитная проницаемость среды заполняющей катушку, μ0 = 4π∙10–7 Гн/м – магнитная постоянная. Площадь сечения соленоида определим как площадь круга:
[ S=frac{pi cdot D^{2}}{4}. ]
Подставим в формулу индуктивности, и выразим число витков:
[ begin{array}{l} {L=mu cdot mu _{0} cdot frac{N^{2} cdot pi cdot D^{2} }{lcdot 4} ,} \ {N=sqrt{frac{4cdot lcdot L}{mu cdot mu _{0} cdot pi cdot D^{2}}}.}end{array} ]
Ответ: 60 витков
Записан
Дмирий
Что вы помогаете.У меня подобная задача была. Теперь вижу,что решил правильно
Записан
Галина Валерьевна
Спасибо за решение. Оказывается всё так просто, если учитывать площадь сечения соленоида(как площадь круга).
Записан
|
Оглавление |
||
|
ЛАБОРАТОРНАЯ РАБОТА № 13……………………………………………………………………………………………….. |
2 |
|
|
1. |
ВВЕДЕНИЕ …………………………………………………………………………………………………………………………….. |
2 |
|
2. |
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ ……………………………………………………. |
3 |
|
3. |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ………………………………………………………………………………… |
4 |
|
ЧАСТЬ 1. ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ СОЛЕНОИДОВ L1 И L2……………………… |
4 |
|
|
ЧАСТЬ 2. ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТЕЙ L’, L» И ВЗАИМНОЙ |
||
|
ИНДУКТИВНОСТИ М ………………………………………………………………………………………………………….. |
5 |
|
|
4. |
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ……………………………………………………………………. |
5 |
|
ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТЕЙ L1, L2……………………………………………………………………. |
5 |
|
|
ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТЕЙ L’, L» И ВЗАИМНОЙ ИНДУКТИВНОСТИ …М 6 |
||
|
ТЕОРЕТИЧЕСКИЙ РАСЧЁТ L1, L2 И M……………………………………………………………………………… |
6 |
|
|
ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ………………………………………………………………………………………… |
7 |
|
|
5. |
КОНТРОЛЬНЫЕ ВОПРОСЫ……………………………………………………………………………………………….. |
7 |
2
Лабораторная работа № 13
ИЗМЕРЕНИЕ ИНДУКТИВНОСТИ
СИСТЕМЫ КАТУШЕК
Цель работы: определение индуктивности двух разных соленоидов, индуктивности системы этих соленоидов при различных способах их включения и взаимной индуктивности системы этих катушек, вставленных друг в друга.
1. Введение
Собственное магнитное поле контура с током I создает магнитный поток самоиндукции (потокосцепление) сквозь поверхность, натянутую на этот контур. Величина пропорциональна магнитной индукции В, которая в свою очередь по закону Био-Савара-Лапласа пропорциональна силе тока, вызвавшего поле. Отсюда вытекает, что ток в контуре I и создаваемый им полный магнитный поток пропорциональны друг другу: Ψ = LI. Коэффициент пропорциональности L называется индуктивностью контура. Следовательно, индуктивность – это величина, численно равная магнитному потоку самоиндукции, пронизывающему данный контур при силе тока в нем, равной единице. Индуктивность контура в отсутствие ферромагнетиков зависит только от геометрии контура (т. е. его формы, размеров, числа витков). В частности, индуктивность длинного соленоида (диаметр много меньше длины) можно рассчитать по формуле
где N – число витков; S – площадь поперечного сечения соленоида; l – его длина; μ0 = 4π 10–7 Гн/ м – магнитная постоянная.
Теперь рассмотрим два контура, расположенных достаточно близко друг к другу (РИС. 1). Если в контуре I течёт ток силы I1, то он создает через площадь, ограниченную контуром II, полный магнитный поток Ψ21 пропорциональный току I1:
|
21 M21I1 Аналогично при протекании тока I2 по |
II |
|
|
второму контуру возникает магнитный поток, сцеп- |
I |
|
|
ленный с контуром I: 12 M12I2 . Коэффициенты про- |
||
|
порциональности М12 и М21 называются взаимными |
||
|
индуктивностями контуров. Их величина зависит |
I1 |
|
|
от геометрии и взаимного расположения контуров и |
||
|
не зависит от силы токов I1 и I2 при условии отсут- |
Рис. 1 |
|
|
ствия ферромагнетиков. В этом случае расчёт даёт, |
что M21 = M12.
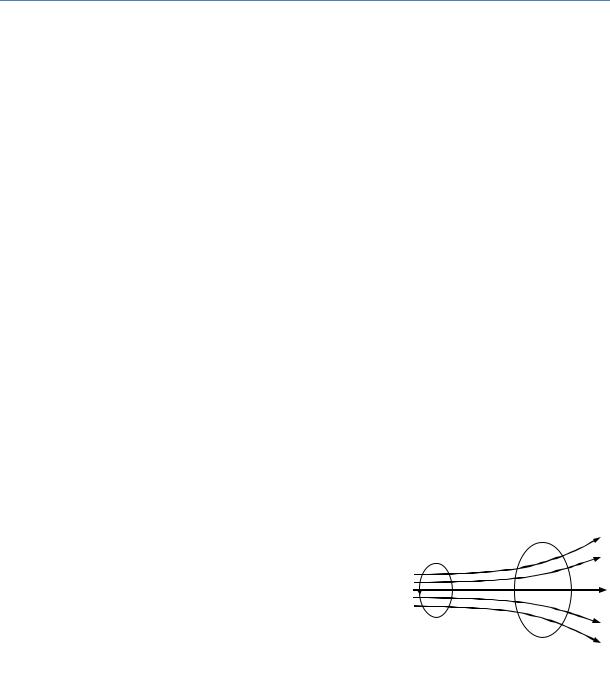
Для двух длинных соленоидов (РИС. 2), надетых друг на друга, коэффициент взаимной индукции
|
M |
μ0N1N2S2 |
, |
(2) |
|
l1 |
3
l1 l2
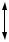
Рис. 2
где N1 и N2 – число витков внешнего L1 и внутреннего L2 соленоидов; S2 – площадь сечения внутреннего соленоида; l1 – длина внешнего соленоида. Рассмотрим
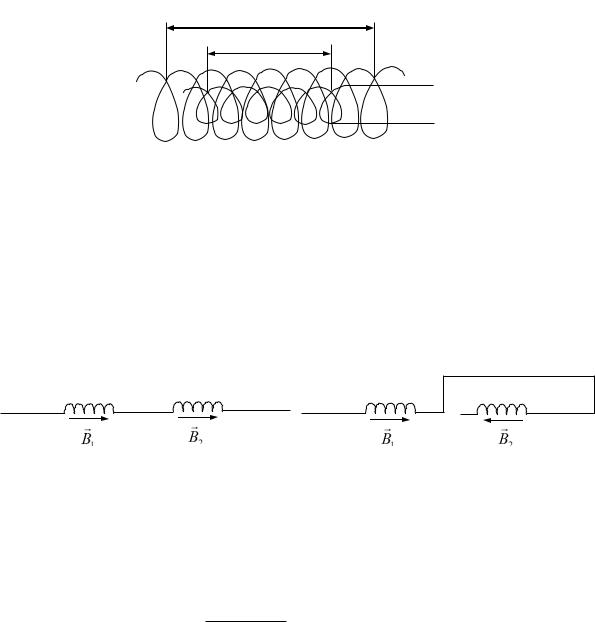
индуктивность системы двух соленоидов L1, L2 для двух различных способов их соединения, изображённых на РИС. 3А И 3Б. Индуктивность системы катушек, надетых друг на друга, в том случае, когда их магнитные поля направлены в одну сторону (РИС. 3А), определяется по формуле
где L1 и L2 – индуктивности каждого соленоида в отдельности, М’ – взаимная индуктивность.
Рис. 3
Если соленоиды подключить так, что их магнитные поля направлены навстречу друг другу (РИС. 3Б), то индуктивность такой системы
L L1 L2 2M .
Из формул (3) и (4) выводят выражения для М’ и М»
|
L |
L |
L L |
||||||
|
M |
L |
, M |
L |
|||||
|
1 |
2 |
1 |
2 |
|||||
|
2 |
2 |
.
Величины L1, L2, L’, L» находят экспериментально, a M’ и М» вычисляют по формулам (5). При неизменном расположении соленоидов М’ = М» = М. Вывод формул
(1), (3), (4) предлагается студентам провести самостоятельно.
2. Описание установки и метода измерений
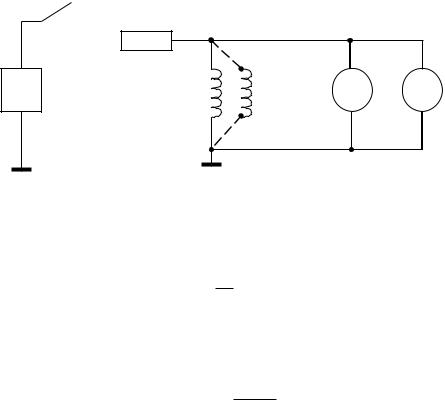
Принципиальная схема установки представлена на РИС. 4. От генератора звуковой
|
частоты Г переменное напряжение U U0 cosωt |
подаётся на последовательно со- |
единённые соленоид L и резистор R. Милливольтметр МВ служит для определения амплитудных значений напряжения, а осциллограф ЭО – для наблюдения качественной картины изменения этого напряжения. Сопротивление R подбирают таким образом, что напряжение на катушке L много меньше, чем на резисторе R. В этом случае проходящий через соленоид ток можно с достаточной степенью точности определить по формуле
4

|
Г |
L1 |
L2 |
МВ |
ЭО |
Рис. 4
где U0 – амплитудное значение напряжения, ω = 2πν – круговая частота, ν – частота. Вследствие изменения потокосцепления самоиндукции соленоида в нём возникает ЭДС самоиндукции
|
ec |
d |
L |
dI |
L |
U |
0 |
ω sinωt UL sinωt , |
||||||||
|
dt |
dt |
R |
|||||||||||||
|
где |
U Lω |
UL |
– амплитудное значение ЭДС самоиндукции. Отсюда находят ин- |
||||||||||||
|
0 |
|||||||||||||||
|
R |
|||||||||||||||
|
дуктивность соленоида |
|||||||||||||||
|
L |
U R |
U R |
. |
(6) |
|||||||||||
|
L |
L |
||||||||||||||
|
U ω |
U |
2πν |
|||||||||||||
|
0 |
0 |
Значения U0 и UL измеряют по милливольтметру МВ, ν – по шкале частот генератора, R задано на установке.
Измерения проводят для двух разных соленоидов L1, L2, а также для системы этих соленоидов, надетых друг на друга, при двух способах их соединения L’, L». По формулам (5) вычисляют М’ и М» и убеждаются в справедливости равенства
М’ = М». Найденные из опыта значения L1, L2 и М сравнивают с их теоретическими значениями, рассчитанными по формулам (1) и (2).
3. Порядок выполнения работы
Перед началом работы обязательно ознакомьтесь с таблицей на стенде.
Часть 1. Определение индуктивности соленоидов L1 и L2
1. Для определения U0 предварительно собирают цепь по схеме (рис. 4) без соленоида. Концы кабелей от генератора, осциллографа, лампового вольтметра с обозначением «Земля» ( ) подключают к нижнему ряду клемм, расположенных на специальной панели.
2. С помощью ручки генератора «Частота» устанавливают = 200 кГц (или
100 кГц).
3. Включают генератор, милливольтметр, осциллограф тумблерами «Сеть». Положения всех ручек этих приборов указаны в таблице к установке.
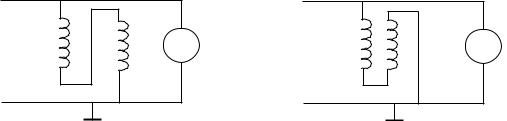
5
4. Напряжение U0 намеряют по милливольтметру. С помощью ручки генератора
«Peг. выхода» добиваются значения U0 примерно 2-3 В. Предварительно устанавливают пределы измерений на вольтметре генератора и на МВ – 3 В.
5.Затем в цепь (РИС. 4) подключают один из соленоидов (например, внешний L1).
6.Записывают показания милливольтметра UL, переключив пределы его измерений на 300, 100 или 30 мВ. Предел необходимо выбирать таким, чтобы отклонение стрелки было близким к максимальному.
7.Отключив соленоид L1, присоединяют внутренний соленоид L2. Записывают показания милливольтметра UL для этого соленоида (U0 и ν не меняют).
8.Наблюдают на осциллографе качественное изменение амплитуды напряжения
UL.
Часть 2. Определение индуктивностей L’, L» и взаимной индуктивности М
1. Для определения индуктивности L’ системы соленоидов (РИС. 3А) их соединяют, как показано на РИС. 5А. Соленоиды при этом должны быть вставлены один в другой.
2. Записывают показания милливольтметра
U L
при указанном в п. 1 расположе-
нии соленоидов, не меняя значений U0 и ν, установленных в предыдущих опытах.
3. Соединение соленоидов L» осуществляют вторым способом, изображенным на
РИС. 5Б (см. РИС. 3Б).
|
при тех же U0 и ν. На экране |
||||||
|
4. Снова записывают показания милливольтметра UL |
||||||
|
осциллографа наблюдают качественную картину изменения напряжения UL и UL . |
||||||
|
1 |
3 |
1 |
3 |
|||
|
L1 |
L2 МВ |
L1 |
L2 |
МВ |
||
|
2 |
4 |
2 |
4 |
|||
|
а |
б |
Рис. 5
5. Все измерения частей 1 и 2 по указанию преподавателя можно повторить в той же последовательности при другой частоте (в пределах от 100 до 200 кГц).
4. Обработка результатов измерений
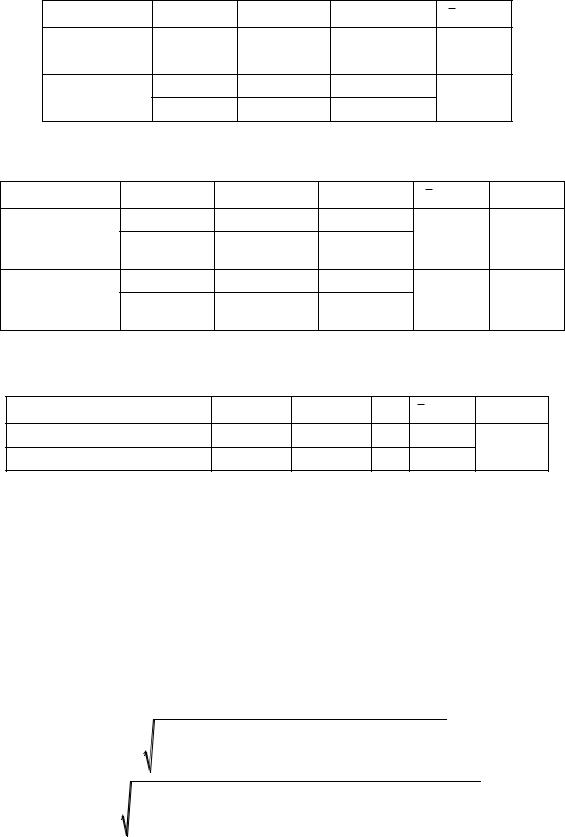
Определение индуктивностей L1, L2
R = 1,00∙103 Ом
|
U0 = 2 |
В |
ν, кГц |
UL, мВ |
L, мкГн |
|
L1, внешний |
||||
|
соленоид |
L2, внутренний соленоид
L
, мкГн
Определение индуктивностей L’, L» и взаимной индуктивности М
|
U0 = 2 В |
ν, кГц |
UL, мВ |
L, мкГн |
L , мкГн |
I соединение,
L
M
II соединение,
L
M
Теоретический расчёт L1, L2 и M
D, мм l, мм N
Внешний соленоид, L1
Внутренний соленоид, L2
1.По формуле (6) находят значения L1, L2 и L’, L».
2.Рассчитывают М’ и М» по (5); окончательно
L
, мкГн
3. Рассчитывают теоретические значения L1, L2, M. Более точные расчёты с учётом неоднородности магнитного поля на концах соленоида приводят к необходимости введения в формулы (1) и (2) коэффициента K, который зависит от соотношения между D и l. Для обоих соленоидов можно принять K 0,9.
4.Сравнить теоретические и экспериментальные значения L1 L2, M.
5.Рассчитывают погрешности величин L1 L2, М по формулам
|
L L |
U |
2 |
R 2 |
U |
2 |
π 2 |
ν 2 |
||||||||||||||||||||
|
L |
R |
U0 |
0 |
π |
, |
||||||||||||||||||||||
|
UL |
ν |
||||||||||||||||||||||||||
|
R |
2 |
U0 |
2 |
π |
2 |
ν |
2 |
U 2 |
U 2 |
||||||||||||||||||
|
М М |
L |
L . |
|||||||||||||||||||||||||
|
R |
U0 |
π |
ν |
U |
|||||||||||||||||||||||
|
U 2 |
|||||||||||||||||||||||||||
|
L |
L |
6.Записывают окончательные результаты для L1, L2, M.
7.Сравнивают М с разностью М’ и М».
7
Дополнительное задание
1.Какой результат можно ожидать, если катушки расположить перпендикулярно или достаточно далеко друг от друга?
2.Как найти число витков соленоида, если их непосредственно подсчитать нельзя?
3.Докажите для частного случая двух надетых друг на друга соленоидов, что
М12 = М21.
5. Контрольные вопросы
1.Что называется индуктивностью контура, взаимной индуктивностью контуров? От чего зависят L и М?
2.Каков принцип работы электрической схемы? Какие величины непосредственно измеряются?
3.Выведите расчётную формулу для определения индуктивности.
4.Чему равна индуктивность системы соленоидов, если магнитные поля в них направлены: а) в одну сторону (L’); б) в противоположные (L»)?
5.Как в работе определяют взаимную индуктивность М?
Соседние файлы в папке II семестр
- #
- #
- #
- #
- #
- #
- #
- #
- #
Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Определение
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как→B. Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B=FAmaxIl
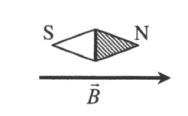
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Определение
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как →H. Единица измерения — А/м.
→H=→Bμμ0
μ — магнитная проницаемость среды (у воздуха она равна 1), μ0 — магнитная постоянная, равная 4π·10−7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: →H↑↑→B.
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора →B магнитной индукции.
Отсюда следует, что:
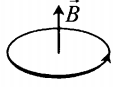
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции →B направлен вверх.
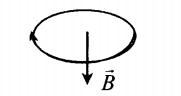
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции →B направлен вниз.
Способы обозначения направлений векторов:
| Вверх | |
| Вниз | |
| Влево | |
| Вправо | |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
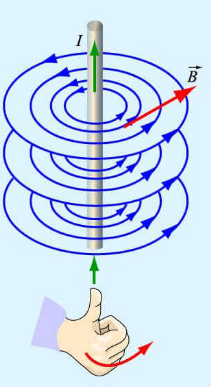
Магнитное поле прямолинейного тока
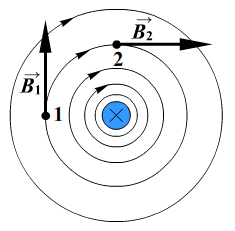
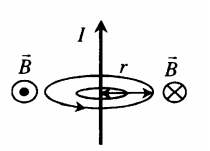
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
Вид сверху:
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B=μμ0I2πr
Модуль напряженности:
H=I2πr
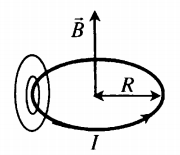
Магнитное поле кругового тока
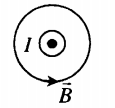
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
B=μμ0I2R
Модуль напряженности в центре витка:
H=I2R
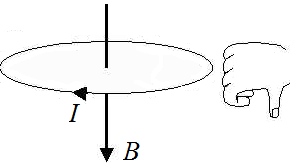
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
Магнитное поле электромагнита (соленоида)
Определение
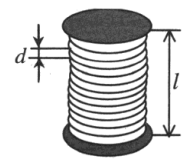
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
N=ld
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
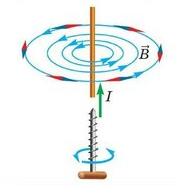
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции →B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B=μμ0INl=μμ0Id
Модуль напряженности магнитного поля в центральной части соленоида:
H=INl=Id
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
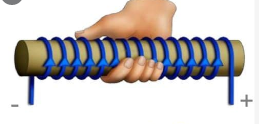
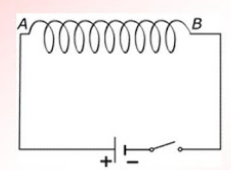
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
Задание EF17530
Ответ:
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
1.Определить правило, по которому можно определить направление вектора магнитной индукции в данном случае.
2.Применить выбранное правило и определить направление вектора магнитной индукции относительно рисунка.
Решение
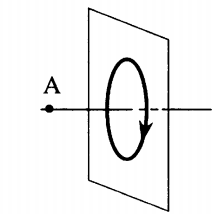
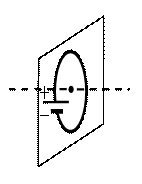
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора →B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18109
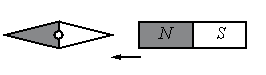
Ответ:
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
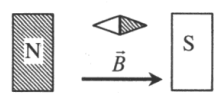
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18266
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
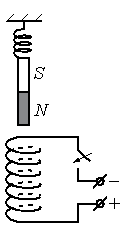
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 22.6k
Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Виды катушек индуктивности
Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности
Расчёт индуктивности катушки.
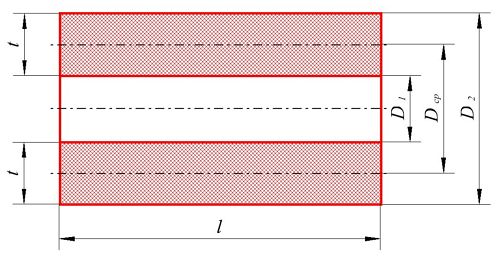
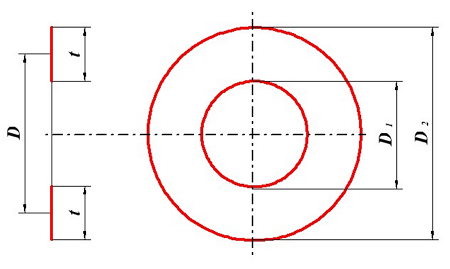
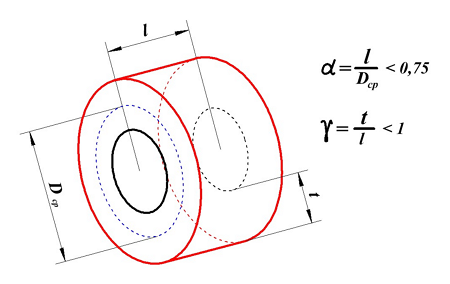
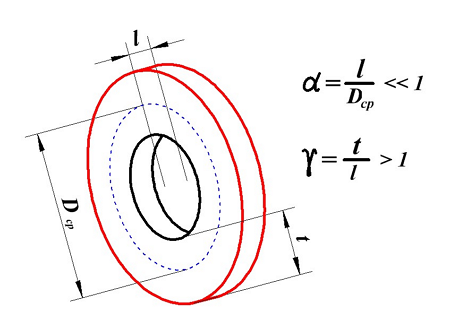
Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:
D1 – внутренний диаметр, D2 – внешний диаметр, Dср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:
если l > Dср – длинная катушка,
если l < Dср – короткая катушка,
если l << Dср – очень короткая катушка,
если l = 0 – плоская катушка,
если t ≈ Dср – толстая катушка,
если t << Dср – тонкая катушка,
если t = 0 – соленоид.
Особенности расчёта катушек индуктивности
Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением
где LР – расчётная индуктивность;
∆L – поправка на «изоляцию», ∆L = ∆1L + ∆2L;
∆1L – поправка учитывающая влияние индуктивности витков;
∆2L – поправка учитывающая влияние взаимной индуктивности витков.
В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности LР, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.
Особенности расчёта круговых катушек индуктивности состоят в следующем:
1. При определении расчётной индуктивности LP, средний диаметр принимается равным среднему диаметру реальной катушки;
2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении
3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.
4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.
5. Так как величина поправки на взаимную индуктивность ∆2L в несколько раз меньше, чем поправка на индуктивность витков ∆1L, то при расчётах можно учитывать только ∆1L.
Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.
Расчёт индуктивности соленоида
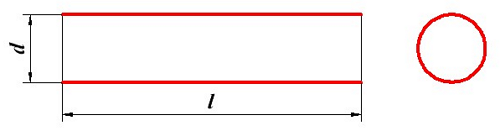
Определение индуктивности соленоида, d – диаметр соленоида, l – длина соленоида.
Соленоид представляет собой катушку, намотанную на каркас в один слой, поэтому толщину слоя можно принять равной нулю t = 0, а расчётная формула индуктивности будет иметь вид
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
d – диаметр соленоида, м;
Φ – коэффициент, который зависит от отношения α = l/D;
l – длина соленоида, м;
Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d
Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит
Для короткого соленоида, то есть α < 0,75, поправочный коэффициент составит
Пример. Необходимо рассчитать соленоид диаметром d = 1 см и длиной l = 5 см, который имеет ω = 75 витков.
Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов.
Online расчёт индуктивности соленоида
Индуктивность плоской катушки
Определение индуктивности плоской катушки, D1 – внутренний диаметр, D2 – внешний диаметр, D – средний диаметр, t – толщина намотки.
В данном случае в качестве плоской катушки представлена идеализированная катушка, длина намотки которой приняли равной нулю l = 0, тогда индуктивность такой катушки можно вычислить по следующей формуле
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
D – средний диаметр катушки, м;
Ψ – коэффициент, который зависит от отношения ρ = t/D;
t – толщина намотки катушки.
Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D
При небольшой толщине намотки, когда ρ < 0,5
При большой толщине намотки, когда ρ > 0,5
где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки
Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.
Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.
Online расчёт индуктивности плоской катушки.
Индуктивность круговой катушки прямоугольного сечения
Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник
Индуктивность прямоугольной катушки.
Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.
Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле
где L0 – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/Dcp;
l – длина катушки, м;
Dcp – средний диаметр катушки, м;
∆ — поправка на форму катушки.
В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру Dcp, можно разделить на несколько типов:
1. Длинная катушка, у которой α > 0,75.
2. Короткая катушка, имеющая α < 0,75 и γ < 1.
3. Очень короткая катушка, имеет α << 1 и γ > 1.
где
Рассмотрим каждый случай по отдельности.
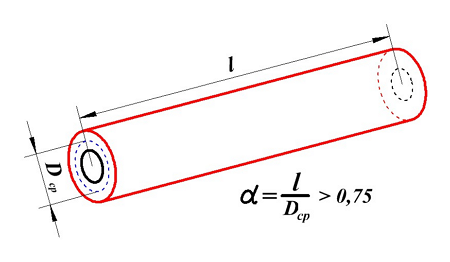
Индуктивность длинной катушки
Длинная катушка.
Для длинной катушки (α > 0,75) величина L0 рассчитывается также как для длинного соленоида, где l – длина соленоида, Dcp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
где D1 – внутренний диаметр, D2 – внешний диаметр.
Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром DCP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.
Индуктивность короткой катушки
Короткая катушка.
Для короткой катушки (α < 0,75, t < l) величина L0 рассчитывается также как для короткого соленоида, где l – длина соленоида, DСР – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
Пример. Рассчитаем индуктивность катушки длиной l = 1 см, средним диаметром DСР = 2 см, толщиной намотки t = 5 мм, количеством витков ω = 50.
Индуктивность очень короткой катушки
Очень короткая катушка.
Для очень короткой катушки (α << 1, t > l) величина L0 рассчитывается также как для плоской катушки, где t – толщина намотки, Dcp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ < 1;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
Пример. Рассчитаем индуктивность катушки длиной l = 5 мм, средним диаметром DCP = 7 см, намотка толщиной t = 1 см, количество витков ω = 150.
Online расчёт индуктивности круговой катушки прямоугольного сечения.
Расчёт поправки на собственную индуктивность витков
Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L
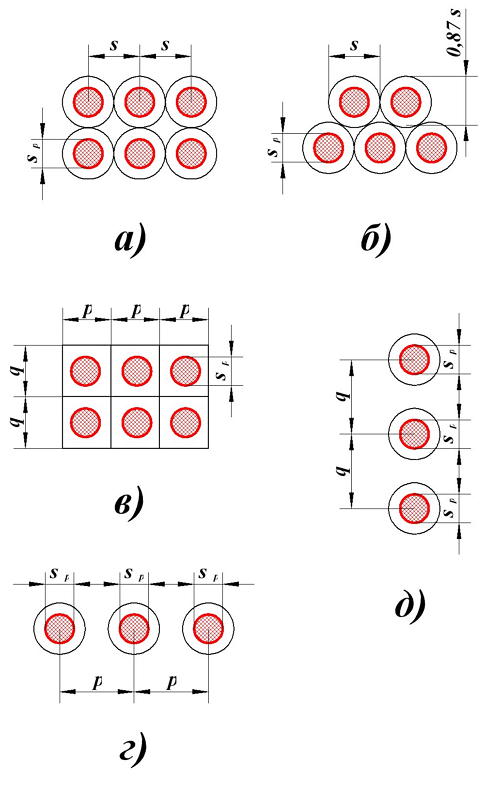
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки
Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I – коэффициент, зависящий от расположения витков катушки.
Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.
Для варианта а), провод намотан с небольшим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта б), провод намотан с большим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен
где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).
Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая
— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен
где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).
Расчёт поправки на взаимную индуктивность витков
В общем случае поправка на взаимную индуктивность витков ∆2L катушки определяется выражением
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
J – коэффициент, зависящий формы катушки и от числа витков катушки.
1. Для катушки выполненной в один слой по длине катушки (соленоид):
а) при определении расчётной индуктивности LP толщина намотки t принята равной шагу намотки р, то коэффициент J составит
где ω – количество витков катушки.
б) при определении расчётной индуктивности LP толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит
где ω – количество витков катушки.
2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):
а) при определении расчётной индуктивности LP длина катушки l принята равной шагу намотки р, то коэффициент J составит
где ω – количество витков катушки.
б) при определении расчётной индуктивности LP длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит
где ω – количество витков катушки.
На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.
Определите число витков селеноида индуктивностью 2, 5 Гн, если сила тока в нём равна 5 А, а магнитный поток через площадь одного витка селеноида равен 0, 005 Вб.
Вы перешли к вопросу Определите число витков селеноида индуктивностью 2, 5 Гн, если сила тока в нём равна 5 А, а магнитный поток через площадь одного витка селеноида равен 0, 005 Вб?. Он относится к категории Физика,
для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот
вариант ответа не полностью вас удовлетворяет, то с помощью автоматического
умного поиска можно найти другие вопросы по этой же теме, в категории
Физика. В случае если ответы на похожие вопросы не раскрывают в полном
объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части
сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете
ознакомиться с вариантами ответов пользователей.