Метод интервалов: решение простейших строгих неравенств
12 ноября 2017
- Домашнее задание
- Ответы
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
(x − 5)(x + 3) > 0
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
x2 − 2x − 15 > 0
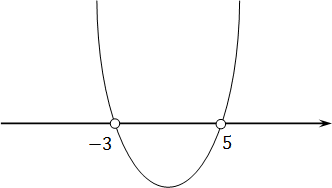
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
(x − 7)(x − 1)(x + 4)(x + 9) < 0
Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.
Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.
Что такое метод интервалов
Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
- Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
- Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
- Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
- Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.
На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:
Задача. Решите неравенство:
(x − 2)(x + 7) < 0
Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:
(x − 2)(x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f (x) = (x − 2)(x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f(3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
Вернемся к исходному неравенству, которое имело вид:
(x − 2)(x + 7) < 0
Итак, функция должна быть меньше нуля. Значит, нас интересует знак минус, который возникает лишь на одном интервале: (−7; 2). Это и будет ответ.
Задача. Решите неравенство:
(x + 9)(x − 3)(1 − x) < 0
Шаг 1: приравниваем левую часть к нулю:
(x + 9)(x − 3)(1 − x) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f (x) = (x + 9)(x − 3)(1 − x);
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197 < 0.
Шаг 4: расставляем остальные знаки. Помним, что при переходе через каждый корень знак меняется. В итоге наша картинка будет выглядеть следующим образом:
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
(x + 9)(x − 3)(1 − x) < 0
Это неравенство вида f (x) < 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:
x ∈ (−9; 1) ∪ (3; +∞)
Это и есть ответ.
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
- Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
- Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одном интервале дают один и тот же знак. Помните об этом.
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
Итак, знак функции на правом куске числовой оси. Этот кусок имеет вид (a; +∞), где a — самый большой корень уравнения f (x) = 0. Чтобы не взрывать мозг, рассмотрим конкретный пример:
(x − 1)(2 + x)(7 − x) < 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
Требуется найти знак функции f (x) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f (x) = −1 и f (x) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f (x) = (x − 1)(2 + x)(7 − x)
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: (x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
(+) · (+) · (−) = (−)
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
Исходное неравенство имело вид:
(x − 1)(2 + x)(7 − x) < 0
Следовательно, нас интересуют интервалы, отмеченные знаком минус. Выписываем ответ:
x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Задача. Решите неравенство:
x(2x + 8)(x − 3) > 0
Заменяем неравенство уравнением и решаем его:
x(2x + 8)(x − 3) = 0;
x = 0;
2x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f (x) = x(2x + 8)(x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
x ∈ (−4; 0) ∪ (3; +∞)
Смотрите также:
- Метод интервалов: случай нестрогих неравенств
- Тест по методу интервалов для строгих неравенств
- Сводный тест по задачам B12 (2 вариант)
- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
- Формулы приведения: ускоряем вычисления в тригонометрии
- Задачи B4: перевозка груза тремя фирмами
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
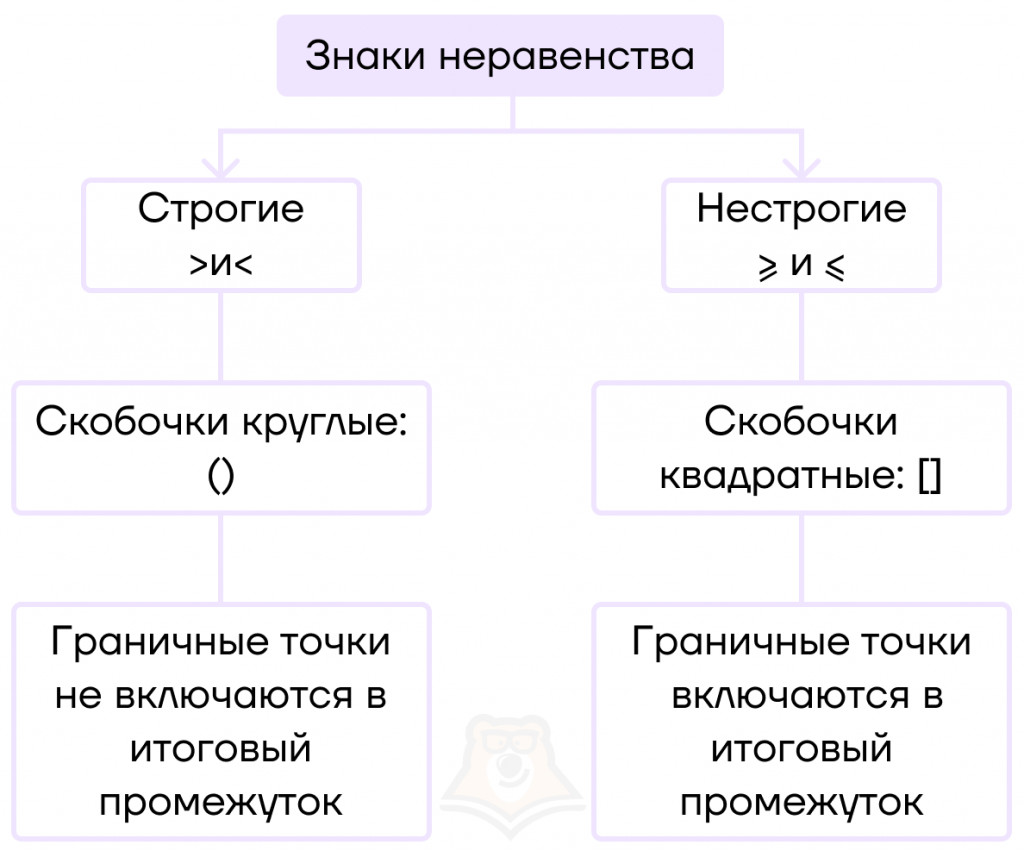
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
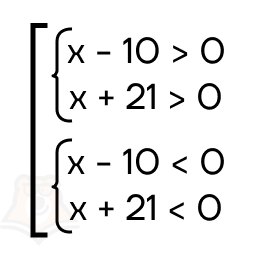
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
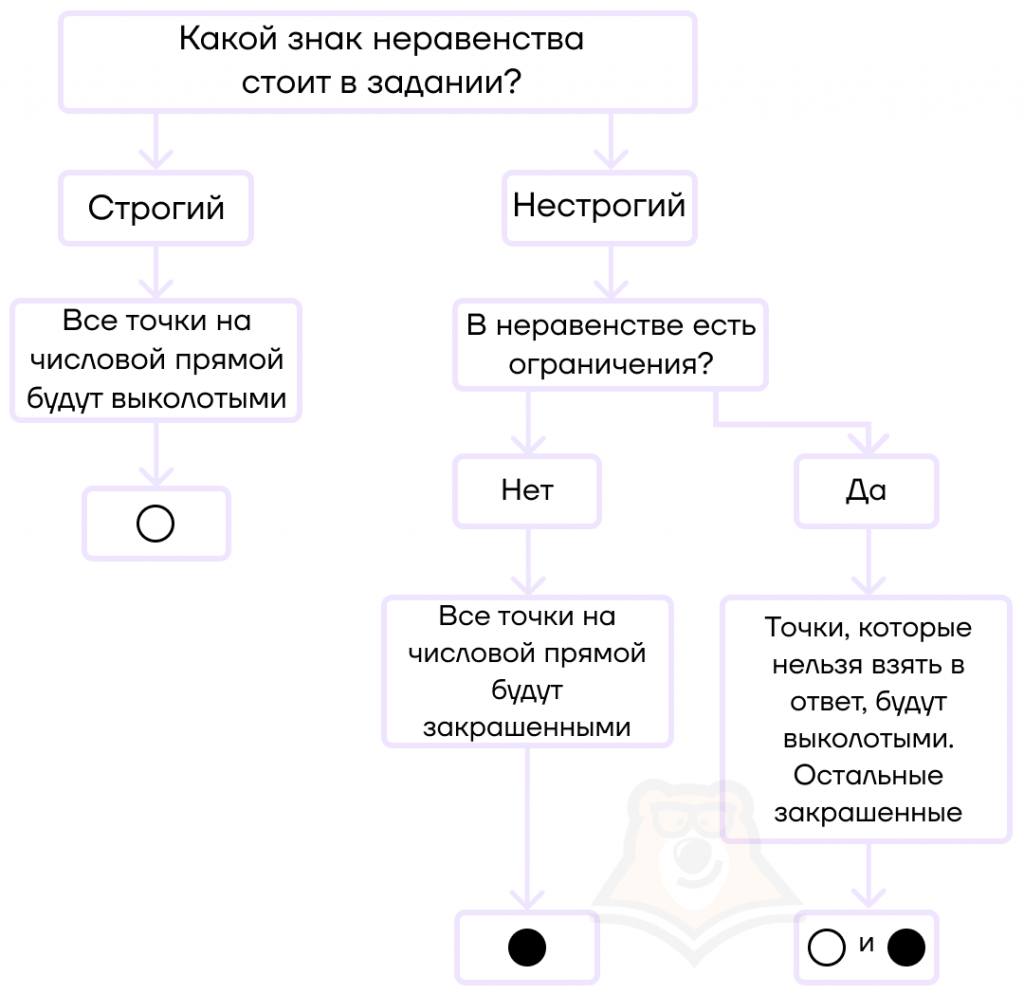
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
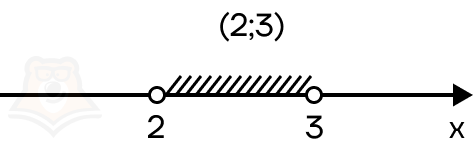
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
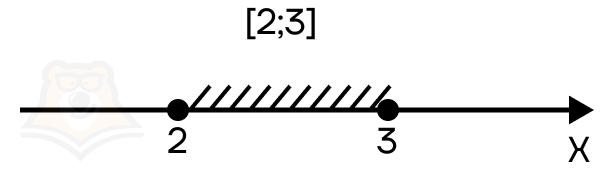
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
В случае сомнений мы всегда можем проверить себя по простой схеме.
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
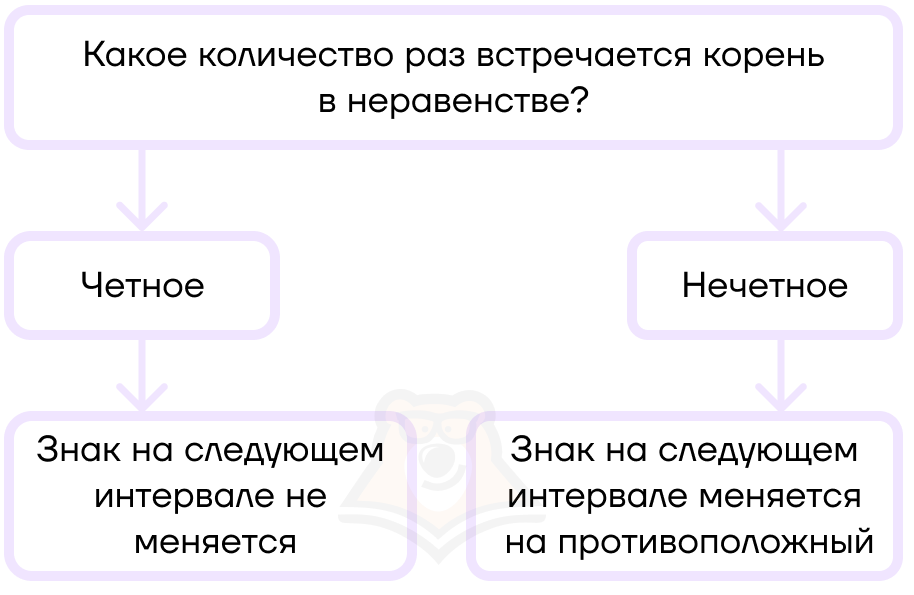
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
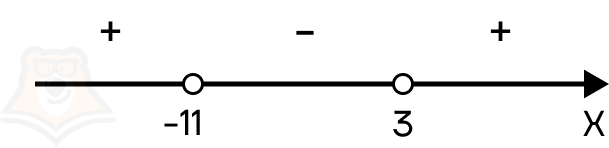
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
The addition x + a on the number line. All numbers greater than x and less than x + a fall within that open interval.
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers x satisfying 0 ≤ x ≤ 1 is an interval which contains 0, 1, and all numbers in between. Other examples of intervals are the set of numbers such that 0 < x < 1, the set of all real numbers 
Real intervals play an important role in the theory of integration, because they are the simplest sets whose «length» (or «measure» or «size») is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure.
Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical approximations, and arithmetic roundoff.
Intervals are likewise defined on an arbitrary totally ordered set, such as integers or rational numbers. The notation of integer intervals is considered in the special section below.
Terminology[edit]
An open interval does not include its endpoints, and is indicated with parentheses.[1] For example, (0, 1) means greater than 0 and less than 1. This means (0, 1) = {x | 0 < x < 1}.
This interval can also be denoted by ]0, 1[, see below.
A closed interval is an interval which includes all its limit points, and is denoted with square brackets.[1] For example, [0, 1] means greater than or equal to 0 and less than or equal to 1.
A half-open interval includes only one of its endpoints, and is denoted by mixing the notations for open and closed intervals.[2] For example, (0, 1] means greater than 0 and less than or equal to 1, while [0, 1) means greater than or equal to 0 and less than 1.
A degenerate interval is any set consisting of a single real number (i.e., an interval of the form [a, a]).[2] Some authors include the empty set in this definition. A real interval that is neither empty nor degenerate is said to be proper, and has infinitely many elements.
An interval is said to be left-bounded or right-bounded, if there is some real number that is, respectively, smaller than or larger than all its elements. An interval is said to be bounded, if it is both left- and right-bounded; and is said to be unbounded otherwise. Intervals that are bounded at only one end are said to be half-bounded. The empty set is bounded, and the set of all reals is the only interval that is unbounded at both ends. Bounded intervals are also commonly known as finite intervals.
Bounded intervals are bounded sets, in the sense that their diameter (which is equal to the absolute difference between the endpoints) is finite. The diameter may be called the length, width, measure, range, or size of the interval. The size of unbounded intervals is usually defined as +∞, and the size of the empty interval may be defined as 0 (or left undefined).
The centre (midpoint) of a bounded interval with endpoints a and b is (a + b)/2, and its radius is the half-length |a − b|/2. These concepts are undefined for empty or unbounded intervals.
An interval is said to be left-open if and only if it contains no minimum (an element that is smaller than all other elements); right-open if it contains no maximum; and open if it contains neither. The interval [0, 1) = {x | 0 ≤ x < 1}, for example, is left-closed and right-open. The empty set and the set of all reals are both open and closed intervals, while the set of non-negative reals, is a closed interval that is right-open but not left-open. The open intervals are open sets of the real line in its standard topology, and form a base of the open sets.
An interval is said to be left-closed if it has a minimum element or is left-unbounded, right-closed if it has a maximum or is right unbounded; it is simply closed if it is both left-closed and right closed. So, the closed intervals coincide with the closed sets in that topology.
The interior of an interval I is the largest open interval that is contained in I; it is also the set of points in I which are not endpoints of I. The closure of I is the smallest closed interval that contains I; which is also the set I augmented with its finite endpoints.
For any set X of real numbers, the interval enclosure or interval span of X is the unique interval that contains X, and does not properly contain any other interval that also contains X.
An interval I is subinterval of interval J if I is a subset of J. An interval I is a proper subinterval of J if I is a proper subset of J.
Note on conflicting terminology[edit]
The terms segment and interval have been employed in the literature in two essentially opposite ways, resulting in ambiguity when these terms are used. The Encyclopedia of Mathematics[3] defines interval (without a qualifier) to exclude both endpoints (i.e., open interval) and segment to include both endpoints (i.e., closed interval), while Rudin’s Principles of Mathematical Analysis[4] calls sets of the form [a, b] intervals and sets of the form (a, b) segments throughout. These terms tend to appear in older works; modern texts increasingly favor the term interval (qualified by open, closed, or half-open), regardless of whether endpoints are included.
Notations for intervals[edit]
The interval of numbers between a and b, including a and b, is often denoted [a, b]. The two numbers are called the endpoints of the interval. In countries where numbers are written with a decimal comma, a semicolon may be used as a separator to avoid ambiguity.
Including or excluding endpoints[edit]
To indicate that one of the endpoints is to be excluded from the set, the corresponding square bracket can be either replaced with a parenthesis, or reversed. Both notations are described in International standard ISO 31-11. Thus, in set builder notation,
Each interval (a, a), [a, a), and (a, a] represents the empty set, whereas [a, a] denotes the singleton set {a}. When a > b, all four notations are usually taken to represent the empty set.
Both notations may overlap with other uses of parentheses and brackets in mathematics. For instance, the notation (a, b) is often used to denote an ordered pair in set theory, the coordinates of a point or vector in analytic geometry and linear algebra, or (sometimes) a complex number in algebra. That is why Bourbaki introduced the notation ]a, b[ to denote the open interval.[5] The notation [a, b] too is occasionally used for ordered pairs, especially in computer science.
Some authors such as Yves Tillé use ]a, b[ to denote the complement of the interval (a, b); namely, the set of all real numbers that are either less than or equal to a, or greater than or equal to b.
Infinite endpoints[edit]
In some contexts, an interval may be defined as a subset of the extended real numbers, the set of all real numbers augmented with −∞ and +∞.
In this interpretation, the notations [−∞, b] , (−∞, b] , [a, +∞] , and [a, +∞) are all meaningful and distinct. In particular, (−∞, +∞) denotes the set of all ordinary real numbers, while [−∞, +∞] denotes the extended reals.
Even in the context of the ordinary reals, one may use an infinite endpoint to indicate that there is no bound in that direction. For example, (0, +∞) is the set of positive real numbers, also written as 

Integer intervals[edit]
When a and b are integers, the notation ⟦a, b⟧, or [a .. b] or {a .. b} or just a .. b, is sometimes used to indicate the interval of all integers between a and b included. The notation [a .. b] is used in some programming languages; in Pascal, for example, it is used to formally define a subrange type, most frequently used to specify lower and upper bounds of valid indices of an array.
An integer interval that has a finite lower or upper endpoint always includes that endpoint. Therefore, the exclusion of endpoints can be explicitly denoted by writing a .. b − 1 , a + 1 .. b , or a + 1 .. b − 1. Alternate-bracket notations like [a .. b) or [a .. b[ are rarely used for integer intervals.[citation needed]
Classification of intervals[edit]
The intervals of real numbers can be classified into the eleven different types listed below[citation needed], where a and b are real numbers, and 
Properties of intervals[edit]
The intervals are precisely the connected subsets of 
The intervals are also the convex subsets of 


The intersection of any collection of intervals is always an interval. The union of two intervals is an interval if and only if they have a non-empty intersection or an open end-point of one interval is a closed end-point of the other – e.g., ![(a,b)cup [b,c]=(a,c]](https://wikimedia.org/api/rest_v1/media/math/render/svg/20dd7d6ce8ba23bfb9de0d90487008656b91eb94)
If 
Any element x of an interval I defines a partition of I into three disjoint intervals I1, I2, I3: respectively, the elements of I that are less than x, the singleton ![[x,x]={x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08cd03413513401836efbed8ca64419d73d3f481)
Dyadic intervals[edit]
A dyadic interval is a bounded real interval whose endpoints are 



Dyadic intervals have the following properties:
- The length of a dyadic interval is always an integer power of two.
- Each dyadic interval is contained in exactly one dyadic interval of twice the length.
- Each dyadic interval is spanned by two dyadic intervals of half the length.
- If two open dyadic intervals overlap, then one of them is a subset of the other.
The dyadic intervals consequently have a structure that reflects that of an infinite binary tree.
Dyadic intervals are relevant to several areas of numerical analysis, including adaptive mesh refinement, multigrid methods and wavelet analysis. Another way to represent such a structure is p-adic analysis (for p = 2).[6]
Generalizations[edit]
Multi-dimensional intervals[edit]
In many contexts, an 



For 

In higher dimensions, the Cartesian product of 
A facet of such an interval 






Complex intervals[edit]
Intervals of complex numbers can be defined as regions of the complex plane, either rectangular or circular.[7]
Topological algebra[edit]
Intervals can be associated with points of the plane, and hence regions of intervals can be associated with regions of the plane. Generally, an interval in mathematics corresponds to an ordered pair (x,y) taken from the direct product R × R of real numbers with itself, where it is often assumed that y > x. For purposes of mathematical structure, this restriction is discarded,[8] and «reversed intervals» where y − x < 0 are allowed. Then, the collection of all intervals [x,y] can be identified with the topological ring formed by the direct sum of R with itself, where addition and multiplication are defined component-wise.
The direct sum algebra 
Every interval can be considered a symmetric interval around its midpoint. In a reconfiguration published in 1956 by M Warmus, the axis of «balanced intervals» [x, −x] is used along with the axis of intervals [x,x] that reduce to a point. Instead of the direct sum 
- z = (x + y)/2 + j (x − y)/2.
This linear mapping of the plane, which amounts of a ring isomorphism, provides the plane with a multiplicative structure having some analogies to ordinary complex arithmetic, such as polar decomposition.
See also[edit]
- Arc (geometry)
- Inequality
- Interval graph
- Interval finite element
- Interval (statistics)
- Line segment
- Partition of an interval
- Unit interval
References[edit]
- ^ a b «Intervals». www.mathsisfun.com. Retrieved 2020-08-23.
- ^ a b Weisstein, Eric W. «Interval». mathworld.wolfram.com. Retrieved 2020-08-23.
- ^ «Interval and segment — Encyclopedia of Mathematics». encyclopediaofmath.org. Archived from the original on 2014-12-26. Retrieved 2016-11-12.
- ^ Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. pp. 31. ISBN 0-07-054235-X.
- ^ «Why is American and French notation different for open intervals (x, y) vs. ]x, y[?». hsm.stackexchange.com. Retrieved 28 April 2018.
- ^ Kozyrev, Sergey (2002). «Wavelet theory as p-adic spectral analysis». Izvestiya RAN. Ser. Mat. 66 (2): 149–158. arXiv:math-ph/0012019. Bibcode:2002IzMat..66..367K. doi:10.1070/IM2002v066n02ABEH000381. S2CID 16796699. Retrieved 2012-04-05.
- ^ Complex interval arithmetic and its applications, Miodrag Petković, Ljiljana Petković, Wiley-VCH, 1998, ISBN 978-3-527-40134-5
- ^ Kaj Madsen (1979) Review of «Interval analysis in the extended interval space» by Edgar Kaucher[permanent dead link] from Mathematical Reviews
- ^ D. H. Lehmer (1956) Review of «Calculus of Approximations»[permanent dead link] from Mathematical Reviews
Bibliography[edit]
- T. Sunaga, «Theory of interval algebra and its application to numerical analysis» Archived 2012-03-09 at the Wayback Machine, In: Research Association of Applied Geometry (RAAG) Memoirs, Ggujutsu Bunken Fukuy-kai. Tokyo, Japan, 1958, Vol. 2, pp. 29–46 (547-564); reprinted in Japan Journal on Industrial and Applied Mathematics, 2009, Vol. 26, No. 2-3, pp. 126–143.
External links[edit]
- A Lucid Interval by Brian Hayes: An American Scientist article provides an introduction.
- Interval computations website Archived 2006-03-02 at the Wayback Machine
- Interval computations research centers Archived 2007-02-03 at the Wayback Machine
- Interval Notation by George Beck, Wolfram Demonstrations Project.
- Weisstein, Eric W. «Interval». MathWorld.
Метод интервалов
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
1. Рассмотрим неравенство:
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .
, где
и
— корни квадратного уравнения
.
Получим:
Рисуем ось X и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Нули знаменателя и
— выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя).
Напомним, что мы изображаем точку на числовой прямой выколотой (пустой), если соответствующее значение переменной никак не может быть решением неравенства. В нашем примере точки и
выколотые, потому что в них знаменатель обращается в ноль.
Нули числителя и
— закрашены, так как неравенство нестрогое. При
и
наше неравенство выполняется, так как обе его части равны нулю.
Эти точки разбивают ось X на 5 промежутков.
Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным — либо «плюс», либо «минус».
И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например,
и проверим знак выражения
в левой части неравенства. Каждая из «скобок» отрицательная. Левая часть имеет знак
.
Следующий промежуток:
. Проверим знак при
. Получаем, что левая часть поменяла знак на
.
. Возьмем
. При
выражение положительно — следовательно, оно положительно на всем промежутке от
до
.
При
левая часть неравенства отрицательна.
И, наконец,
. Подставим
и проверим знак выражения в левой части неравенства. Каждая «скобочка» положительна. Следовательно, левая часть имеет знак
.
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Ответ: .
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
, или
, или
, или
(в левой части — дробно-рациональная функция, в правой — нуль).
Затем — отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого — записываем ответ. Вот и всё.
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
2. Рассмотрим еще одно неравенство:
Решение:
Снова расставляем точки на оси X. Точки и
— выколотые, поскольку это нули знаменателя. Точка
— тоже выколота, поскольку неравенство строгое, и значение переменной
не может быть решением неравенства.
При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например,
. Левая часть имеет знак
:
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак
:
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак
:
Наконец, при все множители положительны, и левая часть имеет знак
:
Ответ: .
Почему нарушилось чередование знаков? Потому что при переходе через точку 2 «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку
знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Решение:
Левая часть та же, что и в предыдущем примере. Та же будет и картина знаков:
Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при
и левая, и правая части неравенства равны нулю — следовательно, эта точка является решением.
Ответ: .
В задачах на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
Решение:
Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения
при всех
одинаков, а конкретно — положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.
И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех
.
Придём к равносильному неравенству:
Решим неравенство методом интервалов. Действуем по алгоритму: числитель левой части равен нулю при а знаменатель обращается в ноль при
. Отметим эти точки на координатной прямой. Точки выколоты, потому что неравенство строгое. Эти точки разбивают числовую ось на три интервала. Найдем знаки на каждом из интервалов. На крайнем правом знак положителен, а дальше знаки чередуются.
Нам нужен «интервал со знаком минус», то есть такой, где Выпишем ответ.
Ответ:
Обратите внимание — мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Решение:
Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь
может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину — знак неравенства меняется.
Мы поступим по-другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Применим метод интервалов.
Действуем по алгоритму. Отметим на координатной прямой точки и
. Они выколотые, потому что неравенство строгое. Эти точки разбивают ось Х на три интервала. Расставим знаки на каждом из них.
Ответ:
6. Решите неравенство:
Решение:
Приведем левую часть неравенства к общему знаменателю и преобразуем числитель:
Применим метод интервалов:
Числитель равен нулю при Знаменатель обращается в ноль при
или
. Неравенство строгое, поэтому все эти точки на числовой оси отмечаем как пустые.
Если , то
. Далее знаки чередуются.
Нам нужны «интервалы со знаком минус». Выпишем их и получим ответ.
Ответ:
7. Решите неравенство
Решение:
Приведем неравенство к виду:
Для этого все перенесем в левую часть, приведем к общему знаменателю и разложим числитель и знаменатель на множители. Применяем формулу разности квадратов и формулу разложения квадратного трехчлена на множители
Получим:
Найдем нули числителя и знаменателя и отметим их на числовой оси:
Выпишем интервалы, где неравенство выполняется, и получим ответ.
Ответ:
8. Решите неравенство:
Решение:
Разложим левую часть неравенства на множители.
Для этого вынесем общий множитель за скобки, а затем воспользуемся формулой:
Получим:
Применим метод интервалов.
Левая часть неравенства обращается в ноль, если ,
или
. Нанесем эти точки на координатную прямую. Все точки закрашенные, так как неравенство нестрогое, в нем присутствует знак «меньше или равно».
Ответ:
9. Решите неравенство:
Решение:
Разложим числитель на множители с помощью группировки:
Знаменатель тоже разложим на множители:
Неравенство примет вид:
Мы видим, что числитель равен нулю при
Знаменатель равен нулю при . Множитель
стоит в числителе и в знаменателе, и он не может равняться нулю.
Отметим полученные точки на координатной прямой. Две из них закрашены (это 3 и 1), а две нет (это -1 и -2). Найдем знаки на каждом промежутке.
При переходе через точку знак не меняется, так как множитель
присутствует и в числителе, и в знаменателе.
Выпишем ответ.
Ответ:
10. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Напомним, что выражение мы разложили на множители, решив квадратное уравнение:
Неравенство примет вид:
Воспользуемся методом интервалов.
Числитель дроби в левой части неравенства равен нулю, если Знаменатель обращается в ноль, если
или
. Отметим эти точки на координатной прямой и определим знаки на интервалах.
Ответ:
11. Решите неравенство:
Решение:
Можно сразу применить метод интервалов.
Но лучше, чтобы не запутаться со знаками, умножить обе части неравенства на (-1) и не забыть поменять знак неравенства на противоположный.
Теперь применим метод интервалов.
Отметим на координатной прямой нули числителя и знаменателя и определим знаки на интервалах.
Обратите внимание, что знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени.
Ответ:
12. Решите неравенство:
Решение:
Разложим числитель и знаменатель на множители:
Сократим на множитель при условии, что
.
Здесь мы действуем чуть иначе, чем в задаче 9.
Неравенство равносильно системе:
Решаем второе неравенство системы методом интервалов:
Второму неравенству удовлетворяют точки .
Точка в этот промежуток не входит.
Ответ:
13. Решите неравенство:
Решение:
Разложив числитель на множители, получим:
Применим метод интервалов.
Отметим на числовой оси точки, в которых числитель и знаменатель обращаются в ноль. Обратите внимание, что точки -1 и 5 закрашены, а точки 2 и 4 пустые.
Определим знаки на интервалах.
Знак не меняется при переходе через точку , так как множитель
входит в выражение в левой части неравенства в четной степени. При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.
В ответе запишем интервалы, на которых неравенство выполняется.
Ответ:
14. Решите неравенство:
Разложим числитель и знаменатель на множители, используя формулы сокращенного умножения: суммы и разности кубов, разности квадратов.
Кажется, что неравенство сложное. Попробуем разложить на множители выражения и
Оказывается, что дискриминанты соответствующих квадратных уравнений отрицательны, поэтому и
при всех х.
Разделим обе части неравенства на эти положительные выражения.
Получим:
Неравенство равносильно системе:
Решим первое неравенство системы методом интервалов:
Его решением является промежуток [1;4], причем точка в этот промежуток не входит.
Ответ:
Мы показали на различных примерах, как применяется метод интервалов.
Сделаем вывод:
Метод интервалов помогает решать дробно-рациональные неравенства по алгоритму. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Метод интервалов» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Как построить интервальный ряд
Когда ряд распределения уже дан, можно сразу приступать к его исследованию. Но в некоторых задачах в качестве исходных данных представлены просто числа (вес, сумма, количество – любые значения параметра или признака). В таком случае для того, чтобы начать анализ, сначала нужно построить интервальный ряд.

Вам понадобится
- — значения параметра.
Инструкция
Если значения параметра изменяются с течением времени, используйте в качестве интервалов временные промежутки, например, час, день, месяц, год. При выборе минимального промежутка учитывайте количество и разброс данных, старайтесь, чтобы ряд распределения оказался максимально информативным и в то же время компактным. Например, если вам даны данные по месяцам в течение двух лет, разбивка на годы ни о чем не сможет сказать, а использование в качестве интервала месяц в некоторых случаях приведет к размыванию данных. Оптимальным решением при этом станет разбивка по кварталам.
Если время для составления выборки не имеет значения, сформируйте интервальные промежутки в зависимости от значений. Для этого оцените разброс данных, их максимальное и минимальное значение и выберите величину интервала. Можно использовать такой метод: вычтите из максимального значения минимальное и полученную разность разделите на желаемое количество интервалов. Затем установите границы, конечно, лучше, если это будут целые числа. Например, вам даны числа 32, 33, 35, 38, 45, 47, 48, 50, 58, 59, 63. После расчетов вы получите (63-32)/5=6,2. Округлите размер интервала до 7. Таким образом, вы получите интервалы: (32-39), (40-47), (48-55), (56-63).
Обратите внимание, лучше всего делать границы интервалов не пересекающимися, то есть следующий интервал начинайте не с того же числа, а с большего на единицу. Благодаря этому вы сможете избежать разногласий и недоразумений.
После того как вы распределите все интервалы, посчитайте количество значений в каждом из них. Запишите полученные результаты в таблицу, где в одной строке будут указаны границы, в другой – количество значений, лежащих в границах этого интервала. В рассмотренном выше примере расчет количества результатов будет выглядеть так: в интервал (32-39) входят значения 32, 33, 35, 38 – всего 4 значения. Значит, в первой ячейке таблицы под этим интервалом укажите число 4. Точно так же рассчитайте значения для следующих интервалов: (40-47) – 2, (48-55) – 2, (56-63) – 3.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

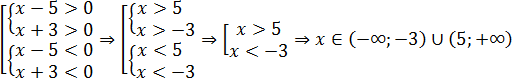


![{displaystyle {begin{aligned}{color {Maroon}(}a,b{color {Maroon})}={mathopen {color {Maroon}]}}a,b{mathclose {color {Maroon}[}}&={xin mathbb {R} mid a{color {Maroon}{}<{}}x{color {Maroon}{}<{}}b},\{}{color {DarkGreen}[}a,b{color {Maroon})}={mathopen {color {DarkGreen}[}}a,b{mathclose {color {Maroon}[}}&={xin mathbb {R} mid a{color {DarkGreen}{}leq {}}x{color {Maroon}{}<{}}b},\{}{color {Maroon}(}a,b{color {DarkGreen}]}={mathopen {color {Maroon}]}}a,b{mathclose {color {DarkGreen}]}}&={xin mathbb {R} mid a{color {Maroon}{}<{}}x{color {DarkGreen}{}leq {}}b},\{}{color {DarkGreen}[}a,b{color {DarkGreen}]}={mathopen {color {DarkGreen}[}}a,b{mathclose {color {DarkGreen}]}}&={xin mathbb {R} mid a{color {DarkGreen}{}leq {}}x{color {DarkGreen}{}leq {}}b}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0410c727e5c09b33b3074d6f7cfa99a624883079)






















