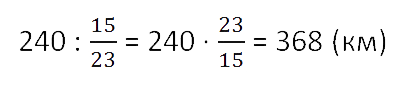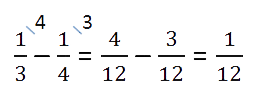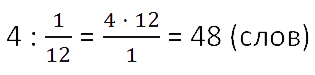Как можно найти какое то число - Исправление недочетов и поиск решений вместе с Examum.ru

Можно найти любое число, если знать какую-то его часть и условие, сколько эта известная часть составляет от искомого целого числа.

Поясним на примере:

Задача 1

Необходимо найти длину отрезка, если известно, что (4 over 9) этого отрезка составляет 16 см.

Итак, нам надо найти число, которое в этом примере является длиной отрезка. Это число нам не известно. Но нам известно, что (4 over 9) длины этого отрезка составляет 16 см. То есть, нам известна часть этого отрезка – 16 см. И эта часть составляет ровно (4 over 9) от длины всего отрезка.

Правило нахождения искомого числа звучит так:

«Чтобы найти число, зная его часть, выраженную дробью, необходимо это число разделить на эту дробь»

В нашем случае, зная, что при делении числа на дробь, мы деление заменяем умножением и «переворачиваем» дробь, получим:

(16 : {4 over 9}=16*{9over4}={16*9over4}={4*9over1}=36)

Искомое число – 36. Это значит, что длина отрезка составляет 36 см.

Давайте решим еще одну задачу, чтобы закрепить полученные знания.

Трактор вспахал (2over5) всего поля. Площадь вспаханной части составила 1200 м². Найдите площадь всего поля.

Решение

Обозначим искомое число за «х».

Воспользуемся правилом нахождения числа, если известна его часть:

«Чтобы найти число, зная его часть, выраженную дробью, необходимо это число разделить на эту дробь»:

(x = 1200:{2over5}=1200*{5over2}={1200*5over2}={600*5over1}=3000)

Получаем, что если (2over5) всего поля составляет 1200 м², то площадь поля составляет 3000 м².

Ответ: 3000 м².

Источник

Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.

Бинарный поиск

Линейный поиск
Бинарный поиск
Бинарный поиск с вещественными числами
Поиск максимума выпуклой функции: тернарный поиск, бинарный поиск
Бинарный поиск по ответу

Линейный поиск

Мы считаем, что вы уже знаете линейный поиск, а именно умеете решать задачи такого типа:

Проверить, есть ли в массиве число X
Найти максимум в массиве
Найти сумму чисел в массиве
Найти первое четное число в массиве

Все такие задачи решаются с помощью одного прохода по массиву с помощью цикла for. Все такие алгоритмы работают за (O(n)). И даже можно понять, что быстрее, чем (O(n)) решить ни одну из этих задач не получится.

Задание

Убедитесь, что вы умеете решать эти задачи. Докажите, что быстрее, чем O(n) их решить в худшем случае нельзя.

Бинарный поиск

Однако иногда найти число X в массиве можно и быстрее! Для этого надо добавить условие на то, что массив отсортирован. Но давайте начнем не с этого.

Задание

Я загадал число X от 1 до 100. Вы можете спрашивать, больше ли мое число чем число T, я отвечаю “да” или “нет”. За сколько вопросов в худшем случае вы сможете найти число X? Как нужно действовать?

Решение и состоит в идее бинарного (двоичного) поиска — нужно первым вопросом спросить “число X больше, чем 50?”. После этого, если ответ “нет”, надо спросить “число X больше, чем 25”? И так далее, нужно уменьшать отрезок возможных значений в два раза каждый раз.

Почему нужно делить обязательно пополам? Почему бы не спросить “число X больше, чем 80?” первым же вопросом? Но если вдруг ответ “нет”, то мы останемся с 80 вариантами вместо 100. То есть деление отрезка ровно пополам гарантирует, что в худшем случае мы останемся не более чем с половиной вариантов.

Чтобы понять, как быстро это работает, введём новую математическую функцию. Логарифмом по основанию (a) от (b) будем называть число (c), такое что (a ^ c = b). Обозначается как (log_a b = c). Чаще всего мы будем работать с двоичным логарифмом, то есть в какую степень (c) нужно возвести двойку, чтобы получить (b). Поэтому договоримся, что запись (log n) означает двочный логарифм (n).

Теперь вернёмся к нашей задаче. Можно понять, что такой алгоритм работает как раз за (O(log n)) вопросов (если число 100 на заменить абстрактную переменную (n)). Несложно убедиться, что именно логарифм раз нужно поделить число на два, чтобы получилось 1.

Общий принцип

А теперь представьте такую задачу: у вас есть массив, состоящий из некоторого количества подряд идущих нулей, за которыми следует какое-то количество подряд идущих единиц.

a = [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
n = len(a)
n

Вам дан массив, и вам нужно найти позицию первой единицы, то есть найти такое место, где заканчиваются нули, и начинаются единицы. Это можно сделать с помощью линейного поиска за один проход по массиву, но хочется сделать это быстрее.

Давайте обратимся к идее бинарного поиска. Посмотрим на элемент посередине массива. Если это нуль, то первую единицу стоит искать в правой половину массива, а если единица — то в левой.

Есть много способов писать бинарный поиск, и в его написании люди очень часто путаются. Очень удобно в данном случае воспользоваться инвариантом (это слово значит “постоянное свойство”):

Пусть переменная left всегда указывает на (0) в массиве, а переменная right всегда указывает на (1) в массиве.

Дальше мы будем переменные left и right постепенно сдвигать друг к другу, и в какой-то момент они станут соседними числами. Это и будет означать, что мы нашли место, где заканчиваются нули и начинаются единицы.

Чему равны left и right изначально, когда мы ничего про массив не знаем? Первая приходящая в голову идея — поставить их на (0) и (n-1) соответственно. Увы, в общем случае это может быть неверно, потому что a[0] может быть единицей, а a[n-1] может быть нулём. Правильнее сделать вот так:

left = -1
right = n

То есть изначально left и right указывают на несуществующие индексы. Но это нормально — например в массиве [1, 1, 1, 1] в конце алгоритма как раз должно быть left == -1, right == 0.

Осталось нам написать цикл while:

while right - left > 1:
    middle = (left + right) // 2 # именно такая формула для среднего индекса между left и right
    if a[middle] == 1:
        right = middle # right всегда должна указывать на 1
    else:
        left = middle # left всегда должна указывать на 0
print left, right
print a[left], a[right]

8 9
0 1

Мы решили задачу для ноликов и единичек, но это легко обобщается на абсолютно любую задачу, где есть какое-то свойство, которое в начале массива не выполняется, а потом выполняется.

Например, если мы хотим найти, есть ли число (X) в отсортированном массиве, то мы просто представим, что (0) — это числа, меньшие (X), а (1) — это числа, большие или равные (X). Тогда достаточно найти первую “единицу” и проверить, равно ли это число (X).

a = [1, 3, 4, 10, 10, 10, 11, 80, 80, 81] # отсортированный массив
def bin_search(a, x):
    n = len(a)
    left = -1
    right = n
    while right - left > 1:
        middle = (left + right) // 2
        if a[middle] >= x: # практически единственная строка, которая меняется от задачи к задаче
            right = middle
        else:
            left = middle
    if right != n and a[right] == x: # ответ лежит в right
        return True
    else:
        return False

print (bin_search(a, 1))
print (bin_search(a, 10))
print (bin_search(a, 20))
print (bin_search(a, 79))
print (bin_search(a, 80))
print (bin_search(a, 81)

True
True
False
False
True
True

Задание

Придумайте, как с помощью бинарного поиска решить такие задачи: * Найти первое число, равное X в отсортированном массиве, или вывести, что таких чисел нет * Найти последнее число, равное X в отсортированном массиве, или вывести, что таких чисел нет * Посчитать, сколько раз встречается число X в отсортированном массиве (в решении помогают два предыдущих пункта) * Дан массив чисел, первая часть состоит из нечетных чисел, а вторая — из четных. Найти индекс, начиная с которого все числа четные.

Все эти задачи решаются бинарным поиском за (O(log{n})). Правда нужно понимать, что в чистом виде такую задачу решать двоичным поиском бессмысленно — ведь чтобы создать массив размера (n), уже необходимо потратить (O(n)) операций.

Поэтому зачастую такие задачи сформулированы таким образом:

Дан отсортированный массив размера (n). Нужно ответить на (m) запросов вида “встречается ли число (x_i) в массиве n”?

Задание

Найдите время работы, за которое решается эта задача?

Решение: Такая задача решается за (O(n + mlog{n})) — нужно создать массив за (O(n)) и (m) раз запустить бинарный поиск.

Задание

Решите 3 первые задачи в этом контесте:

https://informatics.msk.ru/moodle/mod/statements/view.php?id=33216

Бинарный поиск с вещественными числами

У нас все еще есть функция f(x), которая сначала равна 0, а потом равна 1, и мы хотим найти это место, где она меняет значение. Но теперь аргумент функции — вещественное число. Например: * (f(x) = 1), если (x^2 > 2) * (f(x) = 0), если (x^2 leq 2)

Понятно, что при (x = sqrt 2) (f(x) = 0), а при любом даже немного большем значении (f(x) = 1). Если мы научимся решать такую задачу, то мы научимся находить корень из двух!

Увы, возникает проблема: действительные числа хранятся в компьютере неточно

# известный пример
0.1 + 0.1 + 0.1

0.30000000000000004

Тем более не сможем найти точное значение (sqrt 2), потому что это бесконечная непериодическая дробь. Так что давайте снова воспользуемся бинарным поиском, причем всегда (f(left) = 0), (f(right) = 1), и мы остановимся тогда, когда left и right будет очень-очень близко.

И тут снова возникает проблема. Помимо того, что бесконечную дробь в принципе невозможно точно хранить в компьютере, ещё и арифметические операции понижают эту точность. Поэтому, чтобы явно не использовать разность между правым и левым указателем, можно задать фиксированное число шагов, которое будет выполняться.

Так как мы знаем, что двоичный поиск работает за двоичный логарифм, можно сказать, что на угадывание десятичного разряда числа потребуется примерно три шага бинпоиска (т. к. $ $). Значит, например, если нам нужно посчитать значение функции до шести знаков после запятой, то нам нужно ещё примерно 18 шагов уже после того, как расстояние между left и right достигло одного.

Чтобы каждый раз об этом не думать, можно считать, что ста шагов бинпоиска хватит для почти любых разумных целей.

left = 0.0 # 0^2 < 2, а значит f(0) = 0
right = 10.0 # 10^2 > 2, а значит f(10) = 1
for i in range(100):
    middle = (left + right) / 2 # теперь деление не нацело, а вещественное
    if middle ** 2 > 2:
        right = middle # right всегда должна указывать на 1
    else:
        left = middle # left всегда должна указывать на 0
print left, right
print left ** 2, right ** 2

1.41421356237 1.41421356237
2.0 2.0

Вот мы и нашли корень из 2 с достаточно высокой точностью.

На самом деле, так можно искать ноль любой непрерывной функции (мы сейчас искали ноль функции (x^2 — 2)), у которой вы знаете значение меньше нуля и значение больше нуля.

Задание

Придумайте, как с помощью вещественного бинпоиска найти * (sqrt[leftroot{-2}uproot{2}17]{1000}) * какой-нибудь корень уравнения (x^4 + 3x = 5)

Поиск максимума выпуклой функции: тернарный поиск, бинарный поиск

Так мы только что научились находить корень непрерывной функции, у которой мы знаем значение меньше и больше 0. Но можно ли найти с помощью бинарного поиска локальный максимум функции? Можно!

Как известно, локальный максимум функции (f) — это просто такое (x_0), что для всех близких к нему (x) значения (f(x) < f(x_0)). Для непрерывных функций выполняется более крутая вещь: слева от максимума функция возрастает, а справа от максимума функция убывает. Так это как раз отличное условие для нашего вещественного бинарного поиска!

Если вы знаете (x_1) такое, что в его окрестности f(x) возрастает, и (x_2) такое, что в его окрестности f(x) убывает, то можно запустить между ними бинпоиск и найти точку (x_0) такую, что слева от нее возрастает значение функции, а справа — убывает. Это и есть локальный максимум.

А если функция выпуклая, то она вообще выглядит красиво: сначала возрастает, потом максимум, потом убывает.

Проблема только в одном: как по точке понять, в ее окрестности значение функции убывает или возрастает? Достаточно тыкнуть две точки очень-очень рядом с ней и сравнить их значения!

Задание

Придумайте, как с помощью вещественного бинпоиска найти * максимум функции (x — e^x) (она выпуклая, и максимум ровно один) * какой-нибудь локальный максимум функции (31x+x^3-x^4)

Тернарный поиск

Другой способ искать максимум — это тернарный поиск. Пусть известно, что максимум находится между left и right. Поделим отрезок на три равные части: * middle_left = (2 * left + right) / 3 * middle_right = (left + 2 * right) / 3

Тогда если f(middle_left) < f(middle_right), то можно спокойно заменить left на middle_left (максимум точно не левее middle_left), а если f(middle_left) > f(middle_right), то можно спокойно заменить right на middle_right. Он будет работать не за двоичный логарифм, а за логарифм по основанию полтора, что больше (но асимптотически то же самое, так как отличается в константу раз).

Оба способа работают быстро, и обобщаются на дискретный случай (то, что было в начале — когда дан массив, значения в котором сначала возрастают, а потом убывают). Но проблема есть в том, что если функция нестрого возрастает и нестрого убывает, а именно если там есть отрезки постоянства, то алгоритм не работает. В случае, когда значения функции равны, никак нельзя понять, с какой стороны искать максимум — он может быть с любой стороны.

Задание

Решите 4 и 5 задачи в этом контесте:

https://informatics.msk.ru/moodle/mod/statements/view.php?id=33216

Бинарный поиск по неотсортированному массиву

Заметьте, что в первоначальной задаче условие на то, что сначала идут нули, а потом идут единицы несущественно. Главное, чтобы мы знали индекс, который показывает на 0, и индекс, который показывает на 1. После этого бинарным поиском мы таким же способом найдем пару соседних нуля и единицы в массиве.

Поэтому бинарный поиск работает и не для возрастающих массивов / функций, если наша задача состоит именно в поиске двух соседних индексов, в которых условие выполняется и не выполняется.

Например, если мы знаем, что (f(x_0) < 0) и (f(x_1) > 0), и функция непрерывная, то бинарным поиском можно найти ноль этой функции между (x_0) и (x_1), даже если функция не монотонная!

Или, например, если нужно в массиве найти соседние четное и нечетное числа, и известно положение какого-то четного числа и какого-то нечетного числа, то это тоже можно легко сделать с помощью бинарного поиска.

Полезно иметь это в виду, это применяется в нескольких задачах контестов.

Бинарный поиск по ответу

Рассмотрим такую задачу:

Пример: “Корова в стойла”

Условие: На прямой расположены N стойл (даны их координаты на прямой), в которые необходимо расставить K коров так, чтобы минимальное расcтояние между коровами было как можно больше. Гарантируется, что (1 < K < N).

Решение:

Если решать задачу в лоб, то вообще неясно что делать. Нужно решать обратную задачу: давайте предположим, что мы знаем это расстояние X, ближе которого коров ставить нельзя. Тогда сможем ли мы расставить самих коров?

Ответ — да, можно ставить их довольно просто: самую первую ставим в самое левое стойло, это всегда выгодно. Следующие несколько стойл надо оставить пустыми, если они на расстоянии меньше X. В самое левое стойло из оставшихся надо поставить вторую корову и так далее. Даже ясно как это писать: надо идти слева направо по отсортированному массиву стойл, хранить координату последней коровы, и либо пропускать стойло, либо ставить в него новую корову.

То есть если мы знаем расстояние X, то мы можем за O(n) проверить, можно ли расставить K коров на таком расстоянии. Ну так давайте запустим бинпоиск по X, ведь при слишком маленьком X коров точно можно расставить, а при слишком большом — нельзя, и как раз эту границу и просят найти в задаче (“как можно больше”).

Осталось точно определить границы, то есть изначальные значения left и right. Нам точно хватит расстояния 0, так как гарантируется, что коров меньше, чем стойл. И точно не хватит расстояния max_coord — min_coord + 1, так как по условию есть хотя бы 2 коровы.

coords = [2, 5, 7, 11, 15, 20] # координаты стойл
k = 3 # число коров

def is_correct(x): # проверяем, можно ли поставить K коров в стойла, если между коровами расстояние хотя бы x
    cows = 1
    last_cow = coords[0]
    for c in coords:
        if c - last_cow >= x:
            cows += 1
            last_cow = c
    return cows >= k

left = 0 # расставить коров на расстоянии хотя бы 0 можно всегда
right = max(coords) - min(coords) + 1 # при таком расстоянии даже 2 коровы поставить нельзя
while right - left != 1:
    middle = (left + right) // 2
    if is_correct(middle): # проверяем, можно ли поставить K коров в стойла, если между коровами расстояние хотя бы middle
        left = middle # left всегда должна указывать на ситуацию, когда можно поставить коров
    else:
        right = middle # right всегда должна указывать на ситуацию, когда нельзя поставить коров
print left # left - максимальное расстояние, на котором можно расставить коров в стойла

Общий принцип

Такой метод и называется бинпоиск по ответу. Он очень важный и очень распространен на олимпиадах, очень рекомендую решать на него задачи.

По сути мы просто взяли задачу “найдите максимальное X, такое что какое-то свойство от X выполняется” и решили её бинпоиском. Самое сложное — увидеть такую формулировку в задаче. Поэтому рассмотрим еще один пример.

Пример: “Очень Легкая Задача”

Условие: есть два принтера, один печатает лист раз в (x) минут, другой раз в (y) минут. За сколько минут они напечатают (N) листов? (N > 0)

Решение: Здесь, в отличие от предыдущей задачи, кажется, существует прямое решение с формулой. Но вместо того, чтобы о нем думать, можно просто свести задачу к обратной. Давайте подумаем, как по числу минут (T) (ответу) понять, сколько листов напечатается за это время? Очень легко: [lfloorfrac{T}{x}rfloor + lfloorfrac{T}{y}rfloor]

Ясно, что за (0) минут (N) листов распечатать нельзя, а за (xN) минут один только первый принтер успеет напечатать (N) листов. Поэтому (0) и (xN) — это подходящие первые границы для бинарного поиска.

Примечание: заметьте, что задача в контесте немного отличается! Прочитайте внимательно условие.

Задание

Решите как можно больше задач в практическом контесте:

https://informatics.msk.ru/mod/statements/view.php?id=34097

Там могут встречаться задачи как на бинпоиск по ответу, так и на тернарный поиск по ответу.

Источник

Случайное число:

Проводите розыгрыш во ВКонтакте?
Мы поможем определить победителя!

новую последовательность из

из диапазона или из списка

отдо

исключить числа

исключить повторения

Записать видео генерации

Приложение во ВКонтакте

Виджет ГСЧ на сайт

Вы можете добавить виджет генератора случайных чисел себе на сайт, просто разместив код:

Пример работы виджета: https://codepen.io/pit69/pen/dyKyGQG

Страница с результатом сохранена по ссылке: и будет доступна в течении часа с момента генерации. По прошествии этого времени страница будет удалена.
Но вы можете навсегда сохранить результат этой генерации. Стоимость сохранения — 150 рублей.

Источник

Если известно сколько составляет часть от целого, то по известной части можно «восстановить»
целое.

Для этого пользуемся правилом нахождения целого (числа)
по его дроби (части).

Запомните!

Чтобы найти число по его части, выраженной дробью, нужно данное число
разделить на дробь.

Пример. Рассмотрим задачу.

Поезд прошёл 240 км, что составило
всего пути.
Какой путь должен пройти поезд?

Решение. 240 км — часть всего пути. Эти же километры
выражены дробью 15/23
от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части,
и 15 таких частей составляют 240 км
(числитель дроби равен 15).
Значит, можно найти, сколько составляет

часть пути.

240 : 15 = 16 (км)

Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью

Значит, чтобы найти весь путь (23 части, каждая из которых по
16 км) нужно:

16 · 23 = 368 (км)

Кратко запись решения такой задачи можно сделать следующим образом.

Ответ: поезд должен пройти 368 км.

Сложные задачи на нахождение числа по его части

Часто задачи данного типа сложнее, чем рассмотренная задача выше, и более сложные задачи приходиться решать в
несколько действий.

Рассмотрим задачу.

При подготовке к диктанту по английскому языку Оля
выучила четверть всех слов, заданных учителем.
Если бы она выучила ещё 4 слова, то была
бы выучена треть всех слов.
Сколько всего слов надо было выучить Оле?

Решение. Как обычно подчеркнём в условии задачи все важные данные.

Как видно из условия, четыре невыученных слова — это часть от всех слов, которую можно найти в виде
разности дробей.

Такую часть всех слов составляют 4 слова.

Итак, 4 слова — это

от всех слов (целого). Теперь по правилу нахождения
числа по его части данное числовое значение разделим на соответствующую ему дробь

Ответ: всего 48 слов надо было выучить к диктанту.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Время на прочтение
6 мин

Количество просмотров 35K

Представьте, что вам нужно сгенерировать равномерно распределённое случайное число от 1 до 10. То есть целое число от 1 до 10 включительно, с равной вероятностью (10%) появления каждого. Но, скажем, без доступа к монетам, компьютерам, радиоактивному материалу или другим подобным источникам (псевдо) случайных чисел. У вас есть только комната с людьми.

Предположим, что в этой комнате чуть более 8500 студентов.

Самое простое — попросить кого-нибудь: «Эй, выбери случайное число от одного до десяти!». Человек отвечает: «Семь!». Отлично! Теперь у вас есть число. Однако вы начинаете задаваться вопросом, является ли оно равномерно распределённым?

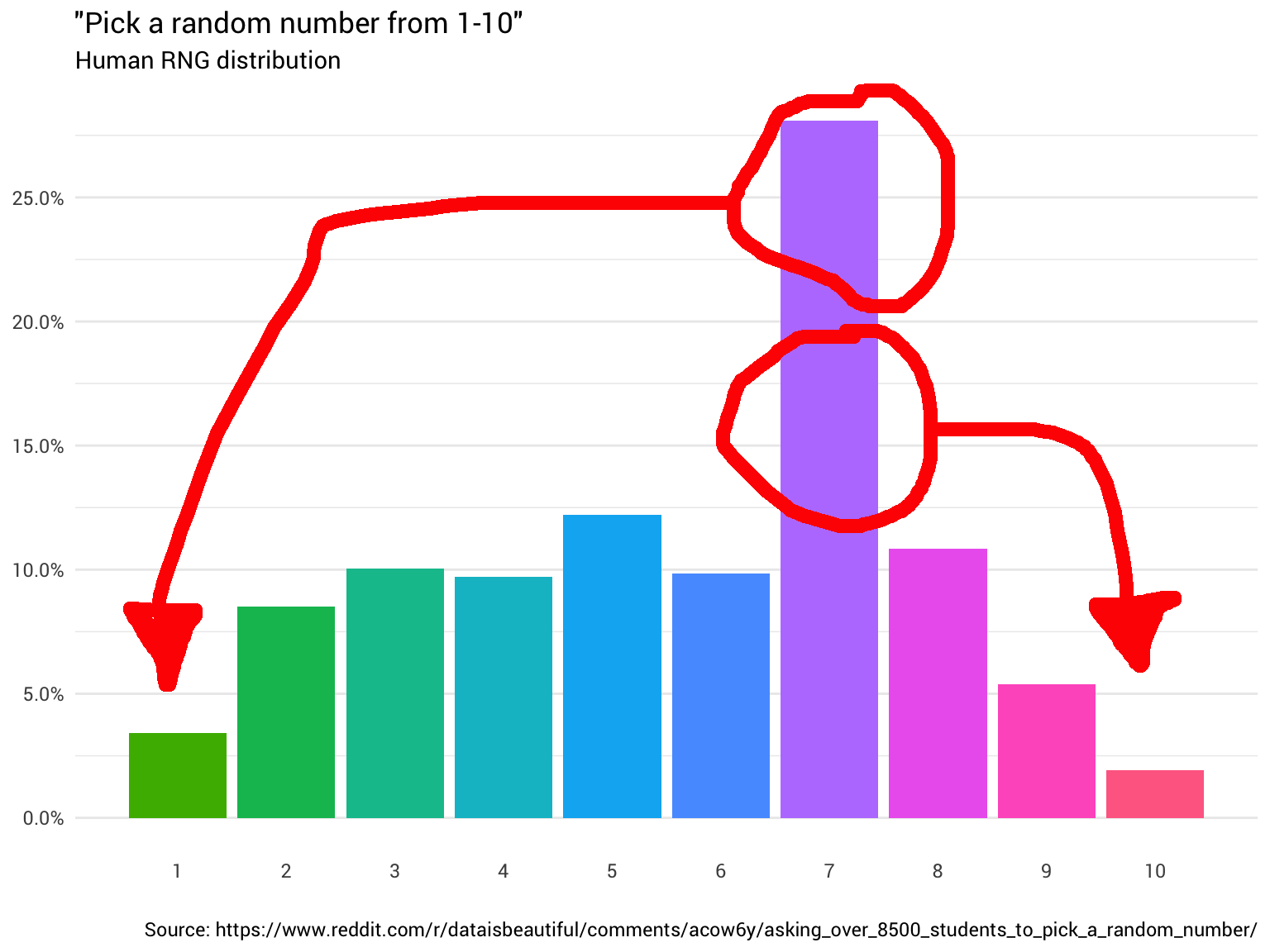
Поэтому вы решили спросить ещё несколько человек. Вы продолжаете их спрашивать и считать их ответы, округляя дробные числа и игнорируя тех, кто думает, что диапазон от 1 до 10 включает 0. В конце концов вы начинаете видеть, что распределение вообще не равномерное:

library(tidyverse)

probabilities <-
  read_csv("https://git.io/fjoZ2") %>%
  count(outcome = round(pick_a_random_number_from_1_10)) %>%
  filter(!is.na(outcome),
         outcome != 0) %>%
  mutate(p = n / sum(n))

probabilities %>%
  ggplot(aes(x = outcome, y = p)) +
  geom_col(aes(fill = as.factor(outcome))) +
  scale_x_continuous(breaks = 1:10) +
  scale_y_continuous(labels = scales::percent_format(),
                     breaks = seq(0, 1, 0.05)) +
  scale_fill_discrete(h = c(120, 360)) +
  theme_minimal(base_family = "Roboto") +
  theme(legend.position = "none",
        panel.grid.major.x = element_blank(),
        panel.grid.minor.x = element_blank()) +
  labs(title = '"Pick a random number from 1-10"',
       subtitle = "Human RNG distribution",
       x = "",
       y = NULL,
       caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/")

Данные с Reddit

Вы хлопаете себя по лбу. Ну конечно, оно не будет случайным. В конце концов, нельзя доверять людям.

Итак, что делать?

Вот бы найти какую-то функцию, которая преобразует распределение «человеческого ГСЧ» в равномерное распределение…

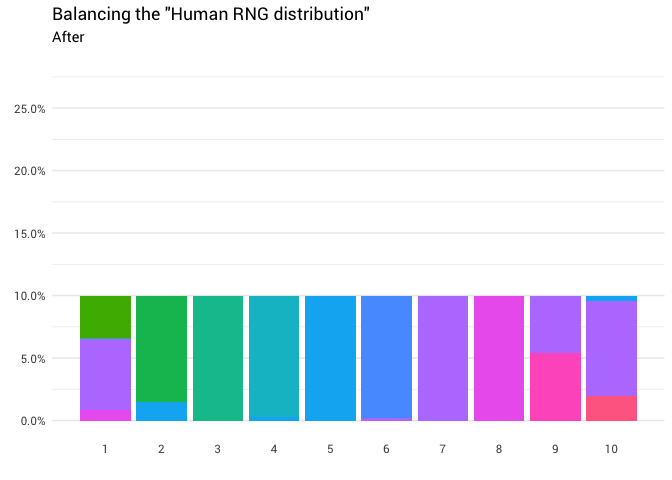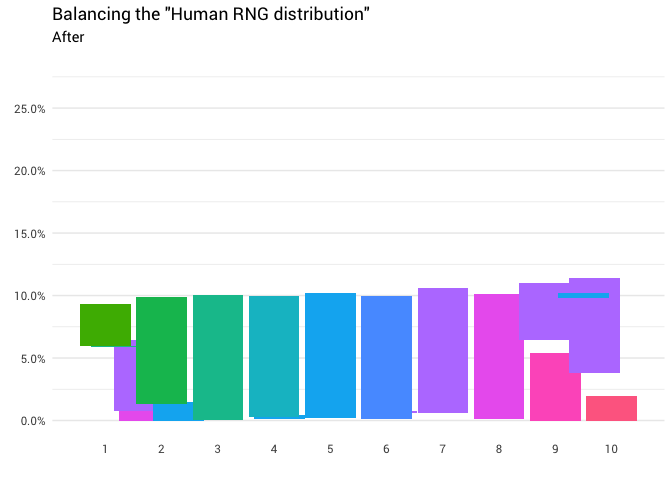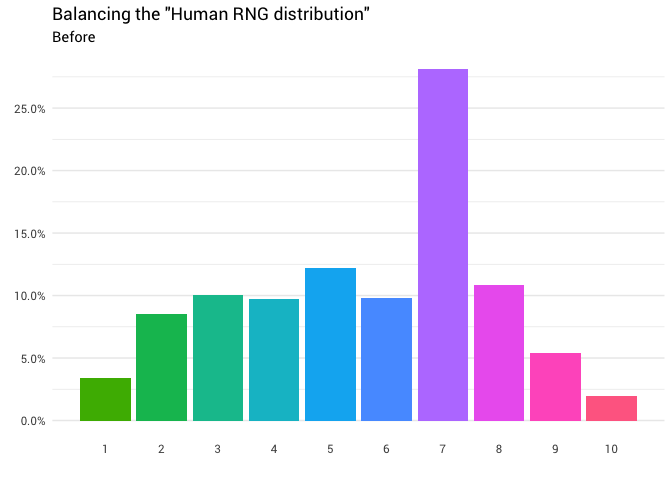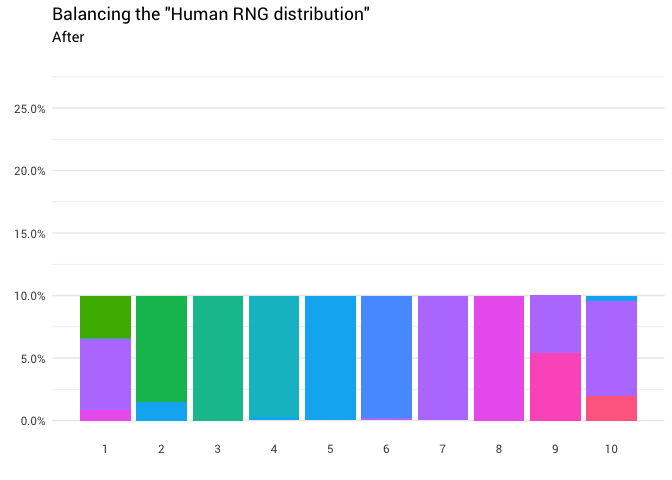
Интуиция тут относительно проста. Нужно всего лишь взять массу распределения оттуда, где она выше 10%, и переместить туда, где она меньше 10%. Так, чтобы все столбцы на графике были одного уровня:

По идее, такая функция должна существовать. Фактически, должно быть много различных функций (для перестановки). В крайнем случае, можно «разрезать» каждый столбец на бесконечно малые блоки и построить распределение любой формы (как кирпичики Lego).

Конечно, такой экстремальный пример немного громоздок. В идеале мы хотим сохранить как можно больше исходного распределения (т. е. сделать как можно меньше измельчений и перемещений).

Как найти такую функцию?

Ну, наше объяснение выше звучит очень похоже на линейное программирование. Из Википедии:

Линейное программирование (LP, также именуется линейной оптимизацией) — метод достижения наилучшего результата… в математической модели, требования которой представлены линейными отношениями… Стандартная форма представляет собой обычную и наиболее интуитивную форму описания задачи линейного программирования. Она состоит из трёх частей:

Линейная функция, которую необходимо максимизировать
Проблемные ограничения следующей формы
Неотрицательные переменные

Аналогично можно сформулировать и проблему перераспределения.

Представление проблемы

У нас есть набор переменных

$(x_{i,j}$ , каждая из которых кодирует долю вероятности, перераспределённую от целого числа

$i$ (от 1 до 10) к целому числу

$j$ (от 1 до 10). Поэтому, если

$(x_{7,1} = 0.2$ , то нам нужно перенести 20% ответов от семёрки к единице.

variables <-
  crossing(from = probabilities$outcome,
           to   = probabilities$outcome) %>%
  mutate(name = glue::glue("x({from},{to})"),
         ix = row_number())

variables

## # A tibble: 100 x 4
##     from    to name       ix
##    <dbl> <dbl> <glue>  <int>
##  1     1     1 x(1,1)      1
##  2     1     2 x(1,2)      2
##  3     1     3 x(1,3)      3
##  4     1     4 x(1,4)      4
##  5     1     5 x(1,5)      5
##  6     1     6 x(1,6)      6
##  7     1     7 x(1,7)      7
##  8     1     8 x(1,8)      8
##  9     1     9 x(1,9)      9
## 10     1    10 x(1,10)    10
## # … with 90 more rows

Мы хотим ограничить эти переменные таким образом, чтобы все перераспределённые вероятности суммировались в 10%. Другими словами, для каждого

$j$ от 1 до 10:

$x_{1, j} + x_{2, j} + ldots x_{10, j} = 0.1$

Можем представить эти ограничения в виде списка массивов в R. Позже свяжем их в матрицу.

fill_array <- function(indices,
                       weights,
                       dimensions = c(1, max(variables$ix))) {
  init <- array(0, dim = dimensions)

  if (length(weights) == 1) {
    weights <- rep_len(1, length(indices))
  }

  reduce2(indices, weights, function(a, i, v) {
    a[1, i] <- v
    a
  }, .init = init)
}

constrain_uniform_output <-
  probabilities %>%
  pmap(function(outcome, p, ...) {
    x <-
      variables %>%
      filter(to == outcome) %>%
      left_join(probabilities, by = c("from" = "outcome"))

    fill_array(x$ix, x$p)
  })

Мы также должны убедиться, что сохраняется вся масса вероятностей из исходного распределения. Так что для каждого

$j$ в диапазоне от 1 до 10:

$x_{1, j} + x_{2, j} + ldots x_{10, j} = 0.1$

one_hot <- partial(fill_array, weights = 1)

constrain_original_conserved <-
  probabilities %>%
  pmap(function(outcome, p, ...) {
    variables %>%
      filter(from == outcome) %>%
      pull(ix) %>%
      one_hot()
  })

Как уже говорилось, мы хотим максимизировать сохранение исходного распределения. Это наша цель (objective):

$maximise (x_{1, 1} + x_{2, 2} + ldots x_{10, 10})$

maximise_original_distribution_reuse <-
  probabilities %>%
  pmap(function(outcome, p, ...) {
    variables %>%
      filter(from == outcome,
             to == outcome) %>%
      pull(ix) %>%
      one_hot()
  })

objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums()

Затем передаём проблему солверу, например, пакету lpSolve в R, объединив созданные ограничения в одну матрицу:

# Make results reproducible...
set.seed(23756434)

solved <- lpSolve::lp(
  direction    = "max",
  objective.in = objective,
  const.mat    = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)),
  const.dir    = c(rep_len("==", length(constrain_original_conserved)),
                   rep_len("==", length(constrain_uniform_output))),
  const.rhs    = c(rep_len(1, length(constrain_original_conserved)),
                   rep_len(1 / nrow(probabilities), length(constrain_uniform_output)))
)

balanced_probabilities <-
  variables %>%
  mutate(p = solved$solution) %>%
  left_join(probabilities,
            by = c("from" = "outcome"),
            suffix = c("_redistributed", "_original"))

Возвращается следующее перераспределение:

library(gganimate)

redistribute_anim <-
  bind_rows(balanced_probabilities %>%
            mutate(key   = from,
                   state = "Before"),
            balanced_probabilities %>%
            mutate(key   = to,
                   state = "After")) %>%
  ggplot(aes(x = key, y = p_redistributed * p_original)) +
  geom_col(aes(fill = as.factor(from)),
           position = position_stack()) +
  scale_x_continuous(breaks = 1:10) +
  scale_y_continuous(labels = scales::percent_format(),
                     breaks = seq(0, 1, 0.05)) +
  scale_fill_discrete(h = c(120, 360)) +
  theme_minimal(base_family = "Roboto") +
  theme(legend.position = "none",
        panel.grid.major.x = element_blank(),
        panel.grid.minor.x = element_blank()) +
  labs(title = 'Balancing the "Human RNG distribution"',
       subtitle = "{closest_state}",
       x = "",
       y = NULL) +
  transition_states(
    state,
    transition_length = 4,
    state_length = 3
  ) +
  ease_aes('cubic-in-out')

animate(
  redistribute_anim,
  start_pause = 8,
  end_pause = 8
)

Отлично! Теперь у нас есть функция перераспределения. Давайте поближе посмотрим, как именно движется масса:

balanced_probabilities %>%
  ggplot(aes(x = from, y = to)) +
  geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) +
  geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) +
  scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) +
  scale_fill_discrete(h = c(120, 360)) +
  scale_x_continuous(breaks = 1:10) +
  scale_y_continuous(breaks = 1:10) +
  theme_minimal(base_family = "Roboto") +
  theme(panel.grid.minor = element_blank(),
        panel.grid.major = element_line(linetype = "dotted"),
        legend.position = "none") +
  labs(title = "Probability mass redistribution",
       x = "Original number",
       y = "Redistributed number")

Эта диаграмма говорит, что примерно в 8% случаев, когда кто-то называет восемь в качестве случайного числа, вам нужно воспринимать ответ как единицу. В остальных 92% случаев он остаётся восьмёркой.

Было бы довольно просто решить задачу, если бы у нас был доступ к генератору равномерно распределённых случайных чисел (от 0 до 1). Но у нас только комната, полная людей. К счастью, если вы готовы примириться с несколькими небольшими неточностями, то из людей можно сделать довольно хороший ГСЧ, не спрашивая более двух раз.

Возвращаясь к нашему исходному распределению, у нас есть следующие вероятности для каждого числа, которые можно использовать для повторного назначения любой вероятности, если необходимо.

probabilities %>%
  transmute(number = outcome,
            probability = scales::percent(p))

## # A tibble: 10 x 2
##    number probability
##     <dbl> <chr>
##  1      1 3.4%
##  2      2 8.5%
##  3      3 10.0%
##  4      4 9.7%
##  5      5 12.2%
##  6      6 9.8%
##  7      7 28.1%
##  8      8 10.9%
##  9      9 5.4%
## 10     10 1.9%

Например, когда кто-то даёт нам восемь в качестве случайного числа, нужно определить, должна ли эта восьмёрка стать единицей или нет (вероятность 8%). Если мы спросим другого человека о случайном числе, то с вероятностью 8,5% он ответит «два». Так что если это второе число равно 2, мы знаем, что должны вернуть 1 как равномерно распределённое случайное число.

Распространив эту логику на все числа, получаем следующий алгоритм:

По этому алгоритму вы можете использовать группу людей для получения чего-то близкого к генератору равномерно распределённых случайных чисел от 1 до 10!

Источник