В этой статье мы увидим, как найти магнитный поток через одиночный контур и проводник с током с числом витков.
Магнитный поток обозначается как произведение магнитного поля, в котором находится материал, и площади, через которую проходит магнитный поток, и определяется соотношением
Как найти плотность магнитного потока?
Наблюдения и советы этой статьи мы подготовили на основании опыта команды магнитный поток Плотность определяется как общее количество линий магнитного потока, пронизывающих единицу площади поверхности материала.
Магнитный поток можно рассчитать, найдя общий поток через проводящий материал и площадь материала, через которую магнитный поток проникает через поверхность.
Магнитный поток через поверхность равен
Следовательно плотность магнитного потока становится магнитным потоком через единицу площади поверхности.
Плотность магнитного потока представляет собой отношение магнитного потока к площади поперечного сечения, через которое проходят силовые линии.
Как найти размер магнитного потока?
Размерность — это математический способ выражения единиц измерения измеряемой величины в простой фигуре.
Размерность магнитного потока можно определить по формуле зная размерность магнитного поля и площадь через которые проходят силовые линии магнитного поля.
Магнитное поле определяется как сила, действующая на заряженную частицу в присутствии магнитного поля скоростью и магнитным потоком через частицу, и, соответственно, размерность магнитного поля основана на размерностях этих величин.
Мы можем математически представить единицу магнитного поля, записав все величины в размерном формате. Сила, действующая на заряды из-за комбинации электрического и магнитного полей, равна
F=qVB
Итак, магнитное поле, в котором находится материал, равно
F=qVB
Теперь нам нужно найти, как мы можем представить эти термины в форме математического измерения.
Мы знаем, что сила определяется как ускорение объекта, когда к нему приложена внешняя сила, в зависимости от массы объекта, поэтому согласно второму закону движения Ньютона мы можем написать F = ma
Единицей ускорения является метр на квадрат времени, поэтому мы можем записать размерность ускорения как M0L1T-2 а единицей массы является кг только соответственно мы можем записать размерность массы как M0L1T-2 что равно М1
Следовательно, размерность магнитная сила is
Ф=М*(М0L1T-2)
Ф = М1L1T-2
Точно так же размерность скорости равна M0L1T-2 так как единица скорости м/с, а заряда М0L1T-2 как I=dQ/dt
Теперь, используя это измерение, мы можем найти размеры магнитного поля как
Б=Ф/кV
Б=М1L1T-2
Магнитный поток является произведением магнитного поля и площади материала, поэтому
Ø=BACosΘ
Θ — безразмерная величина, поэтому ею можно пренебречь и рассматривать размерности остаточных величин.
Ø=[М1L0I-1T-2]*[М0L2T0]
Ø=М1L2-1T-2
Это размер магнитного потока, представленный математически.
Как найти магнитный поток через контур?
Основываясь на направлении магнитного потока, мы можем найти чистое магнитное поле через материал.
Магнитное поле, образованное колеблющимися зарядами в материале, можно рассчитать по всей площади контура и, таким образом, найти магнитный поток через эту площадь.
Рассмотрим круглую петлю радиуса «R» и ток I, протекающий через эту круглую петлю. Пусть начало круга будет «О». Заряд помещен в точку «P», которая находится на расстоянии «x» от начала координат на плоскости оси x. Между линией, соединяющей частицу с началом координат, и контуром с током образуется угол θ.
Пусть dl — малый элемент круглой петли, по которой течет ток I. Магнитное поле через малый элемент dl на круглой петле от заряда, помещенного в точку P, равно
Где мк0/4π – константа пропорциональности, равная 10-7Тм/А
дБ=мк0/4π*IdlrSinθ/r3
дБ=мк0/4π*IdlrSinθ/r2
Направление dB перпендикулярно dl и r, и перпендикулярное магнитное поле компенсируется.
дБ=мк0/4π*холост./об2
Здесь, р2=R2+x2 следовательно, мы можем написать то же уравнение, что и
дБ=мк0/4π*холост./R2+x2
Чистое магнитное поле обусловлено x-компонентой магнитного поля, то есть
дБх=дБКосθ
Поскольку,
Cosθ=R/√x2+R2
Подставляя рассчитанные значения в приведенное выше уравнение, мы получаем
дБх=мк0/4π*IdlR/(R2+x2)3/2
Это уравнение для магнитного поля через небольшой элемент dl на круглом контуре. Теперь найдем магнитное поле на всем контуре.
Bx=∫дБx= μ0/4π∫IdlR/(R2+x2)3/2
Bx= μ0/4π*lR/(R2+x2)3/2∫дл
Bx= μ0/4π*lR/(R2+x2)3/2L
Длина — это полная длина окружности круглой петли, L = 2πR.
Вставка этого в приведенное выше уравнение
Bx= μ0/4π*lR/(R2+x2)3/2*2πr
Отсюда получаем,
Bx= μ0IR2/2((R2+x2)3/2
Если поле находится в центре петли, то x=0 и уравнение примет вид
B0= μ0я/2р
Это магнитное поле через контур, тогда магнитный поток равен
ф=ВА
φ=μ0I/2R*πR2
φ=μ0πIR/2
Это магнитный поток через круговой контур с током, если поле находится в центре контура.
Как найти магнитный поток из магнитного поля?
Линии магнитного потока показывают величину магнитного поля, проникающего через материал.
Линии магнитного поля, падающие на поверхность поперечного сечения материала, образующие определенный угол θ с нормалью к поверхности, дают магнитный поток через эту область.
Предположим, вы поместили проводящий материал площадью A в магнитное поле B так, что линия магнитного поля составляет угол θ с нормальной плоскостью поверхности материала, как показано на рисунке ниже.
Магнитный поток через этот материал будет скалярным произведением линий магнитного поля и площади материала, через которую проходят эти линии.
φ=ВА
φ=BACosθ
Таким образом, мы можем найти магнитный поток через материал от магнитного поля.
Как найти магнитный поток через соленоид?
Чтобы узнать магнитный поток через соленоид, мы должны будем вычислить напряженность магнитного поля через каждую катушку соленоида.
Мы можем определить магнитное поле соленоида, применив закон Био-Савара, который дает связь между током и магнитным полем. Рассчитав магнитное поле, мы можем рассчитать поток через площадь материала.
Рассмотрим цилиндрический соленоид длины ‘2l’ и радиуса ‘a’. Пусть «О» будет точкой в центре соленоида, которая делит соленоид на две половины. Пусть небольшой заряд присутствует в точке P на расстоянии «r» от центральной точки «O». Рассмотрим небольшой сегмент соленоида длиной «dx» на расстоянии «x» от центрального сегмента соленоида. Направление магнитного поля показано на рисунке ниже.
Магнитный поток через этот небольшой сегмент «dx» составляет дБ. Пусть соленоид состоит из n витков на единицу длины соленоида и, следовательно, магнитное поле через этот элемент dx равно
Интегрируя это уравнение, мы получим магнитное поле, создаваемое во всем соленоиде.
В осевом поле r>>a и r>>l тогда
[(прием)2+a2]3/2≅ г3
Следовательно, мы можем записать приведенное выше уравнение как
Магнитный момент m=NIA
Где N — число витков проводника с током вокруг соленоида, I — ток, а A — площадь соленоида.
Здесь количество витков по длине соленоида равно
N=n*2l=2nl
Магнитное поле входит с одной поверхности соленоида и выходит с другого конца.
Площадь, через которую проходит магнитный поток, равна A=πa2
Следовательно, магнитный момент равен
m=n*2l*I*πa2
Поэтому уравнение для магнитного поля мы можем записать в терминах магнитного момента как
В=мк0/4π*2м/р3
Теперь магнитный поток через соленоид равен
ɸ=БА
ɸ=μ0/4π*2м/р3* πа2
ɸ=μ0ma2/ 2r3
Это магнитный поток через соленоид.
Как рассчитать магнитную потокосцепление?
Связь магнитного потока наблюдается в трансформаторе и генераторах, где объединяются магнитные потоки разных контуров.
Связанный магнитный поток дает большое количество магнитного потока через материал. Если магнитный поток через один виток провода равен ɸ =БА тогда катушка, состоящая из n витков, будет давать чистый магнитный поток ɸ =nBA и член λ=nɸ называется утечкой магнитного потока.
Как рассчитать плотность магнитного потока катушки?
Плотность магнитного потока представляет собой полный магнитный поток, проходящий через материал на единицу его площади, и определяется соотношением B=ɸ/A
Плотность магнитного потока можно рассчитать, найдя полный магнитный поток, проникающий через единицу площади материала, находящегося в области магнитного поля.
Какова плотность магнитного потока через квадратный лист длиной 11.3 см, помещенный в область магнитного поля, если магнитный поток через лист равен 1 Вб?
Данный: л = 11.3 см = 0.113 м
ɸ=1Вб
Площадь квадратного листа, через который проходят силовые линии магнитного поля, равна
А=я2= 0.1132= 0.013 м2
У нас есть,
B= ɸ/A
= 76.92Т
B=1T.м2/ 0.013m2= 76.92Т
Следовательно магнитный поток плотность через квадратный лист составляет 76.92 Тл.
Часто задаваемые вопросы
Каков магнитный поток через прямоугольную поверхность длиной 5 см и шириной 2.8 см, помещенную в однородное магнитное поле силой 0.5 Тл, если магнитное поле образует угол 600 с нормалью поверхности?
Данный: л = 5 см = 0.05 м
б = 2.8 см = 0.028 м
В = 0.5 т
Θ = 600
Площадь прямоугольной поверхности равна
А=л*б
=0.05*0.028=0.0014 м2
У нас есть
ɸ=BACosθ
=0.5T* 0.0014 м2
=0.5Т*0.0014м2* 1/2
= 3.5 * 10-4Tm2
Магнитный поток через прямоугольный лист = 3.5*10-4Tm2
Чему равен магнитный поток через круглую петлю с током радиусом 7 см, если сила тока в проводнике равна 2 мА?
Данный: г = 7 см = 0.07 м
I=2 мА
Формула для расчета магнитного потока через круглую петлю имеет вид
ɸ=μ0πIr/2
Вставка заданных значений в это уравнение
ɸ=(4π*10-7Тм/А*π*2*10-3А*0.07м)/2
=4π*π*0.07*10-10Tm2
= 2.76 * 10-10Tm2
Следовательно, магнитный поток через круговой контур с током равен =2.76*10-10Tm2
Магнитный поток
Содержание:
-
Что такое магнитный поток
- В чем измеряется, обозначение и размерность
- От чего зависит величина основного магнитного потока
-
Чему равен магнитный поток, как найти
- Скорость изменения магнитного потока через контур
- Какой формулой определяется величина магнитного потока
- Связь магнитного потока и работы сил магнитного поля
Что такое магнитный поток
Магнитный поток — величина, характеризующая число магнитных силовых линий поля, проходящих через замкнутый контур.
Майкл Фарадей опытным путем пришел к выводу, что при любом соприкосновении проводника и магнитных линий по проводнику проходит заряд (triangle Q). Этот заряд прямо пропорционален количеству( triangle Ф) пересеченных линий и обратно пропорционален сопротивлению R контура. Пересечение линий вызывается или движением проводника, или изменением поля.
Позже, представляя замкнутый контур, в котором действует ЭДС индукции, Джеймс Клерк Максвелл подсчитывал количество силовых линий (triangle Ф), пересекаемых контуром за время (triangle t). Ф он при этом отождествлял с магнитным потоком сквозь всю поверхность.
В чем измеряется, обозначение и размерность
Единица измерения — вебер, сокращенно Вб. Он обозначается буквой Ф.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Размерность — выражение, демонстрирующее связь физической величины с другими величинами данной системы, разложение ее на сомножители из других величин.
Размерность магнитного потока — (В times с = кг times м^{2} times с^{-2} times А^{-1}.)
От чего зависит величина основного магнитного потока
Его можно изменить следующими способами:
- изменив площадь контура;
- изменив угол его наклона;
- изменив магнитное напряжение.
Чему равен магнитный поток, как найти
Магнитный поток в случае однородного магнитного поля равен произведению модуля индукции В этого поля, площади S плоской поверхности, через которую вычисляется поток, и косинуса угла (varphi) между направлением индукции В и нормали к данной поверхности.
Нормаль — перпендикуляр к плоскости контура.
Также поток можно вычислить через индуктивность, которая пропорциональна отношению полного, или суммарного потока к силе тока.
Обозначение суммарного потока — буква ( psi). Он равен сумме потоков, проходящих через всю поверхность. И в простом случае, где рассматриваются одинаковые потоки, проходящие через одинаковые витки катушки, и в случаях, когда поверхность имеет очень сложную форму, эта пропорциональность сохраняется.
Скорость изменения магнитного потока через контур
Закон электромагнитной индукции Фарадея в интегральном виде выглядит следующим образом:
(;underset С{oint;};(overrightarrow{Е;}times;doverrightarrow l) = — frac{1}{c}frac{d}{dt}int underset S{int;};(overrightarrow{B} times doverrightarrow{S}).)
Интеграл в левой части уравнения — циркуляция вектора (overrightarrow{Е;}) по замкнутому контуру С, это отражает знак интеграла, записанный с кругом. В правой части — скорость изменения потока Ф, который вычисляется как интеграл по поверхности S, «натянутой» на С.
Интеграл — целое, определяемое как сумма его бесконечно малых частей.
Если считать изменение потока в замкнутом контуре равномерным, то закон Фарадея примет следующий вид:
(epsilon_{i} = — frac{triangleФ}{triangle t}.)
Какой формулой определяется величина магнитного потока
Математически величину Ф описывают двумя формулами:
(Ф;=;sum_{triangle S};;Btriangle S = B times S times cosvarphi. )
Связь магнитного потока и работы сил магнитного поля
Герман Гельмгольц первым связал закон Фарадея и закон сохранения энергии. Возьмем проводник с током I, находящийся внутри однородного магнитного поля, которое перпендикулярно плоскости контура, и перемещающийся в нем. Под влиянием силы Ампера F проводник перемещается на отрезок dx. Сила F производит работу dA = IdФ.
Работу источника тока можно измерить, сложив работу на джоулеву теплоту и работу по перемещению проводника внутри поля:
(epsilon Idt = I^{2}Rdt + IdФ.)
(I = frac{epsilon — frac{dФ}{dt}}{R}.)
Насколько полезной была для вас статья?
Рейтинг: 4.40 (Голосов: 5)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Вероятно, термин «поток» ассоциируется у вас с потоком воды. Если бы вы хотели описать этот поток количественно, то имели бы в виду определенное количество воды, протекающей через поперечное сечение в определенной точке. Такой поток может нести большое или малое количество воды в зависимости от скорости воды и площади этого поперечного сечения.
Магнитный поток — это физическая величина, тесно связанная с явлением электромагнитной индукции. Это сложная величина, довольно абстрактная. Но, как вы правильно догадались, его название берет свое начало в гидродинамике. Здесь, однако, нет потока материи через поверхность, есть только векторы магнитной индукции B, «пронзающие» поверхность и иногда «скользящие» по ней.
Представьте себе однородное магнитное поле, описываемое вектором магнитной индукции B. Мы помещаем плоскую поверхность с полем S в это поле совершенно произвольным образом, то есть под любым углом по отношению к вектору B (рис. 1). Теперь определим вектор B, перпендикулярный плоскости поверхности. Пусть длина этого вектора равна величине поверхности.
Потоком вектора магнитной индукции ФB через поверхность S называется скалярное произведение векторов B и S.
Итак можно дать следующее определение термину «магнитный поток»:
Магнитный поток — это поток вектора магнитной индукции B через некоторую поверхность. Для бесконечно малого участка равен произведению модуля | B | на площадь участка dS и косинус угла α между B и нормалью n к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам.
Википедия
Зависимости магнитного потока
Используя формулу, можно увидеть, что магнитный поток зависит от трех переменных: магнитного поля B, площади S и угла α.
Магнитный поток линейно зависит от B и S. Например, если увеличить площадь S, но оставить магнитное поле B и угол α прежними, то магнитный поток будет больше. Поэтому большая площадь означает большой поток, а маленькая площадь — маленький магнитный поток.
Если, с другой стороны, увеличить магнитное поле B, то магнитный поток также увеличится. Сильное магнитное поле приводит к большому потоку, слабое поле — к малому магнитному потоку.
В целом, чем больше магнитное поле B или площадь S, тем больше магнитный поток.
Ситуация с углом α немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, тогда ваш угол α = 0° . Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, магнитный поток уменьшается. Когда вы достигаете α = 90°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого он снова начинает увеличиваться.
Единица измерения и обозначение магнитного потока
Магнитное поле B имеет единицу Тесла (T), а площадь — единицу квадратный метр м2 .
Поток является скалярной величиной и его единицей измерения является вебер (Вб): 1 Вб = 1 Т * м2 , то есть [Ф] = Т * м2 . Обозначается магнитный поток как Ф (символ формулы — греческая фи).
Примеры
Приведенные ниже примеры дадут вам лучшее понимание того, что представляет собой новая концепция и аналогия с потоком воды.
- В случае, показанном на рис. 2, поток магнитного поля с магнитной индукцией B через поверхность S составляет: ФB = B * S и при этом его значение максимально, так как:
2. А в каком случае при ненулевой магнитной индукции ФB = 0 ?
Определение магнитного потока показывает, что это тот случай, когда:
потому что cos 90° = 0.
На рис. 3 мы видим, как в этой ситуации располагается плоская поверхность относительно векторов магнитной индукции.
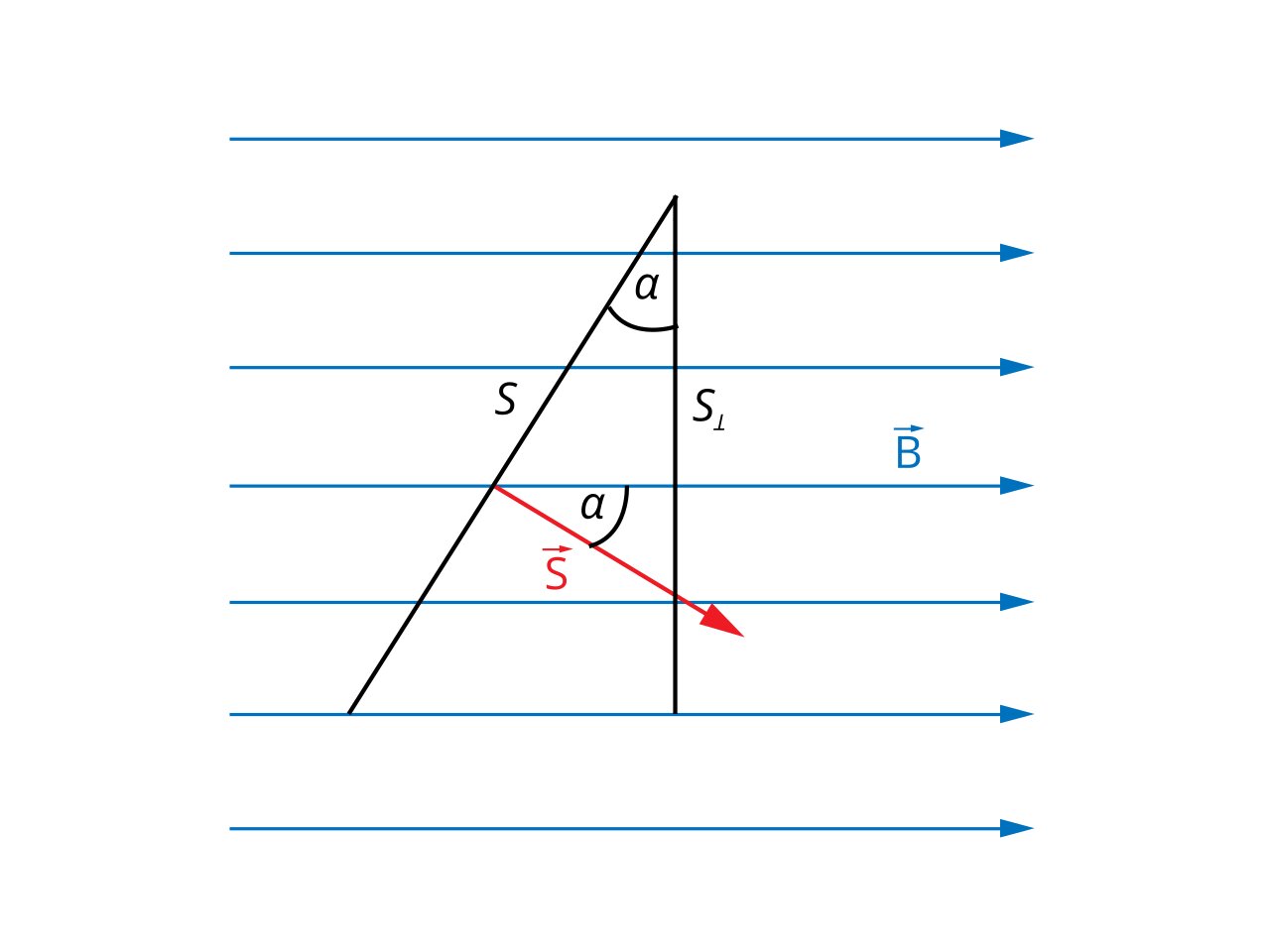
Обратите внимание, что ФB можно представить как произведение В и S⟂, где S⟂ = S * cos α. Аналогично, вы всегда можете рассчитать величину потока магнитного поля, умножив составляющую магнитной индукции, перпендикулярную поверхности, на величину площади поверхности (см. рис. 4а. и 4б.).
Как можно рассчитать поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы делим поверхность, через которую мы должны вычислить поток, на такие маленькие участки, что можно считать, что они плоские и поле однородное. Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:
Вычислять такие интегралы совсем не обязательно, но полезно понимать смысл такой процедуры.
From Wikipedia, the free encyclopedia
This article is about magnetic flux. For the magnetic fields «B» (magnetic flux density) and «H», see Magnetic field.
In physics, specifically electromagnetism, the magnetic flux through a surface is the surface integral of the normal component of the magnetic field B over that surface. It is usually denoted Φ or ΦB. The SI unit of magnetic flux is the weber (Wb; in derived units, volt–seconds), and the CGS unit is the maxwell. Magnetic flux is usually measured with a fluxmeter, which contains measuring coils, and it calculates the magnetic flux from the change of voltage on the coils.
Description[edit]
The magnetic flux through a surface—when the magnetic field is variable—relies on splitting the surface into small surface elements, over which the magnetic field can be considered to be locally constant. The total flux is then a formal summation of these surface elements (see surface integration).
Each point on a surface is associated with a direction, called the surface normal; the magnetic flux through a point is then the component of the magnetic field along this direction.
The magnetic interaction is described in terms of a vector field, where each point in space is associated with a vector that determines what force a moving charge would experience at that point (see Lorentz force).[1] Since a vector field is quite difficult to visualize at first, in elementary physics one may instead visualize this field with field lines. The magnetic flux through some surface, in this simplified picture, is proportional to the number of field lines passing through that surface (in some contexts, the flux may be defined to be precisely the number of field lines passing through that surface; although technically misleading, this distinction is not important). The magnetic flux is the net number of field lines passing through that surface; that is, the number passing through in one direction minus the number passing through in the other direction (see below for deciding in which direction the field lines carry a positive sign and in which they carry a negative sign).[2]
In more advanced physics, the field line analogy is dropped and the magnetic flux is properly defined as the surface integral of the normal component of the magnetic field passing through a surface. If the magnetic field is constant, the magnetic flux passing through a surface of vector area S is
where B is the magnitude of the magnetic field (the magnetic flux density) having the unit of Wb/m2 (tesla), S is the area of the surface, and θ is the angle between the magnetic field lines and the normal (perpendicular) to S. For a varying magnetic field, we first consider the magnetic flux through an infinitesimal area element dS, where we may consider the field to be constant:
A generic surface, S, can then be broken into infinitesimal elements and the total magnetic flux through the surface is then the surface integral
From the definition of the magnetic vector potential A and the fundamental theorem of the curl the magnetic flux may also be defined as:
where the line integral is taken over the boundary of the surface S, which is denoted ∂S.
Magnetic flux through a closed surface[edit]
Some examples of closed surfaces (left) and open surfaces (right). Left: Surface of a sphere, surface of a torus, surface of a cube. Right: Disk surface, square surface, surface of a hemisphere. (The surface is blue, the boundary is red.)
Gauss’s law for magnetism, which is one of the four Maxwell’s equations, states that the total magnetic flux through a closed surface is equal to zero. (A «closed surface» is a surface that completely encloses a volume(s) with no holes.) This law is a consequence of the empirical observation that magnetic monopoles have never been found.
In other words, Gauss’s law for magnetism is the statement:
for any closed surface S.
Magnetic flux through an open surface[edit]
For an open surface Σ, the electromotive force along the surface boundary, ∂Σ, is a combination of the boundary’s motion, with velocity v, through a magnetic field B (illustrated by the generic F field in the diagram) and the induced electric field caused by the changing magnetic field.
While the magnetic flux through a closed surface is always zero, the magnetic flux through an open surface need not be zero and is an important quantity in electromagnetism.
When determining the total magnetic flux through a surface only the boundary of the surface needs to be defined, the actual shape of the surface is irrelevant and the integral over any surface sharing the same boundary will be equal. This is a direct consequence of the closed surface flux being zero.
Changing magnetic flux[edit]
For example, a change in the magnetic flux passing through a loop of conductive wire will cause an electromotive force, and therefore an electric current, in the loop. The relationship is given by Faraday’s law:
where
is the electromotive force (EMF),
- ΦB is the magnetic flux through the open surface Σ,
- ∂Σ is the boundary of the open surface Σ; the surface, in general, may be in motion and deforming, and so is generally a function of time. The electromotive force is induced along this boundary.
- dℓ is an infinitesimal vector element of the contour ∂Σ,
- v is the velocity of the boundary ∂Σ,
- E is the electric field,
- B is the magnetic field.
The two equations for the EMF are, firstly, the work per unit charge done against the Lorentz force in moving a test charge around the (possibly moving) surface boundary ∂Σ and, secondly, as the change of magnetic flux through the open surface Σ. This equation is the principle behind an electrical generator.
Area defined by an electric coil with three turns.
Comparison with electric flux[edit]
By way of contrast, Gauss’s law for electric fields, another of Maxwell’s equations, is
where
- E is the electric field,
- S is any closed surface,
- Q is the total electric charge inside the surface S,
- ε0 is the electric constant (a universal constant, also called the «permittivity of free space»).
The flux of E through a closed surface is not always zero; this indicates the presence of «electric monopoles», that is, free positive or negative charges.
See also[edit]
- Dannatt plates, thick sheets made of electrical conductors
- Flux linkage, an extension of the concept of magnetic flux
- Magnetic circuit is a closed path in which magnetic flux flows
- Magnetic flux quantum is the quantum of magnetic flux passing through a superconductor
References[edit]
- ^ Purcell, Edward; Morin, David (2013). Electricity and Magnetism (3rd ed.). New York: Cambridge University Press. p. 278. ISBN 978-1-107-01402-2.
- ^ Browne, Michael (2008). Physics for Engineering and Science (2nd ed.). McGraw-Hill/Schaum. p. 235. ISBN 978-0-07-161399-6.
{{cite book}}: CS1 maint: uses authors parameter (link)
External articles[edit]
Media related to Magnetic flux at Wikimedia Commons
- US 6720855, Vicci, «Magnetic-flux conduits», issued 2003
- Magnetic Flux through a Loop of Wire by Ernest Lee, Wolfram Demonstrations Project.
- Conversion Magnetic flux Φ in nWb per meter track width to flux level in dB – Tape Operating Levels and Tape Alignment Levels
- wikt:magnetic flux
Поскольку магнитный поток — это мера магнитного поля, проходящего сквозь поверхность определённой площади, его можно измерить магнитометром, точно так же, как и индукцию магнитного поля. Например, представьте, что небольшой щуп магнитометра перемещается (без вращения) по поверхности площадью 0, comma, 5, space, м, squared неподалёку от большого плоского магнетика. Магнитометр показывает во всех точках этой поверхности постоянное значение индукции 5, space, м, Т, л. Тогда магнитный поток, проходящий сквозь эту поверхность, будет равен left parenthesis, 5, dot, 10, start superscript, minus, 3, end superscript, space, Т, л, right parenthesis, dot, left parenthesis, 0, comma, 5, space, м, squared, right parenthesis, equals, 0, comma, 0025, space, В, б. Если же магнитная индукция в разных точках поверхности различается, тогда сначала необходимо найти её среднее значение.
С магнитным потоком тесно связан ещё один термин, с которым вы можете столкнуться, — плотность магнитного потока. Она измеряется в В, б, slash, м, squared. Поскольку мы делим магнитный поток на площадь, плотность магнитного потока можно было бы измерять сразу в тесла. Однако в действительности термин «плотность магнитного потока» часто используется как синоним величины магнитной индукции.
На рисунке 2 показана схема неоднородного магнитного поля неподалёку от большого плоского магнетика. Зелёной линией обозначен замкнутый провод. Чему равен магнитный поток, проходящий сквозь ограниченную им поверхность?