Как можно найти образующую конуса - Исправление недочетов и поиск решений вместе с Examum.ru

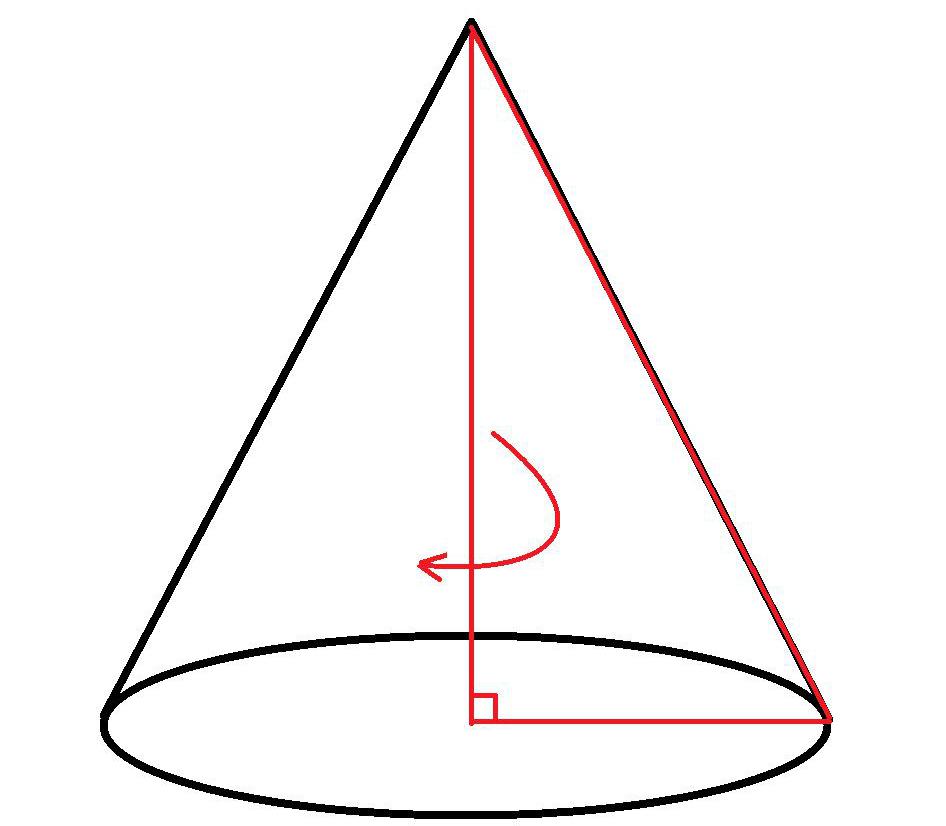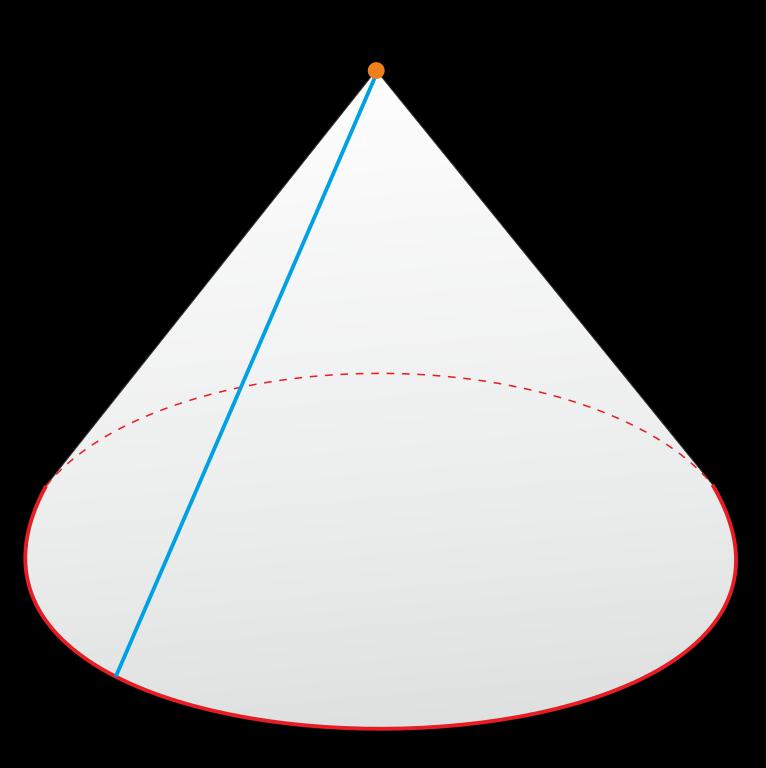
Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.

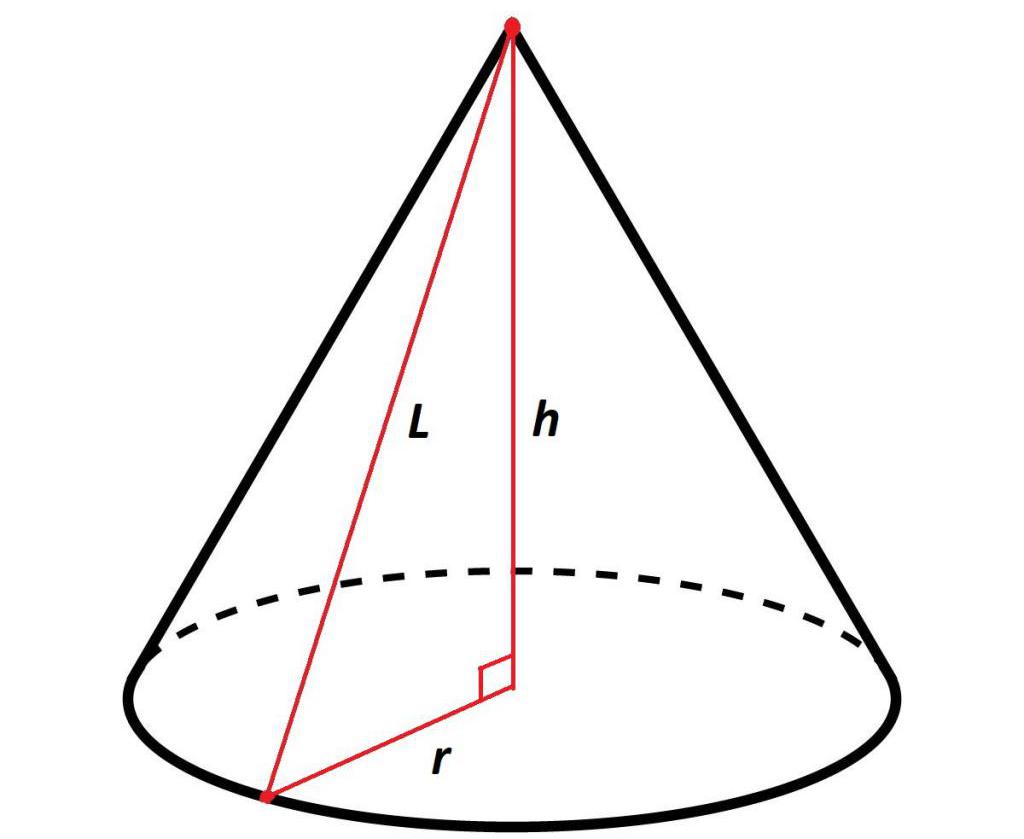
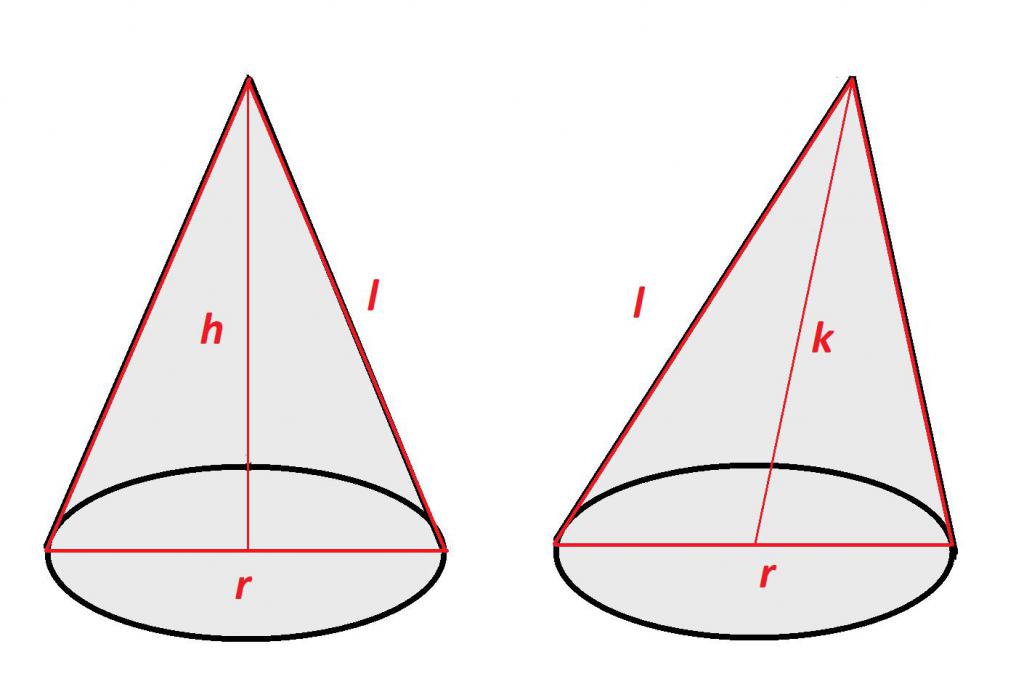
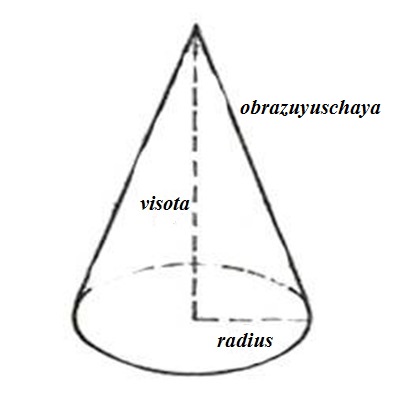
Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.

Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.

Радиус конуса – это радиус его основания.

Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.

Формула образующей конуса

Образующую конуса можно найти, зная ее высоту H и радиус R:

L = √H² + R²

Формула площади боковой поверхности конуса

Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:

S_{бок.пов} = πRL

Формула площади основания конуса

Площадь основания конуса можно вычислить по его радиусу R:

S_осн = πR²

Формула площади конуса

Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:

S = S_{бок.пов} + S_осн = πRL + πR²

Формула объема конуса

Объем конуса можно вычислить, зная его высоту H и площадь основания:

V = 1/3 ⋅ S_осн ⋅ H = 1/3πR²H

Источник

Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.

Конус – это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.

Составляющие конуса

Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.

Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.

Конус состоит из следующих элементов:

Круга, являющегося его основанием.
Боковой поверхности.
Точки, не лежащей в плоскости основания, называющейся вершиной конуса.
Отрезков, которые соединяют точки круга основания геометрического тела и его вершину.

Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.

Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.

Длина образующих в прямом конусе

Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.

То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:

l²= r²+ h² или l = √r²+ h²

где l – образующая;

r – радиус;

h – высота.

Образующая в наклонном конусе

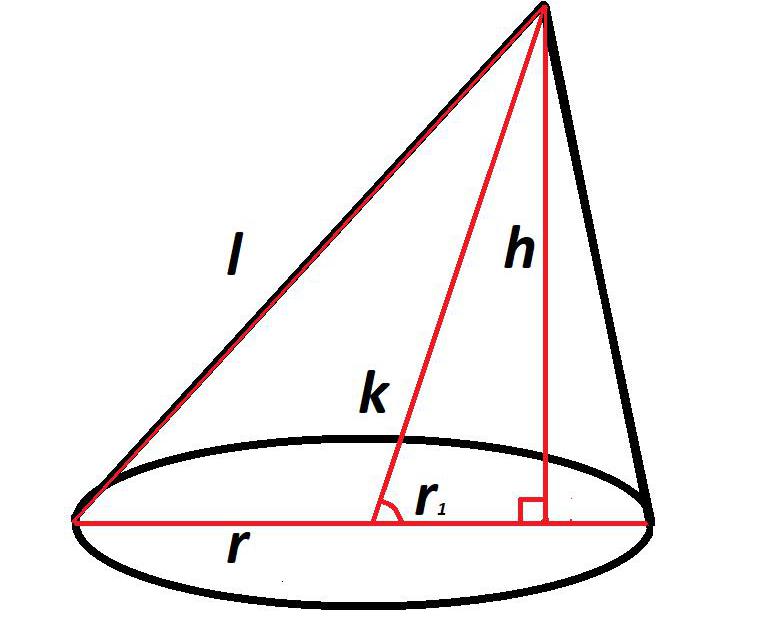
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.

Прежде всего необходимо знать высоту, длину оси и радиус основания.

Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:

r₁= √k²— h²

где r₁ – это часть радиуса между осью и высотой;

k – длина оси;

h – высота.

В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r₁), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:

R = r + r₁

где R – катет треугольника, образованного высотой, образующей и частью диаметра основания;

r – радиус основания;

r₁ – часть радиуса между осью и высотой.

Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:

l = √h²+ R²

или, не производя отдельно расчет R, объединить две формулы в одну:

l = √h² + (r + r₁)².

Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу — использованию теоремы Пифагора.

Сечение конуса

Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.

Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.

Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.

Площадь сечения

Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:

S = 1/2 * d * h или S = 1/2 * 2r * h

где S – это площадь сечения;

d – диаметр основания;

r – радиус;

h – высота.

В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.

Объем

Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м³. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.

Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.

Расчет объема

Формула объема любого конуса выглядит следующим образом:

V = 1/3 * π * h * r²

где V – это объем конуса;

h – высота;

r – радиус;

π — константа, равная 3,14.

Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.

Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a²+ b²= c² или в нашем случае h²+ r²= l², где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:

a = √c²— b²

То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:

h = √l²— r²

Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.

Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:

r = √l²— h²

После чего по той же формуле, что указана выше, рассчитать объем конуса.

Объем наклонного конуса

Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.

Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.

Источник

Как найти образующую конуса обычного и усеченного. Формулы

Пространственные фигуры подробно рассматриваются в старших классах общеобразовательных школ в курсе стереометрии. Данная статья содержит ответ на вопрос о том, как найти образующую конуса круглого прямого и образующую соответствующей усеченной фигуры.

Фигура конус

Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.

Вам будет интересно:Развивающая функция обучения: цель, основные принципы

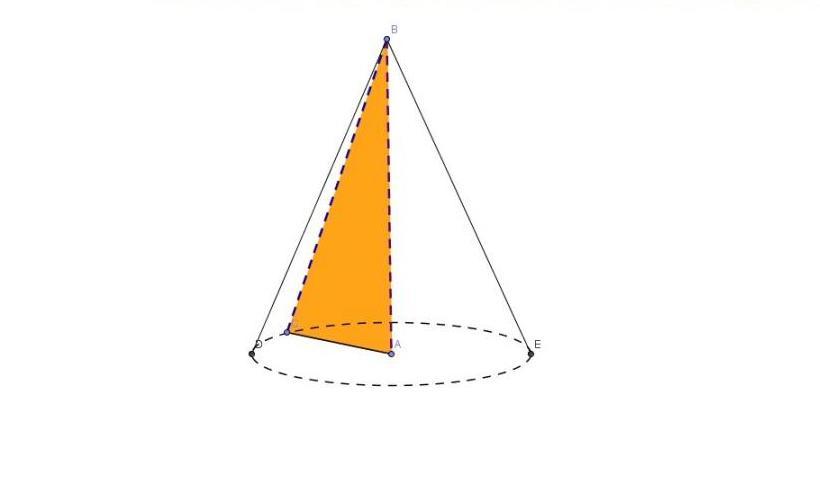
Полученная пространственная фигура имеет следующие характеристики:

Сторона AB треугольника является высотой h конуса. Она лежит на оси вращения фигуры.

Сторона AC треугольника — это радиус r конуса. Круг, который описывает этот радиус, называется основанием фигуры.

Сторона CB треугольника для конуса является его образующей, или генератрисой. Это название она получила за то, что в процессе вращения она описывает коническую поверхность.

Вершина B треугольника — это вершина конуса.

Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.

Образующая конуса

Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:

g = √(r2 + h2)

Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:

g = h/sin(φ);

g = r/cos(φ)

Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.

Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.

Фигура конус усеченный

Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.

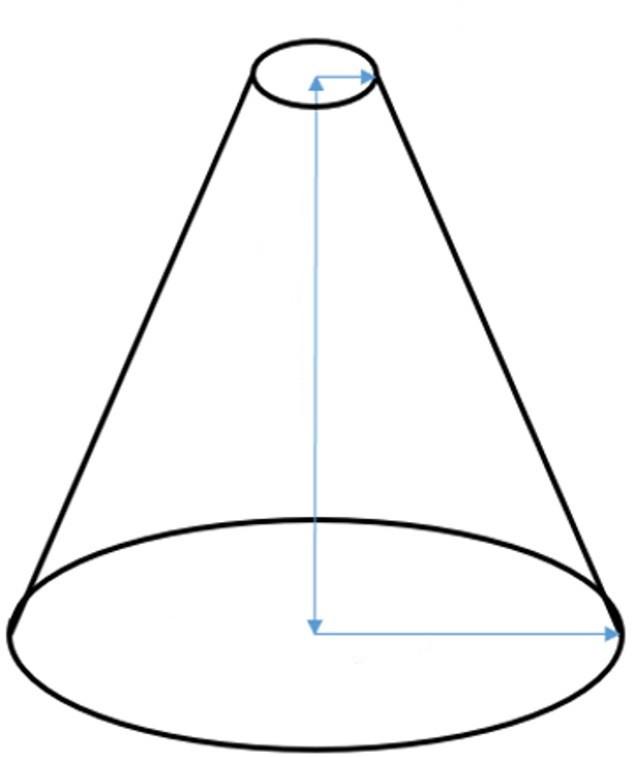
Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок — это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r1 и r2. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.

Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.

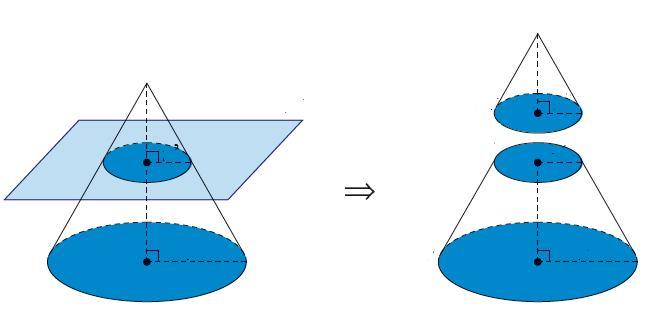
Генератриса усеченной фигуры

Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r1-r2 (катет). Тогда можно записать формулу для определения g:

g = √((r1 — r2)2 + h2)

Соответственно, если дан острый угол φ1 между большим основанием и генератрисой, тогда последнюю можно определить так:

g = h/sin(φ1);

g = (r1 — r2)/cos(φ1)

Если же известен тупой угол φ2 между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:

g = h/sin(φ2);

g = (r2 — r1)/cos(φ2)

Здесь первая формула является точно такой же, как для угла φ1, а во второй формуле радиусы в числителе поменялись местами.

Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.

Автор:

06-12-2018 23:50

Жду ваши вопросы и мнения в комментариях

Источник

Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.

Треугольник (POA) вращается вокруг стороны (PO).

(PO) — ось конуса и высота конуса.

(P) — вершина конуса.

(PA) — образующая конуса.

Круг с центром (O) — основание конуса.

(AO) — радиус основания конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось (PO) конуса.

Осевое сечение конуса — это равнобедренный треугольник.

(APB) — осевое сечение конуса.

∡PAO=∡PBO

— углы между образующими и основанием конуса.

Для конуса построим развёртку боковой поверхности. Это круговой сектор.

Сектор имеет длину дуги, равную длине окружности в основании конуса

2πR

, угол развёртки боковой поверхности

В конусе нельзя обозначить угол развёртки.
На развёртке конуса нельзя обозначить высоту и радиус конуса.

Образующая конуса (l) является радиусом сектора.

Таким образом, боковая поверхность конуса является частью полного круга с радиусом (l):

Длина дуги также является частью длины полной окружности с радиусом (l), но в то же время длина дуги — это длина окружности основания конуса с радиусом (R).

Сравним выражения длины дуги и выразим

через (R):

2πl⋅α360°=2πR;α=2πR⋅360°2πl=R⋅360°l.

Получаем ещё одну формулу боковой поверхности конуса; не используется угол развёртки боковой поверхности:

Sбок.=πl2⋅R⋅360°360°⋅l=πRl

Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом.

Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.

OO1

— ось конуса и высота конуса.

Круги с центрами (O) и

— основания усечённого конуса.

(AO) и

A1O1

— радиусы оснований конуса.

Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось

OO1

конуса.

Осевое сечение конуса — это равнобедренная трапеция.

AA1B1B

— осевое сечение конуса.

Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:

Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1.

Так как

ΔPAO∼ΔPA1O1

, то стороны их пропорциональны:

PAPA1=Rr;l+PA1PA1=Rr;r⋅l+PA1=R⋅PA1;rl=R⋅PA1−r⋅PA1;PA1⋅R−r=rl;PA1=rlR−r.

Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:

Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−r;Sбок.=πRl+πrl=πl⋅R+r.

Источник

Задание.
Как найти образующую конуса, если диаметр его основания равен 12 см, а высота равна 8 см.

Решение.
Изобразим схематически конус, на котором обозначим его высоту, радиус основания и образующую. Образующая конуса соединяет его вершину с одной из точек на окружности основания конуса. Радиус также соединяет центр окружности с любой из точек на этой окружности. Поэтому можем изобразить радиус и высоту на рисунке так, как нам будет удобно использовать их для решения задачи. Пусть концы радиуса и образующей совпадают.

Из рисунка хорошо видно, что из высоты, радиуса и образующей получается прямоугольный треугольник, к которому можно применить теорему Пифагора. Запишем уравнение для данного треугольника:

$[{obrazuyuschaya}^2={visota}^2+{radius}^2]$

Значение высоты известно из условия, радиус можно найти через диаметр. Таким образом, вычислим значение образующей.
Итак, найдем длину радиуса, зная, что диаметр равен 12 см:
$radius=frac{diametr}{2}=frac{12}{2}=6$ (см).
Теперь подставим известные значения в теорему Пифагора:

$[{obrazuyuschaya}^2={visota}^2+{radius}^2]$

$[{obrazuyuschaya}^2=8^2+6^2]$

$[{obrazuyuschaya}^2=64+36]$

$[{obrazuyuschaya}^2=100]$

(см).

Ответ. 10 см.

Источник