Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое правильный шестиугольник?
Правильный шестиугольник — это геометрическая фигура, которая является одним из типов правильных многоугольников. Он имеет шесть равных сторон и шесть равных углов. В правильном шестиугольнике все стороны равны между собой, и все углы равны 120 градусам.
Свойства правильного шестиугольника:
- Равные стороны. Все шесть сторон правильного шестиугольника имеют одинаковую длину.
- Равные углы. Каждый угол в правильном шестиугольнике равен 120 градусам.
- Центральная симметрия. Правильный шестиугольник обладает центральной симметрией, что означает, что его можно повернуть на 60 градусов вокруг центра так, чтобы он выглядел идентично.
- Описанная окружность. Центры описанной окружности правильного шестиугольника и самого шестиугольника совпадают.
По какой формуле калькулятор рассчитывает площадь правильного шестиугольника?
Калькулятор площади правильного шестиугольника — это онлайн инструмент, предназначенный для быстрого и удобного вычисления площади данного геометрического объекта. Он использует математическую формулу, специально разработанную для расчета площади правильного шестиугольника.
Формула для вычисления площади правильного шестиугольника выглядит следующим образом:
Площадь = (3 * √3) * (сторона^2) / 2
где «сторона» обозначает длину каждой стороны правильного шестиугольника.
Расчет производится следующим образом:
- Возведение длины стороны в квадрат (сторона^2).
- Умножение полученного значения на 3 и затем на квадратный корень из 3 (3 * √3).
- Деление полученного значения на 2 ((3 * √3) * (сторона^2) / 2).
Где и как можно использовать шестиугольник?
Шестиугольник может быть применен в различных областях и имеет множество применений. Вот некоторые из них:
- Архитектура и строительство. Шестиугольники могут использоваться в архитектуре для создания уникальных фасадов зданий или в планировке помещений. Например, шестиугольные плитки могут использоваться для создания интересных и гармоничных дизайнов пола и стен.
- Упаковка. Шестиугольные упаковочные контейнеры могут обеспечивать более эффективное использование пространства и обеспечивать прочность и стабильность конструкции.
- Биология и природа. Многие ячейки и пчелиные соты имеют форму шестиугольника, поскольку это оптимальная форма для заполнения пространства с минимальными затратами энергии. Также шестиугольники можно найти в структурах медовых трутней и в некоторых природных образованиях, таких как гексагональные базальтовые колонны.
- Геометрические и математические исследования. Шестиугольники являются одним из простейших правильных многоугольников, и их свойства широко изучаются в математике и геометрии. Они могут использоваться в качестве примеров для изучения углов, сторон и свойств многоугольников в целом.
- Графика и дизайн. Шестиугольники могут быть использованы в графическом дизайне и создании паттернов. Их регулярная форма и симметрия позволяют создавать интересные и гармоничные композиции.
- Игры и головоломки. Шестиугольники могут использоваться в играх и головоломках, где требуется решать задачи, связанные с их свойствами и геометрией.
Это лишь некоторые примеры применения шестиугольника. Фактически, шестиугольник может использоваться везде, где требуется регулярная форма с определенными свойствами и характеристиками.
Пример
Представим ситуацию, в которой вам необходимо покрыть пол шестиугольной комнаты плитками. Для этого вы хотите вычислить площадь правильного шестиугольника, чтобы определить количество плиток, которое вам потребуется для покрытия пола.
Предположим, что сторона вашего правильного шестиугольника равна 4 метра. Теперь, чтобы вычислить площадь, воспользуемся формулой для площади правильного шестиугольника:
Площадь = (3 * √3) * (сторона^2) / 2
Подставим значения:
Площадь = (3 * √3) * (4^2) / 2
Площадь = (3 * √3) * 16 / 2
Площадь = (3 * √3) * 8
Площадь = 24 * √3
Таким образом, площадь вашего правильного шестиугольника составляет 24 * √3 квадратных метра.
Теперь, если вы хотите вычислить количество плиток, которое вам потребуется для покрытия пола, вам нужно знать размер одной плитки. Предположим, что размер плитки составляет 0,25 квадратных метра.
Для вычисления количества плиток, поделите общую площадь пола на площадь одной плитки:
Количество плиток = Площадь пола / Площадь одной плитки
Количество плиток = (24 * √3) / 0,25
Вычислим это:
Количество плиток = 96 * √3
Таким образом, вам потребуется 96 * √3 (приблизительно, 166.286) плиток размером 0,25 квадратных метра для покрытия пола шестиугольной комнаты со стороной 4 метра.
Вычисление площади правильного шестиугольника может быть полезно при планировании различных проектов, таких как покрытие пола, расстановка мебели, зонирование пространства или расчет необходимого материала для строительства или ремонта.
❓ Вопросы и ответы
Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.
Что такое правильный шестиугольник?
Правильный шестиугольник — это многоугольник, у которого все стороны имеют одинаковую длину, а все углы равны 120 градусам.
Как вычислить площадь правильного шестиугольника?
Площадь правильного шестиугольника можно вычислить, используя формулу: Площадь = (3 * √3) * (сторона^2) / 2, где сторона — длина одной стороны шестиугольника.
Могу ли я использовать калькулятор площади правильного шестиугольника для десятичных значений сторон?
Да, вы можете использовать калькулятор площади правильного шестиугольника для десятичных значений сторон. Он примет любые числовые значения и вычислит площадь соответствующего правильного шестиугольника.
Как могу использовать площадь правильного шестиугольника на практике?
Площадь правильного шестиугольника может быть использована при проектировании различных объектов и структур, таких как крыши, мозаики, участки земли, полы, фасады зданий и другие. Вычисление площади поможет вам определить необходимое количество материалов, бюджет, площадь покрытия и другие аспекты проекта.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Как рассчитать площадь правильного шестиугольника
На данной странице калькулятор поможет рассчитать площадь правильного шестиугольника онлайн. Для расчета задайте длину стороны или радиус окружности.
Шестиугольник — многоугольник у которого все стороны равны, а все внутренние углы равны 120°.
Через сторону
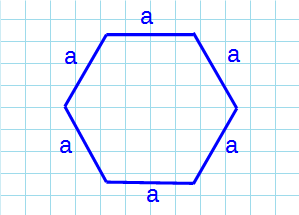
a:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через сторону:
a — сторона шестиугольника.
Через радиус описанной окружности
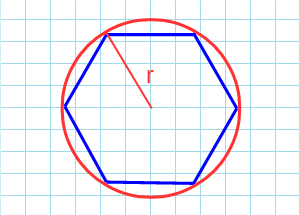
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус описанной окружности:
r — радиус описанной окружности.
Через радиус вписанной окружности
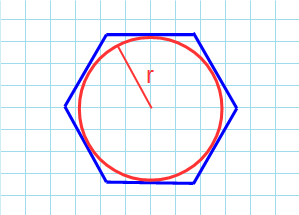
r:
Результат
Ответы:
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности:
r — радиус вписанной окружности.
Калькулятор
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где
— сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольника.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
.
Радиус такой окружности равен .
Ответ: .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Ответ: .
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Правильный шестиугольник: свойства, формулы, площадь» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Download Article
Download Article
A hexagon is a polygon that has six sides and angles. Regular hexagons have six equal sides and angles and are composed of six equilateral triangles. There are a variety of ways to calculate the area of a hexagon, whether you’re working with an irregular hexagon or a regular hexagon. If you want to know how to calculate the area of a hexagon, just follow these steps.
-
1
Write down the formula for finding the area of a hexagon if you know the side length. Since a regular hexagon is comprised of six equilateral triangles, the formula for finding the area of a hexagon is derived from the formula of finding the area of an equilateral triangle. The formula for finding the area of a hexagon is Area = (3√3 s2)/ 2 where s is the length of a side of the regular hexagon.[1]
-
2
Identify the length of one one side. If you already know the length of a side, then you can simply write it down; in this case, the length of a side is 9 cm. If you don’t know the length of a side but know the length of the perimeter or apothem (the height of one of the equilateral triangles formed by the hexagon, which is perpendicular to the side), you can still find the length of the side of the hexagon. Here’s how you do it:
- If you know the perimeter, then just divide it by 6 to get the length of one side. For example, if the length of the perimeter is 54 cm, then divide it by 6 to get 9 cm, the length of the side.[2]
- If you only know the apothem, you can find the length of a side by plugging the apothem into the formula a = x√3 and then multiplying the answer by two. This is because the apothem represents the x√3 side of the 30-60-90 triangle that it creates. If the apothem is 10√3, for example, then x is 10 and the length of a side is 10 * 2, or 20.
Advertisement
- If you know the perimeter, then just divide it by 6 to get the length of one side. For example, if the length of the perimeter is 54 cm, then divide it by 6 to get 9 cm, the length of the side.[2]
-
3
Plug the value of the side length into the formula. Since you know that the length of one side of the triangle is 9, just plug 9 into the original formula. It will look like this: Area = (3√3 x 92)/2
-
4
Simplify your answer. Find the value of equation and write the numerical answer. Since you’re working with area, you should state your answer in square units. Here’s how you do it:[3]
- (3√3 x 92)/2 =
- (3√3 x 81)/2 =
- (243√3)/2 =
- 420.8/2 =
- 210.4 cm2
Advertisement
-
1
Write down the formula for finding the area of a hexagon with a given apothem. The formula is simply Area = 1/2 x perimeter x apothem.[4]
-
2
Write down the apothem. Let’s say the apothem is 5√3 cm.
-
3
Use the apothem to find the perimeter. Since the apothem is perpendicular to the side of the hexagon, it creates one side of a 30-60-90 triangle. The sides of a 30-60-90 triangle are in the proportion of x-x√3-2x, where the length of the short leg, which is across from the 30 degree angle, is represented by x, the length of the long leg, which is across from the 60 degree angle, is represented by x√3, and the hypotenuse is represented by 2x.[5]
- The apothem is the side that is represented by x√3. Therefore, plug the length of the apothem into the formula a = x√3 and solve. If the apothem’s length is 5√3, for example, plug it into the formula and get 5√3 cm = x√3, or x = 5 cm.
- By solving for x, you have found the length of the short leg of the triangle, 5. Since it represents half the length of one side of the hexagon, multiply it by 2 to get the full length of the side. 5 cm x 2 = 10 cm.
- Now that you know that the length of one side is 10, just multiply it by 6 to find the perimeter of the hexagon. 10 cm x 6 = 60 cm
-
4
Plug all of the known quantities into the formula. The hardest part was finding the perimeter. Now, all you have to do is plug the apothem and perimeter into the formula and solve:
- Area = 1/2 x perimeter x apothem
- Area = 1/2 x 60 cm x 5√3 cm
-
5
Simplify your answer. Simplify the expression until you’ve removed the radicals from the equation. State your final answer in square units.[6]
- 1/2 x 60 cm x 5√3 cm =
- 30 x 5√3 cm =
- 150√3 cm =
- 259. 8 cm2
Advertisement
-
1
List the x and y coordinates of all the vertices. If you know the vertices of the hexagon, the first thing you should do is create a chart with two columns and seven rows. Each row will be labeled by the names of the six points (Point A, Point B, Point C, etc), and each column will be labeled as the x or y coordinates of those points. List the x and y coordinates of Point A to the right of Point A, the x and y coordinates of Point B to the right of Point B, and so on. Repeat the coordinates of the first point at the bottom of the list. Let’s say you’re working with the following points, in (x, y) format:[7]
- A: (4, 10)
- B: (9, 7)
- C: (11, 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (again): (4, 10)
-
2
Multiply the x coordinate of each point by the y coordinate of the next point. You can think of this as drawing a diagonal line to the right and downward one row from each x coordinate. List the results to the right of the chart. Then, add the results.[8]
- 4 x 7 = 28
- 9 x 2 = 18
- 11 x 2 = 22
- 2 x 5 = 10
- 1 x 7 = 7
- 4 x 10 = 40
- 28 + 18 + 22 + 10 + 7 + 40 = 125
-
3
Multiply the y coordinates of each point by the x coordinates of the next point. Think of this as drawing a diagonal line from each y coordinate downward and to the left, to the x coordinate below it. Once you multiply all of these coordinates, add the results.[9]
- 10 x 9 = 90
- 7 x 11 = 77
- 2 x 2 = 4
- 2 x 1 = 2
- 5 x 4 = 20
- 7 x 4 = 28
- 90 + 77 + 4 + 2 + 20 + 28 = 221
-
4
Subtract the sum of the second group of coordinates from the sum of the first group of coordinates.[10]
Just subtract 221 from 125. 125 — 221 = -96. Now, take the absolute value of this answer: 96. Area can only be positive. -
5
Divide this difference by two.[11]
Just divide 96 by 2 and you’ll have the area of the irregular hexagon. 96/2 = 48. Don’t forget to write your answer in square units. The final answer is 48 square units.
Advertisement
-
1
Find the area of a regular hexagon with a missing triangle. If you know you’re working with a regular hexagon that is missing one or more of its triangles, then the first thing you need to do is find the area of the entire regular hexagon as if it were whole. Then, simply find the area of the empty or «missing» triangle, and that subtract that from the overall area. This will give you the area of the remaining irregular hexagon.[12]
- For example, if you’ve found that the area of the regular hexagon is 60 cm2 and you’ve found that the area of the missing triangle is 10 cm2 simply subtract the area of the missing triangle from the entire area: 60 cm2 — 10 cm2 = 50 cm2.
- If you know that the hexagon is missing exactly one triangle, you can also just find the area of the hexagon by multiplying the total area by 5/6, since the hexagon is retaining the area of 5 of its 6 triangles. If it’s missing two triangles, you can multiply the total area by 4/6 (2/3), and so on.
-
2
Break up an irregular hexagon into other triangles. You may find that the irregular hexagon is actually composed of four triangles that are irregularly shaped. To find the area of the whole irregular hexagon, you need to find the area of each individual triangle and then add them up. There are a variety of ways to find the area of a triangle depending on the information that you have.[13]
-
3
Look for other shapes in the irregular hexagon. If you can’t simply pick apart a few triangles, look through the irregular hexagon to see if you can locate other shapes — maybe a triangle, a rectangle, and/or a square. Once you’ve outlined the other shapes, just find their areas and add them up to get the area of the entire hexagon.[14]
- One type of irregular hexagon is comprised of two parallelograms. To get the areas of the parallelograms, just multiply their bases times their heights, just as you would do to find the area of a rectangle, and then add up their areas.
Advertisement
Hexagon Area Calculator, Practice Problems, and Answers
Add New Question
-
Question
I was only given the length of the diagonal. What do I do?
1/3rd of the length of the diagonal is the side of the hexagon. Using this, you can calculate the area.
-
Question
I know the area, nothing else. I need a regular hexagon. What do I do?
Assuming you’re looking for the length of a side, solve for s using the area formula in Method 1 above. Then plug in the known area.
-
Question
What is the area of a regular hexagon where the length of each side is 7m?
The side is 1/2 of 7 = 3.5. The area of a regular hexagon is (3√3 *3.5^2)/2 =31.82 or 32 cm, approximately.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
About This Article
Article SummaryX
To calculate the area of a hexagon, use the formula a = 3 × square root of 3 × s^2 divided by 2, where a is the area and s is the length of a side of the hexagon. Just plug in the length of one of the sides and then solve the formula to find the area. If you don’t have one of the side lengths but you do have the apothem, you can use the formula a = 1/2 × perimeter × apothem, where a is the area. To learn more, like how to calculate the area of an irregular hexagon, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,405,611 times.
Did this article help you?
Загрузить PDF
Загрузить PDF
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников. Есть несколько способов найти площадь шестиугольника, в зависимости от того, имеете ли вы дело с правильным или неправильным шестиугольником. Из этой статьи вы узнаете, как именно находить площадь этой фигуры.
-
1
Запишите формулу. Так как правильный шестиугольник состоит из 6 равносторонних треугольников, то формула образована из формулы нахождения площади равностороннего треугольника: Площадь = (3√3 s2)/ 2 где s — длина стороны правильного шестиугольника.[1]
-
2
Определите длину одной стороны. Если известна длина стороны, то просто запишите ее. В нашем случае длина стороны — 9 см. Если длина стороны неизвестна, но известен периметр или апофема (высота одного из шести равносторонних треугольников, перпендикулярная стороне), то можно найти и длину стороны. Вот, как это делается:
- Если известен периметр, то просто разделите его на 6 и получите длину стороны. Если, например, периметр — 54 см, то, разделив 54 на 6, мы получим 9 см, длину стороны.[2]
- Если известна только апофема, то длину стороны можно вычислить, подставив апофему в формулу a = x√3 и затем умножив ответ на 2. Это делается потому, что апофема представляет собой сторону x√3 образуемого ей треугольника с углами 30-60-90 градусов. Если, например, апофема — 10√3, то x — 10 и длина стороны будет равна 10 * 2 или 20.
- Если известен периметр, то просто разделите его на 6 и получите длину стороны. Если, например, периметр — 54 см, то, разделив 54 на 6, мы получим 9 см, длину стороны.[2]
-
3
Подставьте значение длины стороны в формулу. Просто подставляем 9 в изначальную формулу. Получаем: площадь = (3√3 x 92)/2
-
4
Упростите ответ. Решите уравнение и запишите ответ. Ответ должен быть указан в квадратных единицах, ведь мы имеем дело с площадью. Вот, как это делается:
- (3√3 x 92)/2 =
- (3√3 x 81)/2 =
- (243√3)/2 =
- 420.8/2 =
- 210.4 см2
Реклама
-
1
Запишите формулу. Площадь = 1/2 x периметр x апофему.[3]
-
2
Запишите апофему. Скажем, она равна 5√3 см.
-
3
Используйте апофему для нахождения периметра. Апофема перпендикулярна стороне шестиугольника и создает треугольник с углами 30-60-90. Стороны такого треугольника соответствуют пропорции x-x√3-2x, где сторона короткой стороны, лежащей напротив угла в 30 градусов, представлена x, длина длинной стороны, лежащей напротив угла в 60 градусов, представлена x√3, а гипотенуза представлена 2x.[4]
- Апофема — сторона, представленная x√3. Таким образом, подставляем апофему в формулу a = x√3 и решаем. Если, например, длина апофемы — 5√3, то подставляем это число в формулу и получаем 5√3 см = x√3, или x = 5 см.
- Решая через x, мы нашли длину короткой стороны треугольника — 5 см. Эта длина представляет собой половину длины стороны шестиугольника. Умножив 5 на 2, мы получаем 10 см, длину стороны.
- Подсчитав, что длина стороны равна 10, умножаем это число на 6 и получаем периметр шестиугольника. 10 см х 6 = 60 см.
-
4
Подставьте все известные данные в формулу. Сложнее всего найти периметр. Теперь надо лишь подставить апофему и периметр в формулу и решить:
- Площадь = 1/2 x периметр x апофему
- Площадь = 1/2 x 60 см x 5√3 см
-
5
Упрощайте ответ до тех пор, пока не избавитесь от квадратных корней. Окончательный ответ укажите в квадратных единицах.
- 1/2 x 60 см x 5√3 см =
- 30 x 5√3 см =
- 150√3 см =
- 259. 8 см2
Реклама
-
1
Запишите координаты всех вершин по осям x и y. Если известны вершины шестиугольника, то первым делом надо начертить таблицу с двумя колонками и семью рядами. Каждый ряд будет назван по названию по одной из шести точек (точка А, точка В, точка С и так далее), каждая колонка будет названа по осям x или у, соответствующим координатам точек по этим осям. Запишите координаты точки А по осям x и у справа от точки, координаты точки В — справа от точки В и так далее. Внизу повторно укажите координаты первой точки. Для примера скажем, что мы имеем дело со следующими точками, в формате (x, у):[5]
- A: (4, 10)
- B: (9, 7)
- C: (11, 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (снова): (4, 10)
-
2
Умножьте координаты каждой точки по оси x на координаты по оси у следующей точки. Это можно представить себе так: мы проводим диагональ вниз и вправо от каждой координаты по оси x. Запишем результаты справа от таблицы. Затем сложим их.
- 4 x 7 = 28
- 9 x 2 = 18
- 11 x 2 = 22
- 2 x 5 = 10
- 1 x 7 = 7
- 4 x 10 = 40
- 28 + 18 + 22 + 10 + 7 + 40 = 125
-
3
Умножьте координаты каждой точки по оси у на координаты по оси x следующей точки. Это можно представить себе так: мы проводим диагональ вниз и влево от каждой координаты по оси у. Перемножив все координаты, складываем результаты.
- 10 x 9 = 90
- 7 x 11 = 77
- 2 x 2 = 4
- 2 x 1 = 2
- 5 x 4 = 20
- 7 x 4 = 28
- 90 + 77 + 4 + 2 + 20 + 28 = 221
-
4
Вычтите из первой суммы координат вторую сумму координат. Вычитаем 221 из 125 и получаем -96. Итак, ответ: 96, площадь может быть только положительной.
-
5
Разделите разность на два. Делим 96 на 2 и получаем площадь неправильного шестиугольника. Окончательный ответ: 48 квадратных единиц.
Реклама
-
1
Найдите площадь правильного шестиугольника с отсутствующим треугольником. Если вы столкнулись с правильным шестиугольником, в котором отсутствует один или более треугольников, то прежде всего нужно найти его площадь, как если бы он был целым. Потом необходимо найти площадь «отсутствующего» треугольника и вычесть ее из общей площади. В итоге вы получите площадь имеющейся фигуры.[6]
- Например, если мы выяснили, что площадь правильного треугольника — 60 см2, а площадь отсутствующего треугольника — 10 см2, то: 60 см2 — 10 см2 = 50 см2.
- Если известно, что в шестиугольнике не хватает точно одного треугольника, то его площадь можно найти, умножив общую площадь на 5/6, так как мы имеем 5 и 6 треугольников. Если не хватает двух треугольников, то умножаем на 4/6 (2/3) и так далее.
-
2
Разбейте неправильный шестиугольник на треугольники. Найдите площади треугольников и сложите их. В зависимости от имеющихся данных существует множество способов найти площадь треугольника.[7]
-
3
Найдите в неправильном шестиугольнике какие-то другие фигуры: треугольники, прямоугольники, квадраты. Найдите площади составляющих шестиугольник фигур и сложите их.[8]
- Один из видов неправильного шестиугольника состоит из двух параллелограммов. Для нахождения их площадей просто перемножьте основания на высоты и затем сложите их площади.
Реклама
Об этой статье
Эту страницу просматривали 128 862 раза.







































