Как можно найти вершину параболы - Исправление недочетов и поиск решений вместе с Examum.ru

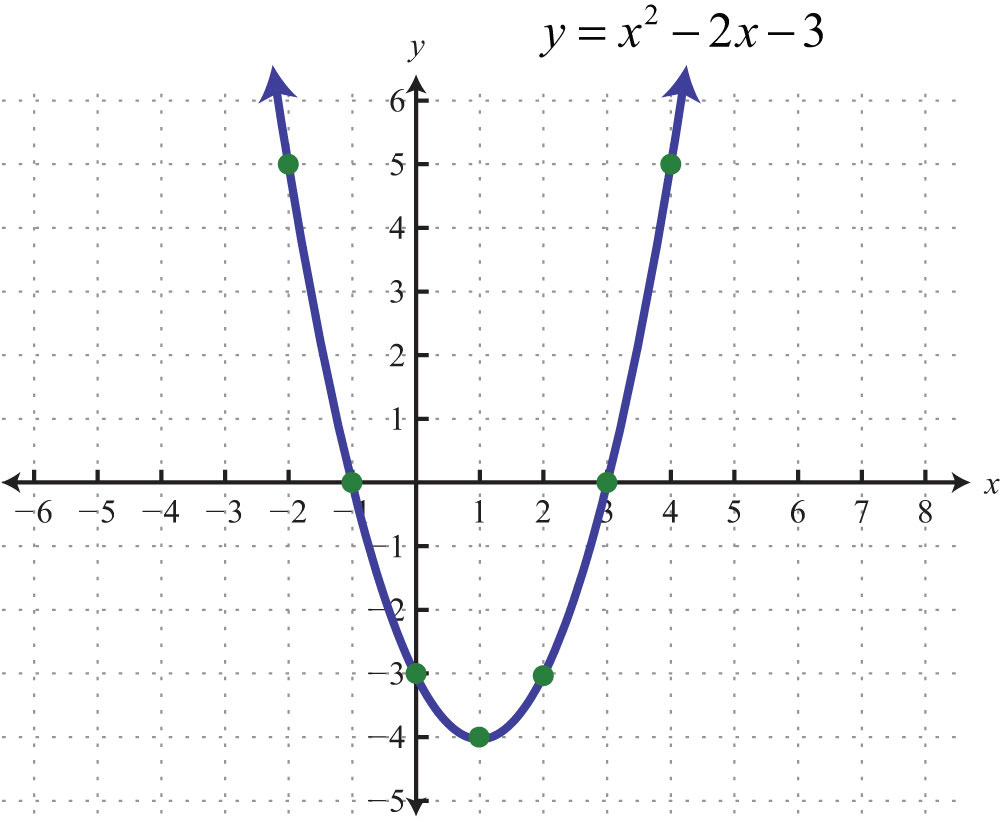
Вершина параболы

Содержание:

Что такое вершина параболы
Вывод формулы координат вершины параболы
Как найти координаты, основные способы
Примеры решения задач

Что такое вершина параболы

Определение

Вершина параболы — это точка, в которой наблюдается пересечение параболой оси координат и ее невозможность держать направление выше или ниже в координатной плоскости.

Чтобы найти ВП, необходимо применить формулу:

(lbrackfrac{-b}{2a};-frac{b^2-4ac}{4a}rbrack)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Исходя из координат, можно узнать расположение вершины параболы и построить ее.

Вывод формулы координат вершины параболы

Рассматриваемую формулу используют для решения квадратных уравнений, которые имеют вид:

(y;=;ax^2;+;bx;+;c)

Ее график представляет собой параболу, формулу которой мы определили выше. Но не всегда требуется пользоваться данной формулой, так как сначала можно найти значение х, а затем подставить его в уравнение и найти y.

Для того, чтобы вывести формулу ВП, нужно преобразовать квадратную функцию к виду:

(y;=;f(x;+;l);+;m)

Делают это с помощью метода выделения полного квадрата, то есть (left(a+bright)^2) преобразуют в (a^2+2ab+b^2.)

Функции вида (y;=;f(x;+;l);+;m) отличаются от (y;=;f(x)) сдвигом из графиков по оси абсцисс на –l и по оси ординат на m. l в переписанной квадратичной функции равняется:

(frac{-b}{2a}, а frac{left(4ac-b^2right)}{4a})

Получается, что l и m — это координаты x₀ и y₀.

Приведем доказательство:

Соединяем первые два члена многочлена: (y;=;(ax^2;+;bx);+;c.)
Выносим коэффициент a за скобку, b при этом делим на a: (y=aleft(x^2+frac baxright)+c.)
Представляем, что у нас есть квадрат суммы, в котором x является слагаемым, а из выражения в скобках необходимо рассчитать его полный квадрат суммы. Одночлен (frac bax) умножаем на два и делим на два одновременно. Далее прибавляем и вычитаем квадрат второго слагаемого квадрата суммы. Получаем: (y=aleft(x^2+2frac b{2a}x+frac{b^2}{4a^2}-frac{b^2}{4a^2}right)+c.)
Выделяем квадрат суммы: (y=aleft(left(x+frac b{2a}right)^2-frac{b^2}{4a}right)+c.)
Умножаем на a: (y=aleft(x+frac b{2a}right)^2-frac{b^2}{4a}+c.)
Приводим свободные члены к общему знаменателю: (y=aleft(x+frac b{2a}right)^2-frac{b^2+4ac}{4a}.)
Меняем знак: (y=aleft(x+frac b{2a}right)^2+frac{b^2-4ac}{4a}.)

Мы привели функцию (y;=;ax^2;+;bx;+;c) к виду (y;=;a{(x;+;l)}^2;+;m,) что соответствует (y;=;f(x;+;l);+;m,) где (f(x);=;ax^2. )

Как найти координаты, основные способы

Существует несколько способов нахождения координат ВП:

(x_0=frac{-b}{2a}) — подходит в том случае, если дискриминант квадратного уравнения равен нулю.
(y_0=-frac{b^2-4ac}{4a}) — это формула дискриминанта, поделенная на 4а.
(x_0=frac{x_1+x_2}2) — среднее арифметическое между нулями функции. Можно использовать, если в выражении есть нули.
Если функция имеет вид (y=aleft(x-x_0right)^2+y_0), то в ее вершиной совпадают координаты (left(x_0;y_0right).)

Примеры решения задач

Задача №1

Найти вершину параболы для уравнения: (y=x^2-5x+7.)

Решение: В выражение (x=-frac b{2a}) подставляем известные числа и получаем (x=frac52=2,5). Теперь подставляем x в исходное уравнение: (2,5^2-5times2,5+7=0,75.)

Ответ: (2,5; 0,75).

Задача №2

Найти ВП для уравнения: y=5(x-1)(x+7).

Решение: Ищем нули функции: 5(x-1)(x+7)=0. Тогда x-1=0 либо x+7=0. Из этого x=1; x=-7.

Подставляем и получаем: (x_0=frac{x_1+x_2}2=frac{1+left(-7right)}2=-3.)

Второе: (y_0=5timesleft(-3-1right)left(-3+7right)=-80.)

Ответ: (-3; -80).

Задача №3

Найти вершину параболы для уравнения: (y=x^2-7x+3 ).

Решение: (х_0=-frac b{2a}=-frac{left(-7right)}{2times1}=3,5.)

Второе: (y_0=3,5^2-7times3,5+3=-9,25.)

Ответ: (3,5; -9,25).

Насколько полезной была для вас статья?

Рейтинг: 2.50 (Голосов: 8)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Загрузить PDF

Вершина параболы квадратного уравнения — это самая высокая или самая низкая ее точка. Чтобы найти вершину параболы, вы можете воспользоваться специальной формулой или методом дополнения до полного квадрата. Ниже описано, как это сделать.

1

Найдите величины a, b, и c. В квадратном уравнении коэффициент при x² = a, при x = b, постоянная (коэффициент без переменной) = c. Например, возьмем уравнение: y = x² + 9x + 18. Здесь a = 1, b = 9, and c = 18.^[1]
2
Воспользуйтесь формулой для вычисления значения координаты x вершины. Вершина также является точкой симметрии параболы. Формула для нахождения координаты x параболы: x = -b/2a. Подставьте в нее соответствующие значения для вычисления x.
- x=-b/2a
- x=-(9)/(2)(1)
- x=-9/2
3
Подставьте найденное значение x в исходное уравнение для вычисления значения y. Теперь, когда вам известно значение x, просто подставьте его в исходное уравнение для нахождения y. Таким образом, формулу для нахождения вершины параболы можно записать в виде функции: (x, y) = [(-b/2a), f(-b/2a)]. Это значит, что для нахождения y необходимо сначала найти x по формуле, а затем подставить значение x в исходное уравнение. Вот, как это делается:
- y = x² + 9x + 18
- y = (-9/2)² + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 — 162 + 72)/4
- y = -9/4
4

Запишите значения x и y в виде пары координат. Теперь, когда вам известно, что x = -9/2, а y = -9/4, запишите их как координаты в виде: (-9/2, -9/4). Вершина параболы находится по координатам (-9/2, -9/4). Если вам нужно нарисовать эту параболу, то ее вершина лежит в нижней точке, так как коэффициент при x² положительный.

Реклама

1

Запишите уравнение. Дополнение до полного квадрата — еще один способ найти вершину параболы. Применив этот метод, вы найдете координаты x и y сразу, без необходимости подставлять x в исходное уравнение. Например, дано уравнение: x² + 4x + 1 = 0.^[2]
2

Разделите каждый коэффициент на коэффициент при x². В нашем случае коэффициент при x² равен 1, поэтому мы можем пропустить этот шаг. Деление на 1 ничего не изменит.
3
Перенесите постоянную в правую часть уравнения. Постоянная — коэффициент без переменной. Здесь это 1. Перенесите 1 вправо путем вычитания 1 из обеих частей уравнения. Вот, как это сделать:^[3]
- x² + 4x + 1 = 0
- x² + 4x + 1 -1 = 0 — 1
- x² + 4x = — 1
4
Дополните до полного квадрата левую часть уравнения. Для этого просто найдите (b/2)² и прибавьте результат к обеим частям уравнения. Подставьте 4 вместо b, так как 4x — это коэффициент b нашего уравнения.
- (4/2)² = 2² = 4. Теперь прибавьте 4 к обеим частям уравнения и получите:
  - x² + 4x + 4 = -1 + 4
  - x² + 4x + 4 = 3
5

Упрощаем левую часть уравнения. Мы видим, что x² + 4x + 4 — полный квадрат. Он может быть записан в виде: (x + 2)² = 3
6

Используйте его для нахождения координат x и y. Вы можете найти x, просто приравняв (x + 2)² к 0. Теперь, когда (x + 2)² = 0, вычисляем x: x =-2. Координата y — это постоянная в правой части полного квадрата. Итак, y = 3. Вершина параболы уравнения x² + 4x + 1 = (-2, 3)

Реклама

Советы

Правильно определяйте a, b, и c.
Записывайте предварительные вычисления. Это не только поможет в процессе работы, но и позволит увидеть, где сделаны ошибки.
Не нарушайте порядок вычислений.

Предупреждения

Проверьте ваш ответ!
Удостоверьтесь, что вы знаете, как определить коэффициента a, b, и c. Если вы не знаете, ответ будет неправильным.
Не паникуйте — решение таких задач требует практики.

Что вам понадобится

Бумага или компьютер
Калькулятор

Об этой статье

Эту страницу просматривали 508 726 раз.

Была ли эта статья полезной?

Источник

Графиком квадратичной функции является парабола.

Если дана квадратичная функция

y=ax2+bx+c¯,гдеa,b,c∈ℝиa≠0,

то абсциссу вершины параболы

(xo;yo)

можно вычислить по формуле:

xo=−b2a

Ординату можно вычислить, подставив полученное значение

в формулу данной функции:

yo=axo2+bxo+c

Пример:

найти координаты вершины параболы

y=−x2+4x−3

(a = -1); (b = 4); (c = -3).

xo=−b2a=−42⋅−1=−4−2=2

Полученное значение подставляем в данную формулу функции:

yo=axo2+bxo+c=−1⋅(2¯)2+4⋅2¯−3=−4+8−3=1

Вершина параболы — точка ((2;1)).

Источник

Определение

Функция вида y=ax²+bx+c, где а, b, с – некоторые числа, причем, а≠0 число, х – переменная, называется квадратичной функцией.

Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Рисунок №1.

Вершина параболы. Формула.

Чтобы найти координаты вершины параболы (х₀; у₀), надо воспользоваться формулой:

х₀=−b2a

для нахождения у₀ можно просто подставить значение х₀ в формулу данной функции y₀=ax²+bx+c вместо х.

Рассмотрим это на примере конкретно заданной функции.

Пример №1

Найти вершину параболы, заданной формулой у=2х² – 8х + 5.

Найдем, чему равны коэффициенты: а=2; b= – 8

Подставим их в формулу и вычислим значение х₀:

х₀=−b2a=82∙2=84=2

Теперь в заданную по условию формулу вместо х подставим найденное значение у₀=2∙2² – 8∙2 + 5=8 – 16 + 5= –3

Итак, мы нашли координаты вершины параболы: (2; –3).

Ответ: (2; –3).

Нули параболы

Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.

Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.

Пример №2

Найти нули функции у=х² +4х – 5

Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х² +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:

х² +4х – 5=0

а=1, b=4, с= –5

D=b² – 4ac=4² – 4∙1∙(−5)=36

x=−b±√D2a

x=−4±√362; х₁=–5; х₂=1

Значит, нули функции равны –5 и 1

Ответ: –5 и 1

Примечание к заданию по нахождению нулей функции без графика

Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).

Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.

Пример №3

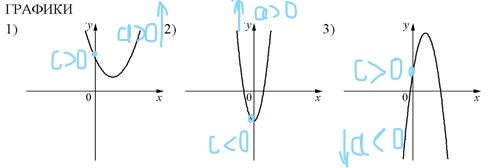
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:

Ответ: 231

Пример №4

Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х₀.

Итак, найдем х₀ для формулы «Б»:

х₀=−b2a=−42∙2=−44=−1

Видим, что х₀ отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.

Запишем в таблицу

Ответ: 231

Задание 11OM21R

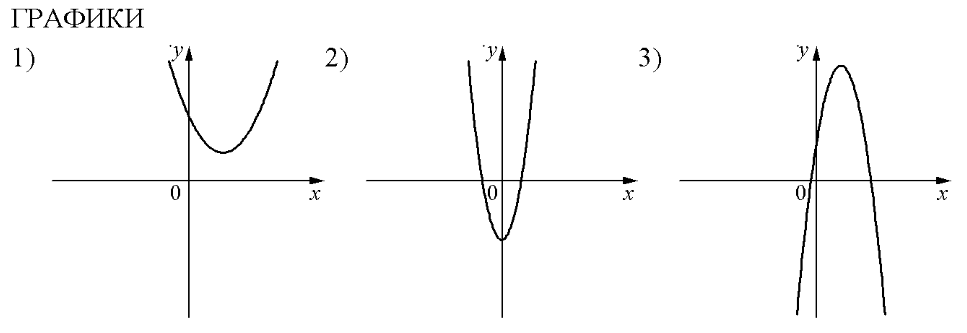
На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов а и с и графиками функций.

КОЭФФИЦИЕНТЫ

А) a>0, с >0 Б) а<0; с>0 В) а>0, с<0

В таблице под каждой буквой укажите соответствующий номер.

Ответ:

Решение

На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a<0 – ветви вниз; а>0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с<0 – пересечение в отрицательном направлении).

Теперь поработаем с графиками и подпишем на каждом из них соответствующие коэффициенты.

Теперь расставим в соответствии с указанными коэффициентами:

А) a>0, с >0 – это график №1

Б) а<0; с>0 – это график №3

В) а>0, с<0 – это график №2

Ответ: 132

pазбирался: Даниил Романович | обсудить разбор

Задание OM1105o

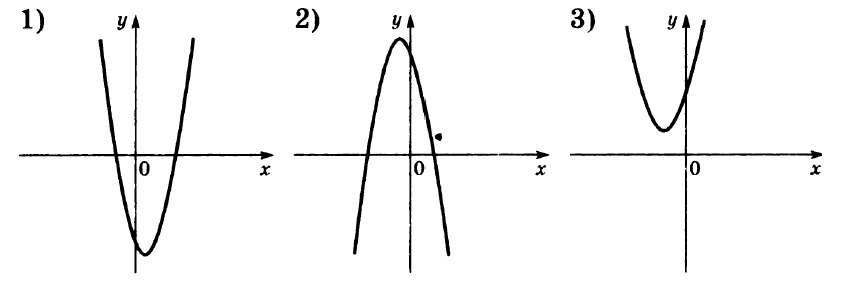
Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А) у=–х²–4х–3 Б) у=–х²+4х–3 В) у=х²+4х+3

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х² (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.

Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3<0 в обоих случаях.

Далее надежнее всего вычислить вершины оставшихся двух парабол из уравнений А и Б по формуле -b/2a. Видим, что случае А (- (-4)) / (2 • -1) = -2, следовательно, вершина левее оси Y, так как x₀ отрицателен, значит, А-1, а Б-2.

Ответ: 123

pазбирался: Даниил Романович | обсудить разбор

Задание OM1101o

На рисунках изображены графики функций вида

y = ax² + bx + c

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Коэффициенты:

А) a > 0, c > 0

Б) a < 0, c > 0

В) a > 0, c < 0

Графики:

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

y = ax² + bx + c

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a < 0, то ветви направлены вниз.

Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.

У первой и третьей ветви направлены вверх, то есть a > 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

если c < 0, то вершина параболы расположена ниже оси x

Так, у первой параболы c < 0, у второй и третьей c > 0.

Из всего вышеперечисленного можно найти ответ:

А) 3

Б) 2

В) 1

Ответ: 321

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 10.8k

Источник

Понятие вершины параболы

Парабола – это геометрическое множество точек, которые равноудалены от точки F, и которая не является частью параболы и прямой, а также не проходит через центр отрезка.

Вершина параболы — это некая точка, которая расположена ближе всего в директрисе параболы. Данная точка является центром любого отрезка, который ограничен точками фокуса параболы и директрисой.

Формула

Каноническое уравнение параболы выглядит следующим образом:

[y^{2}=2 p x]

Где: [p] — параметр параболы; [x] — ось данной параболы.

Данное уравнение будет справедливо только для параболы, вершина которой проходит через центр осей.

Чтобы определить принадлежность точки к графику заданной параболы, нужно точку подставить в уравнение:

[y=a x^{2}+b x+c]

где:

a, b, c — заданные коэффициенты;
х — ось координатной прямой.

Определение вершины кубической параболы

Определение

Кубическая парабола – плоская алгебраическая кривая третьего порядка.

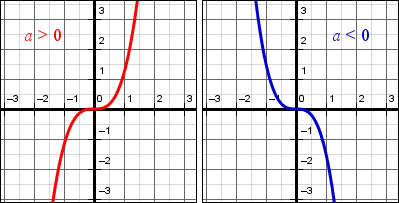
Ее каноническое уравнение в прямоугольной декартовой системе координат имеет вид у = ах³, где а ≠ 0.

Для кубической параболы характерен центр симметрии в самом начале координат. Данная точка является точкой перегиба кривой. Касательная к кубической параболе, в этой же точке именуется как ось абсцисс.

Рисунок 1. Графики кубической параболы

Для того, чтобы определить точки вершин кубической параболы, нужно вычислить ее производную. Точки вершин, иначе еще называют точками минимума и максимума.

После того, как определится производная, нужно ее значение приравнять к нулевому. Затем можно приступать к вычислению значений x и y.

Определение вершин параболы, которая задана квадратичной функцией

Рисунок 2. Уравнение и график параболы квадратичной функции

Квадратичная функция вида: [y=a x^{2}+b x+c] очень часто используется для того, чтобы задать значения параболы.

Вершина такой функции, всегда находится в произвольной точке.

В технических науках не существует единой формулы, чтобы вычислить сразу две вершины параболы. Однако, довольно легко определяются координаты вершины, по уже упомянутому уравнению.

Нет времени решать самому?

Наши эксперты помогут!

Алгоритм решения задач по определению точек вершин параболы

Необходимо выписать коэффициенты a, b, c по условию заданного уравнения. При условии, что коэффициент а будет иметь положительное значение, можно сделать вывод: ветви параболы направлены вверх. Следовательно, если значение отрицательное, то ветви будут направлены вниз.
Вторым действием определяется абсцисса вершины параболы.
(x) по следующей формуле [x=-frac{b}{2 a}], для этого необходимо применить коэффициенты a, b, c из заданного по заданию уравнения.
Найденное значение x нужно подставить в уравнение, решить его, и тем самым будет выполнен окончательный расчет.
В ответ записать найденные координаты вершин параболы x и y.

Пример решения уравнения параболы

Рассмотрим подробно на примере, решение задач данной категории.

Запишем данное уравнение следующего вида: [y=x^{2}-5 x+7].

Воспользуемся алгоритмом решения, и выполним следующие действия:

Зададим коэффициенты параболы. Они равны следующим значениям: a=1, b=-5, с=7.
Чтобы вычислить вершину x параболы, нужно известные коэффициенты a=1, b=-5 подставить в формулу: [x=-frac{b}{2 a}=frac{-5}{2}=2,5].
Вычисленное значение х, нужно подставить в исходное уравнение: [y=2,5^{2}-5 cdot 2,5+7=0,75]
Координаты вершины параболы будут равняться следующим значения: (0,75 и 2,5).

Источник