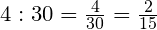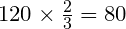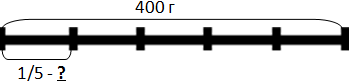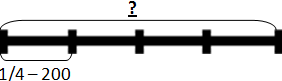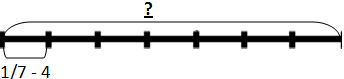Задачи на дроби
- Выражение части в долях целого
- Нахождение дроби от числа
- Нахождение числа по его дроби
Выражение части в долях целого
Чтобы выразить часть в долях целого, нужно часть разделить на целое.
Задача. В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?
Решение:
Ответ: В классе отсутствует 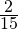
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
Решение: Чтобы найти 
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
Решение:
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение числа по его дроби
Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:
Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.
Задача 1. Потратили 50 рублей, это составило 
Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:
50 · 6 = 300 (р.).
Ответ: Первоначальная сумма — 300 рублей.
Задача 2. Потратили 600 рублей, это составило 
Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):
600 : 2 · 3 = 900 (р.).
Ответ: Первоначальная сумма — 900 рублей.
Второй способ нахождения целого по его части:
Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.
Задача 3. Отрезок AB, равный 42 см, составляет 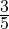
Решение:
Ответ: Длина отрезка CD 70 см.
Задача 4. В магазин привезли арбузы. До обеда магазин продал 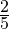
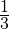
Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):
Итак, мы узнали, что 80 арбузов составляет 

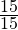
2) 80 : 4 · 15 = 300 (арбузов).
Ответ: Всего в магазин привезли 300 арбузов.
Анализ методической литературы и личного опыта
при проведении уроков по теме “Обыкновенные
дроби” показывает необходимость обобщения и
систематизации материала, связанного с решением
задач на дроби.
Требования к математической подготовке
учащихся 5–6-х классов общеобразовательных
учреждений предполагают, что в результате
изучения курса математики учащиеся должны “решать
основные задачи на дроби”, уметь находить часть
числа и числа по его части [2;6]. С учетом
этого строится тематическое планирование
учебного материала, ориентированное на учебник
“Математика, 5” авторов Н.Я.Виленкина, В.И.Жохова,
А.С.Чеснокова, С.И.Шварцбурда, где говорится, что “с
пониманием смысла дроби связаны три основные
задачи на дроби, осознанного решения которых
важно добиться от учащихся”.
В задачах на дроби речь идет о некоторой
величине а, принятой за единицу (“целое”), и
некоторой ее части в, выраженной дробью :
Тип задачи определяется тем, что неизвестно – а,
в или .
Соответственно, выделяются три типа задач на
дроби:
1. Задачи на нахождение части от числа,
выраженной дробью:
1 – а
– ?
Чтобы найти часть числа, выраженную дробью,
можно это число разделить на знаменатель дроби и
умножить на ее числитель:
b = a : n • m
2. Задачи на нахождение числа по его части,
выраженной дробью:
1 – ?
– в
Чтобы найти число по его части, выраженной
дробью, можно эту часть разделить на числитель
дроби и умножить на ее знаменатель:
a = в : т • п
3. Задачи на нахождение дроби, которую одно
число составляет от другого.
1 – а
? – в
Чтобы найти дробь, которую одно число
составляет от другого, можно первое число
разделить на второе:
= а: в
При изучении темы важно научить учащихся
понимать, что принимается за единицу (целое) в
каждой конкретной задаче, на сколько долей она
разбивается, каково значение одной доли, сколько
долей берут, каково значение всех взятых долей,
каковы правила нахождения дроби от числа, числа
по дроби и дроби, которую одно число составляет
от другого.
Представленный ниже материал можно
использовать как в отдельных фрагментах уроков,
так и в специально выделенных уроках по решению
задач на дроби.
1. Задачи на нахождение части от числа,
выраженной дробью
| № | Текст задачи | Краткая запись | Схема | Решение |
| 889 | Купили кусок ткани длиной 2 м 50 см и из платье для куклы. Сколько сантиметров ткани ушло на это платье? |
250см -1
?см — |
 |
250:5·1=50(см)
Ответ: 50см |
| 890 | От дыни массой 2 кг 400 г Ване отрезали каждого отрезанного куска? Сколько граммов дыни осталось? |
2400г – 1
?г – ?г – ост.–?г |
 |
2400:5·1=480(г)
2400:6·1=400(г) 3) 2400––(480+400)= =1520(г)
Ответ: 480г, 400г, 1520г |
| 891 | Петя готовил уроки 1 ч 40 мин. На математику он потратил этого времени, а на историю – минут Петя готовил уроки по математике и сколько по истории? |
120мин-1
?мин- ост.- ?мин ?мин – |
120:5·1=24(мин) 120-24=96(мин) 96:4·1=24(мин)
Ответ: 24 мин, 24 мин |
|
| 902 | На базу в Антарктиду доставили 22 собаки. Из собак составили упряжку, на которой отправились в поход. Сколько собак не вошло в упряжку? |
22с. – 1
?с. – ост. –?с. |
 |
1) 22:11·5=10 (с.)
2) 22-10=12 (с.)
Ответ: 12 собак |
| К задачам №№900; 901; 903; 909; 928; 929; 960; 968; 1134(1,2); 1141; 1337; 1338; 1296(1,2); 1681(1,2); 980; 983; 1001; 1014; 1015; 1019;1043; 1044; 1733; 1343; 1344; 1345; 1377; 1494; 1595 можно |
2. Задачи на нахождение части от числа,
выраженной дробью
| № | Текст задачи | Краткая запись | Схема | Решение |
| 904 | Сколько молока в бидоне, если составляет 13 л? |
13 л – ? л – 1(все молоко) |
 |
13:1·5=65(л)
Ответ: 65 л |
| 905 | Дорога от Фабричного до Кратова равна 5 км, что составляет Найдите расстояние от Фабричного до Ильинского. |
5 км – ? км – 1(расстояние от Ф.до И.) |
 |
5:5·8=8(км)
Ответ: 8 км |
| 906 | Человек прошел дороги, если он прошел 4 км? |
4 км – ? км – 1(вся дорога) |
 |
4:2·3=6(км)
Ответ: 6 км |
| 907 | Велосипедист проехал дороги, если он проехал 40 км? |
40 км – ? км – 1(вся дорога) |
 |
40:2·9=180(км)
Ответ:180 км |
| 908 | Миша исписал 10 страниц тетради, что составляет всей тетради. Сколько страниц в тетради? |
10 стр. – ? стр. – 1(вся тетрадь) |
 |
10:5·6=12 (стр.)
Ответ: 10 страниц |
| К задачам №№930; 931; 962; 969; 981; 1046; 1824; 982; 1002; 1020; 1021; 1731; 1732; 1346; 1347; 1378; 1481(1,2); 1495; 1594 можно составить аналогично краткую |
3. Задачи на нахождение дроби, которую одно
число составляет от другого
| № | Текст задачи | Краткая запись | Схема | Решение |
| 896 | Дорога от Фабричного до Ильинского равна 8 км. Лена прошла по этой дороге 3 км. Какую |
8 км – 1
3 км – ? часть (от всей дороги) |
 |
3:8= Ответ: |
| 897 | В январе 31 день, а в году 365 дней. Какую часть года составляет январь? |
365 дней – 1
31 день (январь) – ? часть (от |
 |
31:365= Ответ: |
| 898 | В январе 1995 года с 1 января по 10 января были зимние каникулы. 15, 22 и 29 января были воскресными днями, а остальные – учебными. Какую часть января составили свободные от учебы дни? Какую |
31 день – 1
13 дней (свободные) – ? часть 18 дней (учебные) – ? часть (от января) |
 |
13:31= 18:31=
Ответ: |
| 899 | Площадь поля 16 км2. Пшеницей засеяли 11 км2, а рожью – 5 км2. Какая часть поля засеяна пшеницей и какая рожью? |
16 км2 – 1
11 км2 – ? часть (от 5 км2 – ? часть (от поля) |
 |
1) 11:16= 2) 5:16=
Ответ: |
| К задачам №№926; 956; 957; 958; 959; 961; 1037(1,2); 1045; 1069; 1070; 1727; 1822; 1823; 1245; 1013; 1729; 1730 можно |
Литература:
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд
С.И. Математика: учебник для 5 класса
общеобразовательных учреждений в двух частях.
Часть 2 (Дробные числа)/, – 18-е издание. – Москва:
Мнемозина, 2006. - Жохов В.И. Разработки уроков, нормативные и
контрольно-методические материалы: Математика,
5-6: Книга для учителя. – Москва: ИЛНКСА, 2007. - Шевкин А. В. Материалы курса “Текстовые задачи в
школьном курсе математики”: Лекции 1-4, 5-8. –
Москва: Педагогический университет “Первое
сентября”, 2006. - Петерсон Л.Г. Математика. 4 класс. Часть 1, 2. –
Москва: Издательство “Ювента”. 2005. - Дорофеев Г.В., Петерсон Л.Г. Математика. 5 класс.
Часть 2. – Москва: Издательство “Ювента”. 2006. - Программы для общеобразовательных учреждений.
Математика/ Сост. Г.М. Кузнецова, Н.Г. Миндюк, –
Москва, 2000.
Решение задач с помощью дробных рациональных уравнений
Примеры
Пример 1. От посёлка до речки 60 км. Утром турист на скутере отправился на речку. Вечером он возвратился в посёлок, но при этом ехал со скоростью на 10 км/ч меньшей и потратил на дорогу на 18 мин больше. Сколько времени ехал турист от речки к посёлку?
Пусть t — время вечером, на дорогу от речки к посёлку.
Тогда время утром, на дорогу от посёлка к речке t- $frac<18><60>$ = t-0,3 (ч)
По условию разность скоростей равна 10:
$$1,8=t(t-0,3), t neq 0, t neq 0,3$$
$$ D = 0,3^2-4 cdot (-1,8) = 0,09+7,2=7,29 = 2,7^2 $$
$$ t = frac<0,3 pm 2,7> <2>= left[ begin t_1 = -1,1 \ t_2 = 1,5 end right. $$
Выбираем положительный корень, t = 1,5 ч
Пример 2. Катер прошёл по течению 120 км. На этот же путь против течения от тратит времени в 1,5 раза больше. Найдите скорость течения, если скорость катера в стоячей воде 20 км/ч.
Пусть u — скорость течения
По условию время против течения в 1,5 раз больше:
$$ 1,5(20-u) = 20+u, u neq pm 20 $$
Пример 3. В раствор, содержащий 50 г соли, добавили 150 г воды. В результате концентрация соли уменьшилась на 7,5%. Найдите первоначальную массу раствора.
Пусть x — масса воды в первоначальном растворе, в граммах.
По условию разность концентраций:
$$ 50 cdot 150 = frac<75> <1000>(x+50)(x+200), x neq -50, x neq -200 $$
$$ D = 250^2-4 cdot (-90000) = 62500+360000 = 100(625+3600) = $$
$$ = 100 cdot 4225 = 650^2 $$
$$ x = frac<-250 pm 650> <2>= left[ begin x_1 = -450 \ x_2 = 200 end right. $$
Выбираем положительный корень x=200 г – начальное количество воды в растворе. Начальная масса всего раствора: 50+200 = 250 г.
Пример 4. Мастер и его ученик, работая вместе, выполняют норму на 8 ч. Если каждый работает самостоятельно, то мастер тратит на выполнение нормы на 12 ч меньше, чем ученик. Сколько часов тратит каждый из них на выполнении нормы?
Пусть N изделий – это норма, t — время, потраченное мастером.
Из последней строки таблицы получаем:
$$ 8(2t+12) = t(t+12), t neq 0, t neq -12$$
$$ t^2-4t-96 = 0 Rightarrow (t-12)(t+8) = 0 Rightarrow left[ begin t_1 = -8 \ t_2 = 12 end right. $$
Выбираем положительный корень, t=12 ч — время, которое мастер потратит самостоятельно. Ученик потратит 12+12=24 ч.
Ответ: 12 ч и 24 ч
Пример 5*. Один фрилансер может выполнить проект на 12 дней быстрее, чем второй. Над новым проектом первый фрилансер сначала проработал самостоятельно 6 дней, а затем к нему присоединился второй. Через 3 дня совместной работы frac<3> <5>проекта было готово.
За сколько дней каждый из фрилансеров может выполнить проект самостоятельно? За сколько дней проект был фактически выполнен?
Пусть d — количество дней первого фрилансера при самостоятельной работе.
Решение задач с помощью дробных рациональных уравнений табличным методом
Разделы: Математика
Математика в наши дни проникает во все сферы жизни. Овладение практически любой профессией требует тех или иных знаний по математике. Особое значение в этом смысле имеет умение смоделировать математически определённые реальные ситуации. Данное умение интегрирует в себе разнообразные специальные умения, адекватные отдельным элементам математических знаний, их системам, а также различные мыслительные приёмы, характеризующие культуру мышления.
В школьной математике знакомство с математическим моделированием основано, прежде всего, на решении текстовых задач. Текстовая задача несет в себе важные элементы математического моделирования. Решая ее, учащийся некие производственные, экономические, житейские связи зашифровывает с помощью математических символов, придавая им абстрактную математическую форму. Решая уравнения, учащийся расшифровывает результат, согласуя его со здравым смыслом. Вот почему решению текстовых задач, этому важнейшему мостику между математикой и ее приложениями должно уделяться особое внимание. При этом представляется, что техника решения текстовых задач может отрабатываться на любых задачах. Было бы наивным думать, что задача на движение, начинающаяся словами «Два автомобиля:» непременно предназначена для будущих водителей, а для школы со спортивным уклоном она должна начинаться словами «Два лыжника:».
Применение на практике различных задач на составление уравнений позволяет создавать такие учебные ситуации, которые требуют от учащегося умения смоделировать математически определённые физические, химические, экономические процессы и явления, составить план действия в решении реальной проблемы. Практика последних лет говорит о необходимости формирования умений решения задач на составление уравнений различных типов ещё и в связи с включением их в содержание ГИА и ЕГЭ.
Однако, анализ образовательной практики по данному направлению говорит о том, что значительная часть учащихся испытывает серьёзные затруднения при решении задач на составление уравнений. В большей степени это связано с недостаточной сформированностью у учащихся умения составлять план действий, алгоритм решения конкретной задачи, культурой моделирования явлений и процессов. Большинство учащихся решают такие задачи лишь на репродуктивном уровне.
Решению текстовых задач предшествует достаточно долгое время, отводимое на отработку решения уравнений. Начиная с 8 класса, как только выучены дробные рациональные выражения, решения задач по алгебре практически все сводятся к решению дробных рациональных уравнений, которые, в свою очередь, включают чаще всего решение квадратных уравнений.
В 8 классе решение задач с помощью дробных рациональных уравнений как показывает опыт эффективнее решать табличным методом, так как он является более наглядным, что важно для подготовки к ГИА в 9 классе.
Все задачи, решаемые с помощью дробных рациональных уравнений, можно разделить на несколько групп:
- Задачи на движение по местности.
- Задачи на движение по воде.
- Задачи на работу.
- Задачи на нахождение дробей и т.д.
Начинать обучение следует с простых задач, условия которых полностью соответствуют названиям основных типов, и сводящихся к решению дробных рациональных уравнений. Затем можно приступать к решению более сложных задач. Рекомендуется подобрать разноуровневые задачи по каждому типу, что дает возможность работать со школьниками разных математических способностей.
Мы стараемся научить детей строить таблицы с данными величинами задачи, слева обозначаются объекты (автомобили, лодки, пешеходы, самолеты и т.д.), сверху в колонках — величины, характеризующие данную задачу, и обязательно единицы их измерения. И дети понимают, что из трех величин, зная две, всегда можно записать третью.
Приведем пример оформления задачи:
Автобус-экспресс отправился от вокзала в аэропорт, находящийся на расстоянии 120км от вокзала. Пассажир, опоздавший на 10 минут на автобус, решил добраться до аэропорта на такси. Скорость такси на 10км/ч больше скорости автобуса. С какой скорость ехал автобус, если он приехал в аэропорт одновременно с такси?
Пусть 
| Скорость (км/ч) | Время (ч) | Путь (км) | |
| Автобус |  |
 |
 |
| Такси |  |
 |
 |
Т.к. по условию задачи пассажир опоздал на автобус на 10 минут =


720(х+10) — 720х= х (х+10),
Далее решая квадратное уравнение, получаем:
-90 — не входит в ОДЗ, значит, скорость автобуса равна 80 км/ч.
Основная часть класса уверенно заполняет таблицу и составляет уравнение.
В зависимости от выделенного времени, обучаемым может быть предложен широкий спектр мероприятий — семинары, кружки, факультативы, индивидуальные и групповые консультации и т.д., в рамках которых обучаемые более глубоко осваивают решение задач с помощью уравнений.
Практикум по решению задач табличным методом с помощью дробных рациональных уравнений можно провести во второй половине дня на групповой консультации по математике, что целесообразно в рамках школы полного дня.
Список предлагаемых задач:
Числитель обыкновенной дроби на 4 меньше ее знаменателя. Если к числителю этой дроби прибавить 19, а к знаменателю 28, то она увеличится на 
Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 часа. Какова скорость течения реки?
Два комбайна убрали поле за 4 дня. За сколько дней мог убрать поле каждый комбайн, если одному из них для выполнения этой работы потребовалось бы на 6 дней меньше, чем другому?
Моторная лодка прошла против течения 8 км и вернулась обратно, затратив на обратный путь на 30 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
Расстояние 700 км экспресс проходит на 4 часа быстрее товарного поезда, так как его скорость больше скорости товарного поезда на 20 км/ч. Определите скорость каждого из поездов, если известно, что они движутся с постоянной скоростью без остановок.
Мастеру на выполнение заказа потребуется на 5 дней меньше, чем его ученику, но при совместной работе они выполнят заказ на 4 дня быстрее, чем мастер, работающий в одиночку. За сколько дней выполнит заказ мастер, работая в одиночку?
На участке пути длиной 300 км поезд увеличил скорость на 10 км/ч, в результате чего прибыл на конечную станцию на 1 час раньше, чем планировалось по расписанию. С какой скоростью должен был идти поезд по расписанию?
Прозаик хочет набрать на компьютере рукопись объемом 450 страниц. Если он будет набирать на 5 страниц в день больше, чем запланировал, то закончит работу на 3 дня раньше. Сколько страниц в день планирует набирать прозаик?
Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 19 км. Пешеход прошел путь из А в В за 5 часов. Время его движения на спуске составило 4 часа. С какой скоростью пешеход шел на спуске, если скорость его движения на подъеме меньше скорости движения на спуске на 1 км/ч?
Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 88 км. Возвращаясь из В в А, он ехал поначалу с той же скоростью, но через 2 часа пути вынужден был сделать остановку на 10 минут. После этого он продолжил путь в А, увеличив скорость на 2 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
Количество решаемых задач может меняться в зависимости от отводимого на это время.
Используемая литература:
Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
- Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
источники:
http://urok.1sept.ru/articles/571941
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami
Для того чтобы решать задачи, а особенно с дробями, необходимо чертить схемы.
Рассмотрим задачи из учебника Петерсон Л.Г. 4 класс.
Задачи на с.67
Решение:
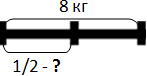
а) Целый арбуз обозначим отрезком. В задаче сказано, что арбуз разделили пополам – это на 2. Значит, отрезок надо разделить на 2 части. Частей немного, поэтому можно начертить отрезок длиной 2, 4 и т.д. см.
2 см – слишком маленький, поэтому чертим длиной 4 см и делим его пополам.
Надо узнать часть от целого (см. статью здесь), т.е. 1/2 от 8. Значит,
8 : 2 = 4 (кг)
Ответ: половина арбуза весит 4 кг.
б) Яблоко – это целое, обозначим отрезком. Надо найти 1/5. Значит, чертим отрезок длиной 5 или 10 см и делим его на 5 равных частей.
Надо узнать часть от целого, т.е. 1/5 от 400. Значит,
400 : 5 = 80 (г)
Ответ: 1/5 часть яблока весит 80 г.
в) эта задача другого вида – нахождение целого по части (см. статью здесь).
Садовый участок – это целое, нам сказано, что известна 1/4, значит, отрезок чертим длиной 4 или 8 кв.м. Удобнее – 8 – будет нагляднее. Делим его на 4 равные части.
Надо узнать целое по известной части: 1/4 это 200. Значит,
200 х 4 = 800 (кв.м)
Ответ: площадь садового участка 800 кв.м.
г) Всех учеников класса обозначим отрезком – это целое. Нам известна 1/7 часть класса. Значит, отрезок надо начертить длиной 7 или 14 см. Но 14 – очень длинный, поэтому начертим длиной 7 см и делим его на 7 равных частей.
Надо узнать целое по его части: 1/7 это 4. Значит,
4 х 7 = 28 (ч.)
Ответ: в классе 28 учеников.
Задачи, которые мы сегодня разобрали, являются самыми простыми. При решении необходимо пользоваться памяткой.
Когда Вы научитесь решать простые задачи, то со сложными справитесь так же просто.
Похожие статьи
Математика
5 класс
Урок № 49
Задачи на дроби (нахождение части от целого)
Перечень рассматриваемых вопросов:
– обыкновенная дробь;
– числитель, знаменатель обыкновенной дроби;
– сократимая, несократимая дробь;
– задачи на дроби.
Тезаурус
Дробьв математике – это число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя.
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя.
Сократимаядробь–это дробь,у которой числитель и знаменатель имеют общий положительный делитель, не равный нулю и единице.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС//С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
«Где учение, там и умение», – гласит известная поговорка.
Сегодня мы научимся не только находить части от целого, но применять свои умения для решения интересных заданий.
В окружающем нас мире очень часто приходится находить часть от чего-либо.
Например, мы можем услышать фразу «Будет сделано через четверть часа». А сколько это минут? Мы знаем, что в 1 часе 60 минут, т. е. чтобы найти четверть часа, нужно разделить шестьдесят на четыре, и получим искомый ответ.
60 : 4 = 15 минут. Четверть часа это 15 минут.
А если нужно найти две трети часа, как быть в этом случае?
Для этого мы снова переведём 1 час в минуты, что соответствует 60 минутам. Будем считать, что 60 минут – это 3/3 часа.
Тогда сначала найдём 1/3 часа. Для этого 60 : 3 = 20 минут. А теперь остаётся найти две части из трёх, т. е. умножить двадцать минут на два, получаем сорок минут.
20 минут · 2 = 40 минут. Это и есть то время, которое соответствует двум третям часа.
Итак, сформулируем правило нахождения части от целого: если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби, и результат умножить на её числитель.
Под нахождением дроби от числа подразумеваетсянахождение той части числа, которая выражена дробью.
Решим ещё одну задачу.
Маша готовит домашнее задание 2 часа 30 минут.
На русский язык она тратит 2/3 этого времени, а на биологию ½ оставшегося времени.
Сколько минут Маша готовит домашнее задание по русскому языку и биологии?
Решение: для решения задачи переведём время в минуты.
1 ч = 60 мин.
2 ч 30 мин. = 2 · 60 + 30 = 150 мин.
Далее найдем время, затраченное на выполнение задания по русскому языку.
150 : 3 · 2 = 100 мин.
Получаем, что Маша выполняет домашнее задание по русскому языку сто минут.
Теперь найдём оставшееся время, как разницу между общим временем и временем выполнения заданий по русскому языку.
150 – 100 = 50 мин.
Остаётся найти половину от этого времени:
50 : 2 = 25 мин.
Это и есть время выполнения заданий по биологии.
Ответ: 100 мин. – на русский язык; 25 мин. – на биологию.
Решим задачу. У хозяина имеется 2 поля. С первого поля он собрал 50 ц картофеля, с другого – в 4 раза больше. 4/5 части всего картофеля он убрал в мешки по 50 кг каждый. Сколько мешков картофеля получилось?
Решение: для решения этой задачи найдём сначала, сколько хозяин собрал картофеля со 2 поля.
1) 50 · 4 = 200 (ц) – картофеля хозяин собрал со 2 участка.
Далее найдём, сколько всего картофеля он собрал с двух участков.
2) 200 + 50 = 250 (ц) – картофеля хозяин собрал с двух участков.
Далее найдём часть, которая будет в мешках.
3) 250 : 5 · 4 = 200 (ц) – картофеля насыпали в мешки.
Теперь найдём, сколько мешков потребуется, для этого 200 ц переведём в кг и разделим на 50.
4) 20000 кг : 50 кг = 400 (мешков) – картофеля получилось.
Ответ: 400 мешков.
Тренировочные задания
№ 1. В 5 классе учится 25 учеников, из них 2/5 класса отличники. Сколько отличников в классе?
Решение: для решения этой задачи нужно использовать правило нахождения части от целого: чтобы найти часть, нужно целое разделить на знаменатель дроби и результат умножить на её числитель.
25 : 5 · 2 = 10 человек
Ответ: 10 человек.
№ 2. Периметр треугольника равен 40 см. Первая сторона составляет 3/10 от периметра, другая составляет 3/2 от первой стороны. Чему равна третья сторона треугольника?
Решение: для решения этой задачи сначала нужно вспомнить, что периметр – это сумма длин всех сторон треугольника, т. е. сумма длин трёх сторон.
Теперь найдём каждую сторону, исходя из условия задачи.
1) 40 : 10 · 3 = 12 см – первая сторона.
2) 12 : 2 · 3 = 18 см – вторая сторона.
Теперь от периметра отнимем сумму длин двух сторон и получим третью сторону.
3) 40 — (18 + 12) = 10 см – третья сторона.
Ответ:10см.