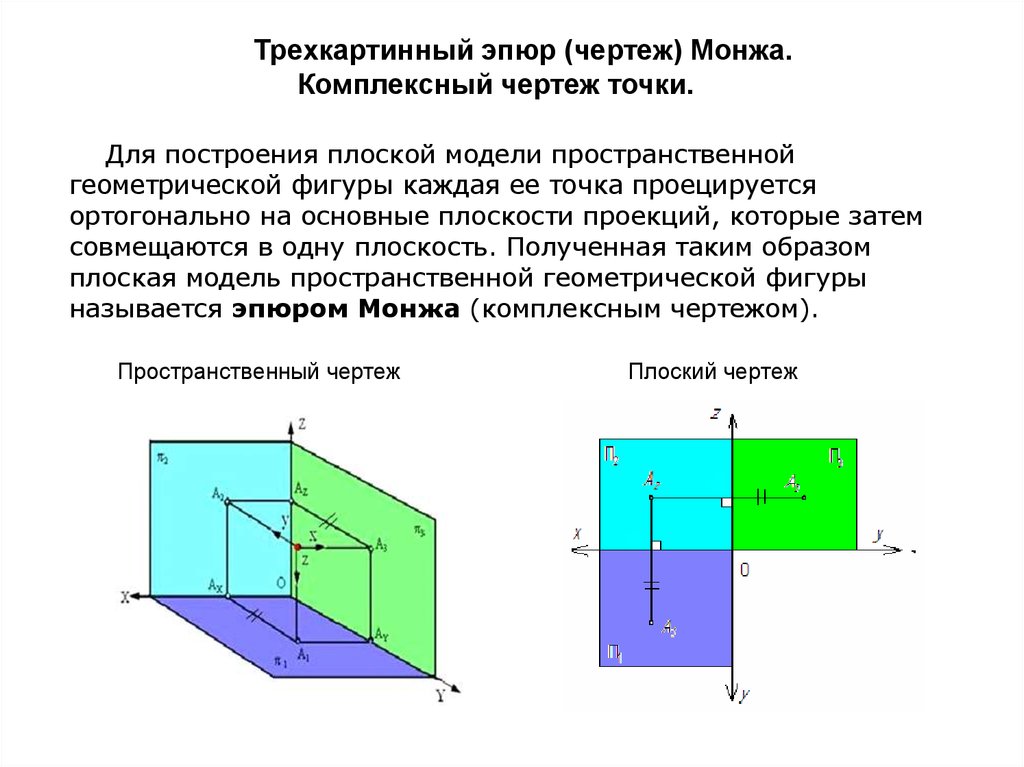
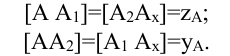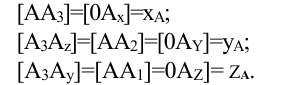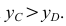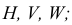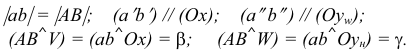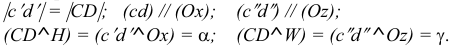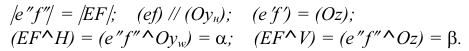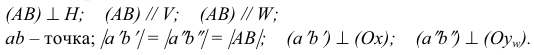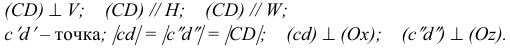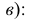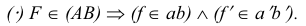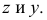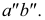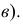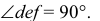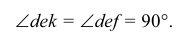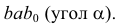Построение ортогональных проекций точек
Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.
По заданному комплексному чертежу точек A и B необходимо:
- Записать их координаты.
- Достроить проекции т. A и B на плоскость П3.
- Определить положение точек в пространстве (октант или плоскость проекций).
- Построить наглядное изображение точек в системе плоскостей П1, П2, П3.
Определение координат точек по их проекциям
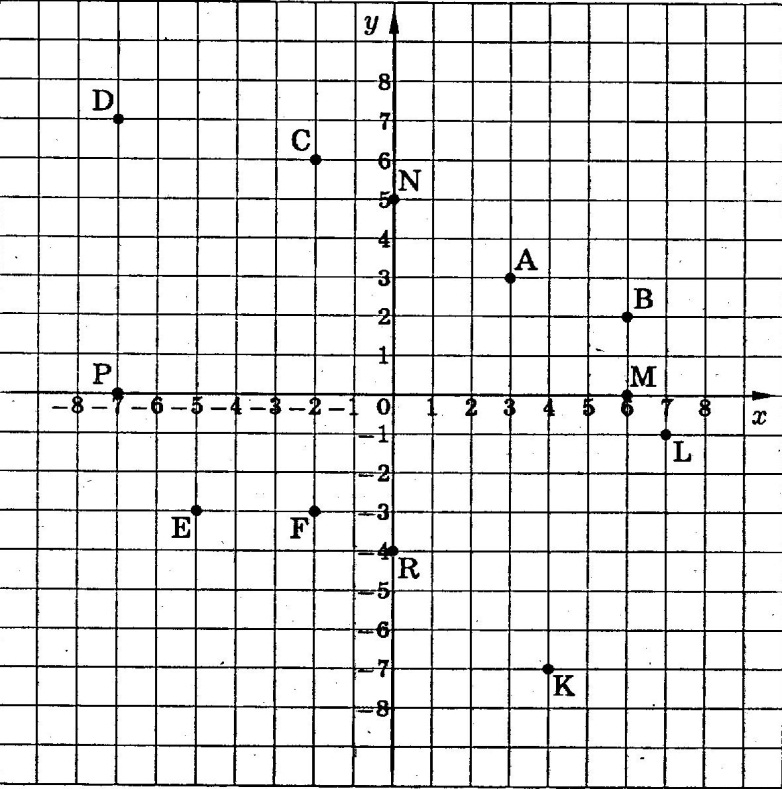
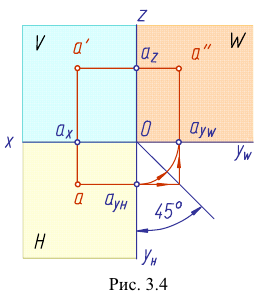
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно Aх, Aу. Координата х для т. A равна длине отрезка AхO со знаком плюс, так как Aх лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка AуO со знаком минус, так как т. Aу лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A» имеет координаты х и z. Опустим перпендикуляр из A» на ось z и найдем Az. Координата z точки A равна длине отрезка AzO со знаком минус, так как Az лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).
Координаты т. B можно записать в виде B (x, y, z). Рассмотрим горизонтальную проекцию точки B – т. В’. Так как она лежит на оси х, то Bx = B’ и координата Bу = 0. Абсцисса x точки B равна длине отрезка BхO со знаком плюс. С учетом масштаба чертежа x = 30. Фронтальная проекция точки B – т. B˝ имеет координаты х, z. Проведем перпендикуляр из B» к оси z, таким образом найдем Bz. Аппликата z точки B равна длине отрезка BzO со знаком минус, так как Bz лежит в области отрицательных значений оси z. С учетом масштаба чертежа определим значение z = –20. Таким образом, координаты B (30, 0, -20). Все необходимые построения представлены на рисунке ниже.
Построение проекций точек
Точки A и B в плоскости П3 имеют следующие координаты: A»’ (y, z); B»’ (y, z). При этом A» и A»’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B» и B»’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса AуO. После этого проведем перпендикуляр из Aу до пересечения с перпендикуляром, восстановленным из точки A» к оси z. Точка пересечения этих двух перпендикуляров определяет положение A»’.
Точка B»’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B» к оси z. Точка пересечении этого перпендикуляра с осью z есть B»’.
Определение положения точек в пространстве
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П1, П2 и П3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П2.
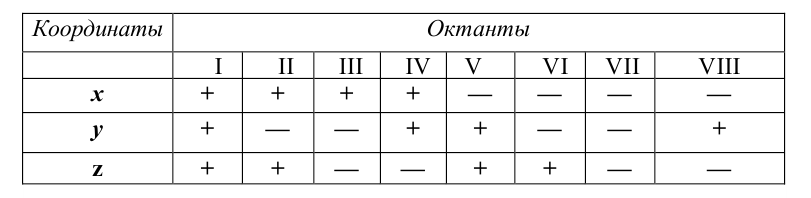
Другим вариантом решения данной задачи является метод исключений. Например, координаты точки A (10, -30, -10). Положительная абсцисса x позволяет судить о том, что точка расположена в первых четырех октантах. Отрицательная ордината y говорит о том, что точка находится во втором или третьем октантах. Наконец, отрицательная аппликата z указывает на то, что т. A расположена в третьем октанте. Приведенные рассуждения наглядно иллюстрирует следующая таблица.
| Октанты | Знаки координат | ||
| x | y | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Координаты точки B (30, 0, -20). Поскольку ордината т. B равна нулю, эта точка расположена в плоскости проекций П2. Положительная абсцисса и отрицательная аппликата т. B указывают на то, что она расположена на границе третьего и четвертого октантов.
Построение наглядного изображения точек в системе плоскостей П1, П2, П3
Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П1, П2, П3, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.
Построение наглядного изображения т. A (10, -30, -10) начнем с её горизонтальной проекции A’. Отложив по оси абсцисс и ординат соответствующие координаты, найдем точки Aх и Aу. Пересечение перпендикуляров, восстановленных из Aх и Aу соответственно к осям x и y определяет положение т. A’. Отложив от A’ параллельно оси z в сторону её отрицательных значений отрезок AA’, длина которого равна 10, находим положение точки A.
Наглядное изображение т. B (30, 0, -20) строится аналогично – в плоскости П2 по осям x и z нужно отложить соответствующие координаты. Пересечение перпендикуляров, восстановленных из Bх и Bz, определит положение точки B.
Точка – это геометрический абстрактный объект, который имеет координаты. Точки также участвуют в создании чертежа.
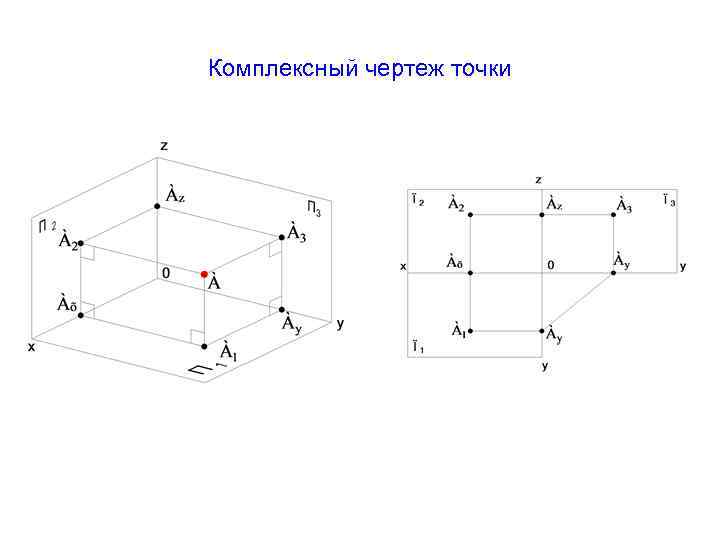
Комплексный чертеж и координаты точки
Комплексным называется чертеж, который был получен на фронтальной и горизонтальной плоскости проекции. Комплексный чертеж получается путем совмещения трех плоскостей проекций в одну.
Существует строгий порядок расположения проекций на чертеже, горизонтальная проекция должна располагаться под фронтальной, профильная проекция должна располагаться справа от фронтальной.
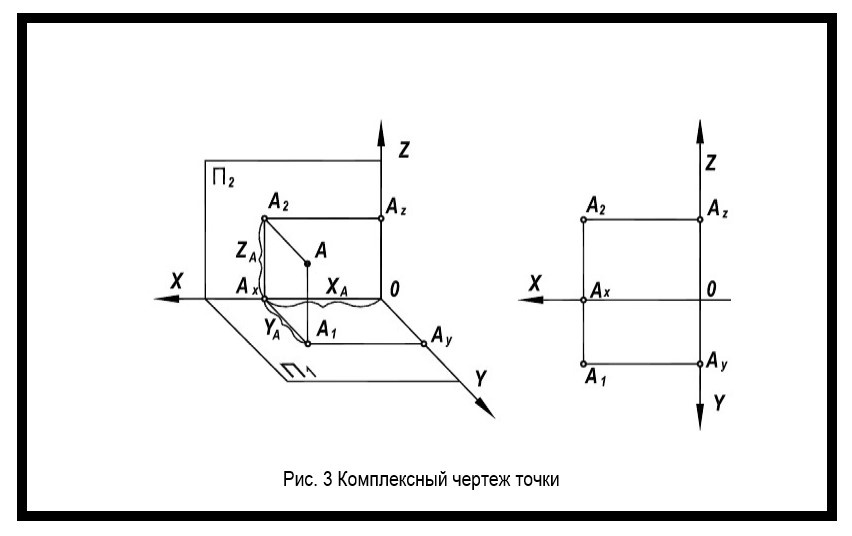
Рисунок 1. Координаты точки
Как найти точки на чертеже
Рассматривая предмет как сочетание граней, вершин и ребер мы можем находить проекции отдельных точек. Для начала нужно определить, какой плоскости или грани точка принадлежит. Затем находят горизонтальные проекции точки, для этого проводят вертикальную прямую линию связи из проекции точек. Видимость проекций определяется исходя из направления взгляда.
Как правильно расставлять точки
Чтобы правильно вычертить вид детали, необходимо уметь строить проекции. С помощью проекций можно определить местоположение точки. Вспомогательные линии позволяют определить место, где ее можно поставить и используются в качестве опорных. Вспомогательные линии двух проекций пересекаются под углом в 45 градусов. В местах пересечения линий связи с проекциями поверхности расставляют точки.
Видимые и невидимые точки
Видимые проекции изображают на чертеже без скобок, а невидимые в скобках, например, А’’ относится к видимой проекции, а (B’’) к невидимой.
Рисунок 2. Видимые и невидимые точки
Точки сопряжения
В месте, где сопрягаются две линии образуется точка перехода или точка сопряжения. Для нахождения точки сопряжения линий прямого угла используется циркуль, его ставят в вершину угла и проводят дугу R до пересечения со сторонами. Чтобы найти центр сопряжения из найденных точек снова проводят окружности радиусом R, в месте их пересечения находится точка центра сопряжения, установив в нее циркуль проводят радиус сопряжения.
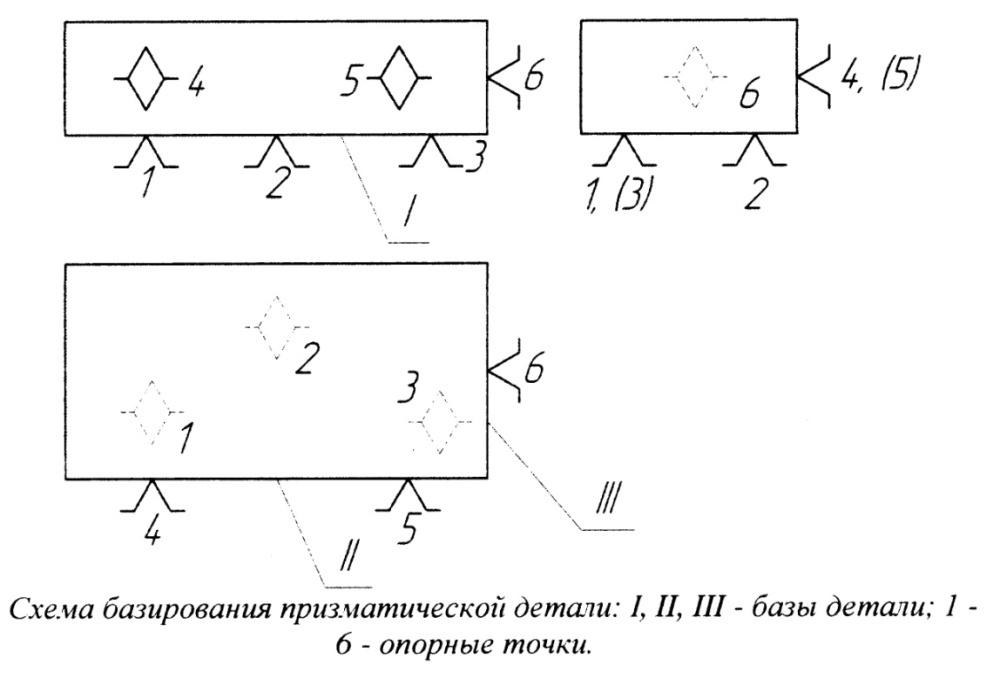
Опорные точки на чертеже
Опорные точки на схеме обозначают условными знакам согласно ГОСТ 21495-76, эти точки символизируют одну из связей заготовки иди изделия с выбранной системой координат. Нумерация опорных точек расставляется, начиная с базы, на которой расположено наибольшее число точек. Также опорные точки называют характерными, их число конечно, они выделяются своим особым положением относительно плоскости проекции и поверхности.
Рисунок 3. Опорные точки на чертеже
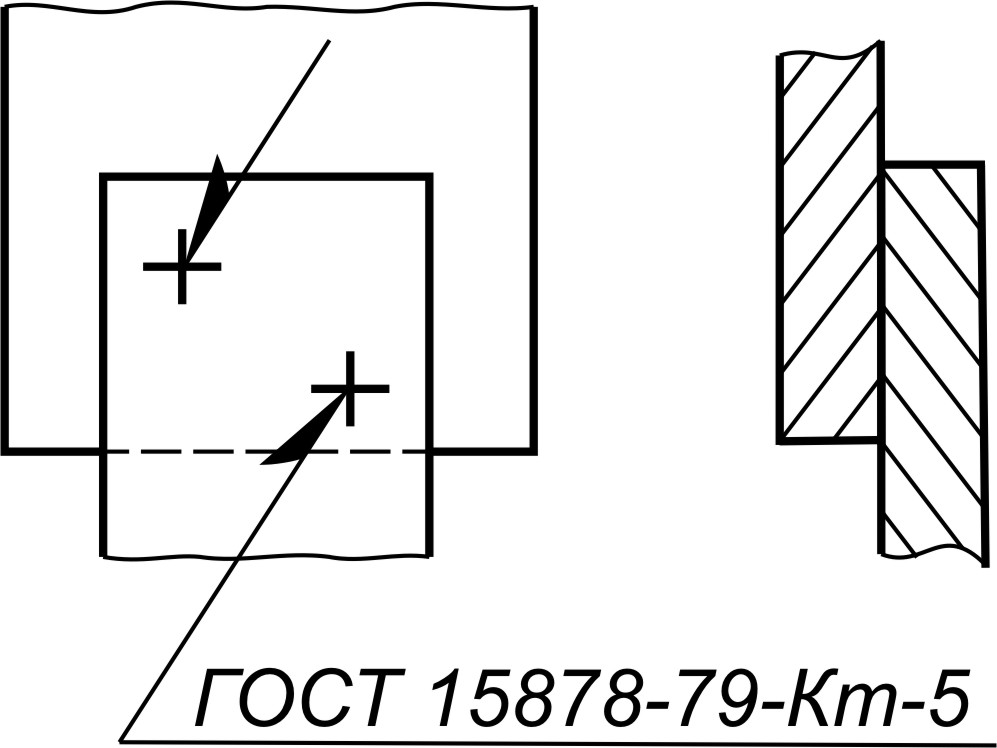
Сварные точки
Если детали соединяются сваркой, то ее также условно изображают на чертеже. В зависимости от расположения сварки можно увидеть шов или одиночную точку. Видимую одиночную точку обозначают знаком «+», невидимые одиночные точки на чертеже не обозначают. Видимый сварной шов обозначают основной сплошной линией, а невидимый штриховой линией.
Рисунок 4. Сварные точки на чертеже
Трехкартинный чертеж точки
Трехкартинный чертеж или чертеж Монка представляет собой прямоугольник, сторонами которого являются линии связи, которые расположены перпендикулярно соответствующим осям проекции. При этом три вершины – проекции точки, а четвертая это точка перелома линии связи.
Рисунок 5. Трехкартинный чертеж точки
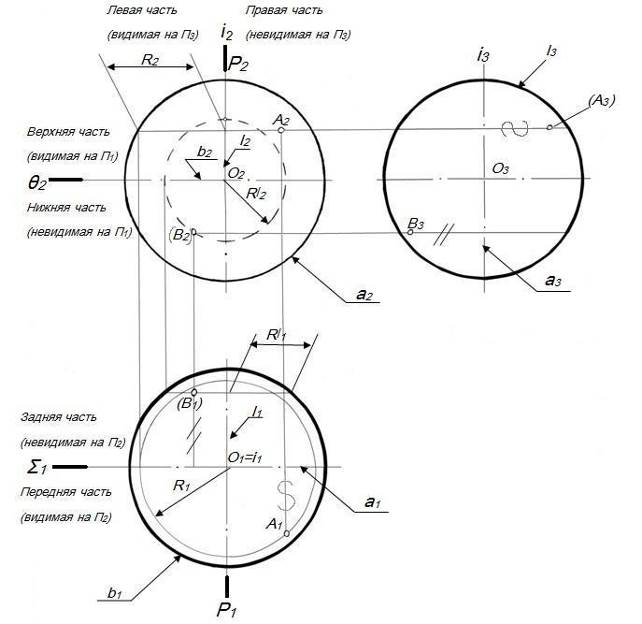
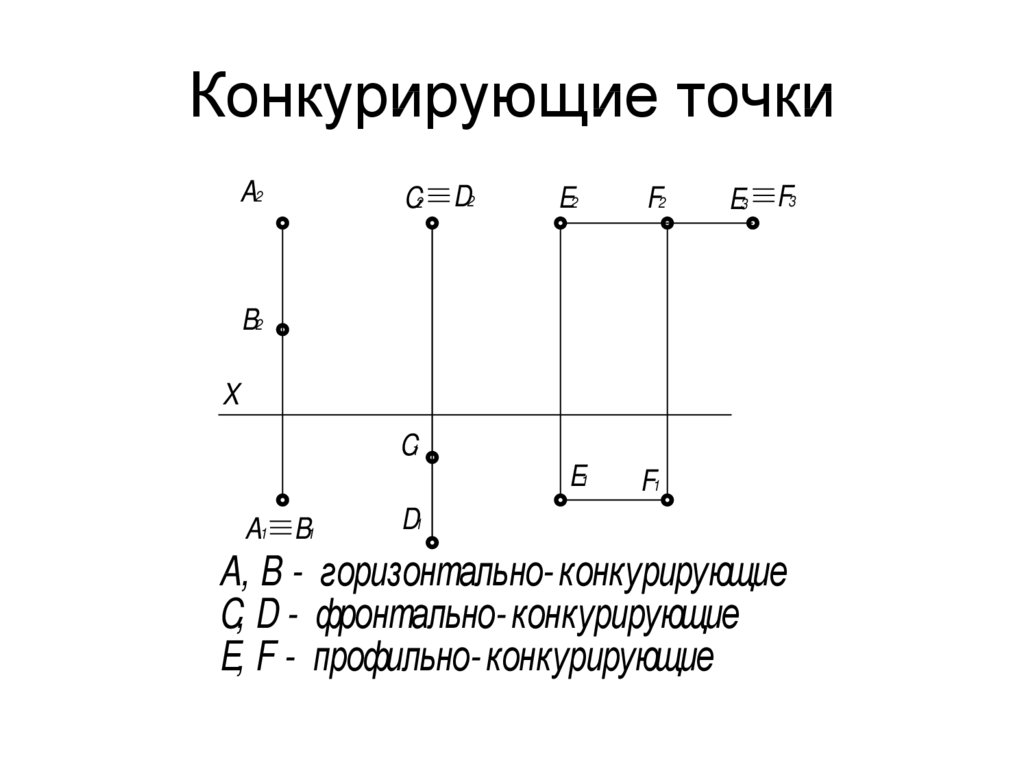
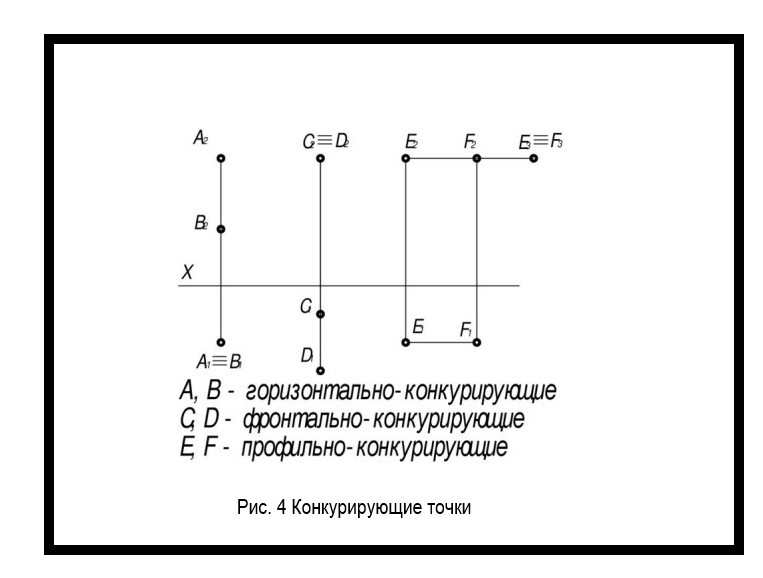
Конкурирующие точки на чертеже
Конкурирующие точки располагаются на одном проецирующем луче, таким образом для наблюдателя одна точка будет видимой, явной, а другая нет, что отразится и на чертеже.
Рисунок 6. Конкурирующие точки на чертеже
Что такое явная точка на чертеже
Одним из важных понятий чертежа является база. Под базой понимается поверхность (точка, ось или сочетание поверхностей), принадлежащие заготовке, которая предназначена для придания изделию требуемого положения. Поверхность, используемая для базирования, может быть установочной ( лишает изделие возможностей перемещения), опорной (лишает одной степени свободы) или направляющей (лишает изделие или заготовку двух степеней свободы). По характеру базы могут быть скрытые и явные. Скрытые находятся в воображаемой плоскости или точке, а явные — в реальной поверхности или точке пересечения рисок.
Как построить комплексный чертеж точки: инструкция
Чтобы построить комплексный чертеж точки используется метод ортогональных или прямоугольных проекций, часто применяемый в инженерной графике. Проекция находится на пересечении проецирующего луча и плоскости.
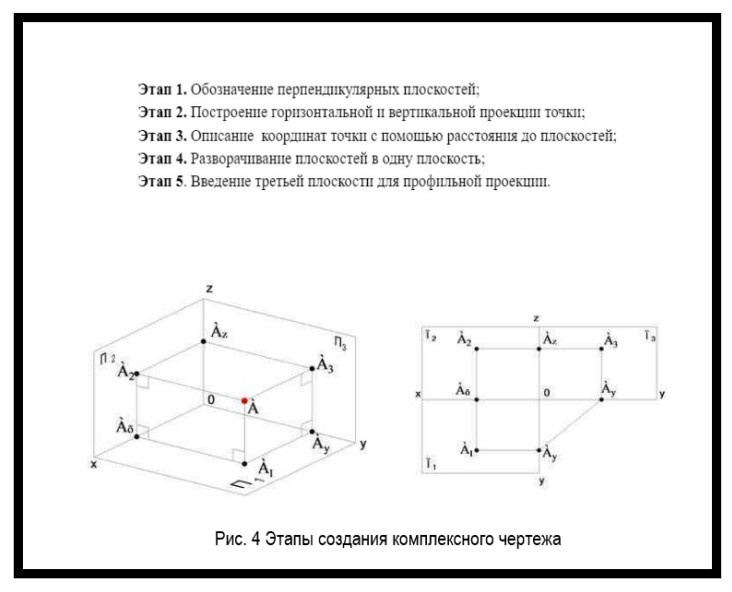
Построение комплексного чертежа точки А состоит следующих этапов:
- возьмем две плоскости, которые перпендикулярны друг другу и назовем их П1 и П2;
- в результате пересечения проецирующих лучей, перпендикулярных каждой из плоскостей получаем горизонтальную и вертикальную проекцию точки А;
- координаты точки описываются с помощью расстояния до плоскостей;
- для построения плоского чертежа плоскость П1 разворачивают так, чтобы она совпадал с плоскостью П2, а прямая соединяющая А1 и А2 называется линией связи;
- третья плоскость вводится для построения профильной проекции.
Рисунок 7. Построение комплексного чертежа точки
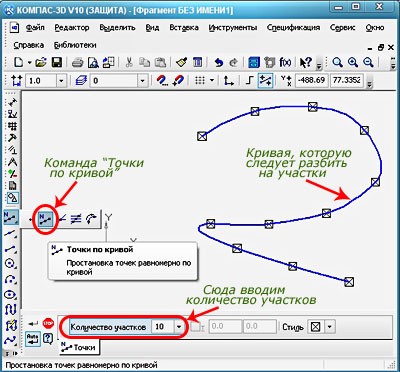
Как поставить точку на чертеже в Компасе
В меню программы Компас есть специальный инструмент «Точка», который позволяет сделать нужное действие за несколько шагов. Точку можно разместить, указав координаты, либо кликнув в месте рабочей области. Помимо основной функции команды, можно использовать расширенный список команд.
Рисунок 8. Как поставить точку в программе Компас
Как убрать точки на чертеже в Компасе
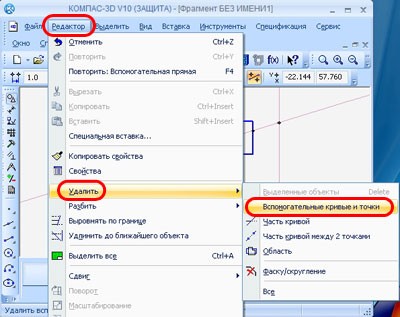
Убрать точки можно выделив их и нажав на клавишу «Delete», либо с помощью команды «Удалить вспомогательные кривые и точки».
Рисунок 9. Как убрать точку в программе Компас
Ответы на вопросы
Как правильно показать невидимую сварную точку?
Невидимые сварные точки не имеют обозначения, в отличие от швов.
Как на чертеже показать характерные точки отрезка?
Характерные точки зависят от объекта, у отрезка они находятся в начале и в конце прямой. Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. При этом длина проекции отрезка прямой общего положения меньше длины самого отрезка.
Чем отличается двухкартинный чертеж точки от трехкартинного?
Разница состоит в количестве проекций на поверхности. В двухкартинном чертеже используются горизонтальная и фронтальная плоскости, такой чертеж вполне позволяет описать форму и размеры фигуры. В трехкартинном чертеже используется еще и третья плоскость.
Чертеж — важный конструкторский документ. Это проекционное изображения предмета. При создании чертежей в начертательной геометрии нужно следовать особым правилам. Все элементы должны находиться в строгой зависимости от положения в пространстве. Простым геометрическим образом пространства является точка. Что такое точки на чертеже? Как их использовать при создании чертежа? Разбираемся в нашем материале.
Что такое точка на чертеже?
Изображение предмета на чертеже состоит из двух или более геометрических фигур, только так можно передать форму изделия. В инженерной графике используются разные элементы графического языка. Одним из них является точка.
Точка — геометрический элемент, не имеющий размеров. Другими словами, все параметры точки равны нулю.
Чтобы изобразить изделие на чертеже, его необходимо перенести на плоскость. В построении любого изображения в инженерной графике применяется метод прямоугольного проецирования, который определяет расположение предмета на области за счет точек.
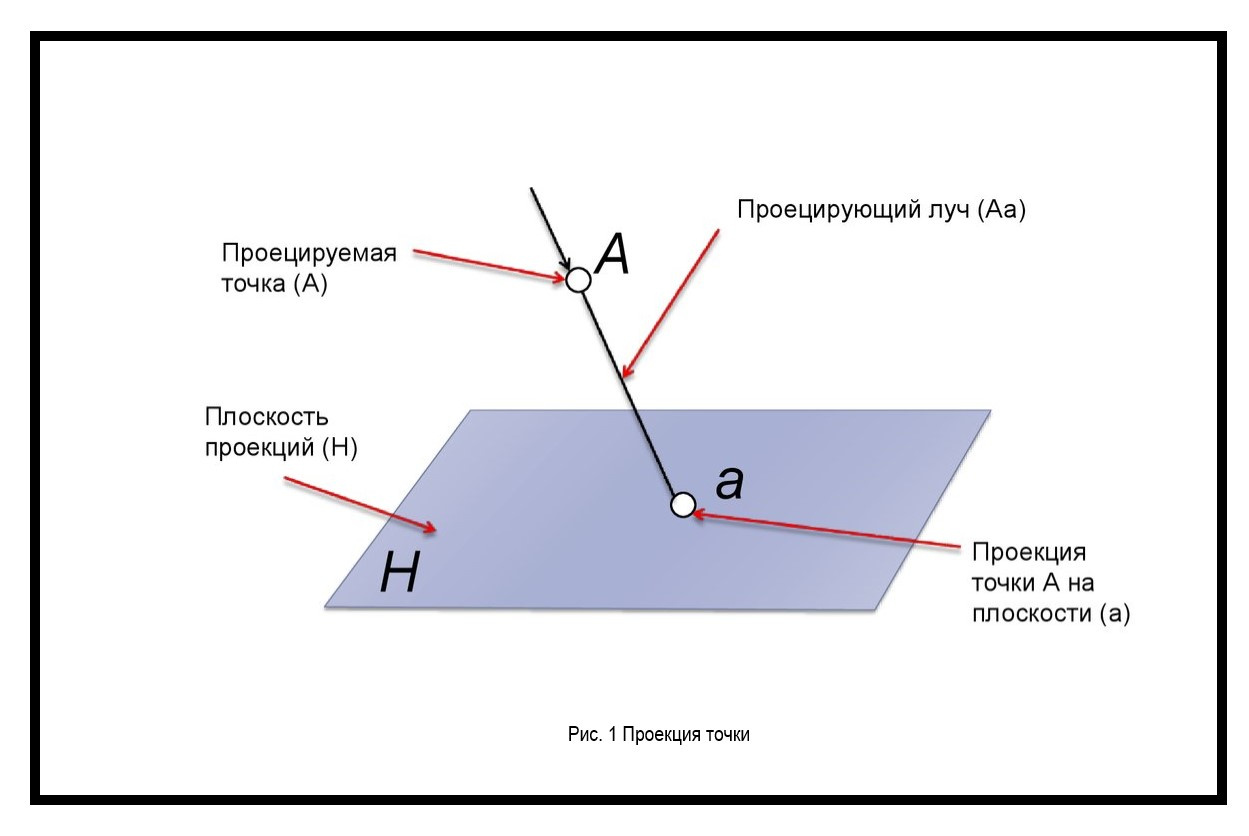
Проекция точки
Это точка пересечения прямой линии с плоскостью (рисунок 1).
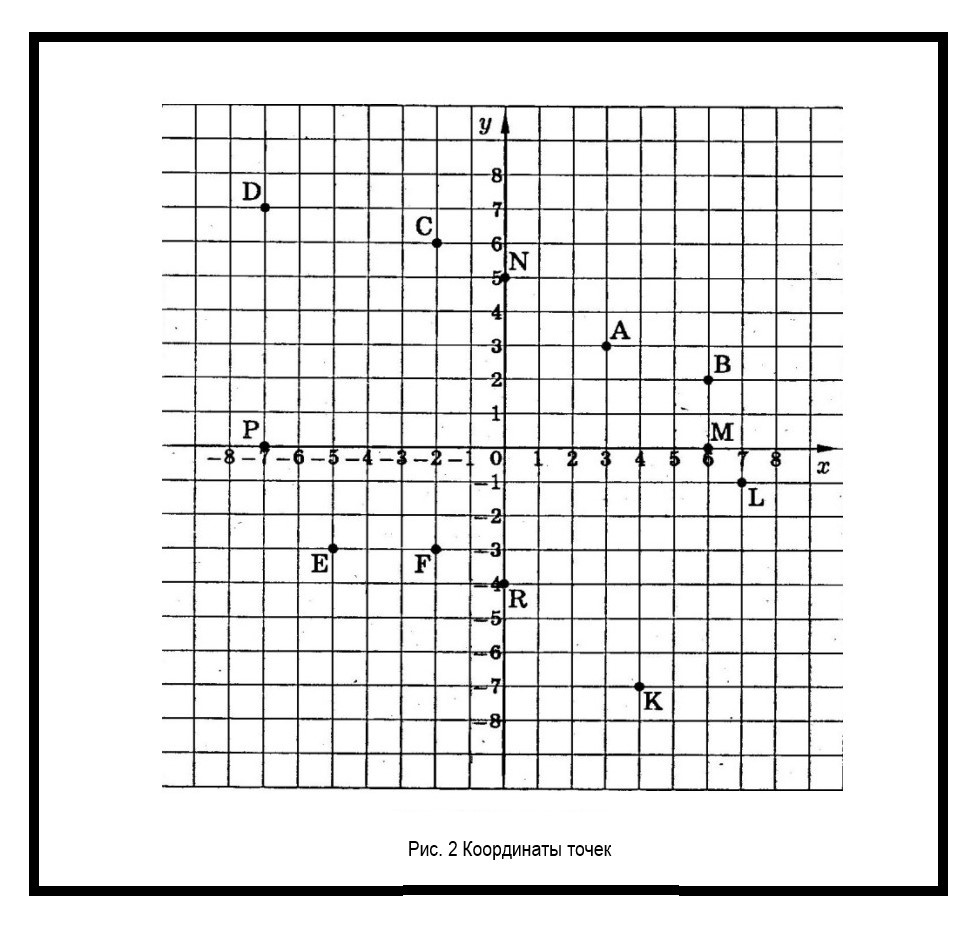
Проецируемая точка на плоскости обозначается как точка проекции. Это позволяет определить ее местоположение на плоскости. Каждая точка на чертеже имеет определенные координаты. Их используют для определения положения других элементов на комплексном чертеже (рисунок 2).
Как определить координаты по проекциям точки?
Для определения координат по проекциям точки используются две ортогональные проекции. Например, фронтальная и профильная. Они позволяют узнать конкретное значение координат точки, а также определить ее октант.
Как определить положение точки в пространстве?
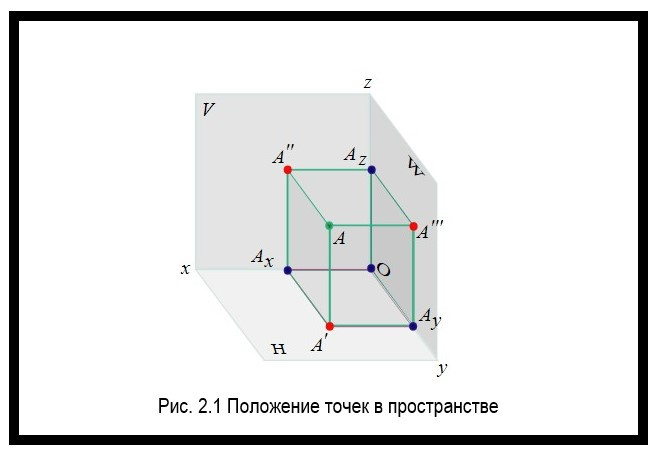
Положение точки в пространстве определяется тремя координатами. Они показывают расстояние точки от плоскостей проекции. Пример представлен на рисунке рисунок 2.1.
Комплексный чертеж точки
Чтобы изображение предмета было понятным, отражающим форму, размер и положение изделия в пространстве, необходимо использовать комплексный чертеж. Он представляет собой изображение предмета на совмещенных плоскостях проекции (рисунок 3).
Построение комплексного чертежа состоит из нескольких этапов (рисунок 4).
На таких чертежах объемный предмет проецируется ортогонально на две взаимно перпендикулярные плоскости. Одна из них — вертикальная, другая — горизонтальная. Прямая пересечения этих плоскостей называется осью проекции
.
Изображение точки на комплексном чертеже
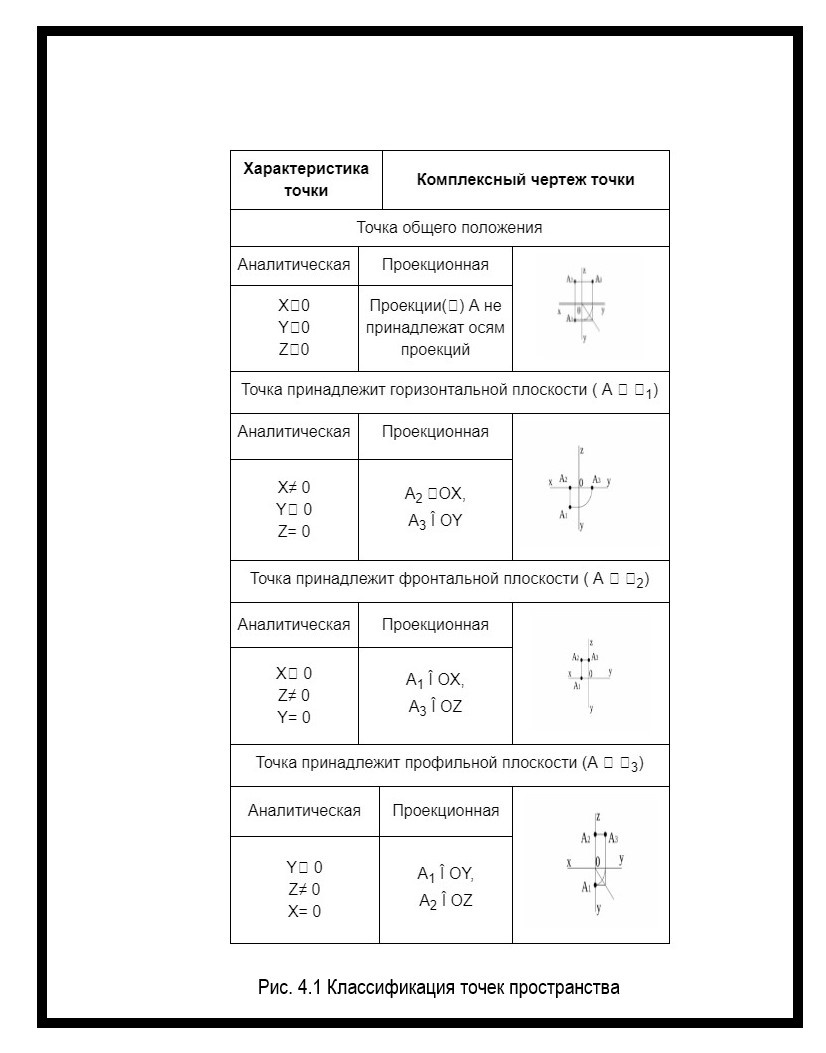
На комплексном чертеже точка — пара координат. Для изображения точки на чертеже нужно провести две перпендикулярные оси: горизонтальную и вертикальную ось. В зависимости от положения точки относительно плоскостей проекции, точки пространства могут быть нескольких видов (рисунок 4.1).
Обозначение точек на чертеже
Обозначение точек на чертеже осуществляется разными способами. Все параметры точек равны нулю, поэтому для их изображения используют условные обозначения (рис. 3.1).
Точка обозначаются буквами (например, точка A, B, C) или цифрами (например, точка 1, 2, 3). Кроме того, она может быть обозначена геометрическими символами кружочком или пересечением двух линий (рисунок 3).
Конкурирующие точки на чертеже
Точки на чертеже с двумя одинаковыми координатами называются конкурирующими (рисунок 4). Это точки, которые лежат на одном проецирующем луче.
Они могут быть нескольких видов, название которых определяет плоскость совпадающих проекций:
- Горизонтально конкурирующие — лежат на одном перпендикуляре к горизонтальной плоскости;
- Фронтально конкурирующие — лежат на одном луче к фронтальной плоскости;
- Профильно конкурирующие — лежат на одном перпендикуляре к профильной плоскости.
Видимые и невидимые конкурирующие точки на чертеже
Видимостью называют изображение близких к наблюдателю точек. Этот параметр помогает улучшить понимание геометрической формы и расположения предмета в пространстве.
Для определения видимости, нужно найти точки предмета на одном луче и обозначить только те, которые расположены ближе к вам (рисунок 5). Без видимости определить положение объекта сложно.
Как обозначить видимость точек на чертеже
Видимость точек обозначается буквами (например, точка C”), невидимость — буквами с круглыми скобками (например, точка (С”)).
Типы точек на чертеже
Точки на чертеже по ГОСТу могут быть следующих типов:
Не хотите тратить время на чертежи? Вы можете заказать готовый чертеж у экспертов Студворк!
Начертательная геометрия: конспект лекций.
4. Координаты точки.
Положение точки в пространстве может быть определено с помощью трех чисел, называемых ее координатами. Каждой координате соответствует расстояние точки от какой-нибудь плоскости проекций.
Расстояние определяемой точки А до профильной плоскости является координатой х, при этом х = а˝А (рис. 15), расстояние до фронтальной плоскости – координатой у, причем у = а́А, а расстояние до горизонтальной плоскости – координатой z, при этом z = аА.
На рисунке 15 точка А занимает ширину прямоугольного параллелепипеда, и измерения этого параллелепипеда соответствуют координатам этой точки, т. е., каждая из координат представлена на рисунке 15 четыре раза, т. е.:
На эпюре (рис. 16) координаты х и z встречаются по три раза:
Все отрезки, которые соответствуют координате х (или z), являются параллельными между собой. Координата у два раза представлена осью, расположенной вертикально:
И два раза – расположенной горизонтально:
Данное различие появилось из-за того, что ось у присутствует на эпюре в двух различных положениях.
Следует учесть, что положение каждой проекции определяется на эпюре только двумя координатами, а именно:
1) горизонтальной – координатами х и у,
2) фронтальной – координатами х и z,
3) профильной – координатами у и z.
Используя координаты х, у и z, можно построить проекции точки на эпюре.
Если точка А задается координатами, их запись определяется так: А (х; у; z).
При построении проекций точки А нужно проверять выполняемость следующих условий:
1) горизонтальная и фронтальная проекции а и а́ должны располагаться на одном перпендикуляре к оси х, так как имеют общую координату х;
2) фронтальная и профильная проекции а́ и а˝ должны располагаться на одном перпендикуляре к оси z, так как имеют общую координату z;
3) горизонтальная проекция а так же удалена от оси х, как и профильная проекция а удалена от оси z, так как проекции а́ и а˝ имеют общую координату у.
В случае, если точка лежит в любой из плоскостей проекций, то одна из ее координат равна нулю.
Когда точка лежит на оси проекций, две ее координаты равны нулю.
Если точка лежит в начале координат, все три ее координаты равны нулю.
Источник
Определение координат точек. Октанты в начертательной геометрии
Страницы работы
Содержание работы
Надо обязательно запомнить, какими координатами задается какая-нибудь проекция точки.
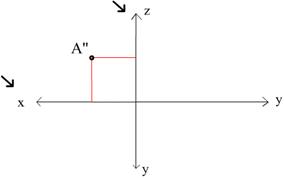
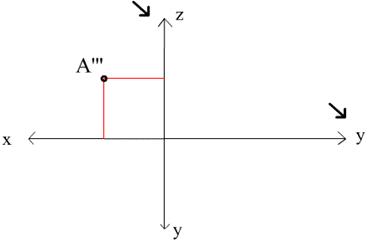
A’’’, профильная проекция точки А, задается координатами Y,Z. Примечание: для A’’’ следует взять ту ось У, которая перпендикулярна оси Z. (рис. 3)
Обратите внимание на то, какие именно оси проекций нужно использовать для определения координат точки (см. рисунки)
1) Определение координат точек.
Пусть вам даны две какие-нибудь проекции точки. Как определить их координаты? Очень просто. Начнем издалека. Как известно, любая точка определяется в пространстве тремя координатами: X, Y и Z. Это понятно.
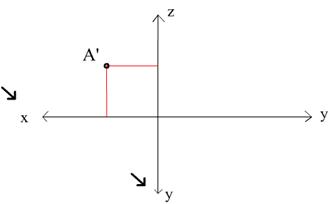
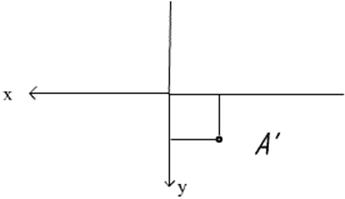
Если вам дана A’, то мы автоматически сможем сказать, какие у этой точки будут координаты Х и У – см. рис. 1. Обратите внимание на знак координаты! Знак определяется в зависимости от того, в какую сторону направлена ось. На рис. 4 очевидно, что координата X точки А отрицательна, а координата У положительна. Повторюсь: мы взяли именно эту ось У, так как она перпендикулярна оси Х, а A’ «зависит» от координаты X. Если бы мы искали координату У с помощью профильной проекции точки (A’’’), то мы бы взяли ось, перпендикулярную оси Z, так как A’’’ «зависит» от координаты Z. Иными словами, оси, по которым определяются две координаты проекции, не могут лежать на одной линии.
В начертательной геометрии существует такое понятие, кок октант. Что такое октант?
Три оси – x,y и z делят пространство на 8 равных частей. Каждая из таких частей и называется октантом.
Чтобы по знакам точки определить, в какой октанте она расположена, достаточно запомнить довольно простую таблицу. Вот она.
Источник
Построение ортогональных проекций точек
Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.
По заданному комплексному чертежу точек A и B необходимо:
Определение координат точек по их проекциям
Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно Aх, Aу. Координата х для т. A равна длине отрезка AхO со знаком плюс, так как Aх лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка AуO со знаком минус, так как т. Aу лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A» имеет координаты х и z. Опустим перпендикуляр из A» на ось z и найдем Az. Координата z точки A равна длине отрезка AzO со знаком минус, так как Az лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).
Построение проекций точек
Точки A и B в плоскости П3 имеют следующие координаты: A»’ (y, z); B»’ (y, z). При этом A» и A»’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B» и B»’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса AуO. После этого проведем перпендикуляр из Aу до пересечения с перпендикуляром, восстановленным из точки A» к оси z. Точка пересечения этих двух перпендикуляров определяет положение A»’.
Точка B»’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B» к оси z. Точка пересечении этого перпендикуляра с осью z есть B»’.
Определение положения точек в пространстве
Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П1, П2 и П3, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П2.
| Октанты | Знаки координат | ||
| x | y | z | |
| 1 | + | + | + |
| 2 | + | – | + |
| 3 | + | – | – |
| 4 | + | + | – |
| 5 | – | + | + |
| 6 | – | – | + |
| 7 | – | – | – |
| 8 | – | + | – |
Построение наглядного изображения точек в системе плоскостей П1, П2, П3
Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П1, П2, П3, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.
Источник
Проецирование точки в начертательной геометрии с примерами
Проецирование точки на две и три плоскости проекций:
Если из точки А, находящуюся в пространстве, относительно двух плоскостей проекций
Они характеризуются координатами, которые численно равны расстоянию от точки А до соответствующих плоскостей проекций. Координаты обозначаются теми же буквами, что и оси вдоль которых измеряется расстояние, с присвоением индекса самой буквы.
Так, для точки А:
Плоскость прямоугольника 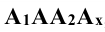
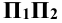
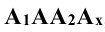
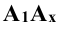
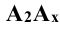
Изображение точки и её проекций на рис.3.1 является пространственным чертежом, что не всегда удобно для практики.
Рис. 2.4 Чтобы получить плоский чертёж, поворачивают плоскость 
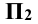
Проекции 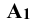
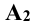
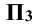
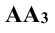
Для получения плоского чертежа в этом случае уже две плоскости 
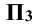
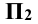
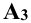
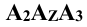
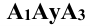
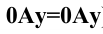
Это не означает, что модули этих величин обязательно равны между собой, т.е. 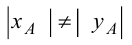
Таким образом, горизонтальная и фронтальная проекции точки А на плоском чертеже лежат на одной линии проекционной связи, перпендикулярной к оси x, а фронтальная и профильная проекции точки А на линии проекционной связи, перпендикулярной к оси z.
Определение по плоскому чертежу принадлежности точки тому или другому октанту пространства
Точка, например А, принадлежит:
Определение по плоскому чертежу принадлежности точки плоскостям проекций
Точка А принадлежит:
Любая точка лежит на оси проекций, если её смежные две проекции совпадают.
Так, точка А лежит на оси х, если 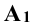
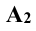
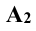
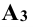
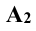
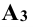
Правила знаков координат проекции точки
При построении проекции точки координата x всегда откладывается от начала координат (точка 0).
Таблица 3.1
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
Начертательная геометрия: конспект лекций
Данное учебное пособие представляет собой курс лекций и предназначено для студентов, сдающих экзамен по специальности «Начертательная геометрия». Подготовлено с учетом требований Министерства образования РФ.
Оглавление
Приведённый ознакомительный фрагмент книги Начертательная геометрия: конспект лекций предоставлен нашим книжным партнёром — компанией ЛитРес.
1. Проекции точки на две плоскости проекций
Рассмотрим проекции точек на две плоскости, для чего возьмем две перпендикулярные плоскости (рис. 4), которые будем называть горизонтальной фронтальной и плоскостями. Линию пересечения данных плоскостей называют осью проекций. На рассмотренные плоскости спроецируем одну точку А с помощью плоской проекции. Для этого необходимо опустить из данной точки перпендикуляры Аа и A на рассмотренные плоскости.
Проекцию на горизонтальную плоскость называют горизонтальной проекцией точки А, а проекцию а́ на фронтальную плоскость называют фронтальной проекцией.
Точки, которые подлежат проецированию, в начертательной геометрии принято обозначать с помощью больших латинских букв А, В, С. Для обозначения горизонтальных проекций точек применяют малые буквы а, b, с… Фронтальные проекции обозначают малыми буквами со штрихом вверху а́, b́, с́…
Применяется также и обозначение точек римскими цифрами I, II,… а для их проекций — арабскими цифрами 1, 2… и 1́, 2́…
При повороте горизонтальной плоскости на 90° можно получить чертеж, в котором обе плоскости находятся в одной плоскости (рис. 5). Данная картина называется эпюром точки.
Через перпендикулярные прямые Аа и Аа́ проведем плоскость (рис. 4). Полученная плоскость является перпендикулярной фронтальной и горизонтальной плоскостям, потому что содержит перпендикуляры к этим плоскостям. Следовательно, данная плоскость перпендикулярна линии пересечения плоскостей. Полученная прямая пересекает горизонтальную плоскость по прямой аах, а фронтальную плоскость — по прямой а́ах. Прямые аах и а́ах являются перпендикулярными оси пересечения плоскостей. То есть Аааха́ является прямоугольником.
При совмещении горизонтальной и фронтальной плоскостей проекции а и а́ будут лежать на одном перпендикуляре к оси пересечения плоскостей, так как при вращении горизонтальной плоскости перпендикулярность отрезков аах и а́ах не нарушится.
Получаем, что на эпюре проекции а и а́ некоторой точки А всегда лежат на одном перпендикуляре к оси пересечения плоскостей.
Две проекции а и а́ некоторой точки А могут однозначно определить ее положение в пространстве (рис. 4). Это подтверждается тем, что при построении перпендикуляра из проекции а к горизонтальной плоскости он пройдет через точку А. Точно так же перпендикуляр из проекции а́ к фронтальной плоскости пройдет через точку А, т. е. точка А находится одновременно на двух определенных прямых. Точка А является их точкой пересечения, т. е. является определенной.
Рассмотрим прямоугольник Aaaха́ (рис. 5), для которого справедливы следующие утверждения:
1) Расстояние точки А от фронтальной плоскости равно расстоянию ее горизонтальной проекции а от оси пересечения плоскостей, т. е.
2) расстояние точки А от горизонтальной плоскости проекций равно расстоянию ее фронтальной проекции а́ от оси пересечения плоскостей, т. е.
Иначе говоря, даже без самой точки на эпюре, используя только две ее проекции, можно узнать, на каком расстоянии от каждой из плоскостей проекций находится данная точка.
Пересечение двух плоскостей проекций разделяет пространство на четыре части, которые называют четвертями (рис. 6).
Ось пересечения плоскостей делит горизонтальную плоскость на две четверти — переднюю и заднюю, а фронтальную плоскость — на верхнюю и нижнюю четверти. Верхнюю часть фронтальной плоскости и переднюю часть горизонтальной плоскости рассматривают как границы первой четверти.
При получении эпюра вращается горизонтальная плоскость и совмещается с фронтальной плоскостью (рис. 7). В этом случае передняя часть горизонтальной плоскости совпадет с нижней частью фронтальной плоскости, а задняя часть горизонтальной плоскости — с верхней частью фронтальной плоскости.
На рисунках 8-11 показаны точки А, В, С, D, располагающиеся в различных четвертях пространства. Точка А расположена в первой четверти, точка В — во второй, точка С — в третьей и точка D — в четвертой.
При расположении точек в первой или четвертой четвертях их горизонтальные проекции находятся на передней части горизонтальной плоскости, а на эпюре они лягут ниже оси пересечения плоскостей. Когда точка расположена во второй или третьей четверти, ее горизонтальная проекция будет лежать на задней части горизонтальной плоскости, а на эпюре будет находиться выше оси пересечения плоскостей.
Фронтальные проекции точек, которые расположены в первой или второй четвертях, будут лежать на верхней части фронтальной плоскости, а на эпюре будут находиться выше оси пересечения плоскостей. Когда точка расположена в третьей или четвертой четверти, ее фронтальная проекция — ниже оси пересечения плоскостей.
Чаще всего при реальных построениях фигуру располагают в первой четверти пространства.
В некоторых частных случаях точка (Е) может лежать на горизонтальной плоскости (рис. 12). В этом случае ее горизонтальная проекция е и сама точка будут совпадать. Фронтальная проекция такой точки будет находиться на оси пересечения плоскостей.
В случае, когда точка К лежит на фронтальной плоскости (рис. 13), ее горизонтальная проекция k лежит на оси пересечения плоскостей, а фронтальная ḱ показывает фактическое местонахождение этой точки.
Для подобных точек признаком того, что она лежит на одной из плоскостей проекций, служит то, что одна ее проекция находится на оси пересечения плоскостей.
Если точка лежит на оси пересечения плоскостей проекций, она и обе ее проекции совпадают.
Когда точка не лежит на плоскостях проекций, она называется точкой общего положения. В дальнейшем, если нет особых отметок, рассматриваемая точка является точкой общего положения.
2. Отсутствие оси проекций
Для пояснения получения на модели проекций точки на перпендикулярные плоскости проекций (рис. 4) необходимо взять кусок плотной бумаги в форме удлиненного прямоугольника. Его нужно согнуть между проекциями. Линия сгиба будет изображать ось пересечения плоскостей. Если после этого согнутый кусок бумаги вновь расправить, получим эпюр, похожий на тот, что изображен на рисунке.
Совмещая две плоскости проекций с плоскостью чертежа, можно не показывать линию сгиба, т. е. не проводить на эпюре ось пересечения плоскостей.
При построениях на эпюре всегда следует располагать проекции а и а́ точки А на одной вертикальной прямой (рис. 14), которая перпендикулярна оси пересечения плоскостей. Поэтому, даже если положение оси пересечения плоскостей остается неопределенным, но ее направление определено, ось пересечения плоскостей может находиться на эпюре только перпендикулярно прямой аа́.
Если на эпюре точки нет оси проекций, как на первом рисунке 14 а, можно представить положение этой точки в пространстве. Для этого проведем в любом месте перпендикулярно прямой аа́ ось проекции, как на втором рисунке (рис. 14) и согнем чертеж по этой оси. Если восстановить перпендикуляры в точках а и а́ до их пересечения, можно получить точку А. При изменении положения оси проекций получаются различные положения точки относительно плоскостей проекций, но неопределенность положения оси проекций не влияет на взаимное расположение нескольких точек или фигур в пространстве.
3. Проекции точки на три плоскости проекций
Рассмотрим профильную плоскость проекций. Проекции на две перпендикулярные плоскости обычно определяют положение фигуры и дают возможность узнать ее настоящие размеры и форму. Но бывают случаи, когда двух проекций оказывается недостаточно. Тогда применяют построение третьей проекции.
Третью плоскость проекции проводят так, чтобы она была перпендикулярна одновременно обеим плоскостям проекций (рис. 15). Третью плоскость принято называть профильной.
В таких построениях общую прямую горизонтальной и фронтальной плоскостей называют осью х, общую прямую горизонтальной и профильной плоскостей — осью у, а общую прямую фронтальной и профильной плоскостей — осью z. Точка О, которая принадлежит всем трем плоскостям, называется точкой начала координат.
Источник
Содержание:
Для полного выявления наружных и внутренних форм деталей и их соединений вводят три и более плоскости проекций.
Введем в систему плоскостей
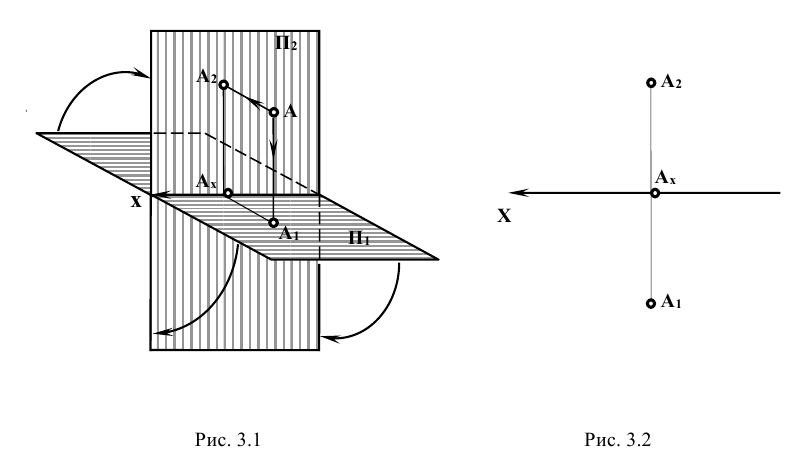
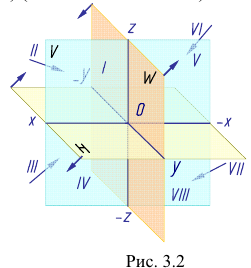
Три взаимно-перпендикулярные плоскости делят пространство на восемь частей, восемь октантов (рис. 3.2) (от лат. octo — восемь).
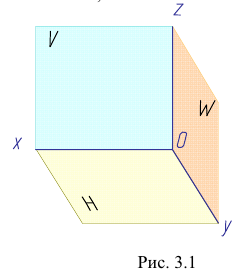
В нашей стране принята европейская система расположения проекций. Ось х направлена от начала координат влево, у — вперед (к нам), z — вверх. Обратные направления координатных осей считаются отрицательными.
Чертеж точки
Опустим из точки А проецирующие лучи (перпендикуляры) до пересечения с плоскостями проекций Н, V и W. Точки пересечения перпендикуляров с плоскостями проекций — это проекции точки на каждую из плоскостей проекций:
- а — горизонтальная;
- а‘ — фронтальная;
- а » — профильная.
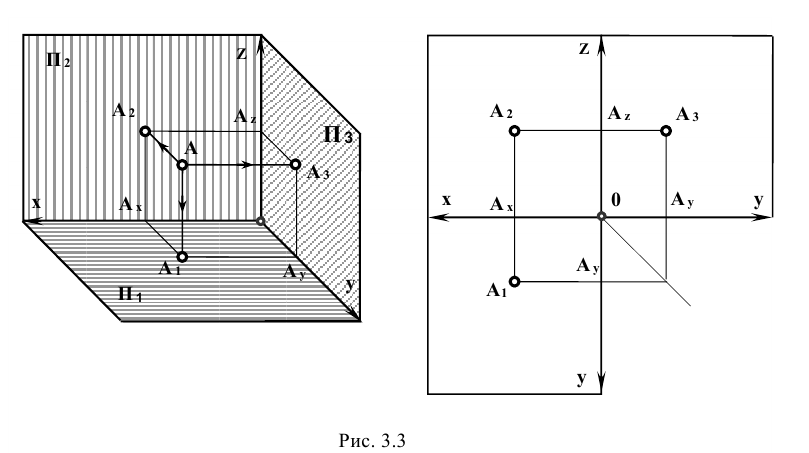
Данное наглядное изображение тонки в системе плоскостей Н, V и W (рис. 3.3) неудобно для черчения из-за сложности. Преобразуем его так, чтобы горизонтальная и профильная плоскости проекций совпали с фронтальной плоскостью проекций, образуя одну плоскость чертежа (рис. 3.4).
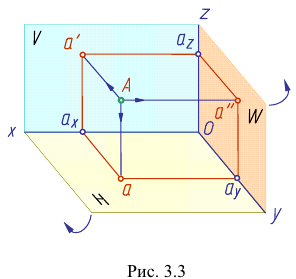
Это преобразование осуществляют путем поворота вокруг оси х плоскости Н на угол 90° вниз и плоскости W на угол 90° вправо вокруг оси z. В результате указанного совмещения плоскостей получаем чертеж, называемый эпюр Монжа (от франц, 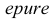
На эпюре мы не можем показать пространственную картину расположения плоскостей проекций и точки. Но эпюр обеспечивает точность изображений при значительной простоте построений.
В дальнейшем эпюр Монжа, а также проекционные чертежи будем называть одним словом — чертеж (или комплексный чертеж).
Горизонтальная и фронтальная проекции точки 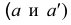
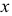
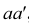
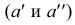
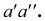
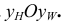
Таким образом, на комплексном чертеже трех ортогональных проекций точки
- две проекции находятся на одной линии связи;
- линии связи перпендикулярны осям проекций;
- две проекции точки определяют положение се третьей проекции;
- две проекции точки определяют ее положение в пространстве.
Положение точки в пространстве задается при помощи трех се координат (абсциссы 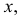
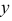
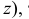
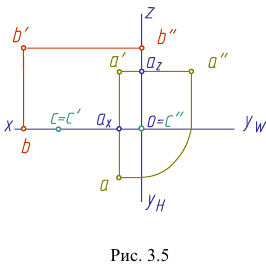
По отношению к плоскостям проекций точка может занимать как общее (точка А), так и частные (точки В и С) положения (рис. 3.5). Если точка лежит в плоскости проекций, то две ее проекции лежат на осях проекций (точка В). У такой точки одна ее координата равна нулю. Если точка принадлежит одновременно двум плоскостям проекций (точка С), то она лежит на оси проекций. Две ее проекции совпадают, а третья совпадает с точкой О — началом координат. В атом случае две ее координаты равны нулю. Если точка принадлежит трем плоскостям проекций, то она расположена в начале координат.
Таким образом, величины отрезков линий связи на чертеже определяют численное расстояние проецируемой точки до плоскости проекций. Отрезок 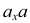
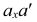
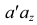
Взаимное положение двух точек. Условия видимости на чертеже
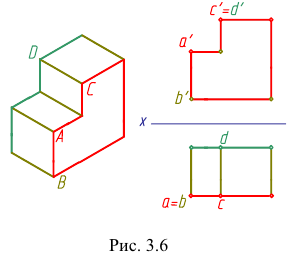
Рассмотрим чертеж модели, изображенной на рис. 3.6. Проекции некоторых точек совпадают, так как они расположены на одной проецирующей прямой. Например, на горизонтальной плоскости совпали проекции а и b вершин А и В — они лежат на одной горизонтально — проецирующей прямой. На фронтальной плоскости совпали проекции с ‘ и d ‘ вершин С и D — они лежат на одной фронтально-проецирующей прямой.
Точки, лежащие на одной проецирующей прямой, называют конкурирующими. А и В — горизонтально-конкурирующие точки, а С и D — фронтально-конкурирующие точки и т.д.
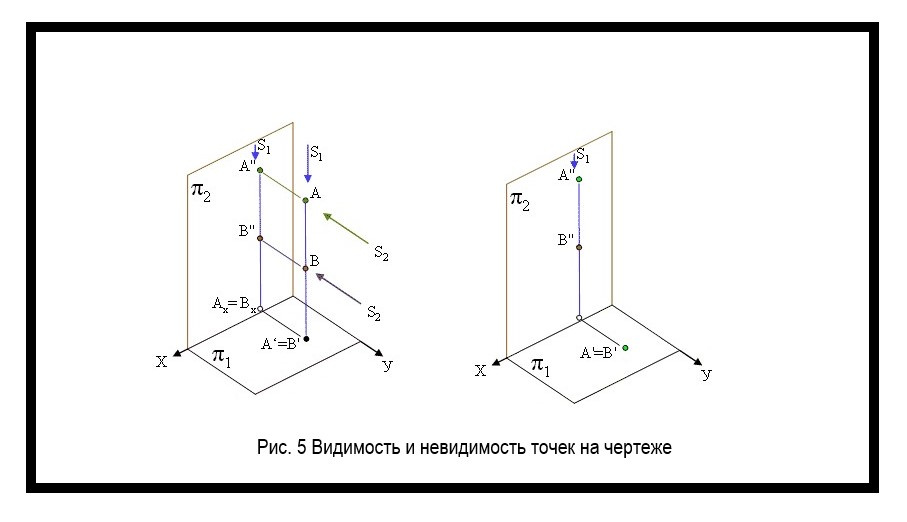
Ясно, что если две точки лежат на одной проецирующей прямой, то одна из них закрывает другую. Как определить, какая из них будет видимая и какая невидимая?
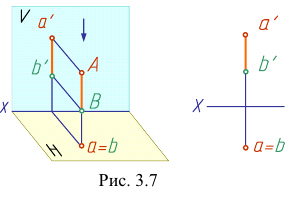
Из двух горизонтально- конкурирующих точек на горизонтальной плоскости видима та, которая расположена в пространстве выше. Анализируя положение фронтальных проекций точек (рис. 3.7), определяем, что точка А имеет большую координату z, чем точка В.
Следовательно, точка А расположена выше точки В и при проецировании на горизонтальную плоскость проекций закроет точку В. Точка А на горизонтальной плоскости видима, точка В — невидима. На фронтальной плоскости они обе видимы.
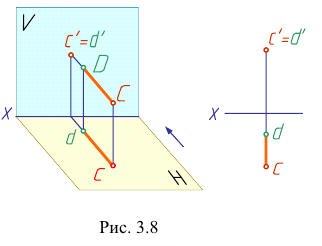
Из двух фронтально- конкурирующих точек на фронтальной плоскости проекций будет видима та, которая расположена ближе к наблюдателю, стоящему лицом к фронтальной плоскости проекций (рис. 3.8).
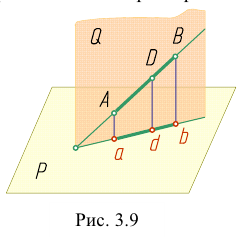
Какая из точек ближе к наблюдателю, можно определить по горизонтальным проекциям. Например, сравнивая горизонтальные проекции точек D и С , заключаем, что на фронтальной плоскости проекций видима точка С, а точка D — невидима, так как
Из двух профильно-конкурирующих точек на профильной плоскости проекций будет видима та точка, которая расположена левее.
Итак, если на чертеже одноименные проекции точек не совпадают или совпадает только одна пара проекций, то такие точки в пространстве не совпадают, а удалены друг от друга на определенное расстояние (рис. 3.7, 3.8).
Чертёж отрезка прямой. Прямые частного положения
Наглядное изображение отрезка АВ прямой и его ортогональное проецирование на плоскость Р показано на рис. 3.9. Рассмотрим ортогональное проецирование отрезка АВ с учетом свойств параллельного проецирования. Проецирующие прямые 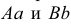
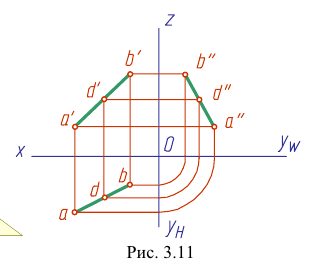
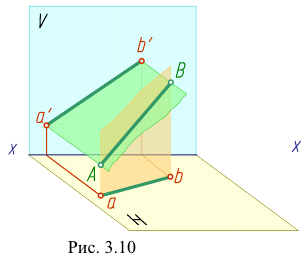
Наглядное изображение проецирования отрезка АВ прямой на две плоскости проекций в системе Н,V показано на рис. 3.10, чертеж — на рис. 3.1 I.
Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. Например, точка D (рис. 3.9) принадлежит прямой АВ, ее проекции — проекциям прямой.
Относительно плоскостей проекции прямая может занимать различные положения:
- — не параллельное ни одной из плоскостей проекций
- — параллельное одной из плоскостей проекций (прямая может и принадлежать этой плоскости);
- — параллельное двум плоскостям проекций, то есть перпендикулярное третьей.
Прямую, не параллельную ни одной из плоскостей проекций, называют прямой общего положения (рис. 3.9 — 3.11).
Прямую, параллельную одной из плоскостей проекций или двум плоскостям проекций (то есть перпендикулярную третьей), называют прямой частного положения.
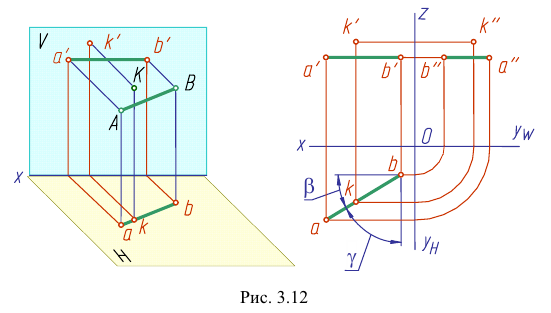
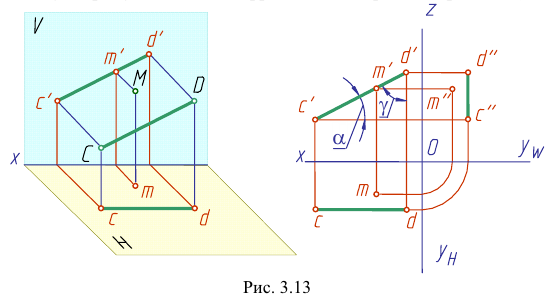
На рис. 3.12 — 3.14 приведены наглядные изображения и чертежи прямых частного положения — прямых, параллельных плоскостям проекций. Такие прямые называют прямыми уровня.
Различают три вида таких прямых.
Прямая АВ параллельна плоскости Н
Такую прямую называют «горизонтальной прямой» (рис. 3.12). Фронтальная проекция прямой 
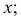
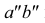
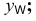
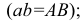
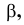
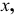
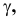
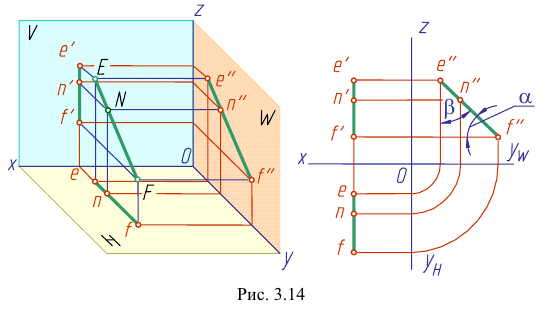
Прямая CD параллельна плоскости V
Такую прямую называют «фронтальной прямой» (рис. 3.13).
Горизонтальная проекция прямой cd параллельна оси х; профильная проекция 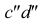
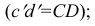
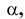
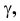
Прямая EF параллельна плоскости IF
Такая прямая носит название «профильная прямая» (рис. 3.14).
Горизонтальная проекция прямой 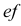
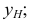
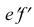
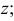
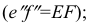
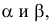
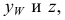
Следовательно, каждая линия уровня проецируется в истинную величину на ту плоскость проекции, которой она параллельна. На ту же плоскость проекций проецируются без искажения и углы, которые эта прямая образует с остальными двумя плоскостями проекций.
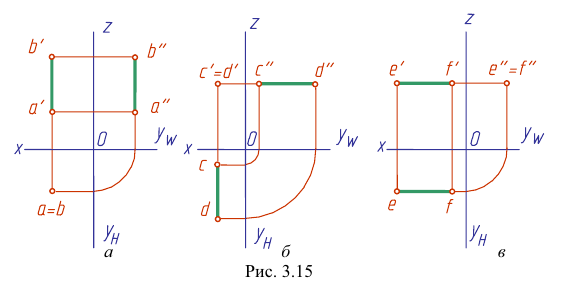
На рис. 3.15 приведены чертежи прямых, перпендикулярных плоскостям проекций. Такие прямые называются проецирующими прямыми. Различают три вида таких прямых.
Прямая АВ перпендикулярна плоскости Н
АВ — горизонтально-проецирующая прямая. Ее проекция 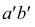
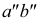
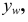
Прямая CD перпендикулярна плоскости V
CD — фронтально-проецирующая прямая. Ее проекция cd перпендикулярна оси х, проекция c»d“ перпендикулярна оси z, проекции с’ и d’ совпадают (рис. 3.15, б):
Прямая EF перпендикулярна плоскости W
EF — профильно-проецирующая прямая. Ее проекция 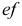
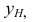
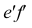
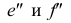
Из чертежа видно, что проецирующая прямая является вместе с тем и прямой двойного уровня, так как она параллельна одновременно двум другим плоскостям проекций
Следовательно, на две плоскости проекций проецирующие прямые проецируются без искажения, то есть в натуральную величину, а на третью — в точку.
Взаимное положение точки и прямой
Точка и прямая в пространстве могут быть различно расположены относительно друг друга и плоскости проекций.
Если точка в пространстве принадлежит прямой, то ее проекции принадлежат соответствующим проекциям этой прямой.
Если это положение нарушается, то точка данной прямой не принадлежит. На рис. 3.12 — 3.14 это положение показано на наглядных изображениях и чертежах прямых линий и точек.
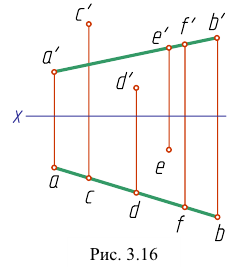
Рассмотрим еще раз это положение на плоскостном чертеже (рис. 3.16). Точка F принадлежит прямой АВ, так как горизонтальная проекция 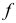
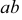
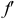
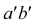
Точка С лежит над прямой АВ, точка D лежит под прямой АВ. точка Е лежит за прямой АВ.
Следы прямой
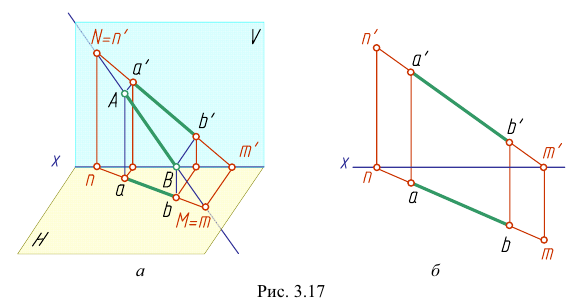
Точки пересечения прямой линии с плоскостями проекций называются следами прямой. На рис. 3.17. а точка М — горизонтальный след прямой, точка 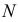
Горизонтальная проекция 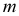
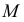
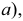
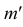
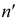
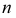
Чтобы построить на плоскостном чертеже горизонтальный след прямой (точки 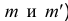
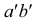
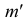
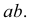
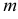
Для построения проекций фронтального следа (точек 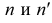
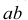
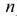
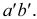
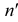
Прямая может пересекать и профильную плоскость проекций, то есть иметь профильный след. Этот след на профильной плоскости проекций совпадает со своей проекцией. Фронтальная и горизонтальная проекции его лежат соответственно на осях
- Чертежи на заказ
Взаимное положение двух прямых
Прямые в пространстве могут занимать различные взаимные положения:
- — пересекаться, то есть иметь одну общую точку;
- — быть параллельными, если точка пересечения прямых удалена в бесконечность;
- — скрещиваться, то есть не иметь обшей точки.
Пересекающиеся прямые
Если прямые пересекаются, то их одноименные проекции пересекаются между собой и точки пересечения проекций лежат на одной линии связи.
Наглядное изображение двух прямых АВ и CD, пересекающихся в точке К, приведено на рис. 3.18, 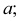
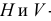
Если одна из прямых профильная, то чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.
На рис. 3.19 все проекции точки 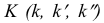
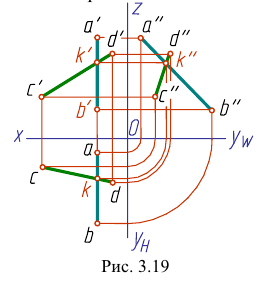
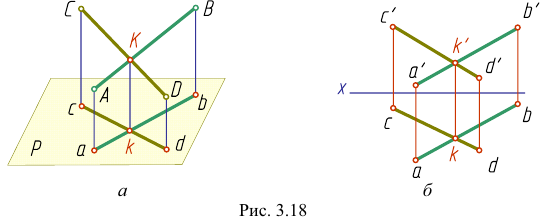
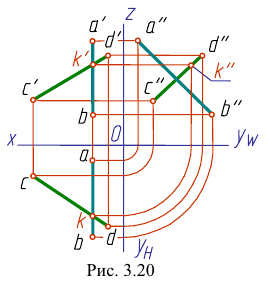
На рис. 3.20 профильная проекция 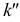
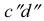
Это значит, что прямые АВ и CD не пересекаются, они скрещиваются.
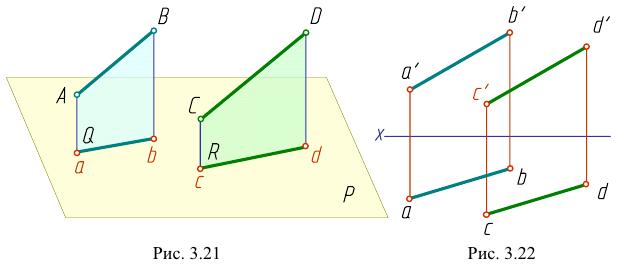
Параллельные прямые
Если прямые в пространстве параллельны, то их одноименные проекции параллельны между собой. Действительно, на рис. 3.21 проецирующие плоскости 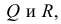
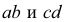
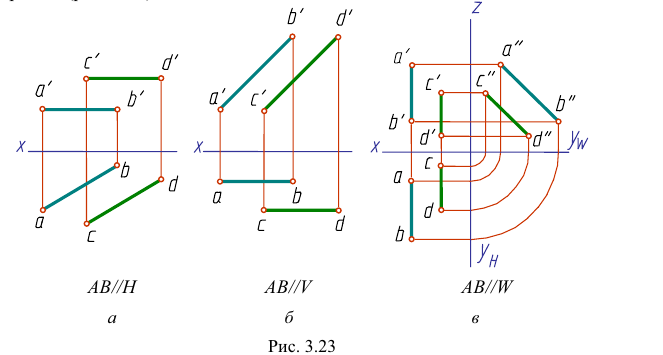
- горизонтальных прямых (рис. 3.23, а);
- фронтальных прямых (рис. 3.23, б);
- профильных прямых (рис. 3.23,
О параллельности прямых в пространстве можно судить по параллельности их одноименных проекций на двух плоскостях проекций.
При этом нужно учитывать некоторые условия.
Для прямых общего положения:
Если одноименные проекции прямых общего положения параллельны в системе двух любых плоскостей проекций, то прямые парал лельны (рис. 3.22).
Для прямых частного положения:
Если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые (рис. 3.23).
Скрещивающиеся прямые
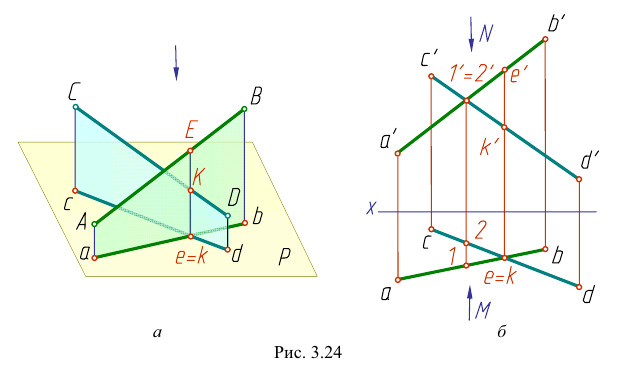
Если прямые в пространстве нс пересекаются, а скрещиваются (рис. 3.24), то хотя на чертеже их одноименные проекции и пересекаются, но точки пересечения проекций не лежат на одной линии связи. Эти точки не являются общими для прямых.
Сравнивая положение таких точек, определяют, какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю. На рис. 3.24, а видно, что точка Е (принадлежащая прямой АВ) расположена выше точки К (принадлежащей прямой CD). При взгляде сверху по указанной стрелке точка Е закрывает точку К. Соответственно и на чертеже (рис. 3.24, б) фронтальная проекция е’ расположена выше фронтальной проекции 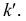
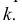
На плоскости V совпадают фронтальные проекции 1′ и 2′ точек прямых АВ и CD. При взгляде спереди по стрелке М видно, что точка 
Проецирование плоских углов
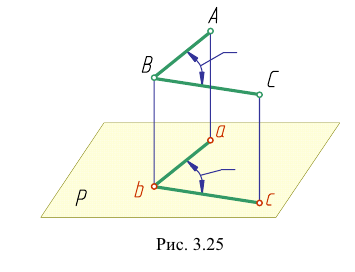
Любой линейный угол образуется двумя пересекающимися прямыми. На плоскости проекций он проецируется в общем случае с искажением. Однако, если обе стороны угла параллельны какой-либо плоскости проекций, то на эту плоскость угол проецируется без искажения. Например, стороны угла АВС (рис. 3.25) параллельны горизонтальной плоскости Р. поэтому угол 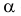
Исключение составляет прямой угол. Он проецируется в истинную величину даже тогда, когда лишь одна из его сторон параллельна плоскости проекций. Рассмотрим теорему о проецировании прямого угла.
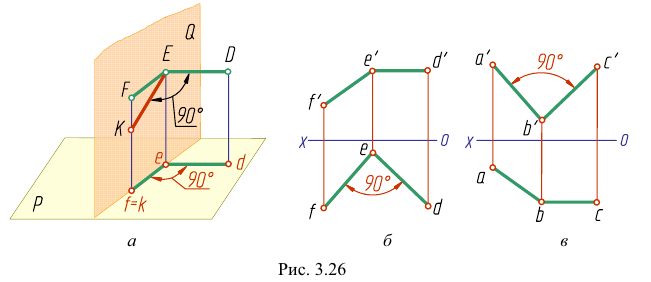
Теорема. Прямой угол проецируется в виде прямого угла, если одна из его сторон параллельна плоскости проекций, а вторая ей не пер пендикулярна. Пусть сторона DE прямого угла DEK параллельна плоскости Р, а сторона ЕК ей нс перпендикулярна (рис. 3.26). Требуется доказать, что его проекция — угол 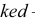
Доказательство. Пусть угол 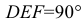
Через прямые EF и Ее проведем дополнительную плоскость 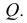
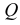
Возьмем на перпендикуляре 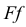
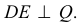
Но, как видно непосредственно из чертежа, только одна сторона DE угла DEK параллельна плоскости Р.
Вторая сторона его ЕК наклонна к плоскости Р.
Итак, для того чтобы прямой угол проецировался в натуральную величину, достаточно, чтобы одна его сторона была параллельна плоскости проекций (рис. 3.26, б, в).
Определение истинной величины отрезка прямой
Отрезки прямых общего положения не проецируются в истинную величину ни на одну из плоскостей проекций. Однако в ряде задач необходимо определить по чертежу длину отрезка прямой общего положения и углы наклона прямой к плоскостям проекций.
В этом случае используют способ построения прямоугольного треугольника.
Теорема. Истинная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка на одну из плоскостей проекций, а другим — разность расстояний концов отрезка до этой же плоскости.
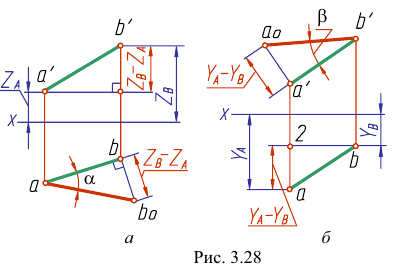
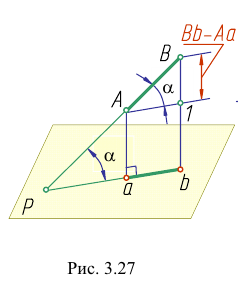
Доказательство. Из рис. 3.27 следует, что истинная величина отрезка АВ будет являться гипотенузой прямоугольного треугольника 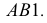
Определим истинную величину отрезка АВ и угол наклона его к плоскости Н (угол 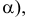
Построим прямоугольный треугольник, у которого одним катетом будет горизонтальная проекция отрезка, а вторым — разность расстояний концов отрезка до плоскости Н (разность z координат точек А и В). Истинная величина отрезка АВ равна гипотенузе abOt а угол наклона его к плоскости Н — угол
На рис. 3.28, 6 показано определение истинной величины отрезка АВ и угла наклона его к плоскости V- угла
- Прямая линия
- Плоскость
- Поверхности
- Изображения и обозначения на чертежах
- Моделирование трехмерных объектов в KOMПAC-3D
- Метод проекций
- Методы проецирования
- Образование проекций