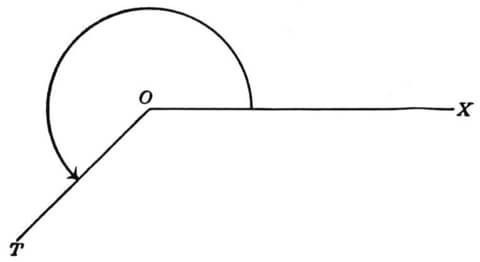
Определение
Тупой угол — это угол, больший прямого, но меньший развёрнутого.
Градусная мера тупого угла — от 90º до 180º.
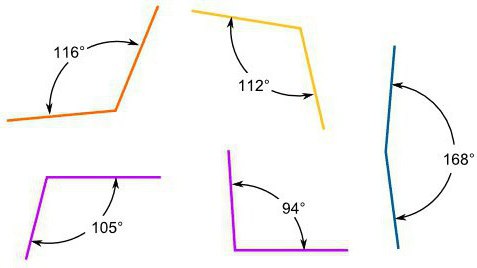
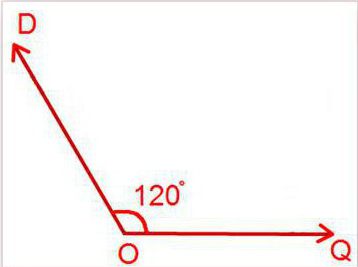
Например,
∠ABC, ∠DEF, ∠PTK — тупые углы.
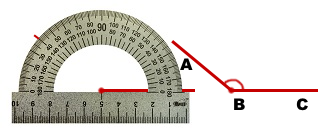
Построить тупой угол заданной градусной меры можно с помощью транспортира.
Пример.
Построить с помощью транспортира угол 140º.
1) Отмечаем точку — вершину угла.
2) От точки проводим луч — сторону угла.
3) Отметку в центре транспортира (у разных моделей отметка может располагаться в разных местах) совмещаем с вершиной угла таким образом, чтобы отметка 0º находилась на стороне угла.
4) Находим 140º на той шкале, где находится 0º, и ставим точку.
5) От вершины угла к отмеченной точке проводим луч — вторую сторону угла.
На рисунках показано построение угла 140º с началом отсчёта по разным шкалам — по нижней и по верхней.
∠ABC=140º
∠MNK=140º
Чтобы найти тупой угол на рисунке при помощи угольника, нужно приложить вершину угольника к вершине угла так, чтобы сторона угольника проходила вдоль одной из сторон угла. Если угол тупой, то его другая сторона выйдет за вторую сторону угольника.
Содержание:
- Определение тупого угла
- Примеры решения задач с тупыми углами
Определение тупого угла
Определение
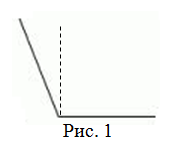
Угол называется тупым, если его
градусная мера лежит в пределах от
$90^{circ}$ до
$180^{circ}$ (рис. 1).
$angle alpha$ — тупой, если
$90^{circ} lt angle alpha < 180^{circ}$.
То есть тупой угол больше
прямого и меньше, чем
развернутый.
Примеры решения задач с тупыми углами
Пример
Задание. Найти тупой угол параллелограмма
$ABCD$, если известно, что его
острый угол равен
$30^{circ}$.
Решение. Известно, что сумма углов параллелограмма, прилежащих к одной стороне, равна
$180^{circ}$. Тогда искомый тупой угол равен
$$angle alpha=180^{circ}-30^{circ}=150^{circ}$$
Ответ. $angle alpha=150^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два угла треугольника равны
$30^{circ}$ и
$40^{circ}$. Найти третий угол треугольника, определить
тупым или острым он является.
Решение. Пусть $alpha$ — искомый угол.
Согласно теореме про сумму углов треугольника имеем, что
$$angle alpha+30^{circ}+40^{circ}=180^{circ}$$
Отсюда получаем
$$angle alpha=110^{circ}$$
Так как $90^{circ} < angle alpha=110^{circ} < 180^{circ}$, то он является тупым.
Ответ. $angle alpha=110^{circ}$
Читать дальше: что такое плоский угол.
Тупой угол
Тупой угол — это угол, больший прямого, но меньший развёрнутого.
Градусная мера тупого угла — от 90º до 180º.
∠ABC, ∠DEF, ∠PTK — тупые углы.
Построить тупой угол заданной градусной меры можно с помощью транспортира.
Построить с помощью транспортира угол 140º.
1) Отмечаем точку — вершину угла.
2) От точки проводим луч — сторону угла.
3) Отметку в центре транспортира (у разных моделей отметка может располагаться в разных местах) совмещаем с вершиной угла таким образом, чтобы отметка 0º находилась на стороне угла.
4) Находим 140º на той шкале, где находится 0º, и ставим точку.
5) От вершины угла к отмеченной точке проводим луч — вторую сторону угла.
На рисунках показано построение угла 140º с началом отсчёта по разным шкалам — по нижней и по верхней.
Чтобы найти тупой угол на рисунке при помощи угольника, нужно приложить вершину угольника к вершине угла так, чтобы сторона угольника проходила вдоль одной из сторон угла. Если угол тупой, то его другая сторона выйдет за вторую сторону угольника.
Тупые углы: описание и особенности
Треугольник – это геометрическая фигура, имеющая три соединенные между собой линиями точки, которые лежат не на единой прямой в плоскости. Вершины треугольника – точки в основании углов, а линии, соединяющие их, называют сторонами треугольника. Чтобы определить площадь такой фигуры, часто используют внутреннее пространство треугольника.
Классификация
Кроме треугольников, имеющих неодинаковые стороны, существуют равнобедренные, то есть обладающие двумя одинаковыми сторонами. Их называют боковыми, а еще одну сторону – основанием фигуры. Существует еще один вид таких многоугольников – равносторонние. Все три их стороны имеют одинаковую длину.
Для треугольников присуща градусная система измерения. Эти фигуры могут иметь разные углы, поэтому их классифицируют так:
- Прямоугольные – имеющие угол 90 градусов. Две стороны, прилежащие к этому углу, называют катетами, а третью – гипотенузой;
- Остроугольные – это треугольники, обладающие всеми острыми углами, не превышающими 90 градусов;
- Тупоугольные – один угол больше 90 градусов.
Определение и параметры треугольника
Как уже было отмечено, треугольник – это один из видов многоугольников, имеющий три вершины и столько же прямых, их объединяющих. Обозначают линии, как правило, одинаково: углы – маленькими латинскими буквами, а противоположные стороны каждого – соответствующей большой буквой.
Если сложить все углы какого-либо треугольника, получится сумма в 180 градусов. Чтобы узнать внутренний угол, нужно из 180 градусов вычесть величину внешнего угла треугольника. Для того чтобы узнать, чему равняется угол, находящийся снаружи, стоит сложить два раздельных от него угла внутри.
В каждом треугольнике, имеет он острые или тупые углы, противоположно большому углу находится наибольшая сторона. Если же прямые между вершинами одинаковы, то, соответственно, и каждый угол равняется 60 градусам.
Тупоугольный треугольник
Тупой угол треугольника всегда больше 90-градусного угла, но меньше развернутого. Таким образом, тупой угол равен от 90 до 180 градусов.
Возникает вопрос: бывает ли более одного тупого угла в такой фигуре? Ответ находится на поверхности: нет, потому что сумма углов должна быть менее 180 0 . Если два угла будут иметь, например, по 95 градусов, то третьему просто не найдется места.
Два тупоугольных многоугольника равны:
- если равны обе их стороны и угол, находящийся между ними;
- если одна сторона и два угла, находящиеся рядом с ней, равны;
- если три стороны тупоугольных треугольников имеют равенство.
Замечательные линии тупоугольного треугольника
Во всех треугольниках, имеющих тупые углы, есть линии, называемые замечательными. Первая из них – высота. Она представляет собой перпендикуляр из одной из вершин на соответствующую ей сторону. Все высоты сталкиваются в точке, которая именуется как ортоцентр. В треугольнике с тупыми углами он будет находиться за пределами самой фигуры. Что касается острых углов, то центр там находится в самом треугольнике.
Еще одна линия – медиана. Это черта, проведенная от вершины к центру соответствующей стороны. Все медианы сходятся в треугольнике, а место их совмещения – это центр тяжести такого многоугольника.
Биссектриса – линия, делящая пополам как тупые углы, так и остальные. Пересечение трех таких линий всегда бывает только в самой фигуре и определяется как центр круга, вписанного в треугольник.
В свою очередь, центр круга, описанного вокруг фигуры, можно получить из трех срединных перпендикуляров. Это линии, которые были опущены из середин прямых, соединяющих вершины. Место пересечения трех срединных перпендикуляров в треугольнике, имеющем тупые углы, находится снаружи фигуры.
Остроугольный, прямоугольный и тупоугольный треугольники.
Виды треугольников
Остроугольный треугольник — это треугольник,
в котором все углы острые.
Прямоугольный треугольник — это треугольник,
в котором один из углов прямой.
Тупоугольный треугольник — это треугольник,
в котором один из углов тупой.
Как определить вид треугольника
Для того, чтобы понять какой треугольник — остроугольный, прямоугольный или тупоугольный
нужно знать какая градусная мера у углов в треугольнике.
Если один из углов в треугольнике прямой, значит треугольник прямоугольный. Все углы острые в треугольнике — значит треугольник остроугольный. Если в треугольнике один из углов тупой, значит треугольник тупоугольный.
В произвольном треугольнике все углы острые, или два угла острые, а третий прямой или тупой. Если в треугольнике вам известно, что один углов тупой или прямой, значит сумма двух других углов не больше 90 градусов.
В прямоугольном треугольнике стороны напротив острых углов называются катетами, а сторона напротив прямого угла называется гипотенузой.
Градусные меры острого, тупого, прямого углов в треугольниках
Чтобы понять как называется угол и как называется треугольник с этими углами — надо знать его градусную меру:
- Острый угол в любом из треугольников не больше 90 градусов.
- Прямой угол в любом из треугольников равен 90 градусам.
- Тупой угол в любом из треугольников больше 90 градусов, но меньше 180 градусов.
http://fb.ru/article/266500/tupyie-uglyi-opisanie-i-osobennosti
http://colibrus.ru/ostrougolnyy-pryamougolnyy-i-tupougolnyy-treugolniki/
В данной публикации мы рассмотрим, что такое тупой угол, а также разберем примеры задач, в которых он участвует.
- Определение тупого угла
- Примеры задач
Определение тупого угла
Угол является тупым, если его градусная мера находится между 90 и 180 градусами.
∠α – тупой, если 90° < α < 180°.
То есть тупой угол больше прямого (90°), но меньше развернутого (180°).
Примеры задач
Задание 1
Дан треугольник, у которого известны два угла – 34° и 27°. Найдем третий и определим, является ли он тупым.
Решение:
Примем неизвестную величину за “α“. Как мы знаем, сумма углов треугольника равняется 180 градусам, значит:
α = 180° – 34° – 27° = 119°.
Следовательно, угол α – тупой.
Задание 2
Дан ромб, площадь (S) которого составляет 12,5 см2, а длина (a) стороны – 5 см. Найдем его углы и определим, являются ли они тупыми.
Решение:
Синус угла ромба (α) можно найти следующим образом (выведено из формулы расчета площади фигуры):
Следовательно, α = 30° (arcsin 0,5), является острым.
Как мы знаем, сумма соседних углов ромба составляет 180 градусов, значит второй угол β равен 150° (180° – 30°), и он является тупым.
План урока:
Угол. Виды углов: прямой, тупой, острый
Прямоугольник. Свойство противоположных сторон прямоугольника
Квадрат
Построение прямого угла, прямоугольника, квадрата на бумаге в клетку
Здравствуйте, дорогие ребята!
Приглашаем вас в сказочную страну Геометрию.
Жил-был король Луч. Была у короля маленькая, смешная и забавная дочка Точка. Отец очень любил и баловал принцессу и никогда не наказывал: не ставил в угол за ее шалости.
Угол. Виды углов: прямой, тупой, острый
Ребята, а вы знаете, что такое угол? Какие бывают углы?
Давайте вместе начертим угол. Сначала поставим точку. Затем проведем из этой точки 2 луча. Например, так:
Лучи – это стороны угла. А точка, из которой мы проводили лучи – вершина угла.
Углы бывают прямые, острые и тупые. Острым углом назовем тот, который меньше прямого, а тупым углом – тот, который больше прямого угла.
Изготовим модель прямого угла из кусочка бумаги.
Можно в качестве модели прямого угла использовать угольник. У него обязательно есть один прямой угол.
Ребята, помогите принцессе Точке определить, какие углы являются прямыми, а какие тупыми и острыми! Сосчитайте, сколько на этом чертеже прямых, острых, тупых углов.
Проверь себя!
Прямых – 6 углов, острых – 4 угла, тупых – 2 угла.
Король Луч решил построить для принцессы Точки игровую площадку. Он долго размышлял, чертил на песке разные фигуры. Посмотрите, после дождя остались лишь очертания. Назовите одним словом, что это?
Верно, это углы. Запишите номера углов в 3 столбика: острые, тупые, прямые.
Проверь себя.
Прямоугольник. Свойства противоположных сторон прямоугольника
Ребята, посмотрите на дворец короля и принцессы. Из каких геометрических фигур он состоит?
Давайте сосчитаем все прямоугольники, квадраты, треугольники и круги.
Прямоугольники – 3.
Квадраты – 5.
Треугольники – 3.
Круги – 5.
Найдите среди этих фигур четырехугольники, у которых все углы прямые. Воспользуйтесь моделью прямого угла, которую мы с вами изготовили.
Проверь себя.
Прямоугольники: 1, 3, 5.
Ребята, у принцессы Точки есть для вас вопросы о прямоугольнике. Попробуйте на них ответить.
Вопрос 1. Равны ли у прямоугольника противоположные стороны (они лежат напротив друг друга)?
На чертеже противоположные стороны обозначены одинаковым цветом.
Вопрос 2. Все ли углы прямые у прямоугольника?
Вопрос 3. Могут ли все стороны прямоугольника, а не только противоположные, быть одинаковыми? Например, так:
Подумайте! Возьмите любой прямоугольник, измерьте линейкой стороны фигуры, с помощью модели прямого угла или угольника проверьте углы.
Сравните свои выводы с правильными ответами.
Ответ 1. Противоположные стороны равны.
Ответ 2. Все углы прямые.
Ответ 3.Все стороны прямоугольника могут быть одинаковыми.
Молодцы! Не огорчайтесь, если не все выводы совпали с правильными ответами. Давайте еще раз повторим о прямоугольнике все, что узнали.
Квадрат
Ребята, отвечая на вопрос принцессы Точки, мы сделали вывод о том, что у прямоугольника все стороны могут быть одинаковой длины. Такой прямоугольник будет называться квадратом.
Задача на смекалку от короля. Помогите принцессе Точке ее решить.
Начерти прямоугольник со сторонами 5 см и 4 см. Сделай из него квадрат! Подсказка: «Можно сделать двумя способами: добавить, убрать».
Проверь себя.
Принцесса отлично справилась с задачей. А теперь попробуйте вы самостоятельно выполнить следующее задание.
Найдите среди этих прямоугольников квадраты. Запишите их номера.
Проверь себя.
Квадраты: 1,3.
Поиграем вместе с принцессой Точкой. Она выложила из счетных палочек такую фигуру:
Сколько квадратов вы видите? Уберите одну палочку так, чтобы осталось два квадрата. Сделать это можно разными способами. Какие еще фигуры, кроме двух квадратов, у вас получились?
Проверь себя.
Кроме двух квадратов, на каждом рисунке есть прямоугольник.
Построение прямого угла, прямоугольника, квадрата на клетчатой бумаге
Как вы заметили, король Луч и принцесса Точка любят чертить. Они приглашают нас, ребята, поучаствовать в этом увлекательном занятии. Вооружитесь тетрадью в клеточку, простым карандашом, угольником.
Задание: построить на бумаге в клеточку прямой угол, прямоугольник со сторонами 6 см и 3 см, квадрат со стороной 7 см.
Посмотрите, как получилось у принцессы. Сравните со своими чертежами.
Ставим точку. Откладываем два луча при помощи угольника или линейки.
Ставим точку. Вверх – 3 см, вправо – 6 см. Помним, что противоположные прямоугольника стороны равны. Чертим их – 6 см и 3 см.
Квадрат
А это тетрадь короля. Он чертил квадрат. Сравните со своим чертежом.
Ставим точку. Помним, что у квадрата все стороны равны. Откладываем вверх 7 см, вправо – 7 см. Чертим противоположные стороны по 7 см.
Молодцы, здорово получилось! Если такое занятие было для вас интересным и увлекательным, попробуйте начертить прямой угол, прямоугольник и квадрат на нелинованной бумаге. Сделать это будет гораздо сложнее. Здесь на помощь придет угольник: проверять прямой угол. Можно воспользоваться моделью прямого угла, которую мы изготовили.
Посмотрите, как это получилось у короля и Точки.
После нелегкого занятия король Луч и его дочка присели отдохнуть. Принцесса попросила рассказать интересную сказку. Давайте и мы послушаем!
Сказка
Жил-был на свете Прямоугольник. Фигура важная, спору нет! Люди ценили и уважали Прямоугольника, потому что при изготовлении многих вещей использовали эту фигуру. Всё хорошо у Прямоугольника, но одиноко как-то. Решил он найти своих родственников. Думает: «Если встречу родственников, сразу узнаю, потому что на меня должны быть похожи!».
Однажды встретил Прямоугольник Квадрата и говорит: «Как тебя зовут? Очень ты, брат, на меня похож!». Отвечает Квадрат: «Если найдем не меньше четырех общих признака, значит, родственники». Стали они друг друга рассматривать и обнаружили четыре сходства:
У каждого было по 4 угла, да все прямые, по 4 стороны, да стороны, которые одна напротив другой – одинаковой длины.
Обрадовались родственники, что нашли друг друга. Поспешили вместе отправиться дальше. Встретили однажды Четырехугольника и спрашивают: «Похож ты на нас. Уж не родня ли?».
Говорит им Четырехугольник: «Я был бы очень рад! Если найдем хотя бы два сходства, значит, родственники». Стали опять внимательно друг к другу приглядываться и увидели два общих признака:
- 4 угла.
- 4 стороны.
Обрадовались фигуры и решили не терять друг друга, держаться всегда рядом.
Понравилась вам сказка? Давайте повторим о фигурах все, что узнали.
В сказочное королевство Геометрия мы вернемся еще не раз. А этот урок подошел к концу. Выберите смайлик вашего настроения.
До скорой встречи в королевстве Геометрия! А сейчас проверьте свои знания. Принцесса Точка справилась с заданиями хорошо, допустила одну небольшую ошибку. Будьте внимательны, не спешите!