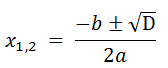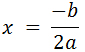Как на java найти корень уравнения - Исправление недочетов и поиск решений вместе с Examum.ru

В этой статье рассмотрим алгоритм решения квадратного уравнения и реализуем его на языке программирования Java.

Пусть нам требуется решить уравнение вида: . Будем решать его через дискриминант. Для получения корней уравнения необходимо выполнить следующий алгоритм:

Вычислим дискриминант по формуле: .
ЕСЛИ дискриминант больше нуля, то вычислим корни уравнения x1 и x2 по формуле:

ИНАЧЕ ЕСЛИ дискриминант равен нулю, значит уравнение имеет единственный корень. Вычислим его по формуле:

ИНАЧЕ (то есть дискриминант меньше нуля) уравнение не имеет действительных корней.

Реализуем этот алгоритм на языке программирования Java.

Приступим к написанию кода программы. В начале импортируем класс Scanner, необходимый для ввода данных:

import java.util.Scanner;

Перейдем к функции main. Объявим необходимые переменные. Для вычислений будем использовать вещественный тип данных повышенной точности double.

Выведем информацию о программе и попросим пользователя ввести данные:

System.out.println(«Программа решает квадратное уравнение вида:»);

System.out.println(«ax^2 + bx + c = 0»);

System.out.println(«Введите a, b и c:»);

Создадим новый объект класса Scanner, он необходим для ввода данных в программу. Инициализируем этот объект класса входным потоком:

Scanner in = new Scanner(System.in);

Считаем переменные a, b и c:

a = in.nextDouble();

b = in.nextDouble();

c = in.nextDouble();

Реализуем алгоритм решения квадратного уравнения, который был описан выше.

D = b * b — 4 * a * c;

if (D > 0) {

double x1, x2;

x1 = (—b — Math.sqrt(D)) / (2 * a);

x2 = (—b + Math.sqrt(D)) / (2 * a);

System.out.println(«Корни уравнения: x1 = « + x1 + «, x2 = « + x2);

}

else if (D == 0) {

double x;

x = —b / (2 * a);

System.out.println(«Уравнение имеет единственный корень: x = « + x);

}

else {

System.out.println(«Уравнение не имеет действительных корней!»);

}

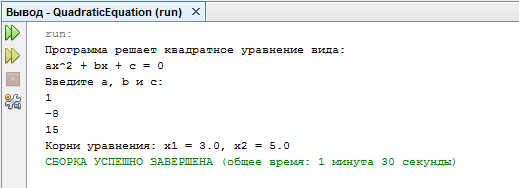
На этом написание функции main закончено. Продемонстрируем работу программы:

Если вы хотите скачать исходник этой программы, написанный в среде программирования NetBeans, то нажмите на кнопку ниже.

Скачать исходник

Источник

В этой статье мы рассмотрим алгоритм решения квадратного уравнение на Java.

Что такое квадратное уравнение

Квадратно уравнение – это уравнение вида:

(1) $begin{equation*}ax^2 + bx + c = 0end{equation*}$

Для вычисления значения x мы сначала вычислим дискриминант по формуле:

(2) $begin{equation*}D = b^2 - 4acend{equation*}$

Далее, если значение дискриминанта больше нуля, вычислим корни уравнения по формулам:

(3) $begin{equation*}x_1 = frac{-b+sqrt D}{2a},quad x_2 = frac{-b-sqrt D}{2a}end{equation*}$

Иначе, если дискриминант равен нулю, единственное значение x вычислим по формуле:

(4) $begin{equation*}x = frac{-b}{2a}end{equation*}$

Иначе, если дискриминант меньше нуля, данное уравнение не имеет решения.

Реализация алгоритма решения квадратного уравнения

Вначале вычитаем исходные данные a, b и c:

Scanner scanner = new Scanner(System.in);

System.out.print("Введите значение a: ");
double a = scanner.nextDouble();

System.out.print("Введите значение b: ");
double b = scanner.nextDouble();

System.out.print("Введите значение c: ");
double c = scanner.nextDouble();

Затем вычислим дискриминант:

double d = b * b - 4 * a * c;

На основании значения дискриминанта вычислим корни уравнения, если таковые имеются:

if (d > 0) {
    double x1 = (-b - Math.sqrt(d)) / (2 * a);
    double x2 = (-b + Math.sqrt(d)) / (2 * a);
    System.out.println("Корни уравнения: x1 = " + x1 + ", x2 = " + x2);
} else if (d == 0) {
    double x;
    x = -b / (2 * a);
    System.out.println("Уравнение имеет единственный корень: x = " + x);
} else {
    System.out.println("Уравнение не имеет действительных корней");
}

Проверка

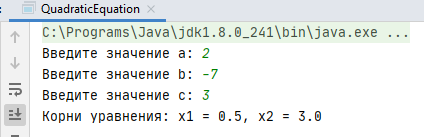
Теперь проверим программу в действии. Для следующих входных данных программа должна выдать такой результат:

(5) $begin{equation*}a = 2, b = -7, c = 3 rightarrow x_1 = 0.5, x_2 = 3end{equation*}$

Результат работы программы:

Исходный код

Полный исходный код программы:

import java.util.Scanner;

public class QuadraticEquation {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        System.out.print("Введите значение a: ");
        double a = scanner.nextDouble();

        System.out.print("Введите значение b: ");
        double b = scanner.nextDouble();

        System.out.print("Введите значение c: ");
        double c = scanner.nextDouble();

        double d = b * b - 4 * a * c;

        if (d > 0) {
            double x1 = (-b - Math.sqrt(d)) / (2 * a);
            double x2 = (-b + Math.sqrt(d)) / (2 * a);
            System.out.println("Корни уравнения: x1 = " + x1 + ", x2 = " + x2);
        } else if (d == 0) {
            double x;
            x = -b / (2 * a);
            System.out.println("Уравнение имеет единственный корень: x = " + x);
        } else {
            System.out.println("Уравнение не имеет действительных корней");
        }
    }
}

Заключение

Мы реализовали программу для решения квадратного уравнения. Вводные данные считываются с помощью Scanner.

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

The roots of a function are the x-intercepts. By definition, the y-coordinate of points lying on the x-axis is zero. Therefore, to find the roots of a quadratic function, we set f (x) = 0, and solve the equation, ax² + bx + c = 0.

Conditions for a quadratic equation –

ax^2 + bx + c = 0 

where 
a, b, c are real numbers and cannot be zero ie, there value must be from {-∞ to -1} and {1 to ∞}

A mathematical formula for finding the roots of a quadratic equation –

roots = (-b ± √(b2-4ac)) / (2a)

± represents there are two roots.

The roots of the quadratic equations are –

first = (-b + √(b2-4ac)) / (2a)
second = (-b - √(b2-4ac)) / (2a)

The (b^2 – 4ac) which is the determinant, tells us about the nature of the roots –

if (b^2 – 4ac) > 0, roots are real and different
if (b^2 – 4ac) == 0, roots are real and equal
if (b^2 – 4ac) < 0, roots are complex and different

Code to find roots of a quadratic equation:

Java

public class Main {

public static void main(String[] args)

{

double a = 7.2, b = 5, c = 9;

double firstroot, secondroot;

double det = b * b - 4 * a * c;

if (det > 0) {

firstroot = (-b + Math.sqrt(det)) / (2 * a);

secondroot = (-b - Math.sqrt(det)) / (2 * a);

System.out.format(

"First Root = %.2f and Second Root = %.2f",

firstroot, secondroot);

}

else if (det == 0) {

firstroot = secondroot = -b / (2 * a);

System.out.format(

"First Root = Second Root = %.2f;",

firstroot);

}

else {

double real = -b / (2 * a);

double imaginary = Math.sqrt(-det) / (2 * a);

System.out.printf("First Root = %.2f+%.2fi",

real, imaginary);

System.out.printf("nSecond Root = %.2f-%.2fi",

real, imaginary);

}

Output

First Root = -0.35+1.06i
Second Root = -0.35-1.06i

Time Complexity: O(log(D)), where D is the discriminant of the given quadratic equation.
Auxiliary Space: O(1)

Last Updated :
11 Jul, 2022

Like Article

Save Article

Источник

Permalink

Cannot retrieve contributors at this time

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters

Show hidden characters

	import java.util.Scanner;

	/**
	* Квадратное уравнение
	*/
	public class QuadraticEquation {
	public static final double EPS = 1e-10;

	/**
	* Решение квадратного уравнения: ax^2 + bx + c = 0
	*
	* @param a коэффициент при x^2
	* @param b коэффициент при x
	* @param c константа
	* @return корни уравнения (значения x)
	*/
	public static double[] solve(double a, double b, double c) {
	if (Math.abs(a) < EPS) {
	if (Math.abs(b) < EPS) {
	if (Math.abs(c) < EPS)
	throw new AnyXException();
	return new double[]{};
	}
	return new double[]{-c / b};
	}
	// Дискриминант
	double D = Math.pow(b, 2) — 4 * a * c;
	if (Math.abs(D) < EPS)
	return new double[]{-b / (2 * a)};
	if (D < 0)
	return new double[]{};
	double d = Math.sqrt(D);
	return new double[]{(-b — d) / (2 * a), (-b + d) / (2 * a)};
	}

	/**
	* Ввод коэффициентов с консоли или из командной строки
	*
	* @param args Аргументы командной строки, например: java QuadraticEquation 1.0 -2.0 1.0
	*/
	public static void main(String[] args) {
	double a, b, c;
	if (args.length == 3) {
	a = Double.parseDouble(args[0]);
	b = Double.parseDouble(args[1]);
	c = Double.parseDouble(args[2]);
	} else {
	Scanner scanner = new Scanner(System.in);
	System.out.print(«Введите a: «);
	a = scanner.nextDouble();
	System.out.print(«Введите b: «);
	b = scanner.nextDouble();
	System.out.print(«Введите c: «);
	c = scanner.nextDouble();
	}
	System.out.printf(«%s x^2 + %s x + %s = 0%n», a, b, c);
	try {
	double roots[] = solve(a, b, c);
	System.out.println(«Количество решений = « + roots.length);
	for (double x : roots) {
	System.out.println(«x = « + x + » -> « + (a * x * x + b * x + c));
	}
	} catch (AnyXException ex) {
	System.out.println(«Вырожденное уравнение: x — любое»);
	}
	}
	}

Источник

public class Equation {

    public static double a;
    public static double b;
    public static double c;

    public int kol;

    public int kolkorni() {
        if (a != 0) {
            if (b * b - 4 * a * c > 0) {
                kol = 2;
            }
        }
        if ((a == 0) && (b != 0) && (c != 0)) {
            kol = 1;
        }
    }
}

задан 27 сен 2012 в 5:11

aaaaa1aaaaaaaaaa1aaaaa

852 золотых знака5 серебряных знаков12 бронзовых знаков

Первое — поубирать все static — они точно здесь не нужны.

public static double a;
public static double b;
public static double c;

их ещё сделать и приватными.

Для корней не принято давать имена k1 и k2, а x1 и x2. Вам то может и понятно, а стороннему человеку (преподавателю к примеру), нужно это будет ещё догадаться.

Метод korni наверное лучше назвать solve, findRoots или что то в этом стиле. Беглый анализ этого метода показывает, что ситуация, когда дескриминант равен нулю не обрабатывается.

Методы printA, printB, printC — излишни (если только не была поставлена задача их написать). Я бы лучше добавил метод «printSolution», который бы распечатал само уравнение, дискриминант и корни в красивой форме.

ответ дан 27 сен 2012 в 6:47

KoVadimKoVadim

112k6 золотых знаков91 серебряный знак158 бронзовых знаков

Если спрашивают кол-во корней, то считать их не будем. Если хотите возвращать в целых, то в третьем случаи вернем максимальный для инта вариант. Один момент еще — double так сравнивать нельзя.

public class Equation {

    private double a;
    private double b;
    private double c;

    public Equation(double a, double b, double c){
        this.set(double a, double b, double c);
    }

    public void set(double a, double b, double c) {
        this.a = a;
        this.b = b;
        this.c = c;
    }

    public double getA() {
        return a;
    }

    public double getB() {
        return b;
    }

    public double getC() {
        return c;
    }

    public int resultsNuber() {
        if (isQuadratic()) {
            double discriminant = this.getDiscriminant();
            if (discriminant > 0) {
                return 2;
            } else if (discriminant == 0.0) {
                return 1;
            } else {
                return 0;
            }
        }

        if (isLinear()) {
            return 1;
        }

        return Integer.MAX_VALUE;
    }

    private boolean isQuadratic() {
        return a != 0;
    }

    private boolean isLinear() {
        return (a == 0) && (b != 0) && (c != 0);
    }

    private double getDiscriminant() {
        return b*b - 4*a*c;
    }

    public void toString() {
        return "" + a + "*x^2 + " + b +"*x + " + c + " = 0";

    }
}

ответ дан 27 сен 2012 в 10:22

Я бы для получение гарантированной 5+ в дополнении к ответу @Антон_Феоктистов создал бы иерархию классов (геттеры/сеттеры намеренно опущены):

public abstract class Equation {
    protected double static epsilon=0.0000001; //значение зависит от задачи
    protected double a;
    protected Equation(double a) {this.a=a;}
    protected boolean isZero(double x) {
        if(Math.abs(x) <= epsilon)
           return true;
        return false;
    }
    public abstract int getNumberOfRoots();
}

public class LinearEquation extends Equation {
    protected double b;
    public LinearEquation(double a, double b) {super(a); this.b=b;}
    public int getNumberOfRoots() {
       if(this.isZero(b)
          return 0;
       return 1;
    }

public class QuadraticEquation extends LinearEquation {
    protected double c;
    public LinearEquation(double a, double b, double c) {super(a, b); this.c=c;}
    public int getNumberOfRoots() {
       //blah-blah
    }
}

ответ дан 27 сен 2012 в 12:11

BarmaleyBarmaley

80.9k7 золотых знаков72 серебряных знака153 бронзовых знака

Опишу то, как я понял эту задачу:

Определить переменные класса. В классе нужно определить поля (в вашем случае типа double) a, b, c.
Конструкторы. Конструктор, навскидку, нужен 1. Он должен устанавливать значения a, b и c.
Метод вычисления количества корней. Исходя из первых 2х пунктов было бы логично сделать метод нестатичным и чтобы он возвращал количество, или записывал бы его в отдельное поле класса (за правильность алгоритма работы самого метода не ручаюсь, ибо вопрос был не об этом).
Метод отображения хранящейся в объекте информации. Для всех полей написать методы print, суть которых сводилась бы просто к выводу на экран значения переменной.
Например,
```
void printA(){
  System.out.println(a);
}
```

ответ дан 27 сен 2012 в 5:39

Источник