Калькулятор тангенса | Calculators.vip
Тангенс острого угла в прямоугольном треугольнике равняется отношение противолежащего катета к прилежащему катету.
.
Поделиться расчетом:
Найти величину
X=SIN(A)X=COS(A)X=TAN(A)X=CTN(A)
A=ARC SIN(X)A=ARC COS(A)A=ARC TAN(X)A=ARC CTN(X)
Первоначальные данные
Градус
Радиан
| Угол в градусах | tg (Тангенс) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0524 |
| 4° | 0.0699 |
| 5° | 0.0875 |
| 6° | 0.1051 |
| 7° | 0.1228 |
| 8° | 0.1405 |
| 9° | 0.1584 |
| 10° | 0.1763 |
| 11° | 0.1944 |
| 12° | 0. |
| 13° | 0.2309 |
| 14° | 0.2493 |
| 15° | 0.2679 |
| 16° | 0.2867 |
| 17° | 0.3057 |
| 18° | 0.3249 |
| 19° | 0.3443 |
| 20° | 0.364 |
| 21° | 0.3839 |
| 22° | 0.404 |
| 23° | 0.4245 |
| 24° | 0.4452 |
| 25° | 0.4663 |
| 26° | 0.4877 |
| 27° | 0.5095 |
| 28° | 0.5317 |
| 29° | 0.5543 |
| 30° | 0.5774 |
| 31° | 0.6009 |
| 32° | 0.6249 |
| 33° | 0.6494 |
| 34° | 0.6745 |
| 35° | 0.7002 |
| 36° | 0.7265 |
| 37° | 0.7536 |
| 38° | 0.7813 |
| 39° | 0.8098 |
| 40° | 0.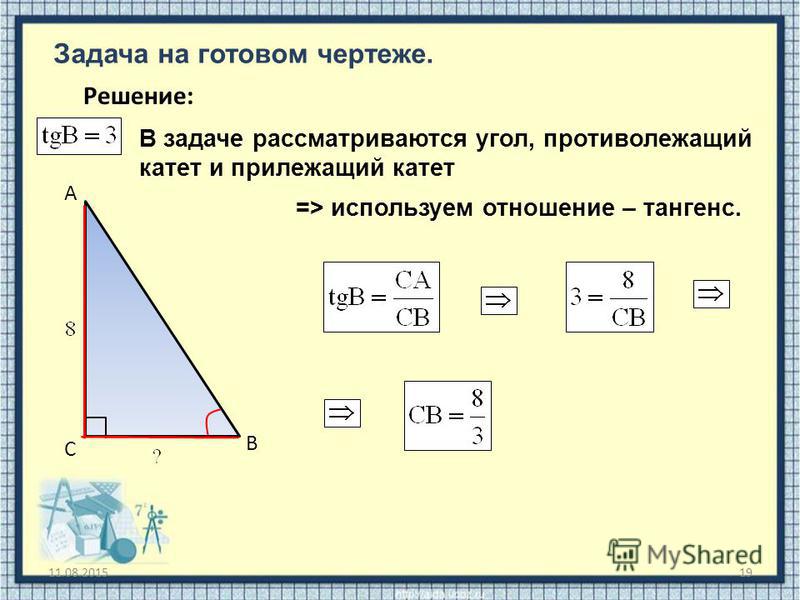 8391 8391 |
| 41° | 0.8693 |
| 42° | 0.9004 |
| 43° | 0.9325 |
| 44° | 0.9657 |
| 45° | 1 |
| 46° | 1.0355 |
| 47° | 1.0724 |
| 48° | 1.1106 |
| 49° | 1.1504 |
| 50° | 1.1918 |
| 51° | 1.2349 |
| 52° | 1.2799 |
| 53° | 1.327 |
| 54° | 1.3764 |
| 55° | 1.4281 |
| 56° | 1.4826 |
| 57° | 1.5399 |
| 58° | 1.6003 |
| 59° | 1.6643 |
| 60° | 1.7321 |
| 61° | 1.804 |
| 62° | 1.8807 |
| 63° | 1.9626 |
| 64° | 2.0503 |
| 65° | 2.1445 |
| 66° | 2.246 |
| 67° | 2.3559 |
| 68° | 2.4751 |
| 69° | 2.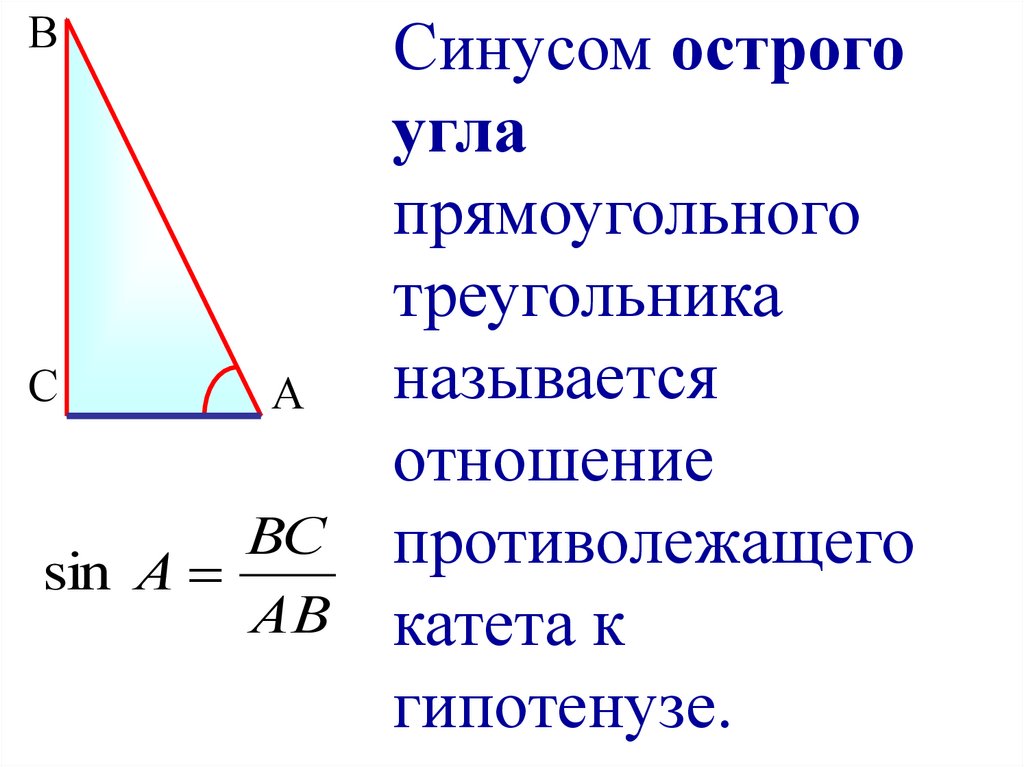 6051 6051 |
| 70° | 2.7475 |
| 71° | 2.9042 |
| 72° | 3.0777 |
| 73° | 3.2709 |
| 74° | 3.4874 |
| 75° | 3.7321 |
| 76° | 4.0108 |
| 77° | 4.3315 |
| 78° | 4.7046 |
| 79° | 5.1446 |
| 80° | 5.6713 |
| 81° | 6.3138 |
| 82° | 7.1154 |
| 83° | 8.1443 |
| 84° | 9.5144 |
| 85° | 11.4301 |
| 86° | 14.3007 |
| 87° | 19.0811 |
| 88° | 28.6363 |
| 89° | 57.29 |
| 90° | ∞ |
Функция тангенса
- Функция тангенса в прямоугольном треугольнике определяется как отношение противолежащего катета к прилежащему.
- Ее график представляет собой тангенсоиду.
- Функция определяется от 90 ° ± k · 180 ° до 270 ° ± k · 180 ° и принимает значения от −∞ до +∞.
прямоугольный треугольник
A
B
C
a
b
c
α
β
$$
begin{aligned}
& tanalpha = frac{a}{b} \ \
& tanbeta = frac{b}{a}
end{aligned}
$$
График
Функция тангенса
α
tan α
[°]
[рад]
0
90°
180°
270°
360°
0,5π
π
1,5π
2π
Калькулятор
Формулы
Функция тангенса
прямоугольный треугольник
A
B
C
a
b
c
α
β
$$ tanalpha = frac{a}{b} $$
$$ tanbeta = frac{b}{a} $$
$$
begin{aligned}
& tanalpha cdot cotalpha = 1 Rightarrow \ \
& cotalpha = frac{1}{tanalpha}
end{aligned}
$$
$$
begin{aligned}
& tanalpha = frac{sinalpha}{cosalpha} \ \
& cotalpha = frac{cosalpha}{sinalpha}
end{aligned}
$$
$$
begin{aligned}
& tan(alpha + beta) = frac{tanalpha + tanbeta}{1 — tanalphatanbeta} \ \
& tan(alpha — beta) = frac{tanalpha — tanbeta}{1 + tanalphatanbeta}
end{aligned}
$$
$$
begin{aligned}
& tan 2alpha = frac{2cdottanalpha}{1 — {tan}^2alpha} \ \
& left|tanfrac{alpha}{2}right| = sqrt{frac{1-cosalpha}{1+cosalpha}} \ \
& tan(-alpha) = -tanalpha
end{aligned}
$$
Если у Вас имеются какие-либо предложения или замечания, мы будем рады узнать о них.
info@calculat.org
На других языках
© 2014 – 2023 Ing. Adam Kašpárek, Jihlava, Czech Republic, IN: 02394260
При предоставлении услуг веб-сайт «Calculat.org» использует файлы куки.
Загрузить PDF
Загрузить PDF
Из этой статьи вы узнаете, как пользоваться основными функциями научного (инженерного) калькулятора. Научный калькулятор пригодится при изучении алгебры, геометрии и тригонометрии.
-
1
Найдите основные функции. На калькуляторе есть несколько функций, которые понадобятся для решения алгебраических, тригонометрических, геометрических и других задач. Найдите на калькуляторе следующие функции:
Основные операции[1]
Операция Описание операции + Сложение — Вычитание (а не знак «минус») x Умножение (для переменных есть отдельная кнопка x) ÷ Деление ^ Возведение в степень yx «y» в степени «x» √ или Sqrt Квадратный корень ex Экспонента sin Синус sin-1 Арксинус cos Косинус cos-1 Арккосинус tan Тангенс tan-1 Арктангенс ln Натуральный логарифм (с основанием e) log Десятичный логарифм (с основанием 10) (-) или neg Знак «минус» () Скобки (указывают порядок операций) π Значение числа Пи Mode Переключение между градусами и радианами -
2
Ознакомьтесь с дополнительными функциями. Наиболее важные функции указаны на самих кнопках (например, SIN для синуса), а дополнительные функции — над кнопками (например, SIN-1 для арксинуса или √ для квадратного корня).
- На некоторых калькуляторах есть кнопка «Shift» вместо кнопки «2ND».
- Во многих случаях цвет кнопки «Shift» или «2ND» соответствует цвету текста функции.
-
3
Всегда закрывайте круглые скобки. Если вы ввели левую скобку, обязательно введите правую (закрывающую) скобку. Если, например, вы ввели пять левых скобок, введите пять правых скобок.
- Это важно при длинных вычислениях с множеством операций — если вы забудете ввести закрывающую скобку, полученный результат будет неверным.
-
4
Переключайтесь между градусами и радианами. Можно работать со значениями в градусах (от 0 до 360) или радианах (вычисляются с помощью числа Пи). Нажмите «MODE» (Режим), кнопками со стрелками выберите опцию «RADIANS» (Радианы) или «DEGREES» (Градусы), а затем нажмите «ENTER».
- Это важно при выполнении расчетов в тригонометрии. Если полученное значение представляет собой десятичную дробь, а не градусы (или наоборот), переключитесь с радианов на градусы (или обратно).
-
5
Научитесь сохранять и восстанавливать результаты. Это понадобится при длинных вычислениях. Существует несколько способов использования сохраненной информации:
- Используйте функцию «Ответ», чтобы вызвать результат, который был показан последним. Например, если вы только что ввели 2^4, введите -10 и нажмите «ENTER», чтобы вычесть 10 из последнего результата.
- Когда получите нужный результат, нажмите «STO» (Сохранить) > «ALPHA», выберите букву, а затем нажмите «ENTER». Так вы сохраните этот результат в памяти под выбранной буквой.[2]
-
6
Очистите экран. Чтобы выйти из меню или удалить несколько строк выражения с экрана калькулятора, нажмите «CLEAR» (Очистить) в верхней части клавиатуры.
- Также можно нажать «2ND» или «Shift», а затем нажать любую кнопку с надписью «QUIT» (Выйти). В большинстве случаев такой кнопкой является «MODE» (Режим).
Реклама
-
1
Извлеките квадратный корень. Например, извлеките квадратный корень из 9. Вам, конечно, известно, что ответом будет число 3, поэтому это хороший способ потренироваться нажимать кнопки в правильном порядке:
- найдите символ квадратного корня (√);
- нажмите кнопку с символом квадратного корня или сначала нажмите кнопку «SHIFT» или «2ND», а затем нажмите кнопку с символом квадратного корня;
- нажмите «9»;
- нажмите «ENTER», чтобы получить ответ.
-
2
Возведите число в степень. В большинстве случаев это делается так: введите первое число (основание степени), нажмите кнопку с символом «^», а затем введите второе число (показатель степени).
- Например, чтобы вычислить 22, введите 2^2 и нажмите «ENTER».
- Чтобы убедиться, что вы не нарушили порядок ввода обоих чисел, вычислите 23. Если в качестве ответа вы получите 8, порядок ввода чисел не нарушен. Если на экране отобразилось число 9, вы вычислили 32.
-
3
Используйте функции тригонометрии. Когда вы работаете с синусами, косинусами и тангенсами, помните о двух вещах: порядке нажатия на кнопки и радианах/градусах.
- Например, вычислите синус 30°. Он равен 0,5.
- Выясните, нужно ли сначала ввести 30 или сначала нажать кнопку «SIN». Если сначала нужно нажать «SIN», а затем ввести 30, ответом будет 0,5; в этом случае калькулятор работает с градусами. Если ответ равен -0,988, калькулятор работает с радианами.
-
4
Введите длинное выражение. Здесь задача немного усложнится, потому что нужно учесть порядок операций и число введенных скобок (). Например, введите в калькулятор следующее выражение: 3^4/(3+(25/3+4*(-(1^2))))
- Обратите внимание, сколько скобок необходимо, чтобы правильно вычислить это выражение. Помните, что число открывающих «(» скобок должно равняться числу закрывающих «)» скобок.
-
5
Изучите сложные функции в меню «MATH» (Математика). Тригонометрические функции, корни, возведение в степень и число Пи указываются на кнопках или над ними, а вот более сложные функции (например, факториалы) можно найти в меню «MATH». Чтобы использовать это меню, выполните следующие действия:
- нажмите кнопку «MATH»;
- кнопками со стрелками прокрутите (вверх/вниз) категории уравнений;
- кнопками со стрелками прокрутите (вправо/влево) уравнения определенной категории;
- нажмите «ENTER», чтобы выбрать уравнение, а затем введите числа или формулу, к которой нужно применить это уравнение;
- нажмите «ENTER», чтобы вычислить уравнение.
Реклама
-
1
Учтите, что не все научные калькуляторы позволяют строить графики. Если на калькуляторе нет кнопки «Y», вы, скорее всего, не сможете построить на нем график линейного уравнения «y = mx + b» (или аналогичного).[3]
- Чтобы вяснить, умеет ли калькулятор строить графики, почитайте инструкцию или поищите кнопку «Y=» в верхней части клавиатуры калькулятора.
-
2
Нажмите кнопку «Y =». Как правило, она находится в верхней части клавиатуры калькулятора. Отобразится список значений Y (например, «Y1», «Y2» и так далее), каждое из которых соответствует определенному графику.
-
3
Введите уравнение. Введите уравнение (например, 3x+4), а затем нажмите «ENTER». Уравнение отобразится справа от значения «Y1».
- Чтобы ввести часть уравнения, в которой находится переменная, нажмите кнопку «X», «T», «Θ», «n» или аналогичную.
-
4
Нажмите GRAPH (График). Как правило, эта кнопка находится в верхней части клавиатуры калькулятора.
-
5
Просмотрите результаты. Через некоторое время на экране отобразится график — прямая/кривая линия и оси координат.
- Чтобы просмотреть координаты отдельных точек графика, нажмите кнопку «TABLE» (Таблица) (или нажмите «Shift»/»2ND», а затем нажмите кнопку «GRAPH») и прокрутите таблицу с координатами точек.
Реклама
Советы
- Расположение функций по кнопкам зависит от модели научного калькулятора. Поэтому найдите время, чтобы ознакомиться с калькулятором. Почитайте инструкцию, если не можете найти определенную функцию.
Реклама
Предупреждения
- Возможно, на старых научных калькуляторах (например, те, которые не умеют строить графики), нет некоторых дополнительных функций, таких как меню «MATH» (Математика).
Реклама
Об этой статье
Эту страницу просматривали 119 196 раз.
Была ли эта статья полезной?
Тангенс угла. Таблица тангенсов.
Тангенс угла через градусы, минуты и секунды
Тангенс угла через десятичную запись угла
Определение тангенса
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
tg(α) = sin(α)/cos(α)
tg(α) = 1/ctg(α)
Таблица тангенсов в радианах
tg(0°) = 0tg(π/12) = tg(15°) = 0.2679491924tg(π/6) = tg(30°) = 0.5773502692tg(π/4) = tg(45°) = 1tg(π/3) = tg(60°) = 1.732050808tg(5π/12) = tg(75°) = 3.732050808tg(π/2) = tg(90°) = ∞tg(7π/12) = tg(105°) = -3.732050808tg(2π/3) = tg(120°) = -1.732050808tg(3π/4) = tg(135°) = -1tg(5π/6) = tg(150°) = -0.5773502692tg(11π/12) = tg(165°) = -0.2679491924tg(π) = tg(180°) = 0tg(13π/12) = tg(195°) = 0.2679491924tg(7π/6) = tg(210°) = 0.5773502692tg(5π/4) = tg(225°) = 1tg(4π/3) = tg(240°) = 1.732050808tg(17π/12) = tg(255°) = 3.732050808tg(3π/2) = tg(270°) = ∞tg(19π/12) = tg(285°) = -3.732050808tg(5π/3) = tg(300°) = -1.732050808tg(7π/4) = tg(315°) = -1tg(11π/6) = tg(330°) = -0.5773502692tg(23π/12) = tg(345°) = -0.2679491924
Таблица Брадиса тангенсы
| tg(0) = 0 | tg(120) = -1.732050808 | tg(240) = 1.732050808 |
| tg(1) = 0.01745506493 | tg(121) = -1.664279482 | tg(241) = 1.804047755 |
| tg(2) = 0.03492076949 | tg(122) = -1.600334529 | tg(242) = 1.880726465 |
| tg(3) = 0.05240777928 | tg(123) = -1.539864964 | tg(243) = 1.962610506 |
| tg(4) = 0.06992681194 | tg(124) = -1.482560969 | tg(244) = 2.050303842 |
| tg(5) = 0.08748866353 | tg(125) = -1.428148007 | tg(245) = 2.144506921 |
| tg(6) = 0.1051042353 | tg(126) = -1.37638192 | tg(246) = 2.246036774 |
| tg(7) = 0.1227845609 | tg(127) = -1.327044822 | tg(247) = 2.355852366 |
| tg(8) = 0.1405408347 | tg(128) = -1.279941632 | tg(248) = 2.475086853 |
| tg(9) = 0.1583844403 | tg(129) = -1.234897157 | tg(249) = 2.605089065 |
| tg(10) = 0.1763269807 | tg(130) = -1.191753593 | tg(250) = 2.747477419 |
| tg(11) = 0.1943803091 | tg(131) = -1.150368407 | tg(251) = 2.904210878 |
| tg(12) = 0.2125565617 | tg(132) = -1.110612515 | tg(252) = 3.077683537 |
| tg(13) = 0.2308681911 | tg(133) = -1.07236871 | tg(253) = 3.270852618 |
| tg(14) = 0.2493280028 | tg(134) = -1.035530314 | tg(254) = 3.487414444 |
| tg(15) = 0.2679491924 | tg(135) = -1 | tg(255) = 3.732050808 |
| tg(16) = 0.2867453858 | tg(136) = -0.9656887748 | tg(256) = 4.010780934 |
| tg(17) = 0.3057306815 | tg(137) = -0.9325150861 | tg(257) = 4.331475874 |
| tg(18) = 0.3249196962 | tg(138) = -0.9004040443 | tg(258) = 4.704630109 |
| tg(19) = 0.3443276133 | tg(139) = -0.8692867378 | tg(259) = 5.144554016 |
| tg(20) = 0.3639702343 | tg(140) = -0.8390996312 | tg(260) = 5.67128182 |
| tg(21) = 0.383864035 | tg(141) = -0.8097840332 | tg(261) = 6.313751515 |
| tg(22) = 0.4040262258 | tg(142) = -0.7812856265 | tg(262) = 7.115369722 |
| tg(23) = 0.4244748162 | tg(143) = -0.7535540501 | tg(263) = 8.144346428 |
| tg(24) = 0.4452286853 | tg(144) = -0.726542528 | tg(264) = 9.514364454 |
| tg(25) = 0.4663076582 | tg(145) = -0.7002075382 | tg(265) = 11.4300523 |
| tg(26) = 0.4877325886 | tg(146) = -0.6745085168 | tg(266) = 14.30066626 |
| tg(27) = 0.5095254495 | tg(147) = -0.6494075932 | tg(267) = 19.08113669 |
| tg(28) = 0.5317094317 | tg(148) = -0.6248693519 | tg(268) = 28.63625328 |
| tg(29) = 0.5543090515 | tg(149) = -0.600860619 | tg(269) = 57.28996163 |
| tg(30) = 0.5773502692 | tg(150) = -0.5773502692 | tg(270) = ∞ |
| tg(31) = 0.600860619 | tg(151) = -0.5543090515 | tg(271) = -57.28996163 |
| tg(32) = 0.6248693519 | tg(152) = -0.5317094317 | tg(272) = -28.63625328 |
| tg(33) = 0.6494075932 | tg(153) = -0.5095254495 | tg(273) = -19.08113669 |
| tg(34) = 0.6745085168 | tg(154) = -0.4877325886 | tg(274) = -14.30066626 |
| tg(35) = 0.7002075382 | tg(155) = -0.4663076582 | tg(275) = -11.4300523 |
| tg(36) = 0.726542528 | tg(156) = -0.4452286853 | tg(276) = -9.514364454 |
| tg(37) = 0.7535540501 | tg(157) = -0.4244748162 | tg(277) = -8.144346428 |
| tg(38) = 0.7812856265 | tg(158) = -0.4040262258 | tg(278) = -7.115369722 |
| tg(39) = 0.8097840332 | tg(159) = -0.383864035 | tg(279) = -6.313751515 |
| tg(40) = 0.8390996312 | tg(160) = -0.3639702343 | tg(280) = -5.67128182 |
| tg(41) = 0.8692867378 | tg(161) = -0.3443276133 | tg(281) = -5.144554016 |
| tg(42) = 0.9004040443 | tg(162) = -0.3249196962 | tg(282) = -4.704630109 |
| tg(43) = 0.9325150861 | tg(163) = -0.3057306815 | tg(283) = -4.331475874 |
| tg(44) = 0.9656887748 | tg(164) = -0.2867453858 | tg(284) = -4.010780934 |
| tg(45) = 1 | tg(165) = -0.2679491924 | tg(285) = -3.732050808 |
| tg(46) = 1.035530314 | tg(166) = -0.2493280028 | tg(286) = -3.487414444 |
| tg(47) = 1.07236871 | tg(167) = -0.2308681911 | tg(287) = -3.270852618 |
| tg(48) = 1.110612515 | tg(168) = -0.2125565617 | tg(288) = -3.077683537 |
| tg(49) = 1.150368407 | tg(169) = -0.1943803091 | tg(289) = -2.904210878 |
| tg(50) = 1.191753593 | tg(170) = -0.1763269807 | tg(290) = -2.747477419 |
| tg(51) = 1.234897157 | tg(171) = -0.1583844403 | tg(291) = -2.605089065 |
| tg(52) = 1.279941632 | tg(172) = -0.1405408347 | tg(292) = -2.475086853 |
| tg(53) = 1.327044822 | tg(173) = -0.1227845609 | tg(293) = -2.355852366 |
| tg(54) = 1.37638192 | tg(174) = -0.1051042353 | tg(294) = -2.246036774 |
| tg(55) = 1.428148007 | tg(175) = -0.08748866353 | tg(295) = -2.144506921 |
| tg(56) = 1.482560969 | tg(176) = -0.06992681194 | tg(296) = -2.050303842 |
| tg(57) = 1.539864964 | tg(177) = -0.05240777928 | tg(297) = -1.962610506 |
| tg(58) = 1.600334529 | tg(178) = -0.03492076949 | tg(298) = -1.880726465 |
| tg(59) = 1.664279482 | tg(179) = -0.01745506493 | tg(299) = -1.804047755 |
| tg(60) = 1.732050808 | tg(180) = 0 | tg(300) = -1.732050808 |
| tg(61) = 1.804047755 | tg(181) = 0.01745506493 | tg(301) = -1.664279482 |
| tg(62) = 1.880726465 | tg(182) = 0.03492076949 | tg(302) = -1.600334529 |
| tg(63) = 1.962610506 | tg(183) = 0.05240777928 | tg(303) = -1.539864964 |
| tg(64) = 2.050303842 | tg(184) = 0.06992681194 | tg(304) = -1.482560969 |
| tg(65) = 2.144506921 | tg(185) = 0.08748866353 | tg(305) = -1.428148007 |
| tg(66) = 2.246036774 | tg(186) = 0.1051042353 | tg(306) = -1.37638192 |
| tg(67) = 2.355852366 | tg(187) = 0.1227845609 | tg(307) = -1.327044822 |
| tg(68) = 2.475086853 | tg(188) = 0.1405408347 | tg(308) = -1.279941632 |
| tg(69) = 2.605089065 | tg(189) = 0.1583844403 | tg(309) = -1.234897157 |
| tg(70) = 2.747477419 | tg(190) = 0.1763269807 | tg(310) = -1.191753593 |
| tg(71) = 2.904210878 | tg(191) = 0.1943803091 | tg(311) = -1.150368407 |
| tg(72) = 3.077683537 | tg(192) = 0.2125565617 | tg(312) = -1.110612515 |
| tg(73) = 3.270852618 | tg(193) = 0.2308681911 | tg(313) = -1.07236871 |
| tg(74) = 3.487414444 | tg(194) = 0.2493280028 | tg(314) = -1.035530314 |
| tg(75) = 3.732050808 | tg(195) = 0.2679491924 | tg(315) = -1 |
| tg(76) = 4.010780934 | tg(196) = 0.2867453858 | tg(316) = -0.9656887748 |
| tg(77) = 4.331475874 | tg(197) = 0.3057306815 | tg(317) = -0.9325150861 |
| tg(78) = 4.704630109 | tg(198) = 0.3249196962 | tg(318) = -0.9004040443 |
| tg(79) = 5.144554016 | tg(199) = 0.3443276133 | tg(319) = -0.8692867378 |
| tg(80) = 5.67128182 | tg(200) = 0.3639702343 | tg(320) = -0.8390996312 |
| tg(81) = 6.313751515 | tg(201) = 0.383864035 | tg(321) = -0.8097840332 |
| tg(82) = 7.115369722 | tg(202) = 0.4040262258 | tg(322) = -0.7812856265 |
| tg(83) = 8.144346428 | tg(203) = 0.4244748162 | tg(323) = -0.7535540501 |
| tg(84) = 9.514364454 | tg(204) = 0.4452286853 | tg(324) = -0.726542528 |
| tg(85) = 11.4300523 | tg(205) = 0.4663076582 | tg(325) = -0.7002075382 |
| tg(86) = 14.30066626 | tg(206) = 0.4877325886 | tg(326) = -0.6745085168 |
| tg(87) = 19.08113669 | tg(207) = 0.5095254495 | tg(327) = -0.6494075932 |
| tg(88) = 28.63625328 | tg(208) = 0.5317094317 | tg(328) = -0.6248693519 |
| tg(89) = 57.28996163 | tg(209) = 0.5543090515 | tg(329) = -0.600860619 |
| tg(90) = ∞ | tg(210) = 0.5773502692 | tg(330) = -0.5773502692 |
| tg(91) = -57.28996163 | tg(211) = 0.600860619 | tg(331) = -0.5543090515 |
| tg(92) = -28.63625328 | tg(212) = 0.6248693519 | tg(332) = -0.5317094317 |
| tg(93) = -19.08113669 | tg(213) = 0.6494075932 | tg(333) = -0.5095254495 |
| tg(94) = -14.30066626 | tg(214) = 0.6745085168 | tg(334) = -0.4877325886 |
| tg(95) = -11.4300523 | tg(215) = 0.7002075382 | tg(335) = -0.4663076582 |
| tg(96) = -9.514364454 | tg(216) = 0.726542528 | tg(336) = -0.4452286853 |
| tg(97) = -8.144346428 | tg(217) = 0.7535540501 | tg(337) = -0.4244748162 |
| tg(98) = -7.115369722 | tg(218) = 0.7812856265 | tg(338) = -0.4040262258 |
| tg(99) = -6.313751515 | tg(219) = 0.8097840332 | tg(339) = -0.383864035 |
| tg(100) = -5.67128182 | tg(220) = 0.8390996312 | tg(340) = -0.3639702343 |
| tg(101) = -5.144554016 | tg(221) = 0.8692867378 | tg(341) = -0.3443276133 |
| tg(102) = -4.704630109 | tg(222) = 0.9004040443 | tg(342) = -0.3249196962 |
| tg(103) = -4.331475874 | tg(223) = 0.9325150861 | tg(343) = -0.3057306815 |
| tg(104) = -4.010780934 | tg(224) = 0.9656887748 | tg(344) = -0.2867453858 |
| tg(105) = -3.732050808 | tg(225) = 1 | tg(345) = -0.2679491924 |
| tg(106) = -3.487414444 | tg(226) = 1.035530314 | tg(346) = -0.2493280028 |
| tg(107) = -3.270852618 | tg(227) = 1.07236871 | tg(347) = -0.2308681911 |
| tg(108) = -3.077683537 | tg(228) = 1.110612515 | tg(348) = -0.2125565617 |
| tg(109) = -2.904210878 | tg(229) = 1.150368407 | tg(349) = -0.1943803091 |
| tg(110) = -2.747477419 | tg(230) = 1.191753593 | tg(350) = -0.1763269807 |
| tg(111) = -2.605089065 | tg(231) = 1.234897157 | tg(351) = -0.1583844403 |
| tg(112) = -2.475086853 | tg(232) = 1.279941632 | tg(352) = -0.1405408347 |
| tg(113) = -2.355852366 | tg(233) = 1.327044822 | tg(353) = -0.1227845609 |
| tg(114) = -2.246036774 | tg(234) = 1.37638192 | tg(354) = -0.1051042353 |
| tg(115) = -2.144506921 | tg(235) = 1.428148007 | tg(355) = -0.08748866353 |
| tg(116) = -2.050303842 | tg(236) = 1.482560969 | tg(356) = -0.06992681194 |
| tg(117) = -1.962610506 | tg(237) = 1.539864964 | tg(357) = -0.05240777928 |
| tg(118) = -1.880726465 | tg(238) = 1.600334529 | tg(358) = -0.03492076949 |
| tg(119) = -1.804047755 | tg(239) = 1.664279482 | tg(359) = -0.01745506493 |
Похожие калькуляторы
|
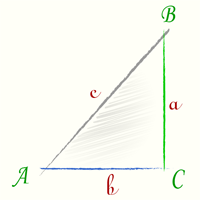
Тангенс угла tg(A) — есть отношение [ tg(A) = frac{a}{b} ] |
Тангенс угла — tg(A), таблица
|
0° Тангенс угла 0 градусов |
$ tg(0°) = tg(0) = 0 $ |
0.000 |
|
30° Тангенс угла 30 градусов |
$ tg(30°) = tgBig(Largefrac{pi}{6}normalsizeBig) = Largefrac{1}{sqrt{3}}normalsize $ |
0.577 |
|
45° Тангенс угла 45 градусов |
$ tg(45°) = tgBig(Largefrac{pi}{4}normalsizeBig) = 1 $ |
1.000 |
|
60° Тангенс угла 60 градусов |
$ tg(60°) = tgBig(Largefrac{pi}{3}normalsizeBig) = sqrt{3} $ |
1.732 |
|
90° Тангенс угла 90 градусов |
$ tg(90°) = tgBig(Largefrac{pi}{2}normalsizeBig) = infin $ |
∞ |
Вычислить, найти тангенс угла tg(A) и угол, в прямоугольном треугольнике
Вычислить, найти тангенс угла tg(A) по углу A в градусах
Вычислить, найти тангенс угла tg(A) по углу A в радианах
Тангенс угла — tg(A) |
стр. 224 |
|---|
