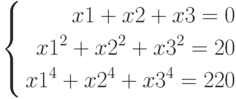На чтение 6 мин Просмотров 1.9к.
Содержание
- 1. Поиск экстремума функции
- 2. Экстремум функции одной переменной
- 3. Условный экстремум
- Александр Малыгин
- 2 Комментарии “ Оптимизация функций одной и нескольких переменных в PTC MathCAD ”
9. Нахождение экстремумов функций 
MathCAD позволяет находить экстремумы функций, которые имеют конечное количество экстремумов. Для нахождения экстремума используются функции Minimize и Maximize .
На рис.14 показан пример использования функции нахождения минимума. Нахождение максимума происходит аналогично, за исключением того, что функцию Minimize необходимо заменить на Maximize . В данном примере показан случай, когда максимум функции не может быть найден.
8.6.1. Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис. 8.8 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканиро-вать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.
Рис. 8.8. График функции f(х)=х 4 +5х 3 -10х
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
- Minimize (f, x1, . ,хм) — вектор значений аргументов, при которых функция f достигает минимума;
- Maximize (f, х1, . ,хм) — вектор значений аргументов, при которых функция f достигает максимума;
- f (x1, . , хм. ) — функция;
- x1, . , xм — аргументы, по которым производится минимизация (максимизация).
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис. 8.8) без дополнительных условий показаны в листингах 8.11- 8.12. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.
Листинг 8.11. Минимум функции одной переменной
Листинг 8.12. Максимум функции одной переменной
Как видно из листингов, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).
1. Поиск экстремума функции
Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и (или) уравнений. В таком случае говорят о задаче на условный экстремум.
Для решения задач поиска максимума и минимума в Mathcad имеются встроенные функции Minerr, Minimize и Maximize. Все они используют те же градиентные численные методы, что и функция Find для решения уравнений.
2. Экстремум функции одной переменной
Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремума. Последние называют еще задачами оптимизации. Рассмотрим конкретный пример функции f(x), показанной графиком на рис.2 на интервале (-2,5). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум на правой границе интервала (в порядке слева направо).
В Mathcad с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения и потом выбрать из них наибольший (наименьший), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности. Последний путь таит в себе некоторую опасность уйти в зону другого локального экстремума, но часто может быть предпочтительнее из соображений экономии времени.

Построим график заданной функции (рис.1). По графику видны участки локальных экстремумов функции.
Для поиска локальных экстремумов имеются две встроенные функции, которые могут применяться как в пределах вычислительного блока, так и автономно.
· Minimize (f, x1, … ,хм) — вектор значений аргументов, при которых функция f достигает минимума;
· Maximize (f, х1, … ,хм) — вектор значений аргументов, при которых функция f достигает максимума;
Всем аргументам функции f предварительно следует присвоить некоторые значения, причем для тех переменных, по которым производится минимизация, они будут восприниматься как начальные приближения. Примеры вычисления экстремума функции одной переменной (рис.1) без дополнительных условий показаны в листинге на рис.2. Поскольку никаких дополнительных условий в них не вводится, поиск экстремумов выполняется для любых значений.


Как видно из листинга, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются локальные различные экстремумы. В последнем случае численный метод вообще не справляется с задачей, поскольку начальное приближение х=-10 выбрано далеко от области локального максимума, и поиск решения уходит в сторону увеличения f (х).
3. Условный экстремум
В задачах на условный экстремум функции минимизации и максимизации должны быть включены в вычислительный блок, т. е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемой функции. На рис.3 показаны примеры поиска условного экстремума на различных интервалах, определенных неравенствами. Сравните результаты работы этого листинга с двумя предыдущими.

Рис. 3. Три примера поиска условного экстремума функции
Не забывайте о важности выбора правильного начального приближения и в случае задач на условный экстремум. Например, если вместо условия — 3 Скачать пример
Александр Малыгин
Объект обсуждения – программное обеспечение для выполнения автоматизированного конструкторского и технологического проектирования, разработки управляющих программ, вопросы, связанные с разработкой прикладных САПР.
2 Комментарии “ Оптимизация функций одной и нескольких переменных в PTC MathCAD ”
Спасибо, очень информативано! Скажите, а для 9 переменных такая же функция и такой же принцип используется?
Функция будет другая. Вы сами подбираете вид функции, остальное аналогично.
Пример решения задачи оптимизации в программе Mathcad
Пример
Дана нелинейная целевая функция
f(x,y)=x4–2y→min
Ограничения
4x+y–2=0
x2+y2≤50
Решение
Для поиска минимального или максимального значения функции в Mathcad имеются функции:
Minimize(f, x1, x2, …xn)
Maximize(f, x1, x2, …xn)
f — функция без аргументов для максимизации и минимизации значений;
x1, x2, …xn — скалярные переменные, найденные в системе уравнений.
Записываем решение в пакете Mathcad
3088
Теперь рассмотрим решение задачи на поиск минимума и максимума с применением функций Maximize и Minimize. Первая часть документа, реализующая решение данной задачи, представлена на рисунке 4.2. Здесь показано задание самого уравнения, построение графика функции и геометрическое представление ограничительных условий. Тут полезно особо отметить, что решение задачи оптимизации с ограничениями в принципе намного сложнее, чем без таковых. Алгоритм решения данной задачи с применением средств Mathcad показан на рисунке 4.3. Следует отметить, что функция Minimize (или Maximize) может вычислять минимум (или максимум) как при отсутствии ограничений, так и при их наличии.
Рис. 4.2 Начало документа с решением задачи поиска минимума и максимума функции с учетом ограничений
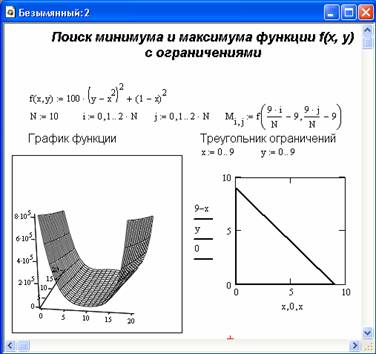
Объективности ради надо заметить, что результаты решения сильно зависят от выбора начальных значений переменных и далеко не всегда имеют устраивающую пользователя погрешность.
Рис. 4.3 Конец документа с решением задачи поиска минимума и максимума функции с учетом ограничений
4.4. Задачи оптимизации
В программе MathCAD с успехом решаются задачи оптимизации. Задача оптимизации (линейного программирования) — определение значений аргументов функции, при которых функция имеет экстремальное (минимальное, максимальное) значение. Условия, налагаемые на аргументы функции — заданные ограничения. Используется методика решения системы уравнений помощью блока Given. При этом вместо функции Find используется функция Maximize(), если определяется максимум, и функция Minimize() , если определяется минимум оптимизируемой функции. Последовательность действий следующая:
- ввести оптимизируемую функцию,
- определить начальные значения аргументов,
- в блоке Given ввести уравнения (неравенства) ограничений,
- ввести функцию Maximize () (Minimaze() ),
- определить решение.
Задача решается в алгебраическом и матричном виде. В матричном виде начальное значение корней, ограничения задаются в виде матриц. Решение в обоих случаях получается в виде матрицы.
Пример 4.11
Найти максимум функции
при ограничениях
Листинги решения в алгебраическом и матричном виде.
Оптимизируемая функция – поиск максимума,
Начальные значения:
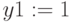
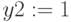
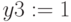
Ограничения:
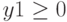
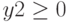
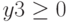
Решение:
Максимальное значение функции:
Матрица коэффициентов функции:
Матрица левых частей ограничений:
Матрица правых частей ограничений:
Начальные значения:
Решение:
Максимальное значение функции:
Основные итоги
В лекции представлены методы численного решения уравнений и систем уравнений с использованием функций MathCAD. Рассмотрены функция Root (), функция для поиска корней полинома polyroots(), вычислительные блоки Given .Find() и Given Minerr().. Описано численное решение систем линейных уравнений, а также способы аналитического решения : с помощью матриц, функции lsolve(), символьного оператора solve. Показано решение задач оптимизации.
Задания для самостоятельного выполнения
- Построить графики функций. Решить уравнения с применением функции root()
а)
для
б)
в)
(2 корня)
- Решить с применением функции polyroots() следующие уравнения
а)
б)
- Решить системы уравнений с использованием блока Given Find(.)
а)
найти 3 корня
б)
найти 2 корня
в)
г)
д)
- Решить систему уравнений тремя способами.
Ключевые термины
root() – функция для численного решения нелинейного уравнения с одним неизвестным. Возвращает с заданной точностью значение переменной, при котором функция равна нулю.
polyroot() — функция для численного поиска корней полинома. Возвращает вектор длиной n+1 всех корней полинома степени n.
Given Find() – вычислительный блок для численного решения нелинейных уравнений и систем уравнений.
Given Minerr() вычислительный блок для приближенного численного решения нелинейных уравнений и систем уравнений.
Maximize () – функция для поиска значений переменных функции, при которых функция имеет максимальное значение.
Minimaze() — , функция для поиска значений переменных функции, при которых функция имеет минимальное значение.
lsolve(A,B) — функция аналитического решения системы линейных уравнений, представленной в виде AX=B.
Mathcad: ищем экстремум функции двух переменных
Поиск экстремума функции двух переменных принципиально не отличается от случая одной переменной и выполняется стандартными функциями Minimize и Maximize. Проблема состоит в том, как правильно выбрать начальную точку (x,y), от которой будет выполняться поиск решения. Если у анализируемой функции несколько стационарных точек, может быть найден только «мусор», точней, найдётся ближайшая к начальной стационарная точка, не являющаяся экстремумом, или не найдётся ничего:
экстремум функции 2 переменных не находится — неверные начальные точки
Поэтому более правильным путём представляется реализация анализа функции на экстремум, ведь Mathcad математики не отменял 
Для заданной функции Z(x,y) = x3+2xy+y2 найдём первые и вторые частные производные, определим стационарные точки, в которых обращаются в ноль первые частные производные, затем выполним проверку достаточных условий локальных экстремумов:
D=Zxx*Zyy-Zxy2>0, Zxx>0— точка локального минимума,D>0, Zxx<0— точка локального максимума.
После этого выполним поиск экстремума от точки, близкой к найденной, с помощью стандартной функции MathCAD, которая годится, скорее, для уточнения решений, чем для анализа.
правильный поиск экстремума функции 2 переменных в Mathcad
Скачать этот пример в архиве .zip с документом .xmcd для Mathcad 14/15 (58 Кб)
22.03.2017, 13:27 [16171 просмотр]





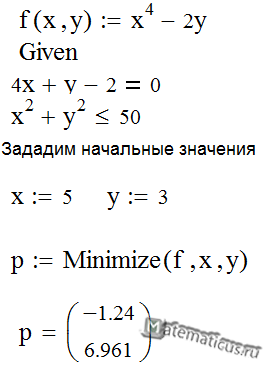


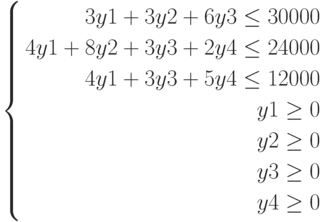

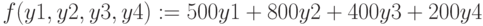


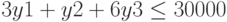

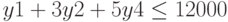
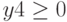

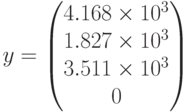
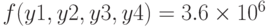
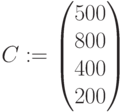
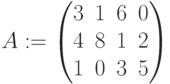
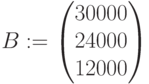
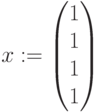
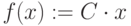



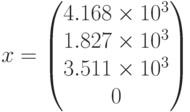
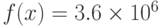
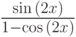 для
для 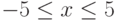
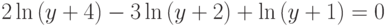
 (2 корня)
(2 корня)
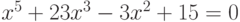
 найти 3 корня
найти 3 корня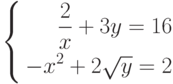 найти 2 корня
найти 2 корня