Как найди диаметр правильного шестиугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти диаметр описанной окружности шестиугольника

Гексагон

Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.

Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.

Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.

Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.

Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.

При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.

Свойства правильного шестиугольника

все внутренние углы равны между собой
каждый внутренний угол правильного шестиугольника равен 120 градусам
все стороны равны между собой
сторона правильного шестиугольника равна радиусу описанной окружности
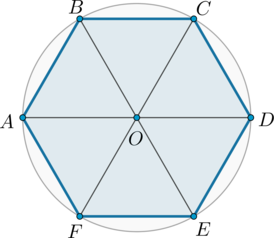
большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
меньшая диагональ правильного шестиугольника в ( sqrt ) раз больше его стороны.
vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
правильный шестиугольник заполняет плоскость без пробелов и наложений
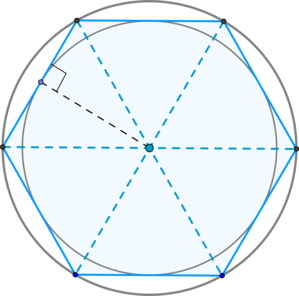
диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .

Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Радиус вписанной окружности правильного шестиугольника равен апофеме:

(r = m = alargefrac > normalsize)

Радиус описанной окружности равен стороне правильного шестиугольника:

Периметр правильного шестиугольника

Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Как найти диаметр описанной окружности шестиугольника

Правильный шестиугольник

1. Все углы правильного шестиугольника равны 120°

2. Все стороны правильного шестиугольника равны между собой

3. Периметр правильного шестиугольника

4. Формула площади правильного шестиугольника

5. Радиус описанной окружности правильного шестиугольника

6. Диаметр описанной окружности правильного шестиугольника

7. Радиус вписанной окружности правильного шестиугольника

8. Соотношения между радиусами вписанной и описанной окружностей

9. Угол , угол , угол , откуда следует, что треугольник — прямоугольный с гипотенузой равной . Следовательно,

10. Длина дуги AB равна

11. Формула площади сектора

Как найти диаметр описанной окружности шестиугольника

Периметр правильного шестиугольника равен 42. Найдите диаметр описанной окружности.

Это задание ещё не решено, приводим решение прототипа.

Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

Найдем сторону шестиугольника: 72 : 6 = 12.

Рассмотрим треугольник AOB. Радиус описанной вокруг шестиугольника окружности равен его стороне, а диаметр вдвое больше. Поэтому он равен 24.

Как найти диаметр описанной окружности в шестиугольнике

Периметр правильного шестиугольника равен 138. Найдите диаметр описанной окружности.

Это задание ещё не решено, приводим решение прототипа.

Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

Найдем сторону шестиугольника: 72 : 6 = 12.

Как найти диаметр описанной окружности в шестиугольнике

Правильный шестиугольник

1. Все углы правильного шестиугольника равны 120°

2. Все стороны правильного шестиугольника равны между собой

3. Периметр правильного шестиугольника

4. Формула площади правильного шестиугольника

5. Радиус описанной окружности правильного шестиугольника

6. Диаметр описанной окружности правильного шестиугольника

7. Радиус вписанной окружности правильного шестиугольника

8. Соотношения между радиусами вписанной и описанной окружностей

9. Угол , угол , угол , откуда следует, что треугольник — прямоугольный с гипотенузой равной . Следовательно,

10. Длина дуги AB равна

11. Формула площади сектора

источники:

http://ege.sdamgia.ru/problem?id=54061

http://self-edu.ru/geom.php?id=9

Источник

Как находить диаметр описанной окружности шестиугольника

Правильный шестиугольник

1. Все углы правильного шестиугольника равны 120°

2. Все стороны правильного шестиугольника равны между собой

3. Периметр правильного шестиугольника

4. Формула площади правильного шестиугольника

5. Радиус описанной окружности правильного шестиугольника

6. Диаметр описанной окружности правильного шестиугольника

7. Радиус вписанной окружности правильного шестиугольника

8. Соотношения между радиусами вписанной и описанной окружностей

9. Угол , угол , угол , откуда следует, что треугольник — прямоугольный с гипотенузой равной . Следовательно,

10. Длина дуги AB равна

11. Формула площади сектора

Как находить диаметр описанной окружности шестиугольника

Периметр правильного шестиугольника равен 42. Найдите диаметр описанной окружности.

Это задание ещё не решено, приводим решение прототипа.

Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

Найдем сторону шестиугольника: 72 : 6 = 12.

Гексагон

Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.

Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.

Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.

Свойства правильного шестиугольника

все внутренние углы равны между собой
каждый внутренний угол правильного шестиугольника равен 120 градусам
все стороны равны между собой
сторона правильного шестиугольника равна радиусу описанной окружности
большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
правильный шестиугольник заполняет плоскость без пробелов и наложений
диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .

Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Радиус вписанной окружности правильного шестиугольника равен апофеме:

(r = m = alargefrac<<sqrt 3 >><2>normalsize)

Радиус описанной окружности равен стороне правильного шестиугольника:

Периметр правильного шестиугольника

Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны

(S = pr = largefrac<<3sqrt 3 >><2>normalsize),
где (p) − полупериметр шестиугольника.

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

источники:

http://ege.sdamgia.ru/problem?id=54087

http://calcsbox.com/post/geksagon.html

Источник

Правильный шестиугольник, многоугольнике с 6 вершинами, вычислить его параметры. Шестиугольник-это фигура, из которой можно складывать мозаику (черепицу). Введите одно из известных значений. Затем нажмите кнопку вычислить.

Поделиться расчетом:

Калькулятор шестиугольников

Длина стороны(a)

Большая диагональ(d1)

Меньшая диагональ(d2)

Периметр(p)

Площадь(S)

Радиус вписанной окружности(r)

Вычислить

Очистить

Формулы:

d = 2 * a
d₂ = √3 * a
p = 6 * a
S = 3/2 * √3 * a2
r = √3 / 2 * a
Высота = d₂ = 2 * r
Радиус окружности = a
Внутренние углы: 120°, 9 диагоналей

S- площадь, p — периметр

Стороны и углы равны между собой

Короткие диагонали образуют гексограмму

Длинные диагонали образуют шесть равносторонних треугольников, с длинной ребра а

Вписанная и описанная окружность

Источник

6. Геометрия на плоскости (планиметрия). Часть II

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Правильный шестиугольник

Правильный шестиугольник — выпуклый шестиугольник, у которого все углы равны и все стороны равны.

(blacktriangleright) Каждый угол правильного шестиугольника равен (120^circ).

(blacktriangleright) Около правильного шестиугольника можно описать окружность: ее радиус равен его стороне.

(blacktriangleright) Большие диагонали правильного шестиугольника делят его на (6) равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.

(blacktriangleright) Центры вписанной и описанной около правильного шестиугольника окружностей есть точка пересечения больших диагоналей этого шестиугольника.

(blacktriangleright) Площадь правильного шестиугольника со стороной (a) равна [S=dfrac{3sqrt3}2a^2]

Задание
1

#2430

Уровень задания: Равен ЕГЭ

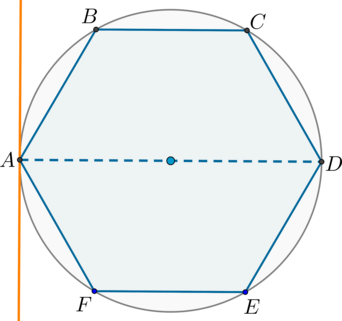
К окружности, описанной около правильного шестиугольника (ABCDEF), в точке (A) проведена касательная. Найдите угол между этой касательной и прямой (AD). Ответ дайте в градусах.

Т.к. центр описанной около правильного шестиугольника окружности есть точка пересечения больших диагоналей, то он лежит на отрезке (AD), то есть (AD) – диаметр описанной окружности. Т.к. радиус, проведенный в точку касания, перпендикулярен касательной, то угол между касательной и (AD) равен (90^circ).

Ответ: 90

Задание
2

#2427

Уровень задания: Равен ЕГЭ

Радиус вписанной в правильный шестиугольник окружности равен (sqrt{12}). Найдите радиус описанной около этого шестиугольника окружности.

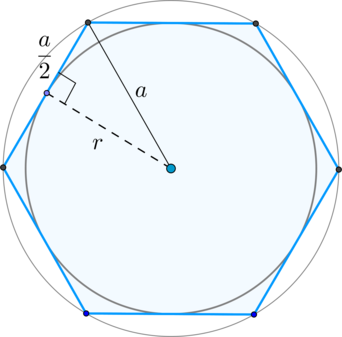
По свойству правильного шестиугольника радиус (r) вписанной окружности равен перпендикуляру, проведенному из центра правильного шестиугольника (центр вписанной и описанной окружности) к стороне шестиугольника; причем этот перпендикуляр падает в середину стороны.

Также по свойству правильного шестиугольника радиус описанной окружности равен его стороне (a). Тогда из прямоугольного треугольника:

[a^2=left(frac a2right)^2+r^2 quad Rightarrow quad a=dfrac 2{sqrt3},r quadRightarrow
quad a=dfrac2{sqrt3}cdot sqrt{12}=4]

Таким образом, и радиус описанной окружности равен (4).

Ответ: 4

Задание
3

#3589

Уровень задания: Равен ЕГЭ

Периметр правильного шестиугольника равен (72). Найдите диаметр описанной окружности.

Если провести все большие диагонали правильного шестиугольника, то они пересекутся в одной точке, которая и будет центром описанной около него окружности (свойство правильного шестиугольника). Рассмотрим чертеж:

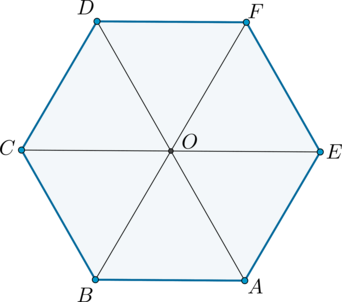
Так как угол правильного шестиугольника равен (180^circ(6-2):6=120^circ), а большие диагонали являются биссектрисами углов, то, например, (angle BAO=angle ABO=60^circ), следовательно, (triangle ABO) – равносторонний. То есть радиус окружности равен (AO) и равен (AB). Так как периметр шестиугольника равен (72), то его сторона равна (72:6=12). Тогда диаметр описанной окружности равен (2cdot 12=24).

Ответ: 24

Задание
4

#3588

Уровень задания: Равен ЕГЭ

Найдите радиус окружности, вписанной в правильный шестиугольник со стороной (sqrt3).

Для любого многоугольника, в который можно вписать окружность, верно (S=pcdot r), где (p) – полупериметр, а (r) – радиус вписанной окружности.
Площадь правильного шестиугольника со стороной (a) равна (S=dfrac{3sqrt3}2a^2), полупериметр равен (3a), тогда [dfrac{3sqrt3}2cdot (sqrt3)^2=3sqrt3cdot rquadRightarrowquad
r=1,5]

Ответ: 1,5

Задание
5

#3587

Уровень задания: Равен ЕГЭ

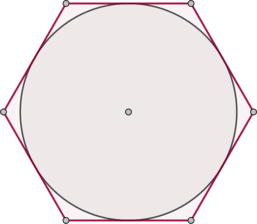
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен (sqrt3).

Ответ: 2

Задание
6

#2429

Уровень задания: Равен ЕГЭ

Площадь правильного шестиугольника равна (24sqrt3). Найдите длину его большей диагонали.

По свойству правильного шестиугольника большая его диагональ в два раза больше его стороны. Следовательно, если (AB=a), то (AD=BF=CE=2a).

Т.к. эти диагонали делят правильный шестиугольник на 6 равносторонних треугольников, причем площадь каждого равна (frac{sqrt3}4 a^2), то площадь всего шестиугольника равна

[S=6cdot dfrac{sqrt3}4a^2=24sqrt3 quad Rightarrow quad a=4 quad Rightarrow
quad AD=2a=8.]

Ответ: 8

Задание
7

#666

Уровень задания: Равен ЕГЭ

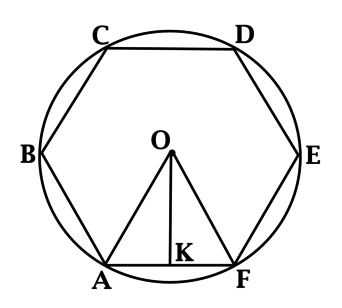
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Расстояние от точки (O) до одной из его сторон равно (4sqrt{3}). Найдите радиус этой окружности.

Радиус описанной около правильного шестиугольника окружности равен стороне этого шестиугольника.

(OK) – высота в треугольнике (AOF), опущенная из (O). Так как расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки на эту прямую, то (OK = 4sqrt{3}).
Пусть (R) – радиус описанной окружности, тогда (OF = R), (KF = 0,5R) (так как (OK) ещё и медиана), таким образом, по теореме Пифагора (R^2 = (0,5R)^2 + (4sqrt{3})^2), откуда (R = .

Ответ: 8

Теме «Правильный шестиугольник и его свойства» в ЕГЭ по математике традиционно отводится сразу несколько заданий. Причем в зависимости от условия от учащегося может требоваться как развернутый, так и краткий ответ. Именно поэтому в процессе подготовки к сдаче аттестационного испытания выпускникам непременно стоит научиться решать задачи на применение свойств этой фигуры, в которых необходимо найти ее стороны, диагонали, радиус окружности со вписанным правильным шестиугольником и т. д.

Восполнить пробелы в знаниях, «прокачать» навыки и улучшить собственные знания по данной теме вам поможет образовательный проект «Школково». Наши специалисты подготовили и изложили весь базовый материал для подготовки к ЕГЭ в максимально доступной форме.

Чтобы школьники могли успешно справляться с задачами по данной теме, мы рекомендуем повторить базовые понятия: каковы свойства правильного шестиугольника, описанного около окружности, как вычисляется его площадь, чему равны его углы и т. д. Весь необходимый материал вы найдете в разделе «Теоретическая справка». Он был разработан нашими сотрудники на основе богатого практического опыта.

Для закрепления полученных знаний предлагаем потренироваться в решении соответствующих задач, а также заданий по теме «Параллелограмм в ЕГЭ». Найти их вы сможете в разделе «Каталог». Для каждого упражнения на сайте представлены алгоритм решения и правильный ответ.

Готовиться к ЕГЭ школьники из Москвы и других городов могут в режиме онлайн. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». В дальнейшем к этому заданию можно будет вернуться и, к примеру, обсудить алгоритм его решения с преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник

Периметр правильного шестиугольника равен 120. Найдите диаметр описанной около этого шестиугольника окружности.

Светило науки — 7610 ответов — 113408 раз оказано помощи

P₆=120 -периметр шестиугольника
P₆=6a
6a=120
a=120:6=20 -сторона шестиугольника
R₆=а=20-диаметр окружности описанной около правильного шестиугольника
D=2R₆=2*20=40-диметр окружности описанной около правильного шестиугольника

Светило науки — 21 ответ — 740 раз оказано помощи

D (диаметр) = 2 * R (радиус)
R = x : ( 2 * sin a/2 ) , Значит D = ( 2 * x ) : ( 2 * sin a/2 ) , где
x — сторона шестиугольника = P (периметр) : 6 = 120 : 6 = 20
a — центральный угол шестиугольника = 360* (градусов) : 6 = 60* (градусов)
D = ( 2 * 20 ) : ( 2 * sin 60/2 ) = 40 : ( 2 * sin 30 ) = 40 : ( 2 * 0,5 ) = 40 : 1 = 40
Ответ: 40.

Источник