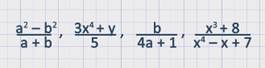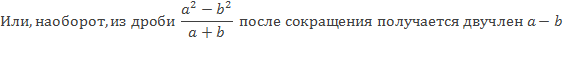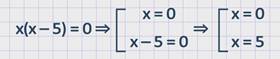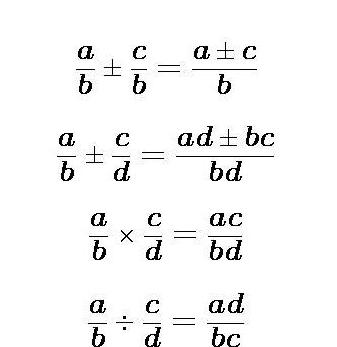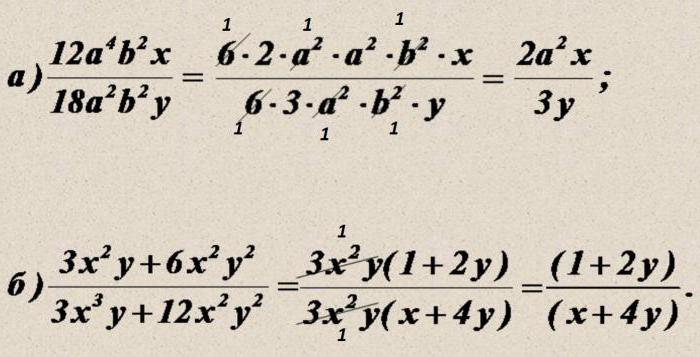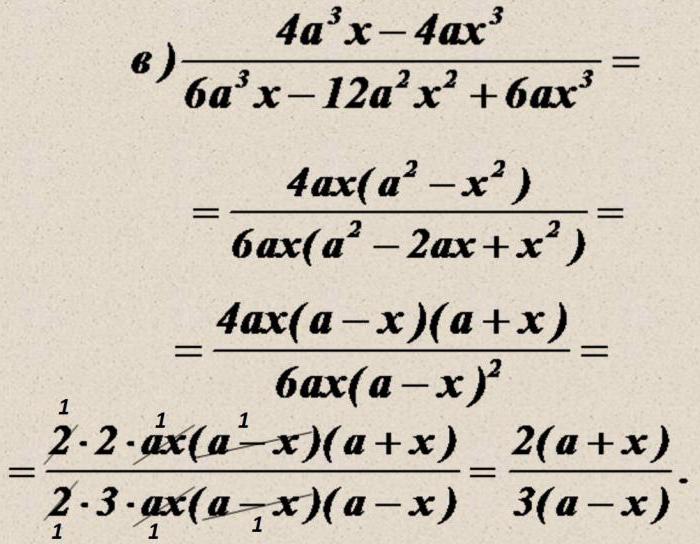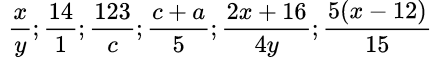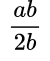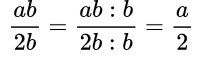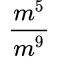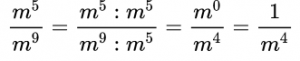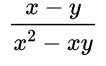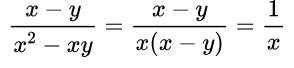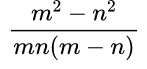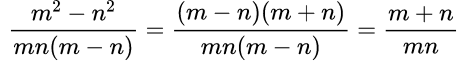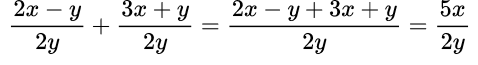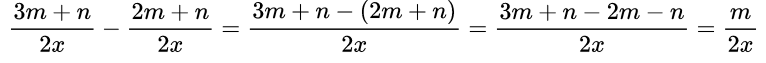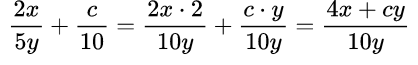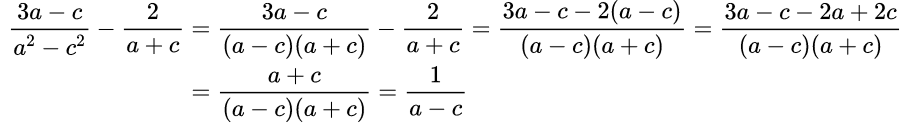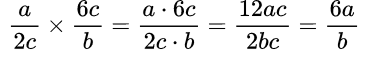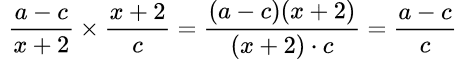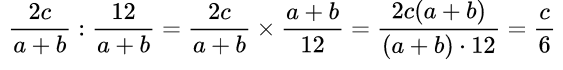Как найди значение алгебраической дроби

Содержание:

• § 1  Понятие алгебраической дроби
• § 2  Допустимые значения переменных алгебраической дроби

Когда ученик переходит в старшую школу, математика разделяется на 2 предмета: алгебру и геометрию. Понятий становится все больше, задания все сложнее. У некоторых возникают трудности с восприятием дробей. Пропустили первый урок по этой теме, и вуаля. Как решать алгебраические дроби? Вопрос, который будет мучить на протяжении всей школьной жизни.

Понятие алгебраической дроби

Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q – знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение.

Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение – часть целого.

Как правило, целое – это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель – делимое, знаменатель – делитель.

Основное правило обыкновенных дробей

Когда учащиеся проходят данную тему в школе, им дают примеры на закрепление. Чтобы правильно их решать и находить различные пути из сложных ситуаций, нужно применять основное свойство дробей.

Оно звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличные от нуля), то значение обыкновенной дроби не изменится. Частным случаем от данного правила является разделение обеих частей выражения на одно и то же число или многочлен. Подобные преобразования называются тождественными равенствами.

Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей.

Математические операции с дробями

Рассмотрим, как решать, основное свойство алгебраической дроби, как применять его на практике. Если нужно перемножить две дроби, сложить их, разделить одну на другую или произвести вычитание, нужно всегда придерживаться правил.

Так, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то нужно опустить этот пункт. Когда общий знаменатель найден, как решать алгебраические дроби? Нужно сложить или вычесть числители. Но! Нужно помнить, что при наличии знака «–» перед дробью все знаки в числителе меняются на противоположные. Иногда не следует производить каких-либо подстановок и математических операций. Достаточно поменять знак перед дробью.

Часто используется такое понятие, как сокращение дробей. Это означает следующее: если числитель и знаменатель разделить на отличное от единицы выражение (одинаковое для обеих частей), то получается новая дробь. Делимое и делитель меньше прежних, но в силу основного правила дробей остаются равными изначальному примеру.

Целью этой операции является получение нового несократимого выражения. Решить данную задачу можно, если сократить числитель и знаменатель на наибольший общий делитель. Алгоритм операции состоит из двух пунктов:

1. Нахождение НОД для обеих частей дроби.
2. Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предшествующей.

Ниже показана таблица, в которой расписаны формулы. Для удобства ее можно распечатать и носить с собой в тетради. Однако, чтобы в будущем при решении контрольной или экзамена не возникло трудностей в вопросе, как решать алгебраические дроби, указанные формулы нужно выучить наизусть.

Несколько примеров с решениями

С теоретической точки зрения рассмотрен вопрос, как решать алгебраические дроби. Примеры, приведенные в статье, помогут лучше усвоить материал.

1. Преобразовать дроби и привести их к общему знаменателю.

2. Преобразовать дроби и привести их к общему знаменателю.

3. Сократить указанные выражения (с использованием изученного основного правила дроби и сокращения степеней)

4. Сократить многочлены. Подсказка: нужно обнаружить формулы сокращенного умножения, привести к подобающему виду, сократить одинаковые элементы.

Задание на закрепление материала

1. Какие действия нужно произвести, что найти скрытое число? Решите примеры.

2. Умножьте и поделите дроби, пользуясь основным правилом.

После изучения теоретической части и расссмотрения практической вопросов больше возникнуть не должно.

Определение алгебраической дроби

Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).

Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю).

Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.

Например: Дробь $frac{x+5}{x-4}$ существует при условии x≠4. Допустимые значения переменной ${x| x in Bbb R, x neq 4 } $.

Дробь $frac{y}{y^2-9}$ существует при условии y≠±3. Допустимые значения переменной $ { y| y in Bbb R, y neq pm 3 }$.

Основное свойство алгебраической дроби

Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:

$$ frac{2x+3y}{4x^2-9y^2} = frac{2x+3y}{(2x+3y)(2x-3y)} = frac{1}{2x-3y} $$

$$ frac{a^3-8}{a-2} = frac{(a-2)(a^2+2a+4)}{a-2} = a^2+2a+4 $$

Приведение алгебраических дробей к общему знаменателю

Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:

$$ frac{1^{(x+1)}}{x-1} — frac{1}{x^2-1} — frac{1^{(x-1)}}{x+1} = frac{x+1-1-(x-1)}{(x-1)(x+1)} = frac{1}{x^2-1} $$

Например: привести к общему знаменателю $frac{1}{xy^2}, frac{x}{y}, frac{-4}{x}$

Шаг 1. Наименьшее общее кратное: $xy^2$

Шаг 2. Дополнительные множители

$$ frac{1}{xy^2}, frac{x^{xy}}{y}, -frac{4^{y2}}{x}$$

Шаг 3. Результат:

$$ frac{1}{xy^2}, frac{x^2 y}{xy^2}, -frac{4y^2}{xy^2} $$

Перемена знака у члена дроби

Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:

$$ frac{x}{y} = frac{-x}{-y} $$

Дробь также не изменится, если провести следующие перемены знаков:

$$ frac{x}{y} = frac{-x}{y} = -frac{x}{-y} $$

Ещё несколько полезных формул, связанных с переменой знаков:

$$ frac{a-b}{b-a} = -1, frac{(a-b)^2}{(b-a)^2} = 1, frac{1}{a-b} = -frac{1}{b-a}, frac{1}{(a-b)^2} = frac{1}{(b-a)^2} $$

Примеры

Пример 1. Найдите допустимые значения переменных, входящих в дробь:

а)$ frac{5}{a^2-4}$

$ a^2-4 neq 0 iff (a-2)(a+2) neq 0 iff a neq pm 2$

${a| a in Bbb R, a neq pm 2}$ — все действительные числа, кроме $pm 2$

б)$ frac{7x+y}{3x-1}$

$ 3x-1 neq 0 iff x neq frac{1}{3}$

${x|x in Bbb R, x neq frac{1}{3}}$ — все действительные числа, кроме $frac{1}{3}$

в)$ frac{k^2-1}{k+1}$

$k+1 neq 0 iff k neq -1 $

${k|k in Bbb R, k neq -1}$ — все действительные числа, кроме -1

Обратите внимание: несмотря на то, что дробь сокращается $frac{k^2-1}{k+1} = frac{(k+1)(k-1)}{k+1} = k-1$ требование $k neq -1$ сохраняется.

г) $ frac{5}{x^2+6x+9}$

$x^2+6x+9 neq 0 iff (x+3)^2 neq 0 iff x neq -3 $

$ {x|x in Bbb R, x neq -3}$ — все действительные числа, кроме -3

д)*$ frac{1}{x-frac{4}{x}} $

$$ x- frac{4}{x} neq 0 iff frac{x^2-4}{x} neq 0 iff {left{ begin{array}{c} x^2-4 neq 0 \ x neq 0 end{array} right.} iff x neq {0; pm2}$$

${x|x in Bbb R, x neq {0;pm2}}$ — все действительные числа, кроме $0,pm2$

е)*$ frac{5}{y^2-3|y|} $

$ y^2-3|y| neq 0 iff |y|(|y|-3) neq 0 iff {left{ begin{array}{c} |y| neq 0 \ |y| neq 3 end{array} right.} iff y neq {0; pm3} $

${y|y in Bbb R, y neq {0; pm3} }$ — все действительные числа, кроме $0, pm3$

Пример 2. Сократите дроби:

а) $$ frac{a^2-9}{2a+6} = frac{(a-3)(a+3)}{2(a+3)} = frac{a-3}{2}$$

б)$$ frac{x^2+2x+1}{x^2-1} = frac{(x+1)^2}{(x+1)(x-1)} = frac{x+1}{x-1}$$

в) $$ frac{12x^2-8xy}{3xy-2y^2} = frac{4x(3x-2y)}{y(3x-2y)} = frac{4x}{y} $$

г) $$ frac{b+5}{b^3-125} = frac{b+5}{(b+5)(b^2-5b+25)} = frac{1}{b^2-5b+25} $$

Пример 3. Упростите выражение:

а) $$ frac{a-b}{(b-a)^2} = frac{a-b}{(a-b)^2} = frac{1}{a-b}$$

б) $$ frac{(-a-b)^2}{a+b} = frac{(-1)^2 (a+b)^2}{a+b} = a+b $$

в) $$ frac{(-a-b)^2}{(a+b)^2} = frac{(a+b)^2}{(a+b)^2} = 1 $$

г) $$ frac{(a-b)^2}{b-a} = frac{(b-a)^2}{b-a} = b-a $$

Пример 4. Постройте график функции:

(О графике линейной функции – см. §38 справочника для 7 класса)

$а) y(x) = frac{x^2-4}{2x+4}$

$$ y(x) = frac{(x-2)(x+2)}{2(x+2)} = {left{ begin{array}{c} frac{x-2}{2} \ x neq -2 end{array} right.} $$

График – прямая y(x) = 0,5x-1, кроме точки (-2;-2), т.к. $x neq -2$.

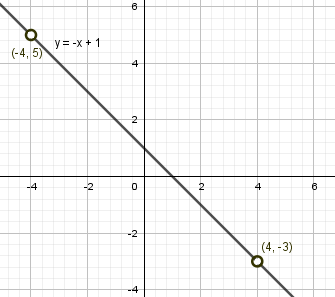
$б) y(x) = frac{x^3-16x}{x^2-16}-2x+1$

$$ y(x) = frac{x(x^2-16)}{x^2-16}-2x+1 = {left{ begin{array}{c} -x+1 \ x neq pm 4 end{array} right.} $$

График – прямая y(x) = -x+1, кроме точек (-4;5) и (4;-3), т.к. $x neq pm 4$.

Определение

Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения.

Примеры алгебраических дробей:

Для алгебраических дробей применяются правила, аналогичные обыкновенным дробям.

Сокращение алгебраической дроби

Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на одно и то же выражение, на их общий множитель (одночлен, его степень или многочлен) – применяется основное свойство дроби. Причем и числитель, и знаменатель должны содержать множители.

Пример №1. Сократим дробь:

В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:

Промежуточные действия можно не записывать, а выполнять устно.

Пример №2. Сократим дробь:

Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на  m⁵:

Пример №3. Сократим дробь:

В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).

Пример №4. Сократим дробь:

Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m²– n²=(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).

Сложение и вычитание алгебраических дробей с одинаковым знаменателем

При сложении и вычитании алгебраических дробей с одинаковыми знаменателями знаменатель остается прежним, а числители складывают или вычитают (из числителя первой вычитают числитель второй дроби).

Пример №5. Выполним сложение дробей:

Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.

Пример №6. Выполним вычитание дробей:

В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.

Сложение и вычитание алгебраических дробей с разными знаменателями

Алгоритм действий

Чтобы сложить или вычесть дроби с разными знаменателями, необходимо:

1. найти общий знаменатель, который может состоять из таких множителей, как числа, степени, многочлены и т.д.
2. Найти дополнительный множитель к каждой дроби.
3. Умножить каждый числитель на его дополнительный множитель.
4. Выполнить сложение (вычитание) дробей с одинаковыми знаменателями.
5. При необходимости сократить полученную дробь.

Пример №7. Выполнить сложение дробей:

Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.

Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.

Пример №8. Выполнить вычитание дробей:

Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а² – с²=(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).

Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).

Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).

Умножение алгебраических дробей

Алгоритм действий

Чтобы перемножить алгебраические дроби, надо числитель перемножить с числителем, а знаменатель со знаменателем. При необходимости выполнить сокращение алгебраической дроби, используя правило.

Пример №9. Выполнить умножение дробей:

Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.

Пример №10. Выполнить умножение дробей:

Здесь в числителях и знаменателях  – многочлены. Поэтому при записи умножения обязательно заключаем  их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.

Деление алгебраических дробей

Алгоритм действий

Чтобы разделить одну алгебраическую дробь на другую, надо первую дробь умножить на дробь, обратную второй (то есть умножить на дробь, у которой числитель равен знаменателю второй дроби, а знаменатель числителю второй дроби). Далее – выполнить умножение дробей по уже известному алгоритму.

Пример №11. Выполнить деление дробей:

Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.

 

Алла Василевская | Просмотров: 8.3k