Как найдите меру лебега

From Wikipedia, the free encyclopedia

In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called n-dimensional volume, n-volume, or simply volume.^[1] It is used throughout real analysis, in particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set A is here denoted by λ(A).

Henri Lebesgue described this measure in the year 1901 which, a year after, was followed up by his description of the Lebesgue integral. Both were published as part of his dissertation in 1902.^[2]

Definition[edit]

For any interval , or , in the set of real numbers, let denote its length. For any subset , the Lebesgue outer measure^[3] is defined as an infimum

The above definition can be generalised to higher dimensions as follows.^[4]
For any rectangular cuboid which is a product of open intervals, let denote its volume.
For any subset ,

Some sets satisfy the Carathéodory criterion, which requires that for every ,

The set of all such forms a σ-algebra. For any such , its Lebesgue measure is defined to be its Lebesgue outer measure: .

A set that does not satisfy the Carathéodory criterion is not Lebesgue-measurable. ZFC proves that non-measurable sets do exist; an example is the Vitali sets.

Intuition[edit]

The first part of the definition states that the subset of the real numbers is reduced to its outer measure by coverage by sets of open intervals. Each of these sets of intervals covers in a sense, since the union of these intervals contains . The total length of any covering interval set may overestimate the measure of because is a subset of the union of the intervals, and so the intervals may include points which are not in . The Lebesgue outer measure emerges as the greatest lower bound (infimum) of the lengths from among all possible such sets. Intuitively, it is the total length of those interval sets which fit most tightly and do not overlap.

That characterizes the Lebesgue outer measure. Whether this outer measure translates to the Lebesgue measure proper depends on an additional condition. This condition is tested by taking subsets of the real numbers using as an instrument to split into two partitions: the part of which intersects with and the remaining part of which is not in : the set difference of and . These partitions of are subject to the outer measure. If for all possible such subsets of the real numbers, the partitions of cut apart by have outer measures whose sum is the outer measure of , then the outer Lebesgue measure of gives its Lebesgue measure. Intuitively, this condition means that the set must not have some curious properties which causes a discrepancy in the measure of another set when is used as a «mask» to «clip» that set, hinting at the existence of sets for which the Lebesgue outer measure does not give the Lebesgue measure. (Such sets are, in fact, not Lebesgue-measurable.)

Examples[edit]

• Any closed interval [a, b] of real numbers is Lebesgue-measurable, and its Lebesgue measure is the length b − a. The open interval (a, b) has the same measure, since the difference between the two sets consists only of the end points a and b, which each have measure zero.
• Any Cartesian product of intervals [a, b] and [c, d] is Lebesgue-measurable, and its Lebesgue measure is (b − a)(d − c), the area of the corresponding rectangle.
• Moreover, every Borel set is Lebesgue-measurable. However, there are Lebesgue-measurable sets which are not Borel sets.^[5][6]
• Any countable set of real numbers has Lebesgue measure 0. In particular, the Lebesgue measure of the set of algebraic numbers is 0, even though the set is dense in R.
• The Cantor set and the set of Liouville numbers are examples of uncountable sets that have Lebesgue measure 0.
• If the axiom of determinacy holds then all sets of reals are Lebesgue-measurable. Determinacy is however not compatible with the axiom of choice.
• Vitali sets are examples of sets that are not measurable with respect to the Lebesgue measure. Their existence relies on the axiom of choice.
• Osgood curves are simple plane curves with positive Lebesgue measure^[7] (it can be obtained by small variation of the Peano curve construction). The dragon curve is another unusual example.
• Any line in , for , has a zero Lebesgue measure. In general, every proper hyperplane has a zero Lebesgue measure in its ambient space.

Properties[edit]

The Lebesgue measure on Rⁿ has the following properties:

1. If A is a cartesian product of intervals I₁ × I₂ × ⋯ × I_n, then A is Lebesgue-measurable and
2. If A is a disjoint union of countably many disjoint Lebesgue-measurable sets, then A is itself Lebesgue-measurable and λ(A) is equal to the sum (or infinite series) of the measures of the involved measurable sets.
3. If A is Lebesgue-measurable, then so is its complement.
4. λ(A) ≥ 0 for every Lebesgue-measurable set A.
5. If A and B are Lebesgue-measurable and A is a subset of B, then λ(A) ≤ λ(B). (A consequence of 2.)
6. Countable unions and intersections of Lebesgue-measurable sets are Lebesgue-measurable. (Not a consequence of 2 and 3, because a family of sets that is closed under complements and disjoint countable unions does not need to be closed under countable unions: .)
7. If A is an open or closed subset of Rⁿ (or even Borel set, see metric space), then A is Lebesgue-measurable.
8. If A is a Lebesgue-measurable set, then it is «approximately open» and «approximately closed» in the sense of Lebesgue measure.
9. A Lebesgue-measurable set can be «squeezed» between a containing open set and a contained closed set. This property has been used as an alternative definition of Lebesgue measurability. More precisely, is Lebesgue-measurable if and only if for every there exist an open set and a closed set such that and .^[8]
10. A Lebesgue-measurable set can be «squeezed» between a containing G_δ set and a contained F_σ. I.e, if A is Lebesgue-measurable then there exist a G_δ set G and an F_σ F such that G ⊇ A ⊇ F and λ(G  A) = λ(A  F) = 0.
11. Lebesgue measure is both locally finite and inner regular, and so it is a Radon measure.
12. Lebesgue measure is strictly positive on non-empty open sets, and so its support is the whole of Rⁿ.
13. If A is a Lebesgue-measurable set with λ(A) = 0 (a null set), then every subset of A is also a null set. A fortiori, every subset of A is measurable.
14. If A is Lebesgue-measurable and x is an element of Rⁿ, then the translation of A by x, defined by A + x = {a + x : a ∈ A}, is also Lebesgue-measurable and has the same measure as A.
15. If A is Lebesgue-measurable and , then the dilation of by defined by is also Lebesgue-measurable and has measure
16. More generally, if T is a linear transformation and A is a measurable subset of Rⁿ, then T(A) is also Lebesgue-measurable and has the measure .

All the above may be succinctly summarized as follows (although the last two assertions are non-trivially linked to the following):

The Lebesgue-measurable sets form a σ-algebra containing all products of intervals, and λ is the unique complete translation-invariant measure on that σ-algebra with

The Lebesgue measure also has the property of being σ-finite.

Null sets[edit]

A subset of Rⁿ is a null set if, for every ε > 0, it can be covered with countably many products of n intervals whose total volume is at most ε. All countable sets are null sets.

If a subset of Rⁿ has Hausdorff dimension less than n then it is a null set with respect to n-dimensional Lebesgue measure. Here Hausdorff dimension is relative to the Euclidean metric on Rⁿ (or any metric Lipschitz equivalent to it). On the other hand, a set may have topological dimension less than n and have positive n-dimensional Lebesgue measure. An example of this is the Smith–Volterra–Cantor set which has topological dimension 0 yet has positive 1-dimensional Lebesgue measure.

In order to show that a given set A is Lebesgue-measurable, one usually tries to find a «nicer» set B which differs from A only by a null set (in the sense that the symmetric difference (A − B) ∪ (B − A) is a null set) and then show that B can be generated using countable unions and intersections from open or closed sets.

Construction of the Lebesgue measure[edit]

The modern construction of the Lebesgue measure is an application of Carathéodory’s extension theorem. It proceeds as follows.

Fix n ∈ N. A box in Rⁿ is a set of the form

where b_i ≥ a_i, and the product symbol here represents a Cartesian product. The volume of this box is defined to be

For any subset A of Rⁿ, we can define its outer measure λ*(A) by:

We then define the set A to be Lebesgue-measurable if for every subset S of Rⁿ,

These Lebesgue-measurable sets form a σ-algebra, and the Lebesgue measure is defined by λ(A) = λ*(A) for any Lebesgue-measurable set A.

The existence of sets that are not Lebesgue-measurable is a consequence of the set-theoretical axiom of choice, which is independent from many of the conventional systems of axioms for set theory. The Vitali theorem, which follows from the axiom, states that there exist subsets of R that are not Lebesgue-measurable. Assuming the axiom of choice, non-measurable sets with many surprising properties have been demonstrated, such as those of the Banach–Tarski paradox.

In 1970, Robert M. Solovay showed that the existence of sets that are not Lebesgue-measurable is not provable within the framework of Zermelo–Fraenkel set theory in the absence of the axiom of choice (see Solovay’s model).^[9]

Relation to other measures[edit]

The Borel measure agrees with the Lebesgue measure on those sets for which it is defined; however, there are many more Lebesgue-measurable sets than there are Borel measurable sets. The Borel measure is translation-invariant, but not complete.

The Haar measure can be defined on any locally compact group and is a generalization of the Lebesgue measure (Rⁿ with addition is a locally compact group).

The Hausdorff measure is a generalization of the Lebesgue measure that is useful for measuring the subsets of Rⁿ of lower dimensions than n, like submanifolds, for example, surfaces or curves in R³ and fractal sets. The Hausdorff measure is not to be confused with the notion of Hausdorff dimension.

It can be shown that there is no infinite-dimensional analogue of Lebesgue measure.

See also[edit]

• Lebesgue’s density theorem
• Lebesgue measure of the set of Liouville numbers
• Non-measurable set
  • Vitali set

References[edit]

Мера Лебега числового множества является
обобщением понятия длины промежутка
числовой оси. При определении меры
Лебега будем руководствоваться тем
принципом, что введенная мера множества,
в частном случае, когда множество
является интервалом, должна совпадать
с такой характеристикой интервала как
длина.

Процедуру определения меры Лебега
начнем с определения меры множества,
имеющего наиболее простую структуру —
открытого множества.

Определение 1.2.1.Мерой интервала
называется число
,
т.е..

Определение 1.2.2. Мерой непустого
ограниченного открытого множества
называется число, равно сумме длин всех
составляющих интервалов множества,
т.е.

Согласно теореме 1.1.2, любое замкнутое
множество
имеет представление,
где,
а— открытое множество.

Определение 1.2.3.Мерой непустого
ограниченного замкнутого множестваназывается число

.

Перейдем к построению меры Лебега
произвольного ограниченного множества
на прямой. С этой целью определим понятия
внешней и внутренней меры множества.

Определение 1.2.4.Внешней мерой
ограниченного множества
называется точная нижняя грань мер
всевозможных открытых ограниченных
множеств, содержащих множество,
т.е.

.

Отметим, что в силу ограниченности
множества
,
внешняя мера множества всегда существует
и принимает конечное значение
.

Определение 1.2.5. Внутренней
мерой
ограниченного множества
называется точная верхняя грань мер
всевозможных замкнутых множеств,
содержащихся во множестве,
т. е

.

Справедливы

Теорема 1.2.1.Еслии— произвольные открытое и замкнутое
множества соответственно, то

и.

Для всякого ограниченного множества
справедливо неравенство.

Теорема 1.2.2.Если— ограниченные множества и,
тои.

Определение 1.2.6.Если для ограниченного
множествасправедливо равенство,
то говорят, что множествоизмеримо по Лебегу, а общее значениеиназываетсямерой Лебега множества .

Из определения 1.2.6 и теоремы 1.2.1 следует,
что

1. всякое ограниченное открытое множество
   измеримо и его мера совпадает с мерой,
   предложенной в определении 1.2.2;

2. всякое ограниченное замкнутое множество
   измеримо по Лебегу и его мера совпадает
   с мерой введенной в определении 1.2.3.

1.3. Свойства измеримых по Лебегу множеств.

Введенная мера Лебега ограниченного
множества обладает рядом свойств.
Сформулируем и докажем некоторые из
них.

Теорема 1.3.1.(Регулярность меры)Пусть— ограниченное, измеримое множество.
Для любогонайдутся такие замкнутое множествои открытое множество,
что справедливы включенияи неравенства

.

Утверждение теоремы непосредственно
следует из определения точных верхней
и нижней граней числового множества.

Теорема 1.3.2. (Инвариантность меры)Если— измеримое множество и— произвольное число, то множествоизмеримо, причем.

Доказательство.Согласно теореме
1.3.1, для произвольного,
найдутся такие открытое множествои замкнутое множество,
чтои

.

Множества
иявляются замкнутым и открытым
соответственно. При этом справедливы
включения.

Покажем, что мера открытого множества
инвариантна относительно сдвига. Как
открытое множество, множествопредставимо в виде.
Тогдаи.

Замкнутое множество
имеет представление.

Отсюда
и.

Как показано выше, мера открытого
множества
инвариантна относительно сдвига, поэтому

.

В конечном итоге получаем

.

Таким образом, для любого
справедливо неравенство

.

Сопоставляя полученное неравенство с
неравенством (1.3.1), и учитывая произвольность
выбора
,
делаем вывод, что.

Теорема доказана.

Теорема 1.3.3. (монотонность меры)Если— ограниченные измеримые множества и,
то

.

Теорема 1.3.4. (счетная аддитивность)
Если ограниченное множествоявляется объединением не более чем
счетного числа ограниченных измеримых
множеств,
и эти множества попарно не пересекаются,
то множествоизмеримо, причем

.

Доказательство.Согласно теореме
1.2.1 для произвольного ограниченного
множествасправедливо неравенство.

Покажем справедливость неравенства
.
С этой целью произвольно зафиксируем.
В соответствии с утверждением теоремы
1.3.1 для каждого множестванайдется такое открытое множество,
что

и.

Можно показать, что если множества
попарно не пересекаются, то,
в случае непустого попарного пересечения
множеств,
справедливо неравенство.

Так как
,
то, по теореме 1.3.3, имеем

.

В силу произвольности выбора
,
можем заключить.

Аналогично можно показать, что
.

В итоге имеем цепь неравенств

из которой следует, что
.
Иными словами, множествоизмеримо.

Теорема доказана.

Теорема 1.3.5. (Полуаддитивность
меры)Для произвольных измеримых
множествсправедливо неравенство

.

Доказательство.Введем множества,,.

Множество
представимо в виде.
При этом множествапопарно не пересекаются и измеримы как
разность двух измеримых множеств (см.
упражнение 10). Согласно теореме 1.3.4
множествоизмеримо.

Докажем справедливость неравенства
.
С этой целью произвольно зафиксируем.
В соответствии с утверждением теоремы
1.3.1 для каждого множестванайдется такое открытое множество,
чтои.

Так как
,
то в силу монотонности меры (Т. 1.3.3),

.

В силу произвольности выбора
имеем.

Теорема доказана.

Теорема 1.3.6.Пусть множестваизмеримы и.
Если множествоограничено, то оно измеримо, причем.

Доказательство.Множествопредставим в виде

.

Множества
иприне пересекаются, поэтому, в силу теоремы
1.3.4 , имеем

.

Можно показать, что если
,
то

.

С учетом последнего равенства
.

В силу ограниченности множества
рядсходится и его частичная сумма равна.

Поэтому
.

Теорема доказана.

Как следствие теоремы 1.3.6 получим
следующее утверждение.

Теорема 1.3.7.Пусть— измеримые множества и.
Если при этом,
то.

Доказательство.Множествоизмеримо и потому ограничено, поэтому
существует.
Для дополнений множествдо отрезкавыполнены все условия предыдущей
теоремы. Действительно,измеримы,и.

В силу теоремы 1.3.6
.

С другой стороны
.

Отсюда
.

Теорема доказана.

Определение 1.3.1.Множество,
представимое в виде пересечения или
объединения не более чем счетного числа
замкнутых множеств называетсяборелевским
множеством типа
,а множество представимое в виде
пересечения или объединения не более
чем счетного числа открытых множеств
называетсяборелевским множеством
типа.

Справедлива

Теорема 1.3.8. (структура измеримого
множества) Для любого ограниченного
и измеримого множестванайдутся множестватипа
итипа
такие, что

и,.

Теорема 1.3.8 утверждает, что всякое
ограниченное измеримое множество
является множеством типа
или
с точностью до множества нулевой меры.

Доказательство.Согласно свойству
регулярности меры, для произвольного
натурального числанайдется такое открытое множество,
что.
Отсюда.

Множество
является борелевским множеством типа
идля любого.

В силу монотонности меры,
при.

Таким образом,
.

Аналогично можно доказать второе
утверждение теоремы.

Теорема доказана.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Мера Лебе́га на — мера, являющаяся продолжением меры Жордана на более широкий класс множеств, была введена Лебегом в 1902 году.

Построение меры на прямой

Внешняя мера

Для произвольного подмножества числовой прямой можно найти сколь угодно много различных систем из конечного или счётного числа интервалов, объединение которых содержит множество . Назовём такие системы покрытиями. Так как сумма длин интервалов, составляющих любое покрытие, есть величина неотрицательная, она ограничена, и, значит, множество длин всех покрытий имеет нижнюю грань. Эта грань, зависящая только от множества , и называется внешней мерой:

Варианты обозначения внешней меры:

Очевидно, внешняя мера любого интервала совпадает с его длиной.
Свойства внешней меры:

где — открытое множество. И действительно, достаточно в качестве взять сумму интервалов, составляющих покрытие , такую что . Возможность существования такого покрытия следует из определения точной нижней грани.

Внутренняя мера

Если множество ограничено, то внутренней мерой множества называется разность между длиной сегмента , содержащего , и внешней мерой дополнения в :

Для неограниченных множеств определяется как точная верхняя грань по всем отрезкам .

Измеримые множества

Множество называется измеримым по Лебегу, если его внешняя и внутренняя меры равны. Тогда общее значение последних называется мерой множества по Лебегу и обозначается , , или .

Пример неизмеримого множества

Рассмотрим на прямой отрезок . Если две точки отстоят друг от друга на рациональное расстояние, то будем считать, что они принадлежат одному классу эквивалентности. Разобъем весь отрезок на такие классы эквивалентности. Далее, из каждого каждого класса эквивалентности выберем по представителю — одной точке. Тогда полученное множество представителей будет неизмеримым.

Действительно, если сдвинуть его счётное число раз, — то оно заполнит весь отрезок. Если бы у построенного множества существовала мера, то она должна либо быть равна нулю, либо быть больше нуля. По счётной аддитивности меры Лебега , что невозможно (если , то и сумма ряда равна нулю, а если , то сумма ряда равна бесконечности)
а значит не существует.

Заметим, что построение этого, как и любого другого примера неизмеримого множества на отрезке, было бы невозможно без принятия аксиомы выбора (было бы невозможно выбрать по представителю в каждом классе эквивалентности).

Литература

• Гелбаум, Олмстед «Контрпримеры в анализе».

Эта статья содержит материал из статьи Мера Лебега русской Википедии.

Мера множества

Понятие меры множества является далеко идущим обобщением понятия длины отрезка. В простейшем случае (которым только мы и будем заниматься) задача состоит в том, чтобы дать определение длины не только для отрезков, но также и для более сложных точечных множеств, расположенных на прямой.

Примем за единицу измерения отрезок . Тогда длина произвольного отрезка , очевидно, равна . Точно так же если имеется два непересекающихся отрезка и , то под длиной множества , состоящего из этих двух отрезков, естественно понимать число . Однако далеко не так ясно, что следует понимать под длиной множества более сложной природы, расположенного на прямой; например, чему равна длина канторова множества. Отсюда вывод: понятие длины множества, расположенного на прямой, нуждается в строгом математическом определении.

Задача определения длины множеств, или, как говорят еще, задача измерения множеств, весьма важна, так как она имеет существенное значение для обобщения понятия интеграла. Понятие меры множества применяется и в других вопросах теории функций, а также в теории вероятностей, топологии, функциональном анализе и т.д.

Ниже излагается определение меры множеств, предложенное французским математиком А. Лебегом и лежащее в основе данного им определения интеграла.

---

Мера открытого и замкнутого множества

Начнем с определения меры произвольного открытого или замкнутого множества. Как уже отмечалось, всякое открытое множество на прямой является конечной или счетной суммой попарно не пересекающихся интервалов.

Мерой открытого множества называется сумма длин составляющих его интервалов.

Таким образом, если и интервалы попарно не пересекаются, то мера равна . Обозначая вообще меру множества через , можем написать . В частности, мера одного интервала равна его длине .

Всякое замкнутое множество , содержащееся в отрезке и такое, что концы отрезка принадлежат , получается из отрезка путем удаления из него некоторого открытого множества . В соответствии с этим мерой замкнутого множества , где , называется разность между длиной отрезка и мерой открытого множества , дополнительного к (относительно отрезка ).

Итак,

Нетрудно усмотреть, что, согласно этому определению, мера произвольного отрезка равна его длине , а мера множества, состоящего из конечного числа точек, равна нулю.

---

Определение меры множества

Для того чтобы дать определение меры множеств более общей природы, чем открытые и замкнутые, нам понадобится одно вспомогательное понятие. Пусть — некоторое множество, лежащее на отрезке . Рассмотрим всевозможные покрытия множества , т. е. всевозможные открытые множества , содержащие . Мера каждого из множеств уже определена. Совокупность мер всех множеств есть некоторое множество положительных чисел. Это множество чисел ограничено снизу (хотя бы числом 0) и потому имеет нижнюю грань, которую мы обозначим через . Число называется внешней мерой множества .

Пусть — внешняя мера множества , а — внешняя мера его дополнения относительно отрезка .

Если удовлетворяется соотношение

то множество называется измеримым, а число — его мерой: ; если соотношение (3) не удовлетворяется, то говорят, что множество неизмеримо; неизмеримое множество не имеет меры.

Отметим, что всегда

Сделаем несколько пояснений. Длина простейших множеств (например, интервалов и отрезков) обладает рядом замечательных свойств. Укажем важнейшие из них.

1. Если множества и измеримы и , то , т.е. мера части множества не превосходит меры всего множества .

2. Если множества и измеримы, то множество измеримо и , т.е. мера суммы не превосходит суммы мер слагаемых.

3. Если множества измеримы и попарно не пересекаются, , то их сумма измерима и , т.е. мера конечной или счетной суммы попарно непересекающихся множеств равна сумме мер слагаемых. Это свойство меры называется ее полной аддитивностью.

4. Мера множества не меняется, если его сдвинуть как твердое тело.

Желательно, чтобы основные свойства длины сохранялись и для более общего понятия меры множеств. Но, как можно совершенно строго показать, это оказывается невозможным, если приписывать меру произвольному множеству точек на прямой. Поэтому-то в данном выше определении и появляются множества, имеющие меру или измеримые, и множества, не имеющие меры или неизмеримые. Впрочем, класс измеримых множеств настолько широк, что это обстоятельство не вносит каких-либо существенных неудобств. Даже построение примера неизмеримого множества представляет известные трудности.

Приведем несколько примеров измеримых множеств.

---

Мера канторова совершенного множества

При построении канторового множества из отрезка выбрасывается сперва один смежный интервал длины , затем два смежных интервала длины , затем четыре смежных интервала длины и т. д. Вообще, на -м. шаге выбрасывается смежных интервалов длины . Таким образом, сумма длин всех выброшенных интервалов равна

Члены этого ряда представляют собою геометрическую прогрессию с первым членом и знаменателем . Поэтому сумма ряда равна .

Итак, сумма длин всех смежных к канторовому множеству интервалов равна 1. Иначе говоря, мера дополнительного к канторовому множеству открытого множества равна 1. Поэтому само множество имеет меру .

Как показывает этот пример, множество может иметь мощность континуума и тем не менее иметь меру, равную нулю.

---

Мера множества R всех рациональных точек отрезка [0, 1]

Покажем прежде всего, что . Как известно, множество счетно. Расположим точки множества в последовательность

Далее, зададим и окружим точку интервалом длины . Сумма есть открытое множество, покрывающее . Интервалы могут пересекаться, поэтому

Так как можно выбрать сколь угодно малым, то .

Далее, согласно (3) имеем , т. е. . Так как содержится в отрезке , то .

Итак, , откуда

Этот пример показывает, что множество может быть всюду плотным на некотором отрезке и тем не менее иметь меру, равную нулю.

Множества меры нуль во многих вопросах теории функций не играют никакой роли, и ими следует пренебрегать. Например, функция интегрируема по Риману в том и только в том случае, если она ограничена и множество её точек разрыва имеет меру нуль. Можно было бы привести значительное число таких примеров.

---

Измеримые функции

Переходим к одному из наиболее блестящих приложений понятия меры множеств, а именно к описанию того класса функций, с которыми фактически оперирует математический анализ и теория функций. Точная постановка задачи такова. Если последовательность функций , заданных на некотором множестве , сходится в каждой точке , кроме, быть может, точек множества меры нуль, то будем говорить, что последовательность сходится почти всюду.

Какие функции можно получить из непрерывных функций путем повторного применения операции построения предела почти всюду сходящейся последовательности функций и алгебраических операций?

Для ответа на этот вопрос нам потребуется несколько новых понятий.

Пусть функция определена на некотором множестве и — произвольное действительное число. Обозначим через множество тех точек , для которых . Например, если функция определена на отрезке и на этом отрезке , то множества равны для , равны для и пусты для .

Функция , определенная на некотором множестве , называется измеримой, если само множество измеримо и для любого действительного числа измеримо множество .

Можно показать, что произвольная непрерывная функция, заданная на отрезке, измерима. Однако к числу измеримых функций принадлежат также и многие разрывные функции, например функция Дирихле, равная 1 для иррациональных точек отрезка и равная 0 для остальных точек этого отрезка.

Отметим без доказательства, что измеримые функции обладают следующими свойствами.

1. Если и — измеримые функции, определенные на одном и том же множестве , то функции

и

также измеримы (последняя, если ).

Это свойство показывает, что алгебраические операции над измеримыми функциями снова приводят к измеримым функциям.

2. Если последовательность измеримых функций , определенных на множестве , сходится почти всюду к функции , то эта функция также измерима.

Таким образом, операция построения предела почти всюду сходящейся последовательности измеримых функций вновь приводит к измеримым функциям.

Эти свойства измеримых функций были установлены Лебегом. Глубокое исследование измеримых функций было произведено советскими математиками Д. Ф. Егоровым и Н. Н. Лузиным. В частности, Н. Н. Лузин показал, что всякую измеримую функцию, заданную на отрезке, можно превратить в непрерывную, изменив ее значения на некотором множестве сколь угодно малой меры.

Этот классический результат Н. Н. Лузина и перечисленные выше свойства измеримых функций позволяют показать, что измеримые функции и представляют собой тот класс функций, о котором шла речь в начале этого пункта. Измеримые функции имеют также большое значение для теории интегрирования, именно, понятие интеграла может быть обобщено таким образом, чтобы всякая ограниченная измеримая функция оказалась интегрируемой. Подробнее об этом рассказывается в разделе интеграл Лебега.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

В теории меры, разделе математики, мера Лебега, названный в честь французского математика Анри Лебега, является стандартным способом присвоения меры подмножествам n-мерного Евклидово пространство. Для n = 1, 2 или 3 он совпадает со стандартной мерой длина, площадь или объем. В общем, его также называют n-мерным объемом, n-объемом или просто объемом . Он используется во всем реальном анализе, в частности, для определения интеграции Лебега. Множества, которым может быть назначена мера Лебега, называются измеримыми по Лебегу ; здесь мера измеримого по Лебегу множества A обозначается через λ (A).

Анри Лебег описал эту меру в 1901 году, а в следующем году он описал интеграл Лебега. Оба были опубликованы как часть его диссертации в 1902 году.

Мера Лебега часто обозначается dx, но ее не следует путать с отдельным понятием формы тома.

Содержание

• 1 Определение
  • 1.1 Интуиция
• 2 Примеры
• 3 Свойства
• 4 Нулевые наборы
• 5 Построение меры Лебега
• 6 Связь с другими мерами
• 7 См. Также
• 8 Ссылки

Определение

Для подмножества E ⊆ R { displaystyle E substeq mathbb {R}}с длиной interval I = [a, b] (или I = (a, b)) { displaystyle I = [a, b] { text {(или}} I = (a, b))}задается как ℓ (I) = b — a { displaystyle ell (I) = ba}, внешняя мера Лебега λ ∗ ( E) { displaystyle lambda ^ {*} (E)}определяется как

λ ∗ (E) = inf ⁡ {∑ k = 1 ∞ ℓ (I k): (I k) k ∈ N — это последовательность открытых интервалов с E ⊆ ⋃ k = 1 ∞ I k} { displaystyle lambda ^ {*} (E) = operatorname {inf} left { sum _ {k = 1 } ^ { infty} ell ( I_ {k}): {(I_ {k}) _ {k in mathbb {N}}} { text {- последовательность открытых интервалов с}} E substeq bigcup _ {k = 1} ^ { infty} I_ {k} right }}.

Мера Лебега определена на σ-алгебре Лебега, которая представляет собой набор всех множеств E { displaystyle E}, которые удовлетворяют «критерию Каратеодори », который требует, чтобы для каждого A ⊆ R { displaystyle A substeq mathbb {R}},

λ ∗ (A) знак равно λ ∗ (A ∩ E) + λ ∗ (A ∩ E c) { displaystyle lambda ^ {*} (A) = lambda ^ {*} (A cap E) + lambda ^ {*} ( A cap E ^ {c})}

Для любого множества в σ-алгебре Лебега его мера Лебега задается его внешней мерой Лебега λ (E) = λ ∗ (E) { displaystyle lambda (E) = lambda ^ {*} (E)}.

Множества, не входящие в σ-алгебру Лебега, не измеримы по Лебегу. Такие наборы действительно существуют (например, наборы Витали ), т. Е. Содержание σ-алгебры Лебега в наборе мощности из R { displaystyle mathbb {R}}строгий.

Интуиция

Первая часть определения гласит, что подмножество E { displaystyle E}действительных чисел сокращено до внешней меры за счет покрытия наборами открытых интервалов. Каждый из этих наборов интервалов I { displaystyle I}охватывает E { displaystyle E}в том смысле, что, когда интервалы объединяются вместе путем объединения, они содержат E { displaystyle E}. Общая длина любого набора интервалов покрытия может легко переоценить меру E { displaystyle E}, потому что E { displaystyle E}является подмножеством объединение интервалов, и поэтому интервалы могут включать точки, которые не находятся в E { displaystyle E}. Внешняя мера Лебега возникает как точная нижняя граница (infimum) длин из всех возможных таких множеств. Интуитивно понятно, что это общая длина тех наборов интервалов, которые наиболее точно соответствуют E { displaystyle E}и не перекрываются.

Это характеризует внешнюю меру Лебега. Переводит ли эта внешняя мера в собственно меру Лебега, зависит от дополнительного условия. Это условие проверяется путем взятия подмножеств A { displaystyle A}действительных чисел с использованием E { displaystyle E}в качестве инструмента для разделения A { displaystyle A}на два раздела: часть A { displaystyle A}, которая пересекается с E { displaystyle E}и оставшаяся часть A { displaystyle A}, которая не находится в E { displaystyle E}: установленная разница A { displaystyle A}и E { displaystyle E}. Эти разделы A { displaystyle A}подлежат внешней мере. Если для всех возможных таких подмножеств A { displaystyle A}вещественных чисел, разделы A { displaystyle A}разделены на E { displaystyle E}имеют внешние меры, сумма которых является внешней мерой A { displaystyle A}, а затем внешней мерой Лебега E { displaystyle E}дает меру Лебега. Интуитивно это условие означает, что набор E { displaystyle E}не должен обладать любопытными свойствами, которые вызывают несоответствие в измерениях другого набора, когда E { displaystyle E}используется как «маска» для «отсечения» этого множества, намекая на существование множеств, для которых внешняя мера Лебега не дает меры Лебега. (Такие множества, на самом деле, не измеримы по Лебегу.)

Примеры

• Любой открытый или закрытый интервал [a, b] из действительных чисел является Измеримы по Лебегу, а его мерой по Лебегу является длина b — a. Открытый интервал (a, b) имеет ту же меру, поскольку разница между двумя наборами состоит только из конечных точек a и b и имеет нулевую меру.
• Любое декартово произведение интервалов [a, b] и [c, d] измеримо по Лебегу, и его мера по Лебегу равна (b — a) (d — c), площадь соответствующего прямоугольник.
• Более того, любое борелевское множество измеримо по Лебегу. Однако существуют измеримые по Лебегу множества, которые не являются борелевскими.
• Любое счетное множество действительных чисел имеет меру Лебега 0. В частности, мера Лебега множества алгебраические числа равны 0, даже если набор плотный в R.
• Набор Кантора и набор чисел Лиувилля являются примерами бесчисленные множества с мерой Лебега 0.
• Если выполняется аксиома детерминированности, то все множества действительных чисел измеримы по Лебегу. Однако детерминированность несовместима с аксиомой выбора ..
• Множества Витали являются примерами множеств, которые не измеримы по отношению к мере Лебега. Их существование основывается на аксиоме выбора .
• Кривые Осгуда представляют собой простые плоские кривые с положительной мерой Лебега (ее можно получить небольшим изменением кривая Пеано построение). Драконья кривая — еще один необычный пример.
• Любая строка в R n { displaystyle mathbb {R} ^ {n}}для n ≥ 2 { displaystyle n geq 2}, имеет нулевую меру Лебега. В общем, каждая правильная гиперплоскость имеет нулевую меру Лебега в ее окружающем пространстве.

Свойства

Трансляционная инвариантность: мера Лебега

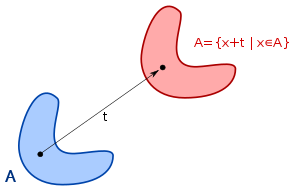
A { displaystyle A}

и

A + t { displaystyle A + t}

одинаковы.

Мера Лебега на R имеет следующие свойства:

1. Если A — декартово произведение из интервалов I1× I 2 ×… × I n, тогда A измеримо по Лебегу и λ (A) = | I 1 | ⋅ | I 2 | ⋯ | I n |. { displaystyle lambda (A) = | I_ {1} | cdot | I_ {2} | cdots | I_ {n} |.}Здесь | I | обозначает длину интервала I.
2. Если A является непересекающимся объединением счетного числа непересекающихся множеств, измеримых по Лебегу, то A само измеримо по Лебегу и λ (A) равно сумме (или бесконечному ряду ) мер участвующих измеримых множеств.
3. Если A измеримо по Лебегу, то его дополнение.
4. λ (A) ≥ 0 для любого измеримого по Лебегу множества A.
5. Если A и B измеримы по Лебегу и A является подмножеством B, то λ (A) ≤ λ (B). (Следствие 2, 3 и 4.)
6. Счетные объединения и пересечения множеств, измеримых по Лебегу, измеримы по Лебегу. (Не является следствием 2 и 3, поскольку семейство множеств, замкнутое относительно дополнений и непересекающихся счетных объединений, не обязательно должно быть замкнутым относительно счетных объединений: {∅, {1, 2, 3, 4}, { 1, 2}, {3, 4}, {1, 3}, {2, 4}} { displaystyle { emptyset, {1,2,3,4 }, {1,2 }, {3,4 }, {1,3 }, {2,4 } }}.)
7. Если A является открытым или закрытым подмножеством R (или даже борелевское множество, см. метрическое пространство ), то A измеримо по Лебегу.
8. Если A — лебеговское измеримое множество, то оно «приблизительно открыто» и «приблизительно замкнуто» в смысле меры Лебега (см. теорему регулярности для меры Лебега ).
9. Измеримое по Лебегу множество можно «втиснуть» между содержащим открытым множеством и содержащееся замкнутое множество. Это свойство использовалось в качестве альтернативного определения измеримости по Лебегу. Точнее, E ⊂ R { displaystyle E subset mathbb {R}}измеримо по Лебегу тогда и только тогда, когда для каждого ε>0 { displaysty le varepsilon>0}существует открытый набор G { displaystyle G}и закрытый набор F { displaystyle F}такие, что F ⊂ E ⊂ G { displaystyle F subset E subset G}и λ (G ∖ F) < ε {displaystyle lambda (Gsetminus F)<varepsilon }.
10. Измеримое по Лебегу множество можно «втиснуть» между содержащим Gδмножеством и содержит Fσ. Т.е. если A измеримо по Лебегу, то существуют Gδмножество G и Fσ F такие, что G ⊇ A ⊇ F и λ (G A) = λ (A F) = 0.
11. мера Лебега и локально конечна, и внутренняя регулярная, поэтому она мера Радона.
12. мера Лебега строго положительна на непустых открытых множествах, и поэтому его опорой является все R.
13. Если A — измеримое по Лебегу множество с λ (A) = 0 (нулевое множество ), то каждое подмножество A также является нулевым множеством. Тем более, каждое подмножество A измеримо.
14. Если A измеримо по Лебегу и x является элементом R, то преобразование A на x, определяется как A + x = {a + x: a ∈ A}, также измеримо по Лебегу и имеет ту же меру, что и A.
15. Если A измеримо по Лебегу и δ>0 { displaystyle delta>0}, затем расширение A { displaystyle A}на δ { displaystyle delta}, определяемое δ A = { δ x: x ∈ A} { displaystyle delta A = { delta x: x in A }}также измеримо по Лебегу и имеет меру δ n λ (A). { displaystyle delta ^ {n} lambda , (A).}
16. В более общем смысле, если T — линейное преобразование, а A — измеримое подмножество R, то T (A) также измеримо по Лебегу и имеет меру | det (T) | λ (A) { displaystyle left | det (T) right | la mbda (A)}.

Все вышесказанное можно кратко резюмировать следующим образом:

Измеримые по Лебегу множества образуют σ-алгебру, содержащую все произведения интервалов, а λ — единственное полная трансляционно-инвариантная мера на этой σ-алгебре с λ ([0, 1] × [0, 1] × ⋯ × [0, 1 ]) = 1. { displaystyle lambda ([0,1] times [0,1] times cdots times [0,1]) = 1.}

Мера Лебега также обладает свойством σ-конечное.

Нулевые множества

Подмножество R является нулевым множеством, если для каждого ε>0 оно может быть покрыто счетным числом произведений n интервалы, общий объем которых не превосходит ε. Все счетные наборы являются пустыми.

Если подмножество R имеет размерность Хаусдорфа меньше n, то это нулевое множество по отношению к n-мерной мере Лебега. Здесь размерность Хаусдорфа относится к евклидовой метрике на R (или любой эквивалентной ей метрике Липшица ). С другой стороны, набор может иметь топологическую размерность меньше n и иметь положительную n-мерную меру Лебега. Примером этого является множество Смита – Вольтерры – Кантора, которое имеет топологическую размерность 0, но имеет положительную одномерную меру Лебега.

Чтобы показать, что данное множество A измеримо по Лебегу, обычно пытаются найти «более хорошее» множество B, которое отличается от A только нулевым набором (в том смысле, что симметричный разница (A — B) ∪ { displaystyle cup}(B — A) — нулевое множество), а затем показать, что B может быть сгенерирован с использованием счетных объединений и пересечений из открытых или закрытые наборы.

Построение меры Лебега

Современное построение меры Лебега — это приложение теоремы Каратеодори о продолжении. Происходит это следующим образом.

Зафиксируем n ∈ N . A коробка в R представляет собой набор формы

B = ∏ i = 1 n [ai, bi], { displaystyle B = prod _ {i = 1 } ^ {n} [a_ {i}, b_ {i}] ,,}

где b i ≥ a i, а символ произведения здесь представляет декартову товар. Объем этого ящика определяется как

vol ⁡ (B) = ∏ i = 1 n (b i — a i). { displaystyle operatorname {vol} (B) = prod _ {i = 1} ^ {n} (b_ {i} -a_ {i}) ,.}

Для любого подмножества A из R, мы можем определить его внешнюю меру λ * (A) следующим образом:

λ ∗ (A) = inf {∑ B ∈ C vol ⁡ (B): C — счетный набор ящиков, объединение которых покрывает A}. { displaystyle lambda ^ {*} (A) = inf left { sum _ {B in { mathcal {C}}} operatorname {vol} (B): { mathcal {C}} { text {- счетный набор ящиков, объединение которых покрывает}} A right }.}

Затем мы определяем множество A как измеримое по Лебегу, если для каждого подмножества S из R,

λ ∗ (S) = λ ∗ (S ∩ A) + λ ∗ (S ∖ A). { displaystyle lambda ^ {*} (S) = lambda ^ {*} (S cap A) + lambda ^ {*} (S setminus A) ,.}

Эти множества, измеримые по Лебегу образуют σ-алгебру, а мера Лебега определяется как λ (A) = λ * (A) для любого измеримого по Лебегу множества A.

Существование множеств, которые не являются Измеримость по Лебегу является следствием определенной теоретико-множественной аксиомы, аксиомы выбора, которая не зависит от многих традиционных систем аксиом для теории множеств. Теорема Витали, которая следует из аксиомы, утверждает, что существуют подмножества R, которые не измеримы по Лебегу. Принимая аксиому выбора, неизмеримые множества со многими удивительными свойствами были продемонстрированы, например, из парадокса Банаха – Тарского.

. В 1970 году Роберт М. Соловей показал, что существование множеств, не измеримых по Лебегу, не может быть доказано в рамках теории множеств Цермело – Френкеля в отсутствие аксиомы выбора (см. модель Соловея ).

Связь с другими мерами

Мера Бореля согласуется с мерой Лебега на тех множествах, для которых она определена; однако существует намного больше измеримых по Лебегу множеств, чем измеримых по Борелю множеств. Мера Бореля трансляционно-инвариантна, но не полной.

Мера Хаара может быть определена на любой локально компактной группе и является обобщением меры Лебега (R со сложением — локально компактная группа).

Мера Хаусдорфа является обобщением меры Лебега, которая является полезной ul для измерения подмножеств R более низких размерностей, чем n, таких как подмногообразия, например, поверхности или кривые в R и фрактале наборы. Меру Хаусдорфа не следует путать с понятием размерности Хаусдорфа.

. Можно показать, что не существует бесконечномерного аналога меры Лебега.

См. Также

Литература