Как найти 8 битное число - Исправление недочетов и поиск решений вместе с Examum.ru

Двоичная система счисления

Если в десятичной системе счисления числа записываются с помощью десяти различных символов (от 0 до 9), то в двоичной системе — с помощью всего двух символов: 0 и 1. Такая система необходима для всех устройств, в которых информация представлена в виде последовательностей двух возможных состояний носителя, а это практически вся современная вычислительная техника.

Так же, как в десятичной системе разряды являются степенями основания 10, в двоичной системе разряды являются степенями основания 2:

10 000 000 000	1 000 000 000	100 000 000	10 000 000	1 000 000	100 000	10 000	1000	100	10	1
10 10	10 9	10 8	10 7	10 6	10 5	10 4	10 3	10 2	10 1	10 0

1024	512	256	128	64	32	16	8	4	2	1
2 10	2 9	2 8	2 7	2 6	2 5	2 4	2 3	2 2	2 1	2 0

При этом значением числа будет сумма значений всех разрядов. Например, переведем в привычный десятичный вид двоичное число 110001:

1 * 2 5 + 1 * 2 4 + 0 * 2 3 + 0 * 2 2 + 0 * 2 1 + 1 * 2 0 = 49

Или то же самое чуть иначе:

1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 49

Биты и байты

В современных вычислительных системах информация представлена не в виде непрерывного потока двоичных символов (условных нолей и единиц), а за единицу информации, как правило, принимается байт (byte).
Байт состоит из восьми битов (т.е. это восьмиразрядное двоичное число), соответственно, он имеет 256 (2 8 ) возможных значений.

Именно поэтому стандартные варианты разрядности кратны восьми. Например, для операционных систем это 32 или 64 разряда (или бита), а для цифрового звука: 8, 16, 24 и 32.

Важно не запутаться в трех основных значениях, которые определяются разрядностью числа: количество возможных значений, максимальное значение и значение старшего бита/разряда.
Например, для 8-разрядного числа количество возможных значений = 256 (0 — 255), максимальное значение = 255, а значение старшего бита = 128.

Что такое восьмибитная двоичная запись числа

Тип 5 № 16882

Автомат обрабатывает натуральное число N (0 ≤ N ≤ 255) по следующему алгоритму:

1. Строится восьмибитная двоичная запись числа N.

2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).

3. Полученное число переводится в десятичную запись.

4. Из нового числа вычитается исходное, полученная разность выводится на экран.

Пример. Дано число N = 13. Алгоритм работает следующим образом.

1. Восьмибитная двоичная запись числа N: 00001101.

2. Все цифры заменяются на противоположные, новая запись 11110010.

3. Десятичное значение полученного числа 242.

4. На экран выводится число 242 − 13 = 229.

Какое число нужно ввести в автомат, чтобы в результате получилось 111?

Заметим, что инверсия двоичной восьмибитной записи числа в сумме с исходным числом дает 11111111, то есть 255. (В исходном примере: 00001101 + 11110010 = 11111111.) Следовательно, если исходное число равно N, то инвертированное число равно 255 − N. Затем автомат осуществляет вычитание, вычисляя 255 − 2N.

Поэтому, чтобы найти число, которое нужно ввести в автомат для получения 111, нужно решить уравнение 255 − 2N = 111. Тем самым, искомое число равно 72.

Заметим, что по условию из нового числа вычитается исходное, следовательно, для получения разности 111 новое число должно быть больше исходного, а значит, исходное число должно быть не более 127.

Представление целых чисел: прямой код, код со сдвигом, дополнительный код

Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:

не требовал усложнения архитектуры процессора для выполнения арифметических операций с отрицательными числами,
не усложнял арифметические действия,
хранил бы одинаковое количество положительных и отрицательных чисел.

Рассмотрим разные методы представления.

Содержание

Прямой код [ править ]

При записи числа в прямом коде (англ. Signed magnitude representation) старший разряд является знаковым разрядом. Если его значение равно нулю, то представлено положительное число или положительный ноль, если единице, то представлено отрицательное число или отрицательный ноль. В остальных разрядах (которые называются цифровыми) записывается двоичное представление модуля числа. Например, число [math] -5 [/math] в восьмибитном типе данных, использующем прямой код, будет выглядеть так: [math] 10000101 [/math] .

Таким способом в [math] n [/math] -битовом типе данных можно представить диапазон чисел [math] [-2^ + 1; 2^ — 1] [/math] .

Достоинства представления чисел с помощью прямого кода [ править ]

Получить прямой код числа достаточно просто.
Из-за того, что [math]0[/math] обозначает [math]+[/math] , коды положительных чисел относительно беззнакового кодирования остаются неизменными.
Количество положительных чисел равно количеству отрицательных.

Недостатки представления чисел с помощью прямого кода [ править ]

Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого).
Существуют два нуля: [math] -0 [/math] [math](100 ldots 000) [/math] и [math] +0 [/math] [math] (000 ldots 000) [/math] , из-за чего усложняется арифметическое сравнение.

Из-за весьма существенных недостатков прямой код используется очень редко.

Код со сдвигом [ править ]

При использовании кода со сдвигом (англ. Offset binary) целочисленный отрезок от нуля до [math] 2^n [/math] ( [math] n [/math] — количество бит) сдвигается влево на [math] 2^ [/math] , а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от [math] 000 dots 0 [/math] до [math] 111 dots 1 [/math] . Например, число [math] -5 [/math] в восьмибитном типе данных, использующем код со сдвигом, превратится в [math] -5 + 128 = 123 [/math] , то есть будет выглядеть так: [math] 01111011 [/math] .

По сути, при таком кодировании:

к кодируемому числу прибавляют [math] 2^ [/math] ;
переводят получившееся число в двоичную систему исчисления.

Можно получить диапазон значений [math] [-2^; 2^ — 1][/math] .

Достоинства представления чисел с помощью кода со сдвигом [ править ]

Не требуется усложнение архитектуры процессора.
Нет проблемы двух нулей.

Недостатки представления чисел с помощью кода со сдвигом [ править ]

При арифметических операциях нужно учитывать смещение, то есть проделывать на одно действие больше (например, после «обычного» сложения двух чисел у результата будет двойное смещение, одно из которых необходимо вычесть).
Ряд положительных и отрицательных чисел несимметричен.

Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.

Дополнительный код (дополнение до единицы) [ править ]

В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones’ complement).

Алгоритм получения кода числа:

если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число;
если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код);
если число является нулем, то его можно представить двумя способами: [math] +0 [/math] [math](000 ldots 000) [/math] или [math] -0 [/math] [math] (111 ldots 111) [/math] .

Пример: переведём число [math] -13 [/math] в двоичный восьмибитный код. Прямой код модуля [math] -13 [/math] : [math] 00001101 [/math] , инвертируем и получаем [math] 11110010 [/math] . Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода.

Таким способом можно получить диапазон значений [math] [-2^+1; 2^ — 1] [/math] .

Достоинства представления чисел с помощью кода с дополнением до единицы [ править ]

Простое получение кода отрицательных чисел.
Из-за того, что [math]0[/math] обозначает [math]+[/math] , коды положительных чисел относительно беззнакового кодирования остаются неизменными.
Количество положительных чисел равно количеству отрицательных.

Недостатки представления чисел с помощью кода с дополнением до единицы [ править ]

Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора.
Существуют два нуля: [math] +0 [/math] и [math] -0 [/math] .

Дополнительный код (дополнение до двух) [ править ]

Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two’s complement).

Алгоритм получения дополнительного кода числа:

если число неотрицательное, то в старший разряд записывается ноль, далее записывается само число;
если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице.

В качестве примера переведём число [math] -5 [/math] в дополнительный восьмибитный код. Прямой код модуля [math] -5 [/math] : [math] 0000101 [/math] , обратный — [math] 1111010 [/math] , прибавляем [math] 1 [/math] , получаем [math] 1111011 [/math] , приписываем [math] 1 [/math] в качестве знакового разряда, в результате получаем [math] 11111011 [/math] .

Также дополнительный код отрицательного числа [math] A [/math] , хранящегося в [math] n [/math] битах, равен [math] 2^n — |A| [/math] . По сути, дополнительный код представляет собой дополнение [math] |A| [/math] до [math] 0 [/math] : так как в [math] n [/math] -разрядной арифметике [math] 2^ = 0 [/math] (двоичная запись этого числа состоит из единицы и [math] n [/math] нулей, а в [math] n [/math] -разрядную ячейку помещаются только [math] n [/math] младших разрядов, то есть [math] n [/math] нулей), то верно равенство [math] 2^n — |A| + |A| = 0 [/math] .

Для получения из дополнительного кода самого числа нужно инвертировать все разряды кода и прибавить к нему единицу. Можно проверить правильность, сложив дополнительный код с самим числом: результат должен быть равен [math] 2^n [/math] . Переведём [math] 11111011 [/math] обратно. Инвертируем — [math] 00000100 [/math] , прибавляем [math] 1 [/math] , получаем [math] 00000101 [/math] — модуль исходного числа [math] -5 [/math] . Проверим: [math] 11111011 + 00000101 = 100000000 [/math] .

Можно получить диапазон значений [math] [-2^; 2^ — 1] [/math] .

Длинная арифметика для чисел, представленных с помощью кода с дополнением до двух [ править ]

Дополнительный код также удобно использовать для вычислений в длинной арифметике, особенно для операций сложения и вычитания. Это операции удобно выполнять с числами одинаковой длины, поэтому в старшие разряды меньшего числа нужно поместить нули (если число положительно) или единицы (если число отрицательно). Тогда числа будут выглядеть следующим образом: в старших разрядах бесконечное число нулей (единиц), а в младших разрядах уже встречаются и нули, и единицы, которые кодируют само число, а не знак. Удобство заключается в том, что нам не обязательно проделывать операции сложения с каждой парой бит, если мы знаем, что на этом отрезке в числах стоят либо единицы, либо нули. Таким образом, на этом отрезке в получившемся числе тоже будут либо только единицы, либо только нули. Операцию сложения можно выполнить только один раз для старших битов, таким образом мы узнаем знак получившегося числа. Вычитание тоже выполняется просто: инвертируем число, прибавляем один и получаем это число с минусом, затем просто делаем сложение. Однако умножение с числами, представленными дополнительным кодом, выполнять не всегда оптимально: алгоритм либо слишком медленный (наивный алгоритм работает за [math]O(n^2)[/math] ), либо слишком сложный. Лучше для умножение использовать прямой код (бит под знак). Тогда можно числа перевести в десятичную систему счисления, выполнить быстрое преобразование Фурье за [math]O(n log n)[/math] , затем перевести их обратно в двоичную. Обычно такой алгоритм работает быстрее, чем выполнение операции напрямую с двоичными числами. Для деления обычно тоже лучше использовать прямой код.

Достоинства представления чисел с помощью кода с дополнением до двух [ править ]

Возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие.
Нет проблемы двух нулей.

Недостатки представления чисел с помощью кода с дополнением до двух [ править ]

Ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел.
В отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности.

Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.

Источник

Все целые числа можно записать в двоичной системе счисления:
$$
begin{aligned}
5_{10} &= 101_2 = 4 + 1
\ 42_{10} &= 101010_2 = 32 + 8 + 2
\ 256_{10} &= 100000000_2 = 2^8
end{aligned}
$$

Так как на уровне схем почти вся логика бинарная, ровно такое представление и используется для хранения чисел в компьютерах: каждая целочисленная переменная указывает на какую-то ячейку из 8 (char), 16 (short), 32 (int) или 64 (long long) бит.

#Эндианность

Единственная неоднозначность в таком формате возникает с порядком хранения битов — также называемый эндианностью. Зависимости от архитектуры он может быть разным:

При схеме little-endian сначала идут младшие биты. Например,
число $42_{10}$ будет храниться так: $010101$.
При записи в формате big-endian сначала идут старшие биты. Все
примеры из начала статьи даны в big-endian формате.

Хотя big-endian более естественный для понимания — на бумаге мы ровно так обычно и записываем бинарные числа — по разным причинам на большинстве современных процессоров по умолчанию используется little endian.

Иными словами, «$i$-тый бит» означает «$i$-тый младший» или «$i$-тый справа», но на бумаге мы ничего не инвертируем и записываем двоичные числа стандартным образом.

#Битовые операции

Помимо арифметических операций, с числами можно делать и битовые, которые интерпретируют их просто как последовательность битов.

#Сдвиги

Битовую запись числа можно «сдвигать» влево (x << y) или вправо (x >> y), что эквивалентно умножению или делению на степень двойки с округлением вниз.

Обычное умножение и деление — не самые быстрые операции, однако все битовые сдвиги всегда работают ровно за один такт. Как следствие, умножение и деление на какую-то фиксированную степень двойки всегда работает быстро — даже если вы не используете сдвиги явно, компилятор скорее всего будет проводить подобную оптимизацию.

#Побитовые операции

Помимо &&, || и !, существуют их побитовые версии, которые применяют соответствующую логическую операцию к целым последовательностям битов: &, |, ~.

Также помимо них есть ещё операция исключающего «или» (XOR), которая записывается как ^.

Например:

$13$ & $7$ = $1101_2$ & $0111_2$ = $0101_2$ = $5$
$17$ | $10$ = $10001_2$ | $01010_2$ = $11011_2$ = $27$
$17$ ^ $9$ = $10001_2$ ^ $01001_2$ = $11000_2$ = $24$

Все побитовые операции тоже работают за один такт, вне зависимости от типа данных. Для больших не вмещающихся в один регистр битовых последовательностей существует битсет.

#Маски

Бинарные последовательности можно поставить в соответствие подмножествам какого-то фиксированного множества: если на $i$-той позиции стоит единица, то значит $i$-тый элемент входит множество, а иначе не входит.

Битовые операции таким образом часто используются операций над множествами, представляемыми битовыми мазками — например, в задачах на полный перебор или динамическое программирование.

#Выделить i-й бит числа

(x >> i) & 1 или x & (1 << i). Во втором случае результат будет либо 0, либо $2^i$.

Это часто используется для проверки, принадлежит ли $i$-тый элемент множеству:

if ((num >> i) & 1)
    cout << "YES";
else
    cout << "NO";

Напомним, что нумерация идет с младших бит и начинается с нуля.

#Получить число, состоящее из k единиц

(1 << k) - 1, также известное как $(2^k-1)$ и соответствующее маске полного множества.

#Инвертировать все биты числа

x = ~x

#Добавить i-й элемент в множество

x |= (1 << i)

#Удалить $i$-й элемент из множества

x &= ~(1 << i)

#Удалить i-й элемент из множества, если он есть

x ^= (1 << i)

Также добавляет этот элемент, если его нет.

#Знаковые числа

Целочисленные переменные делятся на два типа — знаковые (signed) и беззнаковые (unsigned).

Если сложить две unsigned int переменные, сумма которых превосходит $2^{32}$, произойдет переполнение: сумму нельзя будет представить точно, и поэтому вместо неё результатом будут только нижние 32 бит. Все операции с беззнаковыми числами как бы проходят по модулю какой-то степени двойки.

Знаковые же типы нужны для хранения значений, которые могут быть и отрицательными. Для этого нужно выделить один бит для хранение знака — отрицательное ли число или нет — немного пожертвовав верхней границей представимых чисел: теперь самое большое представимое число это $2^{31}-1$, а не $2^{32}-1$.

Инженеры, которые работают над процессорами, ещё более ленивые, чем программисты — это мотивировано не только стремлением к упрощению, но и экономией транзисторов. Поэтому когда в signed типах происходит переполнение, результат в битовом представлении считается так же, как и в случае с unsigned числами. Если мы хотим ничего не менять в плане того, как работают unsigned числа, представление отрицательных чисел должно быть таким, что число $-x$ как бы вычитается из большой степени двойки:

$$
begin{aligned}
-x = 2^{32} — x
end{aligned}
$$

Несколько следствий:

Все неотрицательные числа записываются в точности как раньше.
У всех отрицательных чисел самый большой бит будет единичным.
Если прибавить к $2^{31}-1$ единицу, то результатом будет $-2^{31}$, представляемое как 10000000 (в целях изложения мы будем записывать 8 бит, хотя в int их 32).
Зная двоичную запись положительного числа x, запись -x можно получить как ~x + 1.
-1 записывается как ~1 + 1 = 11111110 + 00000001 = 11111111.
-42 записывается как ~42 + 1 = 11010101 + 00000001 = 11010110.
После -1 = 11111111 идет 0 = -1 + 1 = 11111111 + 00000001 = 00000000.

Упражнение. Каких чисел больше: положительных или отрицательных?

Осторожно. В стандарте C/C++ прописано, что переполнение знаковых переменных приводит к undefined behavior, поэтому полагаться на описанную логику переполнения нельзя, хотя равно это скорее всего и произойдет.

#128-битные числа

Общих регистров размера больше 64 в процессорах нет, однако умножение и несколько смежных инструкций могут использовать два последовательных регистра как один большой. Это позволяет быстро перемножать два 64-битных числа и получать 128-битный результат, разделенный на нижние биты и верхние.

Это весьма специфичная операция, и поэтому в языках программирования нет полноценной поддержки 128-битных переменных. В C++ однако есть «костыль» — тип __int128_t — который фактически просто оборачивает пару из двух 64-битных регистров и поддерживает арифметические операции с ними.

__int128_t x = 1;
int64_t hi = x >> 64; // получить верхние 64 бит
int64_t lo = (int64_t) x; // получить нижние 64 бит

Базовые арифметические операции с ним чуть медленнее, его нельзя напрямую печатать, и деление и прочие сложные операции будут вызывать отдельную библиотеку и поэтому работать очень долго, однако в некоторых ситуациях он оказывается очень полезен.

Источник

ГЛАВА 2
ПРЕДСТАВЛЕНИЕ ДАННЫХ
(часть 2/4)

Почему в байте именно 8 бит?

Ранние ЭВМ имели размеры машинных слов и байтов, отличные от 8 бит, как правило, кратные шести. В 1950-х–1960-х годах многие ЭВМ использовали 6-битную кодировку символов, поэтому длина байта была первоначально кратна шести битам. Восемь бит в байте использовалось в IBM System/360. Это стало стандартом де-факто. С начала 1970-х в вычислительной технике используют байты, состоящие из 8 бит, и машинные слова, кратные 8 битам. Появление 8-битных байтов у System/360 связано, вероятно, с использованием BCD-форматом представления числа (BCD — binary-coded decimal — двоично-десятичный код): по 4 бита на каждую цифру (0-9), таким образом один байт представлял две десятичные цифры. В System/360 были специальные инструкции для обработки данных такого формата, для представления BCD было бы трудно использовать 6-битные байты, поэтому 8 бит в байте стало наилучшим решением. По другой версии, 8-битный размер байта связан c 8-битным числовым представлением символов в кодировке EBCDIC: один байт — один символ. Остается удивляться прозорливости пиратов, которые в XVII веке назвали битом именно 1/8-ю монеты!

Группа из 16 взаимосвязанных бит (двух взаимосвязанных байт) называется машинным словом (WORD). Соответственно группа из четырех взаимосвязанных байтов (32 бита или два слова) называется удвоенным словом (DOUBLE WORD). Группа из восьми байтов (64 бита или два удвоенных слова) — учетверенным словом (QUADRUPLE WORD), группа из 16 байтов (128 бит или два учетверенных слова) — параграфом (PARAGRAPH) или двойным учетверенным словом (DOUBLE QUADRUPLE WORD), группа из 4096 байтов (256 параграфов) — страницей памяти (MEMORY PAGE) (таблица 2.1.4).

Термины «бит», «байт» и «слово» используются для описания как элементов данных, которые обрабатывает компьютер, так и элементов памяти.

Типы данных

Тип в ассемблере	Сокращение	Соответствие в ЯВУ	Количество
		C/C++	Pascal/Delphi	байт	бит
байт	byte	b	char	Byte (Shortint)	1	8
слово	word	w	short	Word (Integer)	2	16
двойное слово	dword	d	int	Longint	4	32
учетверенное слово	qword	q	long	—	8	64
двойное учетверенное слово	oword	o	Long long	—	16	128
параграф	paragraph	para	—	—	16	128
страница	page	page	—	—	256	2048
страница памяти	memory page	mempage	—	—	4096	32768

Таблица 2.1.4
Представление отрицательных двоичных целых чисел

В общем случае под целое число можно отвести любое число соседних битов памяти, однако система команд компьютера поддерживает работу с числами размером в байт, слово, двойное слово. Поэтому целые числа представляются только байтом, словом, двойным словом и так далее.
Рано или поздно возникает потребность представлять в двоичном коде отрицательные числа. А как в двоичной системе представить отрицательное число, если мы не можем использовать для этой цели минус как в традиционной десятичной системе? Как, например, должно выглядеть в
двоичной системе -1?
По определению, для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n, которое дополняет n до нуля:

n + (-n) = 0.

Найдем такое 4-битное число, которое при сложении с числом 5 (0101b) дало бы нам ноль, переносом в 5-й бит мы пренебрегаем (рис 2.2.1).

рис 2.2.1

Теперь самостоятельно заполните таблицу 2.2.1.

hex-число	двоичное число n	двоичное число -n
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101	1011
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011	0101
C	1100
D	1101
E	1110
F	1111

Таблица 2.2.1

Так как n = -(-n), поэтому, таблицу 2.2.1 можно сократить в два раза

число n	число —n
Hex	bin	Hex	bin
0	0000	0	0000
1	0001	F	1111
2	0010	E	1110
3	0011	D	1101
4	0100	C	1100
5	0101	B	1011
6	0110	A	1010
7	0111	9	1001
8	1000	8	1000

При этом оказалось, что числа 0 и 8 являются сами для себя отрицательными числами. Если не рассматривать числа 0 и 8, числа в левой половине таблицы объединяет то, что самый старший (четвертый) бит у них равен 0, а у чисел в правой половине самый старший бит равен 1. Пусть самый старший бит считается знаковым. Если он равен 0, число будем считать положительным, если 1 — отрицательным. Мы только что изобрели способ представления положительных и отрицательных чисел в двоичной системе, так называемый код дополнения до двух, или дополнительный код. При этом, число 0 может быть только положительным, а четырех битовое число 8 — только отрицательным.

Положительное 4-битное число n	Отрицательное 4-битное число —n
десятичное	hex	bin	десятичное	hex	bin
+0	0	0000	-0	—	—
+1	1	0001	-1	F	1111
+2	2	0010	-2	E	1110
+3	3	0011	-3	D	1101
+4	4	0100	-4	C	1100
+5	5	0101	-5	B	1011
+6	6	0110	-6	A	1010
+7	7	0111	-7	9	1001
+8	—	—	-8	8	1000

Компьютер различает целые числа без знака (неотрицательные) и целые числа со знаком (таблица 2.2.2).

Рис. 2.2.2. Форматы представления целых чисел
Дополнительный код

дополнительный двоичный код	Hex	число со знаком	число без знака
0000 0000	0	0	0
0000 0001	1	1	1
0000 0010	2	2	2
…
0111 1111	7Fh	127	127
1000 0000	80h	-128	128
1000 0001	81h	-127	129
…
1111 1110	0FEh	-2	254
1111 1111	0FFh	-1	255

Для целых чисел со знаком положительное число записывается в прямом коде (как есть). Отрицательное — в дополнительном коде. Преобразовать положительное число в отрицательное можно тремя способами.

Способ первый — классический: взять число в прямом коде, преобразовать его в инверсный код. Для этого все нули этого числа необходимо заменить на единицы, а единицы на нули. К числу в инверсном коде добавить 1. На рис. 2.2.3 пример преобразования числа +7 в –7.

Рис. 2.2.3

Способ второй — практический: возьмем максимальное число (для байта 2⁸=256, для слова 2¹⁶=65536, для двойного слова 2³²=4294967296) и отнимем от него наше число, получившееся число преобразуем в двоичный или hex-код:
256 – 7 = 249 = 1111 1001b = 0F9h = – 7.

Способ третий — студенческий: щелкаем по клавише «Пуск», открываем стандартные приложения, запускаем калькулятор в режиме инженерный, теперь щелкаем по клавише 7 и «+/–» на экранчике калькулятора появится –7. А теперь жмем на клавишу F8 или мышкой по переключателю с надписью «Bin». Что мы видим на экране калькулятора? Число 11111111111111111111111111111001b. Многовато, на экране — двойное слово. Жмем на F4 или мышью по переключателю с надписью Byte. Наше число приобрело нормальный вид 11111001b.
На самом деле, нет необходимости пересчитывать отрицательные числа. Вы пишете –7, а транслятор автоматически подставит туда, где нужно число 11111001b.
Если мы пренебрегаем знаковым разрядом, то диапазон чисел увеличивается в 2 раза:
$https://www.cyberforum.ru/cgi-bin/latex.cgi?2^{7}=128$ ; $https://www.cyberforum.ru/cgi-bin/latex.cgi?2^{8}=256$ .
Попрактикуемся и найдем 8-битный эквивалент –5:
0000 0101b двоичное представление +5.
1111 1010b инвертируем все биты.
1111 1011b добавляем 1.
Проделаем обратное преобразование:
1111 1011b двоичное представление –5.
0000 0100b инвертируем все биты.
0000 0101b добавляем 1 и получаем +5.
А теперь поэкспериментируем с 16-битными положительными и отрицательными числами: 7FFFh (+32767, наибольшее 16-битное положительное число), 4000h (+16384), 0 и 8000h (–32768, наименьшее 16-битное отрицательное число).
Получим отрицательные эквиваленты чисел:
0111 1111 1111 1111b 7FFFh (+32767)
1000 0000 0000 0000b инвертируем все биты (8000h)
1000 0000 0000 0001b добавляем 1 (8001h или –32767)
0100 0000 0000 0000b 4000h (16384)
1011 1111 1111 1111b инвертируем все биты (0BFFFh)
1100 0000 0000 0000b добавляем 1 (0C000h или –16384)
0000 0000 0000 0000b 0
1111 1111 1111 1111b инвертируем все биты (0FFFFh)
0000 0000 0000 0000b добавляем 1 (0)
«Ноль» — он и в Африке «ноль».
Получим положительный эквивалент числа 8000h:
1000 0000 0000 0000b 8000h (–32768)
0111 1111 1111 1111b инвертируем все биты (7FFFh)
1000 0000 0000 0000b добавляем 1 (8000h или –32768).
После смены знака число 8000h не изменилось! –(–32768)=–32768. Почему? Дело в том, что число +32768 нельзя представить как 16-битное число со знаком (вспомните, то же самое у нас получилось с четырехбитным числом 8). При выполнении операции смены знака у числа –32768 микропроцессор x86 выставит признак арифметического переполнения.

Расширение знака и расширение нуля

Возьмем десятичное число –64. Ему соответствует 8-битное число 0C0h, 16-битное 0FFC0h и 32-битное 0FFFFFFC0h. Для числа +64 8-битный эквивалент 40h, 16-битный — 0040h и 32-битный — 00000040h.

Примеры расширения знака

8-битное число	16-битное число	32-битное число
80h	0FF80h	0FFFFFF80h
28h	0028h	00000028h
9Ah	0FF9Ah	0FFFFFF9Ah
7Fh	007Fh	0000007Fh
—	1020h	00001020h
—	8088h	0FFFF8088h

Разницу между 8 и 16/32/64-битными эквивалентами можно выразить следующими словами: «если число отрицательное, то слева к 8-битному эквиваленту дописывается 0FF/0FFFFFF/0FFFFFFFFFFFFFF, а если число положительное, то к 8-битному числу слева дописываются нули» или, другими словами, происходит «растягивание» знакового бита.
Если мы рассматриваем беззнаковое десятичное число 128, то ему соответствует 8-битное число 80h, 16-битное — 0080h и 32-битное — 00000080h. Для расширения 8-битного числа до 16/32/64-битного к нему слева дописывают недостающие нули, происходит «расширение нуля».

Примеры расширения нуля

8-битное число	16-битное число	32-битное число
80h	0080h	00000080h
28h	0028h	00000028h
9Ah	009Ah	0000009Ah
7Fh	007Fh	0000007Fh
—	1020h	00001020h
—	8088h	00008088h

Таблица 2.3.2

Иногда, для сокращения размера кода команд, вместо 32-битного числа используют его 8-битный эквивалент, но это можно проделать лишь с ограниченным диапазоном чисел от –128 до +127.
0FFFFFF80h (–128) можно сократить до 8 бит (80h)
00000040h (+64) можно сократить до 8 бит (40h)
0FFFFFE40h (–448) нельзя сократить до 8 бит
00000100h (+256) нельзя сократить до 8 бит.

Представление чисел с плавающей запятой

У десятичных чисел каждая позиция числа соответствует степени числа 10, то есть число 1234,56=1*10³+2*10²+3*10¹+4*10⁰+5*10^-1+6*10^-2.
Запятая показывает границу между позицией, соответствующей 10⁰, и дробной частью. В дробной части позиции числа также являются степенями числа 10, но эти степени теперь отрицательные. Дробные двоичные числа записываются аналогично дробным десятичным, но основание системы счисления здесь 2, а не 10. Например, $https://www.cyberforum.ru/cgi-bin/latex.cgi?1,101b=1+frac{1}{2}+frac{1}{8}=1frac{5}{8}=1,625$
Чтобы получить эквивалент целого числа в двоичной системе, мы использовали последовательное деление на 2. Чтобы получить эквивалент десятичной дроби, используем обратную операцию — последовательное умножение на 2.
Для перевода десятичной дроби в двоичную систему можно использовать три способа, а уж который из них Вам покажется более удобным — выбирайте сами.

Способ первый. Дробную часть числа последовательно умножают на 2 пока либо дробная часть не станет равной нулю, либо не будет получено необходимое количество разрядов. Целые значения, получаемые при умножении, будут являться эквивалентом десятичной дроби в двоичной системе. Посмотрите конкретный пример на рис. 2.4.1.

рис. 2.4.1

Способ второй. Умножать на 2 8 раз чтобы получить 8-двоичных разрядов дробной части долго и утомительно. А давайте 0,14159 умножим сразу на 2⁸=256, что получится? 0,14159х256=36,24704₁₀=100100₂. 100100 это шесть разрядов, а если добавить 2 нуля слева? 00100100 ничего не напоминает? Добавим «0,» и «0,00100100» двоичный эквивалент числа 0,14159. Нужно получить 16 разрядов после запятой? Смело умножайте на 2¹⁶=65536, переводите в двоичный вид и не забудьте добавить недостающие нули слева.
Способ третий. Любое дробное двоичное число можно представить как

x₁*0,5 + x₂*0,25 + x₃*0,125 +…,

где x₁, x₂, …x_n — нули или единицы, то есть 0,1=0,0001100b.

Способ четвертый. Переведем в двоичную систему, например, число 0,27=27/100. Ближайшая к 100 степень двойки 2⁷=128.
$https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{27}{100}timesfrac{1,28}{1,28}=frac{34,56}{128}=frac{32+2+1}{128}=frac{1}{4}+frac{1}{64}+frac{1}{128}=2^{-2}+2^{-6}+2^{-7}=0,01_2+0,000001_2+0,0000001_2=0,0100011_2$
Перевод десятичного дробного числа 0,406 в hex-систему делается аналогично переводу к двоичному виду:

0,616*16=9,856 и так далее, то есть 0,406=0,67EF9…h .
Для перевода вещественного целого числа в двоичную или hex-систему необходимо целую и дробную часть перевести по отдельности в двоичную или hex-систему, а затем соединить их. Например, число равное 3,14159 должно выглядеть вот так 11,00100100b, или так 3,243Fh.
Существует два способа записи вещественных чисел:
Первый способ — целая часть числа отделяется от дробной символом запятой, расположенной между конкретными разрядами в фиксированной позиции. Такой способ записи называют представлением вещественных чисел с фиксированной запятой. Если отвести под целую часть числа 8 разрядов, а под дробную 8 разрядов, то максимально большое число, которое можно записать таким способом:, а минимальное возможное число — $https://www.cyberforum.ru/cgi-bin/latex.cgi?00000000,00000001b=frac{1}{256}approx 0,00390625$ .
Второй способ применяется в астрономии, физике, химии, математике для записи очень больших либо очень маленьких чисел. Например, скорость света в вакууме составляет около м/с, а гравитационная постоянная примерно равна Нм²/кг². Для удобства работы с такими числами используют так называемую экспоненциальную форму записи. Вместо пишут , а вместо — $https://www.cyberforum.ru/cgi-bin/latex.cgi?6,67cdot 10^{-11}$ . Любое число представляется в виде , где C — целая часть числа, дробную часть числа представляющую значащие разряды — M, называют мантиссой. R — основание системы счисления. P — показатель степени, определяющий на сколько разрядов вправо или влево необходимо переместить запятую в мантиссе, называется порядком числа. Число C должно быть . Такой способ записи называют представлением вещественных чисел с плавающей запятой.

Если под мантиссу отвести 8 разрядов и 8 разрядов под порядок числа (из 8 разрядов 1 разряд отводится под знак и 7 разрядов под число), то максимально возможное наибольшее число $https://www.cyberforum.ru/cgi-bin/latex.cgi?2^{127}approx 10^{38}$ , а минимальное возможное число $https://www.cyberforum.ru/cgi-bin/latex.cgi?2^{-127}approx 10^{-38}$ .
Для представления в компьютере дробного числа первый разряд числа считается знаковым и обозначает знак мантиссы. За ним следует мантисса (число со значением больше или равным 1 и меньшим 2) и порядок (степень числа 2). Представление чисел в виде мантиссы и порядка позволяют сводить умножение и деление чисел к сложению и вычитанию показателей степеней, а возведение в степень и извлечение корня — к умножению и делению на показатель степени, что упрощает и сокращает сложные вычисления.
Вещественные числа в памяти компьютера хранятся в нормализованном виде, то есть оно обязательно должно иметь следующий вид:

где значение S определяет знак (S=0 — число положительное, S=1 — отрицательное), M — двоичная мантисса числа, P — порядок двоичного числа.
Из-за того, что целая часть вещественного числа в двоичной системе всегда равена 1, его, из соображений увеличения разрядности числа, предпочитают «хранить в уме».
Для упрощения вычислений значение порядка хранят не в дополнительном коде (то есть не в виде целого со знаком), а в смещенном коде (таблица 2.4.1) в виде суммы с некоторым числом, это позволяет облегчить сравнение вещественных чисел — в большинстве случаев достаточно сравнить их экспоненты.
Обратите внимание, что в смещенном порядке у отрицательных чисел и нуля в двоичном представлении старший разряд нулевой. В смещенном коде число суммируется с константой, которая для N-битного кода равна 2^N-1-1.

Десятичное значение	Смещенный код
	8-битный	11-битный	15-битный
-16383	—	—	0000h
-1023	—	000h	3C00h
-127	00h	380h	3F80h
…
-1	7Eh	3FEh	3FFEh
0	7Fh	3FFh	3FFFh
1	80h	400h	4000h
…
128	0FFh	47Fh	407Fh
1024	—	7FFh	43FFh
16384	—	—	7FFFh

Таблица 2.4.1

32/64-разрядные микропроцессоры семейства 80×86 могут работать с 32/64/80-битными вещественными числами (одинарная/двойная/повышенная точность), а также со 128-битными, состоящими из четырех упакованных вещественных чисел одинарной точности (таблица 2.4.2).

Количество бит	Тип	Поле знака	Поле порядка	Константа	Поле мантиссы	Диапазон принимаемых значений
32	REAL4	1 бит	8 бит	2⁷-1=127	23 бита	От +/- 1,1810^-38 до 3,410³⁸
64	REAL8	1 бит	11 бит	2¹⁰-1=1023	52 бита	От +/- 2,2310^-308 до 1,7910³⁰⁸
80	REAL10	1 бит	15 бит	2¹⁴-1=16383	64 бита	От +/-3,3710^-4932 до 1,1810⁴⁹³²

Количество

бит

Тип

Поле

знака

Поле

порядка

Константа

Поле

мантиссы

Диапазон принимаемых значений

REAL4

1 бит

8 бит

2⁷-1=127

23 бита

От +/- 1,18*10^-38 до 3,4*10³⁸

REAL8

1 бит

11 бит

2¹⁰-1=1023

52 бита

От +/- 2,23*10^-308 до 1,79*10³⁰⁸

REAL10

1 бит

15 бит

2¹⁴-1=16383

64 бита

От +/-3,37*10^-4932 до 1,18*10⁴⁹³²

Число 193,75 в формате вещественного числа, занимающего два слова:
$https://www.cyberforum.ru/cgi-bin/latex.cgi?193,75=11000001,11=1,100000111bcdot 2^{7}=4341C000h$
Преобразуем вид числа 4341C000h в бинарное представление:

01000011010000011100000000000000	Знак числа 0=«+» 1=«—»
01000011010000011100000000000000	Порядок 86h=+7 в смещенном коде 10000110₂=134₁₀=7+127
01000011010000011100000000000000	мантисса числа=(1),1000001110000b

Рис. 2.4.2. Форматы представления
вещественных чисел

Запись одного и того же числа в разных представлениях, естественно, будет отличаться. Число 193,75 может быть представлено как:

Количество бит	Тип	hex-представление числа 193,75
32	REAL4	4341C000h
64	REAL8	4068380000000000h
80	REAL10	4060C1C0000000000000h

Преобразуем число 4068380000000000h в бинарное представление:

010000000110100000111000000000000000000000000…00000000000000000

Знак числа 0=«+»

010000000110100000111000000000000000000000000…00000000000000000

Порядок =+7 10000000110₂=1030₁₀=7+1023

010000000110100000111000000000000000000000000…00000000000000000

мантисса числа=(1),1000001110000000000000000000000000…000000000000b

Преобразуем число 4060C1C0000000000000h в бинарное представление:

0100000001100000110000011100000000000000000000000000000000…0000

Знак числа 0=«+»

0100000001100000110000011100000000000000000000000000000000…0000

Порядок =+7 100000001100000₂=16480₁₀=7+16383

0100000001100000110000011100000000000000000000000000000000…0000

мантисса числа=1,10000011100000000000000000000000000000000…0000b

Типы REAL4, REAL8 и REAL10 соответствуют стандартным вещественным типам в Pascal/Delphi Single (4 байта), Double (8 байта) и Extended (10 байт) в C/C++ float (4 байта), double (8 байт), long double (10 байт). Первые два типа (REAL4 и REAL8) являются «упакованными», а REAL10 — «неупакованным» типом, в нем старший, всегда единичный, бит нормализованной мантиссы хранится в явном виде. Все вычисления внутри FPU происходят после автоматического преобразования типов REAL4 и REAL8 в REAL10.
Для записи вещественного числа в программе пересчет вещественного десятичного числа из десятичной системы в hex или двоичную самому делать не обязательно, просто запишите число, используя в качестве разделителя точку вместо запятой:

Assembler

1	pi dt 3.1415926535897932384626433832795

А компилятор сам подставит 32-битный эквивалент в случае с директивой dd, 64-битный для директивы dq или 80-битный для директивы dt.
Теперь читателю предлагается потренироваться в переводе чисел. Пред вами два простых примера: 0.125 и 0.625. Можно усложнить их: 23.125 и 456.625. Проверьте свои ответы, записав результат в переменную типа dword, и посмотрев под отладчиком число в стеке FPU. Автор настаивает на такой практике, даже если вы не новичок.

Битовое поле

Непрерывная последовательность бит, в которой каждый бит является независимым и может рассматриваться как отдельная переменная. Битовое поле может начинаться с любого бита и содержать до 32 бит.

Источник

Mikl___

Супермодератор
Команда форума

Публикаций:

14

Регистрация:

25 июн 2008

Сообщения:

3.581

Системы представления чисел

Если вы всерьез собрались научиться разрабатывать микропроцессорные устройства, тогда вам необходимо знать, как компьютер хранит и обрабатывает числа. К сожалению люди не придумали способа записывать при помощи электронных сигналов числа в том виде как мы их привыкли видеть (вернее пытались, но попытки закончились неудачно), поэтому матемaтикам и инженерам пришлось придумать другой, более подходящий способ.
Система счисления ― это совокупность приемов представления обозначения натуральных чисел. В обычной жизни используются два способа представления чисел ― при помощи индийских и римских цифр. Одно и тоже число можно записать как 2 или как II, как 5 или как V, как 22 или как XXII. Перед нами два альтернативных способа написания чисел. Числа одинаковые, а способы написания разные.
Если есть два способа, почему бы не придумать третий, четвертый и далее? Были придуманы несколько способов представления чисел. Один из этих способов (двоичный способ представления чисел) подходит для реализации его при помощи электроники.
Другие (восьмеричный и шестнадцатеричный) способы помогают удобнее представлять компьютерные данные на бумаге или на экране.
За основу универсального приема, позволяющего создавать различные способы представления чисел были взяты индийские цифры и позиционный способ представления числа. Согласно этому принципу один и тот же цифровой знак имеет различные значения в зависимости от того места (позиции), где он расположен. Такая система счисления основывается на том, что некоторое число из n единиц (основание системы счисления) объединяется в единицу второго разряда, n единиц второго разряда объединяются в единицу третьего разряда и так далее.
«Разрядам» учат в начальных классах школы. Например, у числа 35672 цифра «2» соответствует первому разряду, «7» ― второму, «6» ― третьему, «5» ― четвертому и «3» ― пятому. А «различные значения» цифрового знака «в зависимости от того места, где он расположен» и «объединение в единицу старшего разряда» очень наглядно отображают обыкновенные бухгалтерские счеты.
Чтобы набрать число 35672 мы должны передвинуть влево две «костяшки» на первом «прутике», 7 на втором, 6 на третьем, 5 на четвертом и 3 на пятом. (1 «костяшка» на втором «прутике» ― это то же самое, что и 10 «костяшек» ― на первом, а одна на третьем равна десяти на втором ― и так далее…) Пронумеруем наши «прутики» снизу вверх ― так, чтобы номер первого «прутика» был равен нулю.
35672 = 3⋅10⁴ + 5⋅10³+ 6⋅10² + 7⋅10¹ +2⋅10⁰ → сколько на каждом «прутике» сдвинутых влево «костяшек»;
35672 = 3⋅10⁴ + 5⋅10³+ 6⋅10² + 7⋅10¹+ 2⋅10⁰ → номер «прутика»;
35672 = 3⋅10⁴ + 5⋅10³+ 6⋅10² + 7⋅10¹ +2⋅10⁰ → число «костяшек» на каждом «прутике».
Оттолкнувшись от записи конкретного числа 35672 можно записать любое пятизначное число как

a₄a₃a₂a₁a₀=a₄×10⁴+a₃×10³+a₂×10²+a₁×10+a₀

где a₄, a₃, a₂, a₁ и a₀ ― какие-то десятичные цифры, а число 10 ― основание системы представления. Компактный способ написания разложения (n+1)-значного числа в линейную комбинацию степеней базы выглядит вот так:

a_na_n-1…a₂a₁a₀=[math]displaystyle sum^{n+1}_{k=0}[/math]a_k×10^k

В большинстве стран мира считают одинаково, используя десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Когда доходят до последней цифры, используют двухзначные числа. Когда заканчиваются двухзначные числа ― начинают использовать трехзначные и так далее… Число десять выбрано потому, что у нас на двух руках десять пальцев
Если бы у человека было на каждой руке только по четыре пальца, как у героев диснеевских мультфильмов (рис. #1), тогда бы ему никогда не пришла в голову мысль о системе счисления, основанной на десяти. Вместо нее нормальной и единственно разумной системой счисления считалась бы система, основанная на восьми пальцах. И называлась бы такая система не десятичной (decimal), а восьмеричной (octal). В восьмеричной системе счисления не нужен символ 9. В десятичной системе нет специального символа для десяти, поэтому в восьмеричной системе нет специального символа для 8.
В десятичной системе начало натурального ряда чисел выглядит так: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, … В восьмеричной системе уже так: 0, 1, 2, 3, 4, 5, 6, 7 и… что дальше? Символы-то закончились. Выход один ― после 7 поставить 10. Но эта десятка уже не равна числу пальцев на двух руках человека. В восьмеричной системе 10 ― это количество пальцев на двух руках мультяшки.
Даже когда пальцы на ногах и руках будут исчерпаны, счет в восьмеричной системе можно продолжать. В целом он идет, как и счет в десятичной системе, но без чисел, содержащих цифры 8 и 9:
0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 21, 22, 23, 24, 25, 26, 27, 30, 31, 31, 32, 33, 34, 35, 36, 37, 40, 41, 41, 42, 43, 44, 45, 46, 47, 50, 51, 52, 53, 54, 55, 56, 57, 60, 61, 62, 63, 64, 65, 66, 67, 70, 71, 72, 73, 74, 75, 76, 77, 100…

«Дети шпионов». 2001. Пал Палычи

А теперь представьте себе как считают вот такие существа (рис. #2). На обоих руках у них всего два пальца, поэтому обходятся они всего двумя цифрами: 0 и 1. Система счисления, основанная на двух цифрах, называется двоичной (binary).
В двоичной системе сразу после 1 идет 10. В любой системе счисления, когда заканчиваются одноразрядные числа, первое двухразрядное число ― 10. Начало натурального ряда чисел в двоичной системе:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001…
Закрепим. Если бы у нас было только пять цифр, 0, 1, 2, 3, 4, тогда начало натурального ряда чисел выглядело бы так:
0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34, 40, 41, 42, 43, 44, 100, 101, 102, 103, 104, 110, 111, 112…
«Обычную» систему представления чисел называют «десятичной». Систему представления чисел, которую мы только что рассмотрели ― пятеричной. Число цифр в системе представления чисел (количество пальцев на двух руках) называют «основанием системы представления чисел» или базой.
Если основании системы более десяти, тогда приходится вводить новые «цифры». В качестве «новых цифр» принято использовать латинские буквы. Так, в семнадцатеричной системе представления начало натурального ряда чисел выглядит вот так:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 1G, 20, …, GD, GE, GF, GG, 100, 101, 102, …
Задание #1: При каком достаточно большом основании способ с использованием латинских букв не подойдет?
Разные системы представления чисел ― как разные языки. У одного и того же числа могут быть совершенно разные записи в разных системах представления. Так, десятичному представлению числа 2785 соответствует шестнадцатеричное представление AE1, восмеричное 5341 и двоичное 101011100001. Точно так же, как слова переводят с одного языка на другой, числа можно переводить из одной системы представления в другую. Двоичная система представления чисел используется в компьютерах. К недостатку двоичной системы представления можно отнести «длинную» запись числа (чем меньше в системе представления цифр, тем длиннее будет представление числа) ― четырем цифрам в десятичном представлении числа 2785 соответствует двенадцать цифр в двоичном представлении 101011100001
Шестнадцатеричная (hexadecimal) и восьмеричная системы представления чисел позволяют вместо длинных цепочек из нулей и единиц записывать более «короткие» числа, что облегчает написание и корректировку программ. Шестнадцатеричная и восьмеричная системы ― промежуточное звено между машиной и человеком, между двоичной и десятичной системами представления чисел.
Разумеется, что нули перед числом не изменяют его значение ни в одной из систем представления.

Задание #2: Посчитайте немного в различных системах представления. Возьмите листочек «в клеточку» и пронумеруете строчки сначала в десятичной системе представления, потом в восьмеричной, шестнадцатеричной и двоичной ― получите табличку перевода первых тридцати чисел в наиболее часто используемых системах представления. Напишите на этой таблице также числовые значения всех латинских букв ― это пригодится в дальнейшем.

Вложения:

Mikl___

Mikl___

Супермодератор
Команда форума

Публикаций:: 14

Регистрация:: 25 июн 2008

Сообщения:: 3.581

Для представления бинарных файлов в текстах писем в электронной почте используется 6-ричное кодирование base64, которое при помощи 64(=2⁶) символов (текстово-цифровые латинские символы A-Z, a-z и 0-9 (62 знака) и 2 дополнительных символа, зависящих от системы реализации)
Или вообще попробуйте считать в 256-ричной (=2⁸) системе счисления, используя в качестве «цифр» таблицу ASCII-символов
Компьютер, как известно, считает только в двоичной системе счисления. Человеку привычна десятичная. Так для чего еще и шестнадцатеричную какую-то знать нужно?
Все очень просто. В умных книжках пишут, что «шестнадцатеричная нотация является удобной формой представления двоичных чисел». Что это значит?
Переведите число A23F из шестнадцатеричной «нотации» в двоичную. (Один из возможных алгоритм приведен в #3). В результате длительных манипуляций у вас должно получиться 1010001000111111.
А теперь еще раз посмотрите на таблицу #2. (которую вы как бы уже и выучили) и попробуйте то же самое сделать «в уме»:
A23F →[math]underbrace{1010}_{A};underbrace{0010}_{2};underbrace{0111}_{3};underbrace{1111}_{F}[/math] → 1010 0010 0011 1111
Каждой шестнадцатеричной цифре соответствует тетрада (4 штуки) ноликов и единичек. Все, что потом нужно сделать ― «состыковать» эти тетрады. Круто? Вас еще не то ждет!
Конкретный рисунок цифр не важен. То, что ноль обозначается кружочком, а единица ― палочкой, всего лишь «историческая условность».
Можно «нормально считать» в троичной системе представления чисел с цифрами «%», «!», «^» и тогда начало натурального ряда чисел будет выглядеть вот так:
%, !, ^, !%, !!, !^, ^%, ^!, ^^, !%%, !%!, !%^, !!%, !!!, !!^, !^%, !^!, !^^, ^%%…
Точно также не стоит воспринимать всерьез требования использовать латинские буквы после девятки. ASCII-символы, стоящие после девятки («:;<=>?@») ничем не хуже.
Для указания системы представления надо указывать не ее основание, а вектор (упорядоченный массив) ее «цифр». Считая в системах представления с вектором основания, в котором цифры идут «не по порядку» (например, восьмеричная система с вектором «31276504»), можно существенно затруднить понимание происходящего.
Существует система представления состоящая из двадцати шести латинских букв, с вектором основания «A B C D E F G H I J K L M N O P Q R S T U V W X Y Z» ― со всеми латинскими буквами в алфавитом порядке. В такой системе представления, к примеру, десятичное число 10 будет записываться как «K». Число «DOG», переведенное из этой системы в десятичную, будет равно 2398. (Проверьте.)
Задание #3: Самостоятельно попереводите разные числа из 26-ричной системы в двоичную и десятичную и обратно.
Принято указывать основание системы представления внизу-справа от числа. При этом основание записывается в десятичной системе представления. Например ― 1FC₁₆ обозначает число 1FC в шестнадцатеричной системе представления.
Задание #4: Заметьте (или проверьте по своей таблице), что [math] 1overbrace{000cdots 00_x}^{n} =x^n[/math]
где N ― количество нулей после единицы, а x ― основание системы счисления.
Алгоритм перевода числа из любой системы в десятичную систему

Если перейти от десятичной записи числа к записи числа в p-ричной системе представления, то изменений будет не очень много

[math]a_{n}a_{n-1}cdots a_{1}a_{0}=a_{n}cdot p^{n}+a_{n-1}cdot p^{n-1}+cdots +a_{1}cdot p+a_{0}=displaystyle sum^{n+1}_{k=0} a_{k}cdot p^k[/math]

где a_k∈[math]{0, 1, 2,cdots , p-1}[/math] и a_n ≠ 0 То есть число равно сумме его цифр, умноженных на основание p возведенное в соответствующую степень k. В качестве примеров используем переводы числа «1210» из троичной системы и числа «C00L» из двадцатидвухричной системы в десятичное представление:
1210₃ = 1⋅3³ + 2⋅3² + 1⋅3 + 0 = 27 + 18 + 3 = 48₁₀
C00L₂₂ = 12⋅22³ + 0⋅22² + 0⋅22 + 21 = 127776 + 21 = 127797₁₀
Задание #5: Попробуйте попереводить побольше чисел из самых различных систем представления (желательно без использования калькулятора), выполняя все арифметические действия в уме или на листочке.
Применив «схему Горнера», получим более эффективную версию алгоритма
1210₃ = ((1⋅3+2)⋅3+1)⋅3+0 = 16⋅3 = 48
C00L₂₂ = (((12⋅22+0)⋅22+0)⋅22+21 = 127776 + 21 = 127797
Эффективность алгоритма в том, что не требуется возведение в степень ― перевод получается значительно быстрее и короче.
Задание #6: Переводите числа из любой системы представления в привычный нам десятичный вид.
Вам нужно постоянно быть в боевой готовности ― кто знает, где придется демонстрировать своё искусство .
Если под рукой есть только примитивный калькулятор с четырьмя арифметическими действиями (например, калькулятор в телефоне), то по традиционному методу вам придется где-то записывать, а потом набирать промежуточные результаты. По новому методу вам потребуется лишь набирать между цифрами знак умножения, основание системы представления чисел и знак сложения.
Если под рукой не оказалось даже примитивного калькулятора, тогда новый алгоритм можно использовать для перевода числа столбиком.

Алгоритм перевода числа из десятичной системы в любую систему

Мы переводили числа из «странной записи» в «обычную». При вводе десятичных чисел в компьютер требуется обратное действие ― десятичные числа должны быть переведены в «машинный вид». Хотя эта операция обычно выполняется компьютером, для лучшего понимания мы проделаем эту операцию самостоятельно.
Обратное действие (перевод из десятичной системы представления в произвольную) обычно выполняется, когда мы хотим ввести информацию в компьютер. Мы живем в «десятичном мире», а компьютер ― в двоичном. Для того, чтобы ввести что-нибудь в «мир компьютера», нам придется переводить числа в «чужую» систему представления.
Тут надо уметь делить. Переведем числа обратно в «родную систему представления», последовательно делим число на основание, пока не получится число, меньше чем основание.

Результат собирается из последнего частного и остатков в обратном порядке. В первом случае получаем 1210₃, а во втором ― C00L₂₂.
Задание #7: Попробуйте несколько десятичных чисел перевести во всякие «странные системы представления», а затем переведите получившиеся числа обратно в десятичную систему представления.
Если вы хорошо делите «в уме» (или используете калькулятор), тогда удобнее использовать другую запись:

при каждом делении остаток записывается справа от черты, а частное ― внизу. Ответ считывается в обратном порядке ― снизу вверх.
Задание #8: Напишите программу, выполняющую автоматический перевод в любую систему представления чисел.
Таблица #1. Цифры разных систем представления чисел

Система счисления Основание Используемые цифры

двоичная 2 0,1

четверичная 4 0, 1, 2, 3

восьмеричная 8 0, 1, 2, 3, 4, 5, 6, 7

десятичная 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

шестнадцатеричная 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Таблица #2. Эквиваленты записи чисел в разных системах представления

Двоич-
ная Чет-
ве-
рич-
ная Вось-
ме-
рич-
ная Деся-
тич-
ная Шест-
над-
цате-
рич-
ная Двоично-десятичные
(BCD ― binary-coded decimal)

8.4.2.1 Tele-
commu-
nication
01236 7.4.2.1 8.4.-2.-1 5.4.2.1 2.4.2.1

0

0

0

0

0
0000 0000 01100 01100 1100 1100 0000 0000 0000 0000 0000 0000

1

1

1

1

1
0000 0001 01100 11000 1100 0001 0000 0111 0000 0001 0000 0001

10

2

2

2

2
0000 0010 01100 10100 1100 0010 0000 0110 0000 0010 0000 0010

11

3

3

3

3
0000 0011 01100 10010 1100 0011 0000 0101 0000 0011 0000 0011

100

10

4

4

4
0000 0100 01100 01010 1100 0100 0000 0100 0000 0100 0000 0100

101

11

5

5

5
0000 0101 01100 00110 1100 0101 0000 1011 0000 1000 0000 1011

110

12

6

6

6
0000 0110 01100 10001 1100 0110 0000 1010 0000 1001 0000 1100

111

13

7

7

7
0000 0111 01100 01001 1100 1000 0000 1001 0000 1010 0000 1101

1000

20

10

8

8
0000 1000 01100 00101 1100 1001 0000 1000 0000 1011 0000 1110

1001

21

11

9

9
0000 1001 01100 00011 1100 1010 0000 1111 0000 1100 0000 1111

1010

22

12

10

А
0001 0000 11000 01100 0001 1100 0111 0000 0001 0000 0001 0000

1011

23

13

11

B
0001 0001 11000 11000 0001 0001 0111 0111 0001 0001 0001 0001

1100

30

14

12

C
0001 0010 11000 10100 0001 0010 0111 0110 0001 0010 0001 0010

1101

31

15

13

D
0001 0011 11000 10010 0001 0011 0111 0101 0001 0011 0001 0011

1110

32

16

14

Е
0001 0100 11000 01010 0001 0100 0111 0100 0001 0100 0001 0100

1111

33

17

15

F
0001 0101 11000 00110 0001 0101 0111 1011 0001 1000 0001 1011

10000

100

20

16

10
0001 0110 11000 10001 0001 0110 0111 1010 0001 1001 0001 1100

Система счисления	Основание	Используемые цифры
двоичная	2	0,1
четверичная	4	0, 1, 2, 3
восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7
десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
шестнадцатеричная	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Двоич- ная	Чет- ве- рич- ная	Вось- ме- рич- ная	Деся- тич- ная	Шест- над- цате- рич- ная	Двоично-десятичные (BCD ― binary-coded decimal)
8.4.2.1	Tele- commu- nication 01236	7.4.2.1	8.4.-2.-1	5.4.2.1	2.4.2.1
0	0	0	0	0	0000 0000	01100 01100	1100 1100	0000 0000	0000 0000	0000 0000
1	1	1	1	1	0000 0001	01100 11000	1100 0001	0000 0111	0000 0001	0000 0001
10	2	2	2	2	0000 0010	01100 10100	1100 0010	0000 0110	0000 0010	0000 0010
11	3	3	3	3	0000 0011	01100 10010	1100 0011	0000 0101	0000 0011	0000 0011
100	10	4	4	4	0000 0100	01100 01010	1100 0100	0000 0100	0000 0100	0000 0100
101	11	5	5	5	0000 0101	01100 00110	1100 0101	0000 1011	0000 1000	0000 1011
110	12	6	6	6	0000 0110	01100 10001	1100 0110	0000 1010	0000 1001	0000 1100
111	13	7	7	7	0000 0111	01100 01001	1100 1000	0000 1001	0000 1010	0000 1101
1000	20	10	8	8	0000 1000	01100 00101	1100 1001	0000 1000	0000 1011	0000 1110
1001	21	11	9	9	0000 1001	01100 00011	1100 1010	0000 1111	0000 1100	0000 1111
1010	22	12	10	А	0001 0000	11000 01100	0001 1100	0111 0000	0001 0000	0001 0000
1011	23	13	11	B	0001 0001	11000 11000	0001 0001	0111 0111	0001 0001	0001 0001
1100	30	14	12	C	0001 0010	11000 10100	0001 0010	0111 0110	0001 0010	0001 0010
1101	31	15	13	D	0001 0011	11000 10010	0001 0011	0111 0101	0001 0011	0001 0011
1110	32	16	14	Е	0001 0100	11000 01010	0001 0100	0111 0100	0001 0100	0001 0100
1111	33	17	15	F	0001 0101	11000 00110	0001 0101	0111 1011	0001 1000	0001 1011
10000	100	20	16	10	0001 0110	11000 10001	0001 0110	0111 1010	0001 1001	0001 1100

Вложения:

Mikl___

Супермодератор
Команда форума

Публикаций:

14

Регистрация:

25 июн 2008

Сообщения:

3.581
Теперь от теории перейдем к практике. Вам понадобится переводить из/в шестнадцатеричную, десятичную, восьмеричную, двоичную системы.
Итак, разберем все случаи. Будьте внимательны ― здесь есть подводные камни!
16→2
Это просто ― так как 2⁴=16 поэтому каждой шестнадцатеричной цифре ставятся в соответствие четыре бита («ниббл», «тетрада» или «полубайт») по таблице #2. После перевода всего числа, нолики слева («лидирующие нули»), если они есть, разумеется, можно удалить.
[math]12FC_{16}tounderbrace{{color{red}{000}}1}_{1};underbrace{0010}_{2};underbrace{1111}_{F};underbrace{1100}_{C}to 1001011111100_2[/math]
2→16
Не на много сложнее ― двоичные разряды объединяются в «четверки» СПРАВА, при этом последняя «четверка» может оказаться «тройкой», «двойкой» или даже одной цифрой, тогда в качестве недостающих разрядов слева дописываются нули. Затем из таблицы #2 вместо «четверок» выписываются соответствующие шестнадцатеричные цифры.
[math]1011001011_2tounderbrace{{color{red}{00}}10}_{2};underbrace{1100}_{C};underbrace{1011}_{B}to 2CB_{16}[/math]
8↔2
Переводы из шестнадцатеричной в двоичную систему и из восьмеричной в двоичную очень похожи, только используется разбивка двоичного числа на тройки («триады») битов (2³=8).
[math]276_8to underbrace{{color{red}{0}}10}_{2};underbrace{111}_{7};underbrace{110}_{6}to 10111110_2[/math]
[math]1011001011_2to underbrace{{color{red}{00}}1}_{1};underbrace{011}_{3};underbrace{001}_{1};underbrace{011}_{3}to 1313_8[/math]
ВНИМАНИЕ! Алгоритмы существуют лишь для переводов 16↔2 и 8↔2. Для перевода 16↔8 надо использовать промежуточную двоичную систему представления чисел. Использование же алгоритмов для перевода в десятичную систему или из нее ― грубейшая ошибка!
Вообще, запомните формулу 8↔2↔16.

ВНИМАНИЕ! Распространенное заблуждение!
У каждого программиста в жизни бывает период, когда он вдруг (по какой-то необъяснимой причине) начинает считать, что числа, в которых не используются буквы, не меняются при переводе в десятичную систему. То есть, например, 123₁₆=123₁₀. Так вот, ЭТО НЕ ТАК! Подумайте, почему.
Задание #9: Посчитайте, чему равно 123₁₆
2→10
Часто требуется переводить байты и слова из двоичной системы в десятичную.
1. Лобовое решение, но не самое лучшее
  [math]101011010101001010001=2^{20}+2^{18}+2^{16}+2^{15}+2^{13}+2^{11}+2^9+2^6+2^4+1=[/math]
  [math]=1048576+262144+65536+32768+8192+2048+512+64+16+1=1419857[/math]
2. Можно использовать калькулятор «Пуск» [math]to[/math] «Все программы» [math]to[/math] «Стандартные» [math]to[/math] «Калькулятор» и «Вид» [math]to[/math] «Программист»
2→16→10
Вместо того, чтобы долго и нудно вычислять степени двойки, а потом подсчитывать их сумму, можно быстро перевести число в шестнадцатеричную систему представления чисел, а уже потом из нее ― в десятичную. Экономится куча времени.
[math]underbrace{1010}_{A};underbrace{1001}_{9} = 10cdot 16+9 = 169[/math]
Байт переводится мгновенно и в уме! Запомните несколько степеней 16: 16²=256, 16³=4096 16⁴=65536 и 16⁵=1048576 ― пригодится!

Алгоритм Содена

быстрый алгоритм перевода из двоичной системы в десятичную предложен Уолтером Соденом (Walter Soden) в 1953 году.
1. Сначала переведем число из двоичной системы в восьмеричную. Например,101011010101001010001₂→101.011.010.101.001.010.001₂→5325121₈
2. Далее выполним перевод из восьмеричной системы в десятичную. Разница между системами представления 10 — 8 = 2. Нужно у восьмеричного представления числа удваивать на k-м шаге k ведущих разряда используя десятичную арифметику, и вычесть полученный результат из (k+1) ведущих разрядов при помощи десятичной арифметики. Если заданное число содержит (m+1) восьмеричных цифр, тогда преобразование займет m шагов. Для выделения удваиваемых разрядов используем «разделяющую точку». Это поможет исключить возможные ошибки
3. 101011010101001010001₂→5325121₈→1419857₁₀
Если двоичное число не очень длинное. тогда можно перевести непосредственно из двоичного представления в десятичное, не прибегая к промежуточному восьмеричному представлению. Разница между системами представления 10 — 2 = 8.

1111110001₂→1009₁₀

10→2
1. Алгоритм перевода из десятичной системы в двоичную, предложенный Шарлем Розье (Charles P. Rozier) в 1962 году, почти такой же.
  
  Сначала переводим число в промежуточную восьмеричную запись. Для этого, заданное в десятичном формате число, удвоим на k-м шаге k ведущих разрядов, используя представление в восьмеричном формате, и сложим полученные(k+1) ведущих разрядов при помощи восьмеричной арифметики. Для заданного числа, содержащего (m+1) цифр преобразование закончится через m шагов. Например,
  
  Далее переводим восьмеричное число в двоичное. [math]5325121_8to 101.011.010.101.001.010.001_2to 101011010101001010001_2[/math]
  
  [math]1419857_{10}to 5325121_8to 101011010101001010001_2[/math]
2. получаем двоичный вид числа от последней двоичной цифры к первой. Число последовательно делится на 2 до получения частного равного нулю. Представление числа в двоичной системе – это упорядоченная последовательность остатков от деления в порядке, обратном их получению (старшую цифру числа дает последний остаток, а младшую – первый). Начинаем с n=0
  
  Делим число на 2. Запомним частное q_n и остаток a_n.
  
  Если в результате деления частное q_n ≠ 0, тогда принимаем q_n за новое делимое, увеличиваем n на 1 и возвращаемся к пункту 1.
  
  Если в результате деления частное q_n = 0, тогда выписываем остатки в обратном порядке a_na_n-1…a₁a₀. Это и будет число представленное в двоичной системе счисления.
  
  Получение двоичного вида числа 147:
3. вычисляем двоичный вид числа начиная с первой двоичной цифры. Для этого придется запомнить степени 2 (2¹⁰=1024, 2⁹=512, 2⁸=256, 2⁷=128, 2⁶=64, 2⁵=32, 2⁴=16, 2³=8, 2²=4). Для примера рассчитаем как будет выглядеть двоичное представление того же числа 147, ищем ближайшую степень двойки 2⁷=128 <147< 2⁸=256 Определившись со степенью n – делим десятичное представление числа на 2ⁿ. Результатом будет первая двоичная цифра и остаток. Остаток делится на 2^n-1 и так далее, пока остаток не станет меньше 2, а степень нулевой.
4. похоже на третий вариант, но деление заменено на вычитание. Преобразуем десятичное число 84 в двоичное. Определяем, ЧТО должно стоять в каждом разряде двоичного числа: 1 или 0. Находим наибольшую степень 2, меньше или равную заданному числу 2⁶=64 < 84 < 128=2⁷, и ставим 1 в 6-ой разряд. Далее 84–64 = 20, 20 < 32=2⁵, поэтому в 5-ый разряд ставим 0, 20 > 16=2⁴, в 4-ый разряд ставим 1. Остается 20 –16 = 4. 4 < 8=2³, ставим 0 в третий разряд. 4=2², – ставим 1 во второй разряд и нули в разряды 1 и 0. Собрав все вместе, получаем 84 = 1010100₂
10→16
1. сперва находим последнюю цифру, затем предпоследнюю и так далее… Число в десятичной форме записи 42936 переводится следующим образом:
2. Второй вариант перевода числа из десятичного вида в шестнадцатеричный – сперва находим первую цифру, затем вторую и так далее… Для начала придется запомнить степени 16 (16⁵=1048576, 16⁴=65536, 16³=4096, 16²=256).
  Начинаем с вычисления старшего разряда и определения его порядка в шестнадцатеричном виде числе, если десятичное число между 1 и 16 миллионами – начинаем с деления на 1048576, если между миллионом и 65 тысячами – начнем с деления на 65536 и так далее. Определившись со степенью – делим десятичное представление числа на 16ⁿ. Результатом будет первая шестнадцатеричная цифра и остаток. Остаток делится на 16^n-1 и так далее, пока остаток не станет меньше 16, а степень нулевой. Для примера рассчитаем шестнадцатеричное представление числа:
3. Преобразуем число 333 в шестнадцатеричное. Найдем наибольшую степень шестнадцати, меньшую или равную заданному числу. [math]log_{16}(333)=2,094844592[/math] [math]16^2 = 256 < 333 < 4096 = 16^3[/math]
Mikl___

Супермодератор
Команда форума

Публикаций:

14

Регистрация:

25 июн 2008

Сообщения:

3.581

Число [math]256[/math] содержится в числе [math]333[/math] только один раз, поэтому во второй разряд записываем единицу. [math]333–256=77[/math]. Число [math]16[/math] содержится в числе [math]77[/math] четыре раза, поэтому в первый разряд записываем четверку. Остается [math]77 – 16times 4 = 13 = D_{16}[/math], поэтому в нулевой разряд записываем [math]D[/math]. [math]333_{10} = 14D_{16}[/math]
16→10
Обратный процесс – переведем число из шестнадцатеричного вида в десятичный – возьмем число A7B8 и учтем, что каждая шестнадцатеричная цифра всегда в 16 раз больше ближайшей цифры справа: ((A⋅16+7)⋅16+B)⋅16+8=(167⋅16+11)⋅16+8=2683⋅16+8=42936

Задание #10: Переведите из десятичной системы в двоичную систему число 12345678987654321.
Задание #11: Переведите из двоичной системы в десятичную систему число 10101010101010101

Обозначения

На самом деле, такую глобальную роль шестнадцатеричная и восьмеричная системы представления чисел играют исключительно благодаря тому, что 8=2³, а 16=2⁴. Внутри машина считает исключительно «по-двоичному». Шестнадцатеричная и восьмеричная системы представления чисел позволяют вместо длинных цепочек из нолей и единиц записывать более короткие строки из чисел. Эти системы ― промежуточное звено между машиной и человеком, между двоичной и десятичной системами представления чисел.
Роль систем представления чисел огромна! К примеру, права доступа к файлу в системе UNIX изменяются из shell’а командой chmod. Эта команда требует задания аргумента (прав доступа) в восьмеричной системе представления чисел! Команда
открывает доступ на чтение и запись всем пользователям к файлу паролей в системе UNIX. Даже системные администраторы должны разбираться в восьмеричной системе представления чисел. Так чего же говорить о программистах, пишущих на языке ассемблер!
В различных языках программирования числа в этих системах обозначаются по разному.
Таблица #3. Сводная таблица для основных языков:

C/C++ Pascal BASIC Assembler

DEC 12 12 12 12 ,12d, 12t

HEX 0xC $C &hC 0Ch, 3F800000r

OCT 014 ― &o14 14o, 14q

BIN ― ― &b1100 1100b, 1100y

Нули в начале числа не влияют на его значение. Создатели языка Cи решили по другому. Поскольку никто в здравом уме не начинает числа с нуля (кому охота набивать лишние символы?), ноль в начале числа используется для обозначения признака восьмеричного числа.
При всех способах записи регистр букв неважен. Даже строгий на регистры Cи позволяет начинать шестнадцатеричные числа как с 0x, так и с 0X. Кстати, в ранних версиях компиляторов Cи различных фирм шестнадцатеричные числа надо было начинать с 0x0.
При программировании на ассемблере если шестнадцатеричное число начинается с буквы, перед ним обязательно должен ставится ноль. Иначе ассемблер подумает, что вы имели в виду переменную Ch, а не число C₁₆. Но некоторые не способны запомнить это правило, ставят ноль впереди всех шестнадцатеричных чисел.
В диалект MASM дополнительно к суффиксам D, O, H и B добавлены суффиксы T, Q, R и Y. Дело в том, что с помощью директивы .RADIX ассемблер позволяет менять систему представления чисел, действующую по умолчанию. Раньше, когда систему представления чисел изменяли на шестнадцатеричную, числа вроде 12D, которые с первого взгляда являются обычными шестнадцатеричными, интерпретировались как 12₁₀. Это порождало сеть мелких и незаметных ошибок, мешавших использовать .RADIX 16.
Мы будем использовать все способы записи чисел, используя ассемблерный способ как основной. Вы должны хорошо владеть всеми способами.

Арифметика

В любой их систем представления чисел можно по прежнему складывать, вычитать, делить и умножать.

Попробуйте самостоятельно решить примеры на сложение и вычитание в шестнадцатеричной, восьмеричной и двоичной системах представления чисел.

Задание #11: Попробуйте делить и умножать в этих системах представления чисел. Производите побольше действий в уме, развивайте свои способности быстро считать, запоминать информацию.
Программа hiew позволяет вывести на экран дамп файла. Программа debug.exe имеет команду d, выводящую на экран дамп (dump) памяти. Даже Norton Commander позволяет по F4 выводить содержимое файла в шестнадцатеричном виде.
Теперь вы должны очень хорошо представлять себе и чувствовать шестнадцатеричную и другие системы. Наконец-то вы сможете разобраться в дампе.
Существуют специальные шестнадцатеричные калькуляторы, позволяющие считать в этих широкораспространенных системах представления чисел.

Вложения:

	C/C++	Pascal	BASIC	Assembler
DEC	12	12	12	12 ,12d, 12t
HEX	0xC	$C	&hC	0Ch, 3F800000r
OCT	014	―	&o14	14o, 14q
BIN	―	―	&b1100	1100b, 1100y

Mikl___

Mikl___

Супермодератор
Команда форума

Публикаций:: 14

Регистрация:: 25 июн 2008

Сообщения:: 3.581

Несколько приемов, которые упростят перевод из двоичного в десятеричное представление

[math]2^n = 1overbrace{000cdots 00}^{n}[/math] ― [math](n+1)[/math]-разрядное двоичное число в котором [math]n[/math] нулей

чему равно [math]2^0+2^1+2^2+cdots +2^{n-2}+2^{n-1}=?[/math] перед нами сумма [math]n[/math] первых членов геометрической прогрессии, где каждый следующий член прогрессии больше предыдущего в 2 раза. Любой член геометрической прогрессии может быть вычислен по формуле: [math]b_{n}=b_{1}times q^{n-1}[/math] Формула суммы [math]n[/math]-первых членов геометрической прогрессии [math]S_{n}=frac{b_{1}times (1-q^{n})}{1-q}[/math]
В нашем случае [math]b_1=2^0=1[/math] [math]q=2[/math] [math]S_n=2^n-1[/math]
[math]2^0+2^1+2^2+cdots +2^{n-2}+2^{n-1}=2^n-1[/math] то есть [math]n[/math]-разрядное двоичное число только из единиц соответствует десятичному числу [math]overbrace{111cdots 11}^{n}=2^n-1[/math]

[math]n[/math]-разрядное двоичное число из чередующихся нулей и единиц, заканчивающееся на единицу, соответствует десятичному числу [math]overbrace{1.01.01.01cdots 01.01}^{n}=frac{1}{3}(2^{n+1}-1)[/math]
[math]2^{n+1}[/math] потому что [math]overbrace{1.01.01.01cdots 01.01}^{n}=overbrace{01.01.01.01cdots 01.01}^{n+1}[/math]

[math]n[/math]-разрядное двоичное число из чередующихся нулей и единиц, заканчивающееся на ноль, соответствует десятичному числу [math]overbrace{10.10.10cdots 10.10}^{n}=frac{2}{3}(2^{n}-1)[/math]

[math]n[/math]-разрядное двоичное число из чередующихся двух единиц и нуля, заканчивающееся на ноль, соответствует десятичному числу [math]overbrace{110.110.110cdots 110}^{n}=frac{6}{7}(2^{n}-1)[/math]

[math]n[/math]-разрядное двоичное число из чередующихся единицы и двух нулей, заканчивающееся на ноль, соответствует десятичному числу [math]overbrace{100.100.100cdots 100}^{n}=frac{4}{7}(2^{n}-1)[/math]

Интересно, заметили ли Вы связь между числителем и знаменателем дроби, стоящей перед [math](2^{n}-1)[/math] и повторяющейся частью и периодичностью, с которой эта часть повторяется?

вычислим чему равно произведение [math](2+1)(2^{2}+1)(2^{4}+1)cdots (2^{2^n}+1)=?[/math] Думаете это сложно и нужен калькулятор? Внимание на экран [math]2+1=3=4-1=2^2-1[/math] и [math](a+b)(a-b)=a^2-b^2[/math] тогда
[math](2+1)(2^{2}+1)(2^{4}+1)cdots (2^{2^n}+1)=[/math]
[math]=(2^{2}-1)(2^{2}+1)(2^{4}+1)cdots (2^{2^{n}}+1)=[/math]
[math]=(2^{4}-1)(2^{4}+1)cdots (2^{2^{n}}+1)=cdots =[/math]
[math]=(2^{2^{n}}-1)(2^{2^{n}}+1)=2^{2^{n+1}}-1[/math]

А теперь умножим [math]overbrace{111cdots 11}^{n}=2^n-1[/math] на [math]2^m[/math] В результате получится
[math](2^n-1)cdot 2^m=2^{n+m}-2^m=underbrace{overbrace{11cdots 11}^{n}overbrace{000cdots 00}^{m}}_{n+m}[/math] ― [math](n+m)[/math]-разрядное двоичное число, в котором [math]n[/math] единиц и [math]m[/math] нулей.
В разделе «Алгоритм Содена» переводят двоичное число 1111110001₂ в десятичное 1009₁₀, но можно же сделать и вот так [math]1111110001_{2}=2^{10}-2^{4}+1=1024-16+1=1009_{10}[/math]

Целая часть от [math]underbrace{sqrt{111cdots 11}}_{2n}=underbrace{111cdots 11}_{n}[/math]

[math]11^2=3^2=9=1001[/math]
[math]111^2=7^2=49=110001[/math]
[math]11111^2=31^{2}=961=1111000001[/math]
[math](2^{n}-1)^2=2^{2n}-2cdot 2^{n}+1=2^{2n}-2^{n+1}+1[/math]
[math]{underbrace{11cdots 11}_n}^2=underbrace{11cdots 11}_{n-1}{overbrace{000cdots 00}^n} 1[/math]

Числа со знаком

Прямой (знаковеличинный) код

Рано или поздно возникает потребность представлять в двоичном коде отрицательные числа. А как в двоичной системе представить отрицательное число, если мы не можем использовать для это цели минус как в традиционной десятичной системе? Самое простое — отвести один разряд (скажем, старший) под знак числа, используя остальные для представления величины числа. Этот способ называется знаковеличинным или прямым кодом и соответствует обычной записи числа со знаком. Он используется при выводе чисел на индикацию, в АЦП (аналого-цифровых преобразователях), для представления вещественных и двоично-десятичных чисел. В такой кодировке появляются нули двух типов (+0 и -0)

Смещенный код

Второй способ представления числа со знаком — представление числа в виде смещенного кода. Для получения смещенного кода какого-либо числа, нужно к этому числу, представленному в прямом коде, прибавить половину наибольшего возможного числа. Благодаря этой операции последовательность всех чисел, начиная со старшего отрицательного и заканчивая старшим положительным, будет представлять из себя простую двоичную прогрессию. Информацию о знаке числа здесь также несет старший разряд, нуль становится единственным. Смещенный код используется в АЦП и ЦАП (цифро-аналоговых преобразователях), в смещенном коде представляется степень вещественного числа.

Дополнительный код

При выполнении операций над целыми числами используется представление чисел в форме «дополнения до двух», или в «дополнительном коде». Положительные числа в такой системе записываются как двоичные без знака, а отрицательные выражаются таким числом, которое, если добавить к положительному числу той же величины, даст в результате ноль.

Таблица #4. 4-разрядные двоичные числа, представленные в трех системах

деся-
тичное
представ-
ление
числа двоичное представление числа

прямой
код смещен-
ный
код дополни-
тельный
код

+7

0111

1111

0111

+6

0110

1110

0110

+5

0101

1101

0101

+4

0100

1100

0100

+3

0011

1011

0011

+2

0010

1010

0010

+1

0001

1001

0001

0

0000

1000

0000

-0

1000

—

—

-1

1001

0111

1111

-2

1010

0110

1110

-3

1011

0101

1101

-4

1100

0100

1100

-5

1101

0011

1011

-6

1110

0010

1010

-7

1111

0001

1001

-8

—

0000

1000

деся- тичное представ- ление числа	двоичное представление числа
прямой код	смещен- ный код	дополни- тельный код
+7	0111	1111	0111
+6	0110	1110	0110
+5	0101	1101	0101
+4	0100	1100	0100
+3	0011	1011	0011
+2	0010	1010	0010
+1	0001	1001	0001
0	0000	1000	0000
-0	1000	—	—
-1	1001	0111	1111
-2	1010	0110	1110
-3	1011	0101	1101
-4	1100	0100	1100
-5	1101	0011	1011
-6	1110	0010	1010
-7	1111	0001	1001
-8	—	0000	1000

Вложения:

Последнее редактирование: 30 июн 2019

Mikl___

Mikl___

Супермодератор
Команда форума

Публикаций:: 14

Регистрация:: 25 июн 2008

Сообщения:: 3.581

В таблице #4 видно, числа в дополнительном коде отличаются от чисел в смещенном коде инверсным значением старшего значащего разряда (СЗР). Точно также, как и при других формах представления, СЗР несет информацию о знаке. Здесь имеется только один ноль, представляемый нулевыми состояниями всех разрядов.

Более подробно о дополнительном коде

По определению, для каждого натурального числа [math]n[/math] существует одно и только одно отрицательное число, обозначаемое [math]-n[/math], которое дополняет [math]n[/math] до нуля:

[math]n + (-n) = 0.[/math]

Найдем такое 4-битное число, которое при сложении с числом 5 (0101) дало бы нам ноль, переносом в 5-й бит мы пренебрегаем.

Теперь самостоятельно заполните таблицу #5
Таблица #5

hex-
число двоичное число

n -n

0 0000

1 0001

2 0010

3 0011

4 0100

5 0101 1011

6 0110

7 0111

8 1000

9 1001

A 1010

B 1011 0101

C 1100

D 1101

E 1110

F 1111

Так как [math]n = -(-n)[/math], поэтому, таблицу #5 можно сократить в два раза
Таблица #6

число n число —n

Hex bin Hex bin

0

0000

0

0000

1

0001

F

1111

2

0010

E

1110

3

0011

D

1101

4

0100

C

1100

5

0101

B

1011

6

0110

A

1010

7

0111

9

1001

8

1000

8
1000

При этом оказалось, что числа 0 и 8 являются сами для себя отрицательными числами. Если не рассматривать числа 0 и 8, числа в левой половине таблицы объединяет то, что самый старший (четвертый) бит у них равен 0, а у чисел в правой половине самый старший бит равен 1. Пусть самый старший бит считается знаковым. Если он равен 0, число будем считать положительным, если 1 — отрицательным. Мы только что изобрели способ представления положительных и отрицательных чисел в двоичной системе, так называемый «код дополнения до двух», или «дополнительный код». При этом, число 0 может быть только положительным, а четырехбитовое число 8 — только отрицательным.
Таблица #7

Положительное
4-битное число n Отрицательное
4-битное число —n

десятич-
ное hex bin десятич-
ное hex bin

+0

0

0000

-0

—

—

+1

1

0001

-1

F

1111

+2

2

0010

-2

E

1110

+3

3

0011

-3

D

1101

+4

4

0100

-4

C

1100

+5

5

0101

-5

B

1011

+6

6

0110

-6

A

1010

+7

7

0111

-7

9

1001

+8

—

—

-8

8
1000

Компьютер различает целые числа без знака (неотрицательные) и целые числа со знаком. Положительные и отрицательные числа расположены как бы в «кольце». Если вычитать в цикле из байтовой переменной на каждом шаге единицу, то, когда значение переменной достигнет нуля, следующим вычитанием мы получим в переменной значение FF₁₆=255₁₀ — максимальное беззнаковое число, которое может быть записано в байт, и одновременно значение -1, если рассматривать его, как число со знаком. При продолжающемся вычитании мы проходим весь диапазон отрицательных чисел и достигаем минимального значения, которое может быть записано в байт — 80₁₆=-128₁₀. На следующем шаге мы получаем значение 7F₁₆=+127₁₀ — максимальное знаковое число, которое может быть записано в байт. Если продолжить вычитание — мы опять достигаем значение нуля.

Таблица #8. Дополнительный код

дополни-
тельный
двоичный
код Hex число со
знаком число без
знака

0000 0000

0

0

0

0000 0001

1

1

1

0000 0010

2

2

2

. . . .

0111 1111

7F

127

127

1000 0000

80

-128

128

1000 0001

81

-127

129

. . . .

1111 1110

FE

-2

254

1111 1111

FF

-1

255

Для целых чисел со знаком положительное число записывается в прямом коде (как есть). Отрицательное — в дополнительном коде. Преобразовать положительное число в отрицательное можно пятью способами.
Способ первый — классический:

взять число в прямом коде, преобразовать его в инверсный код. Для этого все нули этого числа необходимо заменить на единицы, а единицы на нули.

К числу в инверсном коде добавить 1.

На рисунке пример преобразования числа +7 в –7.

Способ второй — взять число, отнять от него единицу, преобразовать в двоичный вид, заменить нули на единицы, а единицы на нули. 7-1 = 6 = 0000 0110 → 1111 1001 = -7
Способ третий — быстрый: двигаемся справа налево и пропускаем нули до первой единицы, после нее заменяем единицы на нули, а нули на единицы. 20 = 0001 0100 → 1110 1100 = -20
Способ четвертый — практический: чтобы получить n-разрядное отрицательное число возьмем число [math]2^N[/math](для байта [math]2^8 = 256[/math], для слова [math]2^{16}=65536[/math], для двойного слова [math]2^{32}=4294967296[/math], для учетверенного cлова [math]2^{64}=18446744073709551616[/math]) и отнимем от него наше число, получившееся число преобразуем в двоичный или hex-код:
256 – 7 = 249 = 1111 1001 = F9 = – 7.

Способ пятый — студенческий: щелкаем по клавише «Пуск», открываем стандартные приложения, запускаем калькулятор в режиме «Программист», теперь щелкаем по клавише 7 и «+/–» на экранчике калькулятора появится –7. А теперь жмем на клавишу F8 или мышкой по переключателю с надписью «Bin». Что мы видим на экране калькулятора? Число 1111111111111111111111111111111111111111111111111111111111111001. Многовато, на экране — учетверенное слово. Жмем на F4 или мышью по переключателю с надписью «1 байт». Наше число приобрело нормальный вид 11111001b.
На самом деле, нет необходимости пересчитывать отрицательные числа. Вы пишете –7, а транслятор автоматически подставит туда, где нужно число 11111001b.
Если мы пренебрегаем знаковым разрядом, то диапазон чисел увеличивается в 2 раза: [math]2^7 = 128[/math]; [math]2^8 = 256[/math]

hex- число	двоичное число
n	-n
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101	1011
6	0110
7	0111
8	1000
9	1001
A	1010
B	1011	0101
C	1100
D	1101
E	1110
F	1111

число n	число —n
Hex	bin	Hex	bin
0	0000	0	0000
1	0001	F	1111
2	0010	E	1110
3	0011	D	1101
4	0100	C	1100
5	0101	B	1011
6	0110	A	1010
7	0111	9	1001
8	1000	8	1000

Положительное 4-битное число n	Отрицательное 4-битное число —n
десятич- ное	hex	bin	десятич- ное	hex	bin
+0	0	0000	-0	—	—
+1	1	0001	-1	F	1111
+2	2	0010	-2	E	1110
+3	3	0011	-3	D	1101
+4	4	0100	-4	C	1100
+5	5	0101	-5	B	1011
+6	6	0110	-6	A	1010
+7	7	0111	-7	9	1001
+8	—	—	-8	8	1000

дополни- тельный двоичный код	Hex	число со знаком	число без знака
0000 0000	0	0	0
0000 0001	1	1	1
0000 0010	2	2	2
. . . .
0111 1111	7F	127	127
1000 0000	80	-128	128
1000 0001	81	-127	129
. . . .
1111 1110	FE	-2	254
1111 1111	FF	-1	255

Вложения:

0.jpg

Размер файла:

22,6 КБ

Просмотров:

3.521

Последнее редактирование: 19 фев 2023

Mikl___

Mikl___

Супермодератор
Команда форума

Публикаций:: 14

Регистрация:: 25 июн 2008

Сообщения:: 3.581

Представление чисел с плавающей запятой

У десятичных чисел каждая позиция числа соответствует степени числа 10, то есть число [math]1234,56=1cdot 10^3+2cdot 10^2+3cdot 10^1+4cdot 10^0+5cdot 10^{-1}+6cdot 10^{-2}[/math].
Запятая показывает границу между позицией, соответствующей [math]10^0[/math], и дробной частью. В дробной части позиции числа также являются степенями числа 10, но эти степени теперь отрицательные. Дробные двоичные числа записываются аналогично дробным десятичным, но основание системы счисления здесь 2, а не 10. Например,[math]1,101_2=1+frac{1}{2}+frac{1}{8}=1frac{5}{8}=1,625[/math]
Чтобы получить эквивалент целого числа в двоичной системе, мы использовали последовательное деление на 2. Чтобы получить эквивалент десятичной дроби, используем обратную операцию — последовательное умножение на 2.
Для перевода десятичной дроби в двоичную систему можно использовать четыре способа, а уж который из них Вам покажется более удобным — выбирайте сами.
Способ первый. Дробную часть числа последовательно умножают на 2 пока либо дробная часть не станет равной нулю, либо не будет получено необходимое количество разрядов. Целые значения, получаемые при умножении, будут являться эквивалентом десятичной дроби в двоичной системе. Посмотрите конкретный пример

Способ второй. Умножать на два 8 раз чтобы получить 8-двоичных разрядов дробной части долго и утомительно. А давайте 0,14159 умножим сразу на [math]2^8=256[/math], что получится? [math]0,14159times 256=36,2470410=100100_2[/math]. 100100 это шесть разрядов, а если добавить 2 нуля слева? 00100100 ничего не напоминает? Добавим «0,» и «0,00100100» двоичный эквивалент числа 0,14159. Нужно получить 16 разрядов после запятой? Смело умножайте на [math]2^{16}=65536[/math], переводите в двоичный вид и не забудьте добавить недостающие нули слева.
Способ третий. Любое дробное двоичное число можно представить как

[math]x_1cdot 0,5 + x_2cdot 0,25 + x_3cdot 0,125 +cdots[/math]

где [math]x_1, x_2,cdots x_n[/math] — нули или единицы, то есть [math]0,1_{10}=0,0001100_2[/math].
Способ четвертый. Переведем в двоичную систему, например, число [math]0,27=frac{27}{100}[/math]. Ближайшая к 100 степень двойки [math]2^7=128[/math].

[math]frac{27}{100}timesfrac{1,28}{1,28}=frac{34,56}{128}=frac{32+2+1}{128}=frac{1}{4}+frac{1}{64}+frac{1}{128}=2^{-2}+2^{-6}+2^{-7}=[/math]
[math]=0,01+0,000001+0,0000001=0,0100011_2[/math]

Перевод десятичного дробного числа 0,406 в шестнадцатеричную систему делается аналогично переводу к двоичному виду:

[math]0,616times 16=9,856[/math] и так далее, то есть [math]0,406_{10}=0,67EF9…_{16}[/math] .
Для перевода вещественного целого числа в двоичную или шестнадцатеричную систему необходимо целую и дробную часть перевести по отдельности в двоичную или шестнадцатеричную систему, а затем соединить их. Например, число [math]pi[/math] равное [math]3,14159[/math] должно выглядеть вот так [math]11,00100100_2[/math], или так [math]3,243F_{16}[/math].
Существует два способа записи вещественных чисел:
Первый способ — целая часть числа отделяется от дробной символом запятой, расположенной между конкретными разрядами в фиксированной позиции. Такой способ записи называют представлением вещественных чисел с фиксированной запятой. Возьмем 16 разрядное число и отведем под целую часть числа 8 разрядов, а под дробную 8 разрядов, тогда максимально большое число, которое можно записать таким способом:[math]11111111,11111111_2=255,99609375 approx 256[/math], а минимальное возможное число — [math]00000000,00000001_2=frac{1}{256} approx 0,00390625[/math]. Запомните эти числа.
Второй способ применяется в астрономии, физике, химии, математике для записи очень больших либо очень маленьких чисел. Например, скорость света в вакууме составляет около [math]300000000[/math] м/с, а гравитационная постоянная примерно равна [math]0,0000000000667[/math] Нм²/кг². Для удобства работы с такими числами используют так называемую экспоненциальную форму записи. Вместо [math]300000000[/math] пишут [math]3cdot 10^8[/math], а вместо [math]0,0000000000667[/math] — [math]6,67cdot 10^{-11}[/math]. Любое число представляется в виде [math]pm C,Mcdot R^P[/math], где [math]C[/math] — целая часть числа, дробную часть числа представляющую значащие разряды — [math]M[/math], называют мантиссой. [math]R[/math] — основание системы счисления. [math]P[/math] — показатель степени, определяющий на сколько разрядов вправо или влево необходимо переместить запятую в мантиссе, называется порядком числа. Число [math]C[/math] должно быть [math]1le C < R[/math]. Такой способ записи называют представлением вещественных чисел с плавающей запятой. Как и в первом случае возьмем 16-разрядное число. Под мантиссу отведем 8 разрядов и 8 разрядов под порядок числа (из 8 разрядов 1 разряд отводится под знак и 7 разрядов под число), в этом случае максимальновозможное число [math]2^{127}approx 10^{38}[/math], а минимальновозможное — [math]2^{–127}approx 10^{–38}[/math]. Сравните их с числами полученными в первом случае
Для представления в компьютере дробного числа первый разряд числа считается знаковым и обозначает знак мантиссы. За ним следует мантисса (число со значением больше или равным 1 и меньшим 2) и порядок (степень числа 2). Представление чисел в виде мантиссы и порядка позволяют сводить умножение и деление чисел к сложению и вычитанию показателей степеней, а возведение в степень и извлечение корня — к умножению и делению на показатель степени, что упрощает и сокращает сложные вычисления.
Вещественные числа в памяти компьютера хранятся в нормализованном виде, то есть оно обязательно должно иметь следующий вид:

[math](-1)^Stimes 1,Mtimes 2^P[/math],

где значение [math]S[/math] определяет знак ([math]S=0[/math] — число положительное, [math]S=1[/math] — отрицательное), [math]M[/math] — двоичная мантисса числа, [math]P[/math] — порядок двоичного числа.
Из-за того, что целая часть вещественного числа в двоичной системе всегда равна 1, его, для увеличения разрядности дробной части, предпочитают «хранить в уме».
Для упрощения вычислений значение порядка хранят не в дополнительном коде (то есть не в виде целого со знаком), а в смещенном коде в виде суммы с некоторым числом, это позволяет облегчить сравнение вещественных чисел — в большинстве случаев достаточно сравнить их экспоненты.
Обратите внимание, что в смещенном порядке у отрицательных чисел и нуля в двоичном представлении старший разряд нулевой. В смещенном коде число суммируется с константой, которая для N-битного кода равна [math]2^{N-1}-1[/math].

Десятичное
значение Смещенный код

8-битный 11-битный 15-битный

-16383

—

—

0000h

-1023

—

000h

3C00h

-127

00h

380h

3F80h

. . .

-1

7Eh

3FEh

3FFEh

0

7Fh

3FFh

3FFFh

1

80h

400h

4000h

. . .

128

0FFh

47Fh

407Fh

1024

—

7FFh

43FFh

16384

—

—

7FFFh

Микропроцессоры семейства x86 х64 могут работать с 32/64/80-битными вещественными числами (одинарная/двойная/повышенная точность), а также со 128-битными, состоящими из четырех упакованных вещественных чисел одинарной точности.

Коли-
чество
бит Тип Поле
знака Поле
порядка Константа Поле
мантиссы Диапазон принимаемых значений

32

REAL4

1 бит

8 бит

2⁷-1=127

23 бита
От [math]pm 1,18cdot 10^{-38}[/math] до [math]pm 3,4cdot 10^{38}[/math]

64

REAL8

1 бит

11 бит

2¹⁰-1=1023

52 бита
От [math]pm 2,23cdot 10^{-308}[/math] до [math]pm 1,79cdot 10^{308}[/math]

80

REAL10

1 бит

15 бит

2¹⁴-1=16383

64 бита
От [math]pm 3,37cdot 10^{-4932}[/math] до [math]pm 1,18cdot 10^{4932}[/math]

Число 193,75 в формате вещественного числа, занимающего два слова:

[math]193,75to 4341C000_{16}[/math]

[math]193,75>0 to[/math] знак=0
[math]log_{2}(193,75)=7,598053[/math]
степень [math]7+127=134=10000110_2[/math]
разрядов в мантиссе — степень [math]23-7=16[/math]
мантисса [math](193,75-2^{7})cdot 2^{16}=66,75cdot 2^{16}=66,75cdot 65536=4374528=10000101100000000000000_2[/math]

Преобразуем вид число в бинарное представление:

01000011010000011100000000000000 Знак числа 0=«+» 1=«—»

01000011010000011100000000000000 Порядок 86h=+7 в смещенном коде [math]10000110_2=134_{10}=7+127[/math]

01000011010000011100000000000000 мантисса числа=[math](1),1000001110000_2[/math]

Рис. Форматы представления вещественных чисел

Десятичное значение	Смещенный код
8-битный	11-битный	15-битный
-16383	—	—	0000h
-1023	—	000h	3C00h
-127	00h	380h	3F80h
. . .
-1	7Eh	3FEh	3FFEh
0	7Fh	3FFh	3FFFh
1	80h	400h	4000h
. . .
128	0FFh	47Fh	407Fh
1024	—	7FFh	43FFh
16384	—	—	7FFFh

Коли- чество бит	Тип	Поле знака	Поле порядка	Константа	Поле мантиссы	Диапазон принимаемых значений
32	REAL4	1 бит	8 бит	2⁷-1=127	23 бита	От [math]pm 1,18cdot 10^{-38}[/math] до [math]pm 3,4cdot 10^{38}[/math]
64	REAL8	1 бит	11 бит	2¹⁰-1=1023	52 бита	От [math]pm 2,23cdot 10^{-308}[/math] до [math]pm 1,79cdot 10^{308}[/math]
80	REAL10	1 бит	15 бит	2¹⁴-1=16383	64 бита	От [math]pm 3,37cdot 10^{-4932}[/math] до [math]pm 1,18cdot 10^{4932}[/math]

Вложения:

Mikl___

Mikl___

Супермодератор
Команда форума

Публикаций:: 14

Регистрация:: 25 июн 2008

Сообщения:: 3.581

Запись одного и того же числа в разных представлениях, естественно, будет отличаться. Число 193,75 может быть представлено как:

Коли-
чество
бит Тип шестнадцатеричное представление числа 193,75

32 REAL4 4341C000h

64 REAL8 4068380000000000h

80 REAL10 4006C1C0000000000000h

Преобразуем число 4068380000000000h в бинарное представление:

0100.0000.0110.1000.0011.1000.0000.0000.0000.0000.0000.0…0.0000.0000.0000.0000

Знак числа 0=«+»

010000000110100000111000000000000000000000000…00000000000000000

Порядок =+7 [math]10000000110_2=1030_{10}=7+1023[/math]

010000000110100000111000000000000000000000000…00000000000000000

мантисса числа=(1),1000001110000000000000000000000000…000000000000b

Преобразуем число 4006C1C0000000000000h в бинарное представление:

0100000000000110110000011100000000000000000000000000000000…0000

Знак числа 0=«+»

0100000000000110110000011100000000000000000000000000000000…0000

Порядок =+7 [math]100000001100000_2=16480_{10}=7+16383[/math]

0100000000000110110000011100000000000000000000000000000000…0000

мантисса числа=1,10000011100000000000000000000000000000000…0000b

Типы REAL4, REAL8 и REAL10 соответствуют стандартным вещественным типам в Pascal/Delphi и C/C++

Asm Pascal/Delphi C/C++ Формула

REAL4 Single float [math](-1)^{S}times(1+mtimes 2^{-23})times 2^{P-127}[/math]

REAL8 Double double [math](-1)^{S}times(1+mtimes 2^{-52})times 2^{P-1023}[/math]

REAL10 Extended long double [math](-1)^{S}times mtimes 2^{P-16446}[/math]

Первые два типа (REAL4 и REAL8) являются «упакованными», а REAL10 — «неупакованным» типом, в нем старший, всегда единичный, бит нормализованной мантиссы хранится в явном виде. Все вычисления внутри FPU происходят после автоматического преобразования типов REAL4 и REAL8 в REAL10.
Для записи вещественного числа в программе пересчет вещественного десятичного числа из десятичной системы в hex или двоичную самому делать не обязательно, просто запишите число, используя в качестве разделителя точку вместо запятой:

pi dt 3.1415926535897932384626433832795

А компилятор сам подставит

32-битный эквивалент в случае с директивой dd

64-битный для директивы dq

80-битный для директивы dt

Перевожу 193,75

в REAL4 (мантисса 23 бита, степень смещается на 127)
вычисляем степень [math]log_2(193{,}75)=7{,}598053[/math] округляем в меньшую сторону 7. [math]p=127+7=134=86_{16}[/math]
(193,75-2⁷)x 2^23-7=(193,75-128)x 65536=4308992=41C000₁₆
[math]underbrace{0.100}_{4}underbrace{0 011}_{3}underbrace{0.100}_{4}underbrace{0001}_{1}underbrace{1100}_{C}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}[/math]

в REAL8 (мантисса 52 бита, степень смещается на 1023)
[math]p=1023+7=1030=406_{16}[/math]
(193,75-2⁷)x 2^52-7=2313372464840704=8380000000000₁₆
[math]underbrace{0.100}_{4}underbrace{0 000}_{0}underbrace{0110.}_{6}underbrace{1000}_{8}underbrace{0011}_{3}underbrace{1000}_{8}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}[/math]

в REAL10 (мантисса 63 бита, степень смещается на 16383)
[math]p=16383+7=16390=4006_{16}[/math]
193,75 x 2^63-7=13961158844848537600=C1C0000000000000₁₆
[math]underbrace{0.100}_{4}underbrace{0 000}_{0}underbrace{0000}_{0}underbrace{0110.}_{6}underbrace{1{,}100}_{С}underbrace{0001}_{1}underbrace{1100}_{С}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}underbrace{0000}_{0}[/math]

Задание #12: Теперь читателю предлагается потренироваться в переводе чисел. Пред вами два простых примера: 0.125 и 0.625. Можно усложнить их: 23.125 и 456.625. Проверьте свои ответы, записав результат в переменную типа dword и посмотрите под отладчиком число в стеке FPU.

Asm	Pascal/Delphi	C/C++	Формула
REAL4	Single	float	[math](-1)^{S}times(1+mtimes 2^{-23})times 2^{P-127}[/math]
REAL8	Double	double	[math](-1)^{S}times(1+mtimes 2^{-52})times 2^{P-1023}[/math]
REAL10	Extended	long double	[math](-1)^{S}times mtimes 2^{P-16446}[/math]

Последнее редактирование: 19 июн 2019

Mikl___

Mikl___

Супермодератор
Команда форума

Публикаций:: 14

Регистрация:: 25 июн 2008

Сообщения:: 3.581

Специальные численные значения

Знак Порядок
(79-64 биты) Мантисса
(63-0 биты) Название числа

0
000…00000000 000…00000000000
+0

1
111…11111111 111…11111111111
-0

0
111…11111111 000…00000000000
[math]+infty[/math] (+бесконечность)

1
111…11111111 000…00000000000
[math]-infty[/math] (-бесконечность)

[math]x[/math]
000…00000000 [math]xxx…xxxxxxxx[/math] Денормализованные числа, используются для работы
с очень маленькими числами от [math]pm 10^{-4932}[/math] до [math]pm 10^{-16445}[/math]

[math]x[/math]
111…11111111 10[math]x…xxxxxxxx[/math] Нечисло типа SNAN (Signal Non A Number). Среди [math]x[/math] есть
единицы. FPU реагирует на появление SNAN возбуждением
исключения недействительной операции

Несмотря на большой диапазон вещественных значений, представимых в регистрах данных FPU, значения, например, [math]+infty[/math] и [math]-infty[/math] находятся за пределами этого диапазона. Для того, чтобы иметь возможность реагировать на некоторые вычислительные ситуации, которые могут возникнуть в результате математических операций в блоке FPU, предусмотрены специальные комбинации битов, называемые специальными численными значениями. Над специальными численными значениями можно выполнять некоторые операции. Программист может и сам кодировать специальные численные значения директивой DT (х – любое значение бита).
Если в результате вычислений мантисса и порядок равны нулю, то, несмотря на скрытую единицу в целой части числа REAL4/8, все число полагается равным нулю. Любой конечный результат операции FPU, который из-за ограниченности поля порядка не может быть представлен в 23/52/64 разрядах для REAL4/8/10, соответственно вызывает особый случай некорректности представления числа.

Знак	Порядок (79-64 биты)	Мантисса (63-0 биты)	Название числа
0	000…00000000	000…00000000000	+0
1	111…11111111	111…11111111111	-0
0	111…11111111	000…00000000000	[math]+infty[/math] (+бесконечность)
1	111…11111111	000…00000000000	[math]-infty[/math] (-бесконечность)
[math]x[/math]	000…00000000	[math]xxx…xxxxxxxx[/math]	Денормализованные числа, используются для работы с очень маленькими числами от [math]pm 10^{-4932}[/math] до [math]pm 10^{-16445}[/math]
[math]x[/math]	111…11111111	10[math]x…xxxxxxxx[/math]	Нечисло типа SNAN (Signal Non A Number). Среди [math]x[/math] есть единицы. FPU реагирует на появление SNAN возбуждением исключения недействительной операции

Последнее редактирование: 19 фев 2023

Mikl___

Mikl___

Супермодератор
Команда форума

Публикаций:: 14

Регистрация:: 25 июн 2008

Сообщения:: 3.581

Как быстро перевести вещественное число в десятичном виде в REAL4, REAL8, REAL10

Коли-чество
бит Тип Поле
знака Поле
порядка Константа Целая
часть Поле
мантиссы Диапазон принимаемых значений

32

REAL4

1 бит

8 бит

[math]2^{8-1}-1=127[/math]

скрыта

23 бита
От ± 1,18×10^-38 до 3,4×10³⁸

64

REAL8

1 бит

11 бит

[math]2^{11-1}-1=1023[/math]

скрыта

52 бита
От ± 2,23×10^-308 до 1,79×10³⁰⁸

80

REAL10

1 бит

15 бит

[math]2^{15-1}-1= 16383[/math]

явно
указана

63 бита
От ± 3,37×10^-4932 до 1,18×10⁴⁹³²

Представить число -240,9375 в формате REAL4

-240,9375 < 0 → Знак=1

log₂(240,9375)=7,912515145→ степень =7
степень в смещенном виде 7+127=134=1000.0110b

23 разряда (мантисса) — 7 (степень) = 16

мантисса
2¹⁶×(240,9375-2⁷)=7401472=70F000h=111.0000.1111.0000.0000.0000b

знак степень мантисса

bin
1

100

0011

0

111

0000

1111

0000

0000

0000

hex
C

3

7

0

F

0

0

0

Представить число 15,92 в формате REAL8

15,92>0 → Знак=0

log₂(15,92)=3,992768431 → степень = 3
степень в смещенном виде 3+1023=1026=100.0000.0010b

52 разряда (мантисса) — 3 (степень) = 49

мантисса
2⁴⁹×(15,92-2³)=2⁴⁹×7,92=4458563631096791,04~4458563631096791=FD70A3D70A3D7h=
=1111.1101.0111.0000.1010.0011.1101.0111.0000.1010.0011.1101.0111b

15,92=402FD70A3D70A3D7

знак степень мантисса

bin
0

100

0000

0010

1111

1101

0111

0000

1010

0011

1101

0111

0000

1010

0011

1101

0111

hex
4

0

2

F

D

7

0

A

3

D

7

0

A

3

D

7

Представить число 6,1429 в формате REAL10

6,1429>0 → Знак=0

log₂(6,1429)=2,61892 → степень = 2
степень в смещенном виде 2+16383=16385=100.0000.0000.0001b

63 разряда (мантисса) — 2 (степень) = 61

мантисса
2⁶¹×6,1429=14164563021298800577,7408~14164563021298800578=C492A305532617C2h=
=1100.0100.1001.0010.1010.0011.0000.0101.0101.0011.0010.0110.0001.0111.1100.0010b

6,1429=4001C492A305532617C2

знак степень целая
часть мантисса

bin
0

100

0000

0000

0001

1

100

0100

1001

0010

1010

0011

0000

0101

0101

0011

0010

0110

0001

0111

1100

0010

hex
4

0

0

1

C

4

9

2

A

3

0

5

5

3

2

6

1

7

C

2

Какому числу типа float соответствует 8027B2A6h=1000.0000.0010.0111.1011.0010.1010.0110b ?

знак степень мантисса

1 000.0000.0 010.0111.1011.0010.1010.0110

—
0

2601638

степень нулевая, значит число денормализованное, то есть целая часть равна нулю
Какому числу типа double соответствует запись C06E4D1000000000?

знак степень мантисса

bin
1

100

0000

0110

1110

0100

1101

0001

0000

0000

0000

0000

0000

0000

0000

0000

0000

hex
C

0

6

E

4

D

1

0

0

0

0

0

0

0

0

0

вычисляем знак
знак=1 число <0

порядок 10000000110₂=1030₁₀
вычисляем степень 1030-1023=7

обрабатываем мантиссу
52(разрядов в мантиссе)-7(степень)=45
1110010011010001000000000000000000000000000000000000₂=4025380788764672₁₀
4025380788764672/2⁴⁵=4025380788764672/35184372088832=114,408203125
114,408203125+2⁷=114,408203125+128=242,408203125

учтем, что число отрицательное
результат: -242,408203125

Из шестнадцатеричного представления получить десятичное число
дана шестнадцатеричная свертка 2F16F100₁₆=0010.1111.0001.0110.1111.0001.0000.0000₂
знак.порядок.мантисса=0.01011110.00101101111000100000000
знак=0 —> число положительное
порядок 01011110₂=94₁₀ степень 94-127=-33
мантисса 1.00101101111000100000000₂=9892096₁₀
число (9892096*2^-23)*2^-33= 9892096*2^-56=9892096/72057594037927936=
=+1,3728040926253015641123056411743*10^-10
или вот так
мантисса 00101101111000100000000₂=1503488₁₀
число (1503488*2^-23+1)*2^-33=(1503488+2²³)*2^-23-33=(1503488+8388608)/72057594037927936=+1,3728040926253015641123056411743*10^-10
Формула для расчета денормализованных чисел

REAL4 (-1)^знак ×2^-149× мантисса

REAL8 (-1)^знак ×2^-1074× мантисса

REAL10 (-1)^знак ×2^-16445× мантисса

[math]F=(-1)^{sign}cdot 2^{-149} cdot mantiss =-1 cdot 2^{-149} cdot 01001111011001010100110=[/math]
[math]=-2601638cdot 1,4012984643248170709237295832899cdot 10^{-45} =[/math]
[math]=-3,6456713341290884347638699856112cdot 10^{-39}[/math]
FPU ХАКИ
FPU Hacks, когда вычисления делают приближенно через integer типы. (Естественно это либо через память, либо если FP регистры позволяют делать integer операции над ними.
Быстрая конвертация в Integer

int FastFloatToInt(float f)

return (*((int*) &f) — 0x4ac00000) >> 1;

Быстрый квадратный корень
Ошибка при вычислении не превышает 5%

Approximations that depend on the floating point representation

Вещественное число представляется в формате [math]mtimes 2^{p}[/math] Квадратный корень равен [math]sqrt {m}times 2^{(frac{p}{2})}[/math] аналогичные формулы применимы для кубических корней и логарифмов. На первый взгляд, это не упрощает вычисление квадратного корня, но предположим, что требуется только приближение: тогда просто [math]2^{(frac{p}{2})} [/math] хорошо на порядок. Некоторые степени [math]p[/math] будут нечетными, поэтому при вычисления квадратного корня например от числа 3141.59 = 3.14159×10³ вместо того, чтобы иметь дело с дробными степенями основания, умножаем мантиссу на основание и вычитаем единицу от степени, чтобы сделать степень четной. Скорректированное представление станет эквивалентом [math]sqrt{31.4159×10^{2}} = sqrt{31.4159}times 10^{1}[/math].
Если берется целая часть скорректированной мантиссы, могут быть только значения от 1 до 99, и их можно использовать в качестве индекса в таблице из 99 предварительно вычисленных квадратных корней для завершения оценки.

[math]a[/math] ближайший корень [math]sqrt{a}[/math]

от 1 до 2.5 1(=1²) 1

от 2.5 до 6.5 4(=2²) 2

от 6.5 до 12.5 9(=3²) 3

от 12.5 до 20.5 16(=4²) 4

от 20.5 до 30.5 25(=5²) 5

от 30.5 до 42.5 36(=6²) 6

от 42.5 до 56.5 49(=7²) 7

от 56.5 до 72.5 64(=8²) 8

от 72.5 до 90.5 81(=9²) 9

от 90.5 до 100 100(=10²) 10

Для компьютера с основанием шестнадцать потребуется таблица большего размера, но для компьютера с основанием два потребуются только три записи: возможные биты целой части скорректированной мантиссы равны 01 (степень даже при отсутствии сдвига, помня, что нормализованная число с плавающей запятой всегда имеет ненулевую старшую цифру) или, если степень была нечетной, 10 или 11, это первые два бита исходной мантиссы. Таким образом, 6,25 = 110,01 в двоичном формате, нормализованное до 1,1001 × 2² четной степени, так что парные биты мантиссы равны 01, в то время как 0,625 = 0,101 в двоичной системе нормализуется до 1,01 × 2^-1 нечетной степени, поэтому корректировка составляет 10,1 × 2^-2, а парные биты равны 10. Обратите внимание, что бит младшего разряда мощности отражается эхом в бите старшего разряда попарной мантиссы. У четной мощности бит младшего разряда равен нулю, а скорректированная мантисса начинается с 0, тогда как для нечетной мощности этот бит равен единице, а скорректированная мантисса начинается с 1. Таким образом, когда число уменьшается вдвое, бит младшего разряда сдвигается, чтобы стать первым битом попарной мантиссы.
Таблица только с тремя записями может быть увеличена за счет включения дополнительных бит мантиссы. Однако с компьютерами, чем вычислять интерполяцию в таблицу, часто лучше найти более простые вычисления, дающие эквивалентные результаты. Теперь все зависит от точных деталей формата представления, а также от того, какие операции доступны для доступа и управления частями числа. Например, Fortran предлагает функцию EXPONENT (x) для получения степени. Усилия, затраченные на разработку хорошего начального приближения, должны окупаться за счет исключения дополнительных итераций процесса уточнения, которые потребовались бы для плохого приближения. Поскольку их немного (одна итерация требует деления, сложения и деления пополам), ограничение является серьезным.
Для компьютеров, использующих IEEE представление вещественного числа, методом Ньютона можно получить очень быстрое приближение к квадратному корню. Следующий алгоритм основан на том, что формат с вещественного числа по основанию два аппроксимируется логарифм по основанию 2. Это [math]log _{2}(mtimes 2^{p})=p+log _{2}(m)[/math]

Таким образом, для 32-разрядного числа с плавающей запятой одинарной точности в формате IEEE (где степень суммируется с числом 127), вы можете получить приблизительный логарифм, интерпретируя его двоичное представление как 32-битное целое число, масштабируя это от [math]2^{-23}[/math] и вычитание смещения 127, т. е. [math]x_{text{int}}cdot 2^{-23}-127approx log _{2}(x)[/math].
Например, 1.0 в шестнадцатеричном виде 0x3F800000 будет представлять [math]1065353216=127cdot 2^{23}[/math] если рассматривать как целое число. Используя формулу выше, вы получите [math]1065353216cdot 2^{-23}-127=0[/math], как и ожидалось от [math]log _{2}(1.0)[/math]. Аналогичным образом вы получаете 0,5 из 1,5 (0x3FC00000).

Чтобы получить квадратный корень, разделите логарифм на 2 и преобразуйте значение обратно. Следующая программа демонстрирует эту идею. Обратите внимание, что младшему разряду экспоненты намеренно разрешено распространяться в мантиссу. Один из способов обосновать шаги в этой программе — предположить, что [math]b[/math] — это смещение экспоненты, а [math]n[/math] — количество явно сохраненных бит в мантиссе, а затем показать, что
[math](((x_{text{int}}/2^{n}-b)/2)+b)cdot 2^{n}=(x_{text{int}}-2^{n})/2+((b+1)/2)cdot 2^{n}[/math].

/* Assumes that float is in the IEEE 754 single precision floating point format */

float sqrt_approx(float z)

union { float f; uint32_t i; } val = {z}; /* Convert type, preserving bit pattern */

* To justify the following code, prove that

* ((((val.i / 2^m) — b) / 2) + b) * 2^m = ((val.i — 2^m) / 2) + ((b + 1) / 2) * 2^m)

* m = number of mantissa bits

val.i -= 1 << 23; /* Subtract 2^m. */

val.i >>= 1; /* Divide by 2. */

val.i += 1 << 29; /* Add ((b + 1) / 2) * 2^m. */

return val.f; /* Interpret again as float */

Быстрый обратный квадратный корень
Если x > 0.25, то ошибка меньше 0.6%

float FastInvSqrt(float x)

int tmp = ((0x3f800000 << 1) +

0x3f800000 — *(long*)&x) >> 1;

float y = *(float *)&tmp;

return y * (1.47f — 0.47f * x * y * y);

Алгоритм принимает 32-битное число с плавающей запятой (одинарной точности в формате IEEE 754) в качестве исходных данных и производит над ним следующие операции:

Трактуя 32-битное дробное число как целое, провести операцию y₀ = 0x5F3759DF − (x >> 1), где >> — битовый сдвиг вправо. Результат снова трактовать как 32-битное дробное число.

Для уточнения можно провести одну итерацию метода Ньютона: y₁ = y₀(1,5 − 0,5x(y₀)²).

Корректная по меркам современного Си реализация, с учётом возможных оптимизаций и кроссплатформенности:

float Q_rsqrt( float number )

const float x2 = number * 0.5F;

const float threehalfs = 1.5F;

} conv = {number}; // member ‘f’ set to value of ‘number’.

conv.i = 0x5f3759df — ( conv.i >> 1 );

conv.f *= threehalfs — x2 * conv.f * conv.f;

Коли-чество бит	Тип	Поле знака	Поле порядка	Константа	Целая часть	Поле мантиссы	Диапазон принимаемых значений
32	REAL4	1 бит	8 бит	[math]2^{8-1}-1=127[/math]	скрыта	23 бита	От ± 1,18×10^-38 до 3,4×10³⁸
64	REAL8	1 бит	11 бит	[math]2^{11-1}-1=1023[/math]	скрыта	52 бита	От ± 2,23×10^-308 до 1,79×10³⁰⁸
80	REAL10	1 бит	15 бит	[math]2^{15-1}-1= 16383[/math]	явно указана	63 бита	От ± 3,37×10^-4932 до 1,18×10⁴⁹³²

	знак	степень	мантисса
bin	1	100	0011	0	111	0000	1111	0000	0000	0000
hex	C	3	7	0	F	0	0	0

	знак	степень	мантисса
bin	0	100	0000	0010	1111	1101	0111	0000	1010	0011	1101	0111	0000	1010	0011	1101	0111
hex	4	0	2	F	D	7	0	A	3	D	7	0	A	3	D	7

	знак	степень	целая часть	мантисса
bin	0	100	0000	0000	0001	1	100	0100	1001	0010	1010	0011	0000	0101	0101	0011	0010	0110	0001	0111	1100	0010
hex	4	0	0	1	C	4	9	2	A	3	0	5	5	3	2	6	1	7	C	2

знак	степень	мантисса
1	000.0000.0	010.0111.1011.0010.1010.0110
—	0	2601638

	знак	степень	мантисса
bin	1	100	0000	0110	1110	0100	1101	0001	0000	0000	0000	0000	0000	0000	0000	0000	0000
hex	C	0	6	E	4	D	1	0	0	0	0	0	0	0	0	0

REAL4	(-1)^знак ×2^-149× мантисса
REAL8	(-1)^знак ×2^-1074× мантисса
REAL10	(-1)^знак ×2^-16445× мантисса

[math]a[/math]	ближайший корень	[math]sqrt{a}[/math]
от 1 до 2.5	1(=1²)	1
от 2.5 до 6.5	4(=2²)	2
от 6.5 до 12.5	9(=3²)	3
от 12.5 до 20.5	16(=4²)	4
от 20.5 до 30.5	25(=5²)	5
от 30.5 до 42.5	36(=6²)	6
от 42.5 до 56.5	49(=7²)	7
от 56.5 до 72.5	64(=8²)	8
от 72.5 до 90.5	81(=9²)	9
от 90.5 до 100	100(=10²)	10

Вложения:

Последнее редактирование: 3 ноя 2021

rasstriga и Коцит нравится это.

Mikl___

Супермодератор
Команда форума

Публикаций:

14

Регистрация:

25 июн 2008

Сообщения:

3.581
Программа для перевода REAL10 в строку
$MagicLog2_32 equ 1292913987 ; = log(2) * 2^32

dp_1 equ 17 ; = decimal places minus 1

; ¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤

sub eax,edx ; make number positive

add byte ptr[edi+22],dl;if eax>=0 then «plus» else «minus»

mov edx,4294968 ;2^32/1000

mul edx ;extend first digit

shrd ecx,edx,8 ;digit 1 in ECX

mul esi ;extend second digit

shrd ecx,edx,8 ;digit 2 in ECX

mul esi ;extend third digit

shrd ecx,edx,8 ;digit 3 in ECX

mul esi ;extend fourth digit

shrd ecx,edx,8 ;digit 4 in ECX

or [edi+23],ecx ;make ASCII string

;———————————————

$maxcounter equ 2*$maxexp+1

;———————————————

shifttableX dd shift0X ; +0

;———————————————

dt @CatStr(<1.0e>,%-cntr)

;—————————————————-

; locals, buffer and args

pReal10 equ dword ptr [esp+16+buffer]

iExp equ dword ptr [esp—4];0+4=4

realx equ aExp—4*3 ;8+12=20

temp equ realx—4*3 ;20+12=32

; —————————

; if iExp=0 we use this realx

; —————————

mov edx, dword ptr [ecx+6]

add edx, edx; if CF=1 then negative

sbb eax, eax; if CF=0 then EAX = 0 else EAX = -1

mov [edi], eax; if CF=0 then EAX = 2C0020h else EAX = 2C002Dh

shr edx, 17 ; remove sign and if EDX = 0 go to _expzero

mov [realx+8], edx ; only exponent

jz _expzero ; if exponent = 0

_expnotzero: cmp edx, 7FFFh

jns _erro1 ; if integer = 0 and exponent <> 0 then ERROR

; ————————

; ————————

jz _iszero ; if edx = ebx = ecx = 0 is zero

;————————-

;————————-

fld realexp4931 ; st(0)=1.0e+4931

and [realx+8],7FFFh ; remove sign

;———————————-

; iExp= 4 * Exp because we multiply

; by 2^16 and divide by 2^14 only

;———————————-

mov eax, $MagicLog2_32 ; log(2)*2^32

jz short _getrealx ;edx = 0 ?

je _new ;integer multipication to 10

;————————————————

mov [temp+4],3F000000h ; 0.5

fistp [temp+8] ; round(z)

fisub [temp+8] ;z — round(z)

add [temp+8],3FFFh ; 2^round(z)

fmul ; 2^((mantissa)*round(z))

;———————————————————

_load: shl edx, 2 ; edx = edx*4

fld [PowerTable12+edx+edx*2] ; edx = edx*12

;———————————————————

@@: fmul ; X * 10^expscaleS = d.??????

;—————————————————————-

_getrealx: mov ecx, [realx+8]

sub ecx, 16382 ; 10=> exponent = 16386

_new: mov eax, ebx;[realx+0]

shift4X:: test eax, 60000000h ; 6= 0110B

; ————————

; correct exponent * 10^-1

; exponent = exponent + 1

; ————————

fld [PowerTable12+12] ; = 0.1

; fld st ; NEW get a copy

a6: shld edx, eax, 4 ;ecx=1 ebx+4

shld eax, ebx, 4 ;ecx=2 ebx+8

add ebx, 12;round ;ecx=4 ebx+12

; ——————————-

; fraction bits in EAX:EBX

; shift: EDX <- EAX <- EBX

; ——————————-

shift3X:: shld edx, eax, 3

; ——————————-

; fraction bits in EAX:EBX

; shift: EDX <- EAX <- EBX

; ——————————-

shift2X:: shld edx, eax, 2

; ——————————-

; fraction bits in EAX:EBX

; shift: EDX <- EAX <- EBX

; ——————————-

shift1X:: shld edx, eax, 1

;——————————————————-

; ——————————-

; fraction bits in EDX:EAX:EBX

; ——————————-

shift0X:: adc eax, 0 ; add carry to eax and edx

_aa: adc edx, ‘0’ ; ASCII convert

mov dword ptr [edi+21],’00+E’;ASCII chars for exponent

mov dword ptr [edi+25],’00’

mov [edi+1], dl ;first char in string

;————————————————

; —————————-

; ——————————

;————————————————

mov eax,ecx ; restore EAX

adc edx,‘0’ ; ASCII convert

mov [edi+k], dl ; next char in string

mov eax,ecx ; restore EAX

adc edx,‘0’ ; ASCII convert

mov [edi+k], dl ; last char in string

jz _exit ;if exponent=0 go to exit

_exit: mov edi,[esp+buffer] ;restore edi

mov esi,[esp+buffer+4] ;restore esi

mov ebx,[esp+buffer+8] ;restore ebx

add esp,buffer+12 ;remove buffer,locals

xor eax, eax ;sucsess code

retn 8 ;go to main program

;————————————————————

_isinfinity: test ecx,ecx

jns short _erro1 ; is NAN

jne short _erro1 ; is NAN

mov dword ptr [edi+1], «IFNI»

mov dword ptr [edi+5], «YTIN»

mov edi,[esp+buffer];pop edi

mov esi,[esp+buffer+4];pop esi

mov ebx,[esp+buffer+8];pop ebx

;—————————

; value to be converted = 0

;—————————

_iszero: mov esi,[esp+buffer+4];pop esi

mov dword ptr [edi+1],«0.0»

mov ebx,[esp+buffer+8];pop ebx

mov edi,[esp+buffer];pop edi

mov dword ptr [edi+1], «ORRE»

mov dword ptr [edi+5], «R»

mov edi,[esp+buffer];pop edi

mov esi,[esp+buffer+4];pop esi

mov ebx,[esp+buffer+8];pop ebx

_other: test ecx,0BFFFFFFFh

mov dword ptr [edi+1], «ngiS»

mov dword ptr [edi+5], «nila»

mov dword ptr [edi+9], «aN g»

mov dword ptr [edi+13],«N»

mov edi,[esp+buffer];pop edi

mov esi,[esp+buffer+4];pop esi

mov ebx,[esp+buffer+8];pop ebx

_other1: cmp ecx,0C0000000h

mov dword ptr [edi+1], «ednI»

mov dword ptr [edi+5], «inif»

mov dword ptr [edi+9], «et»

mov edi,[esp+buffer];pop edi

mov esi,[esp+buffer+4];pop esi

mov ebx,[esp+buffer+8];pop ebx

_Quit_NaN: mov dword ptr [edi+1], «eiuQ»

mov dword ptr [edi+5], «aN t»

mov dword ptr [edi+9], «N»

mov edi,[esp+buffer];pop edi

mov esi,[esp+buffer+4];pop esi

mov ebx,[esp+buffer+8];pop ebx
Программа для перевода REAL4 в строку
Программа для перевода REAL8 в строку

integer to float32

integer to float64

integer to float80

Использованы материалы:
1. Чарльз Петцольд «Код. Тайный язык информатики» — М.: Издательско-торговый дом «Русская Редакция», 2001. — 512 с.: ил.
2. Serrgio / HI-TECH «Введение в машинный код» (Архив WASM.RU)
3. Кнут, Дональд Эрвин «Искусство программирования. Том 2: Получисленные алгоритмы», 3-е изд.: — М.: Издательско-торговый дом «Вильямс», 2003. — 832 с.: ил.
4. Сергей Борисович Гашков «Системы счисления и их применение» Серия: «Математическое просвещение» Выпуск 29. М.: МЦНМО, 2004. — 52 с.: ил.
5. Материалы с сайта http://klein.zen.ru/klein/hscool/online/base/b1s1/
Вложения:

Источник

В седьмом вопросе о leetcode упоминалось, что диапазон целых чисел, представленный 32-битным двоичным числом со знаком, составляет: -2 ^ 31 ~ 2 ^ 31-1, так как же это произошло?

Прежде всего, для двоичных чисел, хранящихся в памяти компьютера, конкретное представление остается на усмотрение людей, например:

1000 0001  
Знаковое число означает: -127
 Беззнаковое число означает: 129

Для чисел со знаком старший бит используется для обозначения знака целого числа, 0 означает положительное число, 1 означает отрицательное число.

Если это положительное число, просто переведите его исходный код в десятичный:

Такие как:

0000 0010
 Представляет положительное число:
 Метод интерпретации:
 Просто используйте 2 как право на десятичное число:
1*2^1=2

Если это отрицательное число, оно выражается в дополнительном, например:

1000 0000
 Представляет отрицательное число:
 Метод интерпретации:
 Первый шаг: напрямую расширить остальные биты, кроме самого старшего, на 2 справа: 0
 Шаг 2: Найдите модуль 7 бит после удаления старшего бита: 2 ^ 7 = 128
 Шаг 3: вычтите результат первого шага из результата второго шага: 128-0 = 128
 Шаг 4: Добавьте к результату третьего шага знак минус: -128

Следовательно, диапазон, представленный 8-битным двоичным числом со знаком (-128 ~ 127), а именно (-2 ^ 7 ~ 2 ^ 7-1), можно рассчитать следующим образом:

Минимальное значение: 1000 0000 означает -128
 Максимальное значение: 0111 1111 означает 127

Таким же образом диапазон, представленный 32-битным двоичным числом со знаком, может быть вычислен как: (-2 ^ 31 ~ 2 ^ 31-1)

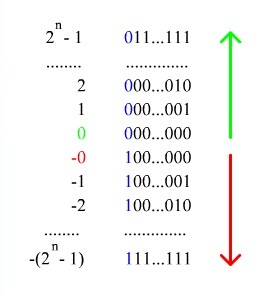
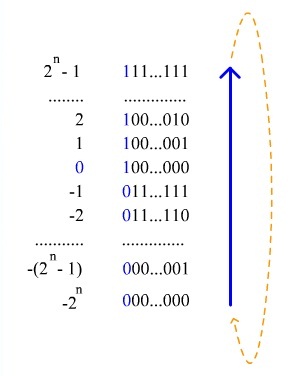
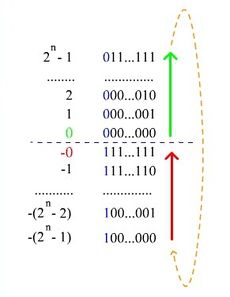
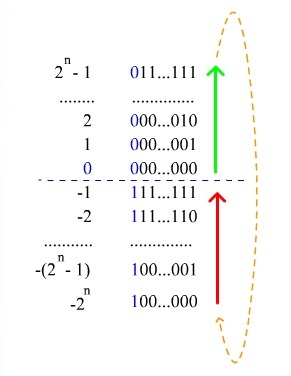
Источник

Двоичная система счисления

Биты и байты

Что такое восьмибитная двоичная запись числа

Представление целых чисел: прямой код, код со сдвигом, дополнительный код

Содержание

Прямой код [ править ]

Достоинства представления чисел с помощью прямого кода [ править ]

Недостатки представления чисел с помощью прямого кода [ править ]

Код со сдвигом [ править ]

Достоинства представления чисел с помощью кода со сдвигом [ править ]

Недостатки представления чисел с помощью кода со сдвигом [ править ]

Дополнительный код (дополнение до единицы) [ править ]

Достоинства представления чисел с помощью кода с дополнением до единицы [ править ]

Недостатки представления чисел с помощью кода с дополнением до единицы [ править ]

Дополнительный код (дополнение до двух) [ править ]

Длинная арифметика для чисел, представленных с помощью кода с дополнением до двух [ править ]

Достоинства представления чисел с помощью кода с дополнением до двух [ править ]

Недостатки представления чисел с помощью кода с дополнением до двух [ править ]

#Эндианность

#Битовые операции

#Сдвиги

#Побитовые операции

#Маски

#Выделить i-й бит числа

#Получить число, состоящее из k единиц

#Инвертировать все биты числа

#Добавить i-й элемент в множество

#Удалить $i$-й элемент из множества

#Удалить i-й элемент из множества, если он есть

#Знаковые числа

#128-битные числа

Mikl___ Супермодератор Команда форума

Системы представления чисел

Вложения:

Mikl___ Супермодератор Команда форума

Вложения:

Mikl___ Супермодератор Команда форума

Алгоритм Содена

10→2

Mikl___ Супермодератор Команда форума

Обозначения

Арифметика

Вложения:

Mikl___ Супермодератор Команда форума

Несколько приемов, которые упростят перевод из двоичного в десятеричное представление

Числа со знаком

Прямой (знаковеличинный) код

Смещенный код

Дополнительный код

Вложения:

Mikl___ Супермодератор Команда форума

Более подробно о дополнительном коде

Вложения:

0.jpg

Mikl___ Супермодератор Команда форума

Представление чисел с плавающей запятой

Вложения:

Mikl___ Супермодератор Команда форума

Mikl___ Супермодератор Команда форума

Специальные численные значения

Mikl___ Супермодератор Команда форума

Approximations that depend on the floating point representation

Вложения:

Mikl___ Супермодератор Команда форума

integer to float32

integer to float64

integer to float80

Использованы материалы:

Вложения:

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума

Mikl___

Супермодератор
Команда форума