Основные понятия
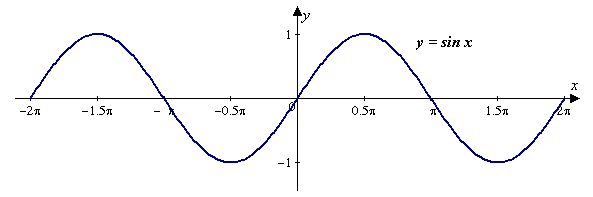
Кривая получается из синусоидальной дуги путём смещения к пи/2 в сторону со знаком минус. Кривая представляет график функции у=sin x. В формуле синусоиды y=a+b cos (cx+d) присутствуют следующие аргументы:
- a: показывает сдвиг графика синусоиды по оси Oy (чем больше значение, тем выше прямая);
- b: описывает растяжения функции по оси Oy (чем выше постоянная, тем сильнее колебания);
- c: определяет растяжение по оси Ох (если постоянная увеличивается, наступает период колебаний);
- d: описывает сдвиг по оси Ох (если d увеличивается, тогда при построении синусоиды учитывается сдвиг в область со знаком минус по оси абсцисс).
Сжатие, растяжение либо сдвиг кривой приводит к изменению величины. Явления называются гармоническими колебаниями. Примеры синусоиды: экспонент или показательная функция в виде винтовой линии, проведённой на плоскости, скрученный провод, развёрнутый рулон бумаги.
Особенности построения
Чтобы выявить свойства синусоиды, необходимо построить её график, провести исследование синуса. В алгебре под функцией представлена плоская кривая, которая выражает закон колебания sin с учётом изменения центрального угла. Сама синусоида строится в схематической последовательности:
- проводится горизонтальная ось, на которой откладывается заданная длина волны;
- отрезок делится на равные части;
- слева чертится окружность с радиусом, равным величине амплитуды;
- окружность делится на 12 одинаковых частей;
- через полученные точки проводятся прямые;
- из точек проводятся перпендикуляры к оси.
График можно построить на онлайн ресурсе либо с помощью специальных программ (Excel). Для расчёта используется калькулятор, основная формула y=sin х. При решении задач учитывается длина волны, которая равна 2 пи. Такое преобразование объясняется тем, что значение функции при любом икс совпадает с её периодичностью x+2π.
Пересечение оси Ох происходит в точках перегиба πK. Максимум достигается при положительном π/2+2πK, а обратное — -π/2+2πK. Свойства кривой проявляются в частном либо комплексном виде:
- размах;
- растяжение/сжатие;
- фазовые колебания;
- круговая частота.
При сдвиге графика влево к значению пи/2 образуется косинусоида. Любое изменение величины характерно для квадрата с гармоническими колебаниями. Примеры подобных явлений: движение маятника, сбои с напряжением в электросети. Другой случай с синусоидальными колебаниями — звук. Он редко бывает чистым, соответствуя y=A sin wt, где:
- А (а) — модуль неизвестной (расстояние от начала координат до точки А);
- w — угловая частота;
- t — время.
Чаще издаются обертоны, для которых характерны низкие амплитуды. Подобные явления изучаются в школе на уроках физики в старших классах.
Свойства и доказательства
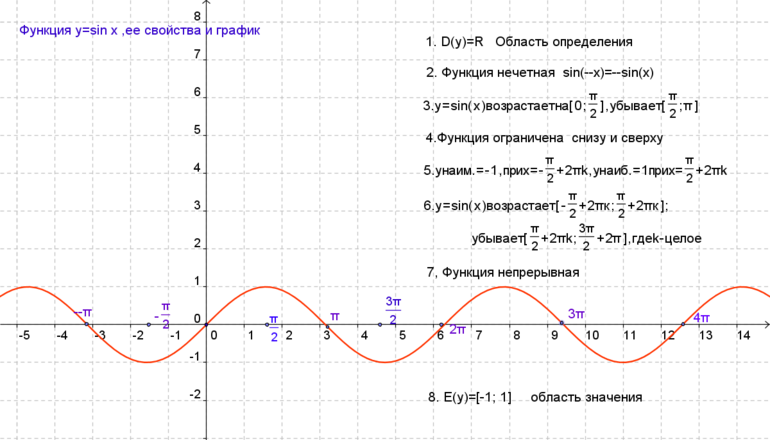
К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.
Так как через круг в одной области можно провести только одну прямую, перпендикулярную оси, поэтому для области определения функции подходят все числа. Такое свойство записывается следующим образом: D (sin x) = R.
Значения ординаты единичной окружности (ЕД) расположены на отрезке [—1; 1]. Они принимают значения от -1 до 1. Через любую точку указанного промежутка оси ординат, равного диаметром ЕД, проводится прямая, перпендикулярная оси ординат. Таким способом получается точка с рассматриваемой ординатой.
Из свойства вытекает следующее: функция y= sin x имеет область значений (-1; 1). Утверждение записывается так: E (sin x)=(-1; 1). Максимальное значение функции равняется единице. Подобное возможно, если соответствующей точкой ЕД является точка А. Минимальное число y равно -1 в случае, когда точкой ЕД является В (х=пи/2 +2пиk, где k принадлежит области Z.
Нечётность и постоянство
Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.
Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.
Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.
Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.
Больше и меньше
С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.
Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.
Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.
Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.
Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.
22
Окт 2013
Категория: Справочные материалыФункции и графики
Графики тригонометрических функций. Синусоида
2013-10-22
2019-09-21
Смешное видео по теме
График функции y=sinx
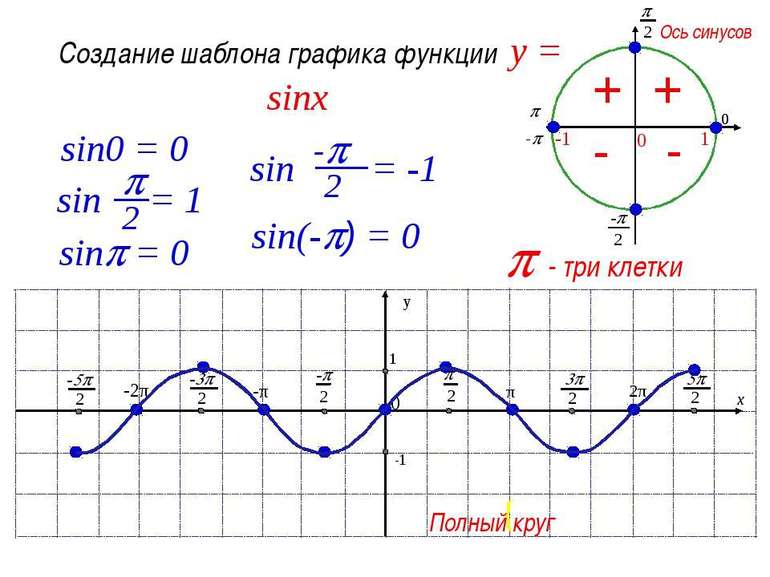
Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции .
Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.

Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.
Нанесенные на координатную плоскость точки подсказывают нам плавную кривую. Это и есть график функции на
Поскольку на тригонометрическом круге значения синуса повторяются через каждый круг (несколько кругов), то не составит труда построить график функции и на всей числовой прямой.
Указанный выше фрагмент графика синуса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :
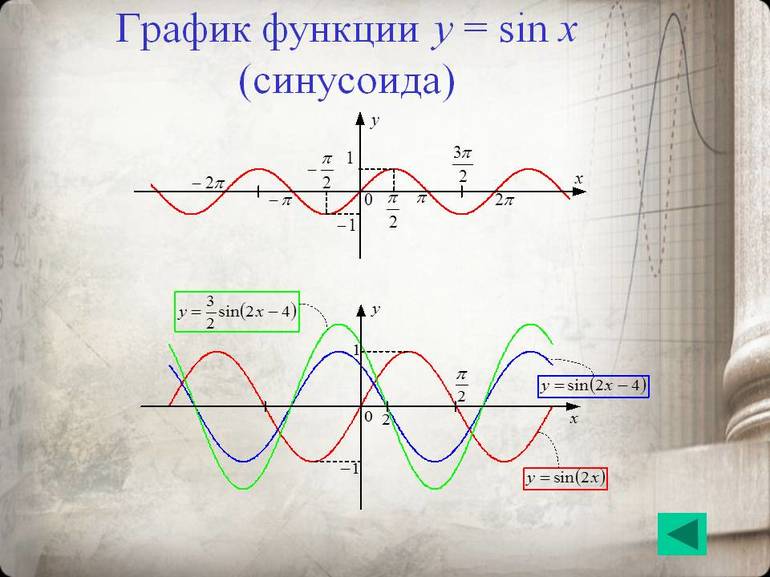
График функции называется синусоидой. График симметричен относительно начала координат.
График функции y=cosx
Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и
.
Поступим несколько иначе.
Согласно формулам приведения .
Из чего мы делаем вывод, что график функции будет получен смещением графика функции
на
единиц влево.
То есть график функции – это все таже синусоида, но теперь уже, симметричная относительно оси ординат.
Преобразования синусоиды
Приглашаю посмотреть небольшой видеоролик о том, как меняется поведение синусоиды в зависимости от умножения аргумента или функции на некоторое число или от прибавления к аргументу или функции некоторого числа.
Автор: egeMax |
Нет комментариев
Печать страницы

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
График синуса
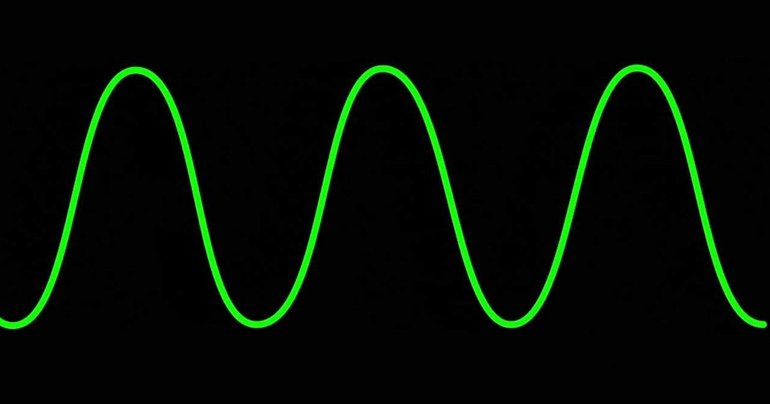
График синуса имеет вид как показано на рисунке 1. Кривая, задающая график синуса, называется синусоидой.
Рис. 1
График функции пересекает ось
в точках
Максимальные значения равные
функция принимает в точках
а минимальные значения, равные (
), в точках
График функции возрастает при
и убывает при
Примеры решения задач
ПРИМЕР 1
| Задание | Построить график функции |
| Решение | Заданный график построим с помощью элементарных преобразований графика функции Рис. 2 Затем, сместив график Рис. 3 |
ПРИМЕР 2
| Задание | Построить график функции
|
| Решение | Построим заданный график с помощью элементарных преобразований графика функции Рис. 4 Затем, сжатием графика Рис. 5 |
| Понравился сайт? Расскажи друзьям! | |
Нужна помощь с
решением задач?
Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб
на первый заказ.
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции 
Свойства функции
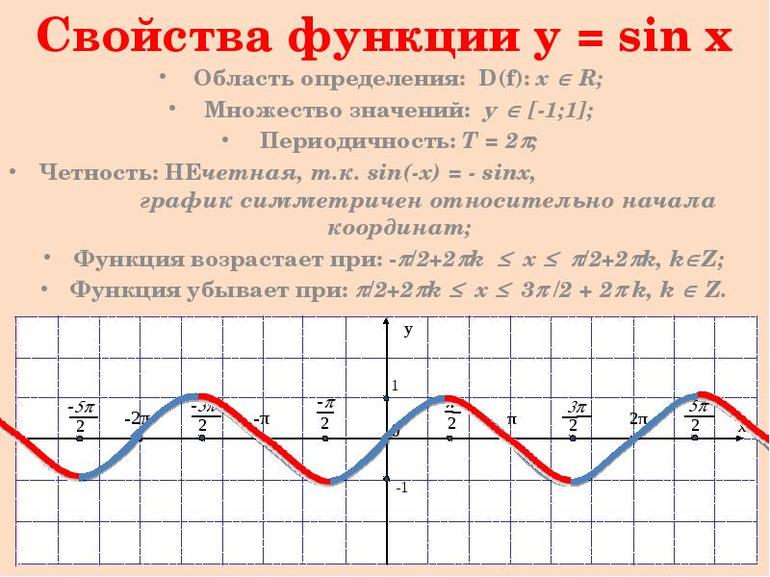
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
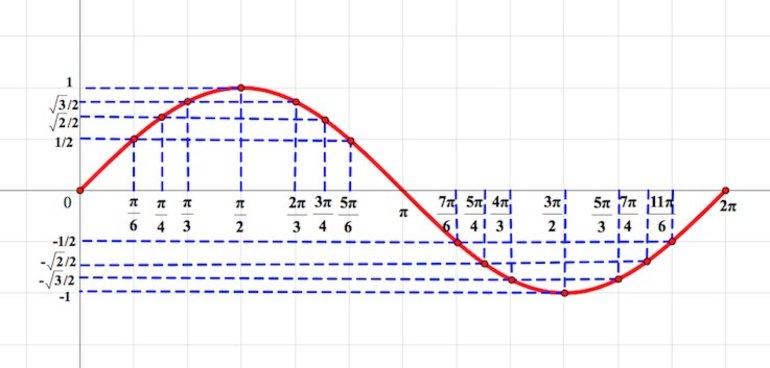
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции 
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции 
. Это можно записать так:
.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции


Синус — нечетная функция: 
Синус — периодическая функция с наименьшим положительным периодом :

вид графика функции

, а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние
, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение
. Тогда соответствующее значение
, то есть график функции
проходит через начало координат.
На оси значение

, при которых


Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, 


Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому 

Промежутки возрастания и убывания. Учитывая периодичность функции 



Если 




Рис.2 Рис.3
Если 




Проведенное исследование позволяет обоснованно построить график функции 







Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной 


на

Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой 
График функции 

. Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой

колебания, 


СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число)
.
- Область значений:
-
Функция четная:
(график симметричен относительно оси
).
- Функция периодическая с периодом
:
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции 

Рис.7
Для точек единичной окружности абсциссы находятся в промежутке 

точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции 

Как видим, наибольшее значение функции 

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при 
Косинус — четная функция: 

Косинус — периодическая функция с наименьшим положительным периодом 



Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси 







Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 


Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому 
Промежутки возрастания и убывания. Учитывая периодичность функции 


Если 





Если 





Рис.8 Рис.9
Проведенное исследование позволяет построить график функции 
. Но график функции


Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки 
абсциссы и ординаты этих точек. Так как 
прямоугольника 



Укажем также формулы, которые нам понадобятся далее:
Тогда,
Таким образом, 
Учитывая, что 

его параллельным переносом вдоль оси


Рис.11
Рис.12
СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции 
Свойства функции 
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
СВОЙСТВО ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
Муниципальное
бюджетное общеобразовательное учреждение
города
Новосибирска
«Средняя
общеобразовательная школа №64»
Синусоида
и ее применение
Выполнил:
Конвиз
Илья Викторович
ученик
10 «А» класса
Руководитель работы:
Прохорова Виктория Александровна,
учитель математики
Новосибирск 2021
Оглавление
Введение
Теоретическая часть
1.1. Возникновение тригонометрии как науки
1.2. Что такое синусоида?
Практическая часть
2.1. Для чего нужны синусы в обычной жизни?
2.2. Тригонометрия в физике
2.3. Тригонометрия в медицине
2.3.1 Анализ расчётных графиков биоритмов
десятиклассников
2.4. Тригонометрия в природе
2.5. Тригонометрия в архитектуре и искусстве
2.6. Результат опроса среди десятиклассников
Заключение
Литература
Приложение
Введение
Недавно,
начиная изучать раздел математики — тригонометрию, я задал себе вопрос: зачем
она нужна, где её применяют, зачем её вообще изучают. Особый интерес у меня
вызвало построение графиков тригонометрических функций – а именно синусоиды;
это график функции y = sin x, она завораживает меня своей грацией, а ее волны, простирающие
от минус бесконечности до плюс бесконечности, уносят меня в просторы
тригонометрии. Преобразование графиков — сжатие, растяжение, параллельный
перенос является увлекательным путешествием в алгебру и начала анализа.
Научившись строить на уроках элементарные графики тригонометрических функций,
мне захотелось узнать о них больше: возможно ли применение синусоиды в других
областях науки? Ведь многие явления, происходящие в природе периодичны, а
периодичность является одним из свойств тригонометрических функций. Такие
явления можно наблюдать в биологии, в физике, медицине. Помимо периодичности
она обладает вертикальной симметрией, а значит, тригонометрические функции
имеют место и в практической деятельности – в архитектуре и искусстве.
Красоту
такого разнообразного раздела математики и хотелось раскрыть этим проектом «Синусоида и ее применение».
Хотя
многие считают, что математика скучна и однообразна, рассмотрение ее через
призму различных областей окружающего мира вызывает большой интерес. Я считаю,
что именно в этом и состоит актуальность данной работы
Объект
исследования
– синусоида;
Предмет
исследования —
области ее практического применения.
Цель: Раскрыть красоту и многообразие
тригонометрии через явления окружающего мира, различные области деятельности
человека
Задачи:
1. Изучить литературу по
данной теме.
2. Выяснить, какие законы природы
выражаются тригонометрической функцией.
3. Найти примеры применения
тригонометрических функций в деятельности человека.
4. Проанализировать и
систематизировать имеющийся материал.
Гипотеза: Всё в мире: и неживая природа,
микро и макромир, живые организмы, в том числе человек и сообщества людей –
государства, империи, мировые религии (идеологии) подчиняются закону синусоиды.
Для исследования мы использовали
такие методы как:
•
Изучение научно- популярной литературы;
•
Проведение опроса среди десятиклассников насчет актуальности
тригонометрии в жизни;
•
Построение и анализ расчетных графиков биоритмов одноклассников.
Теоретическая часть
1.1.
Возникновение тригонометрии как науки
Тригонометрия
– раздел математики, в котором изучаются тригонометрические функции и их
приложения к геометрии. Слово тригонометрия состоит из двух греческих слов:
trigwnon — треугольник и metrew — измерять и в буквальном переводе означает
измерение треугольников. [4]
Историки полагают, что тригонометрию
создали древние астрономы; немного позднее ее стали использовать в геодезии и архитектуре.
Со временем область применения тригонометрии постоянно расширялась, и в наши
дни она включает практически все естественные науки, технику и ряд других
областей деятельности. Особенно полезными тригонометрические функции оказались
при изучении колебательных процессов. [3, c.55]
Первым графиком тригонометрической
функции, появившимся в печати, была синусоида, помещенная в одном из
произведений французского математика Жиля Персона де Роберваля. Вычерчивание и
применение графиков тригонометрических функций вошло в широкое употребление
лишь после появления «Геометрии» Декарта и создания аналитической геометрии. [2,
c.7-10]
Рис.1 Первый график
тригонометрической функции, появившийся в печати.
1.2. Что такое синусоида?
Синусоида
— волнообразная плоская кривая.
Рис.2 Синусоида
[1, с.71]
Если рулончик бумаги разрезать наискось и развернуть его, то край
бумаги окажется разрезанным по синусоиде. Любопытно, что проекция на плоскость
винтовой линии также будет синусоидой.
Изменение какой либо величины по закону синуса называется гармоническим
колебанием. Примеры таких колебаний: колебания маятника, колебания напряжения в
электрической сети, изменение тока и напряжения в колебательном контуре и др.
Практическая часть
2.1. Для чего нужны синусы в обычной жизни?
На практике синусы и косинусы применяются
во всех инженерных специальностях, особенно в строительных. Их используют
моряки и летчики в расчетах курса движения. Не обходятся без синусов и
косинусов геодезисты, и даже путешественники. В географии применяют для
измерения расстояний между объектами, а также в спутниковых навигационных
системах.
2.2.
Тригонометрия в физике
Колебательный процесс — периодический
или почти периодический процесс, который повторяется через одинаковые или почти
одинаковые промежутки времени.
Колебательный процесс включает в себя
гармонические колебания – колебания, при которых изменения физических величин
происходит по закону синуса и косинуса, выражающего связь между амплитудой и
временем (рис. 1) [2, с.155]
рис.3. Понятие колебательного процесса
Выражение, стоящее под знаком косинуса или
синуса, называется фазой колебания:
2.3.
Тригонометрия в медицине
Приходилось ли вам видеть
кривую на бумаге или фотопленке при регистрации деятельности сердца
специальными приборами (ЭКГ)? (рис. 3)
Рис. 4. Электрокардиограмма сердца
Электрокардиограмма – это кривая, которая
отражает биоэлектрическую работоспособность сердца. В момент возбуждения сердца
с его внешней, а также внутренней стороны происходит разность потенциалов,
которая постепенно меняет свою величину и направление. Эти изменения становятся
результатом внедрения в возбуждение иных частей сердца.
Если сравнить график кардиограммы сердца с
графиком функции y=sin x, можно
увидеть, что кардиограмма сердца является искривленной синусоидой (рис. 5,
рис.6)
Рис. 5. ЭКГ сердца
Рис. 6. График синусоиды

человека, как и всё в природе, подвержено влиянию циклических изменений. В
определенные дни, которые рассчитывает этот график (рис. 7). Люди имеют либо максимум,
либо минимум в физическом плане, психологическом плане или интеллектуальном
плане, т.е. они либо имеют большой прилив сил, либо имеете очень позитивный
настрой, либо вы можете решать даже самые сложные для вас задачи.
рис. 7. Расчетный график биоритмов автора
проекта
2.3.1
Анализ расчётных графиков биоритмов десятиклассников
Ряполов Савелий
 |
Сенин Роман
 |
рис. 8-9. Расчетный график биоритмов
одноклассников
Я построил расчетные графики биоритмов
всех своих одноклассников. Проведя парочку исследований, можно выявить то, что
эти данные подтвердились. Я проанализировал поведение двух моих одноклассников
(Савелий Ряполов и Роман Сенин Биоритмы класса 10 «А» (Приложение 1)) и свое,
на протяжении недели, и выявил, что все спады и подъемы полностью совпадают.
2.4.
Тригонометрия в природе
Тригонометрия
встречается и в природе. При полёте птицы траектория взмаха крыльев
образует синусоиду (рис. 10)
Рис. 10.
Траектория взмаха крыльев птицы
Движение
рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку
на хвосте, а потом рассмотреть траекторию движения (рис. 11).
Рис. 11.
Движение рыб в воде
Северное сияние, всеми знакомое нам явление, также связано
с синусоидальным законом:
Проникновение
в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется
взаимодействием магнитного поля планеты с солнечным ветром.
Сила,
действующая на движущуюся в магнитном поле заряженную частицу, называется силой
Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и
скорости движения частицы (рис. 12).
Рис. 12.
Северное сияние
Рис. 13.
Движение Земли вокруг Солнца
Движение
Земли вокруг Солнца иллюстрирует «движение» точки тригонометрической окружности
(рис. 14)
Рис. 14.
«Движение» точки тригонометрической окружности
2.5.
Тригонометрия в архитектуре и искусстве
Широко используется тригонометрия в
строительстве, а особенно в архитектуре. Некоторые композиционные решения и построения
рисунков проходило именно с помощью тригонометрии.
Особый интерес вызвало у меня
архитектурное сооружение в Барселоне каталонского архитектора Антонио Гауди,
построенное в 1888-1894 гг. — школа при монастыре святой Терезы (рис 15).
Рис. 15. Детская школа Гауди в Барселоне
Поверхность крыши школы напоминает синусоидальную
поверхность (рис. 16).
Рис. 16
Уравнение синусоидальной поверхности имеет
вид:
k=1, a=1.[2]
Арочные сооружения, построенные по проекту
испанского архитектора Феликса Канделлы так же вызвали у меня не меньший
интерес. Необычные поверхности зданий напоминают арку, являющуюся элементом
синусоиды (рис. 17, рис.18).
Рис. 17. Океанариум („L’Oceanogràfic“, 1994–2002), Валенсия
Рис. 18 Павильон в Космическом центре, Мехико (1950/1951)
2.6.
Результаты опроса среди десятиклассников
Проведя опрос среди десятиклассников (рис.19), я
пришел к выводу, что не каждый школьник имеет представление об использовании
тригонометрии в жизни.
Рис.19 Результат опроса среди десятикласников
Заключение
В сегодняшнем проекте я выяснил кое-что
важное. Хоть с самого начала кажется, что тригонометрия кажется абсолютно
бесполезной и неприменимой, но это не так. Это благодаря тому, что я привел
несколько примеров о применении синусоиды в различных сферах науки и общества.
Я также решил, что на будущее лучше сделать парочку задач.
Задачи на будущее:
•
Продолжить
изучение синусоиды
•
Продолжить
наблюдение за применением тригонометрии в жизни
•
Познакомить
своих одноклассников с их расчетными графиками биоритмов
И
вывел результаты своей работы.
Результаты работы:
•
Мы изучили историю возникновения
тригонометрии как науки и первое появление синусоиды
•
Изучили
и разобрали «закон синусоиды» на примере разных сфер в науке и обществе
•
Выявили
мнение школьников о применении тригонометрии в жизни
Литература
1. Мордкович
А.Г. и др. «Алгебра и начала математического анализа» Учебник для
10-11 классов общеобразовательных учреждений, М.: Мнемозина, 2012.
2.
Виленкин Н.Я. Функции в природе и техники: Кн. для внеклас. чтения IX-XX кл. –
2-е изд., испр. — М: Просвещение, 1985.
3. Глейзер
Г.И. История математики в школе: IX-X кл. — М.: Просвещение, 1983.
4.https://ru.wikipedia.org/wiki
5.
http://www.math24.ru
Приложение
1
(Таблица расчётных
графиков биоритмов обучающихся 10 «А» класса)
|
№ |
ФИ |
Дата рождения |
Расчетный график биоритмов |
|
1 |
Карина Симанович |
09.04.2005 |
|
|
2 |
Даниил Шатоба |
12.07.2005 |
|
|
3 |
Алина Абдрахманова |
25.05.2005 |
|
|
4 |
Сергей Кобелев |
21.09.2005 |
|
|
5 |
Никита Демиденко |
05.03.2005 |
|
|
6 |
Ксения Кудрина |
25.02.2006 |
|
|
7 |
Елизавета Саморядова |
28.04.2005 |
|
|
8 |
Кирилл Веселов |
14.03.2005 |
|
|
9 |
Савелий Ряполов |
25.11.2005 |
|
|
10 |
Ксюша Календина |
15.01.2005 |
|
|
11 |
Ярослав Лучинин |
13.05.2005 |
|
|
12 |
Екатерина Макарова |
07.06.2005 |
|
|
13 |
Дмитрий Кретинин |
25.04.2005 |
|
|
14 |
Самран Гасанов |
25.12.2005 |
|
|
15 |
Алена Свистунова |
21.04.2005 |
|
|
16 |
Екатерина Белицкая |
17.07.2005 |
|
|
17 |
Арина Гаврилевич |
20.07.2005 |
|
|
18 |
Екатерина Горбунова |
29.07.2005 |
|
|
19 |
Елизавета Горбунова |
27.06.2005 |
|
|
20 |
Артем Злобин |
03.03.2005 |
|
|
21 |
Коротин Данил |
29.05.2005 |
|
|
22 |
Виктория Кузьменко |
23.06.2005 |
|
|
23 |
Владимир Лузин |
17.09.2005 |
|
|
24 |
Максим Москалев |
30.09.2005 |
|
|
25 |
Ульяна Овчинникова |
21.08.2005 |
|
|
26 |
Роман Рогожников |
01.11.2005 |
|
|
27 |
Роман Сенин |
15.10.2005 |
|
|
28 |
Илья Фуркайло |
08.03.2005 |
|
|
29 |
Анна Умрихина |
12.05.2005 |
|
|
30 |
Диана Пацукова |
26.11.2005 |
|
|
31 |
Александра Губаз |
26.12.2005 |
|
|
32 |
Вероника Ощепкова |
05.10.2005 |
|
|
33 |
Анастасия Ядрова |
14.01.2005 |
|
|
34 |
Сергей Сергеев |
28.12.2005 |
|
|
35 |
Конвиз Илья |
21.11.2005 |
|








![file.[2]](https://ya-znau.ru/information/userfiles/73/file.%5B2%5D.jpg)
![file.[3]](https://ya-znau.ru/information/userfiles/73/file.%5B3%5D.jpg)

![file.[4]](https://ya-znau.ru/information/userfiles/73/file.%5B4%5D.jpg)