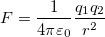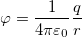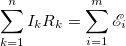Как найти a в физике формула электричество

Основные формулы по физике — ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип

При изучении темы «Постоянный ток» необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении «Магнетизма» необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.

Электрические и магнитные явления связаны особой формой существования материи — электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.

Смотрите также основные формулы оптики

Таблица основных формул электричества и магнетизма

 Физические законы, формулы, переменные

 Формулы электричество и магнетизм

Закон Кулона:
где q1 и q2 — величины точечных зарядов, ԑ1  — электрическая постоянная; 046
ε — диэлектрическая проницаемость изотропной среды (для вакуума ε = 1),
r — расстояние между зарядами.

001

Напряженность электрического поля:

где Ḟ — сила, действующая на заряд q0 , находящийся в данной точке поля.

002

Напряженность поля на расстоянии r от источника поля: 1) точечного заряда

2) бесконечно длинной заряженной нити с линейной плотностью заряда τ:

3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ:

4) между двумя разноименно заряженными плоскостями

Потенциал электрического поля:

где W — потенциальная энергия заряда q0 .

007

Потенциал поля точечного заряда на расстоянии r от заряда:

008

По принципу суперпозиции полей, напряженность:

009

Потенциал:

где Ēi и ϕi — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом.

010

Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ1 в точку с потенциалом ϕ2 :

011

Связь между напряженностью и потенциалом

1) для неоднородного поля:

2) для однородного поля:

1) 

012 

2) 

 013

Электроемкость уединенного проводника:

014

Электроемкость конденсатора:

где U = ϕ1 — ϕ2 — напряжение.

015

Электроемкость плоского конденсатора:

где S — площадь пластины (одной) конденсатора,

d — расстояние между пластинами.

016

Энергия заряженного конденсатора:

017

Сила тока:

018

Плотность тока:

где S — площадь поперечного сечения проводника.

019

Сопротивление проводника:

ρ — удельное сопротивление;

l — длина проводника;

S — площадь поперечного сечения.

020

Закон Ома

1) для однородного участка цепи:

2) в дифференциальной форме:

3) для участка цепи, содержащего ЭДС:

   где ε — ЭДС источника тока,

   R и r — внешнее и внутреннее сопротивления цепи;

4) для замкнутой цепи:

Закон Джоуля-Ленца

 1) для однородного участка цепи постоянного тока:
    где Q — количество тепла, выделяющееся в проводнике с током,
    t — время прохождения тока;

 2) для участка цепи с изменяющимся со временем током:

1)

025

2)

026

Мощность тока:

027

Связь магнитной индукции и напряженности магнитного поля:

где B — вектор магнитной индукции,
μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1),
µ0 — магнитная постоянная 028,
H — напряженность магнитного поля.

029

Магнитная индукция (индукция магнитного поля):
 1) в центре кругового тока
     где R — радиус кругового тока,

 2) поля бесконечно длинного прямого тока
     где r — кратчайшее расстояние до оси проводника;

 3) поля, созданного отрезком проводника с током
    где 

ɑ1 и ɑ2 — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля;
 4) поля бесконечно длинного соленоида
     где n — число витков на единицу длины соленоида.

Сила Лоренца:

по модулю
где F — сила, действующая на заряд, движущийся в магнитном поле,
v — скорость заряда q,
α — угол между векторами v и B.

034

035

Поток вектора магнитной индукции (магнитный поток через площадку S):
 1) для однородного магнитного поля ,
    где α — угол между вектором B и нормалью к площадке,
 2) для неоднородного поля

1)

 036

2)

 037

Потокосцепление (полный поток):
где N — число витков катушки.

038

Закон Фарадея-Ленца:
где ԑi — ЭДС индукции.

039

ЭДС самоиндукции:
 где L — индуктивность контура.

040

Индуктивность соленоида:

где n — число витков на единицу длины соленоида,
V — объем соленоида.

041
042

Энергия магнитного поля:

043

Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур:

где ∆Ф = Ф2 – Ф1 — изменение магнитного потока, R — сопротивление контура.

044

Работа по перемещению замкнутого контура с током I в магнитном поле:

045

Поделитесь ссылкой с друзьями:

Похожие таблицы

Комментарии:

Источник

Формула напряжения в физике — это представление электрической потенциальной энергии на единицу заряда. Если ток был размещен в определенном месте, напряжение указывает на ее потенциальную энергию в этой точке. Другими словами, это измерение силы, содержащейся в электрическом поле или цепи в данной точке. Он равен работе, которую нужно было бы выполнить за единицу заряда против электрического поля, чтобы переместить его из одной точки в другую.

Напряжение является скалярной величиной, у него нет направления. Закон Ома гласит, что интенсивность равна текущему временному сопротивлению.

Сопротивление

Формула механической мощности — средняя и мгновенная мощность

Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.


Резисторы различных типов

Для переменного тока

Нужно понимать, что закон не применим напрямую к переменным цепям, например, с катушками индуктивности, конденсаторами или линиям передач. Закон может использоваться только для чисто резистивных цепей переменного тока без каких-либо изменений. В цепи RLC противодействие току является импедансом Z, который образует комбинацию двух ортогональных частей сопротивления.

Переменный ток

Im=Vm/Z

В этом случае Vm связано с Im с помощью константы пропорциональности Z (импеданса) и константы пропорциональности R. Для чисто резистивных линий, где (Z = R).

Vm = ImZ и Vm = ImR

Z — это общее сопротивление участка к переменному току, состоящее из реальной части — сопротивления и мнимой — реактивности.

Формула ее определяется теоремой Пифагора, поскольку угол Ф зависит от реактивной составляющей.

Интегральная форма

Взаимосвязь параметров электрической цепи

Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.

К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.

Формула напряжения тока закона Ома выглядит следующим образом:

I=U/R.

Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.

Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:

  • I – сила тока;
  • U – напряжение;
  • R – сопротивление.

Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.

Кроме закона Ома, используется формула расчета мощности:

P=U∙I.

Символом P здесь обозначена мощность тока.

Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.

Закон Ома для неоднородного участка цепи

Физическая величина, равная отношению работы сторонних сил Aст при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой (ЭДС) источника Eэдс:

$ E_{эдс} = {A_{cт}over q} $ (1).

Таким образом, ЭДС равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда. При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа электростатического поля равна нулю, а работа сторонних сил равна сумме всех ЭДС, действующих в этой цепи.

Работа электростатических сил по перемещению единичного заряда равна разности потенциалов $ Δφ = φ_1 – φ_2 $ между начальной и конечной точками 1 и 2 неоднородного участка. Работа сторонних сил равна, по определению, электродвижущей силе Eэдс, действующей на данном участке. Поэтому полная работа равна:

$ U_п = φ_1 – φ_2 + E_{эдc} $ (2).

Величина Uп называется напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:

$ U_п = φ_1 – φ_2 $ (3).

Немецкий исследователь Георг Симон Ом в начале XIX века установил, что сила тока I, текущего по однородному проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

$ I = {U over R} $ (4).

Рис. 2. Портрет Георга Ома.

Величина R — это электрическое сопротивление. Уравнение (4) выражает закон Ома для однородного участка цепи. Для участка цепи, содержащего ЭДС, закон Ома записывается в следующем виде:

$ U_п = I * R = φ_1 – φ_2 + E_{эдс} = Δ φ_{12} + E_{эдс}$ (5).

Данное уравнение называется обобщенным законом Ома для неоднородного участка цепи.

Как работает закон в реальной жизни

Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.

Сила тока формула через мощность:

I=P/U;

Сопротивление:

R=U/I.

Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:

R=U2/P.

Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.

Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:

P=U2/R.

Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.

Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.

Облегчить расчеты можно, используя онлайн калькулятор.

Определение через разложение электрического поля

Используя приведенное выше понятие, потенциал не находится на одном месте, когда магнитные поля меняются со временем. В физике иногда полезно обобщать электрическое значение, рассматривая только консервативную часть поля. Это делается с помощью следующего разложения, используемого в электродинамике.

формула для вычисления напряжения

В показанной выше формуле Е — индуцированный — вращательное электрическое поле, обусловленное изменяющимися во времени магнитными фонами. В этом случае сила между точками всегда определяется однозначно.

Пример с обычной водой

Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.

Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.

Различные используемые величины

Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:

  • Кило – 1000;
  • Мега – 1000000;
  • Гига – 1000000000;
  • Милли – 0.001.

Таким образом, получается:

  • Киловольт (кВ) – тысяча вольт;
  • Мегаватт (Мвт) – миллион ватт;
  • Миллиом (мОм) – одна тысячная Ом;
  • Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.

Как найти напряжение

Формула нахождения напряжения как разности потенциалов в электрическом поле:

U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.

Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:

U=A/q, где q – величина заряда.

Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.

Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.

Единицы измерения в формуле

Вам будет интересно:Антиклиналь + синклиналь – это складчатые горы

формула напряжения физика

В формуле, определяющей напряжение, значением СИ является вольт. Таким образом, что 1В = 1 джоуль/кулон. Вольт назван в честь итальянского физика Алессандро Вольта, который изобрел химическую батарею.

Это означает, что в формуле напряжения в физике один кулон заряда получит один джоуль потенциальной энергии, когда он будет перемещен между двумя точками, где разность электрических потенциалов составляет один вольт. При напряжении 12, один кулон заряда получит 12 джоулей потенциальной энергии.

Батарея на шесть вольт имеет потенциал для одного кулона заряда, чтобы получить шесть джоулей потенциальной энергии между двумя местоположениями. Батарея на девять вольт имеет потенциал для одного кулона заряда, чтобы получить девять джоулей потенциальной энергии.

Гидравлическая аналогия

Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:

  • Источник питания – насос;
  • Проводники – трубы;
  • Электроток – движение воды.

Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.

Измерительные приборы

Для измерения параметров электрических цепей служат измерительные приборы:

  • Вольтметр;
  • Амперметр;
  • Омметр.

Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.

Источник


Загрузить PDF


Загрузить PDF

Ампер (обозначение: А) – это единица измерения силы электрического тока. Электрический ток является движением заряженных частиц.[1]
 Эта информация пригодится при подключении электроприбора к сетевой розетке, переменный ток к которой подается непосредственно с электростанции.[2]
[3]

  1. Изображение с названием Find Amps Step 1

    1

    Воспользуйтесь формулой для цепи постоянного тока. Силу электрический тока (I), которая измеряется в амперах (А), можно вычислить, разделив мощность (P), которая измеряется в ваттах (Вт), на напряжение (V), которое измеряется в вольтах (В). Запомните следующую формулу:

    • I(A) = P(Вт) / V(В)[4]

      Или так: Ампер = Ватт / Вольт.

  2. Изображение с названием Find Amps Step 2

    2

    Если в задаче рассматривается цепь переменного тока, уясните определение коэффициента мощности. Коэффициент мощности (PF) – это отношение активной мощности, которая потребляется электроприбором, к полной мощности; значение коэффициента мощности лежит в пределах от 0 до 1. Активная мощность (Р) измеряется в ваттах, а полная мощность (S) – в вольт-амперах (В•А).

    • PF = P / S[5]

  3. Изображение с названием Find Amps Step 3

    3

    Вычислите полную мощность, чтобы найти коэффициент мощности. Полная мощность вычисляется по формуле:

    S = Vrms x Irms

    где S – полная мощность, которая измеряется в вольт-амперах (В•А), Vrms – среднеквадратическое значение напряжения, Irms – среднеквадратическое значение силы тока. Последние две величины можно найти следующим образом:

    • Vrms = Vpeak / √2 (в вольтах, В)
    • Irms = Ipeak / √2 (в амперах, A)

  4. Изображение с названием Find Amps Step 4

    4

    Воспользуйтесь коэффициентом мощности в случае однофазного переменного тока. Здесь сила тока (I) измеряется в амперах (А) и равна отношению активной мощности (P), которая измеряется в ваттах (Вт), к произведению коэффициента мощности (PF) на среднеквадратичное значение (RMS) напряжения, которое измеряется в вольтах (В).

    • I(A) = P(Вт) / (PF x V(В)[6]

      Или так: Ампер = Ватт/(Коэффициент мощности х Вольт)

    Реклама

  1. Изображение с названием Find Amps Step 5

    1

    Убедитесь, что ток является постоянным. Постоянный ток не изменяется по величине и направлению. Если источником тока является батарейка или аккумулятор, то ток будет постоянным.[7]

    • Имейте в виду, что ток, подающийся к электророзеткам, является переменным.[8]
       Переменный ток можно сделать постоянным при помощи трансформатора, выпрямителя и фильтра.[9]

  2. Изображение с названием Find Amps Step 6

    2

    Определите схему электрической цепи. Чтобы вычислить силу тока в цепи, амперметр нужно подключить к определенному участку этой цепи. Чтобы определить схему цепи, отследите электропровода, идущие от положительного к отрицательному полюсу аккумулятора.

  3. Изображение с названием Find Amps Step 7

    3

    Протестируйте работу цепи. Если в ней присутствует разрыв или аккумулятор неисправен, амперметр не сможет измерить силу тока (или измерит ее неточно). Замкните цепь, чтобы убедиться, что она нормально работает.

  4. Изображение с названием Find Amps Step 8

    4

    Разомкните цепь. В некоторых цепях нужно полностью отсоединить аккумулятор. Работая с мощным аккумулятором, вы рискуете получить удар электрическим током, поэтому обязательно обесточьте цепь. Или же наденьте плотные резиновые перчатки, чтобы избежать поражения электрическим током.

  5. Изображение с названием Find Amps Step 9

    5

    Подключитесь к положительной клемме амперметра. У любого амперметра две цветные клеммы (ила два цветных провода): красная, которая соответствует положительному (+) полюсу, и черная, которая соответствует отрицательному (-) полюсу. Положительный полюс аккумулятора подключите к положительной клемме амперметра.[10]

    • Амперметр не воспрепятствует потоку электричества, но измерит силу тока и отобразит ее на экране.

  6. Изображение с названием Find Amps Step 10

    6

    Замкните цепь, подключившись к отрицательной клемме амперметра. Отрицательную клемму амперметра подключите к электропроводу, который вы отсоединили от положительного полюса аккумулятора.[11]

  7. Изображение с названием Find Amps Step 11

    7

    Замкните цепь. В некоторых цепях просто подсоедините аккумулятор. Цепь замкнется, и амперметр измерит и отобразит силу тока в амперах (А) или миллиамперах (мА) (если источник тока небольшой).[12]

    Реклама

  1. Изображение с названием Find Amps Step 12

    1

    Воспользуйтесь законом Ома. Этот закон описывает зависимость между напряжением и силой тока.[13]
     Формулы закона Ома: V = I х R, R = V / I, I = V / R, где:

    • V – напряжение.
    • R – сопротивление
    • I – сила тока, который проходит через резистор.[14]

  2. Изображение с названием Find Amps Step 13

    2

    Определите напряжение в цепи. Например, если напряжение источника тока равно 9 В, то и напряжение в цепи равно 9 В. Напряжение аккумулятора указывается на его корпусе или упаковке; также напряжение определенной модели источника тока можно найти в интернете.

    • Напряжение большинства батареек (типоразмера от ААА до D) равно 1,5 В.[15]

  3. Изображение с названием Find Amps Step 14

    3

    Найдите резисторы, подключенные к цепи. Резисторы обладают определенным сопротивлением, которое препятствует свободному прохождению электрического тока; определите, какие резисторы являются частью цепи. Схемы цепей отличаются друг от друга (в простейших схемах вообще нет резисторов), поэтому изучите схему вашей цепи, чтобы найти резисторы и определить их сопротивление, которое измеряется в омах (ОМ).

    • Электропровода также обладают некоторым сопротивлением. Скорее всего, таким сопротивлением можно пренебречь, если только электропровода не повреждены или не очень длинные.
    • Формула для вычисления сопротивления: сопротивление = (сопротивление х длина) / площадь поперечного сечения.[16]

  4. Изображение с названием Find Amps Step 15

    4

    Воспользуйтесь законом Ома. Так как напряжение источника тока распространяется на всю цепь, чтобы вычислить силу тока, нужно разделить общее напряжение на сопротивление каждого резистора. Так вы найдете силу тока (I), которая измеряется в амперах (А). Формула для вычислений:

    • (V/R1) + (V/R2) + (V/R3), где V – общее напряжение в цепи (в вольтах), R – сопротивление резисторов (в омах).[17]

    Реклама

Предупреждения

  • Соблюдайте меры безопасности, работая с электричеством. Вы рискуете получить удар электрическим током, а высокое напряжение может привести к пожару. Рекомендуется надевать плотные резиновые перчатки.

Реклама

Об этой статье

Эту страницу просматривали 34 572 раза.

Была ли эта статья полезной?

Источник

Электричество Основные формулы

1. Электростатика

1.1 Закон Кулона

Закон Кулона

q1, q2 — величины точечных зарядов,
r — расстояние между зарядами.

1.2 Напряженность поля уединенного точечного заряда

Напряженность поля уединенного точечного заряда

q — величина уединенного точечного заряда,
r — расстояние от заряда.

1.3 Потенциал точки в поле точечного заряда

Потенциал точки в поле точечного заряда

q — величина уединенного точечного заряда,
r — расстояние от заряда.

1.4 Потенциальная энергия заряда в электростатическом поле

Потенциальная энергия заряда в электростатическом поле

φ — потенциал,
q1 — величина заряда.

1.5 Потенциальная энергия заряда q1 в поле точечного заряда

Потенциальная энергия заряда в поле точечного заряда

q — величина уединенного точечного заряда, который создает поле,
r — расстояние между зарядами.

1.6 Теорема Гаусса

Теорема Гаусса

N — поток вектора напряженности электрического поля через замкнутую поверхность,
q — полный заряд, находящийся внутри замкнутой поверхности.

1.7 Напряженность электрического поля вблизи от поверхности проводника

Напряженность электрического поля вблизи от поверхности проводника

σ — поверхностная плотность заряда.

1.8 Емкость плоского кондесатора

Емкость плоского кондесатора

q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.

1.9 Энергия плоского кондесатора

Энергия плоского кондесатора

q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.

2. Постоянный электрический ток

2.1 Закон Ома для участка однородной цепи

Закон Ома для участка однородной цепи

U — напряжение на концах участка,
R — сопротивление участка цепи.

2.2 Закон Ома для замкнутой цепи с источником тока

Закон Ома для замкнутой цепи с источником тока

ЭДС — ЭДС (электродвижущая сила),
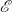
r — внутреннее сопротивление источника ЭДС.

2.3 Работа постоянного тока

Работа постоянного тока

U — напряжение на концах участка цепи,
t — время, за которое совершается работа.

2.4 Закон Джоуля-Ленца

Закон Джоуля-Ленца

Q — теплота,
R — сопротивление проводника,
t — время, за которое выделяется теплота.

2.5 Полная мощность, развиваемая источником тока

Полная мощность, развиваемая источником тока

ЭДС — ЭДС источника тока,
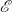
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.6 Полезная мощность

Полезная мощность

ЭДС — ЭДС источника тока,
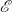
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.7 Коэффициент полезного действия источника тока

Коэффициент полезного действия источника тока

R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.8 Первое правило Кирхгофа

Первое правило Кирхгофа

n — число проводников, сходящихся в узле;
Ik — сила тока в k-м проводнике.

2.9 Второе правило Кирхгофа

Второе правило Кирхгофа

n — число неразветвленных участков в контуре;
m — число ЭДС в контуре.

Источник

Цепь постоянного тока (или, строго говоря, цепь без комплексного сопротивления)

Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока.

  • P = мощность (Ватт)
  • U = напряжение (Вольт)
  • I = ток (Ампер)
  • R = сопротивление (Ом)
  • r = внутреннее сопротивление источнка ЭДС
  • ε = ЭДС источника
  • Тогда для всей цепи:
    • I=ε/(R +r) — закон Ома для всей цепи.

И еще ниже куча формулировок закона Ома для участка цепи :

Основные электротехнические формулы. Мощность. Сопротивление. Ток. Напряжение. Закон Ома

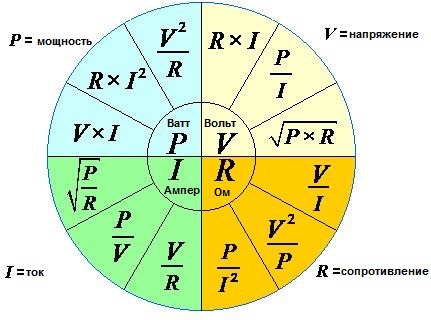
Электрическое напряжение:

  • U = R* I — Закон Ома для участка цепи
  • U = P / I
  • U = (P*R)1/2

Электрическая мощность:

  • P= U* I
  • P= R* I2
  • P = U 2/ R

Электрический ток:

  • I = U / R
  • I = P/ E
  • I = (P / R)1/2

Электрическое сопротивление:

  • R = U / I
  • R = U 2/ P
  • R = P / I2

НЕ ЗАБЫВАЕМ: Законы Кирхгофа они же Правила Кирхгофа для тока и напряжения.

Цепь переменного синусоидального тока c частотой ω.

Применимость формул: пренебрегаем зависимостью сопротивлений от силы тока и частоты.

Напомним, что любой сигнал, может быть с любой точностью разложен в ряд Фурье, т.е. в предположении, что параметры сети
частотнонезависимы — данная формулировка применима ко всем гармоникам любого сигнала.

Закон Ома для цепей переменного тока:

  • U=I*Z

    • где:
      • Естественно, применительно к цепям переменного тока можно говорить и об активной/реактивной мощности.
  • U = U0eiωt  напряжение или разность потенциалов,
  • I  сила тока,
  • Z = Re—iφ  комплексное сопротивление (импеданс)
  • R = (Ra2+Rr2)1/2  полное сопротивление,
  • Rr = ωL — 1/ωC  реактивное сопротивление (разность индуктивного и емкостного),
  • Rа  активное (омическое) сопротивление, не зависящее от частоты,
  • φ = arctg Rr/Ra — сдвиг фаз между напряжением и током.
Источник

Понравилась статья? Поделить с друзьями:
  • Как составить план текста для изложения 4 класс
  • Как найти номер прокси сервер
  • Как найти подписчиков в инстаграме с нуля
  • Как найти репетитора для онлайн занятий
  • Как найти драйвер для блютуз колонки