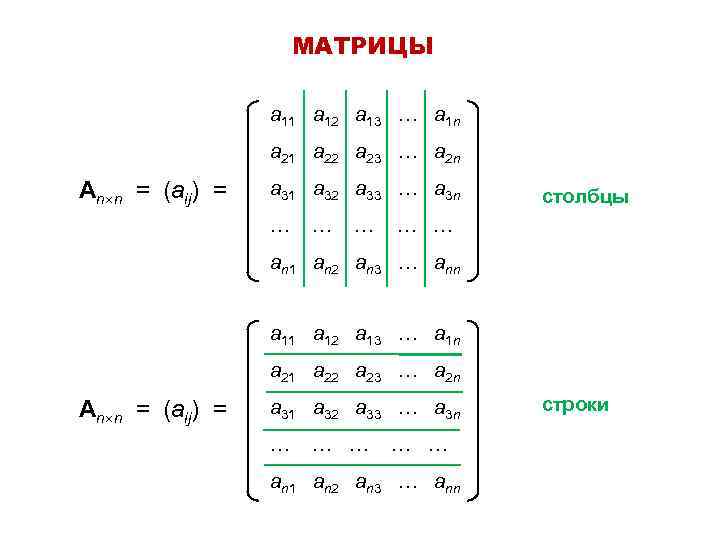
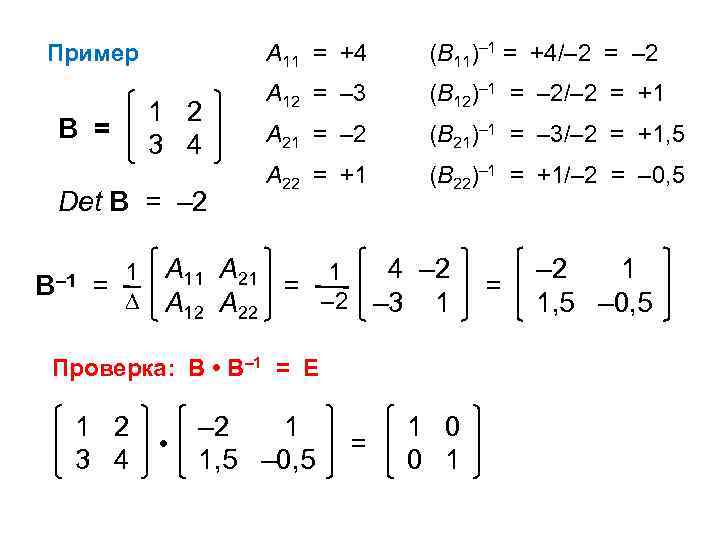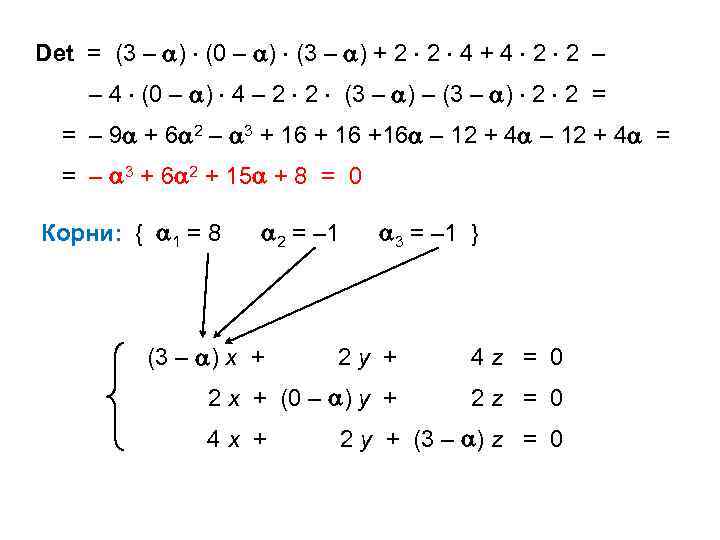МАТРИЦЫ а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n An n = (aij) = a 31 a 32 a 33 … a 3 n … … … столбцы … … an 1 an 2 an 3 … ann а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n An n = (aij) = a 31 a 32 a 33 … a 3 n … … … an 1 an 2 an 3 … ann строки
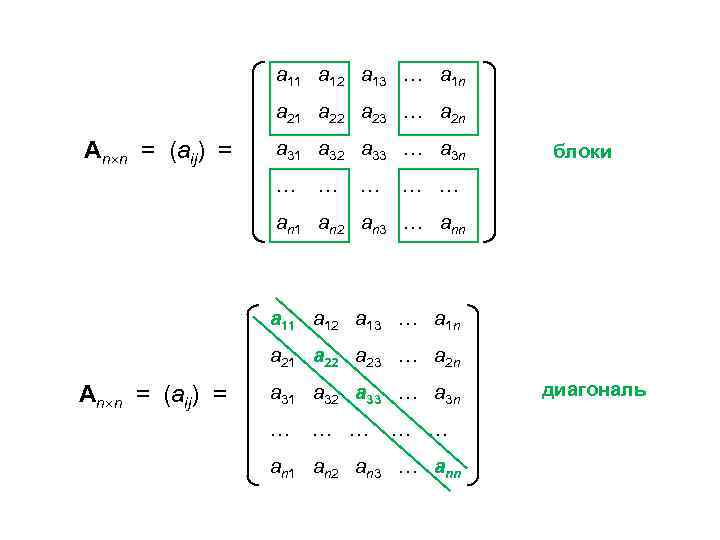
а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n An n = (aij) = a 31 a 32 a 33 … a 3 n … … … блоки … … an 1 an 2 an 3 … ann а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n An n = (aij) = a 31 a 32 a 33 … a 3 n … … … an 1 an 2 an 3 … ann диагональ
Характеристики матриц 1. След Sp = a 11 + a 22 + … + ann = aii 2. Определитель (детерминант) Метод разложения по элементам строки (столбца) 1) выбрать в матрице некоторую строку (обычно выбирается та строка, которая содержит наибольшее количество нулей); 2) записать первый элемент выбранной строки и умножить его на вспомогательную матрицу (минор), которая получается из исходной посредством вычеркивания строки и столбца, на пересечении которых стоит выписанный элемент;
а 11 а 12 а 13 … a 1 n a 21 a 22 a 23 … a 2 n An n = (aij) = a 31 a 32 a 33 … a 3 n … … … an 1 an 2 an 3 … ann а 11 а 12 а 13 … a 1 n a 22 a 23 … a 2 n a 21 a 22 a 23 … a 2 n Det A = a 31 a 32 a 33 … a 3 n … … … an 1 an 2 an 3 … ann = a 11 a 32 a 33 … a 3 n … … +… an 2 an 3 … ann 3) выполнить описанный выше прием для всех элементов выделенной строки;
a 21 a 23 … a 2 n + a 12 a 21 a 22 … a 2 n– 1 a 33 … a 3 n a 31 a 32 … a 3 n– 1 … … an 1 an 3 … ann + … + a 1 n … … an 1 an 2 … ann– 1 4) каждое произведение дополнительно умножить на (– 1)i+j, где i и j — индексы элемента выделенной строки. В итоге большой определитель представляется в виде линейной комбинации определителей, размерность которых на 1 меньше, чем у исходного.
5) применить описанную процедуру ко всем определителям с размерностью (n – 1), в результате чего каждый из них превратится в линейную комбинацию определителей размерностью (n – 2). Систематически повторяя процедуру, мы, в конце концов, придем к длинной линейной комбинации определителей с размерностью 1, т. е. обычных чисел. Для завершения процедуры нужно выполнить все перемножения, сложения и вычитания, что даст в итоге единственное число — определитель матрицы А.
Пример Det A = – 48 Det A = = 2 (5 5 – 7 1) – 4 (3 5 – 7 4) + 8 (3 1 – 5 4) = 2 (25 – 7) – 4 (15 – 28) + 8 (3 – 20) = = 2 (18) – 4 (– 13) + 8 (– 17) = 36 + 52 – 136 = – 48 3. Перманент (плюс-определитель) Метод вычисления тот же самый, что и для определителя, но вместо дополнительного множителя (– 1)i+j используется множитель (+1)i+j
Пример Per A = 420 Per A = = 2 (5 5 + 7 1) + 4 (3 5 + 7 4) + 8 (3 1 + 5 4) = 2 (25 + 7) + 4 (15 + 28) + 8 (3 + 20) = = 2 (32) + 4 (43) + 8 (23) = 64 + 172 + 184 = 420 Алгебраическое дополнение Aij = минор (aij) (– 1)i + j Det A = ai 1 Ai 1 + ai 2 Ai 2 + … + ain Ain
Операции над матрицами 1. Сложение матриц А + В = С Аij + Вij = Сij 2. Умножение матрицы на число А = D Аij = Dij 3. Линейные комбинации А + В + С + … = F Аij + Вij + Сij + … = Fij
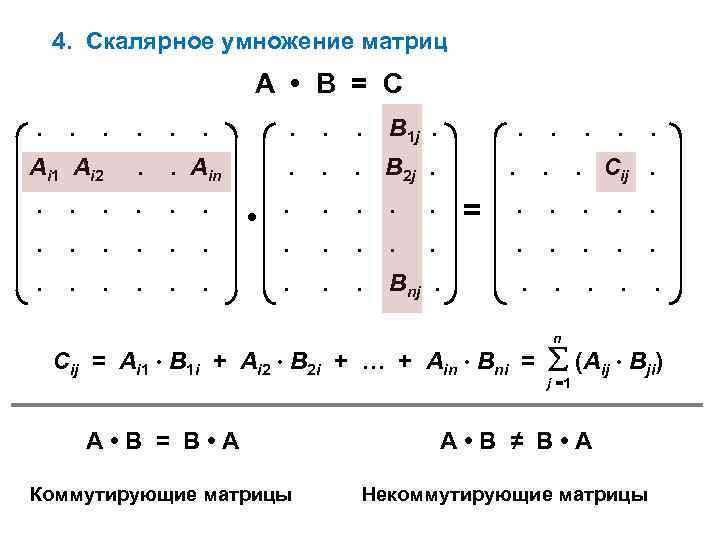
4. Скалярное умножение матриц А • В = С. . . Аi 1 Ai 2 . . Ain . . B 1 j. . • . . . B 2 j. . . . . Cij. . . Bnj. . . = n Cij = Ai 1 B 1 i + Ai 2 B 2 i + … + Ain Bni = (Aij Bji) j =1 A • B = B • A Коммутирующие матрицы A • B ≠ B • A Некоммутирующие матрицы
Примеры 1 2 3 4 5 • 1 2 3 4 5 6 7 8 + • • 5 6 7 8 1 2 3 4 = = 6 8 10 12 5 10 15 20 19 22 43 50 23 34 31 46 Матрицы не коммутируют
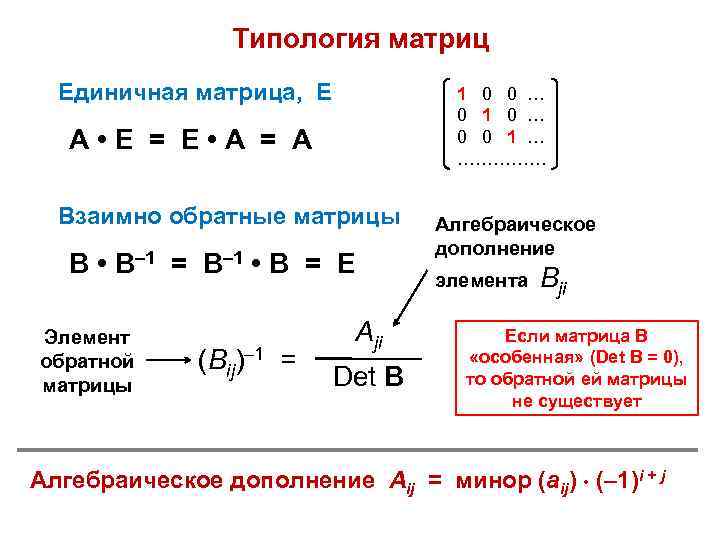
Типология матриц Единичная матрица, Е 1 0 0 … 0 1 0 … 0 0 1 … …………… А • Е = Е • А = А Взаимно обратные матрицы В • В– 1 = В– 1 • В = Е Элемент обратной матрицы (Вij)– 1 = Aji Det В Алгебраическое дополнение элемента Вji Если матрица В «особенная» (Det В = 0), то обратной ей матрицы не существует Алгебраическое дополнение Aij = минор (aij) (– 1)i + j
Пример В = А 11 = +4 1 2 3 4 Det B = – 2 В– 1 1 = (В 11)– 1 = +4/– 2 = – 2 А 12 = – 3 (В 12)– 1 = – 2/– 2 = +1 А 21 = – 2 (В 21)– 1 = – 3/– 2 = +1, 5 А 22 = +1 (В 22)– 1 = +1/– 2 = – 0, 5 А 11 А 21 4 – 2 1 = – 2 А 12 А 22 – 3 1 Проверка: В • В– 1 = Е 1 2 3 4 • – 2 1 1, 5 – 0, 5 = 1 0 0 1 = – 2 1 1, 5 – 0, 5
Взаимно транспонированные матрицы В = 1 2 3 4 1 3 В = 2 4 Т Симметричные матрицы В = В Т Ортогонгальные матрицы В– 1 = В Т В = В– 1 = cos φ – sin φ cos φ sin φ – sin φ cos φ
Комплексно сопряженные матрицы В = 1+i 2–i 3 – 2 i 4 В* = 1–i 2+i 3 + 2 i 4 Эрмитово сопряженные матрицы В = 1+i 2–i 3 – 2 i 4 + В = 1 – i 3 + 2 i 2+i 4 Самосопряженные (эрмитовы) матрицы В = В + Аналоги симметричных матриц Унитарные матрицы В– 1 = В + Аналоги ортогональных матриц
Линейные операторы F 11 F 12. . . F 1 n x 1 y 1 F 22. . . F 2 n x 2 y 2 . . . Fn 1 Fn 2. . . Fnn • . xn F (X) = Y = . yn F ( X) = F (X) F (X + Y) = F (X) + F (Y) ОПЕРАТОР, трансформирующий исходный вектор X в конечный вектор Y ВЕКТОРЫ, принадлежащие к одному ВП Условия линейности
Преобразование векторов-строк F 11 F 12. . . F 1 n ( x 1 x 2 … xn ) • F 21 F 22. . . F 2 n. . . = ( y 1 y 2 … yn ) Fn 1 Fn 2. . . Fnn F (X) = Y «столбец столбец» (X)F = Y «строка строка»
1. Любая квадратная матрица может выступать в роли оператора 2. Любой оператор может быть изображен в виде квадратной матрицы Единичный оператор 1 0 0 x 0 1 0 • y 0 0 1 z Оператор растяжения 2 0 0 x 0 2 0 • y 0 0 2 z Оператор проектирования на ось Z 0 0 0 x 0 0 0 • y 0 0 1 z = x y z = 2 x 2 y 2 z = 0 0 z
Матричные представления операций симметрии Единичная операция E x y z Е x y z 1 0 0 x 0 1 0 • y 0 0 1 z = x y z = –x –y –z Инверсия E x y z i –x –y –z – 1 0 0 x 0 – 1 0 • y 0 0 – 1 z
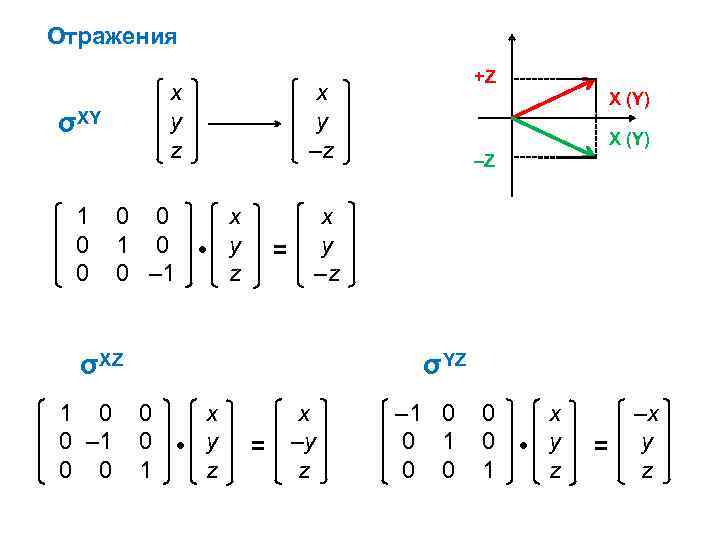
Отражения x y z x y –z 0 0 x 1 0 • y 0 – 1 z x y –z σXY 1 0 0 = σXZ 1 0 0 – 1 0 0 +Z X (Y) –Z σYZ 0 x 0 • y 1 z = x –y z – 1 0 0 0 x 0 • y 1 z = –x y z
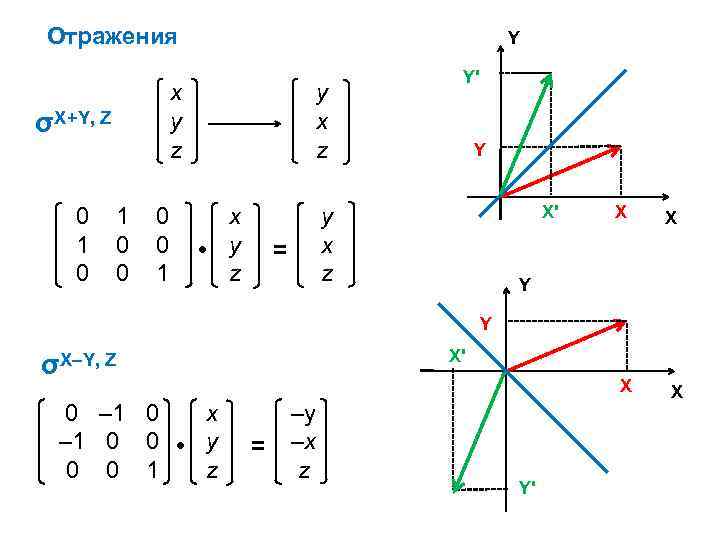
Отражения x y z σX+Y, Z 0 1 0 Y 1 0 0 1 y x z x • y z Y’ Y X’ y x z = X X Y Y X’ σX–Y, Z 0 – 1 0 x – 1 0 0 • y 0 0 1 z X = –y –x z Y’ X
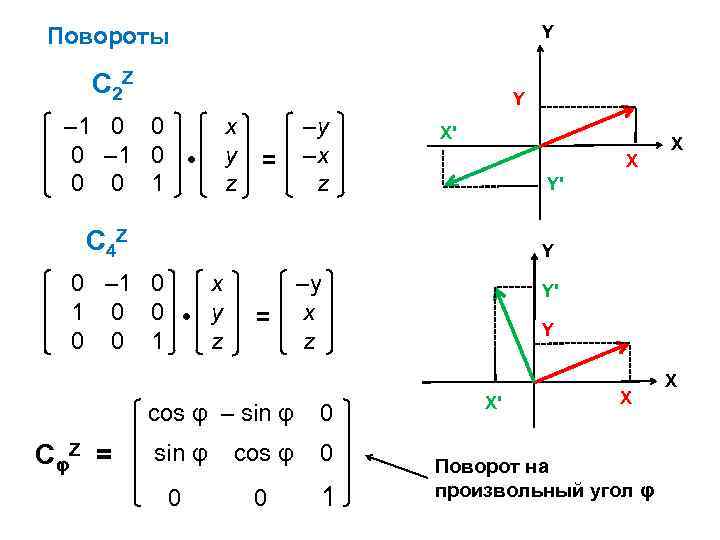
Y Повороты С 2 Z Y – 1 0 0 0 – 1 0 • 0 0 1 x y z = –y –x z X’ X Y’ С 4 Z Y 0 – 1 0 x 1 0 0 • y 0 0 1 z = –y x z cos φ – sin φ Сφ Z = X 0 sin φ cos φ 0 0 0 1 Y’ Y X’ X Поворот на произвольный угол φ X
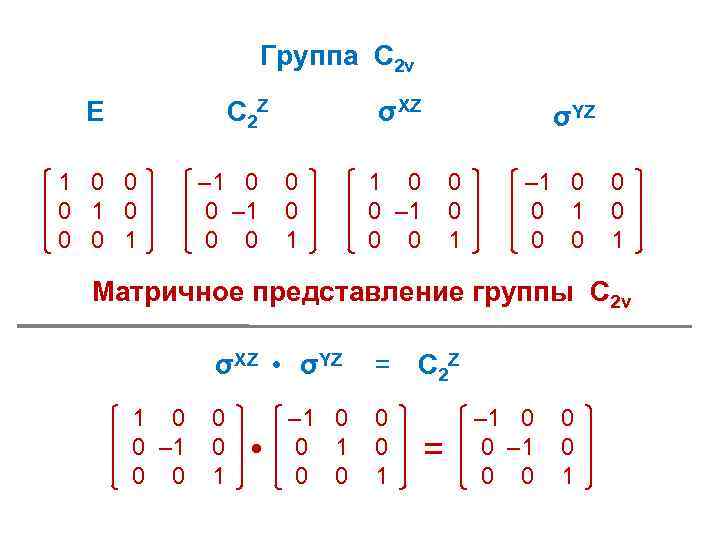
Группа С 2 v E C 2 Z 1 0 0 0 1 – 1 0 0 σXZ 0 0 1 σYZ 1 0 0 – 1 0 0 1 – 1 0 0 0 0 1 Матричное представление группы С 2 v σXZ • σYZ 1 0 0 – 1 0 0 = C 2 Z 0 0 1 • – 1 0 0 = – 1 0 0 0 0 1
Домашнее задание Задача 3. 1. Установить, коммутируют ли между собой заданные операции симметрии, найти коммутатор. 1) найти матричные представления операций 2) найти произведения: F 1 3) найти коммутатор: • F 2 и F 1 и F 2; F 2 • F 1; С = F 1 • F 2 – F 2 • F 1
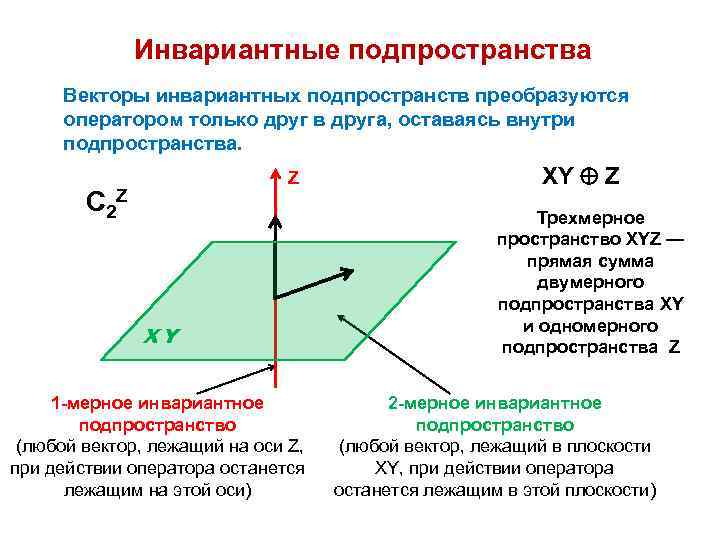
Инвариантные подпространства Векторы инвариантных подпространств преобразуются оператором только друг в друга, оставаясь внутри подпространства. Z C 2 Z ХY 1 -мерное инвариантное подпространство (любой вектор, лежащий на оси Z, при действии оператора останется лежащим на этой оси) XY Z Трехмерное пространство XYZ — прямая сумма двумерного подпространства XY и одномерного подпространства Z 2 -мерное инвариантное подпространство (любой вектор, лежащий в плоскости XY, при действии оператора останется лежащим в этой плоскости)
σXZ σYZ Z Z X Z Y Y X YZ X XZ Y X YZ
Спектральные свойства операторов F (X) = Y Уравнение на собственные значения Собственное значение Y F (А) = А X Спектр оператора Собственный вектор (инвариантное подпространство) 1 2 3 … n A 1 A 2 A 3 … A n n — размерность пространства
F (А) = А F 11 F 12. . . F 1 n a 1 F 21 F 22. . . F 2 n a 2 . . . • . Fn 1 Fn 2. . . = . Fnn . . an an F 11 а 1 + F 12 а 2 +. . . + F 1 n аn = a 1 F 21 а 1 + F 22 а 2 +. . . + F 2 n аn = a 2. . . Fn 1 а 1 + Fn 2 а 2 +. . . + Fnn аn = an
(F 11 – ) а 1 + F 12 а 2 +. . . + F 1 n аn = 0 F 21 а 1 + (F 22 – ) а 2 +. . . + F 2 n аn = 0. . . Fn 1 а 1 + Fn 2 а 2 +. . . + (Fnn – ) аn = 0 Однородная система линейных уравнений Условие разрешимости: Det = 0 (F 11 – ) F 12 . Fn 1 F 1 n (F 22 – ). . . F 2 n F 21. . . . Fn 2 . . . . (Fnn – ) = 0
Сn n + Сn– 1 + Сn– 2 +. . . + С 1 + Co = 0 Характеристическое уравнение Основная теорема алгебры: всякое уравнение степени n имеет n корней Корни: { 1 2 … n } — собственные значения оператора F (F 11 – ) а 1 + F 12 а 2 +. . . + F 1 n аn = 0 F 21 а 1 + (F 22 – ) а 2 +. . . + F 2 n аn = 0. . . Fn 1 а 1 + Fn 2 а 2 +. . . + (Fnn – ) аn = 0
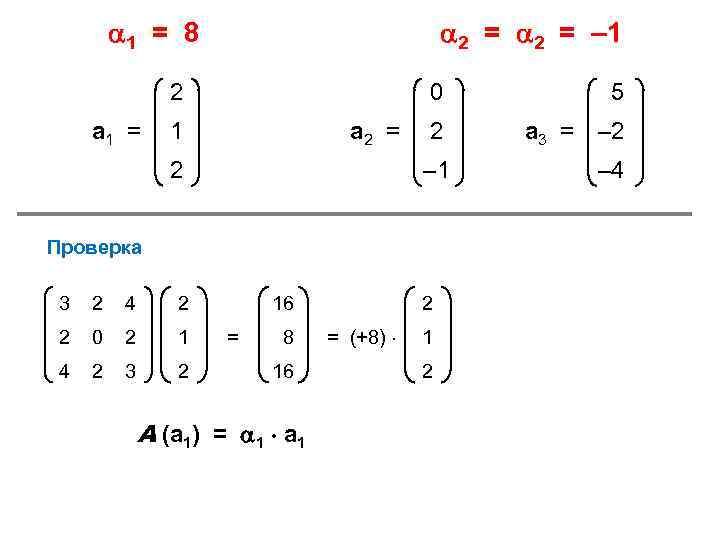
1 a 1 = 2 a 1 a 2 a 2 = … an Пример: an = • • • … an 1 n … an 2 2 4 2 0 2 4 2 3 2 4 2 A = 3– 3 … 0– 2 4 2 3– = 0 n
Det = (3 – ) (0 – ) (3 – ) + 2 2 4 + 4 2 2 – – 4 (0 – ) 4 – 2 2 (3 – ) – (3 – ) 2 2 = = – 9 + 6 2 – 3 + 16 +16 – 12 + 4 = = – 3 + 6 2 + 15 + 8 = 0 Корни: { 1 = 8 2 = – 1 (3 – ) х + 3 = – 1 } 2 y + 4 z = 0 2 x + (0 – ) y + 2 z = 0 4 x + 2 y + (3 – ) z = 0
– 5 х + 2 y + 4 z = 0 2 x – 8 y + 2 z = 0 4 x + 2 y – 5 z = 0 1 = 8 Вычитая третье уравнение из первого, получим: – 9 x + 9 z = 0 или x = z. Подставим этот результат во второе уравнение и получим: 4 х – 8 у = 0 или у = х/2. Теперь мы можем выразить все три координаты вектора через одну, например, через х: х=х у = х/2 z=x x Решение: а 1 = x/2 = (х/2) x 2 1 2
= – 1 4 х + 2 y+ 4 z = 0 2 x + 1 y+ 2 z = 0 4 x + 2 y+ 4 z = 0 Видно, что все три уравнения одинаковы и задают только одно соотношение между тремя неизвестными. Поэтому мы можем произвольно выбрать значения двух неизвестных, а третье уже выразить через эти два. Уравнение 2 x + 1 y + 2 z = 0 определяет некоторую плоскость (двумерное инвариантное подпространство) в трехмерном пространстве. Любой вектор, лежащий на этой плоскости является решением нашей системы и, следовательно, будет собственным для нашего оператора. Экономный способ задать все эти векторы заключается в выборе базиса — двух ортогональных векторов на плоскости.
Первый базисный вектор можно выбрать произвольно. Положим, например, х = 0 и у = 1. Тогда из уравнения плоскости 2 x + 1 y + 2 z = 0 следует, что z = – 1/2. Второй базисный вектор должен удовлетворять как уравнению плоскости (2 x + 1 y + 2 z = 0), так и условию ортогональности: x (0, 1, – 1/2) y = y – 1/2 z = 0 z Решая совместно эти два уравнения, получим: у = – 2/5 х и z = – 4/5 х. 0 а 2 = 1 – 1/2 1 a 3 = – 2/5 – 4/5 0 а 2 = 2 – 1 5 a 3 = – 2 – 4
1 = 8 2 = – 1 2 a 1 = 0 a 2 = 2 2 a 3 = – 2 – 1 1 5 – 4 Проверка 3 2 4 2 2 0 2 1 4 2 3 2 16 = 8 16 А (а 1) = 1 а 1 2 = (+8) 1 2
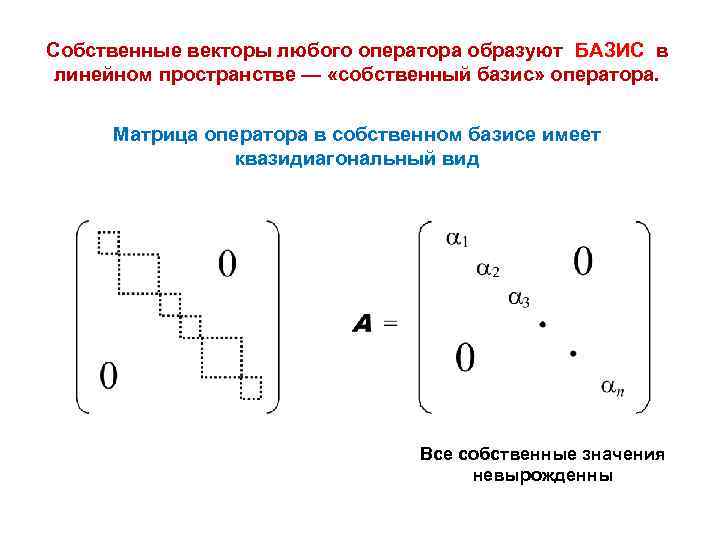
Собственные векторы любого оператора образуют БАЗИС в линейном пространстве — «собственный базис» оператора. Матрица оператора в собственном базисе имеет квазидиагональный вид Все собственные значения невырожденны
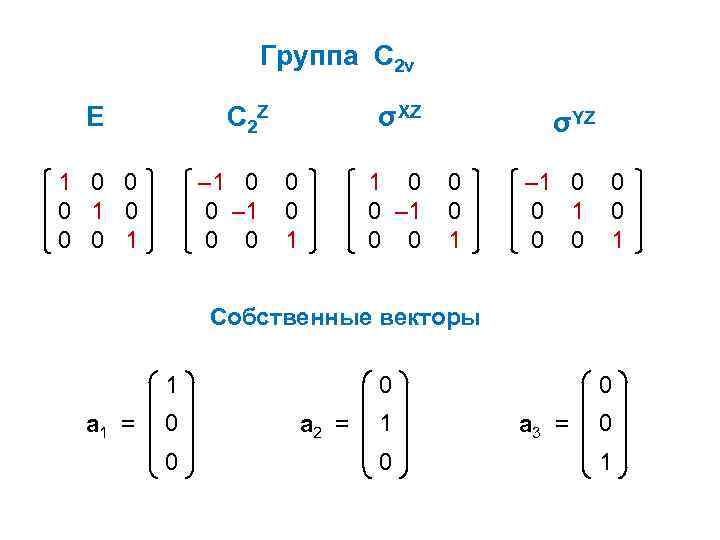
Группа С 2 v E C 2 Z 1 0 0 0 1 – 1 0 0 σXZ 0 0 1 1 0 0 – 1 0 0 σYZ 0 0 1 – 1 0 0 0 0 1 Собственные векторы 1 a 1 = 0 0 0 a 2 = 1 0 0 a 3 = 0 1
Домашнее задание Задача 3. 2. Для заданной матрицы найти собственные значения и собственные векторы: 1 = ? 2 = ? ? ? a 1 = ? ? a 2 = ? ? a 3 = ? ? (все собственные значения являются целыми числами)
Онлайн калькулятор. Определитель матрицы. Детерминант матрицы
Используя этот онлайн калькулятор для вычисления определителя (детерминанта) матриц, вы сможете очень просто и быстро найти определитель (детерминант) матрицы.
Воспользовавшись онлайн калькулятором для вычисления определителя (детерминанта) матриц, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на транспонирование матриц, а также закрепить пройденный материал.
Найти определитель (детерминант) матрицы
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.
1.
Матрицей А Размера
Называется таблица из Т·п чисел
Часто для краткости пишут А = ||Aij||. Числа, из которых состоит матрица, называются Элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент А23 находится на пересечении второй строки и третьего столбца:
Элементы А11, А22, А33, … называются Главной диагональю матрицы
Если матрица А имеет размер то такую матрицу называют Квадратной матрицей порядка П.
Две матрицы одинакового размера А = ||Aij|| и B = ||Bij|| называют Равными (при этом пишут А = В), если
.
Упражнение 1.

Найти А12 и А23.
Решение.
Элемент А12 располагается в первой строке и втором столбце, то есть это второй элемент первой строки: А12 = -1.
Соответственно А23 – элемент, стоящий во второй строке и в третьем столбце;
А23 = -3.
Упражнение 2.
Даны матрицы

При каких A и B А=В?
Решение.
У равных матриц должны быть равными соответствующие элементы. Для элементов, заданных численно, это условие выполняется: A12 = B12 = 1,
A22 = B22 = 3. Поскольку B11 = 4, a A21 = -2, для равенства матриц А и В должны выполняться условия:

Следовательно, A = ±2, B = -2.
Ответ: A = ±2, B = -2.
| < Предыдущая | Следующая > |
|---|
1
Первый слайд презентации
МАТРИЦЫ
а 11 а 12 а 13 … a 1 n
a 21 a 22 a 23 … a 2 n
a 31 a 32 a 33 … a 3 n
… … … … …
a n 1 a n 2 a n 3 … a nn
A n n = ( a ij ) =
столбцы
а 11 а 12 а 13 … a 1 n
a 21 a 22 a 23 … a 2 n
a 31 a 32 a 33 … a 3 n
… … … … …
a n 1 a n 2 a n 3 … a nn
A n n = ( a ij ) =
строки
Изображение слайда
а 11 а 12 а 13 … a 1 n
a 21 a 22 a 23 … a 2 n
a 31 a 32 a 33 … a 3 n
… … … … …
a n 1 a n 2 a n 3 … a nn
A n n = ( a ij ) =
блоки
а 11 а 12 а 13 … a 1 n
a 21 a 22 a 23 … a 2 n
a 31 a 32 a 33 … a 3 n
… … … … …
a n 1 a n 2 a n 3 … a nn
A n n = ( a ij ) =
диагональ
Изображение слайда
Характеристики матриц
1. След
Sp = a 11 + a 22 + … + a nn = a ii
2. Определитель (детерминант)
Метод разложения по элементам строки (столбца)
1) выбрать в матрице некоторую строку (обычно выбирается та строка, которая содержит наибольшее количество нулей);
2) записать первый элемент выбранной строки и умножить его на вспомогательную матрицу ( минор ), которая получается из исходной посредством вычеркивания строки и столбца, на пересечении которых стоит выписанный элемент;
Изображение слайда
а 11 а 12 а 13 … a 1 n
a 21 a 22 a 23 … a 2 n
a 31 a 32 a 33 … a 3 n
… … … … …
a n 1 a n 2 a n 3 … a nn
A n n = ( a ij ) =
а 11 а 12 а 13 … a 1 n
a 21 a 22 a 23 … a 2 n
a 31 a 32 a 33 … a 3 n
… … … … …
a n 1 a n 2 a n 3 … a nn
Det A =
= a 11
a 22 a 23 … a 2 n
a 32 a 33 … a 3 n
… … … …
a n 2 a n 3 … a nn
+ …
3) выполнить описанный выше прием для всех элементов выделенной строки ;
Изображение слайда
+ a 12
a 21 a 23 … a 2 n
a 31 a 33 … a 3 n
… … … …
a n 1 a n 3 … a nn
+ … + a 1 n
a 21 a 22 … a 2 n–1
a 31 a 32 … a 3 n–1
… … … …
a n 1 a n 2 … a nn–1
4) каждое произведение дополнительно умножить на (–1) i+j, где i и j — индексы элемента выделенной строки.
В итоге большой определитель представляется в виде линейной комбинации определителей, размерность которых на 1 меньше, чем у исходного.
Изображение слайда
5) применить описанную процедуру ко всем определителям с размерностью ( n – 1 ), в результате чего каждый из них превратится в линейную комбинацию определителей размерностью ( n – 2).
Систематически повторяя процедуру, мы, в конце концов, придем к длинной линейной комбинации определителей с размерностью 1, т.е. обычных чисел.
Для завершения процедуры нужно выполнить все перемножения, сложения и вычитания,что даст в итоге единственное число — определитель матрицы А.
Изображение слайда
Пример
Det A =
= 2 (5 5 – 7 1) – 4 (3 5 – 7 4) + 8 (3 1 – 5 4)
= 2 (25 – 7) – 4 (15 – 28) + 8 (3 – 20) =
= 2 (18) – 4 (–13) + 8 (–17) = 36 + 52 – 136 = – 48
Det A = –48
3. Перманент (плюс-определитель)
Метод вычисления тот же самый, что и для определителя, но вместо дополнительного множителя (–1) i+j используется множитель (+1) i+j
Изображение слайда
Пример
Per A =
= 2 (5 5 + 7 1) + 4 (3 5 + 7 4) + 8 (3 1 + 5 4)
= 2 (25 + 7) + 4 (15 + 28) + 8 (3 + 20) =
= 2 ( 32 ) + 4 ( 4 3) + 8 ( 23 ) = 6 4 + 172 + 1 84 = 4 20
Per A = 420
Алгебраическое дополнение A ij = минор ( a ij ) (–1) i + j
Det A = a i 1 A i 1 + a i 2 A i 2 + … + a in A in
Изображение слайда
Операции над матрицами
1. Сложение матриц
А + В = С
2. Умножение матрицы на число
А = D
3. Линейные комбинации
А + В + С + … = F
А ij + В ij = С ij
А ij = D ij
А ij + В ij + С ij + … = F ij
Изображение слайда
4. Скалярное умножение матриц
А • В = С
……… B 1 j……
А i 1 A i 2.. A in… B 2 j…. C ij.
…………….
…………….
……… B nj……
•
=
C ij = A i 1 B 1 i + A i 2 B 2 i + … + A in B ni = ( A ij B ji )
j =1
n
A • B = B • A
A • B ≠ B • A
Коммутирующие матрицы
Некоммутирующие матрицы
Изображение слайда
Примеры
1 2
3 4
5 6
7 8
6 8
10 12
+ =
1 2
3 4
=
5 •
5 10
15 20
Матрицы не коммутируют
1 2
3 4
5 6
7 8
19 22
43 50
• =
5 6
7 8
1 2
3 4
23 34
31 46
• =
Изображение слайда
Типология матриц
Взаимно обратные матрицы
В • В –1 = В –1 • В = Е
Если матрица В « особенная» ( Det В = 0), то обратной ей матрицы не существует
( В ij ) –1 =
A ji
Det В
Алгебраическое дополнение элемента В ji
Элемент обратной матрицы
Единичная матрица, Е
А • Е = Е • А = А
1 0 0 …
0 1 0 …
0 0 1 …
……………
Алгебраическое дополнение A ij = минор ( a ij ) (–1) i + j
Изображение слайда
Пример
1 2
3 4
В =
А 11 = +4
А 12 = –3
А 21 = –2
А 22 = +1
( В 11 ) –1 = +4 /–2 = –2
( В 1 2 ) –1 = – 2/–2 = +1
( В 2 1 ) –1 = – 3/–2 = +1,5
( В 22 ) –1 = + 1/–2 = –0,5
Det B = –2
1 2
3 4
– 2 1
1,5 –0,5
•
=
1 0
0 1
Проверка: В • В –1 = Е
В –1 =
А 11 А 21 А 12 А 22
1
=
4 –2 –3 1
1
–2
– 2 1
1,5 –0,5
=
Изображение слайда
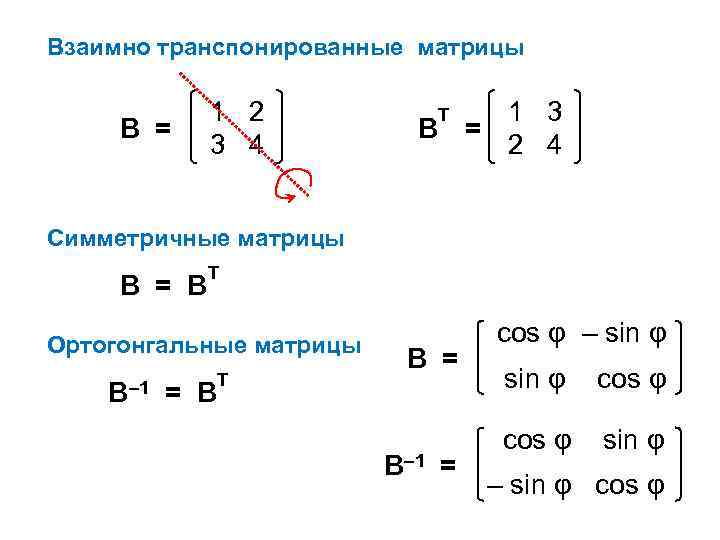
Взаимно транспонированные матрицы
1 2
3 4
В =
1 3
2 4
В Т =
Симметричные матрицы
В –1 = В Т
В = В Т
Ортогонгальные матрицы
cos φ – sin φ
sin φ cos φ
В =
cos φ sin φ
– sin φ cos φ
В –1 =
Изображение слайда
Комплексно сопряженные матрицы
1 + i 2 – i
3 – 2 i 4
В =
В = В +
Самосопряженные (эрмитовы) матрицы
1 – i 2 + i
3 + 2 i 4
В * =
Эрмитово сопряженные матрицы
1 + i 2 – i
3 – 2 i 4
В =
1 – i 3 + 2 i
2 + i 4
В + =
В –1 = В +
Унитарные матрицы
Аналоги симметричных матриц
Аналоги ортогональных матриц
Изображение слайда
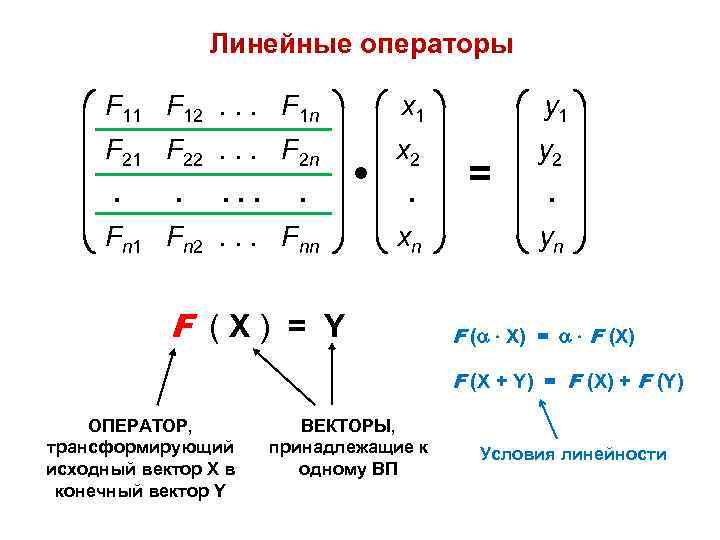
Линейные операторы
F 11 F 12… F 1 n x 1 y 1
F 21 F 22… F 2 n x 2 y 2
……..
F n 1 F n 2… F nn x n y n
• =
F ( X ) = Y
ОПЕРАТОР, трансформирующий исходный вектор X в конечный вектор Y
ВЕКТОРЫ, принадлежащие к одному ВП
F ( X) = F ( X)
F ( X + Y) = F ( X) + F (Y)
Условия линейности
Изображение слайда
F 11 F 12… F 1 n
F 21 F 22… F 2 n
……
F n 1 F n 2… F nn
( x 1 x 2 … x n ) •
= ( y 1 y 2 … y n )
Преобразование векторов-строк
F ( X ) = Y
( X ) F = Y
«столбец столбец»
«строка строка»
Изображение слайда
1. Любая квадратная матрица может выступать в роли оператора
2. Любой оператор может быть изображен в виде квадратной матрицы
Единичный оператор
1 0 0 x x
0 1 0 y y
0 0 1 z z
• =
Оператор растяжения
2 0 0 x 2 x
0 2 0 y 2 y
0 0 2 z 2 z
• =
Оператор проектирования на ось Z
0 0 0 x 0
0 0 0 y 0
0 0 1 z z
• =
Изображение слайда
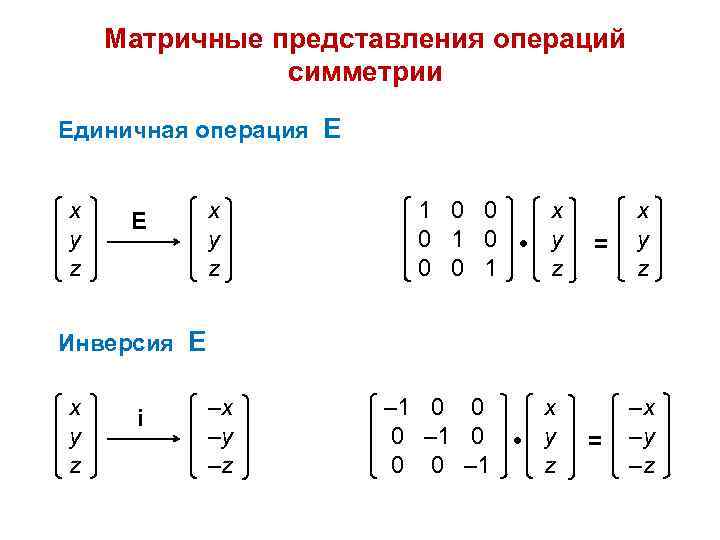
Матричные представления операций симметрии
1 0 0 x x
0 1 0 y y
0 0 1 z z
• =
Единичная операция E
x x
y y
z z
Е
Инверсия E
– 1 0 0 x – x
0 – 1 0 y – y
0 0 – 1 z – z
• =
x – x
y – y
z – z
i
Изображение слайда
σ XY
1 0 0 x x
0 – 1 0 y – y
0 0 1 z z
• =
σ XZ
Отражения
+Z
X (Y)
–Z
X (Y)
1 0 0 x x
0 1 0 y y
0 0 – 1 z – z
• =
x x
y y
z – z
– 1 0 0 x – x
0 1 0 y y
0 0 1 z z
• =
σ YZ
Изображение слайда
σ X+Y, Z
0 –1 0 x –y
–1 0 0 y – x
0 0 1 z z
• =
σ X–Y, Z
Отражения
0 1 0 x y
1 0 0 y x
0 0 1 z z
• =
x y
y x
z z
X
X
Y
Y
X ‘
Y ‘
X
X
Y
Y
X ‘
Y ‘
Изображение слайда
С 2 Z
0 –1 0 x –y
1 0 0 y x
0 0 1 z z
• =
С 4 Z
Повороты
–1 0 0 x – y
0 –1 0 y – x
0 0 1 z z
• =
X
X
Y
Y
X ‘
Y ‘
X
X
Y
Y
X ‘
Y ‘
cos φ – sin φ 0
sin φ cos φ 0
0 0 1
С φ Z =
Поворот на произвольный угол φ
Изображение слайда
Матричное представление группы С 2 v
1 0 0
0 1 0
0 0 1
– 1 0 0
0 – 1 0
0 0 1
E
C 2 Z
1 0 0
0 – 1 0
0 0 1
– 1 0 0
0 1 0
0 0 1
Группа С 2 v
σ XZ
σ YZ
σ XZ
σ YZ
C 2 Z
• =
1 0 0
0 – 1 0
0 0 1
– 1 0 0
0 1 0
0 0 1
– 1 0 0
0 – 1 0
0 0 1
• =
Изображение слайда
Домашнее задание
Задача 3.1. Установить, коммутируют ли между собой заданные операции симметрии, найти коммутатор.
1) найти матричные представления операций F 1 и F 2 ;
2) найти произведения: F 1 • F 2 и F 2 • F 1 ;
3) найти коммутатор: С = F 1 • F 2 – F 2 • F 1
Изображение слайда
Инвариантные подпространства
Векторы инвариантных подпространств преобразуются оператором только друг в друга, оставаясь внутри подпространства.
C 2 Z
2-мерное инвариантное подпространство
(любой вектор, лежащий в плоскости XY, при действии оператора останется лежащим в этой плоскости)
1-мерное инвариантное подпространство
(любой вектор, лежащий на оси Z, при действии оператора останется лежащим на этой оси)
X Y Z
Z
Х Y
Трехмерное пространство X Y Z — прямая сумма двумерного подпространства X Y и одно мерного подпространства Z
Изображение слайда
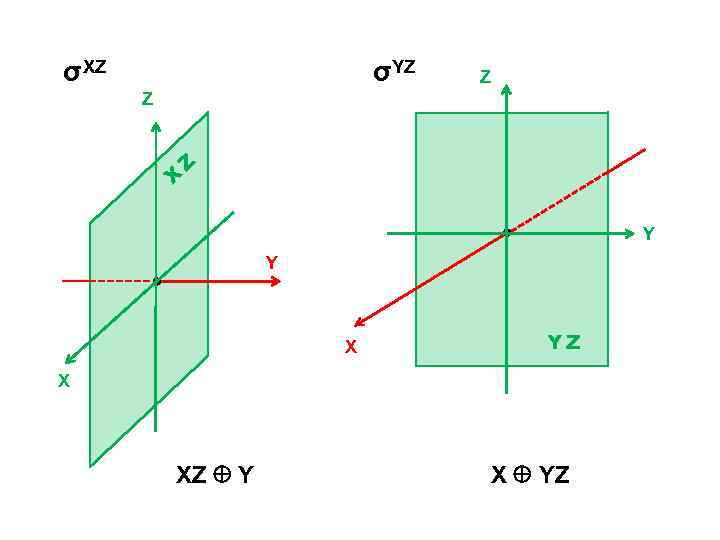
σ XZ
Y
XZ
XZ Y
Z
X
σ YZ
X
YZ
X Y Z
Z
Y
Изображение слайда
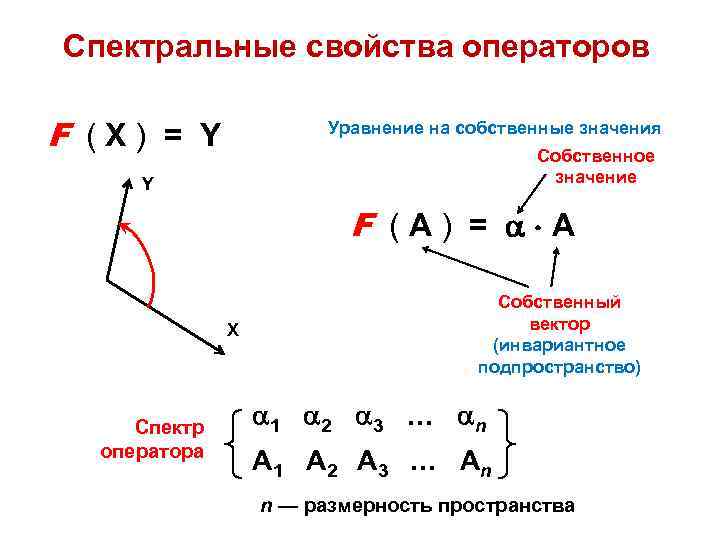
Спектральные свойства операторов
F ( X ) = Y
F ( А ) = А
X
Y
Собственный вектор (инвариантное подпространство)
Собственное значение
Уравнение на собственные значения
1 2 3 … n
A 1 A 2 A 3 … A n
Спектр оператора
n — размерность пространства
Изображение слайда
F ( А ) = А
F 11 F 12… F 1 n a 1 a 1
F 21 F 22… F 2 n a 2 a 2
………
F n 1 F n 2… F nn a n a n
• =
F 11 а 1 + F 12 а 2 +… + F 1 n а n = a 1
F 21 а 1 + F 22 а 2 +… + F 2 n а n = a 2
…………..
F n 1 а 1 + F n 2 а 2 +… + F nn а n = a n
Изображение слайда
( F 11 – ) а 1 + F 12 а 2 +… + F 1 n а n = 0
F 21 а 1 + ( F 22 – ) а 2 +… + F 2 n а n = 0
…………..
F n 1 а 1 + F n 2 а 2 +… + ( F nn – ) а n = 0
Однородная система линейных уравнений
Условие разрешимости: Det = 0
( F 11 – ) F 12… F 1 n
F 21 ( F 22 – )… F 2 n
……….
F n 1 F n 2… ( F nn – )
= 0
Изображение слайда
С n n + С n –1 n –1 + С n –2 n –2 +… + С 1 + C o = 0
Характеристическое уравнение
Основная теорема алгебры:
всякое уравнение степени n имеет n корней
Корни: { 1 2 … n } — собственные значения оператора F
( F 11 – ) а 1 + F 12 а 2 +… + F 1 n а n = 0
F 21 а 1 + ( F 22 – ) а 2 +… + F 2 n а n = 0
…………..
F n 1 а 1 + F n 2 а 2 +… + ( F nn – ) а n = 0
Изображение слайда
a 1
a 2
…
a n
a 1 =
1
1 2 … n
a 1
a 2
…
a n
a 2 =
2
a 1
a 2
…
a n
a n =
n
• • •
3 2 4
2 0 2
4 2 3
A =
Пример:
3 – 2 4
2 0 – 2
4 2 3 –
= 0
Изображение слайда
Det = (3 – ) (0 – ) (3 – ) + 2 2 4 + 4 2 2 –
– 4 (0 – ) 4 – 2 2 (3 – ) – (3 – ) 2 2 =
= – 9 + 6 2 – 3 + 16 + 16 +16 – 12 + 4 – 12 + 4 =
= – 3 + 6 2 + 15 + 8 = 0
Корни: { 1 = 8 2 = –1 3 = –1 }
(3 – ) х + 2 y + 4 z = 0
2 x + (0 – ) y + 2 z = 0
4 x + 2 y + (3 – ) z = 0
Изображение слайда
1 = 8
– 5 х + 2 y + 4 z = 0
2 x – 8 y + 2 z = 0
4 x + 2 y – 5 z = 0
Вычитая третье уравнение из первого, получим:
–9 x + 9 z = 0 или x = z.
Подставим этот результат во второе уравнение и получим:
4 х – 8 у = 0 или у = х /2.
Теперь мы можем выразить все три координаты вектора через одну, например, через х :
х = х у = х /2 z = x
Решение :
x
x /2
x
2
1
2
а 1 = = ( х /2)
Изображение слайда
= –1
4 х + 2 y + 4 z = 0
2 x + 1 y + 2 z = 0
4 x + 2 y + 4 z = 0
Видно, что все три уравнения одинаковы и задают только одно соотношение между тремя неизвестными. Поэтому мы можем произвольно выбрать значения двух неизвестных, а третье уже выразить через эти два.
Уравнение 2 x + 1 y + 2 z = 0 определяет некоторую плоскость (двумерное инвариантное подпространство) в трехмерном пространстве. Любой вектор, лежащий на этой плоскости является решением нашей системы и, следовательно, будет собственным для нашего оператора.
Экономный способ задать все эти векторы заключается в выборе базиса — двух ортогональных векторов на плоскости.
Изображение слайда
Первый базисный вектор можно выбрать произвольно. Положим, например, х = 0 и у = 1. Тогда из уравнения плоскости
2 x + 1 y + 2 z = 0
следует, что z = –1/2.
Второй базисный вектор должен удовлетворять как уравнению плоскости ( 2 x + 1 y + 2 z = 0 ), так и условию ортогональности:
x
y
z
(0, 1, –1/2) = y – 1/2 z = 0
Решая совместно эти два уравнения, получим: у = –2/5 х и z = –4/5 х.
0
1
– 1/ 2
1
–2/5
–4/5
а 2 = a 3 =
0
2
– 1
5
–2
–4
а 2 = a 3 =
Изображение слайда
2
1
2
a 1 =
1 = 8 2 = 2 = –1
0
2
–1
a 2 =
5
–2
–4
a 3 =
Проверка
3 2 4
2 0 2
4 2 3
2
1
2
16
8
16
2
1
2
= = (+8)
А (а 1 ) = 1 а 1
Изображение слайда
Собственные векторы любого оператора образуют БАЗИС в линейном пространстве — «собственный базис» оператора.
Матрица оператора в собственном базисе имеет квазидиагональный вид
Все собственные значения невырожденны
Изображение слайда
1 0 0
0 1 0
0 0 1
– 1 0 0
0 – 1 0
0 0 1
E
C 2 Z
1 0 0
0 – 1 0
0 0 1
– 1 0 0
0 1 0
0 0 1
Группа С 2 v
σ XZ
σ YZ
1
0
0
a 1 =
0
1
0
a 2 =
0
0
1
a 3 =
Собственные векторы
Изображение слайда
39
Последний слайд презентации: МАТРИЦЫ
а 11 а 12 а 13 … a 1 n
a 21 a 22 a 23 … a 2 n
a 31 a 32 a 33 … a 3 n
…
Домашнее задание
Задача 3.2. Для заданной матрицы найти собственные значения и собственные векторы:
?
?
?
a 1 =
?
?
?
a 2 =
?
?
?
a 3 =
1 = ? 2 = ? 2 = ?
(все собственные значения являются целыми числами)
Изображение слайда
Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 — 4cdot5 = 27 — 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) — 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 — 0 — 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 — 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 — 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 — 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 — 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 — 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 — 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |