Как найти абсциссу точки алгебра - Исправление недочетов и поиск решений вместе с Examum.ru

Прямоугольная система координат. Ось абсцисс и ординат

О чем эта статья:

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Как найти абсциссу точки окружности

Как найти координаты точки?

О чем эта статья:

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Координатные оси — это прямые, образующие систему координат.
Ось абсцисс Ox — горизонтальная ось.
Ось ординат Oy — вертикальная ось.
Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

верхний правый угол — первая четверть I;
верхний левый угол — вторая четверть II;
нижний левый угол — третья четверть III;
нижний правый угол — четвертая четверть IV;

Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
Если обе координаты отрицательны, то число находится в третьей четверти.
Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0).
Начало координат — точка O. Ее координаты равны нулю: O (0,0).
Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус.
Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

| A₁A₂| 2 =
= ( x₂ – x₁) 2 + ( y₂ – y₁) 2 .

(1)

что и требовалось доказать.

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

9 класс. Геометрия. Метод координат. Уравнение окружности.

Оглавление
Занятия
Обсуждение
О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Решение задач

Выясните, какие из данных уравнений являются уравнениями окружности.

Найдите координаты центра и радиус каждой окружности.

а)

б)

в)

г) ;

д)

Рассмотрим каждое уравнение в отдельности.

а) – окружность,

б) – окружность,

в)
Выделим полный квадрат:

уравнение не является уравнением окружности.

г) .
Выделим полный квадрат:
– окружность,

д)
Выделим полный квадрат:
– окружность,

На окружности, заданной уравнением , найдите точки

а) с абсциссой –4; б) с ординатой 3.

Решение: построим окружность с центром (0;0) радиуса 5 (рис. 1).

Рис. 1. Иллюстрация к задаче

а) Координаты точек окружности с абсциссой –4 являются решениями системы:

Получаем точку и точку

Рис. 2. Иллюстрация к задаче

б) Координаты точек окружности с ординатой 3 являются решениями системы:

Рис. 3. Иллюстрация к задаче

Получаем точку и ту же самую точку

Ответ: .

Запишите уравнение окружности радиуса r с центром в точке А, если

а)

б)

в)

г)

а) Окружность
Ответ:

б) Окружность .
Ответ:

в) Окружность
Ответ:

г) Окружность
Ответ:

Напишите уравнение окружности с центром в начале координат, проходящей через точку

Рис. 4. Иллюстрация к задаче

Найдем радиус, как расстояние ОВ:

Запишем уравнение окружности с центром О(0;0):

Для контроля проверим, удовлетворяют ли полученному уравнению координаты точки В:

значит, точка В лежит на окружности.

Ответ:

Напишите уравнение окружности, проходящей через точку А(1;3), если известно, что центр окружности лежит на оси абсцисс, а радиус равен 5.

Сколько существует таких окружностей?

Дано: А(1;3) – точка окружности,

Найти: уравнение окружности (С; r=5).

Решение: центр искомой окружности удален от точки А(1;3) на расстояние 5, значит, он лежит на окружности с центром в точке А(1;3) радиуса 5, но он еще лежит и на оси Ох. Построим окружность (А(1;3); r=5) (рис. 5).

Рис. 5. Иллюстрация к задаче

Точек, удовлетворяющих нашим условиям, на оси Ох две:

Для определения координат этих точек составим систему:

Запишем уравнения искомых окружностей:

окружность (

окружность ( и построим эти окружности (рис. 6):

Рис. 6. Иллюстрация к задаче

Ответ: две окружности.

Напишите уравнение окружности, проходящей через две заданные точки и В(0;9), если известно, что центр окружности лежит на оси ординат.

Дано: окружности ;

oкружности .

записать уравнение окружности.

Рис. 7. Иллюстрация к задаче

Запишем уравнение окружности так как окружность проходит через точки А и В, то их координаты удовлетворяют уравнению окружности:

Подставим найденные значения в уравнение.

Ответ:

Напишите уравнение окружности с центром в точке А(6;0), проходящей через точку В(-3;2).

Дано: А(6;0) – центр,

окружности.

Найти: уравнение окружности.

Рис. 8. Иллюстрация к задаче

Находим радиус как расстояние АВ:

Запишем уравнение окружности:

Ответ:

Заключение

Итак, мы рассмотрели серию задач по теме «Окружность» и в каждой задаче использовали уравнение окружности.

На следующем уроке мы выведем уравнение прямой.

Как найти абсциссу и ординату точки на числовой окружности

Единичной окружностью называют окружность радиуса 1.

Числовая окружность — это единичная окружность, точки которой соответствуют определенным действительным числам.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки. Отсчет от точки А против часовой стрелки называется положительным направлением. Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Центр радиуса числовой окружности соответствует началу координат (числу 0). Горизонтальный диаметр соответствует оси x, вертикальный — оси y. Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1: ;

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности. Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2П) против часовой стрелки.

1) Начнем с крайних точек на осях координат. Начальная точка — это 2П (крайняя правая точка на оси х, равная 1). Как вы знаете, 2П — это длина окружности. Значит, половина окружности — это 1П или П. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется П. Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность — это П, то половина полуокружности — это П/2. Одновременно П/2 — это и четверть окружности. Отсчитаем три таких четверти от первой до третьей — и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти — значит имя ей 3П/2.

Определение. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t и обозначают соs t, а ординату точки М называют синусом числа t и обозначают sin t.
Если М(t) = М(х;у), то х = cost, у = sint.

Определение. Отношение синуса числа t к косинусу того же числа называют тангенсом числа t. Отношение косинуса числа t к синусу того же числа называют котангенсом числа t.

источники:

http://b4.cooksy.ru/articles/kak-nayti-abstsissu-tochki-okruzhnosti

http://matematika-ru.1gb.ru/9.html

Источник

Математика 5-6 класс

10 баллов

как найти абсциссу и ординату точки на координатной плоскости?

Влад Тихонов

15.07.2019 15:46:22

Чтобы найти абсциссу, нужно по оси x выбрать то число, которое указано в координатах на первом месте. Чтобы найти ординату, нужно по оси y выбрать то число, которое указано в координатах на втором месте.

Все предметы

Рейтинг пользователей

Калькуляторы
Справочник
Словарь

Источник

Найти абсциссу точки. Друзья! В этой статье для вас размещено ещё несколько заданий связанных с координатной плоскостью. Решение данного типа задач, входящих в состав ЕГЭ очень простенькое – решаются они практически сходу в течение минуты. Если вы забыли, что такое абсцисса и ордината, то посмотрите эту статью.

Суть рассматриваемых ниже задач такая – даны фигуры на плоскости, заданы координаты вершин (не всех), необходимо определить абсциссу или ординату неизвестной вершины. Также имеются задачи на определение длины отрезка. Если у вас развито визуальное (зрительное) представление, то решение вы «увидите» сразу посмотрев на эскиз.

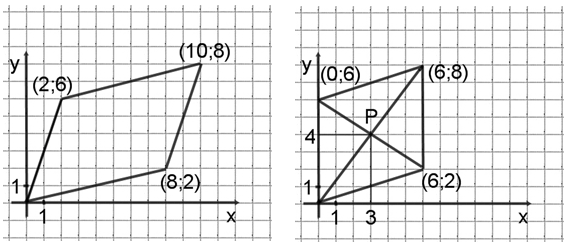
Если есть сложности с визуальным представлением фигур на координатной плоскости, то моя вам «универсальная» рекомендация – постройте фигуру по данным координатам на листе в клетку, далее вы без труда определите координаты (местонахождение) вершины или оговоренной в условии точки и ответите на поставленный вопрос. Посмотрите, как это будет выглядеть такое построение:

Например, абсцисса и ордината точки Р (точка пересечения диагоналей параллелограмма) определяется без труда, соответственно 3 и 4. Рассмотрим задачи:

27673. Точки O (0;0), A (6;8), C (0;6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Точка В смещена относительно точки О в положительном направлении по оси оУ на 2 единицы (также как и точка А смещена относительно точки С), значит её ордината будет равна 0 + 2 = 2.

Ответ: 2

27674. Точки O (0;0), A (6;8), B (4;2) и C являются вершинами параллелограмма. Найдите ординату точки C.

Ордината точки С равна длине стороны ОС. Известно, что противолежащие стороны параллелограмма равны, то есть ОС = АВ = 8 – 2 = 6.

Ответ: 6

Точки O (0;0), A (6;8), B (6;2), C (0;6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей.

Обратите внимание на то, что в условии сказано, что дан четырёхугольник, то есть как бы подразумевается, что это возможно это и не параллелограмм.

Но по координатам видно, что это не что иное, как параллелограмм.

*Для убедительности можно построить данную фигуру на координатной плоскости на листе в клетку.

Известно, что точка пересечения диагоналей равноудалена от противолежащих сторон (лежит посередине). Поэтому абсцисса точки Р будет равна 6:2 = 3.

Ответ: 3

27677. Точки О(0;0), А(10;8), С(2;6) и В являются вершинами параллелограмма. Найдите абсциссу точки В.

Абсцисса точки В на 2 меньше абсциссы точки А (также как абсцисса точки О меньше абсциссы точки С), значит она равна 10 – 2 = 8.

Ответ: 8

27679 (80). Точки O (0;0), A (10;8), B (8;2) и C являются вершинами параллелограмма. Найдите абсциссу и ординату точки C.

Точка С смещена относительно точки О в положительном направлении по оси оХ на 2 единицы (также как и точка А смещена относительно точки В), значит её абсцисса равна 0 + 2 = 2.

Точка С смещена относительно точки О в положительном направлении по оси оУ на 6 единиц (также как и точка А смещена относительно точки В), значит её ордината равна шести.

Ответ: абсцисса равна 2, ордината равна 6.

27681 (2). Точки O (0;0), B (8;2), C (2;6) и A являются вершинами параллелограмма. Найдите абсциссу и ординату точки A.

Точка А смещена относительно точки С в положительном направлении по оси оХ на 8 единиц (также как и точка В смещена относительно точки О), значит её абсцисса равна 2 + 8 = 10.

Точка А смещена относительно точки В в положительном направлении по оси оУ на 6 единиц (также как и точка С смещена относительно точки О), значит её ордината равна 2 + 6 = 8.

Ответ: Абсцисса точки А равна 10, ордината равна 8.

27683 (4). Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите абсциссу и ординату точки P пересечения его диагоналей.

Можно использовать формулу координат середины отрезка. Формула:

Ответ: абсцисса равна 5, ордината равна 4.

27672. Точки O(0;0), B(6;2), C(0;6) и A являются вершинами параллелограмма. Найдите ординату точки A.

Посмотреть решение

27675. Точки O(0;0), A(6;8), B(6;2), C(0;6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.

Посмотреть решение

27678. Точки O(0;0), A(10;8), C(2;6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Посмотреть решение

27685. Точки О(0;0), А(6;8), В(8;2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.

Рекомендация!

Можно использовать формулу координат середины отрезка, а затем зная их вычислить длину отрезка по соответствующей формуле. Но будет проще и быстрее построить фигуру на координатной плоскости на листе в клетку и вычислить длину отрезка по теореме Пифагора.

Посмотреть решение

27686. Точки O(0;0), A(10;0), B(8;6), C(2;6) являются вершинами трапеции. Найдите длину ее средней линии DE.

Рекомендация!

Можно использовать формулы координат середины отрезка и затем длины отрезка или построить трапецию н листе в клетку, но в данном случае удобно воспользоваться формулой средней линии трапеции.

Посмотреть решение

На этом всё! Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Как найти координаты точки

Поддержать сайт

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

находить координаты точки;
найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!

На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.

Особые случаи расположения точек

Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0).
Начало координат — точка O имеет координаты, равные нулю O (0,0).
Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox».
Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy».
Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.

Второй способ

Чтобы найти точку D (−4 , 2) надо:

Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−».
Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Для обозначения числами точного положения точки на плоскости
проведём две перпендикулярные координатные прямые (x) и (y),
которые пересекаются в начале отсчёта — точке (O).

Так мы задали на плоскости прямоугольную систему координат,

а плоскость стала координатной плоскостью.

Начало координат — точка (O) (точка пересечения прямых (x) и (y)),

оси координат — координатные прямые (x) и (y),

координатные углы — прямые углы, образованные при пересечении осей координат.

Координатные углы нумеруют против часовой стрелки:

Отметим в прямоугольной системе координат точку (M).

Проведём через точку (M) прямую, параллельную оси (y).

Прямая пересечёт ось (x) в некоторой точке, координата которой равна (-2).

Эту координату называют абсциссой точки (M).

Далее проведём через точку (M) прямую, параллельную оси (x). Прямая пересечёт ось (y) в некоторой точке, координата которой равна (3).

Эту координату называют ординатой точки (M).

Коротко пишем так: (M(x; y)).

Эту пару чисел называют координатами точки (M).
Абсциссу записываем на первое место, ординату — на второе место.

Имеем (M(-2; 3)).

Число (-2) называют абсциссой точки (M), а число (3) — ординатой точки (M).

Горизонтальную координатную прямую (x) называют осью абсцисс, или осью (x), а

вертикальную координатную прямую (y) — осью ординат, или осью (y).

Координатные углы ещё называют координатными четвертями. Рассмотрим координаты точки (M(x; y)) в разных четвертях и на осях:

в (1) четверти: (x>0; y>0);

во (2) четверти: (x<0; y>0);

в (3) четверти: (x<0; y<0);

в (4) четверти: (x>0; y<0);

на оси (x): координата (y=0), то есть (M(x; 0));

на оси (y): координата (x=0), то есть (M(0; y)).

Каждой точке на координатной плоскости соответствует пара чисел: её абсцисса и ордината — и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.

Для построения этой точки, требуется найти точку пересечения прямых (x=a) и (y=b).

Это будет точка (M(a; b)).

Источник