Как найти абсциссу точки в ромбе - Исправление недочетов и поиск решений вместе с Examum.ru

Математика 5-6 класс

10 баллов

как найти абсциссу и ординату точки на координатной плоскости?

Влад Тихонов

15.07.2019 15:46:22

Чтобы найти абсциссу, нужно по оси x выбрать то число, которое указано в координатах на первом месте. Чтобы найти ординату, нужно по оси y выбрать то число, которое указано в координатах на втором месте.

Все предметы

Рейтинг пользователей

Калькуляторы
Справочник
Словарь

Источник

Собственно, если у вас дагонали dx, dy, и они параллельны осям, а центр — rx, ry, точка — x, y, то проверка сводится к следующей:
|(x — rx) / dx| + |(y — ry) / dy| <= 2.
Всё.

Нужно четыре раза проверить, что точка лежит по одну сторону от прямой, содержащей сторону ромба:

Знак Q определяет, с какой стороны от прямой AB лежит точка T.

Остается проверить это для всех сторон ромба AB, BC, CD, DA, если знак везде одинаков — точка в ромбе.

«Интеграл по контуру».
В общем, суммируете углы AXB, BXC, CXD, DXA.
Если сумма равна ±360°, то точка внутри многоугольника.
Если сумма равна ±180°, то точка на ребре.
В остальных случаях точка снаружи.
Кажется так.

Источник

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №10 ЕГЭ.

Что такое функция

Чтение графика функции

Четные и нечетные функции

Периодическая функция

Обратная функция

5 типов элементарных функций и их графики

Преобразование графиков функций

Построение графиков функций

Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 10 в формате ЕГЭ-2021

Линейная функция

Необходимая теория

1. На рисунке изображён график функции . Найдите значение , при котором

Решение:

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

$left{ begin{array}{c}3k+b=4 \-k+b=-3 end{array}right..$

Вычтем из первого уравнения второе:

$left{ begin{array}{c}4k=7 \-k+b=-3 end{array};right. left{ begin{array}{c}k=frac{7}{4} \b=-frac{5}{4} end{array}right. .$

Уравнение прямой имеет вид:

$displaystyle y=frac{7}{4}x-frac{5}{4}.$

Найдем, при каком значение функции равно -13,5.

$displaystyle frac{7}{4}x-frac{5}{4}=-13,5;$

7x=-49;

x=-7.

Ответ: -7.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция y=-x+1.

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции y=kx+b.

$left{ begin{array}{c}-k+b=-1 \-2k+b=4 end{array}right. .$

Вычтем из первого уравнения второе.

k=-5; тогда b=-6.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

$left{ begin{array}{c}y=-x+1 \y=-5x-6 end{array} ;right. begin{array}{c}-x+1=-5x-6 ; \x=-frac{7}{4}=-1,75. end{array}$

Ответ: -1,75.

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Прямая, расположенная на рисунке ниже, задается формулой y=x+1, так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен $displaystyle frac{3}{2}=1,5.$

Эта прямая проходит через точку (-2; 4), поэтому: b=7, эта прямая задается формулой

Для точки пересечения прямых:

x=-12.

Ответ: -12.

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

Решение:

На рисунке — квадратичная парабола $y={left(x-aright)}^2,$ полученная из графика функции y=x^2 сдвигом на 1 вправо, то есть a=1.

Получим: $fleft(xright)={left(x-1right)}^2=x^2-2x+1;$

b=-2.

Ответ: -2.

5. На рисунке изображен график функции $y={left(x-cright)}^2$ . Найдите с.

Решение:

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при x^2 положительный. График сдвинут относительно графика функции y=x^2 на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид $y={left(x-1right)}^2$ .

Значит, с = 1.

Ответ: 1

6. На рисунке изображён график функции Найдите

Решение:

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

$left{ begin{array}{c}2+b+c=1 \2cdot 4-2b+c=-2 end{array}right. .$

$left{ begin{array}{c}b+c=-1 \-2b+c=-10 end{array};right.$ отсюда b=3, c=-4.

Формула функции имеет вид:

Ответ: 31.

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому c=-3.

График функции g(x) проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

$left{ begin{array}{c}a-b-3=-3 \4a+2b-3=3 end{array};right.$ отсюда a=b=1;

Найдем абсциссу точки B. Для точек A и B:

x=-2 (это абсцисса точки A) или x=6 (это абсцисса точки B).

Ответ: 6.

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций $displaystyle fleft(xright)=frac{k}{x}$ и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

График функции $displaystyle y=frac{k}{x}$ проходит через точку (2; 1); значит, $displaystyle frac{k}{2}=1;$

$displaystyle k=2, ; fleft(xright)=frac{2}{x}.$

График функции проходит через точки (2; 1) и (1; -4), a=5 — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда b=-9.

Для точек A и B имеем:

$displaystyle frac{2}{x}=5x-9;$

Отсюда x=2 (абсцисса точки A) или x=-0,2 (абсцисса точки B).

Ответ: -0,2.

9. На рисунке изображён график функции . Найдите f (6,76).

Решение:

Функция задана формулой:

Ее график проходит через точку (4; 5); значит, k=2,5;

Тогда

Ответ: 6,5.

10. На рисунке изображен график функции . Найдите .

Решение:

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда = 5.

Ответ: 5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции $fleft(xright)=a^{x+b}.$ Найдите

Решение:

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции $fleft(xright)=a^{x+b},$ получим:

$left{ begin{array}{c}a^{-3+b}=1 \a^{1+b}=4 end{array}.right.$

Поделим второе уравнение на первое:

$a^{1+b+3-b}=4; ; a^4=4;; a=sqrt{2}.$

Подставим во второе уравнение:

$displaystyle {sqrt{2}}^{1+b}=4;; 2^{frac{1+b}{2}}=2^2;; 1+b=4;; b=3.$

$displaystyle fleft(xright)={left(sqrt{2}right)}^{x+3};; fleft(-7right)={left(sqrt{2}right)}^{-7+3}={left(sqrt{2}right)}^{-4}=frac{1}{4}=0,25.$

Ответ: 0,25.

12. На рисунке изображен график функции . Найдите

Решение:

График функции проходит через точку Это значит, что

a=2, формула функции имеет вид: .

Ответ: 2.

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции $fleft(xright)={{log}_a left(x+bright)}.$ Найдите

Решение:

График функции $y={{log}_a left(x+bright) }$ проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

$left{ begin{array}{c}{{log}_a left(-3+bright)=1 } \{{log}_a left(-1+bright) }=2 end{array}.right.$

Отсюда: $left{ begin{array}{c}b-3=a \b-1=a^2 end{array}.right.$

Вычтем из второго уравнения первое:

a=2 или a=-1 — не подходит, так как (как основание логарифма).

Тогда $fleft(xright)={{log}_2 left(x+5right) };$

$fleft(11right)={{log}_2 16=4.}$

Ответ: 4.

14. На рисунке изображен график функции $fleft(xright)=a{{log}_5 x }-c$ .

Найдите f(0,2).

Решение:

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

$left{ begin{array}{c}a{{log}_5 1 }-c=-2 \a{{log}_5 5 }-c=3 end{array};right.$

$left{ begin{array}{c}-c=-2 \a-c=3 end{array};right.$

$left{ begin{array}{c}c=2 \a=5 end{array}.right.$

Формула функции: $fleft(xright)=5{{log}_5 x }-2.$

Найдем $displaystyle fleft(0,2right)=fleft(frac{1}{5}right)$ :

$displaystyle 5cdot {{log}_5 frac{1}{5} }-2=-5-2=-7.$

Ответ: -7.

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

Решение:

График функции сдвинут на 1,5 вверх; Значит, b=1,5. Амплитуда a=2 (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на 1,5 .

Ответ: b=1,5.

16. На рисунке изображён график функции

Найдите .

Решение:

На рисунке — график функции Так как b=-1,5.

График функции проходит через точку A $displaystyle (frac{pi}{4}; ; frac{1}{2}).$ Подставим и координаты точки А в формулу функции.

$displaystyle a tg frac{pi}{4}-1,5=frac{1}{2}.$

Так как $displaystyle tg frac{pi}{4}=1,$ получим: a = 2.

Ответ: 2.

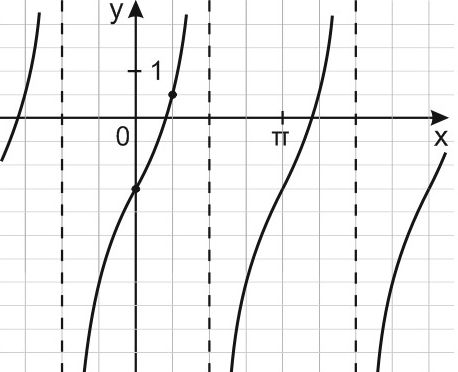
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Решение:

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Ответ: 5.

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Как найти координаты точки

Поддержать сайт

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

находить координаты точки;
найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!

На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.

Особые случаи расположения точек

Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0).
Начало координат — точка O имеет координаты, равные нулю O (0,0).
Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox».
Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy».
Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.

Второй способ

Чтобы найти точку D (−4 , 2) надо:

Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−».
Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Тема 10.

Задачи на свойства графиков функций

Комбинации нескольких графиков

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

задачи на свойства графиков функций

Решаем задачи

На рисунке изображены графики двух линейных функций, пересекающиеся в точке Найдите абсциссу точки

Показать ответ и решение

Найдем уравнения прямых.

Определим коэффициенты и для нижней прямой. Найдём как тангенс угла наклона прямой:

Δy 0− (−2) 2
k = Δx-= 0−-(−1) = 1 = 2

Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом Подставим точку

Значит, первая функция имеет вид

Теперь определим коэффициенты и для верхней прямой. Найдём как тангенс угла наклона прямой:

Δy 4 − 0 4
k = Δx-= 0−-(−4) = 4 = 1

Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом Подставим точку

Значит, вторая функция имеет вид

Теперь найдем абсциссу точки пересечения двух прямых.

На рисунке изображены графики двух линейных функций, пересекающиеся в точке Найдите абсциссу точки

Показать ответ и решение

Найдем уравнения прямых.

Определим коэффициенты и для нижней прямой. Найдём как тангенс угла наклона прямой:

Δy 2 − 0 2
k = Δx-= 1-− 0 = 1 = 2

Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом Подставим точку
(1;2) :

Значит, первая функция имеет вид

Теперь определим коэффициенты и для верхней прямой. Найдём как тангенс угла наклона прямой:

Δy- -3-− 0- 3
k = Δx = 0− (−3) = 3 = 1

Чтобы найти подставим одну из точек на прямой в уравнение с уже расcчитанным коэффициентом Подставим точку

Значит, вторая функция имеет вид

Теперь найдем абсциссу точки пересечения двух прямых.

На рисунке изображены графики двух линейных функций. Найдите ординату
точки пересечения графиков.

xy110

Показать ответ и решение

Способ 1

Найдём уравнение функции график которой из себя представляет убывающую прямую, на которой отмечены
точки (1;4), Найдём угловой коэффициент:

k = Δy-= −2-− 4-= −1,5
Δx 5− 1

Получим уравнение функции

Найдём значение подставив в уравнение точку (1;4):

Получится уравнение

Найдём уравнение функции график которой из себя представляет возрастающую прямую, на которой
отмечены точки (1;2). Найдём угловой коэффициент:

Δg 2− (−5)
k = Δx-= 1−-(−1) = 3,5

Получим уравнение функции

Найдём значение подставив в уравнение точку (1;2):

Получится уравнение

Теперь решим уравнение

Тогда ордината точки пересечения прямых равна

Способ 2

По картинке видим, что целые точки (1;4) и принадлежат графику первой прямой поэтому можем
составить систему из двух уравнений:

( (
{ 4= f1(1) {4 =k1+ b1
( ⇔ ( ⇔
−2(=f1(5) − 2= 5k1+b(1
{ k1 = 4− b1 { b1 = 5,5
⇔ ( ⇔ (
−2 =5(4− b1)+b1 k1 = −1,5

Также целые точки (1;2) и принадлежат графику второй прямой поэтому можем составить
систему из двух уравнений:

( (
{ 2= f2(1) { 2= k2+ b2
( −5 =f2(−1) ⇔ ( −5= − k2 +b2 ⇔
( (
{ k2 = 2− b2 {b2 = −1,5
⇔ ( ⇔ (
−5= − (2 − b2)+ b2 k2 = 3,5

Значит, функции имеют вид и Аналогично первому способу решаем уравнение
и получаем ответ.

На рисунке изображены графики двух функций вида которые
пересекаются в точке Найдите x0.

xy110

Показать ответ и решение

Первый способ.

Пусть — уравнение первой прямой, — уравнение второй прямой.

Заметим, что первая прямая проходит через точки и Если прямая проходит через точку на плоскости, то
координаты этой точки обращают уравнение этой прямой в верное равенство. Тогда мы получаем систему из двух
уравнений:

( ( ( (
{ 4= k1⋅(−1)+ b1 {4 =− k1+ b1 { b1 = 4+ k1 { b1 = 9
⇔ ⇔ ⇔ 2
( 3= k1⋅(−3)+ b1 (1 =2k1 ( k1 = 12 ( k1 = 12

Значит, — уравнение первой прямой. Вторая прямая проходит через точки и Следовательно, мы
можем получить следующую систему:

( ( ( (
{− 1= k2⋅2+ b2 {− 1= 2k2+ b2 { b2 = −(2k2+ 1) { b2 = −3
( ⇔ ( ⇔ ( ⇔ (
− 4= k2⋅(−1)+ b2 3 =3k2 k2 = 1 k2 = 1

Значит, — уравнение второй прямой. Обе прямые проходят через точку по условию, тогда мы имеем
систему:

(
{ y0 = x02+9 ⇒ x − 3= x0-+9 ⇔ 2x − 6= x + 9 ⇔ x = 15
( y0 = x0− 3 0 2 0 0 0

Второй способ.

Если прямая на плоскости проходит через две точки и то мы можем составить ее каноническое
уравнение:

x− x1 y− y1
a: x2−-x1 = y2−-y1

На рисунке видно, что одна из прямых проходит через точки и Тогда мы можем записать ее каноническое
уравнение:

Другая прямая проходит через точки и . Аналогично запишем ее каноническое уравнение:

Если прямая проходит через точку на плоскости, то координаты этой точки обращают уравнение прямой в верное равенство.
Обе прямые проходят через точку по условию, тогда имеем систему:

({ x0+9
y0 = 2 ⇒ x0− 3= x0-+9 ⇔ 2x0− 6= x0+ 9 ⇔ x0 = 15
( y0 = x0− 3 2

Друзья, поздравляем вас с Новым годом! Этот новогодний пробный вариант ЕГЭ подготовлен специально для вас, и, прорешав все задачи правильно, вы можете получить секретный код. Числу, составленному из цифр каждого ответа, соответствует буква в русском алфавите. Тогда правильные ответы ко всем задачам помогут вам составить фразу, которую мы загадали. Введите ее в поле ответа к заданию 19 без пробелов с маленькой буквы.

На рисунке изображены графики функций и которые
пересекаются в точке Найдите абсциссу точки

xy110

Показать ответ и решение

По картинке видим, что точка (4;3) принадлежит графику функции
следовательно,

f(4)= 3 ⇔ a√4-= 3 ⇔
√-
a= 3 ⇒ f(x)= 3 x
2 2

Посмотрим теперь на график функции Это прямая, которой принадлежат
точки и (4;0). Найдем угловой коэффициент:

0−-(−-4) 1
k = 4− (− 4) = 2

Найдем подставив в уравнение точку (4;0) и 1
k = 2 :

1
g(4) = 0 ⇔ 2 ⋅4 +b =0 ⇔
1
b= −2 ⇒ g(x)= 2x − 2

Найдем абсциссу точки приравняв и g :

3√x = 1x− 2 ⇔ 3√x-= x− 4 ⇔
( 2 2 (
{ 9x= (x− 4)2 {− x2+ 17x− 16= 0
( ⇔ ( ⇔
x− 4≥ 0 x ≥ 4
({ x= 1;16
⇔ x =16
( x≥ 4

На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите x0.

xy110A

Показать ответ и решение

Для начала разберемся, какой из графиков какой функции соответствует.

Координата по вершины параболы равна −-(−2) =− 1,
2⋅(−2) 2 что
соответствует правой параболе.

Любую параболу вида 2
g(x)= ax + bx+ c можно представить в виде

Здесь (xB;yB) — координаты ее вершины. По картинке несложно видеть, что
вершина левой параболы имеет координаты значит функция имеет
вид

Также по картинке видно, что в точке -4 функция равна 1. Это условие
можно записать следующим образом:

Теперь мы полностью восстановили функцию она имеет вид

Найдем точки пересечения и g :

Пересечение, соответствующее это точка Тогда координата
точки равна 3.

На рисунке изображены графики функций и
которые пересекаются в точках и Найдите абсциссу точки

xy110A

Показать ответ и решение

Восстановим уравнение функции f(x). По картинке видно, что её график проходит через три целые точки:
и (1;1).

Так как график f(x) проходит через точку то имеем уравнение:

Так как график f(x) проходит через точку (1;1), то имеем уравнение:

f(1)= 1 ⇔ a ⋅12+ b⋅1+ c= 1 ⇔
⇔ a+ b− 4= 1 ⇔ a+ b= 5

Так как график f(x) проходит через точку то имеем уравнение:

Решим систему из двух уравнений:

( (
{ a+ b= 5 { b= 5− a
( 2a− b= 1 ⇔ ( 2a− (5 − a) =1 ⇔
( ( (
{ b= 5− a {b =5 − a {a = 2
⇔ ( ⇔ ( ⇔ (
2a− 5+ a= 1 3a =6 b = 3

Таким образом, мы полностью восстановили уравнение функции f(x):

2
f(x) = 2x +3x − 4

Восстановим уравнение функции g(x). По картинке видно, что её график проходит через целые точки и
Значит, можем составить систему из двух уравнений:

( (
{g(−2)= − 2 ⇔ {− 2k + d= −2 ⇔
(g(−1)= 2 (− k+ d= 2
( ( (
{d = 2k− 2 { k+ 2= 2k− 2 { k = 4
⇔ (d = k+ 2 ⇔ ( d= k+ 2 ⇔ ( d= 6

Таким образом, мы полностью восстановили уравнение функции g(x):

Найдем координаты второй точки пересечения графиков этих функций:

2 2
2x +3x − 4 = 4x + 6 ⇔ 2x − x−⌊10= 0 ⇔
x = −2
⇔ (x+ 2)(2x− 5)= 0 ⇔ ⌈
x = 2,5

Значит, абсцисса точки равна 2,5.

На рисунке изображены графики функций и
которые пересекаются в точках и Найдите ординату точки

xy110A

Показать ответ и решение

По картинке видно, что график функции g(x) проходит через точки (1;2) и (3;4). Если график функции проходит
через определенную точку, то ее координаты обращают уравнение функции в верное равенство. Значит, мы можем составить
систему из трех уравнений:

( ( (
|||g(−1)= 8 ||| a⋅(−1)2+ b⋅(−1)+ c= 8 |||a − b +c = 8
{g(1)= 2 ⇔ { a⋅(1)2 +b ⋅(1)+ c= 2 ⇔ {a +b +c = 2
||| ||| |||
(g(3)= 4 ( a⋅(3)2 +b ⋅(3)+ c= 4 (9a +3b+ c= 4

Из первого уравнения следует, что Тогда, подставив этот результат во второе уравнение, получим:

Подставив и в третье уравнение, получим:

Тогда можем найти

Значит, мы нашли уравнение функции g(x):

По условию функции f(x) и g(x) пересекаются в точках A(3;4) и Тогда координаты точки обращают
уравнения функций f(x) и g(x) в верные равенства:

(
{ f(x0) =y0
( g(x0)= y0 ⇒ f(x0)= g(x0) ⇔

⇔ − 3x0+ 13= x20− 3x0+ 4 ⇔ 9= x20 x⇒⁄=3 x0 = −3
0

Тогда ордината точки равна

На рисунке изображены графики функций

2
f(x)= ax + bx+ c и g(x)= kx+ d

которые пересекаются в точках и Найдите y0.

xy110A

Показать ответ и решение

Заметим, что любую квадратичную функцию можно представить в виде

2
f (x)= a(x− x0) +y0,

где (x0;y0) — координаты вершины параболы. По графику видно, что y0 =1.

Найдём подставив точку в уравнение параболы:

Получим уравнение параболы

Найдём уравнение линейной функции

график которой проходит через точки и (0;3). Найдём значение углового коэффициента

Δg 3 − 0
k = Δx-= 0−-(−1) = 3

Значение коэффициента равно 3, поскольку прямая пересекает ось ординат в точке (0;3).

Получим уравнение функции

Чтобы найти координаты точки надо решить уравнение

−(x+ 2)2 +1 = 3x + 3
2
− x − 4x − 4+ 1= 3x+ 3
x2 +7x +6 = 0
⌊
⌈x =− 1
x =− 6

Первое значение соответствует абсциссе точки тогда второе — абсциссе точки Найдём её ординату, подставив
в уравнение любой из функций. Подставим в

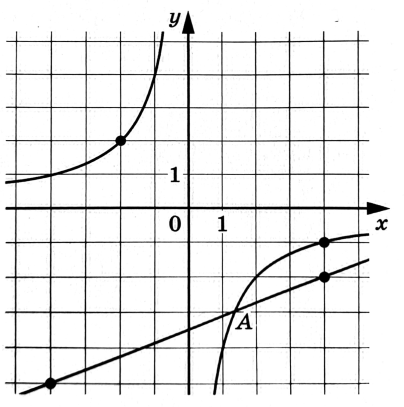
На рисунке изображены графики функций и
которые пересекаются в точках и Найдите ординату точки

xy110

Показать ответ и решение

Определим какой из графиков («верхний» или «нижний») принадлежит функции f(x). Заметим, что
значит, график функции f(x) проходит через точку (0;4), то есть функции f(x) соответствует «верхний»
график.

Восстановим уравнение функции g(x). Заметим, что «нижний» график проходит через точку следовательно
справедливо равенство

2
g(0)= −3 ⇔ a ⋅0 + b⋅0+ c= −3 ⇔ c= − 3

Также график функции g(x) проходит через целые точки и (1;1) , значит, можем составить систему
уравнений:

({ ({ 2
g(−2)= −5 ⇔ a⋅(−2) + b⋅(− 2)+c = −5 ⇔
( g(1) =1 ( a⋅12+ b⋅1+ c= 1
( (
⇔ {4a− 2b− 3= −5 ⇔ {2a− b= − 1 ⇔
(a+ b− 3= 1 (a+ b =4
( ( (
{ b= 2a+ 1 { 2a +1 = 4− a {a = 1
⇔ ( b= 4− a ⇔ ( b= 4− a ⇔ (b = 3

Таким образом, мы полностью восстановили уравнение функции g(x):

2
g(x)= x + 3x− 3

Теперь найдем абциссу второй точки пересечения графиков функций f(x) и g(x) :

2 2 2
2x − 5x+ 4= x + 3x− 3 ⇔ x − 8x+⌊ 7 =0 ⇔
x= 1
⇔ (x− 1)(x − 7) =0 ⇔ ⌈
x= 7

Значит, абсцисса точки равна 7. Тогда ордината точки равна

На рисунке изображены графики функций √ -
f(x) = a x и которые пересекаются в точках и
Найдите y0.

xy110AB

Показать ответ и решение

Найдём уравнение функции g(x). По графику видно, что k = 1, поскольку функция увеличивается на 1 при увеличении
аргумента на 1. Также прямая пересекает ось ординат в точке (0;1), откуда b = 1. Тогда уравнение прямой имеет
вид

Найдём уравнение функции f(x). Подставим точку (4;5) на графике в уравнение функции:

Тогда уравнение корня имеет вид

Найдём координаты точек пересечения графиков, приравняв функции:

Сделаем замену и получим квадратное уравнение:

t2− 2,5t+ 1= 0
2
2t − 5t+ 2= 0
D = 52− 4⋅2⋅2 =52− 42 = 32
5 ±3 1
t= --4- = 2;2

Сделаем обратную замену и получим совокупность

⌊ ⌊
t= 0,5 x = 0,25
⌈t= 2 ⇔ ⌈x = 4

Точке соответствует координата Подставим её в g(x) и получим

На рисунке изображены графики функций √ ----
f(x) =a x− b+ c и
которые пересекаются в точках A(0;1) и Найдите абсциссу точки

xy110A

Показать ответ и решение

Заметим, что область определения функции √ ----
f(x)= a x− b+ c совпадает с
областью определения функции √----
x − b и равна

Из графика видно, что f(x) определена на откуда получаем

Тогда функция примет вид

По графику то есть

Найдем отличную от точку пересечения графиков функций f(x) и
g(x):

pict

Из последней системы получаем x= 8. Тогда абсцисса точки пересечения
графиков равна 8.

На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите xB.

xy110A

Показать ответ и решение

Поскольку f (x) — квадратичная функция, абсцисса вершины ее графика равна
-−(−2) = −0,5.
2 ⋅(− 2)

Тогда по рисунку график функции f(x) — это правая парабола.

Найдём уравнение левой параболы в виде

где — ее вершина. Подставим точку в уравнение
g(x):

Получим

Чтобы найти координаты точки решим уравнение

pict

Значение — это абсцисса точки тогда xB = 3 — это абсцисса
точки

На рисунке изображены графики функций

√ -
f(x) =a x и g(x)= kx+ b,

которые пересекаются в точке Найдите абсциссу точки

xy110

Показать ответ и решение

По картинке видим, что точка (4;3) принадлежит графику функции следовательно,

√-
f(4) = 3 ⇔ a 4= 3 ⇔
⇔ a = 3 ⇒ f(x)= 3√x-
2 2

Посмотрим теперь на график функции По картинке видим, что ему принадлежат точки и (4;0). Найдем угол
наклона

0−-(−4) 1
k = 4− (−4) = 2

Найдем подставив точку (4;0)

g(4)= 0 ⇔ 1 ⋅4+ b= 0 ⇔
2 1
⇔ b= − 2 ⇒ g(x) = 2x− 2

Найдем абсциссу точки приравняв и

3√ - 1 √-
2 x= 2x − 2 ⇔ 3 x= x − 4 ⇔
( (
{9x = (x − 4)2 { −x2+ 17x− 16= 0
⇔ (x − 4 ≥ 0 ⇔ ( x≥ 4 ⇔
(
{x =1;16
⇔ ( ⇔ x = 16
x ≥4

На рисунке изображены графики двух функций: одна из них линейная, другая — вида

√-----
y = a x− x0+ y0

Найдите абсциссу точки пересечения графиков этих функций. Если таких точек несколько, в ответе укажите наименьшую
абсциссу.

xy110

Показать ответ и решение

Для решения найдём уравнения обеих функций, после чего решим уравнение, приравняв эти функции, что и будет означать
пересечение графиков функций.

Найдём уравнение линейной функции. Заметим, что прямая проходит через точки и (3;2). Тогда угловой
коэффициент можно найти по формуле

k = y1−-y0= --2−-0- = 2
x1− x0 3 − (−4) 7

Получим уравнение прямой

y = 2 +b
7

Для нахождения свободного коэффициента подставим произвольную точку на прямой в это уравнение. Подставим точку
(3;2) :

2 8
2 = 7 ⋅3+ b ⇔ b= 7

Получаем уравнение прямой

y = 2 x+ 8
7 7

Найдём уравнение второй функции. Заметим, что график имеет вершину (2;3), из чего можно сделать вывод, что x0 = 2,
y0 = 3. Чтобы найти подставим в полученную функцию координаты точки (3;4), которая находится на
графике.

√ ----
4= a 3− 2+ 3 ⇔ a= 1

Получаем уравнение второй функции

√-----
y = x − 2+ 3

Приравняем полученные функции:

√x-−-2+ 3= 2x + 8
7 7
√x-−-2= 2x− 13 |⋅7
√ ----7 7
7 x− 2= 2x− 13

Возведём в квадрат обе части уравнения, отметив, что правая чать должна быть неотрицательной, то есть

2
49(x− 2)= 4x + 169− 52x
4x2− 101x+ 267= 0
2 2
D = 101 − 4 ⋅4⋅267 = 5929 = 77
101±-77
x1,2 = 8 = 3;22,25

Поскольку решение уравнения существует при , получим единственное решение

На рисунке изображены графики функций и
которые пересекаются в точках и Найдите x0.

xy110A

Показать ответ и решение

Восстановим график функции f(x). Он проходит через точку Значит, можем составить уравнение:

k
f(−3)= −2 ⇔ −3-=− 2 ⇔ k = 6

Значит, f(x) = 6.
x

Восстановим график функции g(x). Он проходит через точку (0;5), следовательно,

Также график g(x) проходит через точку следовательно,

Значит,

Найдем абсциссу точки B :

⌊
-6 2 ⌈x = −2
x = 4x+ 5 ⇔ 4x + 5x− 6= 0 ⇔ x= 0,75 ⇒ x0 = 0,75

На рисунке изображены графики функций

k
f(x)= x и g(x)= ax+ b,

которые пересекаются в точках и Найдите ординату точки

xy110A

Показать ответ и решение

Подставим точку расположенную на графике гиперболы, в функцию f(x):

k
f(−2)= −-2 = 2 ⇔ k = −4

Найдём коэффициент по точкам на графике линейной функции

a = Δy-= −2-− (−5)-= 3
Δx 4− (− 4) 8

Найдём подставив точку

3
− 2= 8 ⋅4+ b ⇔ b= −3,5

Найдём точки пересечения, приравняв f(x) и g(x):

f(x)= g(x)

−4-= 3x− 3,5− 32= 3x2− 28x
x 8 2
3x − 28x+ 32= 0

Решим данное уравнение методом переброски коэффициента. Решим уравнение

По теореме Виета легко находятся корни ′
x1 = 4 и ′
x2 = 24. Тогда у исходного уравнения корни равны

x′1 4 x′2
x1 =-3 = 3 и x2 = 3-= 8

Видно, что точке соответствует координата x1, тогда точке — координата x2. Найдём ординату, подставив в
g(x):

g(8)= 3 ⋅8− 3,5 = −0,5
8

На рисунке изображены графики функций k
f(x) = x и которые пересекаются в точках и
Найдите абсциссу точки

На рисунке изображены графики функций и , которые пересекаются в точках и .
Найдите ординату точки .

На рисунке изображены графики функций

2 √----
f(x)= ax + bx+ c и |g(x)|= k x + r,

которые пересекаются в точках и
Найдите y0.

Показать ответ и решение

Найдем уравнения каждой функции. Пусть ----
g1(x)= k√x+ r, ----
g2(x)= −k√x + r
— функции, задающие второе уравнение условия. Тогда график g2(x) проходит
через точки и , следовательно,

{0 = −k√ −1+-r- {r = 1
−2 =− k√0+-r ⇔ k = 2

Следовательно,

√ -----
|g(x)|= 2 x+ 1

График проходит через точки A,B,C :

( ( 1
|{ 0= a− b+ c |{ a= 35
|( −2= c ⇔ |( b= −3
−4= 9a+ 3b+ c c= −2

Следовательно,

f(x)= 1x2− 5x − 2
3 3

Найдем четвертую точку пересечения, то есть корень уравнения
По картинке можно предположить, что точка — общая для
графиков f(x) и g1(x). Тогда имеем:

x2 − 5x − 6 = 6√x-+-1
√----- √-----
(x − 6)(x+ 1)= 6√x-+1-|: x +1 ⁄= 0
(x− 6) x+ 1= 6
(x− 6)2(x +1)= 36
3 2
x − 11x + 24x = 0 |:x ⁄=0
x2− 11x+ 24= 0

Корни последнего уравнения Мы ищем корень x0 = 8. Тогда

√ ----
y0 = g1(8)= 2 8+ 1= 6

Источник